E3: Temperaturowa zależność oporu przewodników.
Przemysław Kołoczek.

1. Wstęp.

Opór elektryczny jest cechą danego materiału i decyduje jaki prąd przepłynie przez
element obwodu przy przyłożonym do jego końców napięciu. Pierwsze prawo Ohma –
natężenie prądu (I) płynącego przez przewodnik, jest proporcjonalne do napięcia na jego
końcach (U) – można zilustrować równaniem:

𝐼 =

1

𝑅

𝑈

Drugie prawo Ohma – opór przewodnika jest wprost proporcjonalny do jego oporu
właściwego (ρ) i długości (l), a odwrotnie proporcjonalny do powierzchni jego przekroju
poprzecznego (S), przez który płynie prąd – można zilustrować równaniem:

𝑅 = 𝜌

𝑙

𝑆

Pasma energetyczne to przedziały energii, stanowiące układ leżących blisko siebie
podpowłok energetycznych, pochodzących od sąsiednich atomów w sieci krystalicznej.
Stąd też szerokości pasm są różne dla różnych substancji i są zależne tylko od odległości
między atomami. Pasmo walencyjne odpowiada powłokom walencyjnym, pasmo
przewodnictwa odpowiada najbliższym powłokom stanów wzbudzonych, a oba pasma
oddziela pasmo wzbronione, odpowiadające stanom energii, których elektrony nie mogą
przyjąć (bo ich energia jest skwantowana). Prąd będzie płynął w danym ciele, jeśli
elektrony znajdą się w paśmie przewodnictwa, a jest to możliwe tylko wtedy, gdy zostanie
przekroczone pasmo wzbronione. W przypadku izolatorów jest to mało prawdopodobne,
bo pasmo wzbronione ma dużą wartość energii. Z kolei w półprzewodnikach wystarczy
nieznacznie podnieść temperaturę aby zwiększyć ich przewodnictwo, ewentualnie można
użyć domieszek (powstają półprzewodniki typu n z nadmiarem elektronów oraz p – z ich
niedomiarem). Metali nie trzeba nawet podgrzewać, gdyż oba pasma – walencyjne i
przewodnictwa – zachodzą na siebie, więc elektrony mogą swobodnie przeskakiwać z
jednego do drugiego.
Elektrony swobodne, według klasycznej teorii przewodnictwa, stanowiące gaz
elektronowy w przewodniku, zaczynają poruszać się z pewną prędkością (dryfu) po
przyłożeniu zewnętrznego napięcia. Ruch ten jest spowalniany przez oddziaływania z
siecią krystaliczną – albo poprzez drgania cieplne sieci (fonony), albo defekty i domieszki
w sieci. W podwyższonej temperaturze drgania atomów w sieci wzmagają się, co z kolei
jeszcze bardziej spowolnia elektrony swobodne, a to objawia się wzrostem oporu
właściwego danego przewodnika. Dla przewodników zależność ρ(T) jest liniowa:

𝜌

𝑇

= 𝜌

0

+ 𝜌

0

𝛼(𝑇 − 𝑇

0

)

gdzie α jest temperaturowym współczynnikiem oporu właściwego, ρ

0

– oporem

właściwym w temperaturze odniesienia T

0

, a ρ

T

– oporem właściwym w temperaturze T.

Korzystając z zależności między oporem właściwym a oporem elektrycznym otrzymujemy
zależność R(T):

𝑅

𝑇

= 𝑅

0

+ 𝑅

0

𝛼(𝑇 − 𝑇

0

)

Więc:

𝛼 =

𝑅

𝑇

− 𝑅

0

𝑅

0

(𝑇 − 𝑇

0

)

Pierwsze prawo Kirchhoffa – suma natężeń prądów wpływających do węzła (I

i

) jest równa

sumie prądów z niego wypływających (I

j

):

∑ 𝐼

𝑖

𝑛

𝑖=1

= ∑ 𝐼

𝑗

𝑛

𝑗=1

Drugie prawo Kirchhoffa – suma wartości chwilowych SEM (ε

i

) w oczku jest równa sumie

chwilowych spadków napięć (U

j

) na elementach pasywnych oczka:

∑ 𝜀

𝑖

𝑛

𝑖=1

= ∑ 𝑈

𝑗

𝑛

𝑗=1

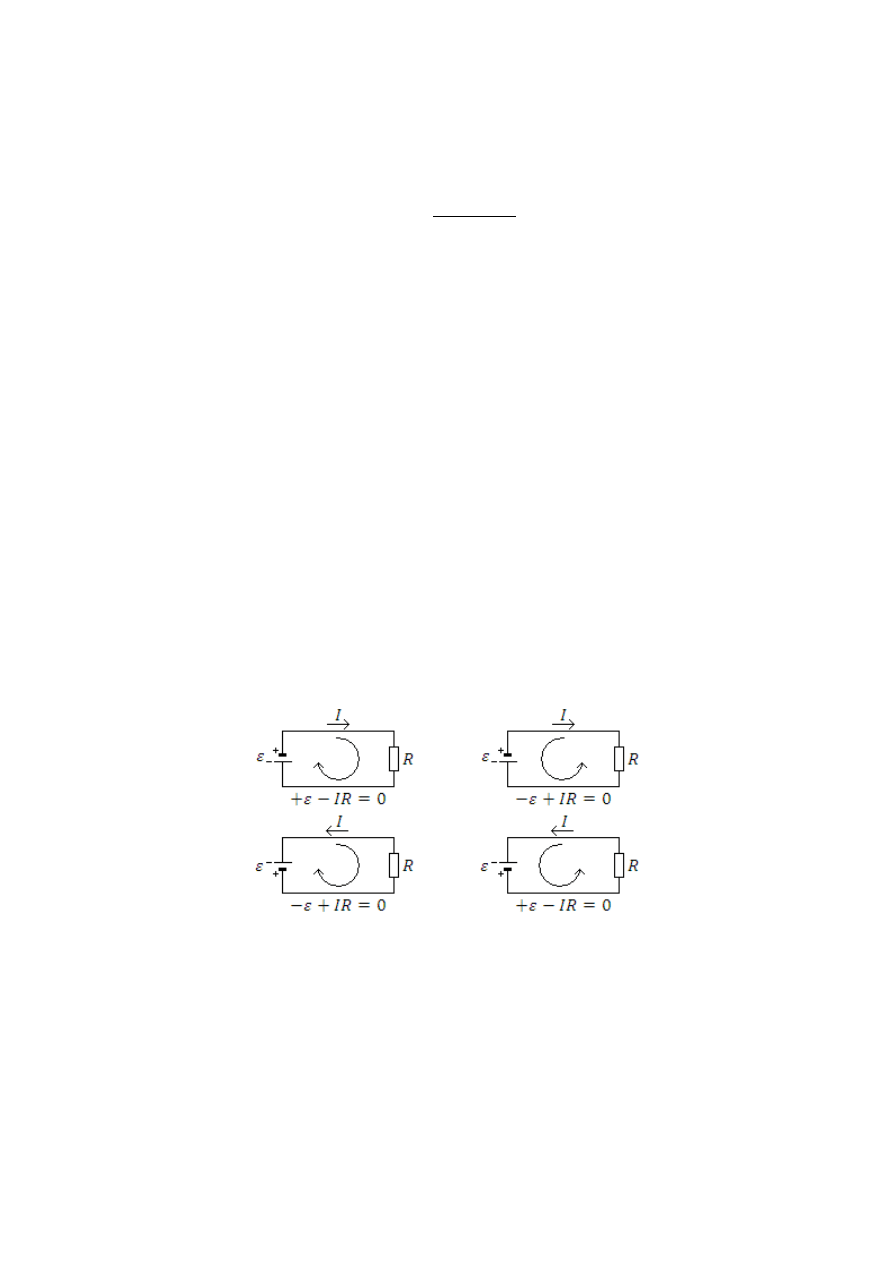
Jeżeli obchodzimy oczko zgodnie z ruchem wskazówek zegara, trafiamy na źródło SEM i
mijając go następuje wzrost potencjału, to SEM źródła zapisujemy ze znakiem plus (gdy
odwrotnie – minus). Jeżeli obchodzimy oczko zgodnie z ruchem wskazówek zegara,
trafiamy na opór, przez który prąd płynie w przeciwnym kierunku do założonego, to
iloczyn oporu i natężenia prądu przez niego płynącego zapisujemy ze znakiem plus (gdy
odwrotnie – minus). Wszystkie możliwości obrazuje Rysunek 1.:












W połączeniu szeregowym przez każdy z oporników płynie ten sam prąd o natężeniu I, a
ponadto na każdym z nich pojawia się spadek napięcia, przy czym spadki te sumują się.
Dodatkowo, korzystając z pierwszego prawa Ohma otrzymujemy ostatecznie opór
zastępczy (R

Z

):

𝑅

𝑍

= ∑ 𝑅

𝑖

𝑛

𝑖=1

Rysunek 1. II prawo Kirchhoffa dla pojedynczego oczka.

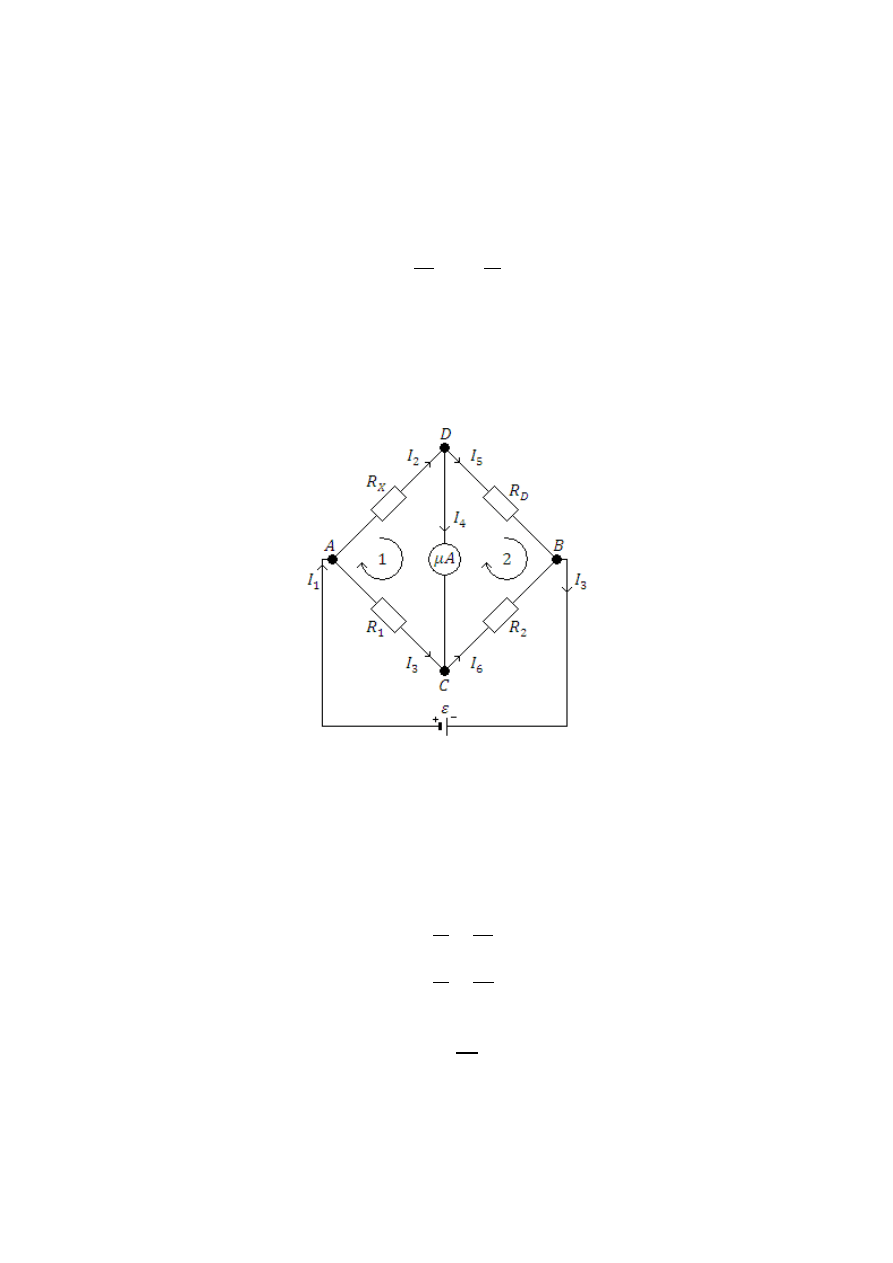
W połączeniu równoległym spadki napięcia na każdym oporniku są takie same i równe
spadkowi napięcia na oporniku zastępczym. Z pierwszego prawa Kirchhoffa wynika, że
suma natężeń prądów, płynących przez oporniki, jest równa natężeniu prądu,
wpływającego do tego układu. Korzystając jeszcze z pierwszego prawa Ohma
otrzymujemy ostatecznie:

1

𝑅

𝑍

= ∑

1

𝑅

𝑖

𝑛

𝑖=1

Mostek Wheatstone’a (Rysunek 2.) pozwala na pomiar oporu bez mierzenia wartości
natężenia i napięcia prądu. Może on znajdować się w dwóch stanach – gdy 𝑈

𝐶𝐷

= 0

(mostek zrównoważony), albo 𝑈

𝐶𝐷

≠ 0 (mostek niezrównoważony). Gdy mostek jest

zrównoważony, to na mocy drugiego i pierwszego prawa Kirchhoffa:

𝑂𝑐𝑧𝑘𝑜 1: − 𝐼

2

𝑅

𝑋

+ 𝐼

3

𝑅

1

= 0 𝑜𝑟𝑎𝑧 𝐼

2

= 𝐼

5

= 𝐼

𝐷

𝑂𝑐𝑧𝑘𝑜 2: − 𝐼

5

𝑅

𝐷

+ 𝐼

6

𝑅

2

= 0 𝑜𝑟𝑎𝑧 𝐼

3

= 𝐼

6

= 𝐼

𝐶

{

𝐼

𝐷

𝐼

𝐶

=

𝑅

1

𝑅

𝑋

𝐼

𝐷

𝐼

𝐶

=

𝑅

2

𝑅

𝐷

𝑅

𝑋

=

𝑅

1

𝑅

2

𝑅

𝐷

Jeżeli R

1

= R

2

, to:

𝑅

𝑋

= 𝑅

𝐷

Rysunek 2. Schemat mostka Wheatstone’a., gdzie:
R

X

– badany opornik,

R

D

– opornica dekadowa,

R

1

, R

2

– oporniki o ustalonym oporze,

μA – mikroamperomierz (galwanometr).

2. Opis doświadczenia.

Zmierzono opory dwóch takich samych oporników, a także ich połączenia szeregowe i
równoległe za pomocą miernika uniwersalnego. Zmierzono opory węgla, niklu i platyny za
pomocą miernika, a także w układzie wcześniej zestawionego mostka Wheastone’a.
Następnie rozłączono układ, wszystkie kable i urządzenia odłożono na miejsce.
Podłączono jeden z oporników (węgiel) zanurzony w parafinie do omomierza i zanurzono
w wcześniej przygotowanej zlewce z wodą na grzejniku elektrycznym, podłączonym do
sieci elektrycznej. Odczekano aż do ustabilizowania się temperatury układu i odczytano
opory dla każdego opornika (węgiel, nikiel, platyna). Włączono ogrzewanie i odczytano
odpowiednie opory co 4°C, aż do ustabilizowania się temperatury układu. Następnie
grzejnik wyłączono, całość wyjęto ze zlewki z wodą i włączono wentylator. Dalej
postępowano analogicznie jak przy ogrzewaniu – odczytywano odpowiednie opory co 4°C,
aż do stabilnej temperatury układu. Wszystkie urządzenia odłączono z sieci elektrycznej,
miernik oddano do magazynu.

3. Plan pracy.

a) Zmierzyć opór dostępnych oporników za pomocą miernika uniwersalnego.
b) Zmierzyć opór tych samych oporników wykorzystując mostek Wheastone’a.
c) Połączyć szeregowo, a następnie równolegle dwa wybrane oporniki, przy czym przy

połączeniu równoległym wybrać dwa podobne i skrajne oporniki i zmierzyć opory tych
połączeń.

d) Wybrać dwa oporniki o porównywalnym oporze, połączyć układ mostka Wheatstone’a.
e) Napełnić zlewkę z wodą do 3/4 objętości. Odczytać ustabilizowane opory dla

temperatury początkowej.

f) Powoli ogrzewać układ, odczytywać odpowiednie opory co kilka stopni, aż do wrzenia

wody, odczytać ustabilizowane opory dla wrzącej wody.

g) Ochładzać układ i ponownie odczytywać opory dla tych samych temperatur, co

podczas ogrzewania.

4. Wyniki.

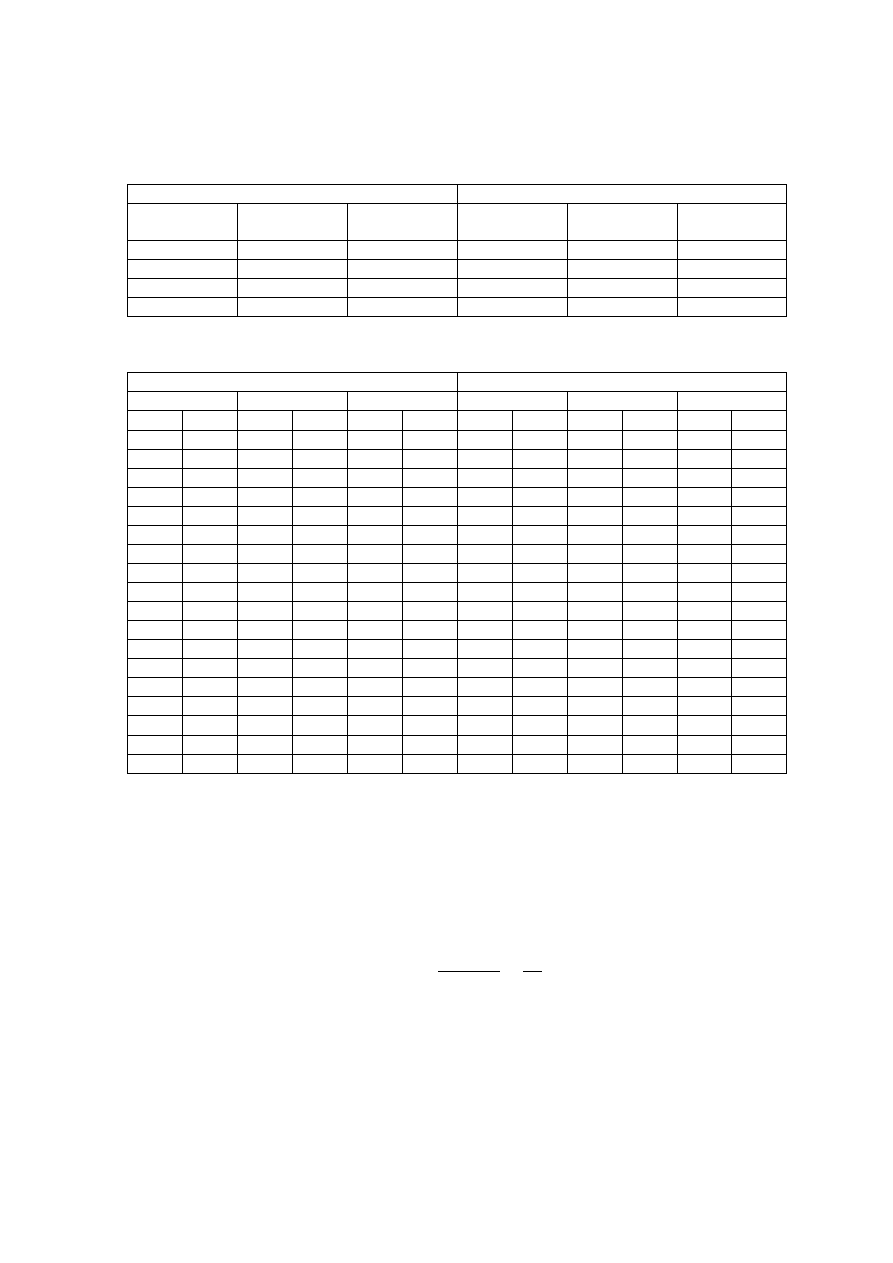
Tabela 1. Wyniki pomiarów pierwszej części ćwiczenia.

Zestaw 1

Zestaw 2

Miernik

(1)

Teoretyczne

(2)

Miernik

(1)

Mostek

(2)

R

1

[Ω]

10,4

10

R

C

[Ω]

99,9

99

R

2

[Ω]

10,3

10

R

Ni

[Ω]

114,4

113

R

S

[Ω]

20,3

20

R

Pt

[Ω]

109,8

109

R

R

[Ω]

0,4

5

Tabela 2. Wyniki pomiarów drugiej części ćwiczenia.

Ogrzewanie

Ochładzanie

C

Ni

Pt

C

Ni

Pt

T [°C]

R [Ω]

T [°C]

R [Ω]

T [°C]

R [Ω]

T [°C]

R [Ω]

T [°C]

R [Ω]

T [°C]

R [Ω]

24

99,8

24

115,2

24

110,0

92

99,8

92

156,7

92

135,8

28

117,5

28

111,4

88

155,3

88

134,7

32

120,0

32

113,2

84

153,8

84

132,7

36

121,4

36

114,6

80

151,4

80

131,2

40

123,2

40

115,0

76

146,5

76

129,8

44

125,3

44

117,6

72

143,4

72

128,3

48

127,8

48

119,0

68

140,7

68

126,8

52

130,4

52

120,6

64

138,2

64

124,8

56

133,0

56

121,1

60

135,7

60

123,5

60

135,6

60

123,6

56

133,2

56

121,9

64

138,0

64

125,0

52

130,6

52

120,4

68

140,8

68

126,6

48

128,4

48

118,9

72

143,4

72

128,1

44

126,0

44

117,4

76

146,0

76

129,7

40

123,6

40

115,9

80

148,6

80

131,2

36

121,2

36

114,3

84

151,4

84

132,7

32

99,8

32

118,8

32

112,8

88

154,2

88

134,4

92

99,8

92

156,9

92

135,8

5. Opracowanie wyników.

a) Część pierwsza.

Obliczono teoretyczne opory zastępcze połączenia szeregowego i równoległego dwóch
takich samych oporników (R

1

= R

2

), na podstawie wzorów:

𝑅

𝑆

= 𝑅

1

+ 𝑅

2

= 2𝑅

1

𝑅

𝑅

=

𝑅

1

𝑅

2

𝑅

1

+ 𝑅

2

=

𝑅

1

2

gdzie:
𝑅

𝑆

– opór zastępczy oporników połączonych szeregowo [Ω],

𝑅

𝑅

– opór zastępczy oporników połączonych równolegle [Ω],

𝑅

1

= 𝑅

2

– opór danych oporników [Ω].

Otrzymane wyniki wprowadzono do Tabeli 1.

Obliczono niepewności pomiarowe danych z Tabeli 1., na podstawie wzorów:

Miernik:

∆(𝑅

𝑛

)

1

= 0,8%(𝑅

𝑛

)

1

+ 0,3 Ω

gdzie:
∆(𝑅

𝑛

)

1

– niepewność oporu badanego opornika [Ω],

(𝑅

𝑛

)

1

– wartość oporu badanego opornika [Ω].

Teoretyczne:

∆(𝑅

1

)

2

= ∆(𝑅

2

)

2

= Δ𝑥

𝑝𝑟𝑜𝑑.

= 10%𝑅 = 1 Ω

gdzie:
∆(𝑅

1

)

2

= ∆(𝑅

2

)

2

– niepewność oporu danych oporników [Ω],

Δ𝑥

𝑝𝑟𝑜𝑑.

– niepewność oporu badanego opornika podana przez producenta [Ω],

𝑅 – wartość oporu badanego opornika [Ω].

Dla teoretycznych oporów zastępczych użyto wzorów:

∆𝑅

𝑆

= √(∆𝑅

1

)

2

+ (∆𝑅

2

)

2

= ∆𝑅

1

√2 = 1 ∙ 1,4 = 1,4 Ω

∆𝑅

𝑅

= |

𝜕𝑅

𝑅

𝜕𝑅

1

∆𝑅

1

| = 0,5 Ω

gdzie:
∆𝑅

𝑆

– niepewność oporu zastępczy oporników połączonych szeregowo [Ω],

∆𝑅

𝑆

– niepewność oporu zastępczy oporników połączonych równolegle [Ω],

∆𝑅

1

= ∆𝑅

2

– niepewność oporu danych oporników [Ω].

Mostek (opornica dekadowa):

∆(𝑅

𝐶

)

2

= ∆(𝑅

𝑁𝑖

)

2

= ∆(𝑅

𝑃𝑡

)

2

= 𝑛

𝑠

∙ 0,05% + 𝑛

𝑑

∙ 0,05% + 𝑛

𝑗

∙ 0,1% + 1

gdzie:
∆(𝑅

𝐶

)

2

– niepewność oporu węgla [Ω],

∆(𝑅

𝑁𝑖

)

2

– niepewność oporu niklu [Ω],

∆(𝑅

𝑃𝑡

)

2

– niepewność oporu platyny [Ω],

𝑛

𝑠

– liczba setek omów na opornicy dekadowej [Ω],

𝑛

𝑑

– liczba dziesiątek omów na opornicy dekadowej [Ω],

𝑛

𝑗

– liczba jednostek omów na opornicy dekadowej [Ω].

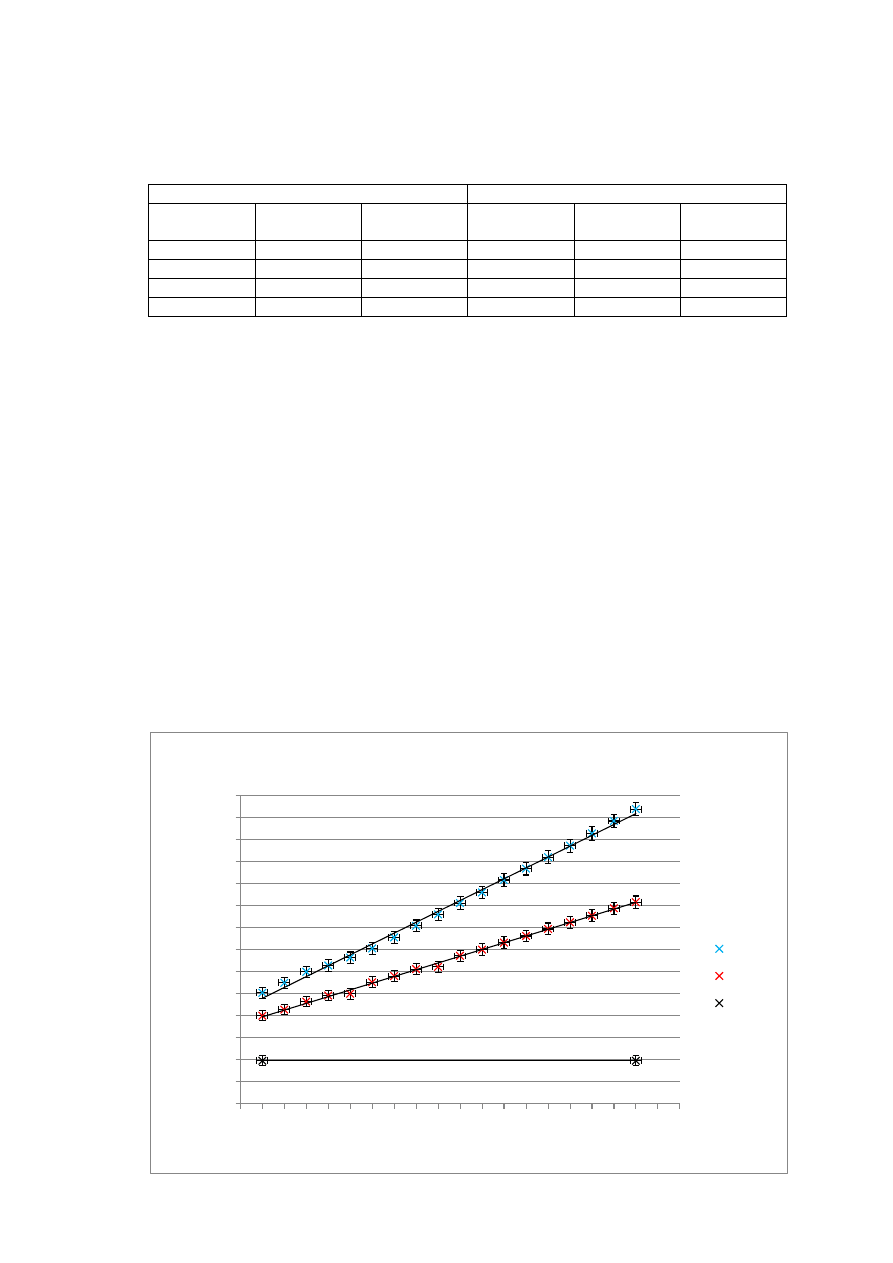
Wykres 1. Zależność R(T) dla ogrzewania badanych przewodników.

Wyniki końcowe:

Tabela 3. Wyniki końcowe pierwszej części ćwiczenia.

Zestaw 1

Zestaw 2

Opornik

R

n

Miernik

(1)

Teoretyczne

(2)

Opornik

R

n

Miernik

(1)

Mostek

(2)

R

1

[Ω]

10,4 ± 0,4

10,0 ± 1,0

R

C

[Ω]

99,9 ± 1,1

99,0 ± 1,1

R

2

[Ω]

10,3 ± 0,4

10,0 ± 1,0

R

Ni

[Ω]

114,4 ± 1,2

113,0 ± 1,1

R

S

[Ω]

20,3 ± 0,5

20,0 ± 1,4

R

Pt

[Ω]

109,8 ± 1,2

109,0 ± 1,1

R

R

[Ω]

0,4 ± 0,2

5,0 ± 0,5

b) Część druga.

Obliczono niepewności pomiarów z Tabeli 2, za pomocą wzorów:

Δ𝑇 = 1℃

∆𝑅

𝑛

= 0,8%𝑅

𝑛

+ 0,3 Ω

gdzie:
∆𝑇 – niepewność temperatury [°C],
∆𝑅

𝑛

– niepewność zmierzonego oporu [Ω],

𝑅

𝑛

– zmierzony opór [Ω].

Sporządzono wykresy zależności R(T) dla niklu i platyny, dopasowano do nich linie
trendu i wyświetlono ich równania, wyznaczono niepewności pomiarowe
współczynników otrzymanych prostych, a także słupki błędów za pomocą arkusza
kalkulacyjnego Excel (funkcja REGLINP) i powyższych danych:

y = 0.6164x + 99.178

R² = 0.9966

y = 0.3816x + 100.62

R² = 0.9983

y = 99.8

90.0

95.0

100.0

105.0

110.0

115.0

120.0

125.0

130.0

135.0

140.0

145.0

150.0

155.0

160.0

20 24 28 32 36 40 44 48 52 56 60 64 68 72 76 80 84 88 92 96 100

R [

Ω

]

T [°C]

Ogrzewanie

Nikiel

Platyna

Węgiel

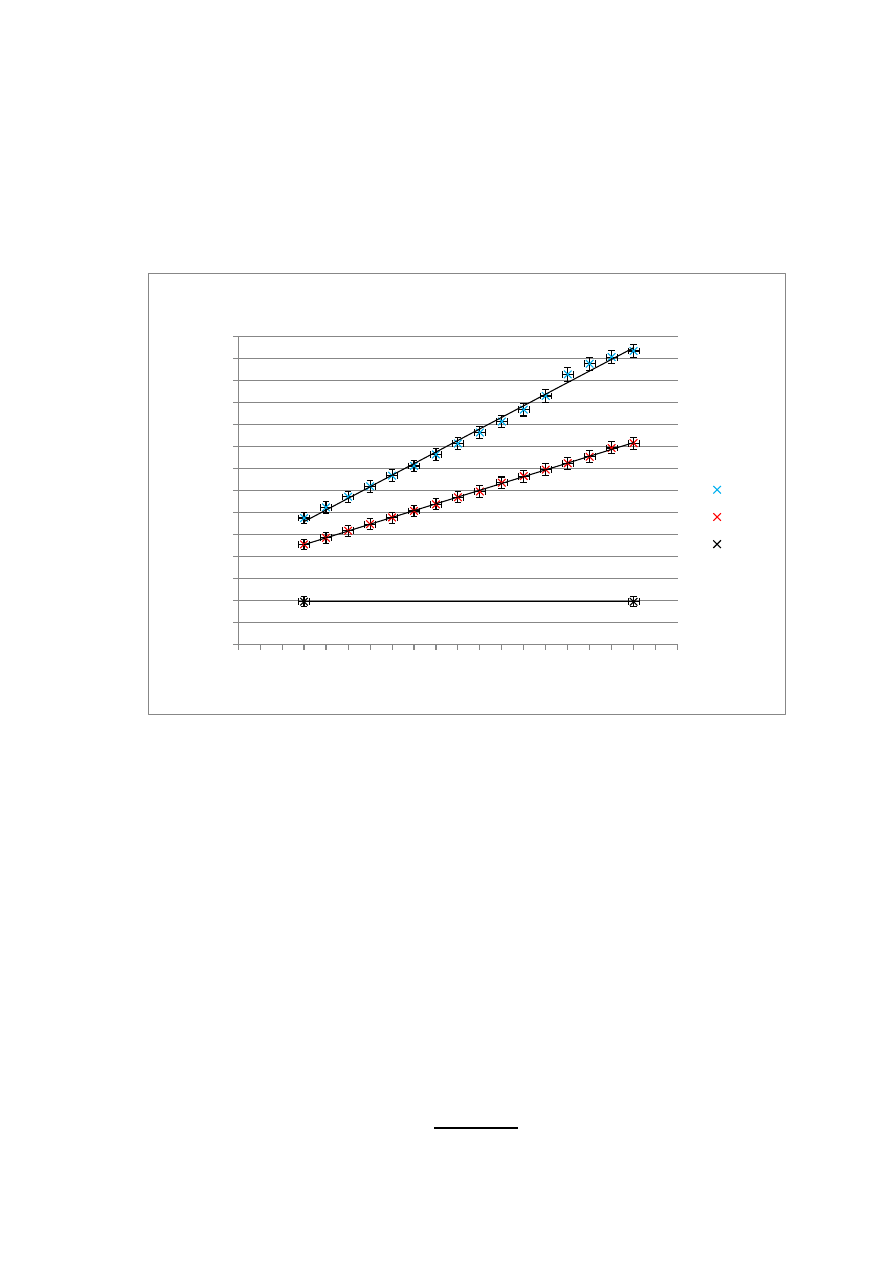
Wykres 2. Zależność R(T) dla ogrzewania badanych przewodników.

𝑎

𝑁𝑖

= 0,6164 Ω/𝐾

∆𝑎

𝑁𝑖

= 0,0090 Ω/𝐾

𝑎

𝑃𝑡

= 0,3816 Ω/𝐾

∆𝑎

𝑃𝑡

= 0,0040 Ω/𝐾

𝑎

𝐶

= 0 Ω/𝐾

∆𝑎

𝐶

= 0 Ω/𝐾

𝑎

𝑁𝑖

= 0,6575 Ω/𝐾

∆𝑎

𝑁𝑖

= 0,0124 Ω/𝐾

𝑎

𝑃𝑡

= 0,3864 Ω/𝐾

∆𝑎

𝑃𝑡

= 0,0020 Ω/𝐾

𝑎

𝐶

= 0 Ω/𝐾

∆𝑎

𝐶

= 0 Ω/𝐾

Obliczono temperaturowe współczynniki oporu przewodników na podstawie wzoru:

𝑅

𝑇

= 𝑅

0

+ 𝑅

0

𝛼(𝑇 − 𝑇

0

)

oraz uzyskanych zależności liniowych:

𝑦 = 𝑎𝑥 + 𝑏

Ostatecznie:

(𝛼

𝑃

)

1

=

𝑅

𝑇

− 𝑅

0

𝑅

0

(𝑇 − 𝑇

0

)

(𝐴)

y = 0.6575x + 96.956

R² = 0.9951

y = 0.3864x + 100.37

R² = 0.9996

y = 99,8

90.0

95.0

100.0

105.0

110.0

115.0

120.0

125.0

130.0

135.0

140.0

145.0

150.0

155.0

160.0

20 24 28 32 36 40 44 48 52 56 60 64 68 72 76 80 84 88 92 96 100

R [

Ω

]

T [°C]

Ochładzanie

Nikiel

Platyna

Węgiel

oraz:

(𝛼

𝑃

)

2

=

𝑎

𝑅

0

(𝐵)

gdzie:
𝛼 – temperaturowy współczynnik oporu [1/K],

(𝛼

𝑃

)

1

– temperaturowy współczynnik oporu dany wzorem A [1/K],

(𝛼

𝑃

)

2

– temperaturowy współczynnik oporu dany wzorem B [1/K],

𝑅

𝑇

– opór przewodnika w temperaturze T [Ω],

𝑅

0

– opór przewodnika w temperaturze T

0

[Ω],

𝑇 – najwyższa zanotowana temperatura układu [°C],
𝑇

0

– najniższa zanotowana temperatura układu [°C],

𝑎 – współczynnik kierunkowy równania uzyskanej prostej [Ω/K],
𝑏 – wyraz wolny równania uzyskanej prostej [Ω].

Ogrzewanie:

𝑇

0

= 24℃

𝑇 = 92℃

(𝛼

𝑁𝑖

)

1

= 0,0053 1/𝐾

(𝛼

𝑁𝑖

)

2

= 0,0054 1/𝐾

(𝛼

𝑃𝑡

)

1

= 0,0034 1/𝐾

(𝛼

𝑃𝑡

)

2

= 0,0035 1/𝐾

(𝛼

𝐶

)

1

= 0 1/𝐾

(𝛼

𝐶

)

2

= 0 1/𝐾

Ochładzanie:

𝑇

0

= 32℃

𝑇 = 92℃

(𝛼

𝑁𝑖

)

1

= 0,0040 1/𝐾

(𝛼

𝑁𝑖

)

2

= 0,0055 1/𝐾

(𝛼

𝑃𝑡

)

1

= 0,0028 1/𝐾

(𝛼

𝑃𝑡

)

2

= 0,0034 1/𝐾

(𝛼

𝐶

)

1

= 0 1/𝐾

(𝛼

𝐶

)

2

= 0 1/𝐾

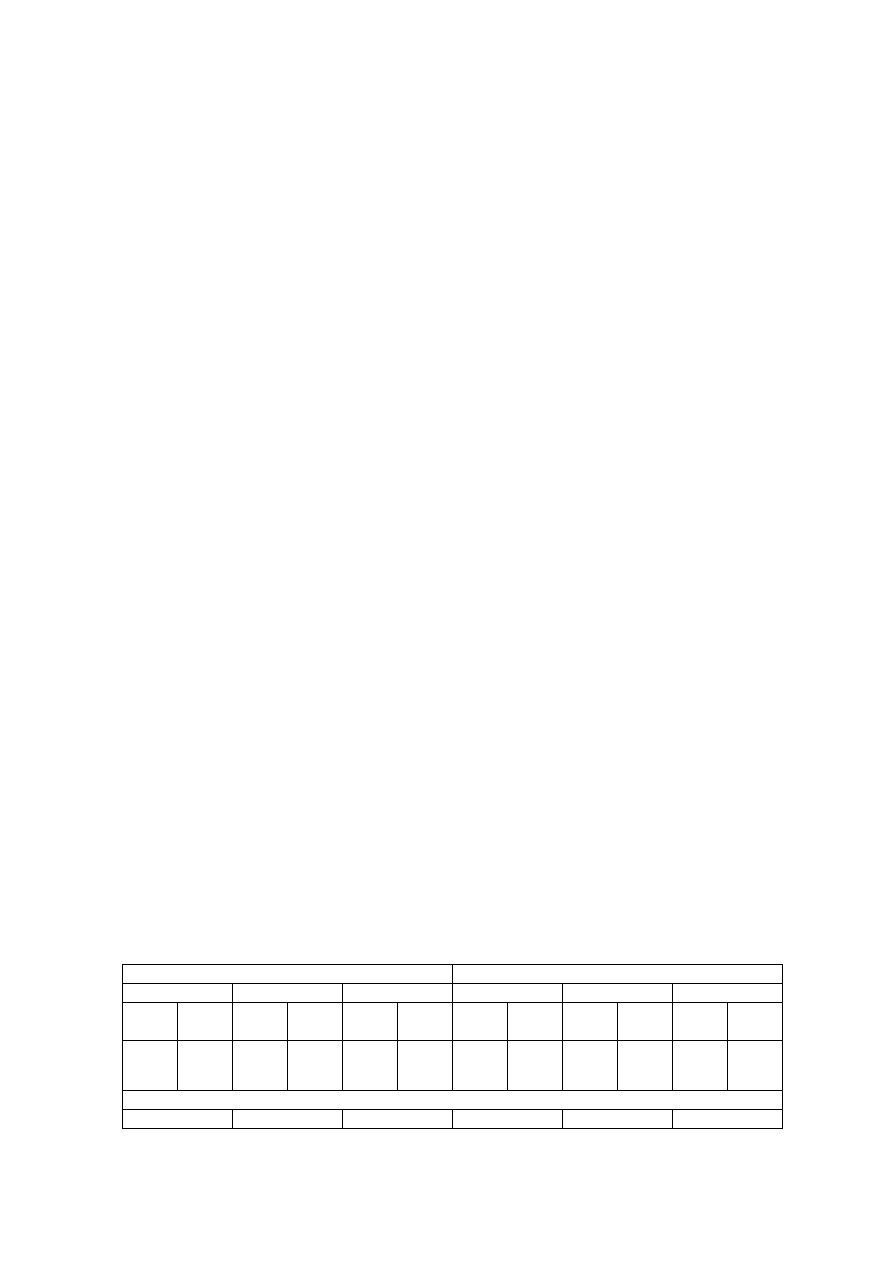
Obliczono niepewności powyższych pomiarów na podstawie wzorów:

∆(𝛼

𝑃

)

1

= |

𝜕(𝛼

𝑃

)

1

𝜕𝑅

𝑇

∆𝑅

𝑇

| + |

𝜕(𝛼

𝑃

)

1

𝜕𝑅

0

∆𝑅

0

| + |

𝜕(𝛼

𝑃

)

1

𝜕𝑇

∆𝑇| + |

𝜕(𝛼

𝑃

)

1

𝜕𝑇

0

∆𝑇

0

| =

=

(𝑇 − 𝑇

0

)(𝑅

0

∆𝑅

𝑇

+ 𝑅

𝑇

∆𝑅

0

) + 𝑅

0

(𝑅

𝑇

− 𝑅

0

)(∆𝑇 + ∆𝑇

0

)

𝑅

0

2

(𝑇 − 𝑇

0

)

2

∆(𝛼

𝑃

)

2

= |

𝜕(𝛼

𝑃

)

2

𝜕𝑎

∆𝑎| + |

𝜕(𝛼

𝑃

)

2

𝜕𝑅

0

∆𝑅

0

| =

1

𝑅

0

∆𝑎 +

𝑎

𝑅

0

2

∆𝑅

0

=

𝑅

0

∆𝑎 + 𝑎∆𝑅

0

𝑅

0

2

gdzie:
𝛼 – temperaturowy współczynnik oporu [1/K],

(𝛼

𝑃

)

1

– temperaturowy współczynnik oporu dany wzorem A [1/K],

(𝛼

𝑃

)

2

– temperaturowy współczynnik oporu dany wzorem B [1/K],

𝑅

𝑇

– opór przewodnika w temperaturze T [Ω],

𝑅

0

– opór przewodnika w temperaturze T

0

[Ω],

𝑇 – najwyższa zanotowana temperatura układu [°C],
𝑇

0

– najniższa zanotowana temperatura układu [°C],

𝑎 – współczynnik kierunkowy równania uzyskanej prostej [Ω/K],
∆𝛼 – niepewność temperaturowego współczynnika oporu [1/K],
∆(𝛼

𝑃

)

1

– niepewność temperaturowego współczynnika oporu danego wzorem A [1/K],

∆(𝛼

𝑃

)

2

– niepewność temperaturowego współczynnika oporu danego wzorem B [1/K],

∆𝑅

𝑇

– niepewność oporu przewodnika w temperaturze T [Ω],

∆𝑅

0

– niepewność oporu przewodnika w temperaturze T

0

[Ω],

∆𝑇 – niepewność najwyższej zanotowanej temperatury układu [°C],
∆𝑇

0

– niepewność najniższej zanotowanej temperatury układu [°C],

∆𝑎 – niepewność współczynnika kierunkowego równania uzyskanej prostej [Ω/K].

Ogrzewanie:

∆(𝛼

𝑁𝑖

)

1

= 0,00057 1/𝐾

∆(𝛼

𝑁𝑖

)

2

= 0,00016 1/𝐾

∆(𝛼

𝑃𝑡

)

1

= 0,00048 1/𝐾

∆(𝛼

𝑃𝑡

)

2

= 0,000090 1/𝐾

∆(𝛼

𝐶

)

1

= 0 1/𝐾

∆(𝛼

𝐶

)

2

= 0 1/𝐾

Ochładzanie:

∆(𝛼

𝑁𝑖

)

1

= 0,00063 1/𝐾

∆(𝛼

𝑁𝑖

)

2

= 0,00018 1/𝐾

∆(𝛼

𝑃𝑡

)

1

= 0,00053 1/𝐾

∆(𝛼

𝑃𝑡

)

2

= 0,000069 1/𝐾

∆(𝛼

𝐶

)

1

= 0 1/𝐾

∆(𝛼

𝐶

)

2

= 0 1/𝐾

Wyniki końcowe:

Tabela 4. Wyniki końcowe drugiej części ćwiczenia.

Ogrzewanie

Ochładzanie

C

Ni

Pt

C

Ni

Pt

α

1

[1/K]

α

2

[1/K]

α

1

[1/K]

α

2

[1/K]

α

1

[1/K]

α

2

[1/K]

α

1

[1/K]

α

2

[1/K]

α

1

[1/K]

α

2

[1/K]

α

1

[1/K]

α

2

[1/K]

0
±
0

0
±
0

0,0053

±

0,00057

0,0054

±

0,00016

0,0034

±

0,00048

0,0035

±

0,000090

0
±
0

0
±
0

0,0040

±

0,00063

0,0055

±

0,00018

0,0028

±

0,00053

0,0034

±

0,000069

Dane tablicowe

-0,0005

0,006

0,0039

-0,0005

0,006

0,0039

6. Omówienie wyników i podsumowanie.

Wartości oporów zmierzone dla danych oporników niewiele odbiegają od wartości
teoretycznej (podanej przez producenta). Analogicznie jest w przypadku połączenia
szeregowego. Z kolei połączenie równoległe zmierzone za pomocą miernika
uniwersalnego znacząco odbiega od wartości teoretycznej (obliczonej). Może to być
spowodowane tylko jednym czynnikiem – nieprawidłowym zestawieniem odwodu
elektrycznego. Porównując wartości oporów oporników zbudowanych z węgla, niklu i
platyny, można dojść do wniosku, że są one zgodne zarówno dla pomiaru miernikiem, jak
i mostkiem Wheatstone’a.
Otrzymane wartości temperaturowych współczynników oporu właściwego niewiele różnią
się od wartości tablicowych. Współczynniki te, otrzymane dwiema różnymi metodami dla
każdej substancji również niewiele się od siebie różnią. Jeżeli chodzi o niepewności, tu
bywa różnie – niekiedy są zgodne (np. nikiel podczas ogrzewania (0,00016 1/K) i
ochładzania (0,00018 1/K) drugą metodą), a niekiedy nie (np. nikiel w przypadku
pierwszej (0,00057 1/K) i drugiej (0,00016 1/K) metody podczas ogrzewania). W
przypadku węgla wszystkie otrzymane wartości wynoszą 0, ze względu na to, iż jego opór
nie uległ żadnej zmianie podczas wszystkich pomiarów. Jest to niezgodne z wartością
tablicową, która wskazuje na to, że opór węgla niewiele, ale mimo wszystko powinien
maleć wraz ze wzrostem temperatury – ma bowiem ujemny temperaturowy współczynnik
oporu właściwego. Wszystkie zależności R(T), poza węglem, zachowują bardzo dobrą
liniowość, co jest widoczne na załączonych wykresach – współczynnik R

2

dla wszystkich

zależności wynosi ponad 0,9950, a w przypadku ochładzania platyny – nawet 0,9996.
Powyższe rozbieżności mogą wynikać z niedokładności użytych przyrządów pomiarowych
(co doskonale widać w przypadku pierwszej części ćwiczenia), niedoskonałości ludzkiego
oka podczas odczytywania temperatury, a także należy wziąć pod uwagę trudności
podczas równoczesnego odczytywania wartości oporu dla kilku oporników w danej
temperaturze.

7. Literatura.

[1] http://www.1pf.if.uj.edu.pl/documents/5046939/5227638/e3%20Kapanowski%208
%2003%2013.pdf, dostęp: 17.04.13 r.
[2] A. Magiera, I Pracownia Fizyczna, IF UJ, Kraków 2010.
[3] D. Halliday, R. Resnick, J. Walker, Podstawy Fizyki 3, PWN, Warszawa 2003.
[4] A. Bielański, Podstawy chemii nieorganicznej 1, PWN, Warszawa 2010, s. 241.
[5] http://pl.wikipedia.org/wiki/Fonon, dostęp: 17.04.13 r.
[6] http://www.1pf.if.uj.edu.pl/materialy/pmc/mas830, dostęp: 17.04.13 r.

8. Załączniki.

Kserokopia wyników pomiarowych.