PODSTAWY LOGIKI

ROZMYTEJ

Dariusz Badura

Czym jest Logika Rozmyta

Fuzzy-Logic?

• Klasyczna logika

bazuje na dwóch wartościach

reprezentowanych najczęściej przez: 0 i 1 lub prawda i fałsz.
Granica między nimi jest jednoznacznie określona i

niezmienna.

• Logika rozmyta

stanowi rozszerzenie klasycznego

rozumowania na rozumowanie bliższe ludzkiemu. Wprowadza
ona wartości pomiędzy standardowe 0 i 1; ‘rozmywa’ granice
pomiędzy nimi dając możliwość istnienia wartości z pomiędzy
tego przedziału (np.: prawie fałsz, w połowie prawda).

Logika Rozmyta

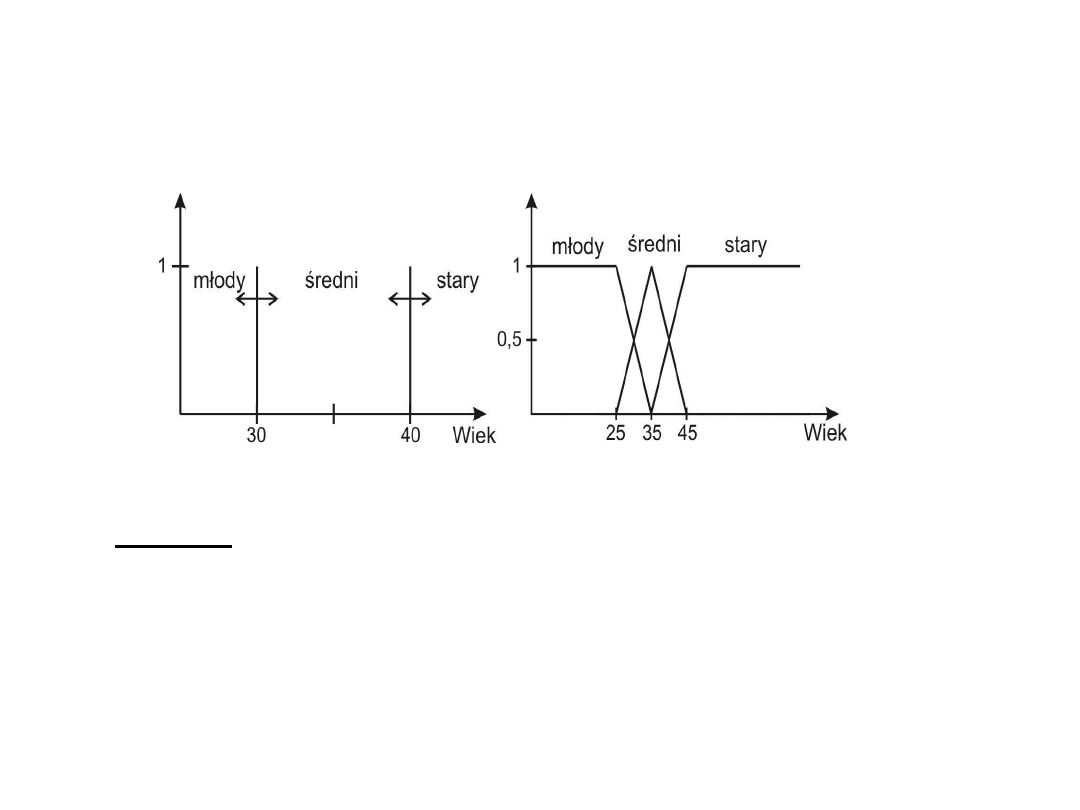
• Przykład: Polem naszego przykładu niech będzie wiek ludzi. Chcemy

określić granice między ludźmi młodymi, w średnim wieku i starymi. W
klasycznej logice będziemy zmuszeni przyjąć stałe niezmienne granice,
jak na przykład dla ludzi młodych moglibyśmy przyjąć 0 a 30 lat, dla ludzi
w średnim wieku 30 a 40 lat i dla ludzi starych 40 i więcej lat.

Logika Rozmyta

Klasyczna logika

Logika rozmyta

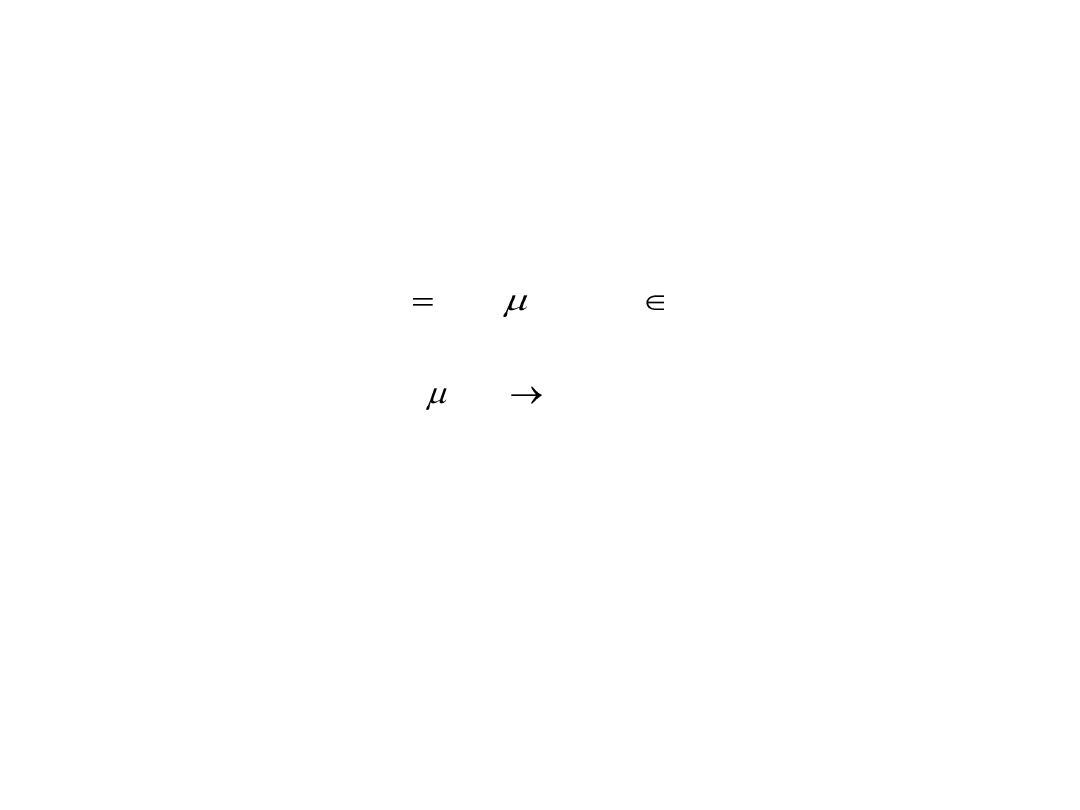
Definicja zbioru rozmytego

jest funkcją przynależności zbioru rozmytego A. Funkcja ta każdemu
elementowi x

∈ X przypisuje jego stopień przynależności do zbioru rozmytego

A, przy czym można wyróżnić 3 przypadki:
μ

A

(x

) = 1 oznacza pełną przynależność do zbioru rozmytego A, tzn. x

∈ A,

μ

A

(x

) = 0 oznacza brak przynależności elementu x do zbioru rozmytego A, tzn.

x

∉ A,

0 <

μ

A

(x

) < 1 oznacza częściową przynależność elementu x do zbioru

rozmytego A.

Zbiorem rozmytym A w pewnej (niepustej) przestrzeni X, co zapisujemy jako A

⊆

X

, nazywamy zbiór par

}

));

(

,

{(

A

X

x

x

x

A

gdzie:

]

1

,

0

[

: X

A

Zastosowanie logiki rozmytej

• Logika rozmyta jest stosowana wszędzie tam, gdzie użycie klasycznej

logiki stwarza problem ze względu na trudność w zapisie matematycznym
procesu lub gdy wyliczenie lub pobranie zmiennych potrzebnych do
rozwiązania problemu jest niemożliwe.

• Ma szerokie zastosowanie w różnego rodzaju sterownikach. Sterowniki te

mogą pracować w urządzeniach tak pospolitych jak lodówki czy pralki, jak
również mogą być wykorzystywane do bardziej złożonych zagadnień jak
przetwarzanie obrazu, rozwiązywanie problemu korków ulicznych czy
unikanie kolizji.

• Sterowniki wykorzystujące logikę rozmytą są również używane na

przykład w połączeniu z sieciami neuronowymi.

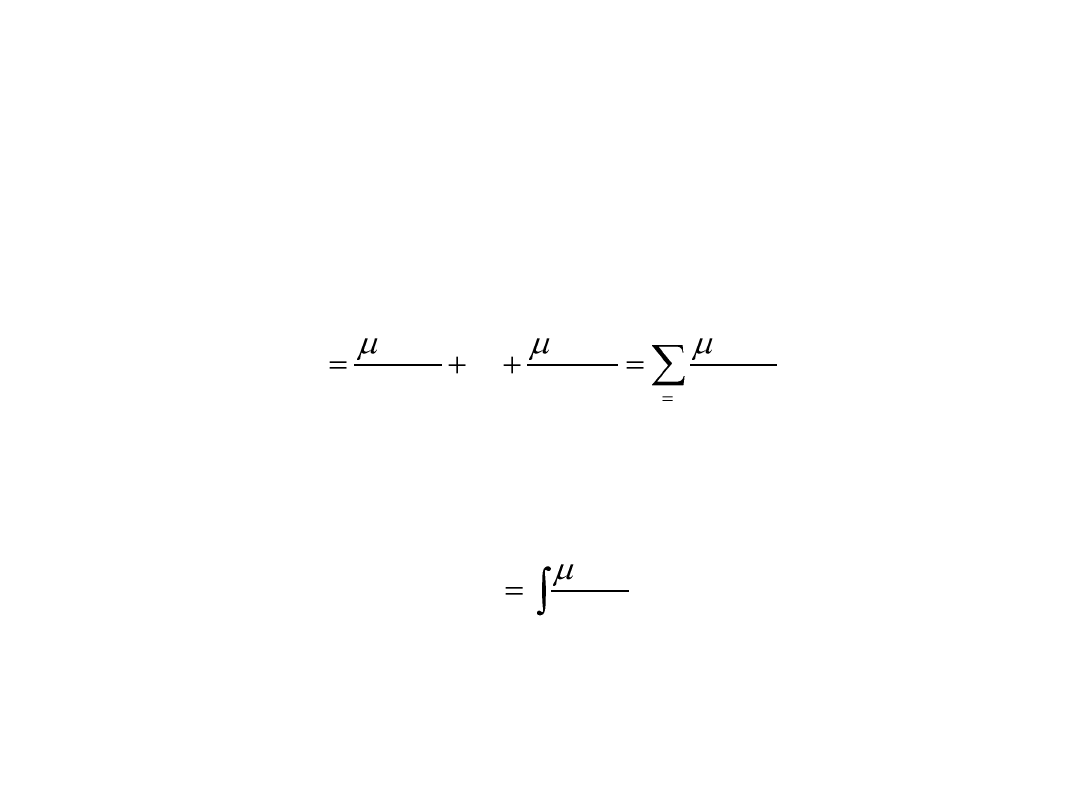
Zapis symboliczny zbiorów rozmytych

X

jest przestrzenią o skończonej liczbie elementów, X = {x

1

, ..., x

n

}:

n

i

i

i

A

n

n

A

A

x

x

x

x

x

x

1

1

1

)

(

)

(

)

(

A



X

jest przestrzenią o nieskończonej liczbie elementów:

X

A

x

x)

(

A

Podstawy matematyczne

• Przykład: weźmy zbiór mieszkańców pewnego miasta. Podzbiorem będą

osoby posiadające samochód. Osoby należące do tego zbioru możemy
również przedstawić za pomocą argumentów składających się dwóch
wartości. Pierwszą z nich jest wartość odpowiadająca osobie, natomiast
drugą jest liczba 1 lub 0, w zależności czy dana osoba posiada samochód
czy też nie. Mając w ten sposób oznaczone elementy zbioru, aby
stwierdzić, czy są częścią naszego podzbioru wystarczy odszukać te, które
na drugiej pozycji mają jedynkę. Zbiór taki może mieć następujące
elementy:

• Miasto1 = { Marek,1; Ania,0; Piotr,0; Maja,1 }

Dzięki takiemu zapisowi wiemy, że osobami posiadającymi samochód i

należącymi do naszego podzbioru są Marek i Maja.

Zbiory – logika klasyczna

Zbiory rozmyte

• Podzbiór rozmyty Z zbioru Y tak samo może być reprezentowany przez

dwuargumentowy zestaw wartości, w których pierwszy element odpowiada
wartości zbioru Y, a drugi przyjmuje wartości ze zbioru [0;1].

• Podobnie jak w zwykłym zbiorze drugi element określa przynależność do

podzbioru Z, z tą różnicą, że oprócz ‘całkowitej’ przynależności do niego
(dla 1) i ‘całkowitym’ brakiem tej przynależności (dla 0), posiadamy
informacje o tzw. „stopniu przynależności” do podzbioru Z (określoną
wartościami z przedziału 0-1).

• Stopień Przynależności stanowi dla nas informację, jak daleko element y

jest oddalony od naszego podzbioru Z. Określamy go dzięki

Funkcji

Przynależności.

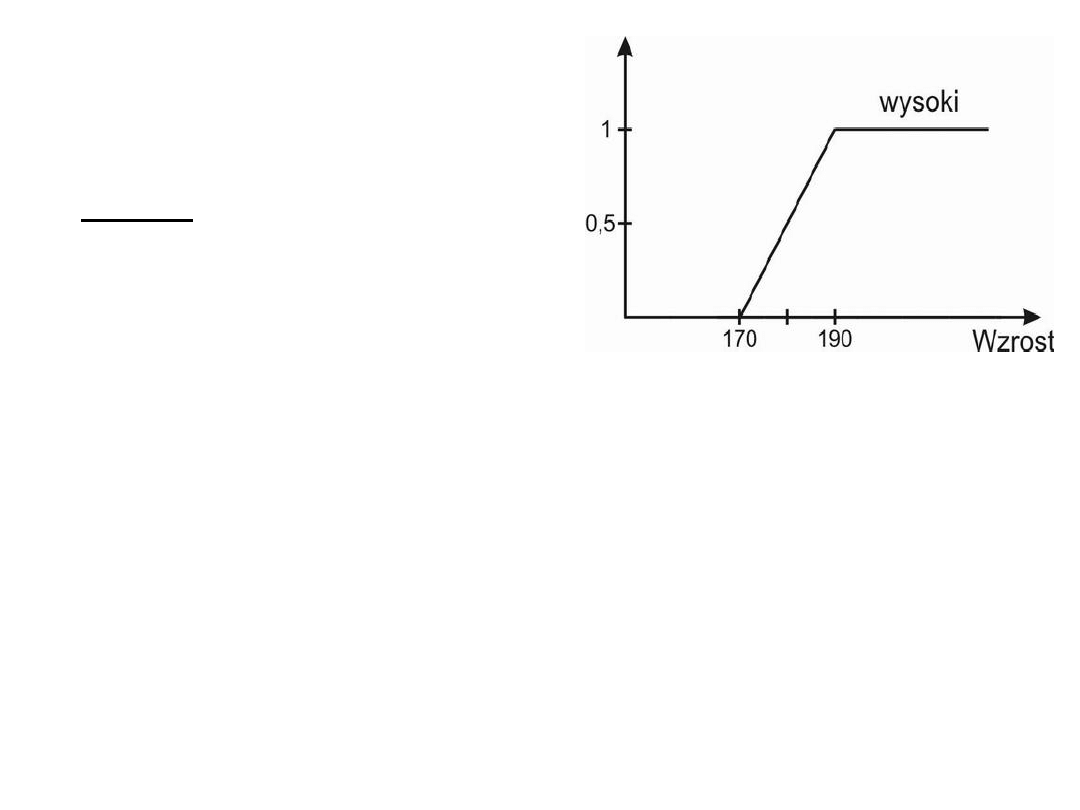
Zbiory rozmyte

•

Przykład.

Niech naszym

- zbiorem Y będą osoby, a

- zbiorem rozmytym Z – osoby wysokie.

Zbiór Z będzie nam mówił, w jakim stopniu dana osoba ze zbioru Y
przynależy do zbioru osób wysokich. W tym celu musimy ułożyć funkcję
przynależności dla naszego zbioru rozmytego bazującą na wzroście.

Np.:

Z(y) = ( 0  wzrost < 170 cm

[Z(y) – 170]/20  170 cm > wzrost < 190 cm

1  wzrost > 190 cm )

Zbiory rozmyte c.d.

Osoba Y

Wzrost

Stopień

Przynależności

d

o Z

Osoba Y

Wzrost

Stopień

Przynależności

d

o Z

Kamil

139

0

Darek

193

1

Sławek

182

0,6

Zbyszek

128

0

Mariusz

179

0,45

Karol

175

0,25

Jacek

187

0,85

Dzięki zastosowanej funkcji przynależności uzyskujemy następujące
dane:

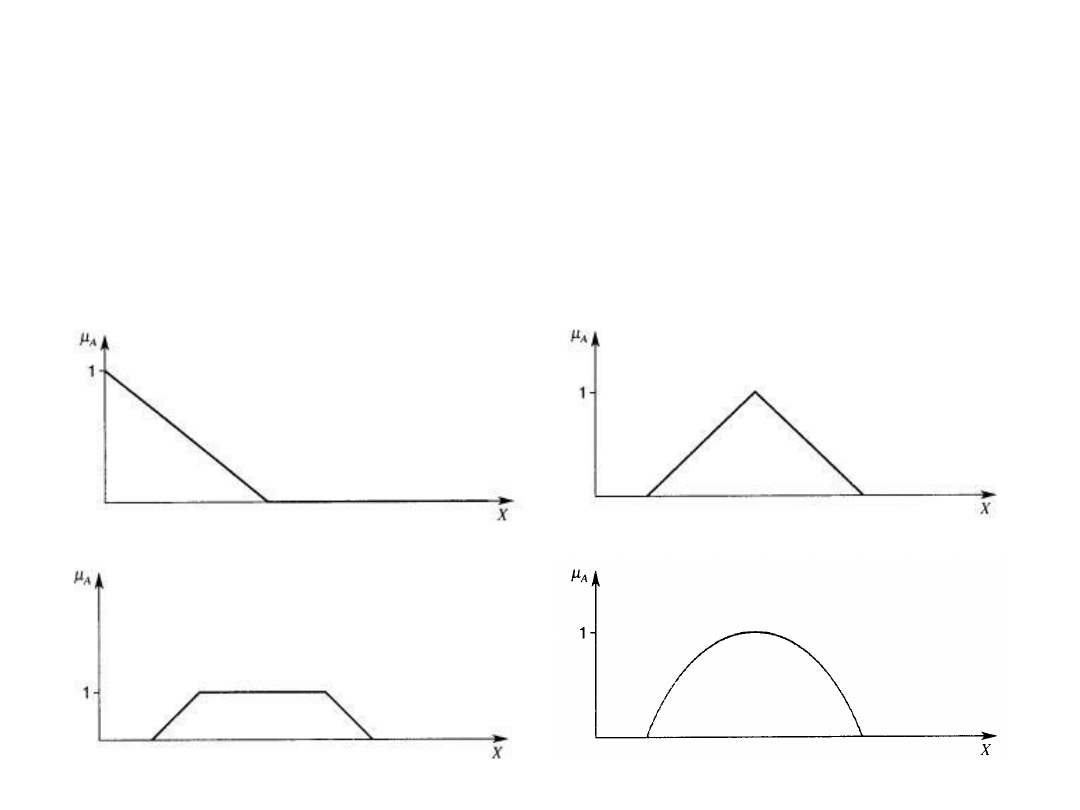
Funkcje przynależności

Funkcja przynależności może mieć bardziej złożony kształt. W zdecydowanej
większości przypadków jako funkcje przynależności stosuje się trójkąty, ale
mogą to być też trapezy lub parabole

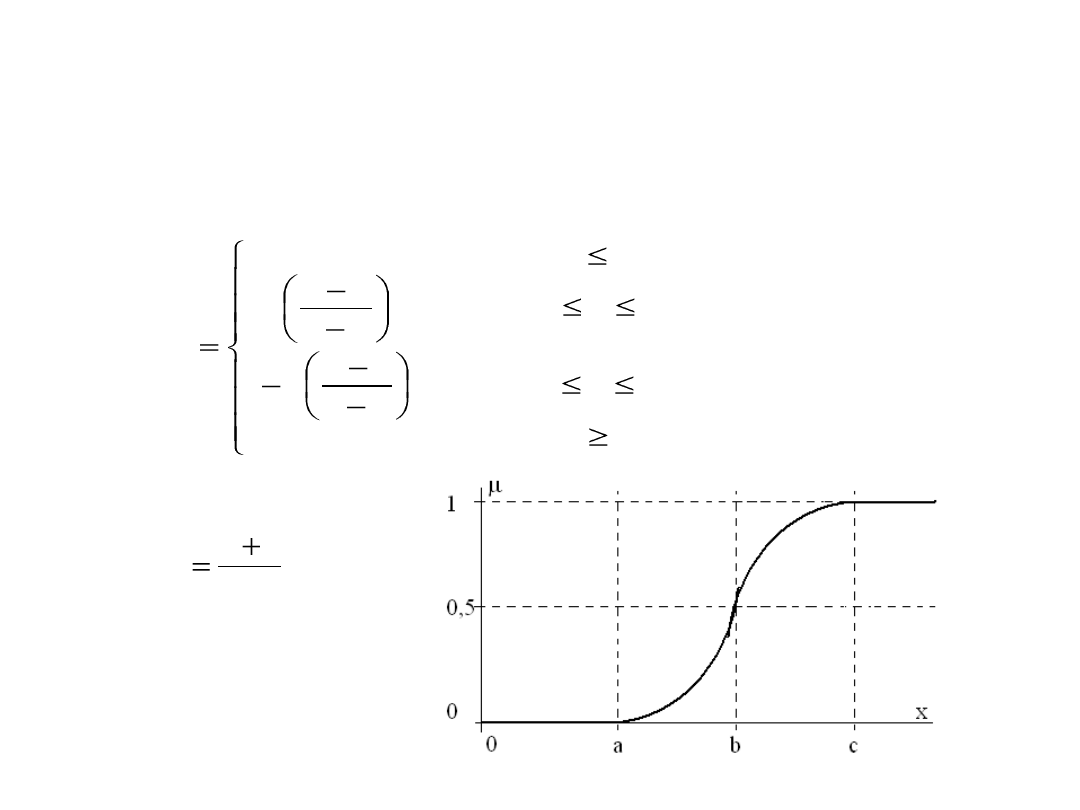
Standardowe postaci funkcji

przynależności

1. Funkcja przynależności klasy s:

c

x

c

x

b

a

c

c

x

b

x

a

a

c

a

x

a

x

c

b

a

x

s

dla

1

dla

2

1

dla

2

dla

0

)

,

,

;

(

2

2

gdzie

2

c

a

b

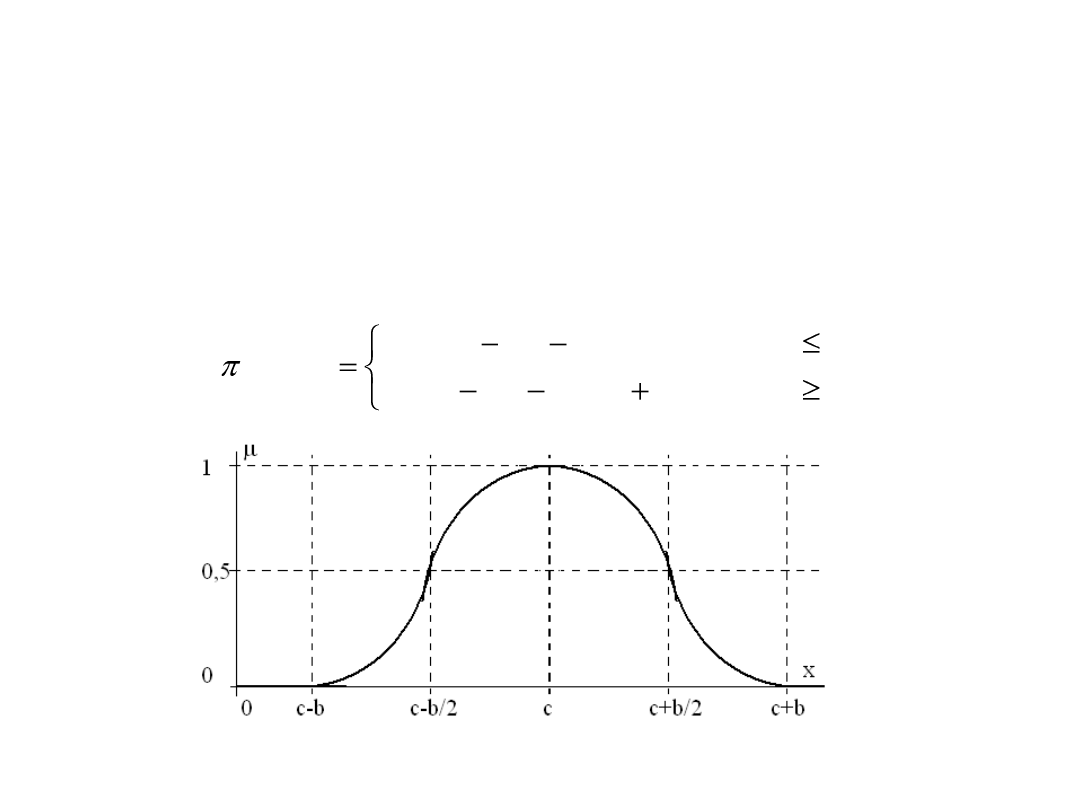
Standardowe postaci funkcji

przynależności

2. Funkcja przynależności klasy π:

c

x

b

c

b

c

b

c

x

s

c

x

c

b

c

b

c

x

s

c

b

x

dla

)

,

2

/

,

;

(

dla

)

,

2

/

,

;

(

)

,

;

(

zdefiniowana poprzez klasę s

Standardowe postaci funkcji

przynależności

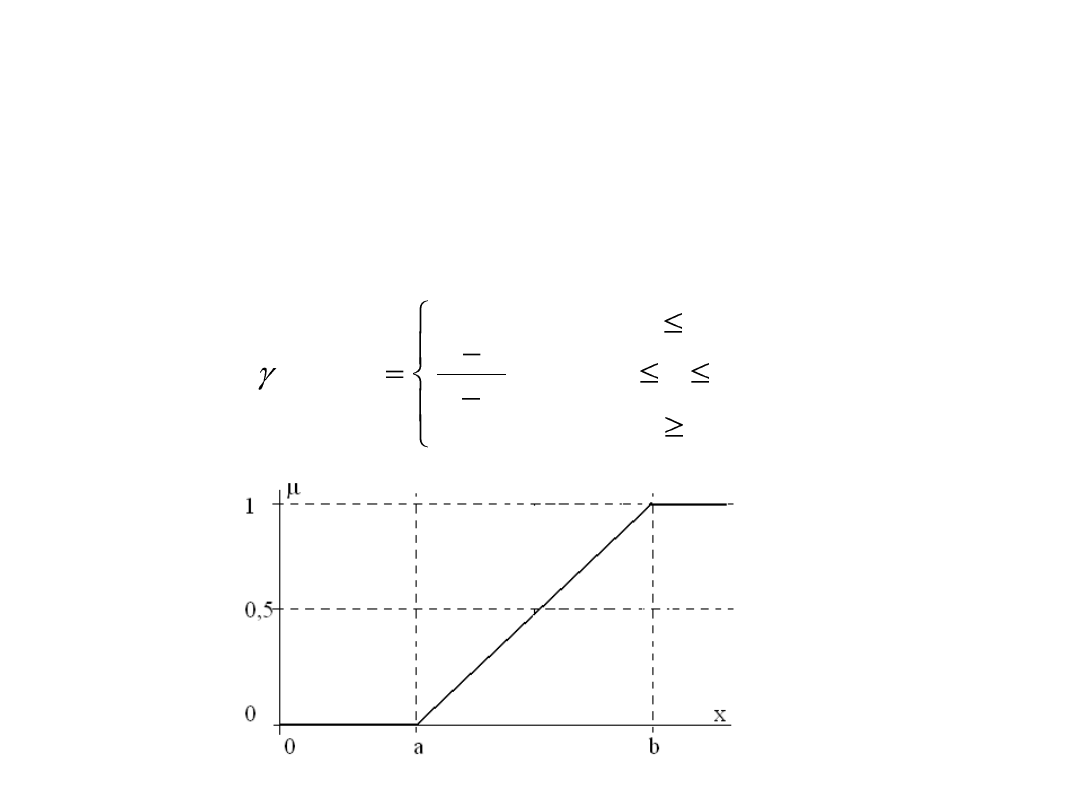
3. Funkcja przynależności klasy γ:

b

x

b

x

a

a

b

a

x

a

x

b

a

x

dla

1

dla

dla

0

)

,

;

(

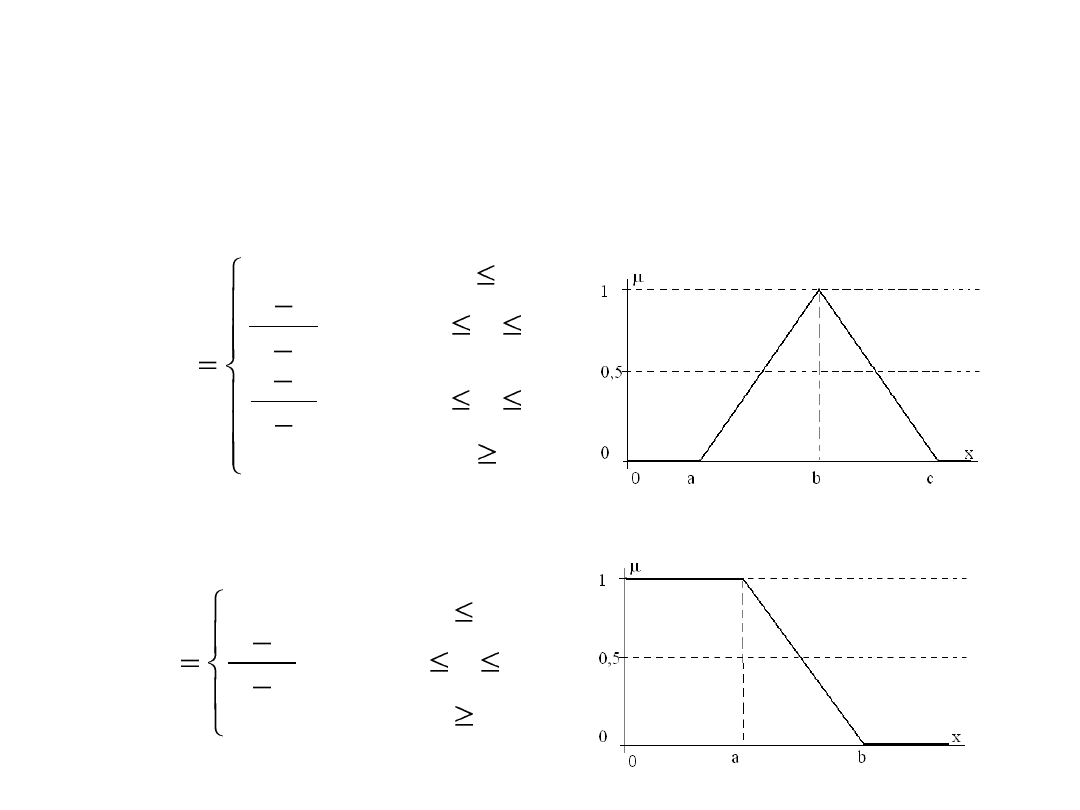
Standardowe postaci funkcji

przynależności

4. Funkcja przynależności klasy t:

5. Funkcja przynależności klasy L:

c

x

c

x

b

b

c

x

c

b

x

a

a

b

a

x

a

x

c

b

a

x

t

dla

0

dla

dla

dla

0

)

,

,

;

(

b

x

b

x

a

a

b

x

b

a

x

b

a

x

L

dla

0

dla

dla

1

)

,

;

(

Standardowe postaci funkcji

przynależności

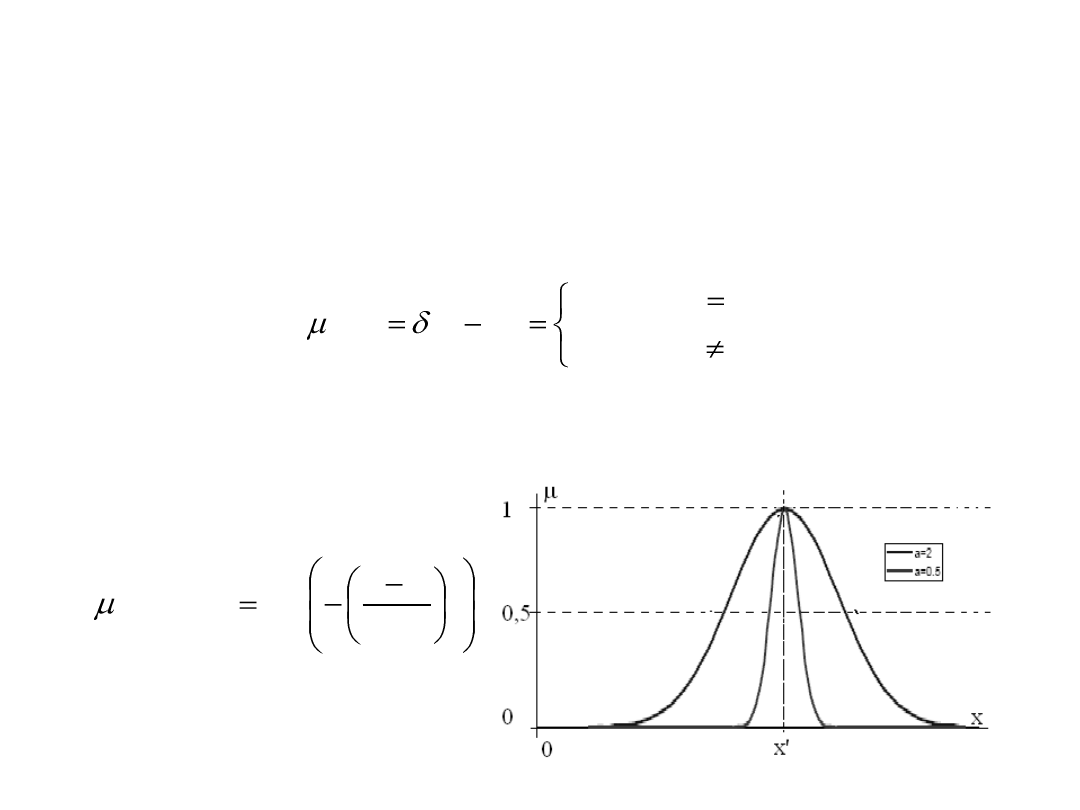
6. Funkcja przynależności klasy singleton:

'

dla

0

'

dla

1

)

'

(

)

(

x

x

x

x

x

x

x

A

7. Funkcja przynależności Gaussa:

2

'

exp

)

,

'

,

(

a

x

x

a

x

x

A

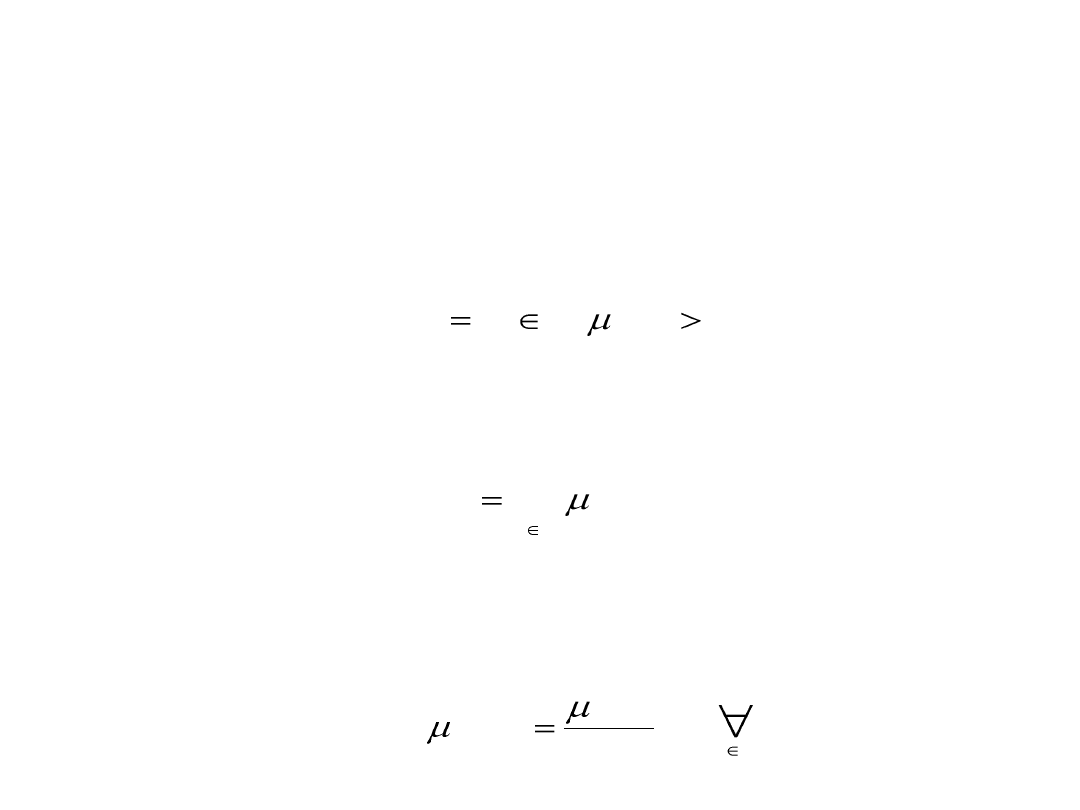
Definicje

Definicja

nośnika:

Zbiór elementów przestrzeni X, dla których μ

A

(x) > 0 nazywamy

nośnikiem zbioru rozmytego A i oznaczamy supp A (ang. support).
Zapisujemy

}

0

)

(

;

{

A

supp

x

x

A

X

Definicja

wysokości:

Wysokość zbioru rozmytego A oznaczamy h(A) i określamy jako

)

(

sup

)

A

(

x

h

A

A

x

Definicja zbioru rozmytego normalnego:
Zbiór rozmyty A nazywamy normalnym wtedy i tylko wtedy, gdy h(A) = 1.
Jeżeli zbiór rozmyty A nie jest normalny, to można go znormalizować za
pomocą przekształcenia

)

A

(

)

(

)

(

h

x

x

A

A

N

X

x

Definicje

Definicja zbioru rozmytego pustego:
Zbiór rozmyty A jest pusty, co zapisujemy A = Ø, wtedy i tylko wtedy, gdy
μ

A

(x

) = 0 dla każdego x

∈ X.

Definicja zawierania się zbiorów rozmytych:
Zbiór rozmyty A zawiera się w zbiorze rozmytym B, co zapisujemy A

⊂

B, wtedy i tylko wtedy, gdy

μ

A

(x)

≤ μ

B

(x

) dla każdego x

∈ X.

Definicja równości zbiorów rozmytych:
Zbiór rozmyty A jest równy zbiorowi rozmytemu B, co zapisujemy A = B,
wtedy i tylko wtedy, gdy

μ

A

(x) =

μ

B

(x

) dla każdego x

∈ X.

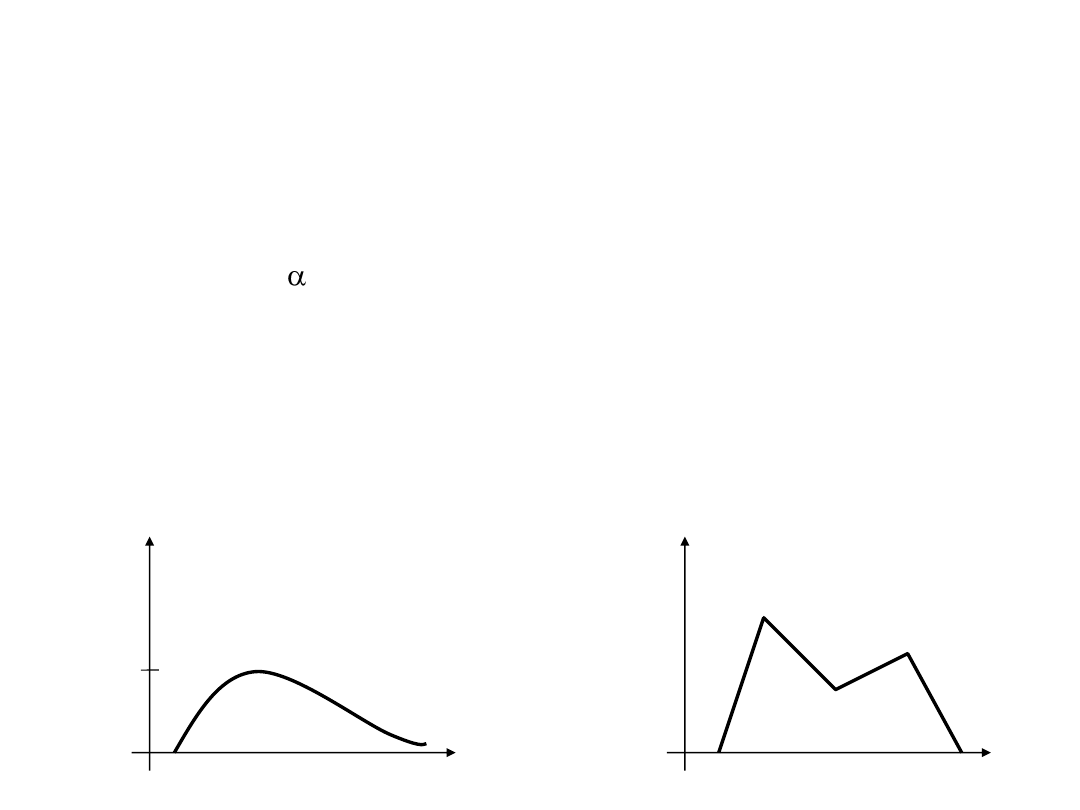
Właściwości zbiorów rozmytych

• Dla zbiorów rozmytych wprowadzono również pojęcia:

– Przekroju ,

– Wypukłości zbioru rozmytego (funkcji przynależności),

– Wklęsłości zbioru rozmytego.

x

μ

A

(x)

1

x

μ

A

(x)

Zbiór rozmyty wklęsły:

Zbiór rozmyty wypukły:

Operacje na zbiorach rozmytych

• Podstawowymi operacjami na zbiorach

rozmytych są:

– negacja (NOT)
– suma (OR)
– iloczyn (AND)

• W przypadku sumy i iloczynu logicznego mamy

parę możliwości uzyskania wyników. Do

obliczania ich zaproponowanych zostało kilka

wzorów matematycznych, różnych dla każdej z
tych operacji.

Definicja normy S

Funkcję dwóch zmiennych S

nazywamy S-

normą, jeżeli:



funkcja S

jest nierosnąca względem obu argumentów

S(a, c)

≤ S(b, d) dla a ≤ b c ≤ d



funkcja S

spełnia warunek przemienności

S(a, b) = S(b, a)



funkcja S

spełnia warunek łączności

S(S(a, b), c) = S(a, S(b, c))



funkcja S

spełnia warunki brzegowe

S(a, 0) = a, S(a, 1) = 1

gdzie a, b, c, d

∈ [0,1].

]

1

,

0

[

]

1

,

0

[

]

1

,

0

[

:

S

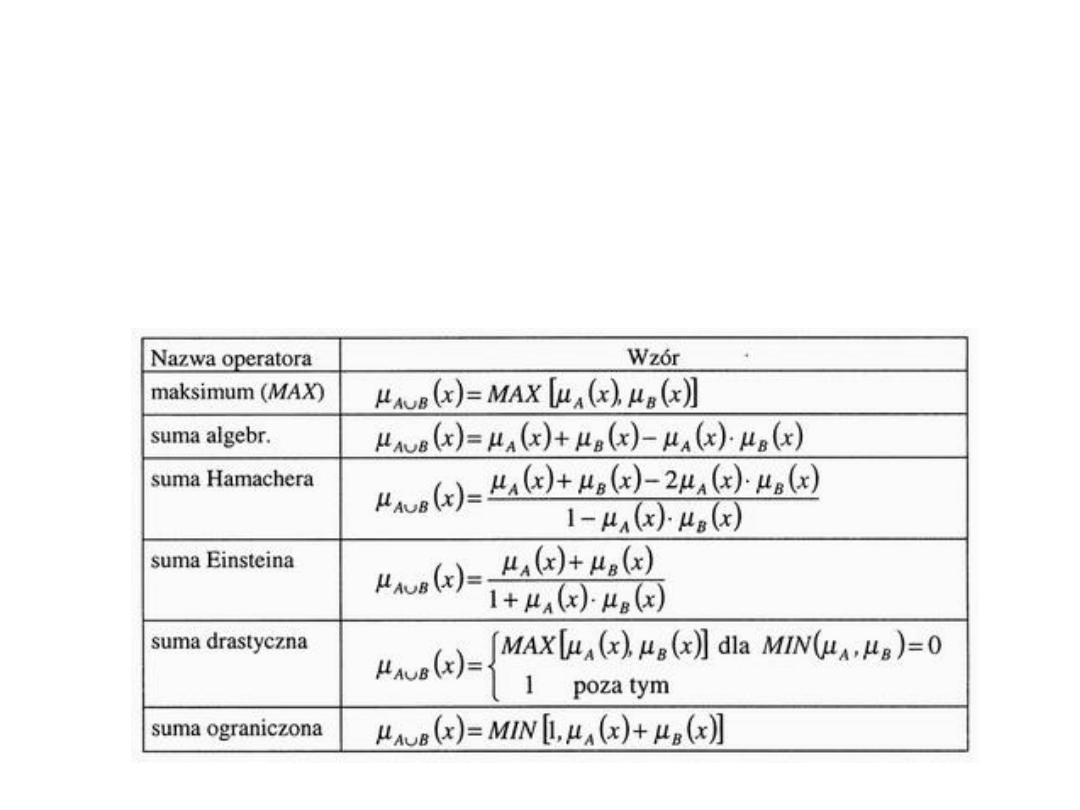
Suma logiczna zbiorów rozmytych

• Dla sumy logicznej zbiorów rozmytych stosowane

operatory S-normy,

Definicja normy T

Funkcję dwóch zmiennych T

nazywamy T-

normą, jeżeli:



funkcja T

jest nierosnąca względem obu argumentów

T(a, c)

≤ T(b, d) dla a ≤ b c ≤ d



funkcja T

spełnia warunek przemienności

T(a, b) = T(b, a)



funkcja T

spełnia warunek łączności

T(T(a, b), c) = T(a, T(b, c))



funkcja T

spełnia warunki brzegowe

T(a, 0) = 0, T(a, 1) = a

gdzie a, b, c, d

∈ [0,1].

]

1

,

0

[

]

1

,

0

[

]

1

,

0

[

:

T

Funkcja S

nosi także nazwę ko-normy lub normy dualnej względem

T-normy.

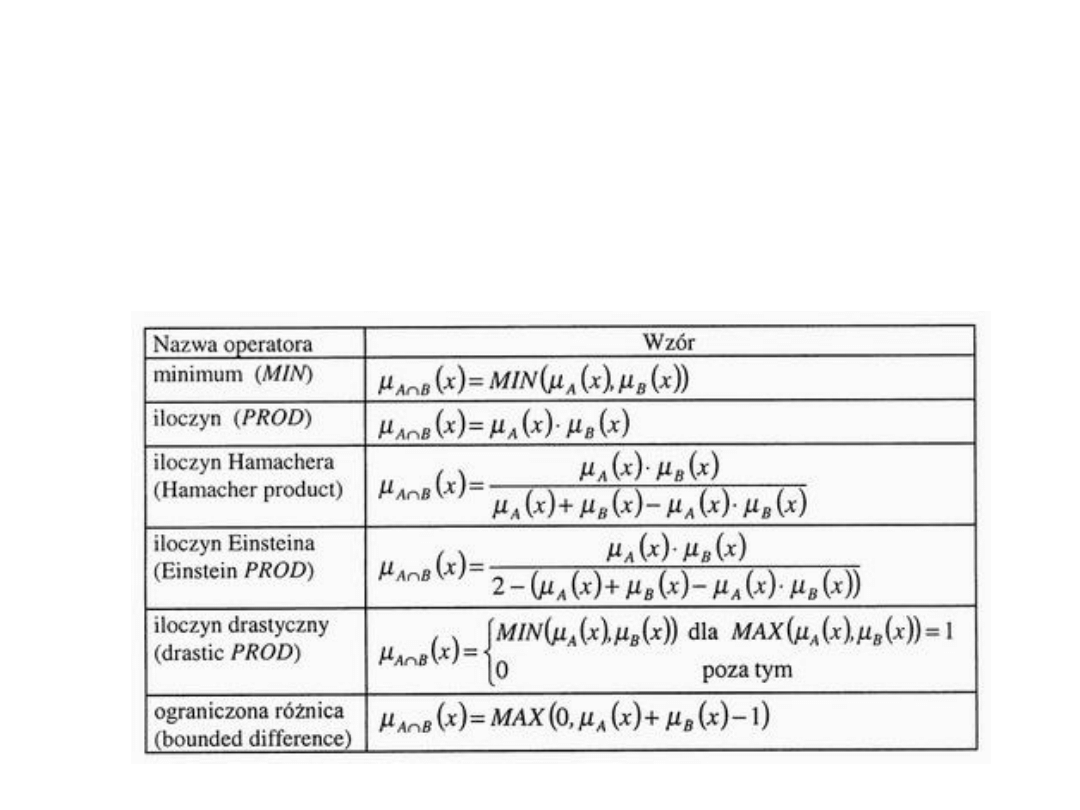
Iloczyn logiczny zbiorów rozmytych

• Dla iloczynu logicznego zbiorów rozmytych

stosowane są operatory T-normy

Negacja zbiorów rozmytych

• Negacja zbiorów rozmytych jest natomiast bardzo

zbliżona do negacji zwykłych zbiorów.

• W odróżnieniu od powyższych operacji istnieje tylko

jeden sposób otrzymywania wyniku.

• Aby go obliczyć wystarczy odjąć stopień

przynależności danego elementu od jedności.

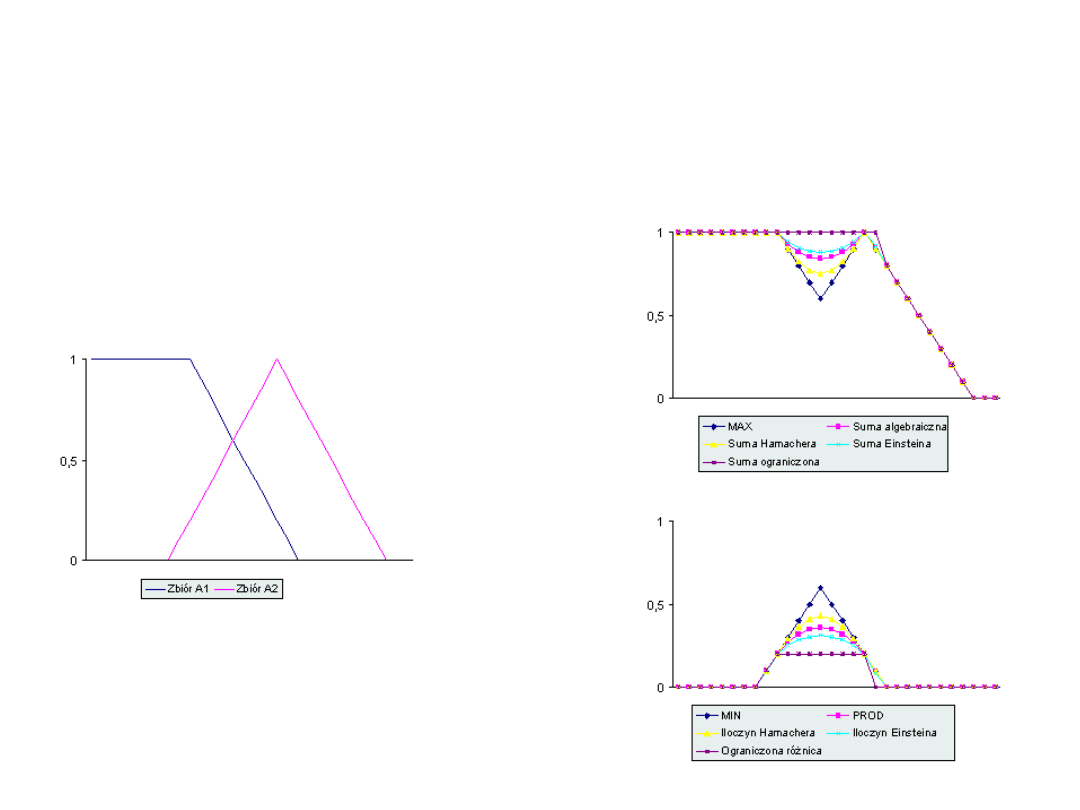
Ilustracje obliczeń sumy i iloczynu

logicznego

suma

iloczyn

Stosowanie operatorów

T-normy MIN, i S-normy MAX.

NEGACJA:
Jeżeli mamy dany podzbiór rozmyty A zbioru Y, to jego

negacją jest podzbiór Ā=Y-A. Czyli dla każdego y

należącego do A mamy Ā(y)=1-A(y)

Jeżeli A={ a/1;

b/0,4;

c/0,8;

d/0,2;

e/0 }

to Ā={ a/0;

b/0,6;

c/0,2;

d/0,8;

e/1 }

Przykład

SUMA

Jeżeli mamy dane podzbiory rozmyte A i B zbioru Y, to ich

sumą jest podzbiór C=A or B. Czyli dla każdego y
należącego do Y mamy C(y)=Max[A(y), B(y)]

A={

a/1;

b/0,3;

c/0,8;

d/0;

e/0,1 }

B={

a/0,6;

b/0,4;

c/0,9;

d/0,5;

e/0,7 }

C={

a/1;

b/0,4;

c/0,9;

d/0,5;

e/0,7 }

Przykład

ILOCZYN

Jeżeli mamy dane podzbiory rozmyte A i B zbioru Y, to ich

iloczynem jest podzbiór C=A and B. Czyli dla każdego y
należącego do Y mamy C(y)=Min[A(y), B(y)]

Przykład

A={

a/1;

b/0,3;

c/0,8;

d/0;

e/0,1 }

B={

a/0,6;

b/0,4;

c/0,9;

d/0,5;

e/0,7 }

C={

a/0,6;

b/0,3;

c/0,8;

d/0;

e/0,1 }

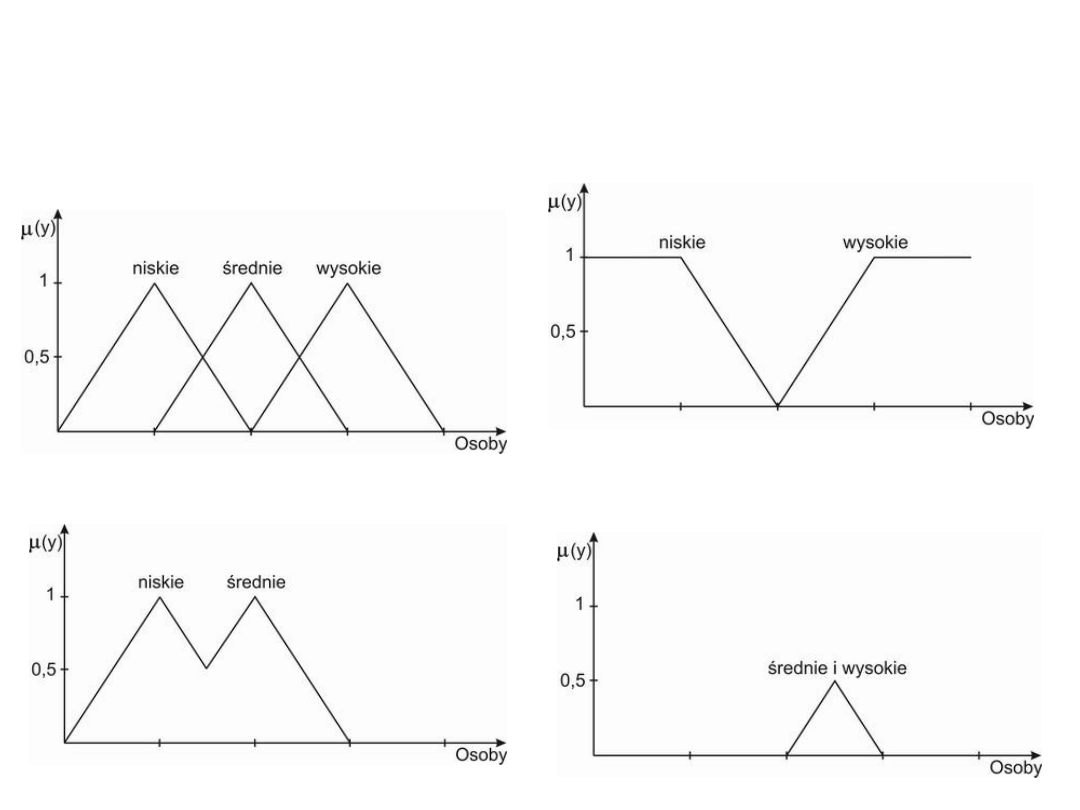
Przykład

trzy podzbiory rozmyte
odpowiadające za wzrost

zbiór osób nie średnich

zbiór osób niskich lub średnich

zbiór osób zarówno średnich jaki i
wysokich

Przykład z dwoma zmiennymi

Z(y) = ( 0  wzrost < 170 cm
[Z(y) – 170]/20  170 cm > wzrost < 190 cm
1  wzrost > 190 cm )

V(y) = ( 0  wiek < 40 lat
[V(y) – 40]/20  40 lat >= wiek < 60 lat
1  wiek >= 60 lat )

Przykład z dwoma zmiennymi

Utwórzmy następujące zbiory rozmyte:

- zbiór ludzi wysokich lub starych

A = Z

LUB

V

- zbiór ludzi wysokich i starych

B = Z

I

V

Osoba Y

Wzrost

Wiek

Stopień

Przynależności

do Z

Stopień

Przynależności

do V

A

B

Darek

193

18

1

0

1

0

Kamil

139

53

0

0,82

0,82

0

Zbyszek

128

25

0

0,1

0,1

0

Sławek

182

74

0,6

1

1

0,6

Karol

175

35

0,25

0,36

0,36

0,25

Mariusz

179

48

0,45

0,69

0,69

0,45

Jacek

187

27

0,85

0,2

0,85

0,2

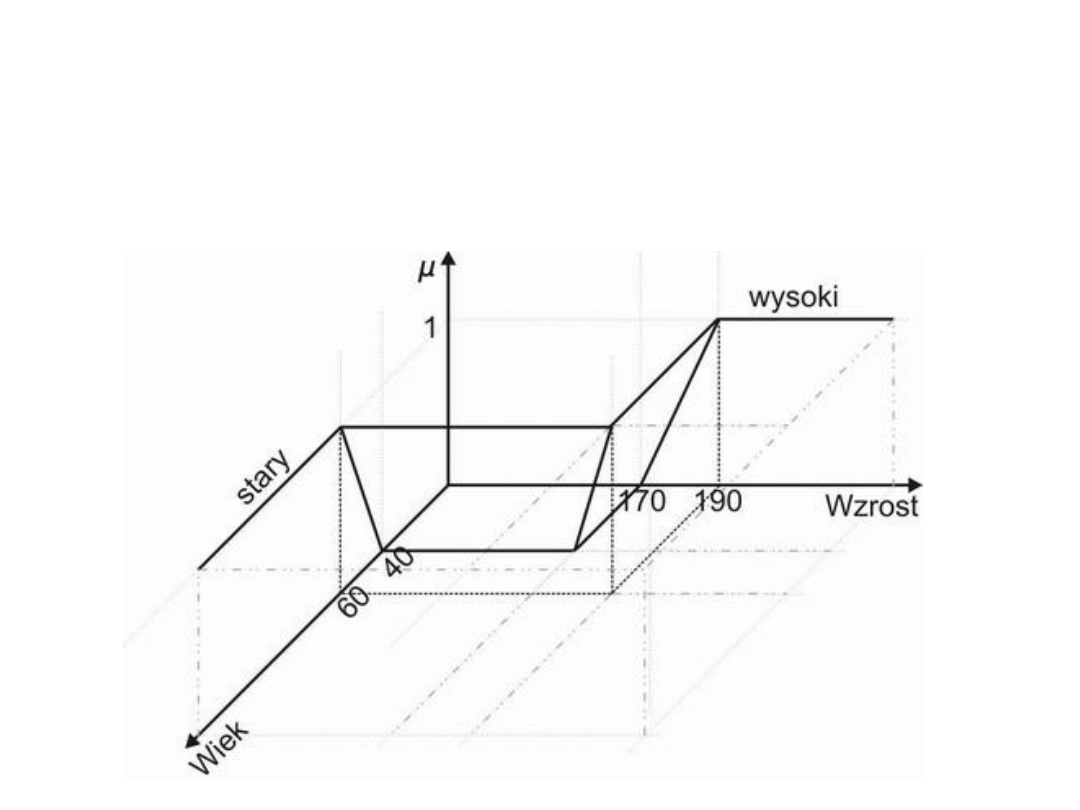
Interpretacja geometryczna

Graficzne prezentacja operacji (osoby_stare) LUB (osoby_wysokie):

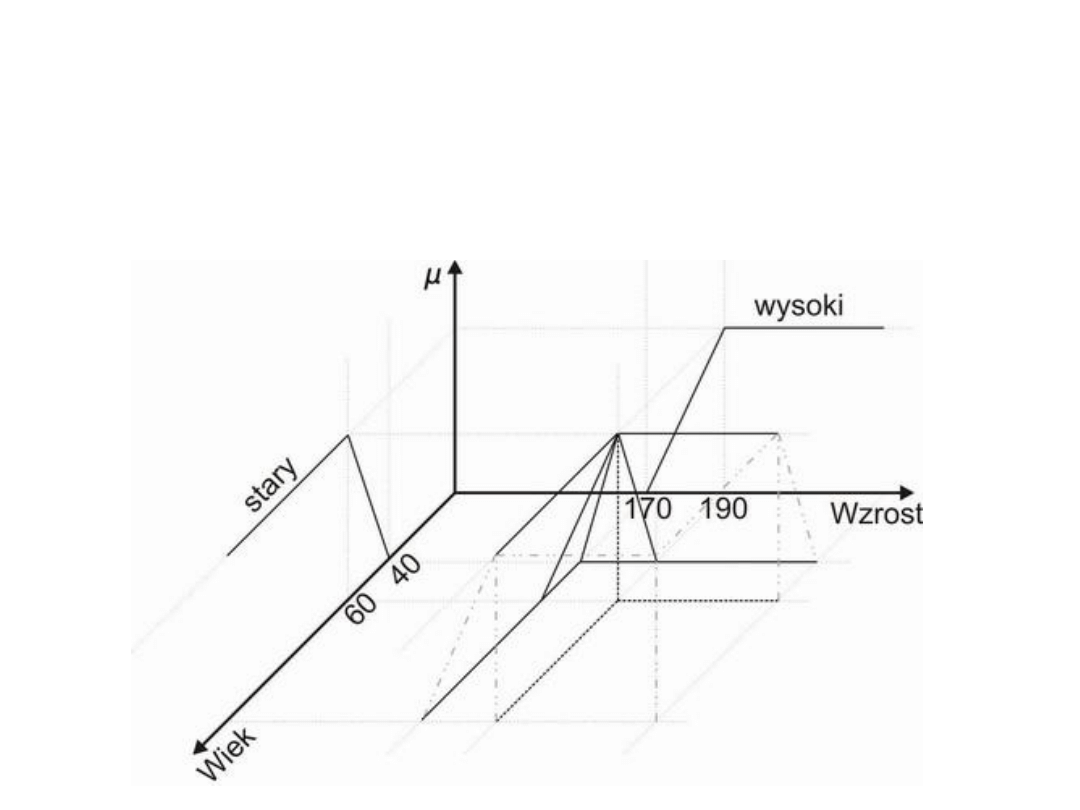
Interpretacja geometryczna

Graficzne prezentacja operacji (osoby_stare) I (osoby_wysokie):

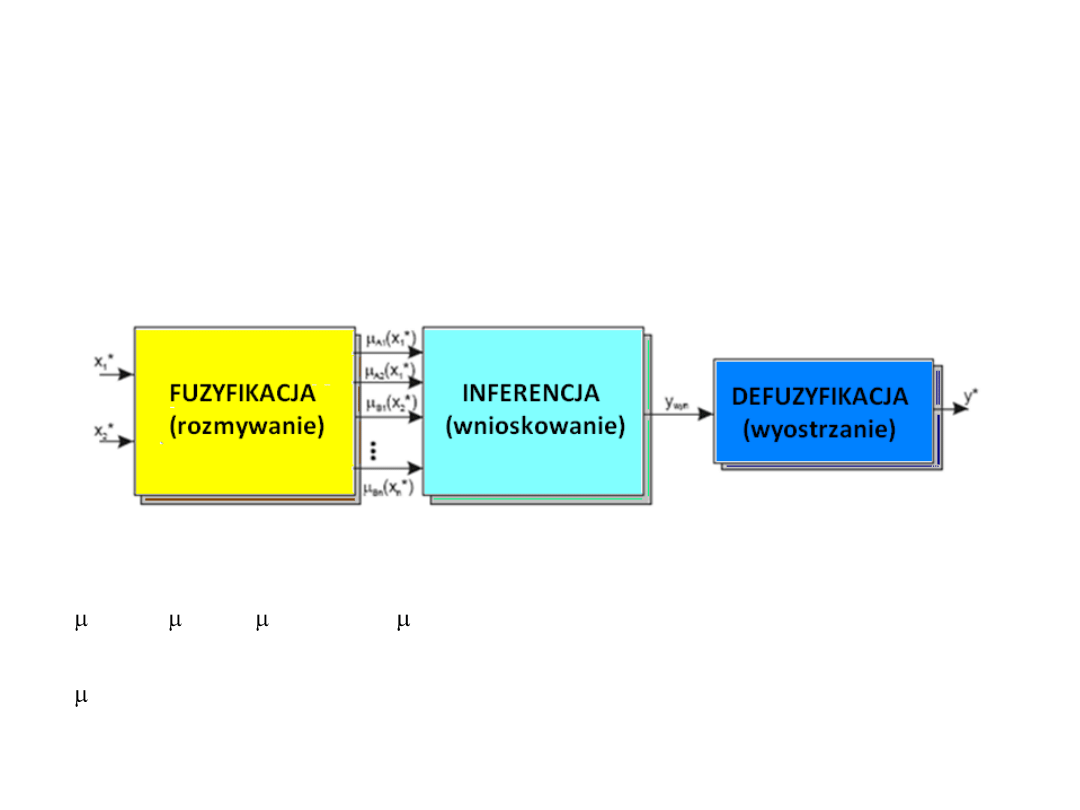
Regulatory rozmyte

Struktura przykładowego regulatora rozmytego o 2

wejściach i jednym wyjściu

X

1

*

, X

2

*

-

ostre wartości sygnałów wejściowych

A1

(X

1

*

),

A2

(X

1

*

)

B1

(X

2

*

), ... ,

Bn

(X

2

*

)

– stopnie przynależności ostrych wartości

wejściowych do odpowiednich wejściowych zbiorów rozmytych

wyn

(Y)

– wynikowa funkcja przynależności wyjścia

Y

*

-

ostra wartość sygnału wyjściowego

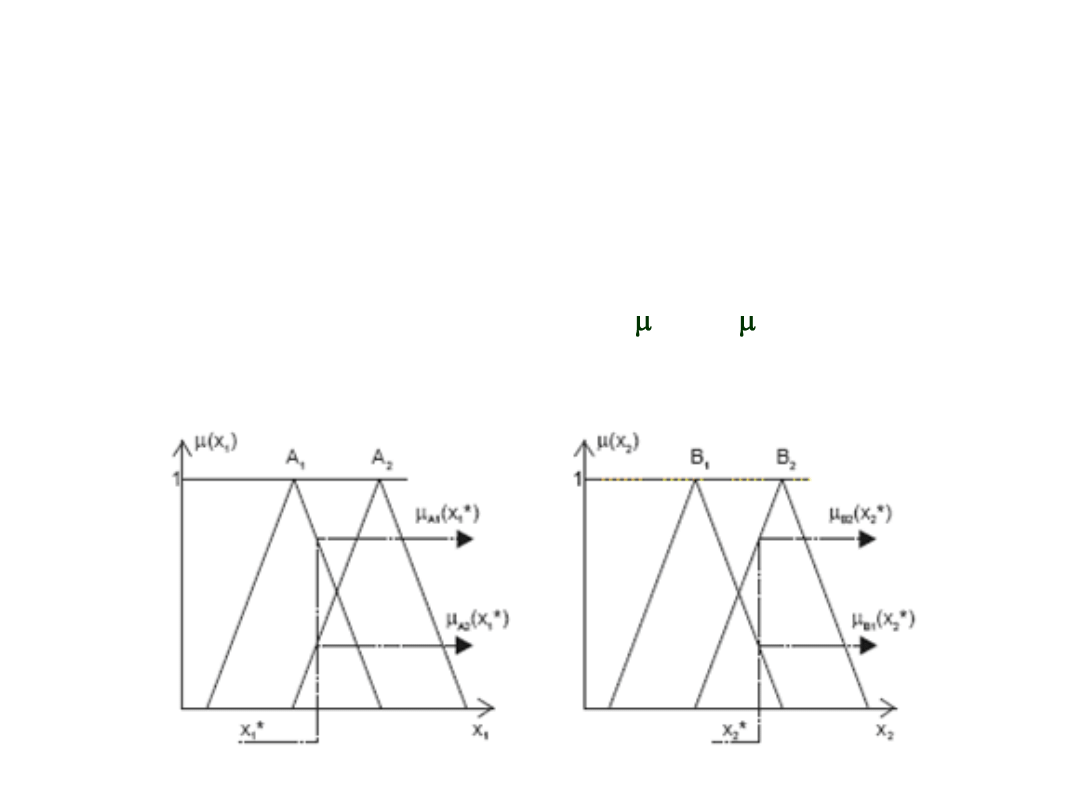
Fuzyfikacja

W bloku

FUZYFIKACJA

przeprowadzana jest operacja rozmywania czyli

obliczania stopnia przynależności do poszczególnych zbiorów rozmytych A

i

, B

j

wejść. Aby operację tę przeprowadzić blok

FUZYFIKACJA

musi posiadać

dokładnie zdefiniowane funkcje przynależności:

A

i

(x

1

)

,

B

j

(x

2

)

do zbiorów

rozmytych poszczególnych wejść.

Fuzyfikacja c.d.

Obliczone i podane na wyjściu bloku FUZYFIKACJA

wartości stopni przynależności A

i

(x

1

*

), B

j

(x

2

*

) informują o

tym, jak wysoka jest przynależność ostrych wartości wejść

x

1

*

, x

2

*

do poszczególnych zbiorów rozmytych wejść, tzn. na

przykład jak bardzo wartości te są małe (A

1

, B

1

) lub duże (A

2

,

B

2

).

Inferencja

Blok INFERENCJA oblicza na podstawie wejściowych stopni
przynależności A

i

(x

1

), B

j

(x

2

) tzw. wynikową funkcję

przynależności

wyn

(y) wyjścia regulatora. Funkcja ta ma często

złożony kształt, a jej obliczanie odbywa się w drodze tzw.
Inferencji (wnioskowania), która może być matematycznie
zrealizowana na wiele sposobów. Aby przeprowadzić obliczenia
inferencyjne blok INFERENCJA musi zawierać następujące,
ściśle zdefiniowane elementy:

• bazę reguł,
• mechanizm inferencyjny,
• funkcje przynależności wyjścia y modelu.

Inferencja c.d.

Baza reguł zawiera reguły logiczne określające zależności
przyczynowo-skutkowe istniejące w systemie pomiędzy
zbiorami rozmytymi wejść i wyjść.

Reguła:

JEŚLI

przesłanki

TO

konkluzja

Przesłanki mają zwykle postać funkcji logicznej.

Przykładowa baza reguł może mieć następującą postać:

reguła 1:

JEŚLI

(X

1

A

1

)

I

(X

2

B

1

)

TO

(Y C

1

)

reguła 2:

JEŚLI

(X

1

A

2

)

I

(X

2

B

1

)

TO

(Y C

2

)

reguła 1:

JEŚLI

(X

1

A

1

)

LUB

(X

2

B

2

)

TO

(Y C

2

)

przesłanki

operator

konkluzja

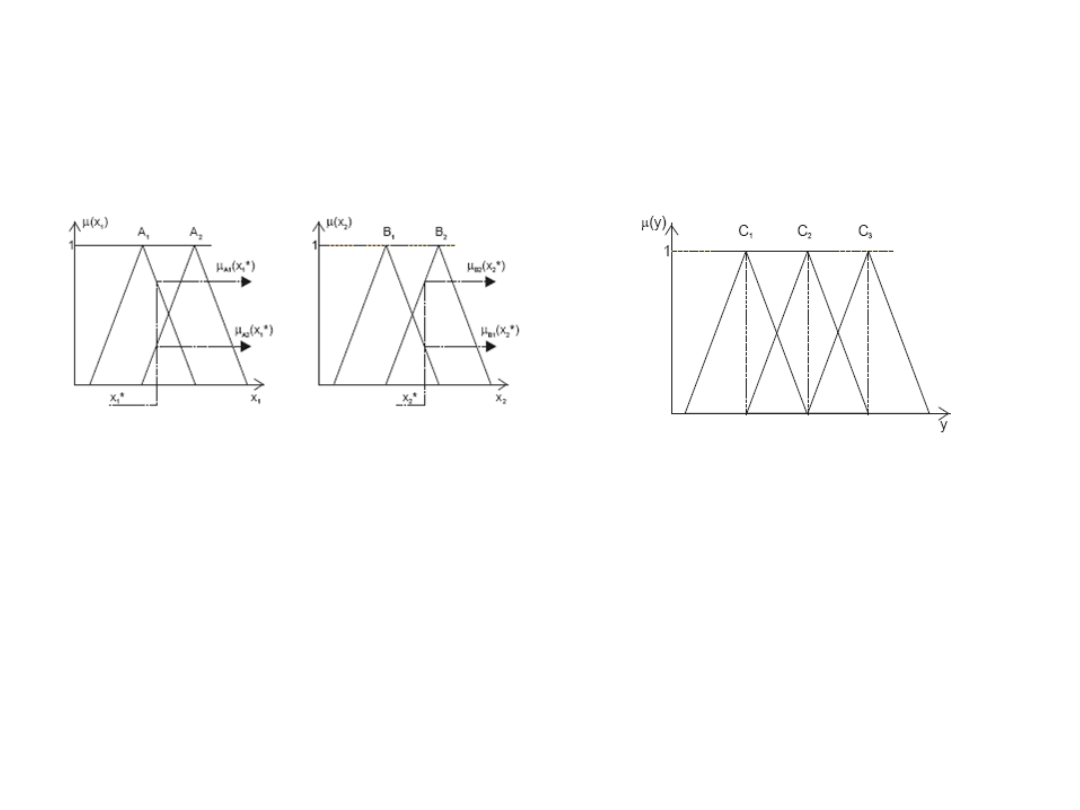
Inferencja - przykład

Mechanizm inferencyjny realizuje zadanie bloku INFERENCJA, tzn.

obliczanie wynikowej funkcji przynależności mwyn(y). Składa się on z

następujących części:

– Części, która na podstawie stopni spełnienia przesłanek poszczególnych reguł z

uwzględnieniem wykorzystywanych w nich operatorów (I albo LUB) oblicza

stopień aktywizacji konkluzji reguł.

– Części określającej wynikową postać funkcji przynależności wyjścia mwyn(y)

na podstawie stopni aktywizacji konkluzji poszczególnych reguł.

Przykładowe zbiory rozmyte wejść (A1
– mały, A2 – duży)

zbiory rozmyte wyjścia (C1 –
mały, C2 – średni, C3 – duży)

DEFUZYFIKACJA

Mając daną funkcję przynależności wyjścia mwyn(y) regulator
może obliczyć ostrą wartość wyjściową y*. Operację tę realizuje
blok DEFUZYFIKACJA.

Przez defuzyfikację zbioru rozmytego scharakteryzowanego
wyjściową funkcją przynależności

wyn

(y) uzyskaną w wyniku

inferencji należy rozumieć operację określania ostrej wartości
y*, reprezentującej ten zbiór w sposób jak najbardziej
"sensowny".

DEFUZYFIKACJA c.d.

Oczywiście mogą istnieć różne kryteria oceny sensowności

reprezentanta y* zbioru rozmytego. O ilości tych kryteriów
świadczy ilość metod defuzyfikacji, z których najbardziej

znane to:

• Metoda środka maksimum (Middle of Maxima)
• Metoda pierwszego maksimum (First of Maxima)
• Metoda ostatniego maksimum (Last of Maxima)
• Metoda środka ciężkości (Center of Gravity)
• Metoda wysokości (Height Method)

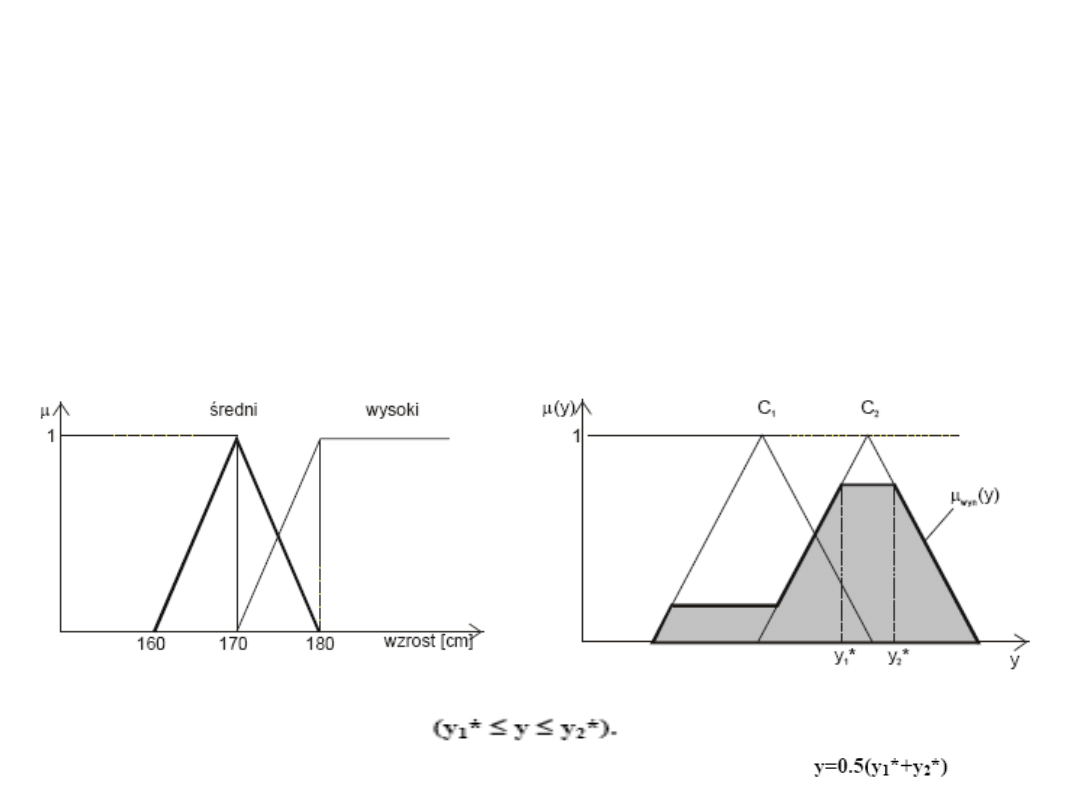
Metoda środka maksimum

Funkcję przynależności do zbioru rozmytego można rozumieć jako funkcję
informującą o podobieństwie poszczególnych elementów zbioru do elementu
najbardziej typowego dla tego zbioru.
Przykład

Wynikowa funkcja przynależności z nieskończoną ilością elementów y o najwyższej
przynależności

Metoda środka maksimum

• Zaletą metody jest prostota obliczeniowa ułatwiająca

zastosowanie tańszych elementów w układzie sterowania.
Prostota obliczeniowa okupiona jest jednak pewnymi wadami.

• Wadą metody jest to, że na wynik metody wpływa tylko ten

zbiór rozmyty, który jest najbardziej zaktywizowany. Zbiory
mniej zaktywizowane nie mają wpływu. Oznacza to również,
że na wynik w postaci ostrej wartości wyjściowej y* mają
wpływ tylko te reguły bazy reguł, które mają ten zbiór w
swojej konkluzji (często jest to tylko jedna reguła). W ten
sposób defuzyfikacja staje się "niedemokratyczna", bowiem
nie wszystkie reguły biorą udział w "głosowaniu".

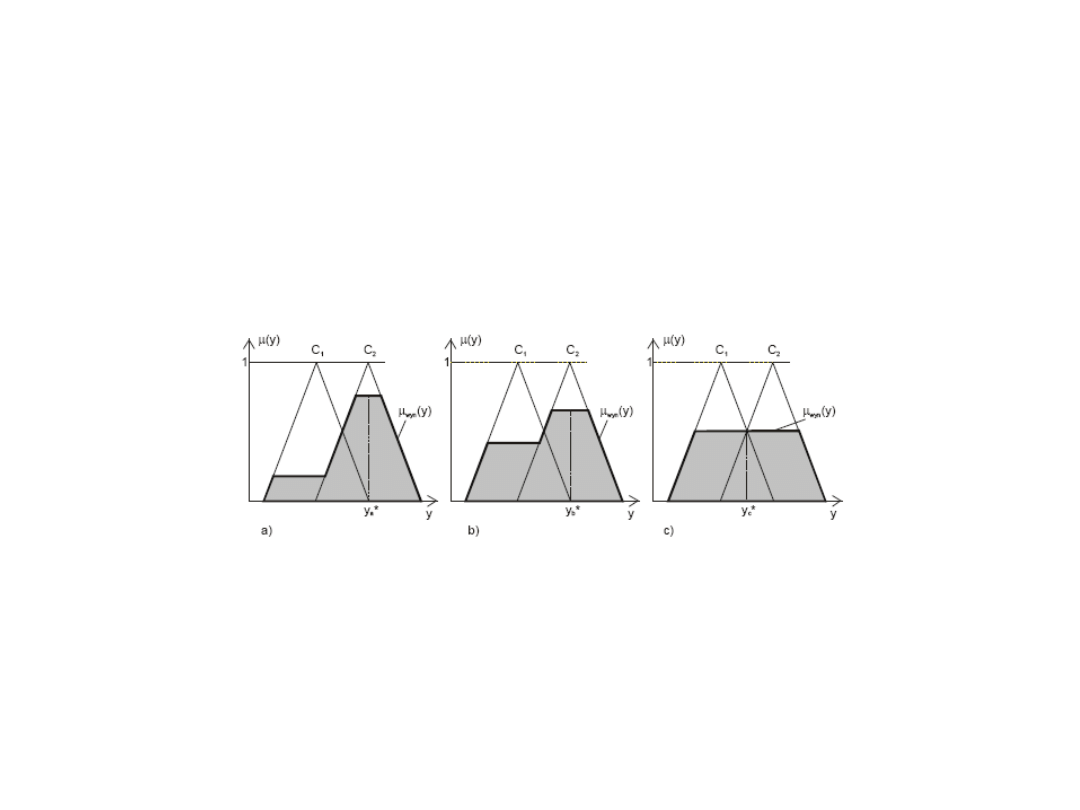
Metoda środka maksimum c.d.

Czułość metody defuzyfikacji i wynikająca stąd czułość regulatora rozmytego
można zdefiniować jako istnienie reakcji wyjścia Dy regulatora na zmiany stopni
aktywizacji zbiorów rozmytych konkluzji reguł.

Ilustracja wad metody środka maksimum (SM).

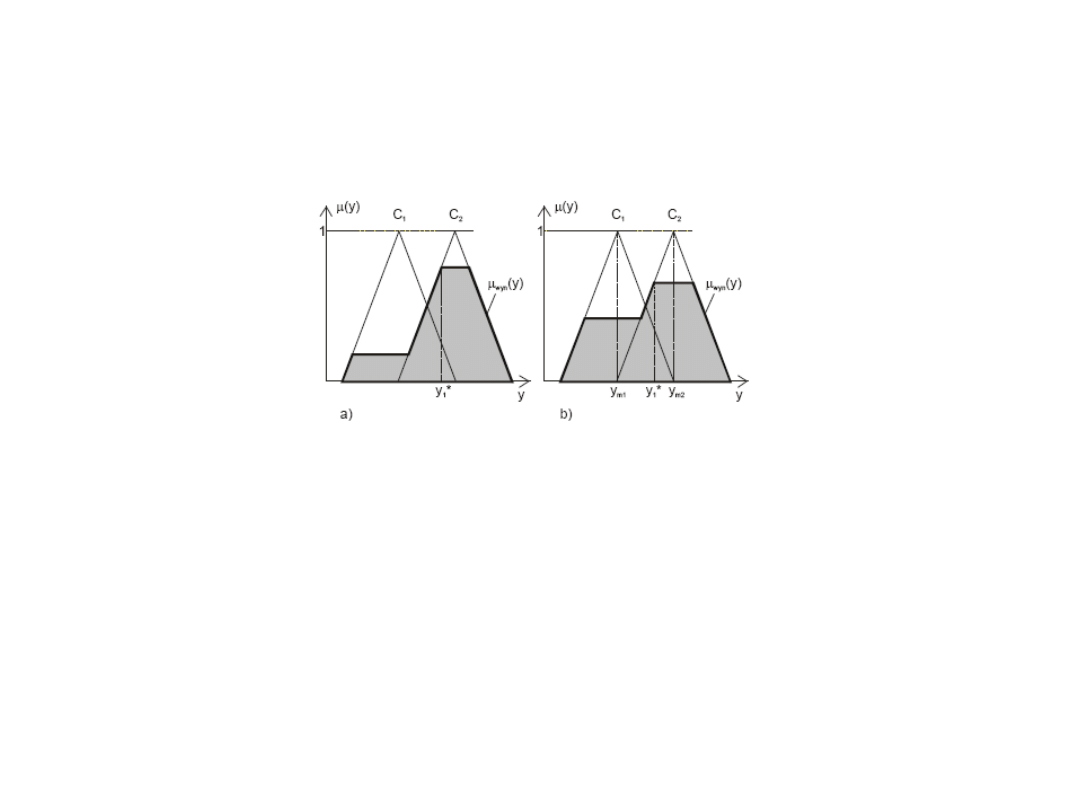
Metoda pierwszego maksimum

Zalety metody pierwszego maksimum:
· mały nakład obliczeniowy,
· większa (względem metody średniego maksimum) czułość na zmiany stopnia
aktywizacji konkluzji reguł.
Wady metody pierwszego maksimum:
· nieciągłość,
· uwzględnianie w procesie defuzyfikacji tylko jednego, najbardziej
zaktywizowanego
zbioru.

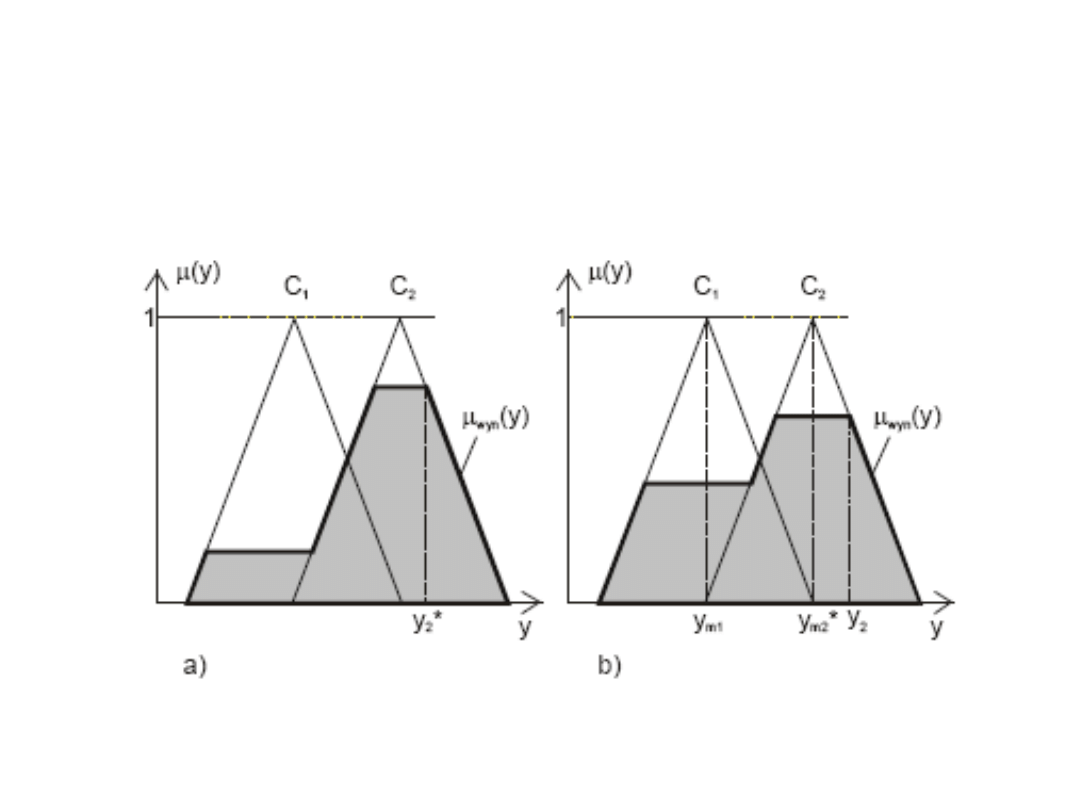
Metoda ostatniego maksimum

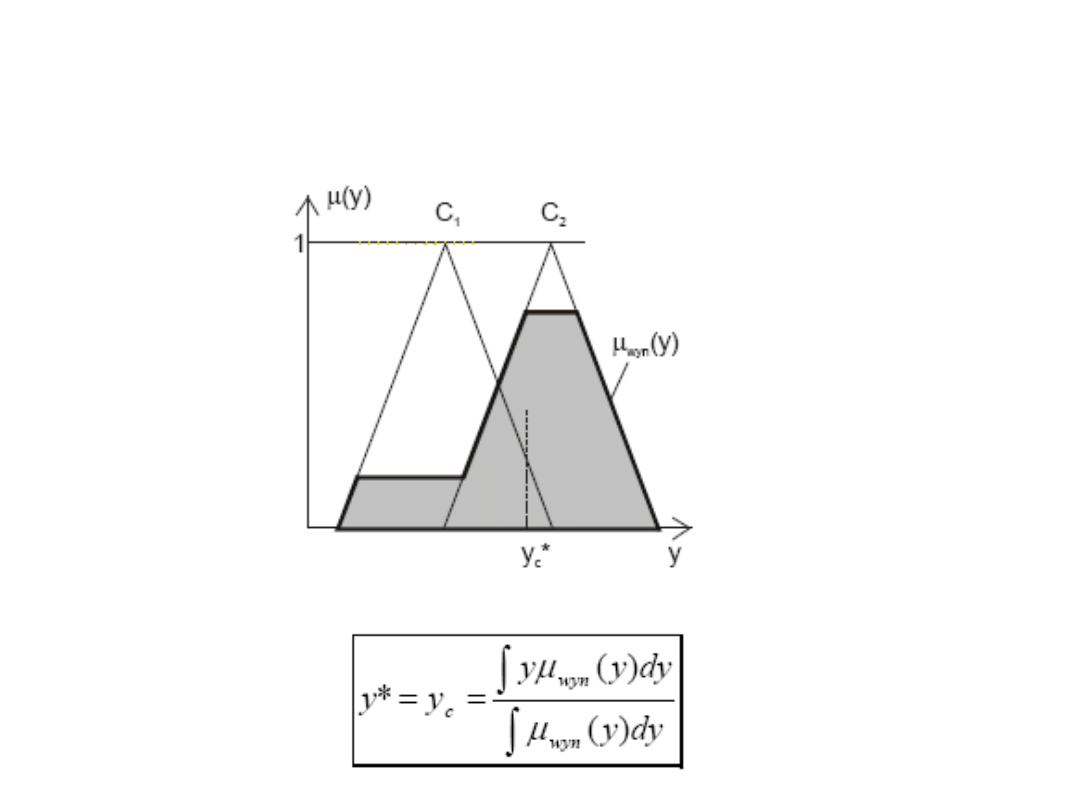
Metoda środka ciężkości

Uproszczenie metody

Uproszczenie polega na:

• zastąpieniu znaku całkowania z licznika wzoru na ostrą

wartość wyjściową znakiem sumy.

• przy sumowaniu uwzględniamy po kolei punkty

charakterystyczne wynikowej funkcji przynależności, tak jak
to przedstawia rysunek

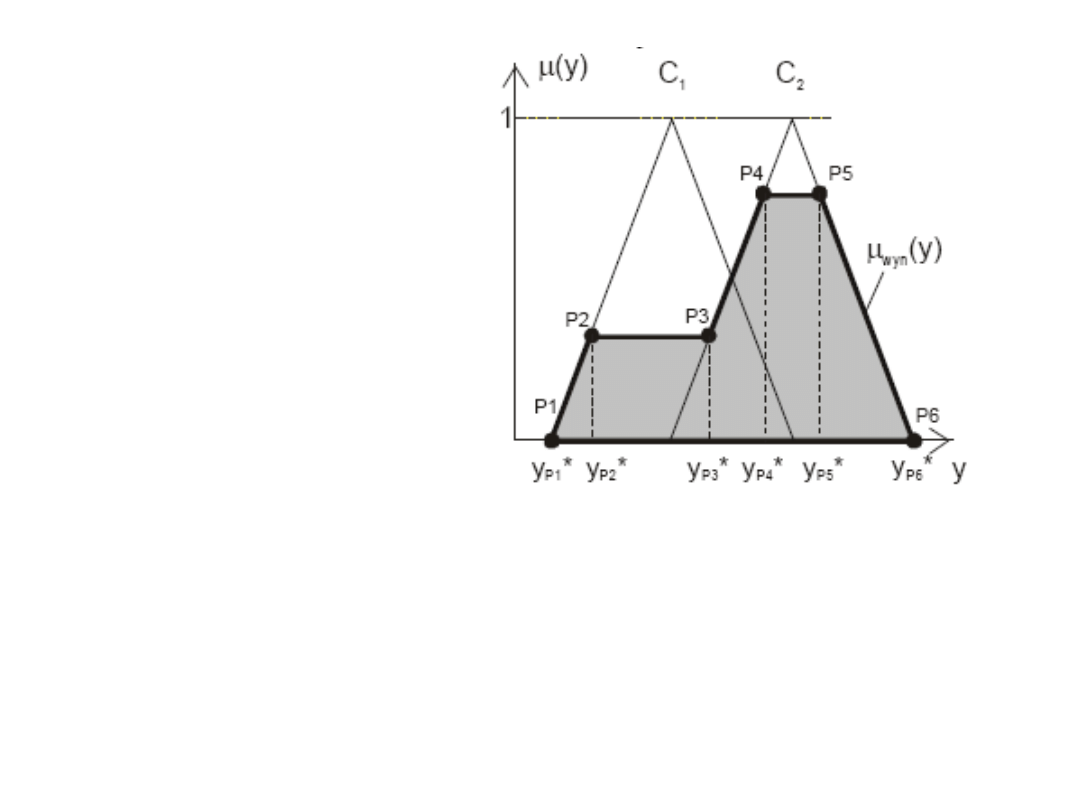
Zalety metody środka ciężkości:
Wszystkie zaktywizowane funkcje przynależności konkluzji
(wszystkie aktywne reguły) biorą udział w procesie defuzyfikacji.
Jest ona "demokratyczna". Gwarantuje to większą niż w
przypadku poprzednio przedstawionych reguł czułość regulatora
rozmytego na zmiany jego wejść.

Metoda środka
ciężkości

Metoda środka ciężkości

Wady metody środka ciężkości
· Duża ilość skomplikowanych obliczeń, co jest związane z
całkowaniem powierzchni o nieregularnym kształcie. Istnieje
kilka metod upraszczania obliczeń dla metody środka
ciężkości, jak na przykład użycie prostokątnych funkcji
przynależności.
· Zawężenie zakresu defuzyfikacji

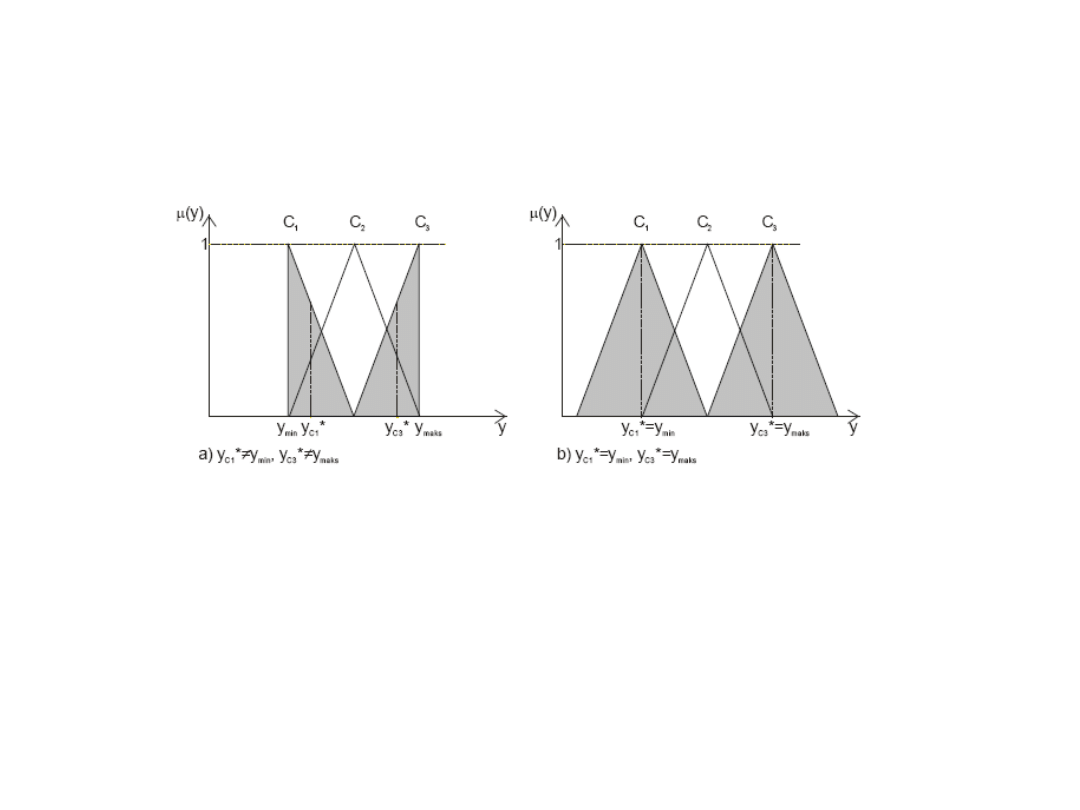
Metoda środka ciężkości -

modyfikacja

Wyjście y modelu (regulatora) rozmytego nie może osiągnąć minimalnej
(maksymalnej) wartości możliwego zakresu nastaw. Regulator nie mógłby więc
wygenerować większych sygnałów sterujących, co obniżyłoby jakość regulacji.

Wadę tę można usunąć przez rozszerzenie brzegowych zbiorów rozmytych (Patrz
rysunek b.), dzięki czemu współrzędne środka ciężkości tych zbiorów pokrywają
się z granicami zakresu działania ymin, ymax.

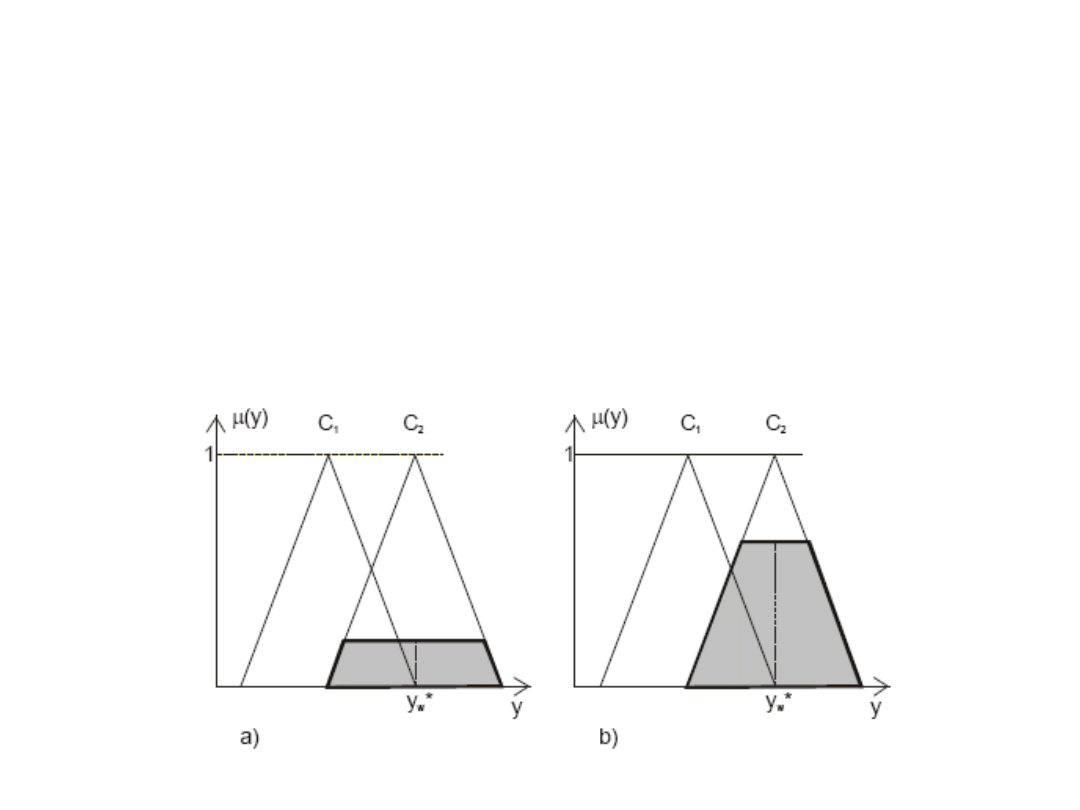
Metoda środka ciężkości – wady c.d.

• Nieczułość metody w przypadku aktywizacji tylko jednej funkcji przynależności

wyjścia. Jeżeli kilka reguł ma identyczną konkluzję lub aktywizowana jest tylko
jedna reguła (patrz rysunek), to mimo zmiany stopnia aktywizacji zbioru
wynikowego, współrzędna środka ciężkości yw nie zmienia się. Oznacza to
nieczułość metody na zmiany wejścia.

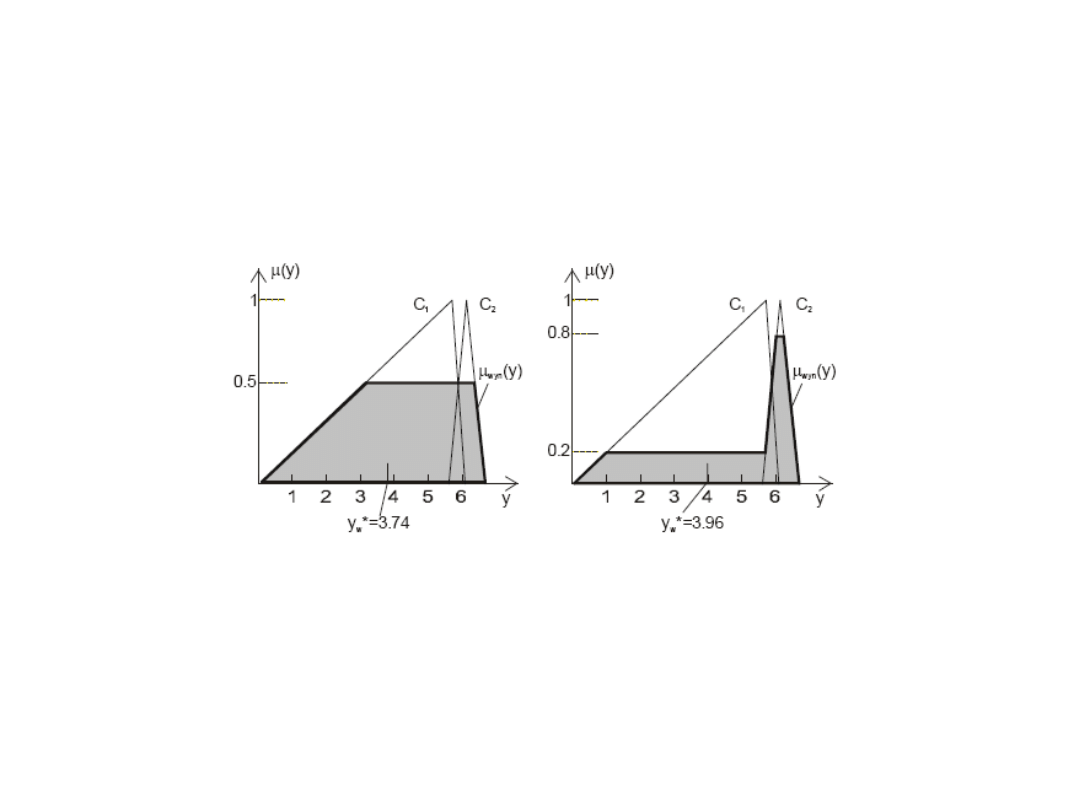
Metoda środka ciężkości – wady c.d.

Zmniejszenie czułości metody środka ciężkości przy dużym zróżnicowaniu
wielkości nośników zbiorów wyjściowych.

Duża zmiana stopnia aktywacji zbiorów składowych (ma: 0.5 – 0.2, mb: 0.5 – 0.8)
powoduje minimalne przesunięcie współrzędnej środka ciężkości (y*=yc: 3.74 –
3.96). Powodem tego jest duże zróżnicowanie powierzchni zbiorów składowych C1
i C2. Aby uzyskać większy wpływ zmiany stopni aktywizacji ma(y) i mb(y) na
zmianę wartości yc nośniki obu zbiorów powinny być podobne. Warunkiem
wysokiej czułości metody jest więc małe zróżnicowanie wielkości poszczególnych
zbiorów wynikowych reguł.

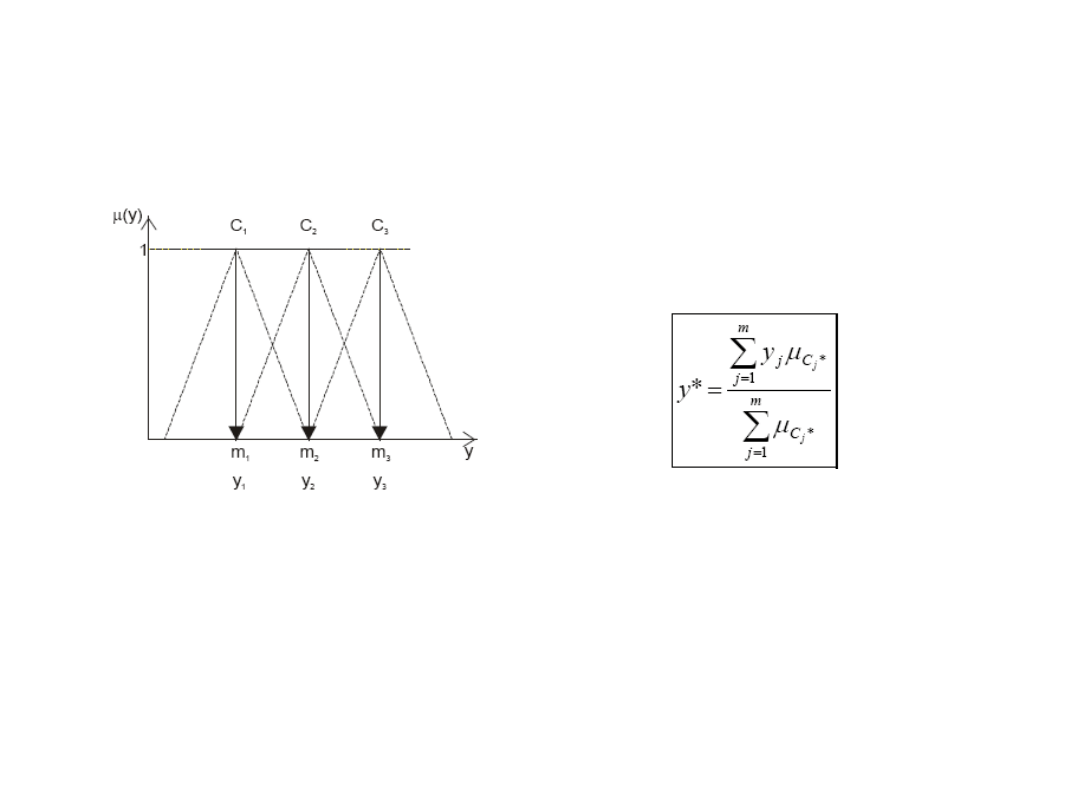
Metoda wysokości

Zastępowanie zbiorów rozmytych zbiorami jednoelementowymi.

Do obliczania wyjścia modelu y* (wyniku
defuzyfikacji) stosujemy wzór:

Zalety metody wysokości:
• znaczne zmniejszenie ilości obliczeń w porównaniu z metodą środka ciężkości,
• ciągłość,
• duża czułość.

Zastosowanie regulatora rozmytego

do sterowania suwnicą

przenoszącą kontenery

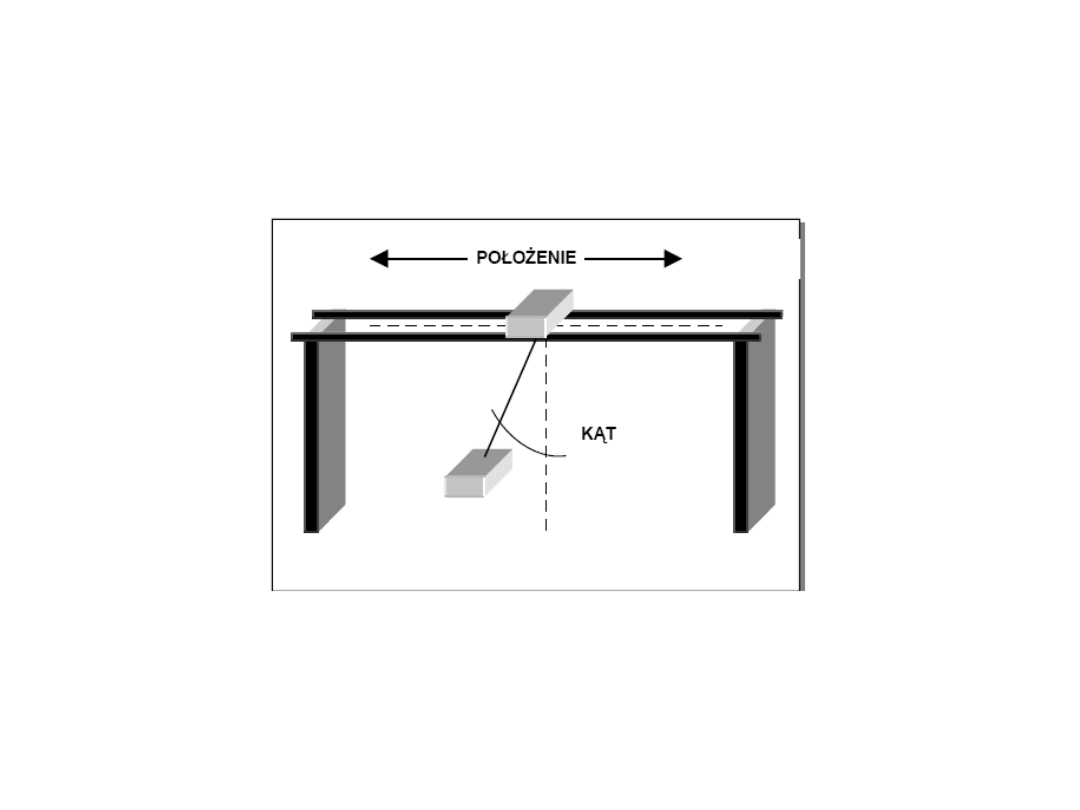
Model suwnicy

Sygnały wejściowe wykorzystywane w procesie sterowania to:
d

– odległość wózka z kontenerem od zadanej pozycji docelowej,

Q -

kąt wychylenia liny z kontenerem od pionu.

Fuzyfikacja

Jak zostało to opisane w części teoretycznej fuzyfikacja jest procesem rozmywania

ostrych wartości wejściowych czyli określania ich stopnia przynależności do
właściwych zbiorów rozmytych wejścia. W przypadku modelu suwnicy mamy do
czynienia z następującymi wejściowymi zbiorami rozmytymi:

• dla sygnału "odległość od miejsca docelowego" zbiory:

UJEMNA DUŻA,

UJEMNA MAŁA, ZERO, DODATNIA DUŻA, DODATNIA MAŁA

,

• dla sygnału "kąt wychylenia" zbiory:

UJEMNY DUŻY, UJEMNY MAŁY, ZERO,

DODATNI MAŁY, DODATNI DUŻY

.

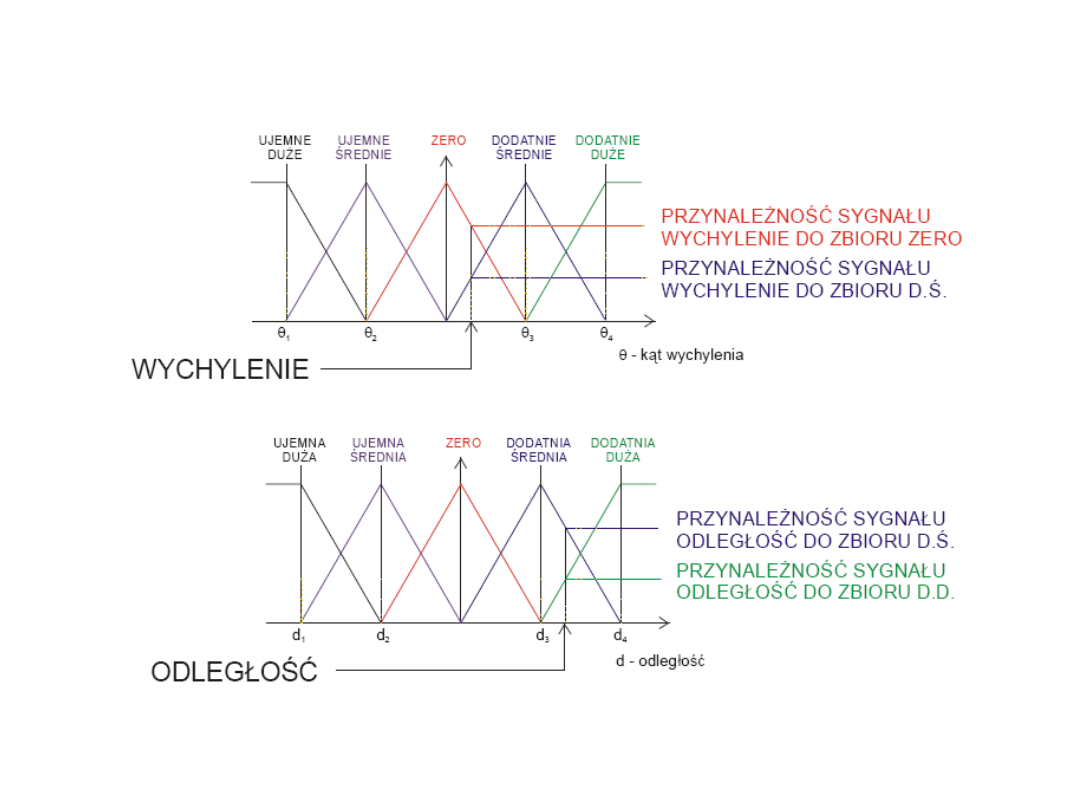
Inferencja

Zadaniem bloku INFERENCJA jest zbudowanie tzw. wynikowej funkcji
przynależności mwyn(y) wyjścia regulatora.

Właściwe sterownie mają nam zapewnić odpowiednio dobrane reguły:

R1: JEŚLI (d = duża) TO (P = duża)
R2: JEŚLI (d = mała) I (kąt = ujemny duży) TO (P = dodatnia średnia)
R3: JEŚLI (d = mała) I (kąt = ujemny mały LUB zero LUB dodatni mały) TO (P =

dodatnia średnia)

R4: JEŚLI (d = mała) I (kąt = dodatni duży) TO (P = ujemna średnia)
R5: JEŚLI (d = zero) I (kąt = dodatni duży LUB mały) TO (P = ujemna średnia)
R6: JEŚLI (d = zero) I (kąt = zero) TO (P = zero)
R7: JEŚLI (d = zero) I (kąt = ujemny mały) TO (P = dodatnia średnia)
R8: JEŚLI (d = zero) I (kąt = ujemny duży) TO (P = dodatnia duża)

gdzie: d

– odległość od celu, P – moc

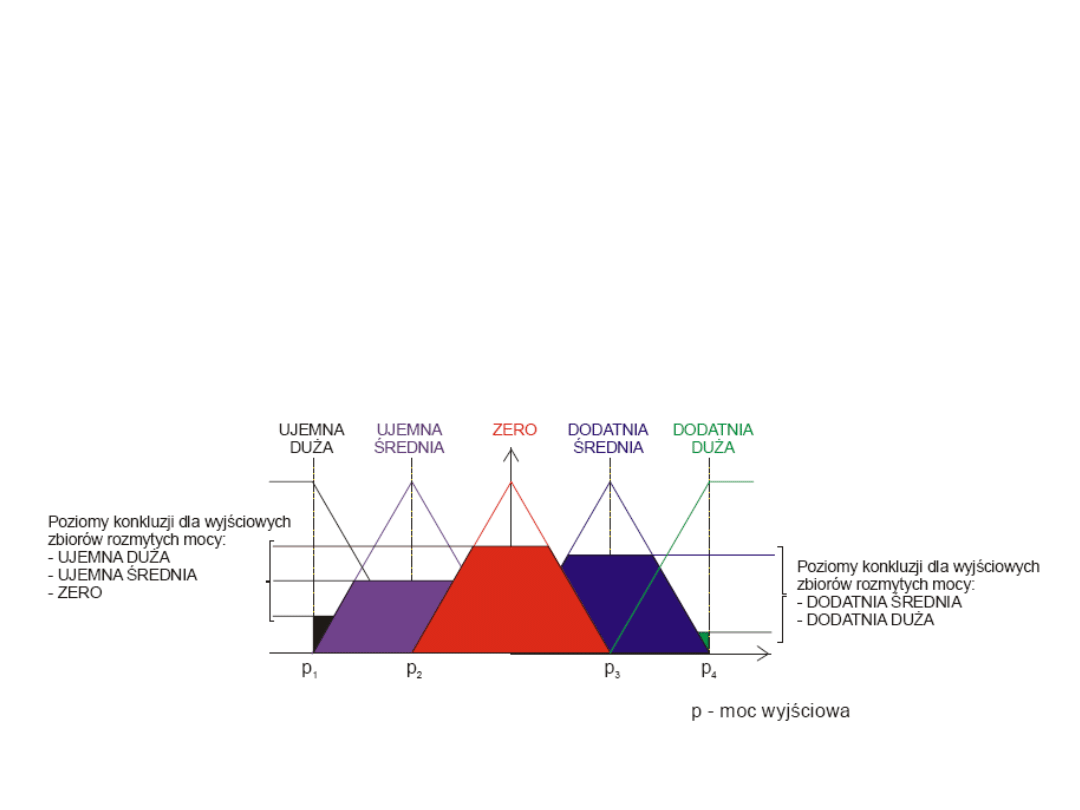
Ilustracja wyznaczania wynikowej funkcji

przynależności na podstawie wyliczonych

przez bazę reguł stopni aktywacji konkluzji

poszczególnych reguł oraz wyjściowych zbiorów

rozmytych.

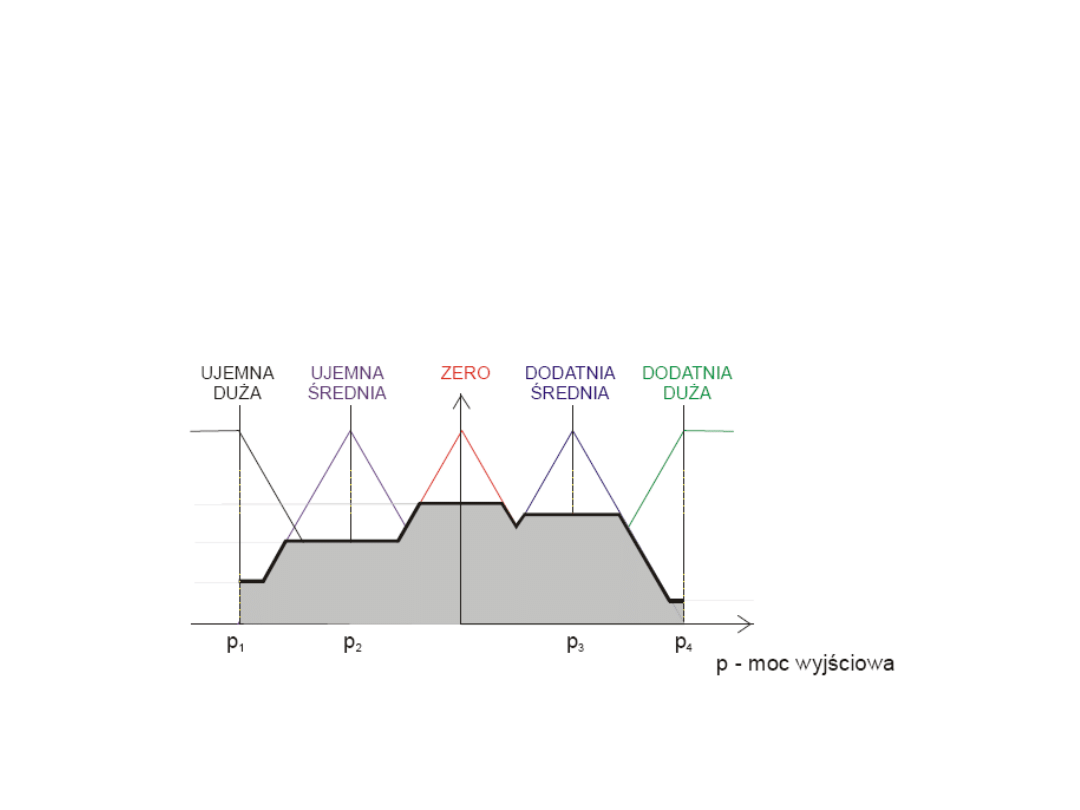
Ostateczny kształt wynikowej

funkcji przynależności m

wyn

(y)

Zastosowanie sieci neuronowych

w zbiorach rozmytych

Sieci neuronowe rozmyte

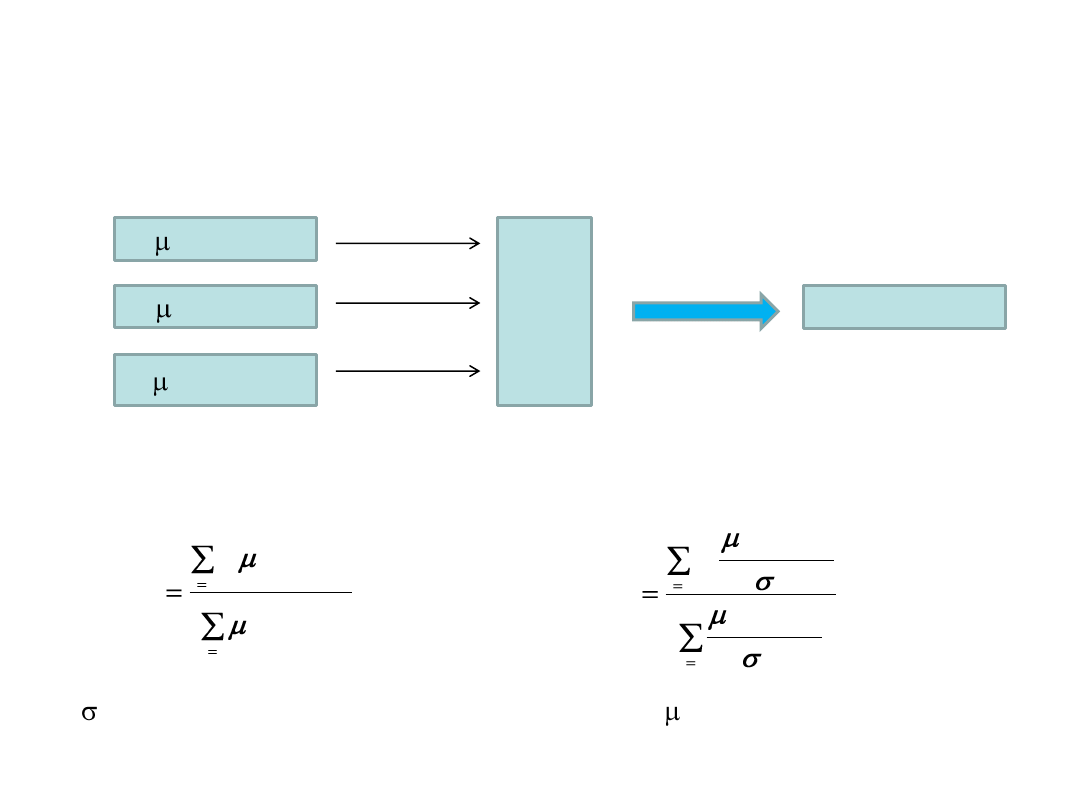
Defuzyfikator

Rodzaje defuzyfikatorów:
a) według średnich wartości centrów b) według ważonych średnich wartości centrów

M

l

l

F

M

l

l

F

l

x

x

c

y

l

l

1

)

(

1

)

(

)

(

)

(

)

(

)

(

M

l

l

l

F

M

l

l

l

F

l

x

x

c

y

l

l

1

)

(

)

(

1

)

(

)

(

)

(

)

(

)

(

)

(

c

l

,

(l)

– centrum (dyspersja) zbioru rozmytego G(l);

F(l)

– funkcja przynależności

zbiorów rozmytych F

(l)

odpowiadających danemu wektorowi wejściowemu

... konwertuje wartości „rozmyte ” do dziedziny wartości „ostrych”.

N

(x) = 0.0

S

(x) = 0.2

W

(x) = 0.9

De

fu

zy

fi

ka

tot

y= ‘wysoki’

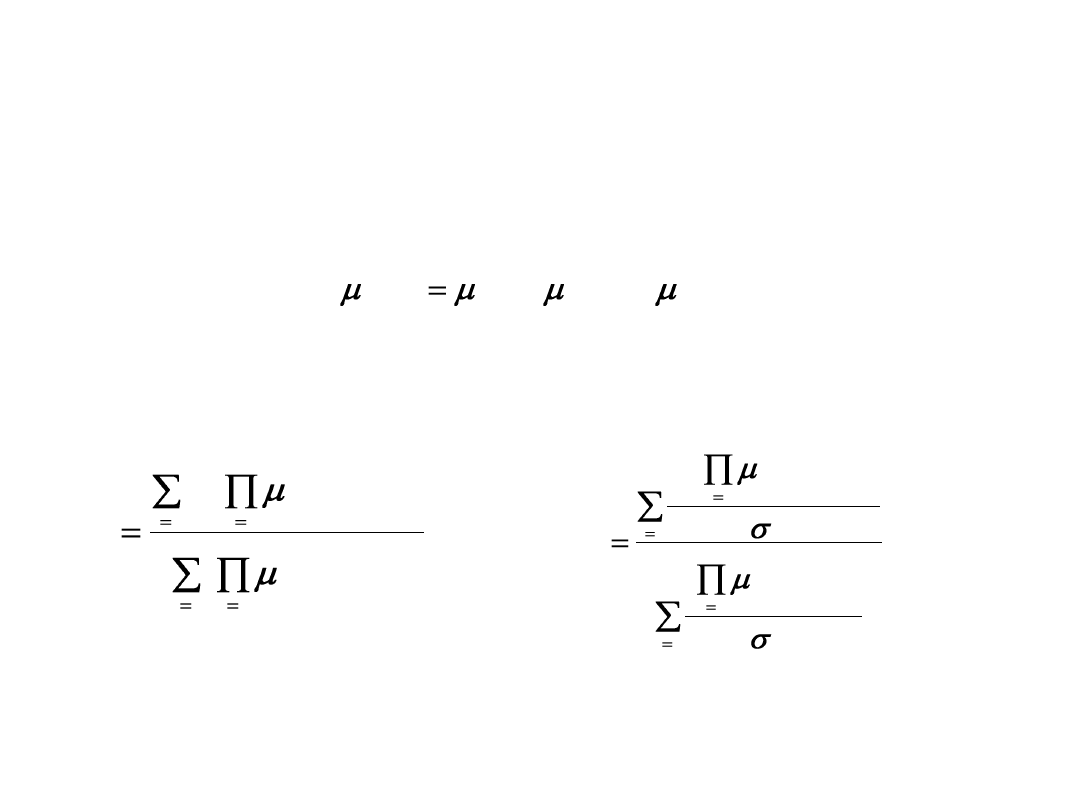
Defuzyfikator

Korzystając z opisów defuzyfikatora dowolną funkcją ciągłą f(x) o n elementowym
wektorze x można opisać przy wykorzystaniu pojęć logiki rozmytej. Stosując
interpretację iloczynową funkcji przynależności:

M

l

N

i

l

i

F

M

l

N

i

l

i

F

l

x

x

c

y

l

i

l

i

1

1

)

(

1

1

)

(

)

(

(

)

)

(

(

)

(

)

(

)

(

)...

(

)

(

)

(

2

1

x

y

x

x

n

F

F

F

A

otrzymuje się dla defuzyfikatora
a) średnich wartości centrów b) ważonych średnich wartości centrów

M

l

l

N

i

l

i

F

M

l

l

N

i

l

i

F

l

x

x

c

y

l

i

l

i

1

)

(

1

)

(

1

)

(

1

)

(

)

(

(

)

)

(

(

)

(

)

(

gdzie l=1,2,.., M

oznacza kolejną regułę logiczną.

Sieci neuronowe o logice rozmytej

• Możliwość reprezentacji dowolnej funkcji nieliniowej wielu zmiennych za

pomocą sumy funkcji rozmytych scharakteryzowanych przez funkcje
przynależności uzasadnia możliwość zastosowania funkcji rozmytych do
odwzorowania dowolnych procesów nieliniowych i stanowi alternatywne
podejście do klasycznych sieci neuronowych jednokierunkowych

• Postać funkcji f(x) umożliwia jej implementację jako równoległej struktury

wielowarstwowej, podobnie jak w przypadku sieci sigmoidalnych i

radialnych

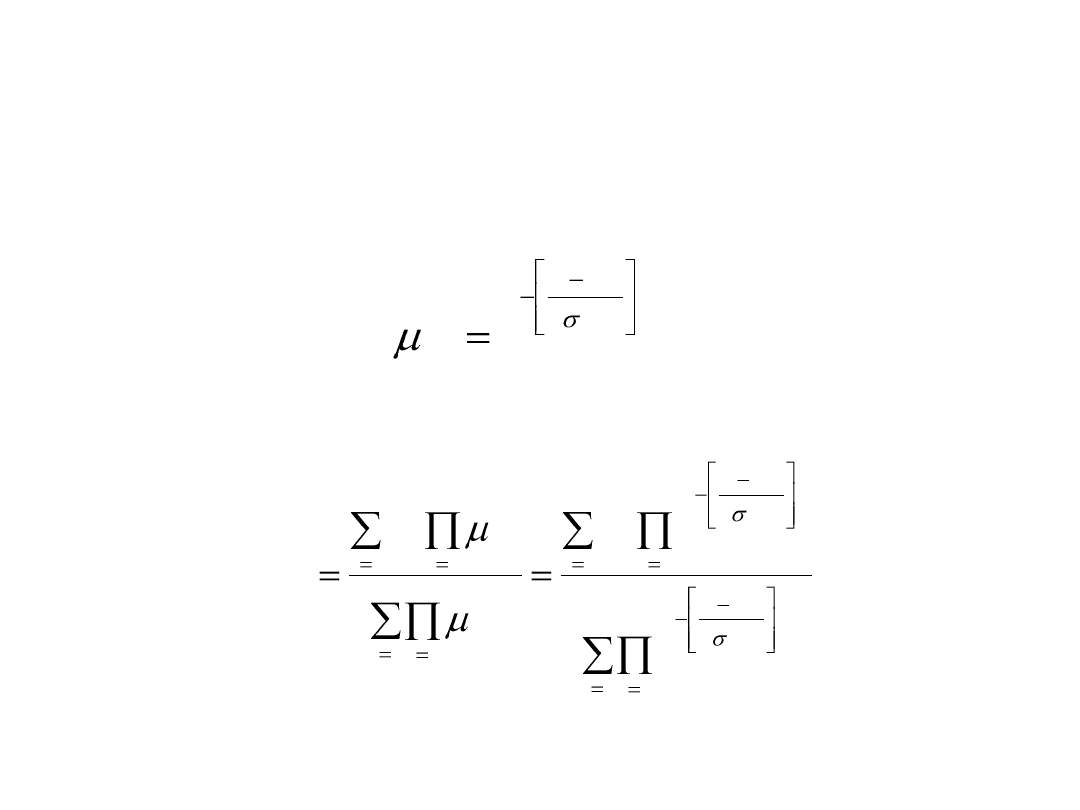
Sieci neuronowe o logice rozmytej

2

)

(

)

(

)

(

l

i

l

i

i

c

x

l

i

e

Przyjmując gaussowską postać funkcji przynależności dla i-tej zmiennej
x

i

odpowiadającej l-tej regule w postaci:

funkcja aproksymująca f(x) wyrażoną przez średnie wartości centrów
można zapisać jako:

w której W

l

jest centrum zbioru rozmytego zmiennej wyjściowej.

M

l

N

i

c

x

M

l

N

i

c

x

l

M

l

N

i

l

i

M

l

N

i

l

i

l

l

i

l

i

i

l

i

l

i

i

e

e

W

W

x

f

1

1

1

1

1

1

)

(

1

1

)

(

2

)

(

)

(

2

)

(

)

(

)

(

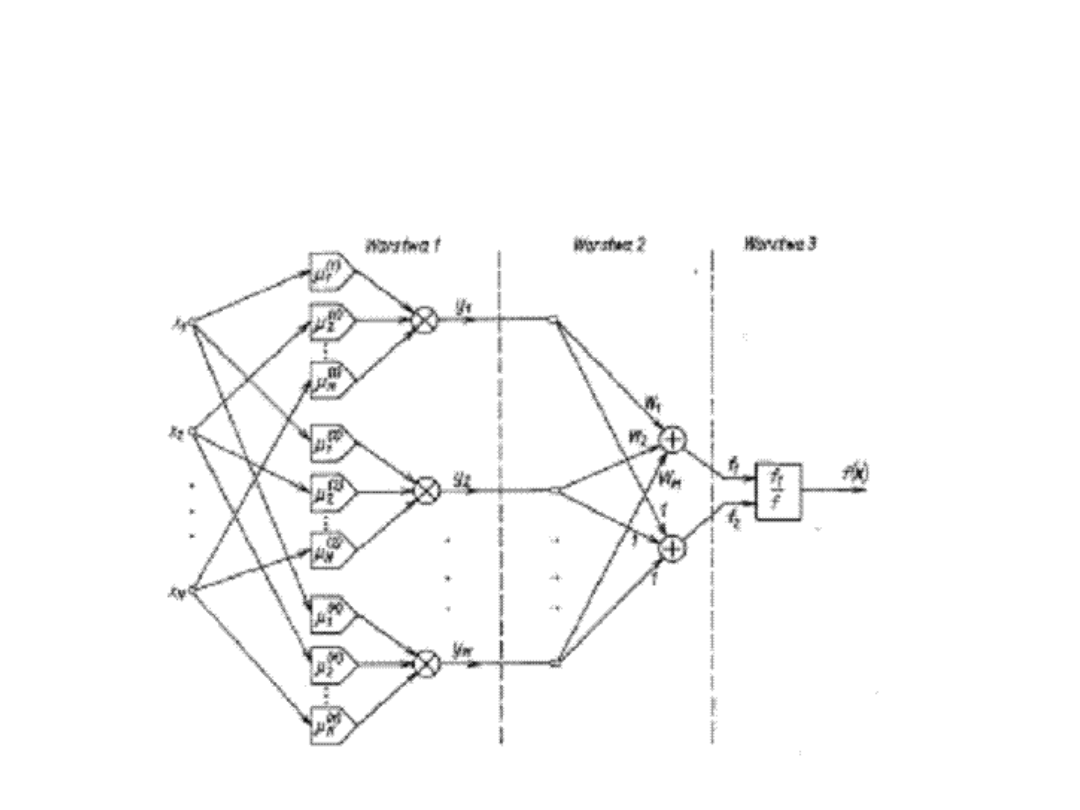
Sieci neuronowe o logice rozmytej –

schemat

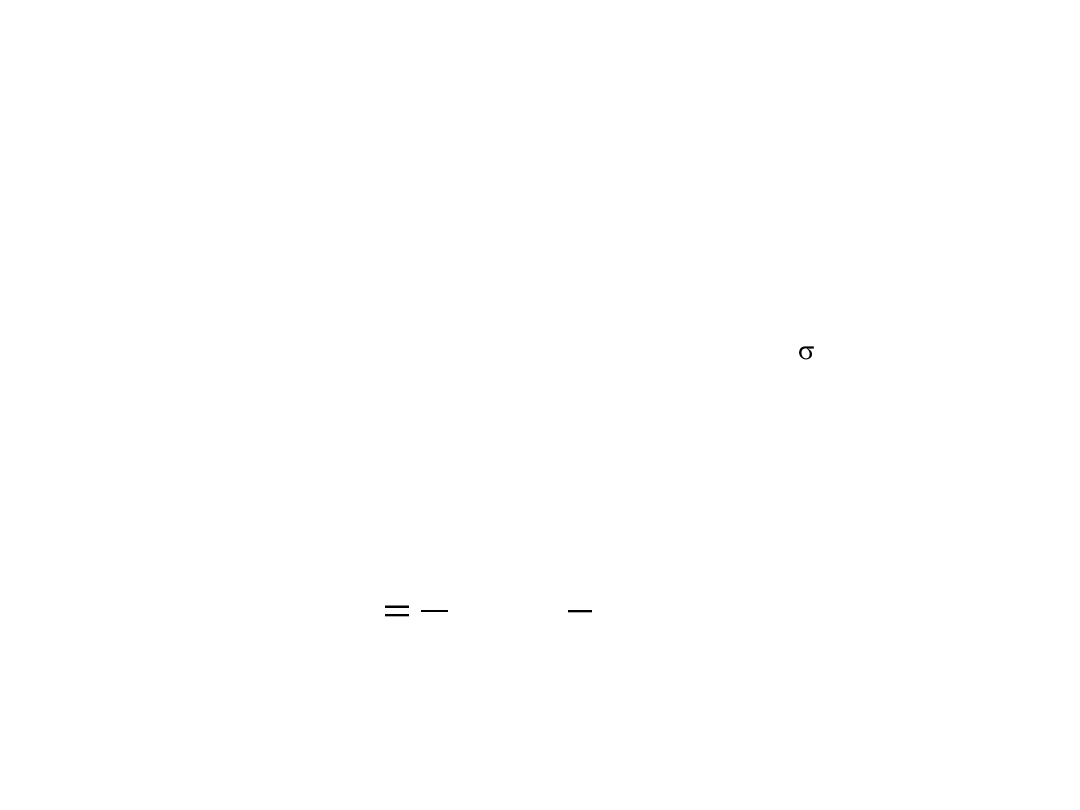
Metoda gradientowa

• Zadaniem sieci jest odwzorowanie par danych wejście-wyjście (x,d) w taki

sposób, aby wartość żądana d stanowiąca pożądaną odpowiedź systemu,
była odwzorowana przez funkcję f(x).

• Uczenie sieci polega na doborze parametrów W

l

, c

i

(l)

oraz

i

(l)

(i=1,2,...N,

l=1,2,...,M).

• Uczenie przeprowadza się przez minimalizacją błędu kwadratowego

między wartością żądaną d a jej odwzorowaniem f(x):

2

]

)

(

[

2

1

d

x

f

E

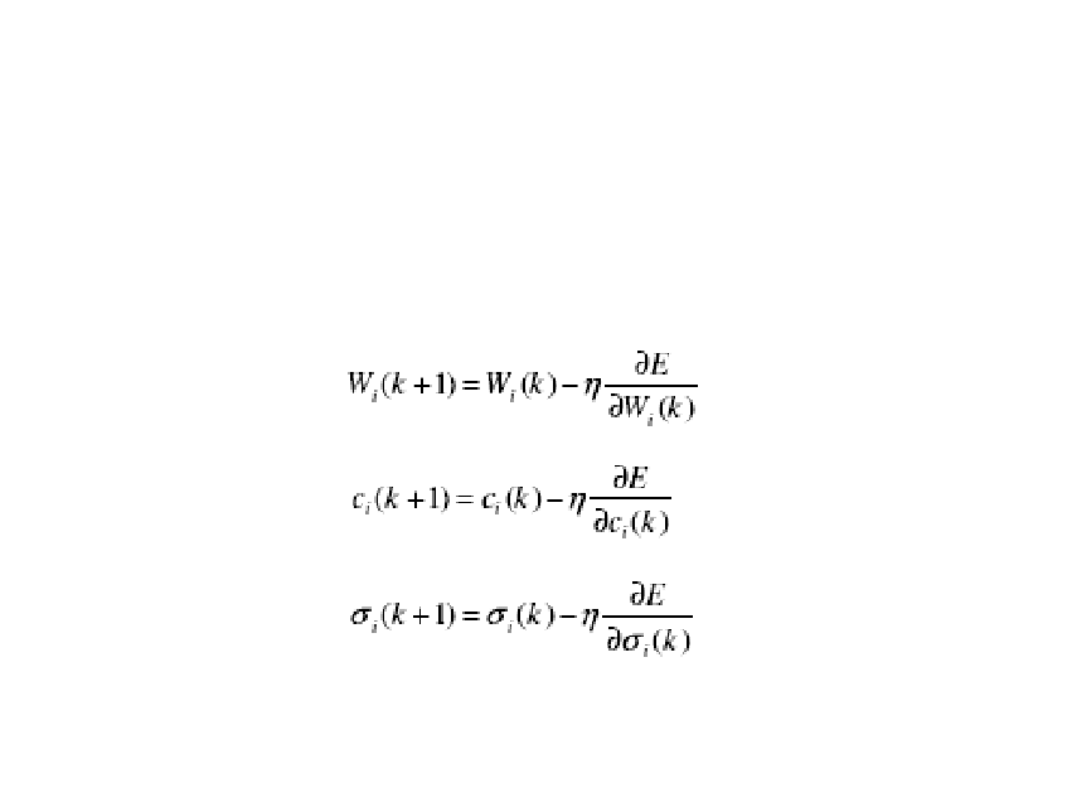
Metoda gradientowa

(Algorytm wstecznej propagacji błędu)

Stosując do minimalizacji metodę największego spadku otrzymujemy w k-tym
kroku uczącym następujące wartości parametrów:

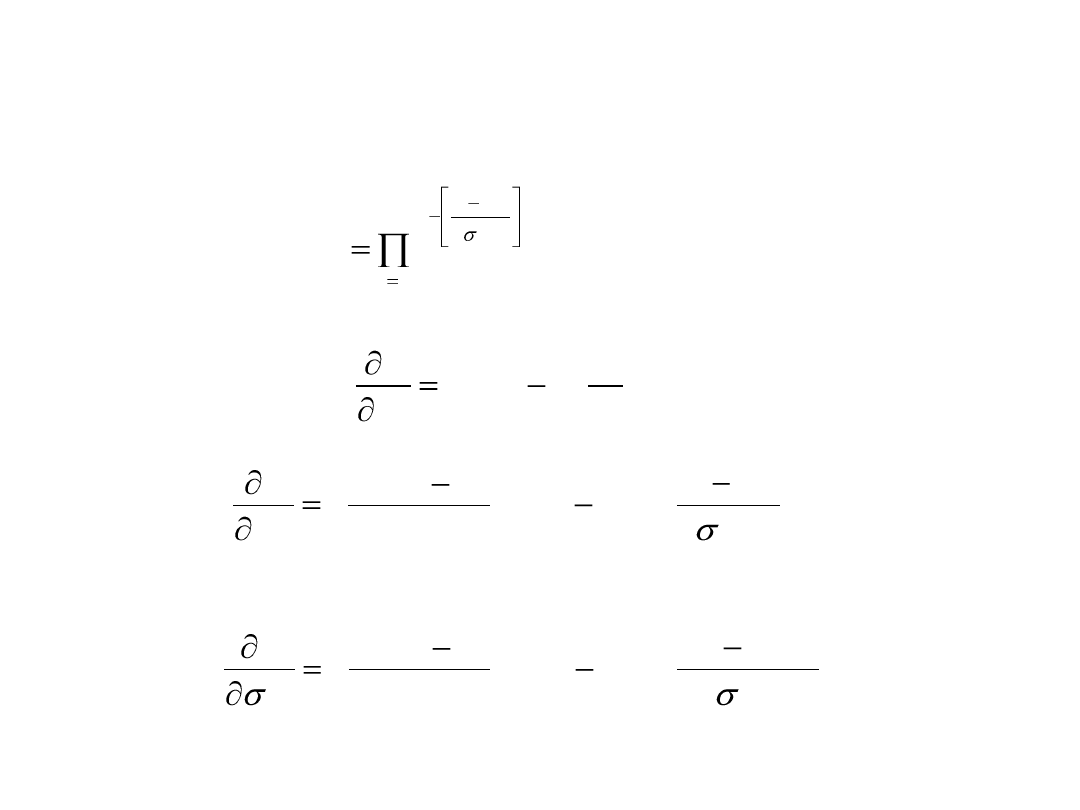
Metoda gradientowa

Przyjmując:

2

)

(

)

(

1

l

i

l

i

i

c

x

N

i

l

e

y

otrzymujemy:

2

)

)

(

(

f

y

d

x

f

W

E

l

l

2

)

(

)

(

2

)

(

]

[

)]

(

[

)

)

(

(

2

l

i

l

i

i

l

l

l

i

c

x

x

f

W

y

f

d

x

f

c

E

3

)

(

2

)

(

2

)

(

]

[

)

(

)]

(

[

)

)

(

(

2

l

i

l

i

i

l

l

l

i

c

x

x

f

W

y

f

d

x

f

E

Fazy algorytmu propagacji wstecznej

• podanie na wejście sieci sygnałów wejściowych tworzących wektor x i

określenie wszystkich sygnałów wewnętrznych oraz wyjściowych sieci,
występujących w wyrażeniu określającym gradient;

• określenie wartości funkcji błędu na wyjściu sieci i przez jego propagację w

kierunku wejścia wyznaczenie wszystkich składowych wektora gradientu;

• adaptacja parametrów sieci odbywa się z kroku na krok według wybranej

metody gradientowej z krokiem uczenia

stałym bądź zmiennym.

Cechy charakterystyczne

Mimo podobieństwa funkcji aproksymującej z funkcjami radialnymi istnieją

różnice:

• charakterystyczna interpretacja parametrów funkcji, wynikająca z faktu,

że postać funkcji f(x) jest odzwierciedleniem zasady wnioskowania
logicznego w zbiorach rozmytych zawierającą część warunkową
„jeśli...” oraz część wynikową „to...”:

– parametry c

i

(l)

oraz

i

(l)

są odpowiednio centrami i szerokościami części

„jeśli”

– wagi W

i

odpowiadają ściśle centrom części „to”

• możliwość włączenia w proces uczenia informacji lingwistycznej,

zawierającej się we wnioskowaniu logicznym. Wiedza eksperta
równolegle do danych pomiarowych może zostać wprzęgnięta w proces
uczenia, szczególnie na etapie wstępnym przy doborze początkowych
wartości parametrów optymalizacyjnych.

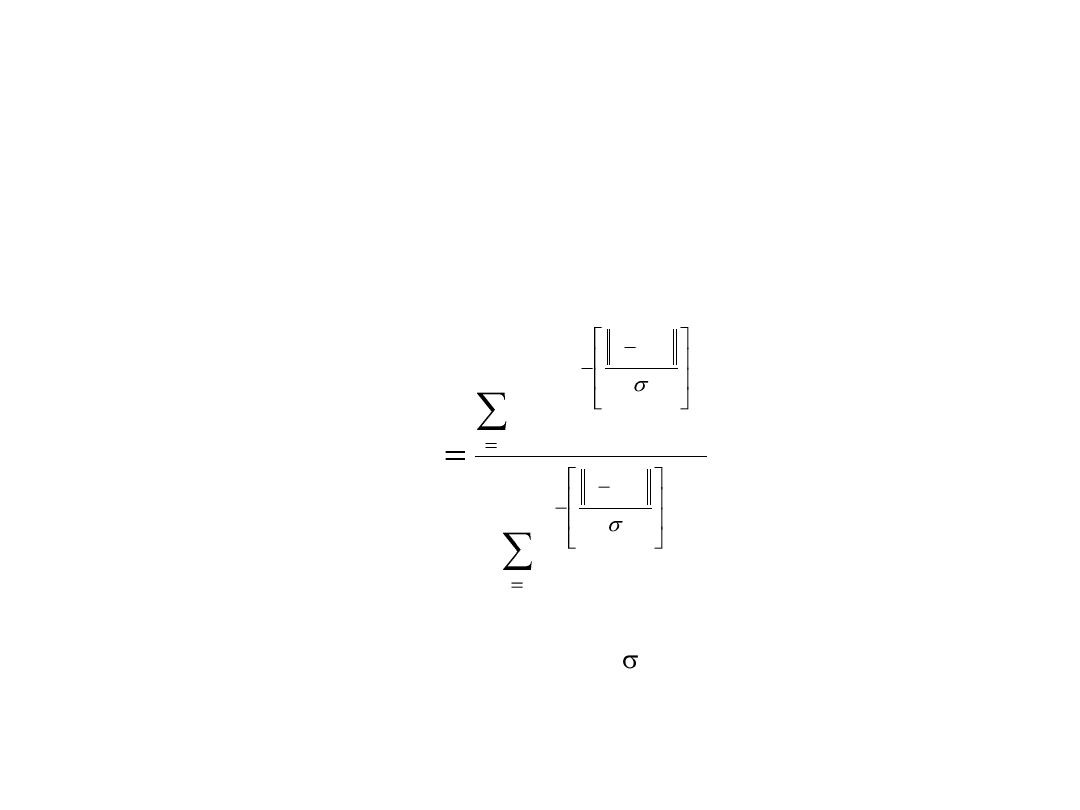
Uczenie samoorganizujące się sieci

rozmytych

p

l

x

x

p

l

x

x

l

l

l

e

e

d

x

f

1

1

)

(

2

)

(

2

)

(

)

(

Zakładamy, że mamy p par uczących, przy czym każda z par jest
reprezentantem reguły logicznej l: (x

(l)

;d

(l)

). Zakładając, że M=p otrzymujemy:

gdzie wartość parametru s, taka sama dla każdej reguły rozmytej, decyduje o
gładkości odwzorowania. Im mniejsza wartość tym lepsze dopasowanie w
danym punkcie i jednocześnie gorsza gładkość funkcji.

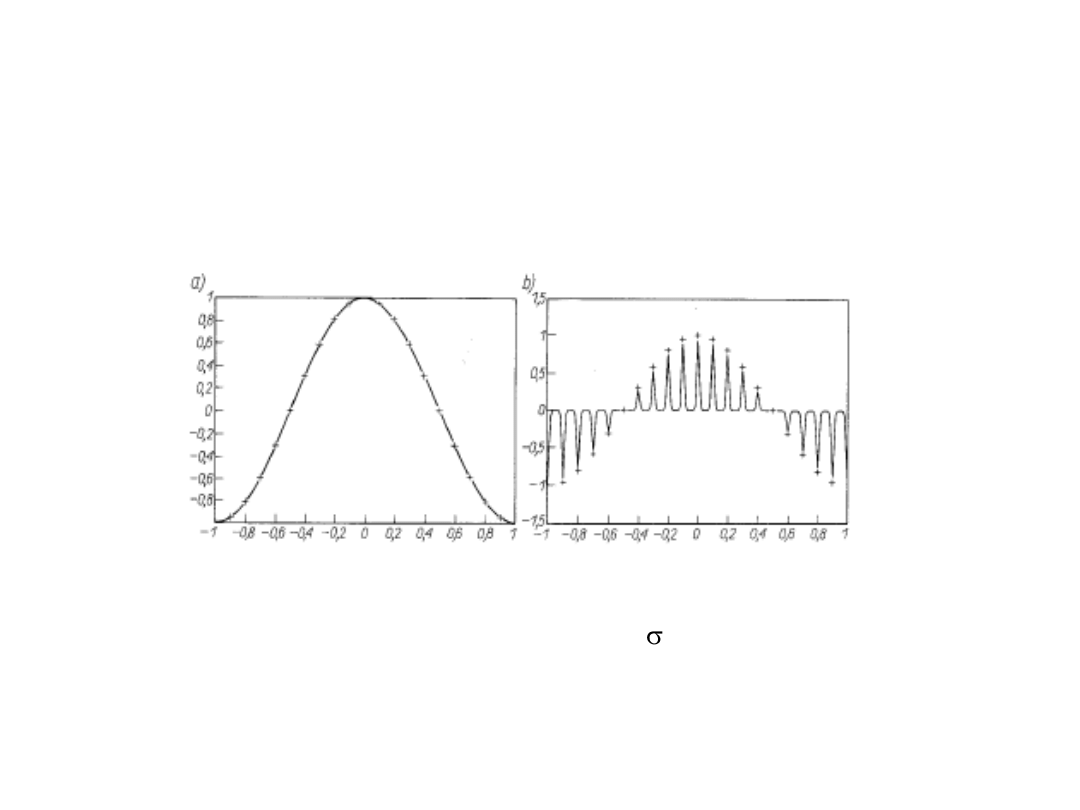
Uczenie samoorganizujące się sieci

rozmytych

Dobór a) właściwego, b) niewłaściwego parametru funkcji rozmytej

Uczenie samoorganizujące się sieci

rozmytych

• Gdy liczba p jest duża przyjęcie M = p jest niepraktyczne. Dane

wówczas mogą być reprezentowane przez M<p klastrów.

• Algorytm automatycznego podziału przestrzeni danych na klastry

(odmiana algorytmu K-

średnich):

– Startując z pierwszej pary danych (x

(1)

, d

(1)

) jest tworzony pierwszy

klaster o centrum c

(1)

=x

(1)

. Zakłada się W

(1)

=d

(1)

oraz liczność zbioru

L

(1)

=1. Niech r będzie oznaczać odległość wektora cech x od centrum,

poniżej której dane będą traktowane jako należące do danego
klastera. (Zakładamy, że w chwili startu istnieje M klastrów).

– Po wczytaniu k-tej pary uczącej (x

(k)

, d

(k)

) następuje wyznaczenie

odległości ||x

(k)

-c

(l)

|| l=1,2,..., M. Określono, że najbliższym centrum jest

c

(z)

.

• jeżeli ||x

(k)

-c

(z)

|| > r zakłada się nowy klaster i ustala odpowiednio jego

parametry (patrz pkt. 1)

Uczenie samoorganizujące się sieci

rozmytych

• jeżeli ||x

(k)

-c

(z)

|| < r uaktualniane są parametry klastra z:

– W

(z)

(k)=W

(z)

(k-1)+d

(k)

– L

(z)

(k)=L

(z)

(k-1)+1

– c

(z)

(k)=[c

(z)

(k-1)L

(z)

(k-1)+x

(k)

] / L

(z)

(k)

Przeprowadzając powyższe kroki do k=p otrzymujemy podział obszaru
danych na M klastrów (odpowiednio dla przyjętej wartości r). Liczebność
każdego z nich jest określona przez L

(l)

(k), centrum przez c

(l)

(k); wartość

skumulowanej funkcji przez W

(l)

(k).

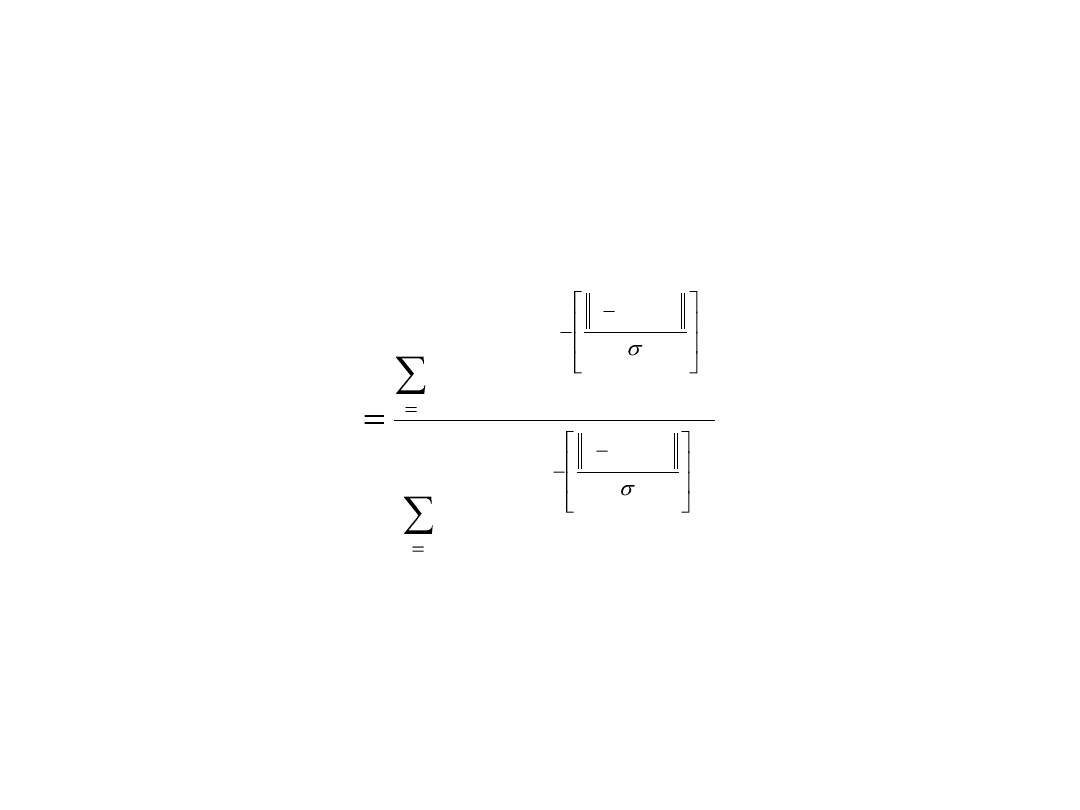
Postać funkcji aproksymującej

p

l

k

c

x

l

p

l

k

c

x

l

l

l

e

k

L

e

k

W

x

f

1

)

(

)

(

1

)

(

)

(

2

)

(

2

)

(

)

(

)

(

)

(

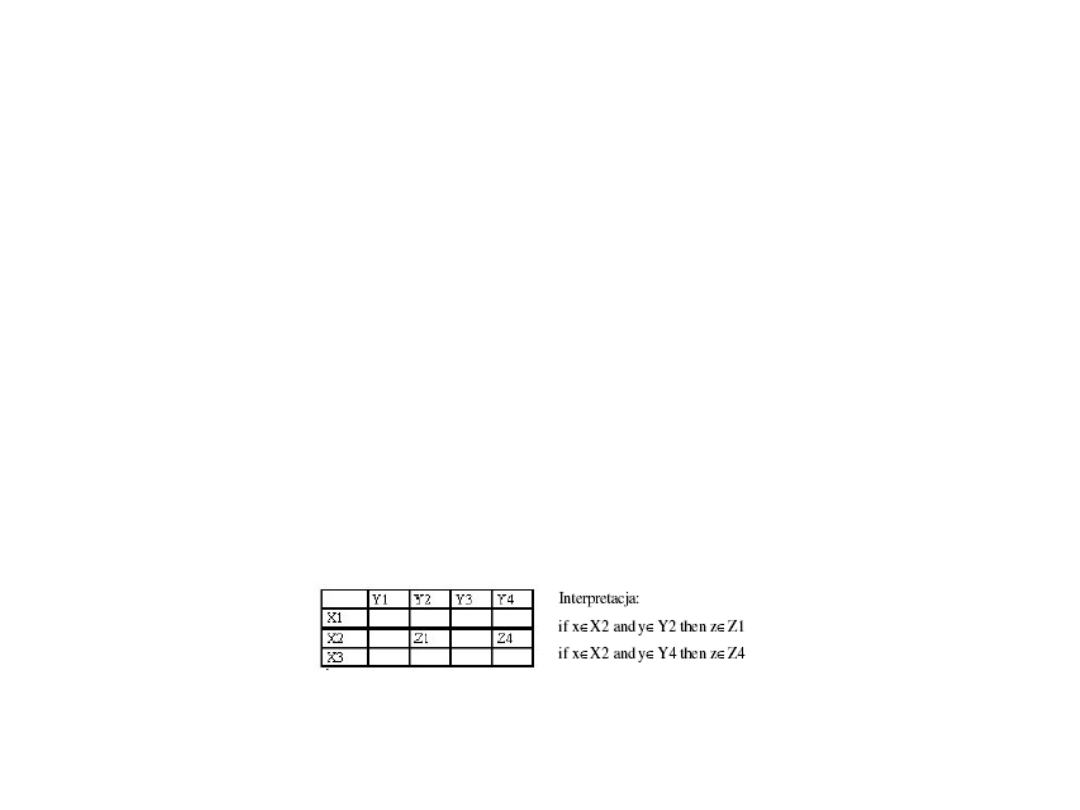
Uczenie na podstawie tabeli przejść

• Etapy uczenia:

– Podział przestrzeni danych wejściowych i wyjściowych na podzbiory rozmyte z

przyporządkowaną odpowiednią funkcją przynależności

– Generowanie reguł rozmytych na podstawie danych uczących i ich podziału na

zbiory rozmyte

– Hierarchizacja reguł - powiązanie z każdą regułą jej stopnia w hierarchii.

W przypadku sprzeczności za obowiązującą przyjmuje się regułę o

największym stopniu

– Określenie tabeli reguł wynikowych podejmowania decyzji:

– Defuzyfikacja

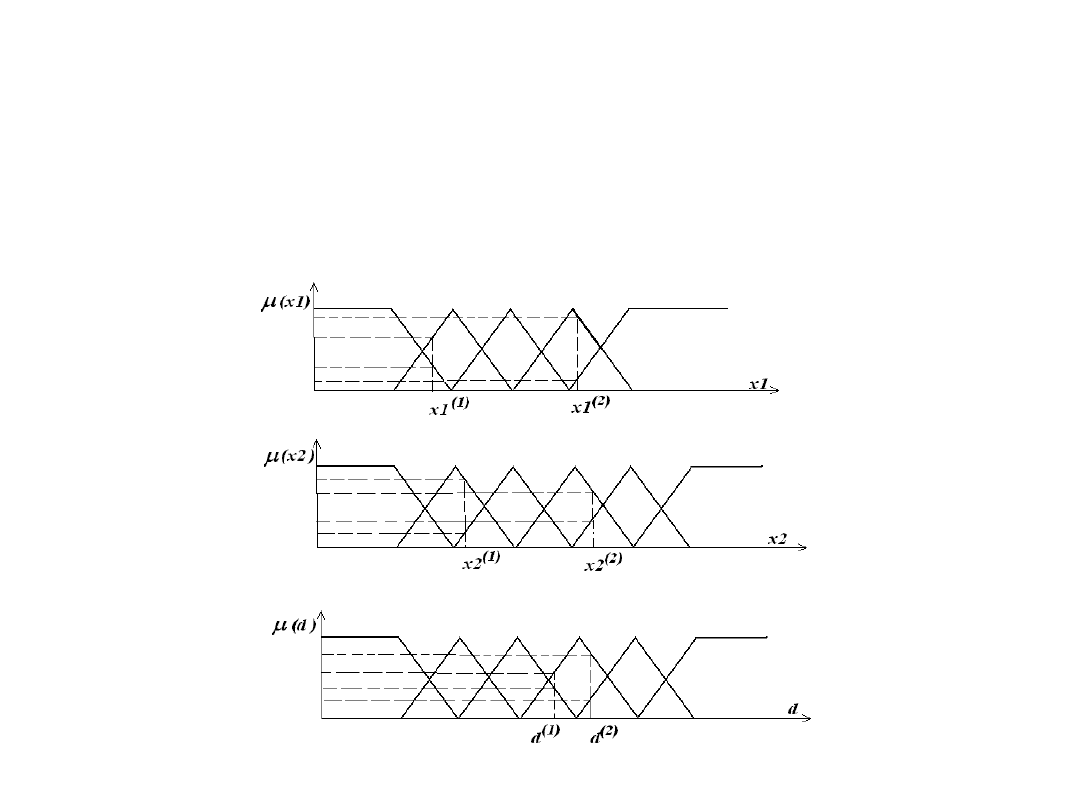
Podział przestrzeni danych wejściowych i

wyjściowych na podzbiory rozmyte

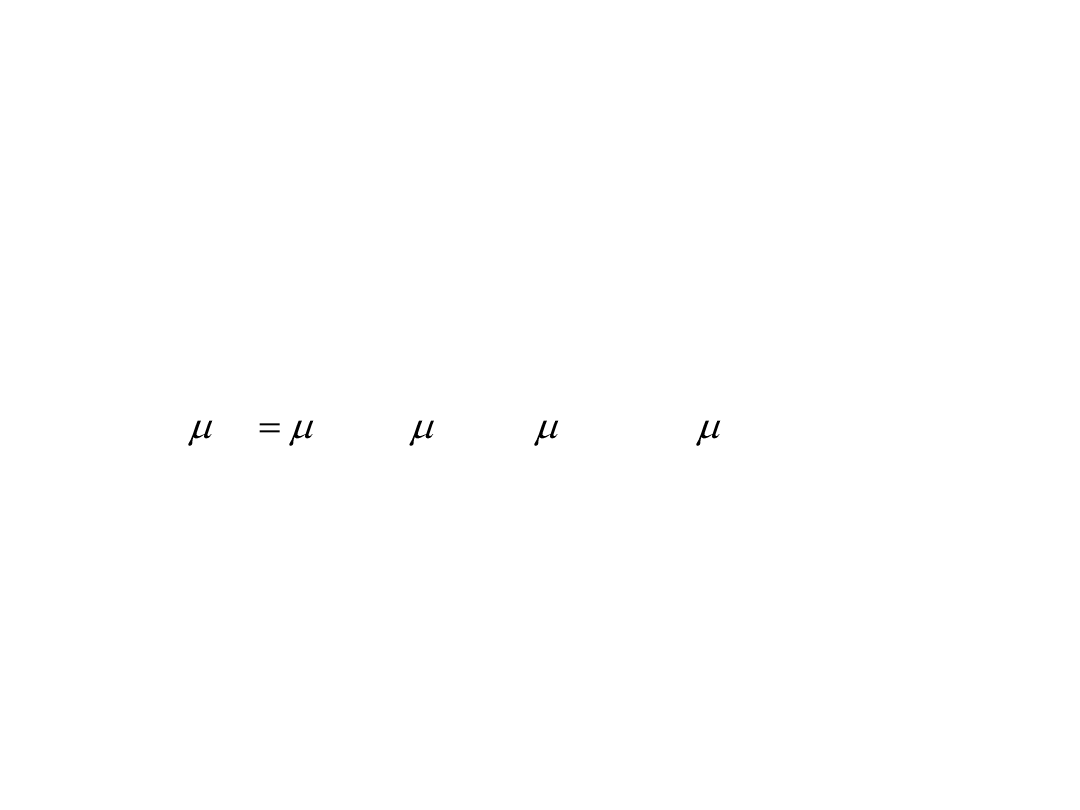
Strategia defuzyfikacji

W celu określenia konkretnej wartości y odpowiadającej wymuszeniu
opisanemu wektorem x

(i)

(i=1,2,...,M) podanemu na wejście układu o

logice rozmytej stosuje się następujące etapy:

• określenie wartości kombinowanej funkcji przynależności wektora x

(i)

do różnych stref zmiennej wyjściowej

)

(

)

(

)

(

)

(

)

(

)

(

3

)

(

2

)

(

1

)

(

3

2

1

)

(

N

I

I

I

I

i

y

x

x

x

x

i

N

i

i

i

i



przy czym y

(i)

oznacza zakres zmiennej wyjściowej odpowiadającej i-

tej regule, a I

j

(i)

– zakres zmiennej wejściowej x

j

odpowiadający i-tej

regule.

• Wyznaczenie wartości zmiennej wyjściowej y odpowiadającej zbiorom

wektorów x(i) według reguły uśrednionych centrów

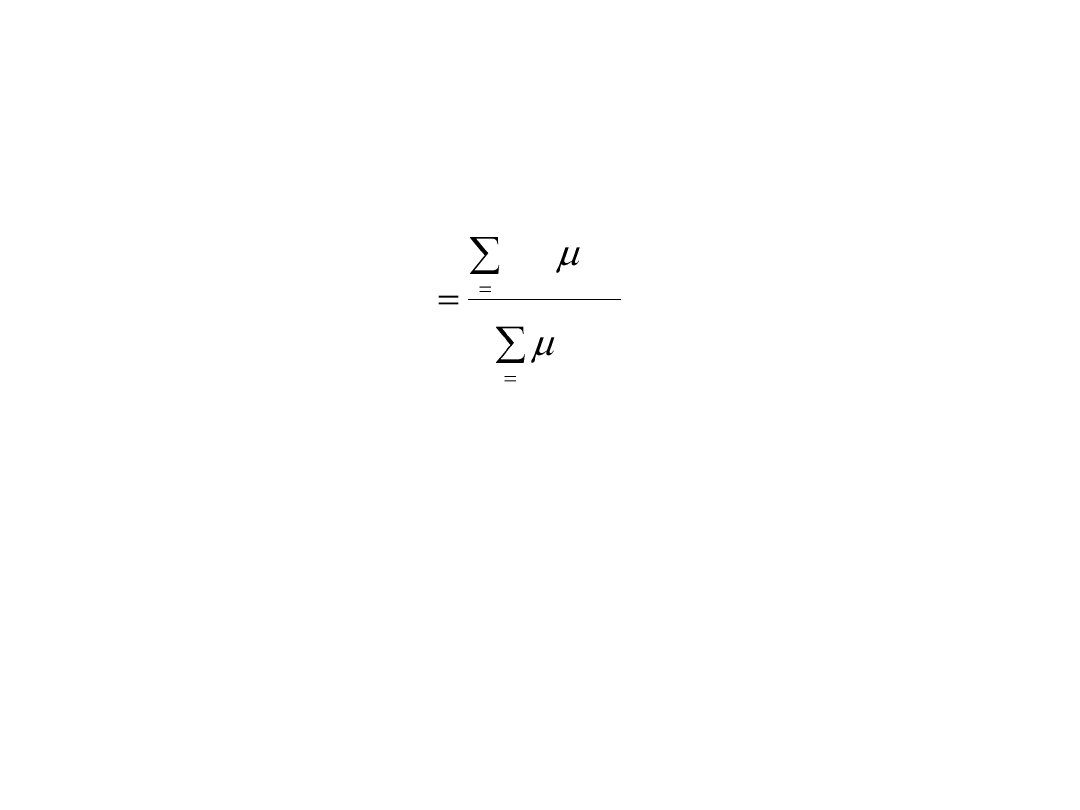
Strategia defuzyfikacji

M

l

i

y

M

l

i

y

i

i

i

d

y

1

)

(

1

)

(

)

(

)

(

)

(

przy czym d

(i)

oznacza wartość centralną i-tego zakresu zmiennej

wyjściowej, a zatem wartość d, przy której funkcja przynależności jest
równa 1. M jest liczbą reguł logicznych zastosowanych do określenia
odpowiedzi układu (liczba różnych wartości wektora wejściowego x).

•

Przy większej liczbie wyjść układu postępuje się identycznie dla każdej
zmiennej wyjściowej.