http://www.if.pwr.wroc.pl/~wozniak/

fizyka1.html

Terminy i miejsce konsultacji (zima 2011/2012):
poniedziałek 12-14, środa 11-13, pokój 18/11 bud. A-1

Dr hab. inż. Władysław Artur Woźniak

Instytut Fizyki Politechniki Wrocławskiej

Dr hab. inż. Władysław Artur Woźniak

Wykład FIZYKA I

1. Sprawy organizacyjne; metodologia;

elementy rachunku wektorowego i

różniczkowo-całkowego

LITERATURA PODSTAWOWA



D. Halliday, R. Resnick, J. Walker, PODSTAWY FIZYKI, tom 1, tom 2,

PWN, Warszawa 2003 oraz J. Walker, PODSTAWY FIZYKI.

Zbiór zadań,

PWN, Warszawa 2005.



J. Orear, FIZYKA, t. I i II, WNT, Warszawa 2008.



J. Massalski, M. Massalska,

Fizyka dla inżynierów, cz. I, Fizyka

klasyczna, WNT, Warszawa 2008.



R.P. Feynman, R.B. Leighton, M. Sands,

Feynmana wykłady z fizyki, T.

1, cz.1; T.1. cz.2; T. 2, cz. 1; T. 2, cz. 2, T. 3



dotyczy mechaniki

kwantowej; PWN, Warszawa 2005-

7; patrz również strona:

http://www.feynmanlectures.info/.



Strona internetowa Instytutu Fizyki http://www.if.pwr.wroc.pl zawiera

wartościowe materiały dydaktyczne.



http://www.if.pwr.wroc.pl/~wozniak/fizyka1.html

Dr hab. inż. Władysław Artur Woźniak

LITERATURA UZUPEŁNIAJĄCA



P.G. Hewitt,

FIZYKA WOKÓŁ NAS, Wydawnictwo Naukowe PWN,

Warszawa 2008.



Cz. Bobrowski,

Fizyka. Krótki kurs, WNT, Warszawa 2007.



K.

Sierański, K. Jezierski, B. Kołodko, Wzory i prawa z objaśnieniami.

Część I. Oficyna Wyd. Scripta, Wrocław 2005;



K.

Sierański, P. Sitarek, K. Jezierski, Repetytorium. Wzory i prawa

z

objaśnieniami, Oficyna Wyd. Scripta, Wrocław 2002;



K. Jezierski, K.

Sierański, I. Szlufarska, Repetytorium. Zadania z

rozwiązaniami, Oficyna Wyd. Scripta, Wrocław 2003. K. Jezierski, B.
Kołodko, K. Sierański, Zadania z rozwiązaniami. Część I. Oficyna Wyd.
Scripta

, Wrocław 2000.

Dr hab. inż. Władysław Artur Woźniak

PROGRAM WYKŁADU FIZYKA I

1. Sprawy organizacyjne: zasady uczestnictwa w

wykładach, zasady zaliczenia

kursu,

podręczniki i materiały dydaktyczne. Metodologia fizyki: cele fizyki;

układy jednostek fizycznych, jednostki podstawowe i pochodne; konwersja
jednostek; przedrostki

wielkości metrycznych; analiza wymiarowa; dokładność w

fizyce. Elementy rachunku wektorowego i operatory

różniczkowe.

2. Kinematyka:

układy współrzędnych, wielkości kinematyczne: podstawowe

definicje, ruch jednostajny, jednostajnie przyspieszony, ruch po

okręgu, ruchy

dwuwymiarowe (rzut

ukośny).

3. Dynamika punktu materialnego: masa,

pęd, siła; zasady dynamiki Newtona.

4. Nieinercjalne

układy odniesienia: siła Coriolisa.

5. Praca i energia mechaniczna: praca, energia (kinetyczna i potencjalna), moc;
zasada zachowania energii (mechanicznej); pola zachowawcze.

6. Zasada zachowania

pędu: pęd, popęd siły, zasada zachowania pędu;

zderzenia.

7. Dynamika ruchu obrotowego

bryły sztywnej: środek masy, moment: siły,

pędu, bezwładności; zasada zachowania momentu pędu, tensor momentu
bezwładności.

Dr hab. inż. Władysław Artur Woźniak

PROGRAM WYKŁADU FIZYKA I – C.D.

8. Grawitacja: pola fizyczne, pole grawitacyjne, prawo powszechnego

ciążenia, prawa Keplera.
9. Ruch okresowy: oscylator harmoniczny prosty.
10. Ruch okresowy:

tłumiony, wymuszony; rezonans mechaniczny.

11. Fale mechaniczne:

równanie falowe; fale sprężyste; prędkość

fazowa i grupowa; zasada superpozycji; interferencja; fale

dźwiękowe.

12. Elementy hydromechaniki

płynów: płyn idealny i rzeczywisty,

hydrostatyka

płynów:

prawa

Pascala

i

Archimedesa,

napięcie

powierzchniowe,

włoskowatość; przepływ płynu, prawa: ciągłości,

Bernoullego; turbulencja.
13.

Termodynamika

fenomenologiczna:

wielkości

i

opis

makroskopowy, zasady termodynamiki i ich wybrane zastosowania;

równanie stanu gazu doskonałego i rzeczywistego.
14. Termodynamika fenomenologiczna: energia

wewnętrzna, entropia,

przemiany gazu

doskonałego, silniki cieplne, zjawiska termoelektryczne.

15. Elementy termodynamiki statystycznej: idee opisu statystycznego,
mikroskopowa interpretacja entropii, funkcje

rozkładu Boltzmanna i

Maxwella, zasada ekwipartycji energii cieplnej, zjawiska dyfuzji i

lepkości.

Dr hab. inż. Władysław Artur Woźniak

NIEZWYKLE WAŻNE

2+2=4

Dr hab. inż. Władysław Artur Woźniak

Warunki zaliczenia: obecności, egzamin.

Dr hab. inż. Władysław Artur Woźniak

FIZYKA - CEL

Cel: poszukiwanie i poznawanie podstawowych praw przyrody.

Nowe prawa, nowe
podejście
do znanych zagadnień

Upraszczanie podstawowych
praw, eliminacja zbędnych,
przestarzałych teorii (brzytwa
Ockhama)

Ostateczna (!?)
prawda o
świecie
fizycznym

(Fizyka a
filozofia)

UKŁADY JEDNOSTEK FIZYCZNYCH

Podstawowe wielkości fizyczne:

długość;
czas;

masa;
natężenie prądu;
natężenia źródła światła;
kąt płaski (kąt bryłowy).

Dr hab. inż. Władysław Artur Woźniak

UKŁADY JEDNOSTEK FIZYCZNYCH



Układy jednostek fizycznych: CGS, MKGS, SI.



Przykład „ewolucji” definicji metra:

-

definicja bazująca na wymiarach Ziemi (1/10000 odległości

bieguna od równika, 1/40000 długości równika);
-

wzorzec metra w Międzynarodowym Biurze Miar i Wag w Sèvres

pod Paryżem (stop platyny z irydem);
-

liczba długości fal jednej z linii widmowych Kryptonu

86

Kr;

-

(obecna, od 1983 r.): droga, którą w próżni przebywa światło w

czasie 1/299792458 sekundy.

Dr hab. inż. Władysław Artur Woźniak

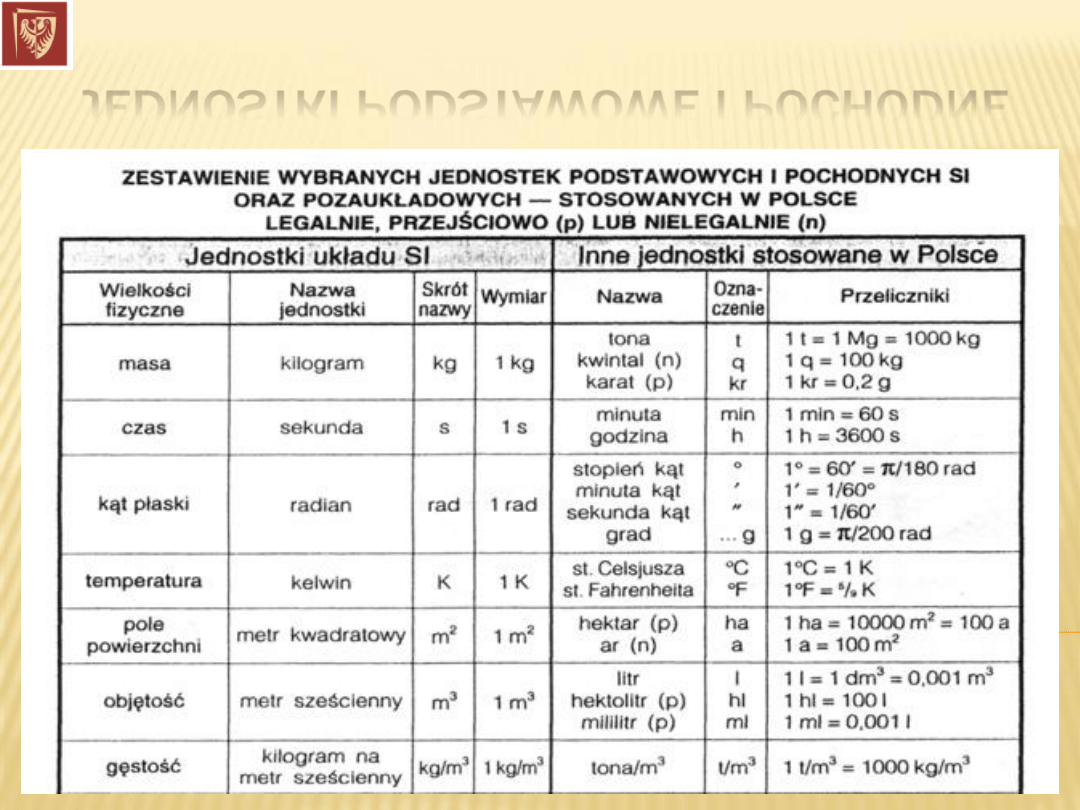
JEDNOSTKI PODSTAWOWE I POCHODNE

Dr hab. inż. Władysław Artur Woźniak

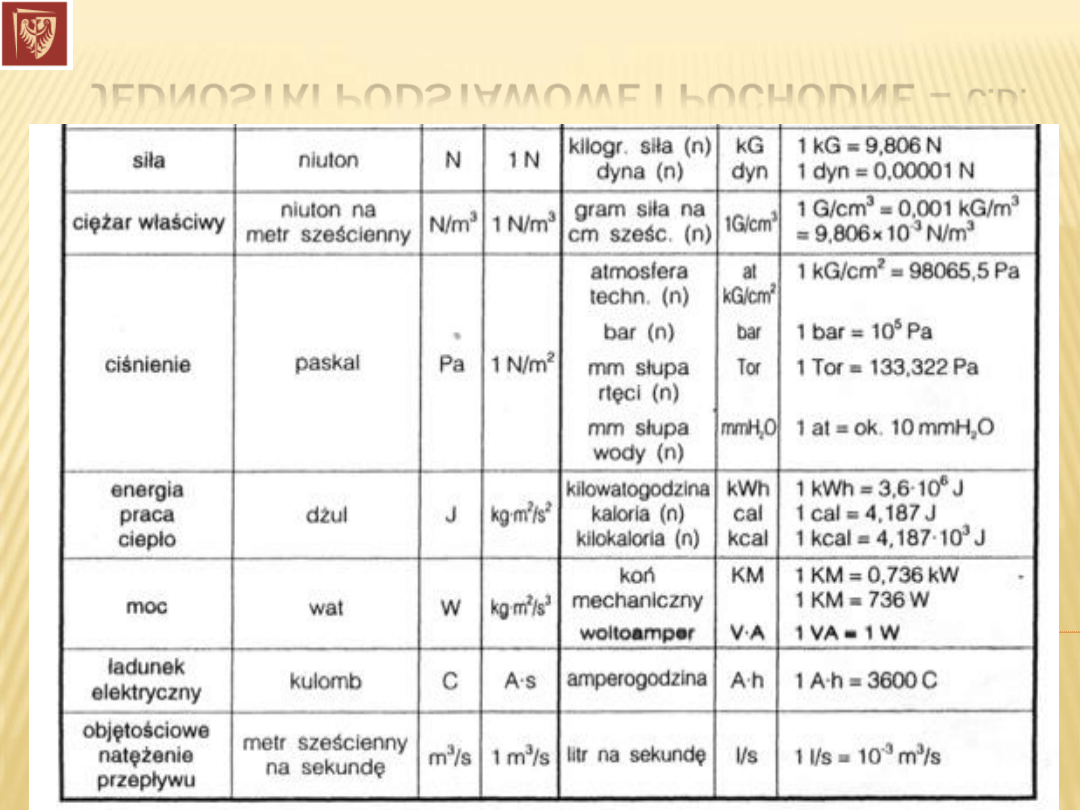
JEDNOSTKI PODSTAWOWE I POCHODNE –

C.D.

Dr hab. inż. Władysław Artur Woźniak

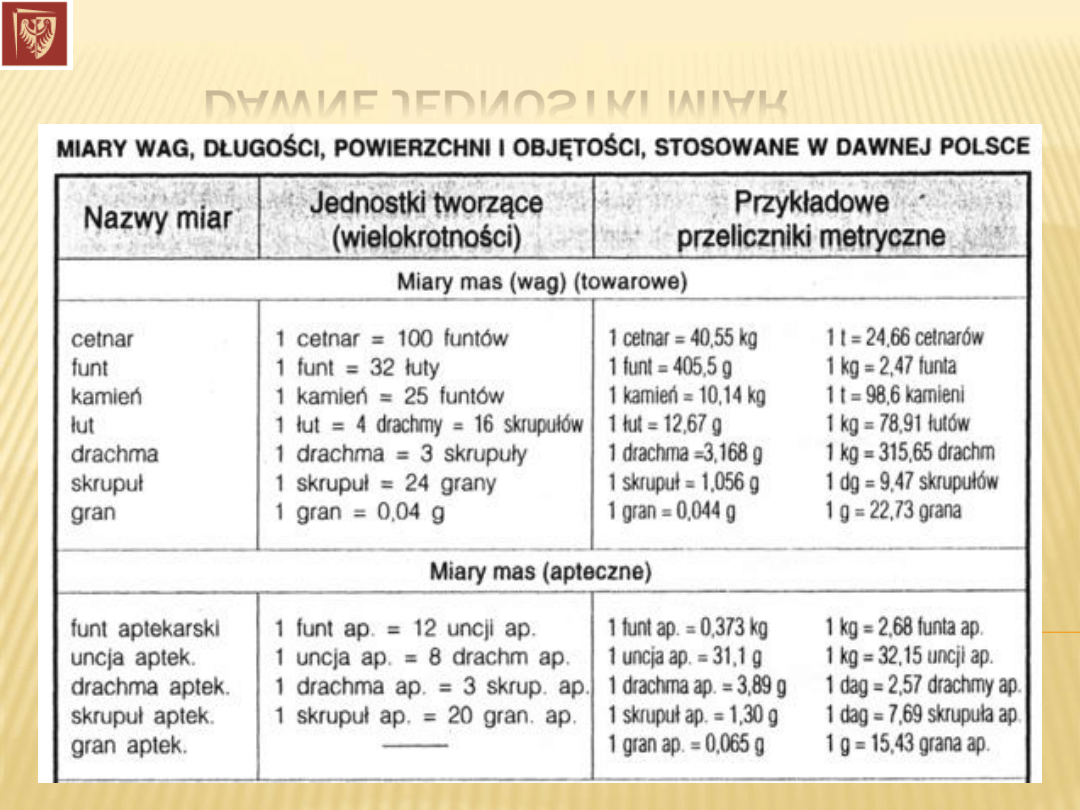
DAWNE JEDNOSTKI MIAR

Dr hab. inż. Władysław Artur Woźniak

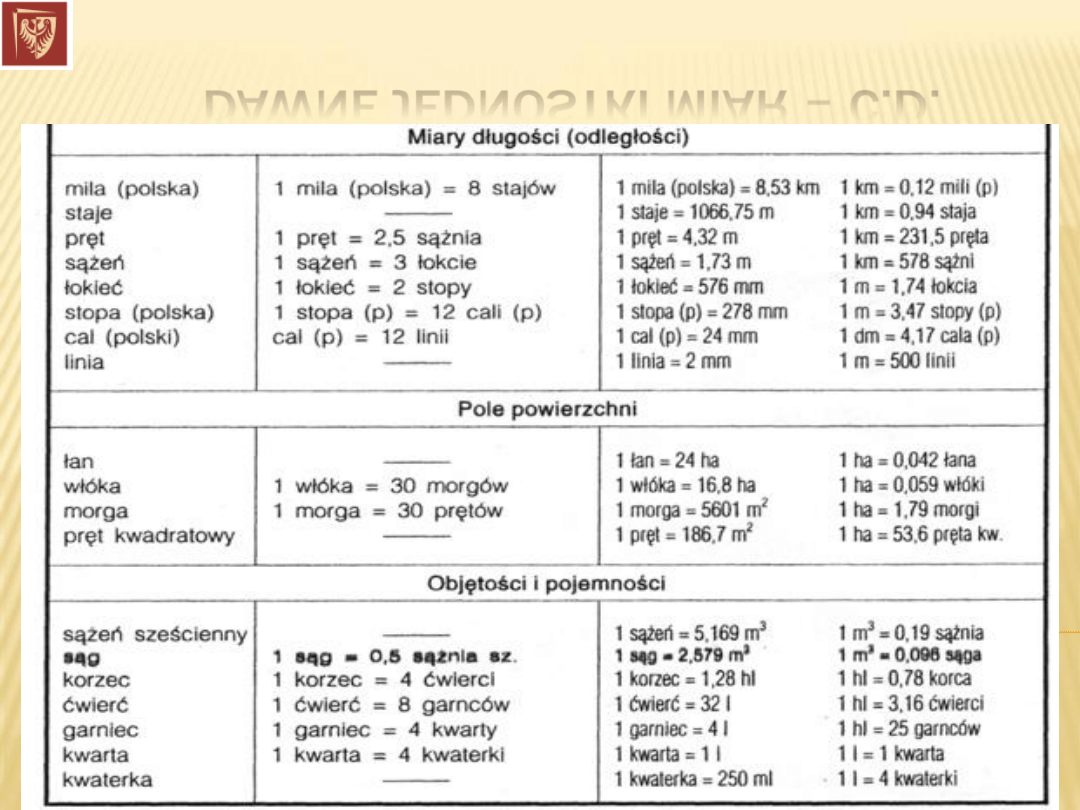
DAWNE JEDNOSTKI MIAR – C.D.

Dr hab. inż. Władysław Artur Woźniak

Dr hab. inż. Władysław Artur Woźniak

PRZEDROSTKI JEDNOSTEK METRYCZNYCH

Przedrostek

Skrót

Potęga dziesięciu

tera

T

12

giga

G

9

mega

M

6

kilo

k

3

centy

c

-2

mili

m

-3

mikro



-6

nano

n

-9

piko

p

-12

femto

f

-15

(peta = 10

15

; eksa = 10

18

; zetta = 10

21

; jotta = 10

24

; atto = 10

-18

; zepto = 10

-21

; jokto = 10

-24

;)

ZASADY ZAPISU ZMIENNOPOZYCYJNEGO

Pojęcie:

Rząd wielkości

Przykłady:

134,22 m = 1,3422



10

2

m

– rząd setek metrów (ale NIE: „rząd stu

trzydziestu

metrów”!)

0,00134 m = 1,34



10

-3

m = 1,34 mm

– rząd milimetrów

Dr hab. inż. Władysław Artur Woźniak

KONWERSJA JEDNOSTEK

Czyli: zamiana z jednego układu jednostek na inny

Przykład:

Dr hab. inż. Władysław Artur Woźniak

 

 

s

m

s

m

h

mi

mph

8

,

26

10

6

,

3

10

61

,

1

1

1

60

60

3

3













ANALIZA WYMIAROWA

Dr hab. inż. Władysław Artur Woźniak

Przykład:
Wzór na prędkość samochodu wyrażoną przez jego przyspieszenie i drogę:

Sprawdzamy wymiary:

q

p

x

a

v



- lewa strona:

 

   





1

1















s

m

s

m

v

- prawa strona:

 

   





p

q

p

q

p

s

m

m

s

m

2

2































stąd: układ dwóch równań

q

p





1

p

2

1







skąd otrzymujemy:

2

1



p

2

1



q

czyli:

ax

v



POJĘCIA WSTĘPNE

Wielkości, występujące w fizyce:

Skalary, wektory, pseudowektory, tensory;

Dr hab. inż. Władysław Artur Woźniak

Język – istotny składnik myśli abstrakcyjnej.

Nowe pojęcia naukowe = nowe słowa.

SKALAR

Wielkość, którą można wyrazić liczbą. Jego wartość nie zależy od wyboru
układu współrzędnych.

Przykłady:

masa, czas, energia, gęstość, objętość, temperatura.

WEKTOR

Dr hab. inż. Władysław Artur Woźniak

Początkowo w astronomii: wyimaginowana linia prosta, łącząca
planetę poruszającą się dookoła środka lub ogniska elipsy z tym
środkiem lub ogniskiem.

Własności zapisu wektorowego:

1.wektorowe

ujęcie praw fizyki jest niezależne od wyboru osi

współrzędnych;
2.zapis wektorowy jest

zwięzły; wiele praw ma w nim prostą i

przejrzystą postać.

WEKTOR

- kierunek

: prosta, na której działa dana wielkość;

Dr hab. inż. Władysław Artur Woźniak



Własności, które musi mieć wielkość fizyczna, aby

przypisać jej cechy wielkości wektorowej, a które nie mogą
zależeć od wyboru układu współrzędnych:

-

wartość: reprezentowana przez długość wektora;

- zwrot:

„orientacja” na danym kierunku;

- (punkt zaczepienia).

WEKTOR

Dr hab. inż. Władysław Artur Woźniak



Aby

wielkość fizyczną można było opisać wektorem,

musi ona

dodawać się jak wektor

(według poniższej reguły)

:

opis „algebraiczny”: każda składowa sumy wektorów jest sumą
odpowiednich składowych tych wektorów;

opis „geometryczny”: reguła równoległoboku:

B

A







A



B



WEKTOR

Dr hab. inż. Władysław Artur Woźniak



Przykłady wielkości wektorowych:

prędkość, przyspieszenie, siła, pęd, moment pędu, natężenie pola
elektrycznego i magnetycznego;



Długość wektora:



Wersor, czyli wektor jednostkowy:



Pochodna wektora:

 

y

x

r

,









2

2

y

x

r

r









r

r

r







ˆ

   





       

dt

t

r

d

t

r

t

r

dt

t

dr

t

r

t

r

dt

d

dt

r

d

ˆ

ˆ

ˆ









ILOCZYN SKALARNY WEKTORÓW



Własności:

1) Przemienność:
2)



Zastosowania:

1) Prawo cosinusów:

jeśli

to:

2) Cosinusy kierunkowe:



Przykład:

Moc jako prędkość wykonywanej pracy przy stałej sile :

Dr hab. inż. Władysław Artur Woźniak

A

B

B

A















0









B

A

B

A









B

A

C











 

B

A

AB

B

A

C





,

cos

2

2

2

2









     

z

A

z

y

A

y

x

A

x

A

ˆ

ˆ

ˆ

ˆ

ˆ

ˆ





















 

v

F

dt

r

d

F

dt

r

F

d

dt

dW

P



























 

B

A

AB

B

A









,

cos







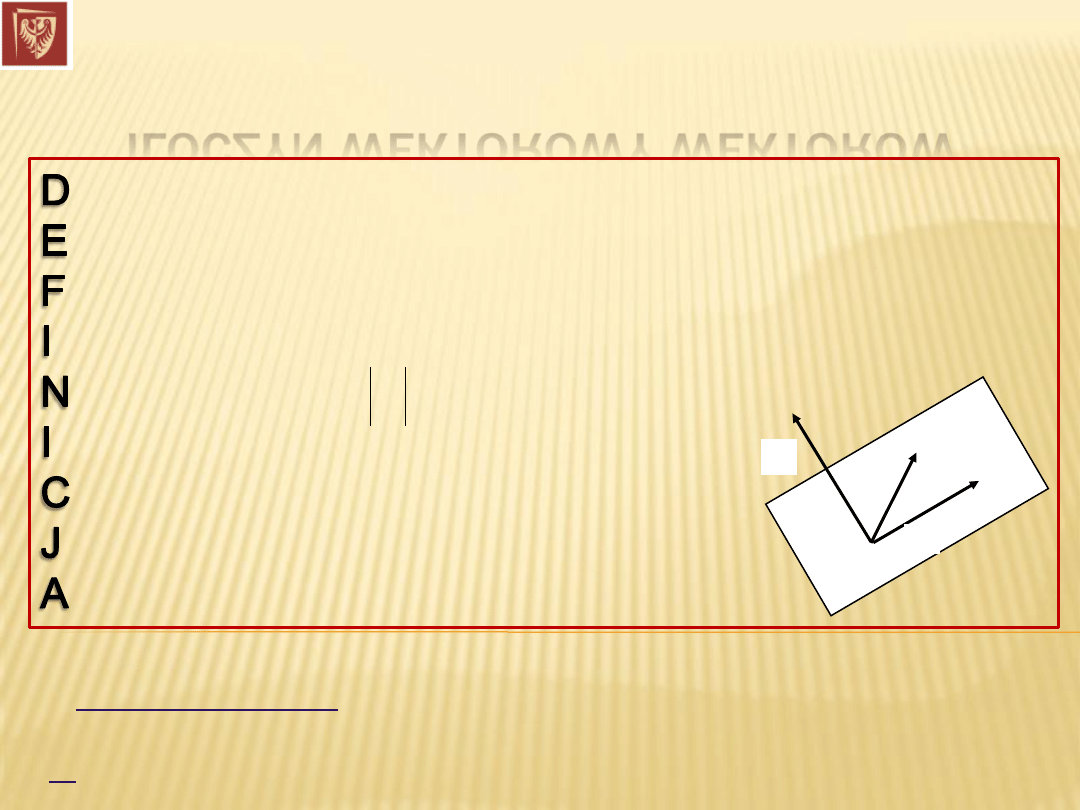
ILOCZYN WEKTOROWY WEKTORÓW

Dr hab. inż. Władysław Artur Woźniak

C

B

A











C



A



B



 

B

A

AB

C

C







,

sin







B

A

C

jest wektorem

prostopadłym do płaszczyzny, w której leżą wektory

o wartości:

a jego zwrot wyznacza reguła śruby prawoskrętnej
(rys):

A

B

B

A

















0









B

A

B

A











Własności:

1)

Antyprzemienność:

2)

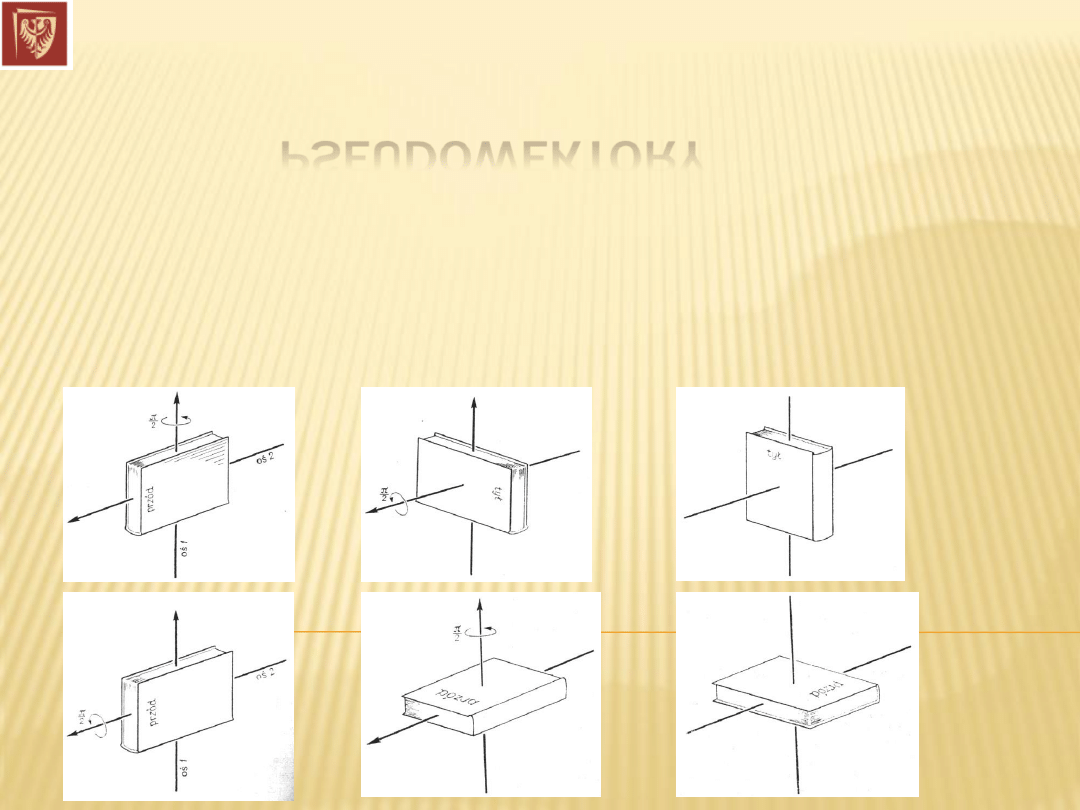
PSEUDOWEKTORY

Dr hab. inż. Władysław Artur Woźniak



Istnieją wielkości fizyczne, którym możemy przypisać nie tylko wartość liczbową, ale

również kierunek i zwrot. Wielkości te jednak nie są wektorami, gdyż nie stosują się do nich

prawa dodawania

wektorów. Nazywamy je pseudowektorami.

Przykład: kąt obrotu bryły sztywnej, podobnie prędkość kątowa i przyspieszenie kątowe.

TENSORY

Dr hab. inż. Władysław Artur Woźniak































































z

y

x

zz

xy

zx

yz

yy

yx

xz

xy

xx

z

y

x

E

E

E

D

D

D





















0

ijk

d

i

ijk

jk

E

d





jk





Wektor

= tensor pierwszego rzędu;



Tensor

drugiego rzędu – reprezentacja macierzowa;

Przykład: związek między wektorem indukcji elektrycznej D i wektorem natężenia pola

elektrycznego E:



Tensor

trzeciego rzędu

Przykład: tensor modułów piezoelektrycznych

gdzie:

jest tensorem (drugiego rzędu) odkształceń.

Tensor drugiego

rzędu ustala zależność między

wektorami.
Inne

przykłady: naprężenia, odkształcenia.

OPERATORY RÓŻNICZKOWE

Dr hab. inż. Władysław Artur Woźniak



Gradient

Operator

różniczkowy, który z wielkości (funkcji) skalarnej tworzy wektor:

B

z

A

z

y

A

y

x

A

x

r

A

A

gradA



































ˆ

ˆ

ˆ





























z

y

x

,

,

-

„nabla”

Przykład: siła jako gradient energii potencjalnej

p

gradE

F







OPERATORY RÓŻNICZKOWE

Dr hab. inż. Władysław Artur Woźniak



Dywergencja

Operator

różniczkowy, który z wektora (funkcji wektorowej) tworzy skalar:

z

B

y

B

x

B

B

B

div

z

y

x





























Przykład:
(jedno z praw Maxwella)

– dywergencja natężenia pola elektrycznego równa

się gęstości przestrzennej ładunku





E

div



OPERATORY RÓŻNICZKOWE

Dr hab. inż. Władysław Artur Woźniak



Rotacja

Operator

różniczkowy, który z wektora (funkcji wektorowej) tworzy wektor

(funkcję wektorową):

Przykład:
W prawach Maxwella

–

proszę sobie znaleźć…





z

B

y

B

B

rot

y

z

x



























































z

y

x

B

B

B

z

y

x

z

y

x

B

B

rot

ˆ

ˆ

ˆ





OPERATORY RÓŻNICZKOWE

Dr hab. inż. Władysław Artur Woźniak



Laplasjan

Operator

różniczkowy, który z pola skalarnego klasy C

2

tworzy skalar

(funkcję skalarną):

Przykład:
Równanie falowe.

Jak

wygląda?





2

2

2

2

2

2

2

,

,

z

A

y

A

x

A

z

y

x

A

A























