DYNAMIKA PŁYNÓW

Dr Stanisław Łuczyński

2

Ogólna postać podstawowych równań mechaniki płynów

1. Zasada zachowania pędu (ilości ruchu)

Pochodna pędu płynu zawartego wewnątrz obszaru V względem czasu jest
równa sumie sił zewnętrznych działających na ten obszar

siła bezwładności = siły masowe + siły powierzchniowe

Równania Naviera-Stokesa

dA

P

dV

F

dV

dt

d

V

A

V

∫∫∫

∫∫

∫∫∫

+

=

r

r

r

ρ

υ

ρ

υ

μ

ρ

υ

ρ

r

r

r

Δ

⋅

+

−

=

gradp

F

dt

d

2. Równanie zachowania krętu (momentu pędu):

Prędkość zmiany momentu pędu płynu zawartego wewnątrz obszaru V równa
się sumie momentów wszystkich sił działających na ten obszar..

dA

P

r

dV

F

r

dV

r

dt

d

V

A

V

∫∫∫

∫∫

∫∫∫

×

+

×

=

×

)

(

)

(

)

(

r

r

r

r

r

r

ρ

υ

ρ

V

r

r

M

&

r

r

r

r

r

ρ

υ

υ

]

)

(

)

[(

1

2

∞

∞

∞

×

−

×

=

Podstawowe równanie maszyn przepływowych:

σ

λ

ρ

υ

&

& +

+

∇

=

D

T

dt

dT

c

2

3. Równanie zasady energii:

wektor naprężeń

gęstość energii wewnętrznej intensywność wewnętrznego źródła ciepła

strumień energii cieplnej z otoczenia

Zmiana całkowitej energii układu płynnego następuje wskutek pracy sił

masowych i powierzchniowych oraz wskutek dostarczenia energii cieplnej ze
źródeł wewnętrznych i z otoczenia przez powierzchnie kontrolną.

∫∫

∫∫∫

∫∫

∫∫∫

∫∫∫

+

+

⋅

+

⋅

=

⎟⎟

⎠

⎞

⎜⎜

⎝

⎛

+

A

n

V

A

n

V

V

dA

q

dV

dA

dV

F

dV

u

dt

d

&

&

r

r

r

r

σ

υ

τ

υ

ρ

υ

ρ

2

2

intensywność dyssypacji
energii mechanicznej

4. Równanie ciągłości:

+ warunki początkowe i brzegowe

M

z

y

x

dt

d

z

y

x

&

=

⎟⎟

⎠

⎞

⎜⎜

⎝

⎛

∂

∂

+

∂

∂

+

∂

∂

+

υ

υ

υ

ρ

ρ

(

)

0

=

M&

gradp

F

dt

d

m

ρ

υ

1

−

=

r

r

x

p

F

z

y

x

t

x

x

z

x

y

x

x

x

∂

∂

−

=

∂

∂

+

∂

∂

+

∂

∂

+

∂

∂

ρ

υ

υ

υ

υ

υ

υ

υ

1

. . .

p

z

y

x

,

,

,

υ

υ

υ

Dynamika płynów doskonałych

)

0

(

=

μ

Równania Eulera

Leonhard Euler
(1707 - 1783).

Traktat „Ogólne
zasady ruchu
płynów” (1755)

0

=

⎟⎟

⎠

⎞

⎜⎜

⎝

⎛

∂

∂

+

∂

∂

+

∂

∂

+

z

y

x

dt

d

z

y

x

υ

υ

υ

ρ

ρ

Założenia:

¾

Przepływ stacjonarny

¾

Płyn bapotropowy

¾

Siły masowe potencjalne

Równanie Bernoulliego

const

gz

p

=

+

+

ρ

υ

ρ

2

2

r

const

gz

p

=

+

+

ρ

υ

2

2

r

Daniel Bernoulli (1700 – 1782),
szwajcarski matematyk i fizyk.
Obszarem jego zainteresowań były
także medycyna i fizjologia.

W Petersburgu przygotował swoją
większą pracę z hydrodynamiki.
W ostatecznej redakcji to klasyczne
dzieło wyszło w Strasburgu w roku
1738 pod tytułem Hydrodynamika,
czyli studia nad siłami i ruchami
cieczy.

W roku 1725 Daniel Bernoulli
został powołany wraz z bratem
Mikołajem do Petersburskiej
Akademii Nauk, w której czynny
był około ośmiu lat.

const

g

p

g

=

+

ρ

υ

2

2

h

g

p =

ρ

4

2

D

A

π

=

3

3

2

2

1

1

A

A

A

⋅

=

⋅

=

⋅

υ

υ

υ

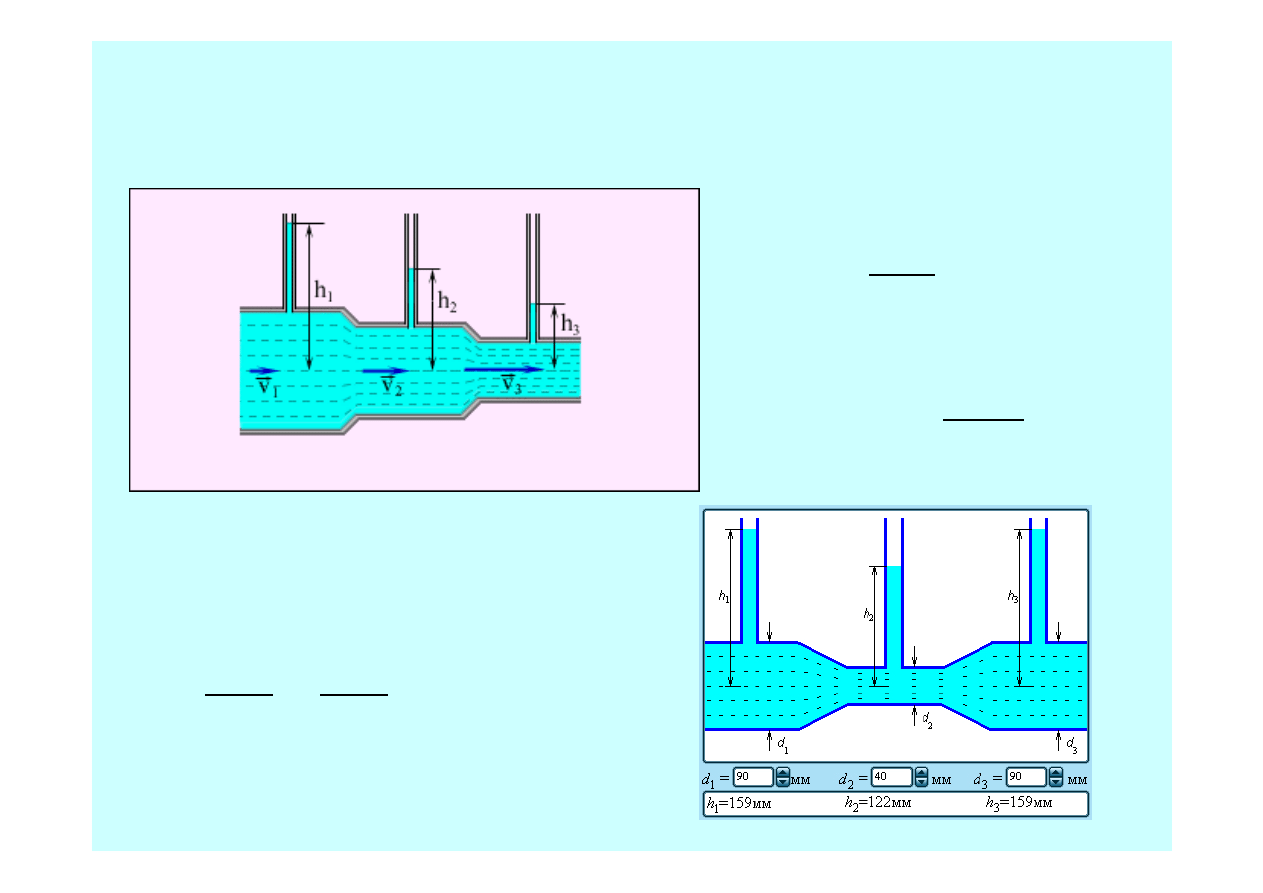
Zastosowania równania Bernoulliego

(

)

∞

∞

∞

−

=

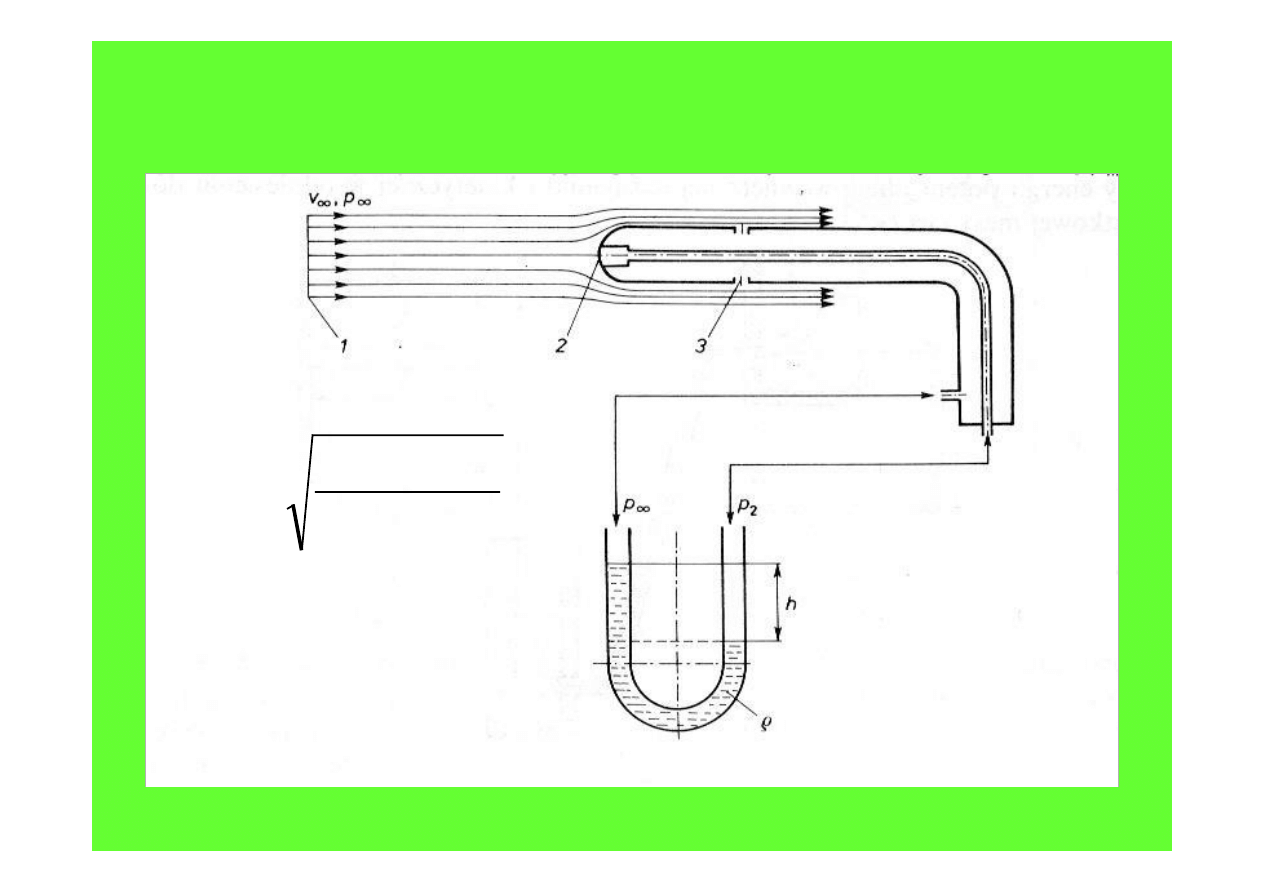
ρ

υ

p

p

2

2

gh

p

p

m

ρ

=

−

∞

2

Rurka Pitota - Prandtla

(

)

⎥

⎥

⎦

⎤

⎢

⎢

⎣

⎡

−

⎟

⎠

⎞

⎜

⎝

⎛

−

=

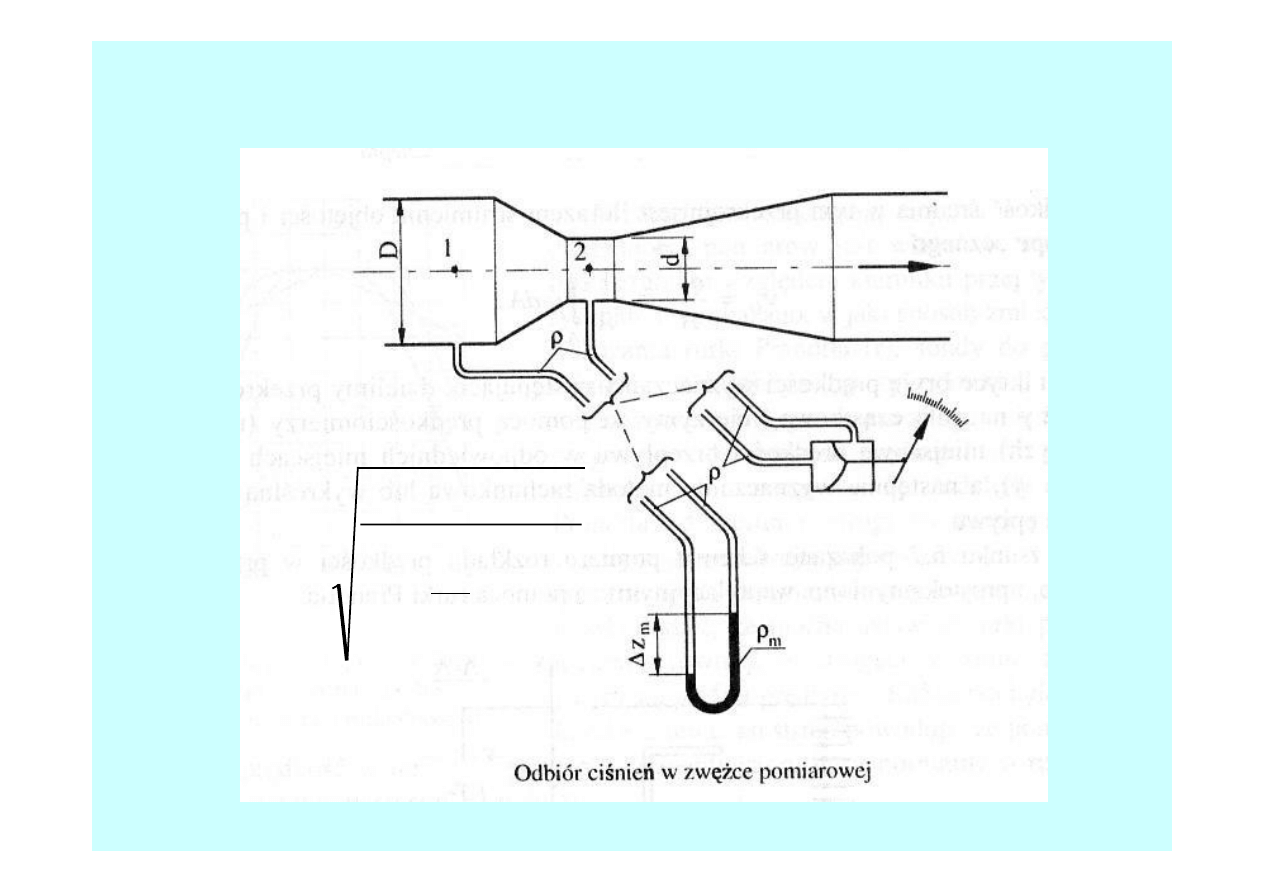
1

2

4

2

1

d

D

p

p

ρ

υ

Zwężka Venturiego

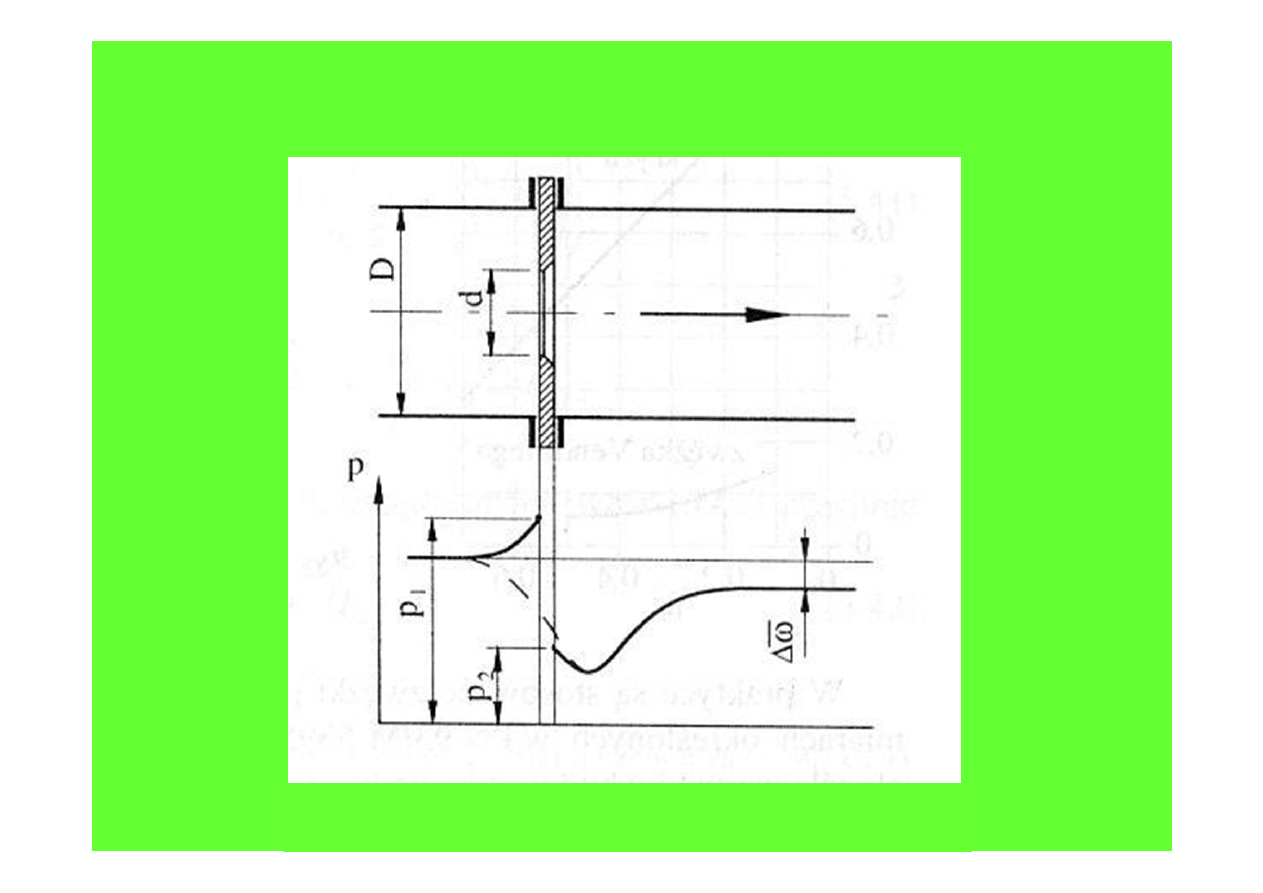
Kryza

gh

2

2

=

υ

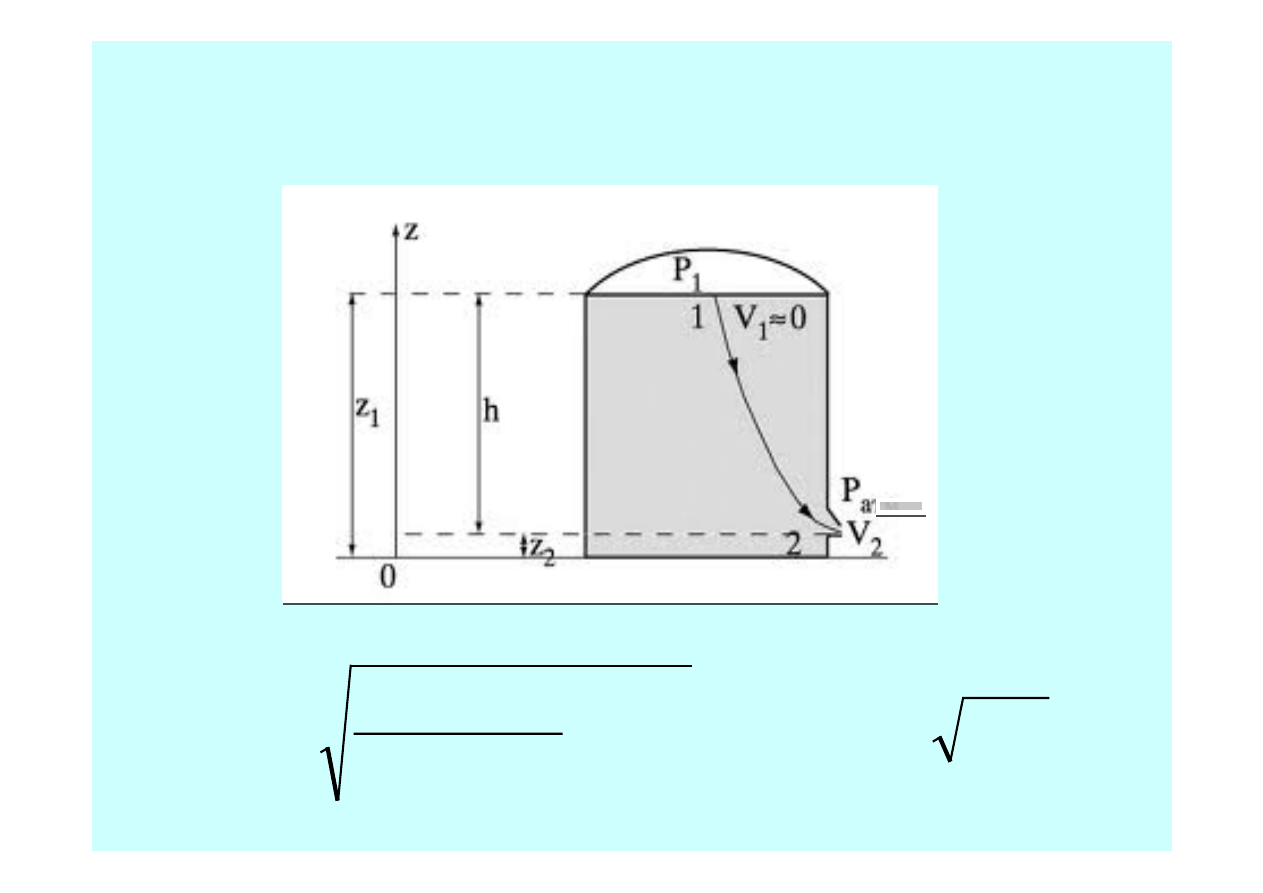
Wypływ cieczy ze zbiornika przez mały otwór

2

2

(

)

gh

p

p

a

2

2

1

2

+

−

=

ρ

υ

Woda wypływa do otoczenia przez mały otwór w zbiorniku,

który znajduje się na głębokości h = 180 cm. Nad zwierciadłem
wody panuje ciśnienie p

1

= 1,035 bar. Z jaką teoretyczną

prędkością wypływa woda, jeżeli ciśnienie otoczenia jest równe
p

a

= 1,01 bar.

Obliczyć strumień objętości oleju o gęstości ρ = 0,8 kg/l
wypływającego ze zbiornika jeżeli średnica przewodu
wynosi d = 32 mm. Nadciśnienie na manometrze przy
zamkniętym i otwartym zaworze wynosi odpowiednio
p

z

= 1,035 bar i p

o

= 1,019 bar.

υ

μ

ρ

υ

ρ

r

r

r

Δ

⋅

+

−

=

gradp

F

dt

d

m

⎟⎟

⎠

⎞

⎜⎜

⎝

⎛

∂

∂

+

∂

∂

+

∂

∂

+

∂

∂

−

=

⎟⎟

⎠

⎞

⎜⎜

⎝

⎛

∂

∂

+

∂

∂

+

∂

∂

+

∂

∂

2

2

2

2

2

2

z

y

x

x

p

F

z

y

x

t

x

x

x

x

x

z

x

y

x

x

x

υ

υ

υ

μ

ρ

υ

υ

υ

υ

υ

υ

υ

ρ

. . .

. . .

)

(

y

υ

)

(

z

υ

Podstawy dynamiki płynów rzeczywistych

Równania Naviera-Stokesa

Claude Louis Marie Henri Navier (1785-1836)

francuski inżynier i fizyk

George Gabriel Stokes (1819-1903),

irlandzki matematyk i fizyk

Przepływy laminarne i turbulentne

Doświadczenia

Reynoldsa (1883)

ν

υ

μ

ρυ

D

D

Re

=

=

2000

÷ 2300

=

kr

Re

Osborne Reynolds (1842 – 1912),

irlandzki inżynier

Przepływ przez kratkę

Turbulencja jednorodna

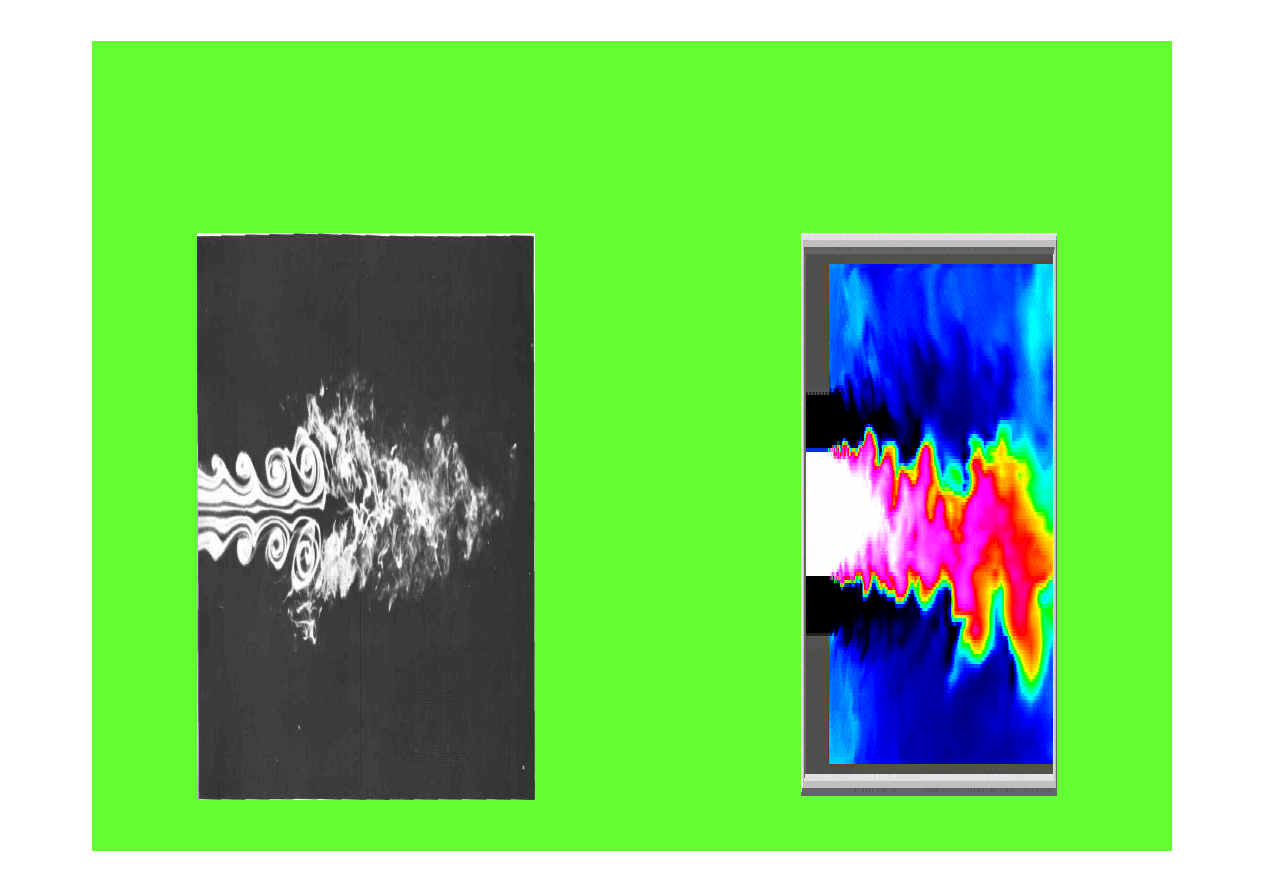
Struga

Re =10000

wody dymu

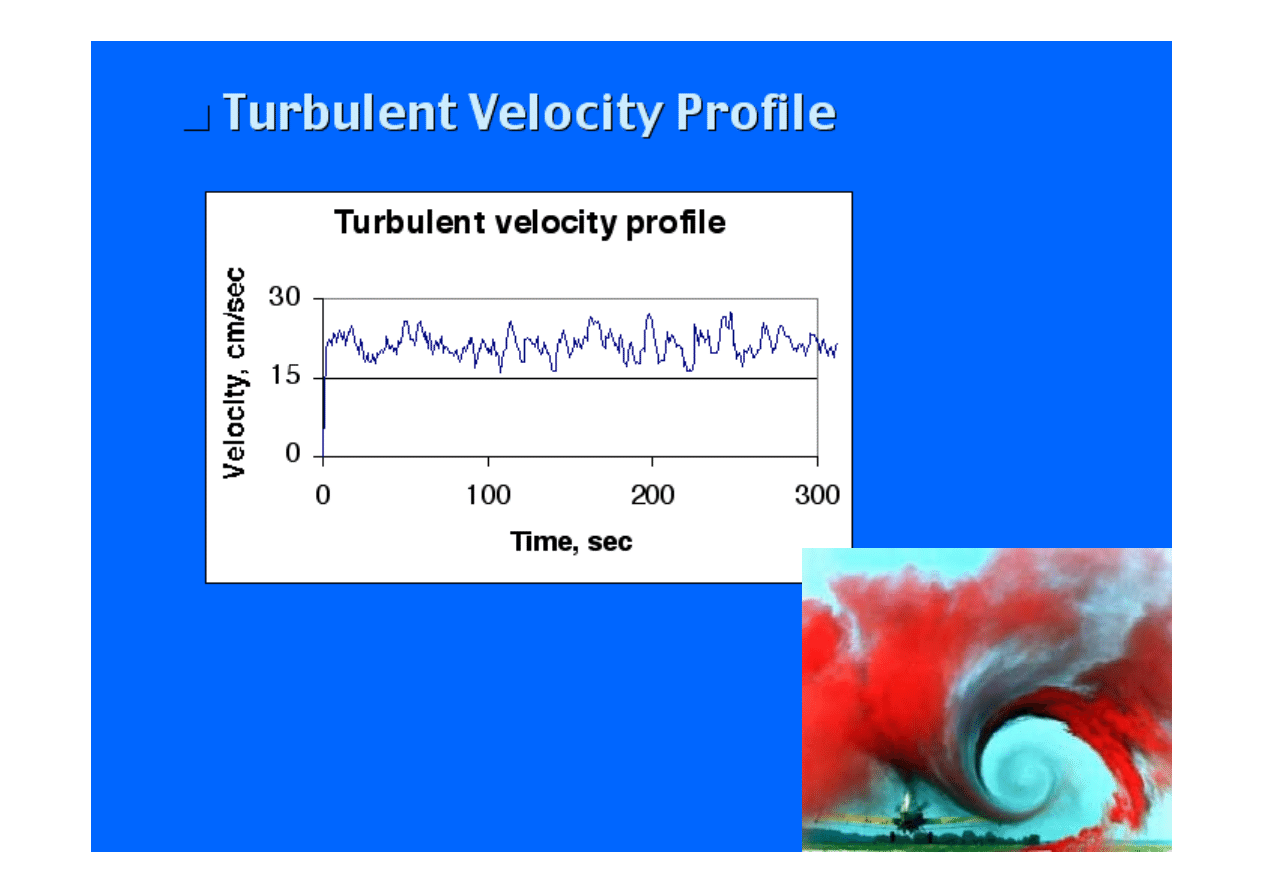
Reguły Reynoldsa Reguły uśredniania

x

x

x

υ

υ

υ

′

+

=

P

P

P

′

+

=

y

y

y

υ

υ

υ

′

+

=

z

z

z

υ

υ

υ

′

+

=

wartość

wartość

pulsacja

chwilowa średnia (fluktuacja)

0

=

−

=

−

=

′

x

x

x

x

x

υ

υ

υ

υ

υ

0

≠

′

′

y

x

υ

υ

x

x

υ

υ

=

L

0

2

≠

′

=

′

′

x

x

x

υ

υ

υ

jednopunktowe momenty korelacyjne

∫

−

=

2

1

1

2

1

t

t

x

x

dt

t

t

υ

υ

Przepływ turbulentny, nieściśliwy, stacjonarny

, gdzie

0

=

∂

∂

t

i

υ

,

const

=

ρ

Równania Reynoldsa

z

y

x

z

y

x

x

p

F

z

y

x

z

x

y

x

x

x

x

x

x

x

z

x

y

x

x

∂

′

′

∂

−

∂

′

′

∂

−

∂

′

∂

−

⎟⎟

⎠

⎞

⎜⎜

⎝

⎛

∂

∂

+

∂

∂

+

∂

∂

+

+

∂

∂

−

=

⎟⎟

⎠

⎞

⎜⎜

⎝

⎛

∂

∂

+

∂

∂

+

∂

∂

)

(

)

(

)

(

2

2

2

2

2

2

2

υ

υ

ρ

υ

υ

ρ

υ

ρ

υ

υ

υ

μ

ρ

υ

υ

υ

υ

υ

υ

ρ

[ ]

⎥

⎥

⎥

⎥

⎦

⎤

⎢

⎢

⎢

⎢

⎣

⎡

′

−

′

′

−

′

′

−

′

′

−

′

−

′

′

−

′

′

−

′

′

−

′

−

=

2

2

2

z

y

z

x

z

z

y

y

x

y

z

x

y

x

x

ij

υ

ρ

υ

υ

ρ

υ

υ

ρ

υ

υ

ρ

υ

ρ

υ

υ

ρ

υ

υ

ρ

υ

υ

ρ

υ

ρ

τ

L

Tensor naprężeń turbulentnych (Reynoldsa)

x

x

x

υ

υ

ε

2

′

=

y

y

y

υ

υ

ε

2

′

=

z

z

z

υ

υ

ε

2

′

=

Stopień lub intensywność turbulencji

2

2

2

2

2

z

y

x

q

υ

υ

υ

′

+

′

+

′

=

Energia kinetyczna turbulencji

Współczynnik korelacji (autokorelacji)

2

2

y

x

y

x

xy

R

υ

υ

υ

υ

′

′

′

′

=

Makro- i mikroskale turbulencji

( )

dx

x

R

xx

x

Δ

Λ

∫

∞

=

0

2

1

0

2

2

2

1

−

=

⎟

⎟
⎠

⎞

⎜

⎜
⎝

⎛

−

=

x

xx

x

dx

R

d

Δ

λ

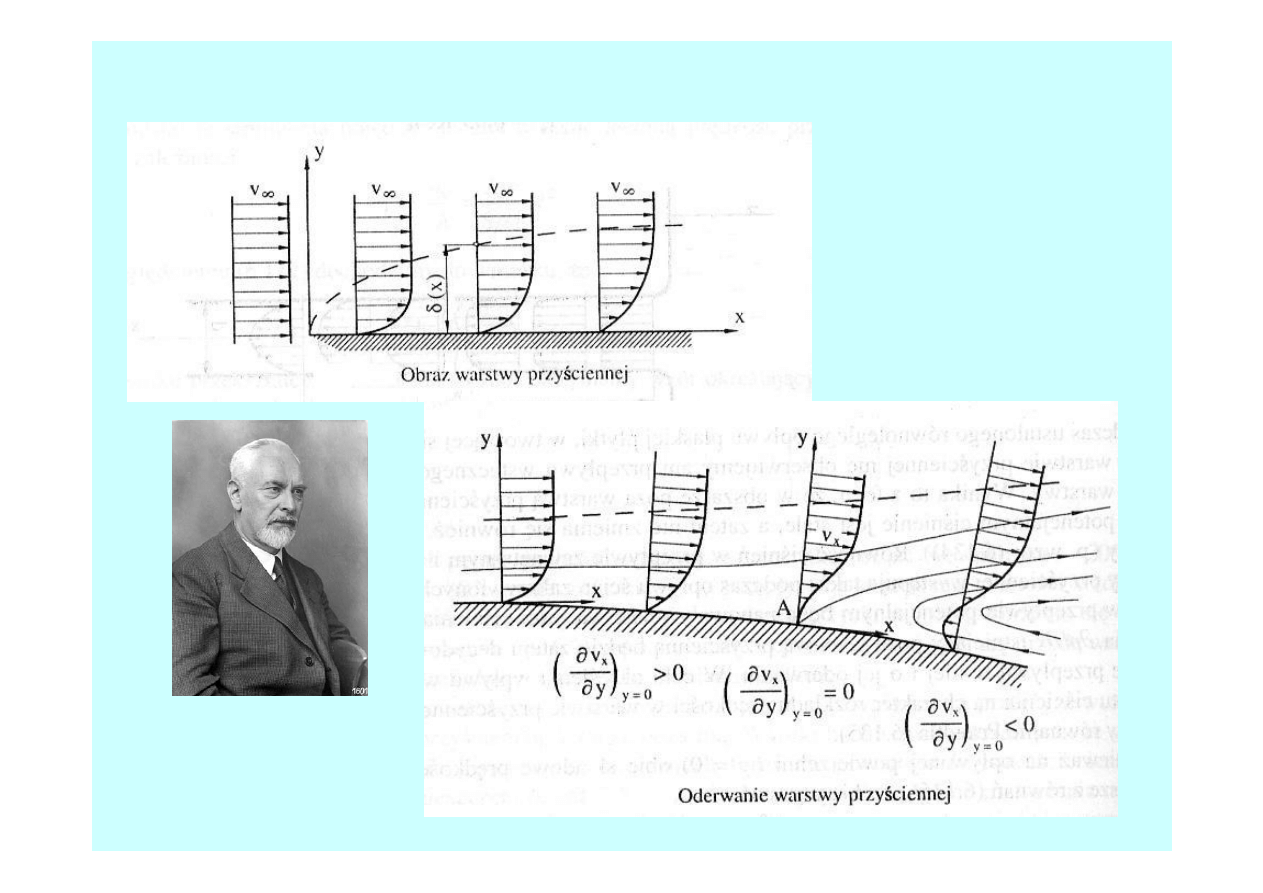
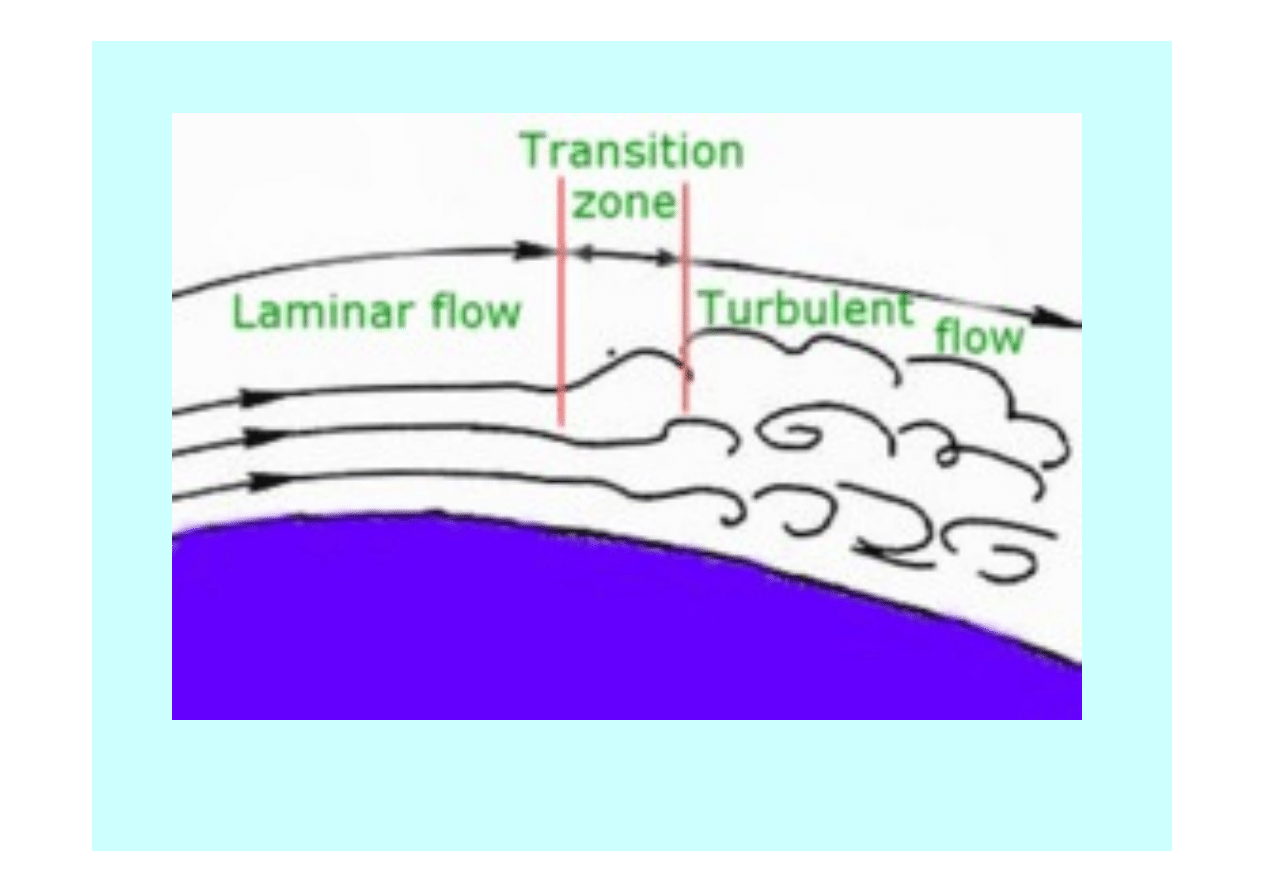
Warstwa przyścienna

−

)

x

(

δ

grubość
warstwy
przyściennej

Ludwig Prandtl (1875 - 1953),

niemiecki fizyk

v =

1

mm/s

Re = 13

Re = 26

Walec

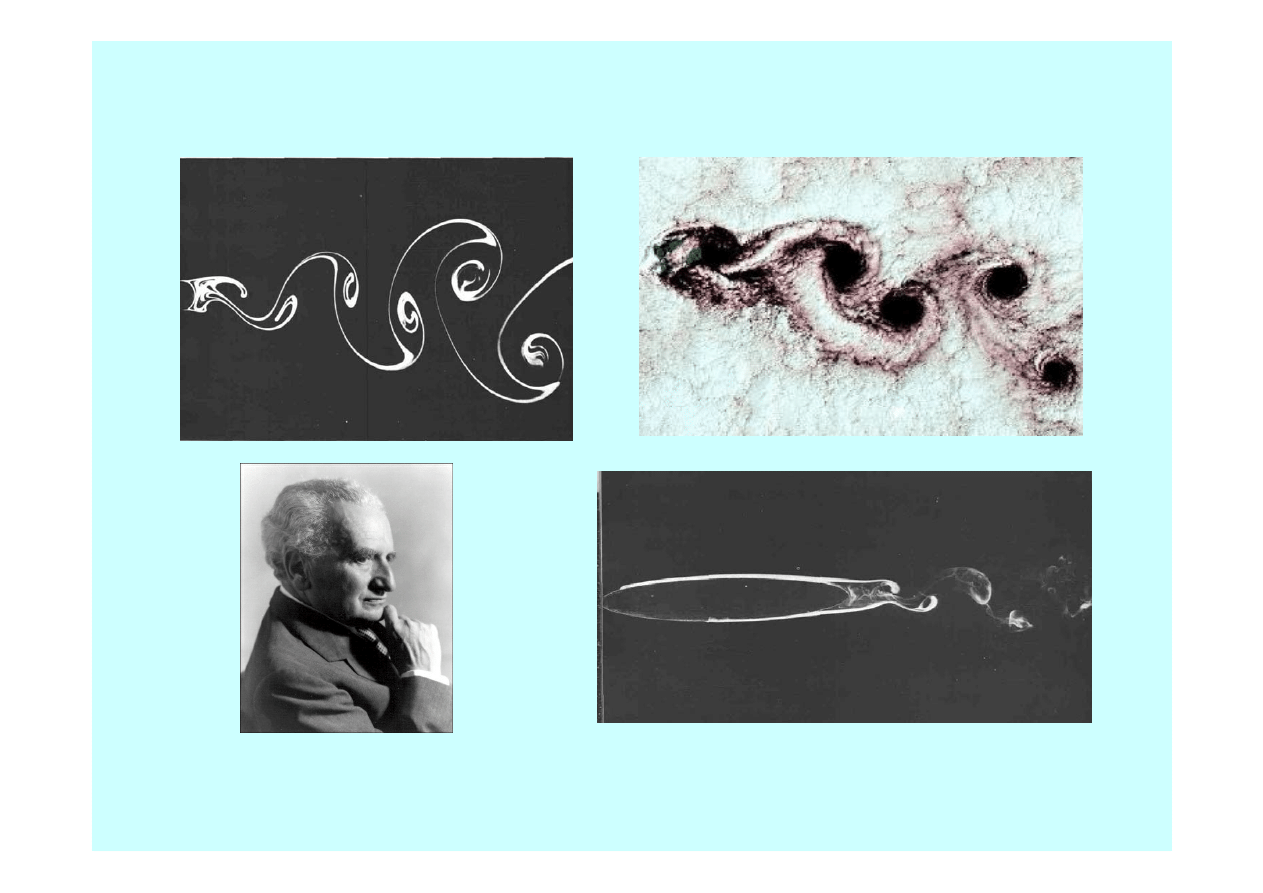
Ścieżka wirowa Karmana

Theodore von Kármán (węg. Szőllőskislaki
Kármán Tódor) (1881 - 1963) jest uważany za
pioniera nowoczesnej aerodynamiki.

Re = 26,8

Re = 15000

Kula

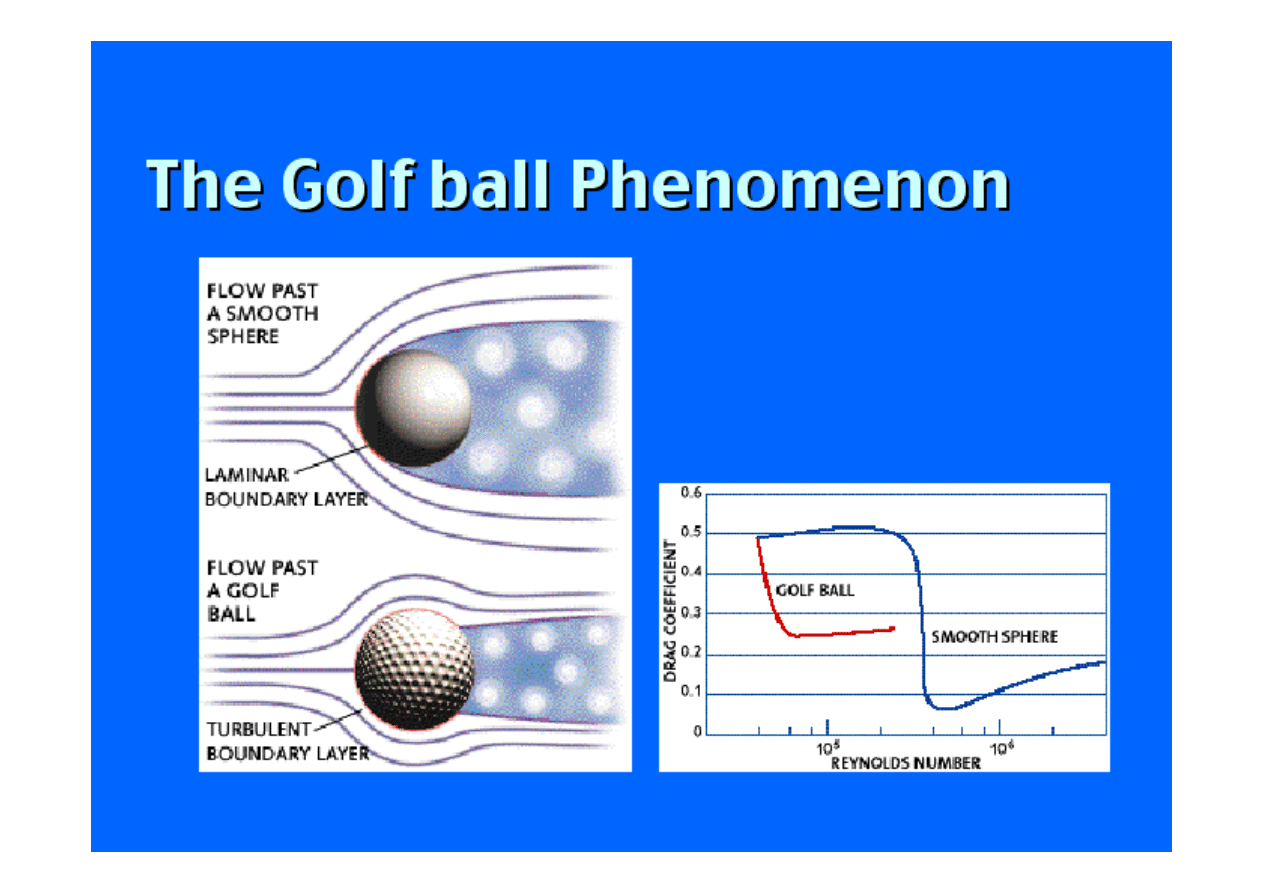
Ciecz o gęstości ρ = 0,85 kg/l płynie rurociągiem o
średnicy d = 30 mm z natężeniem przepływu Q = 2,5 l/s.
Lepkość dynamiczna cieczy µ = 0,05 Pa·s. Określić
charakter przepływu.

Przy jakim natężeniu przepływu cieczy nastąpi stan
krytyczny, jeżeli średnica rury d = 20 mm, a lepkość
kinematyczna ν = 0,05·10־³ m²/s?

Woda płynie rurociągiem z natężeniem przepływu Q = 0,2
l/s. Lepkość dynamiczna wody µ = 0,001 Pa·s. Jaka może
być wartość średnicy rury aby przepływ został
laminarnym?

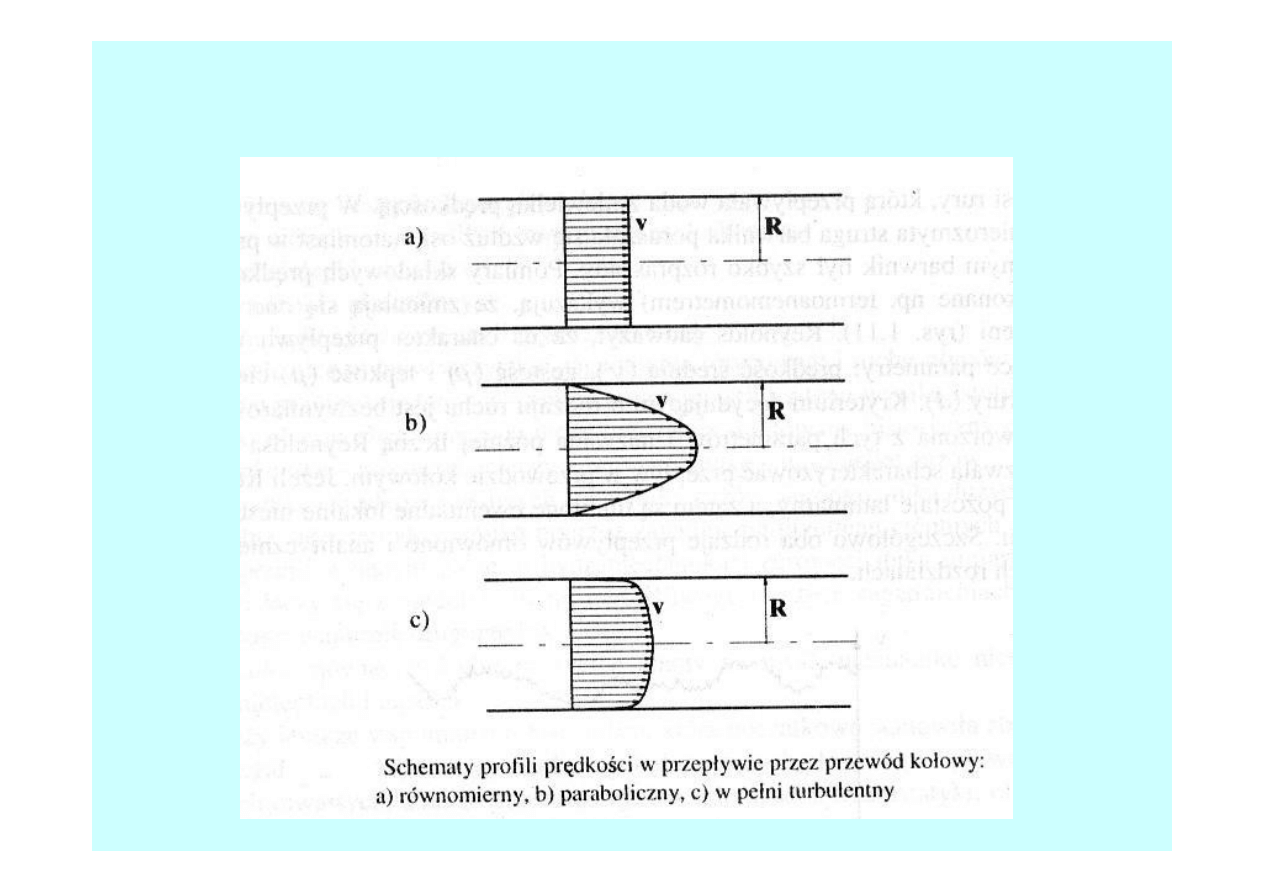
Przepływy w przewodach pod ciśnieniem

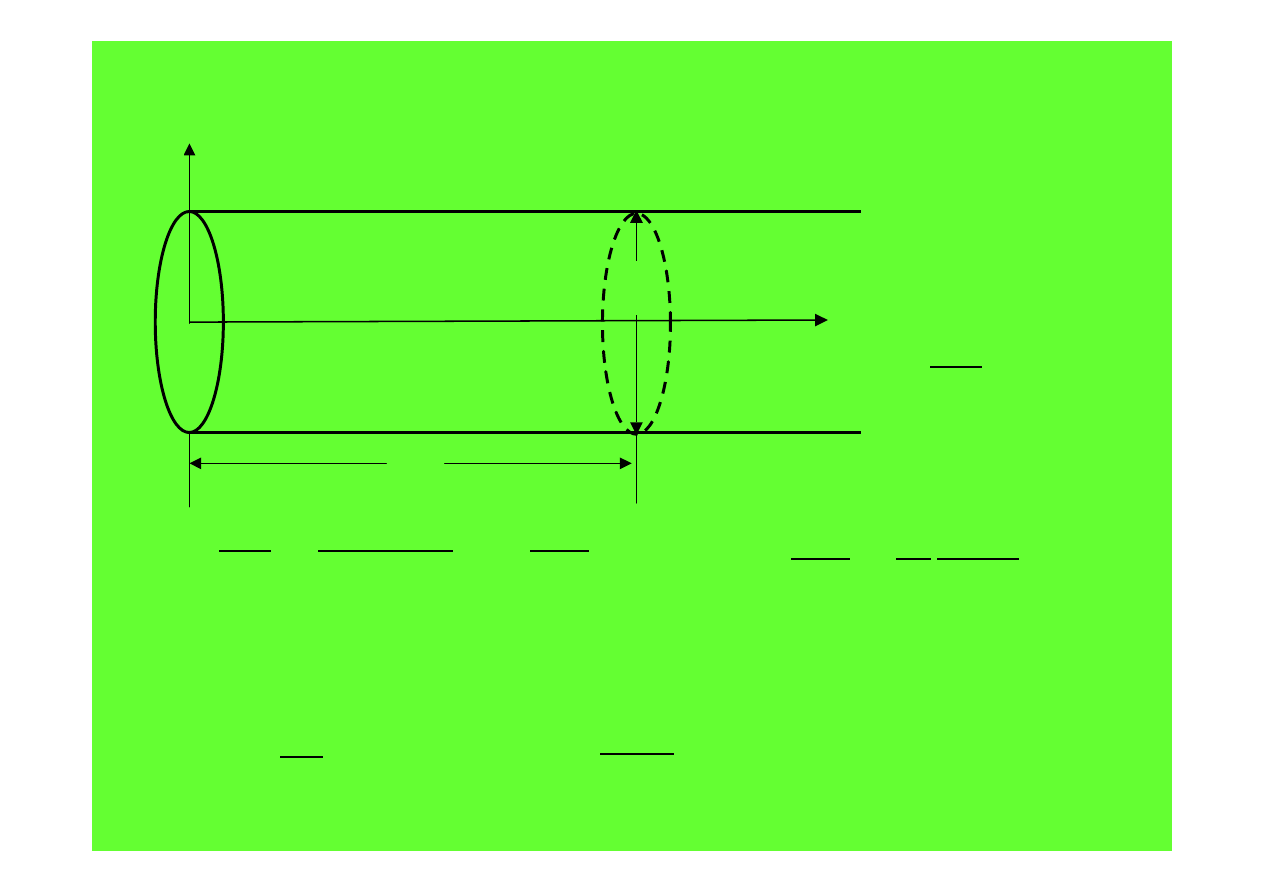
2

2

ρυ

λ

d

L

p =

Δ

Straty liniowe

L

p

L

p

p

x

p

Δ

−

=

−

=

∂

∂

1

2

0

=

∂

∂

y

p

p

p

p

Δ

=

−

2

1

λ

- współczynnik oporów liniowych

U

A

d

h

4

=

d

k

=

ε

)

(Re,

f

ε

λ

=

A - powierzchnia przekroju
U - obwód zwilżony

P

1

P

2

d

x

y

L

O

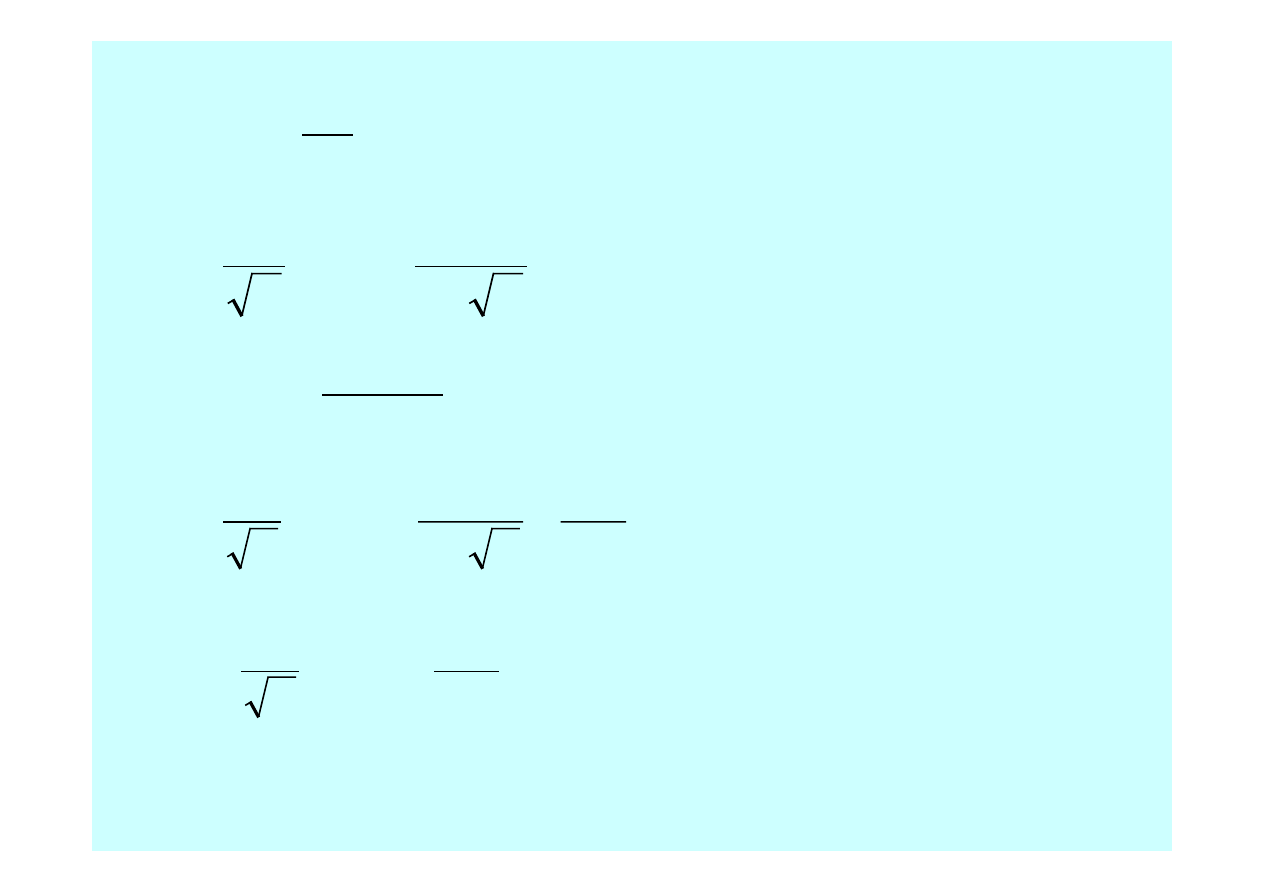
Re

64

=

λ

dla przepływów laminarnych
Re < 2000 ÷ 2300

(wzów Pioseuille’a)

λ

λ

Re

,

lg

51

2

2

1

−

=

k

L

>

δ

dla rur hydraulicznie gładkich

Re > 4 000 (wzór Prandtla – Karmana)

4

1

3164

0

/

Re

,

=

λ

(wzór Blasiusa ) 4 000 < Re < 100 000

⎟⎟

⎠

⎞

⎜⎜

⎝

⎛

+

−

=

71

3

51

2

2

1

,

Re

,

lg

ε

λ

λ

(wzór Colebrooka – White’a)

w strefie przejściowej

⎟

⎠

⎞

⎜

⎝

⎛

−

=

71

3

2

1

,

lg

ε

λ

(wzór Prandtla – Nikuradsego)

w strefie kwadratowej

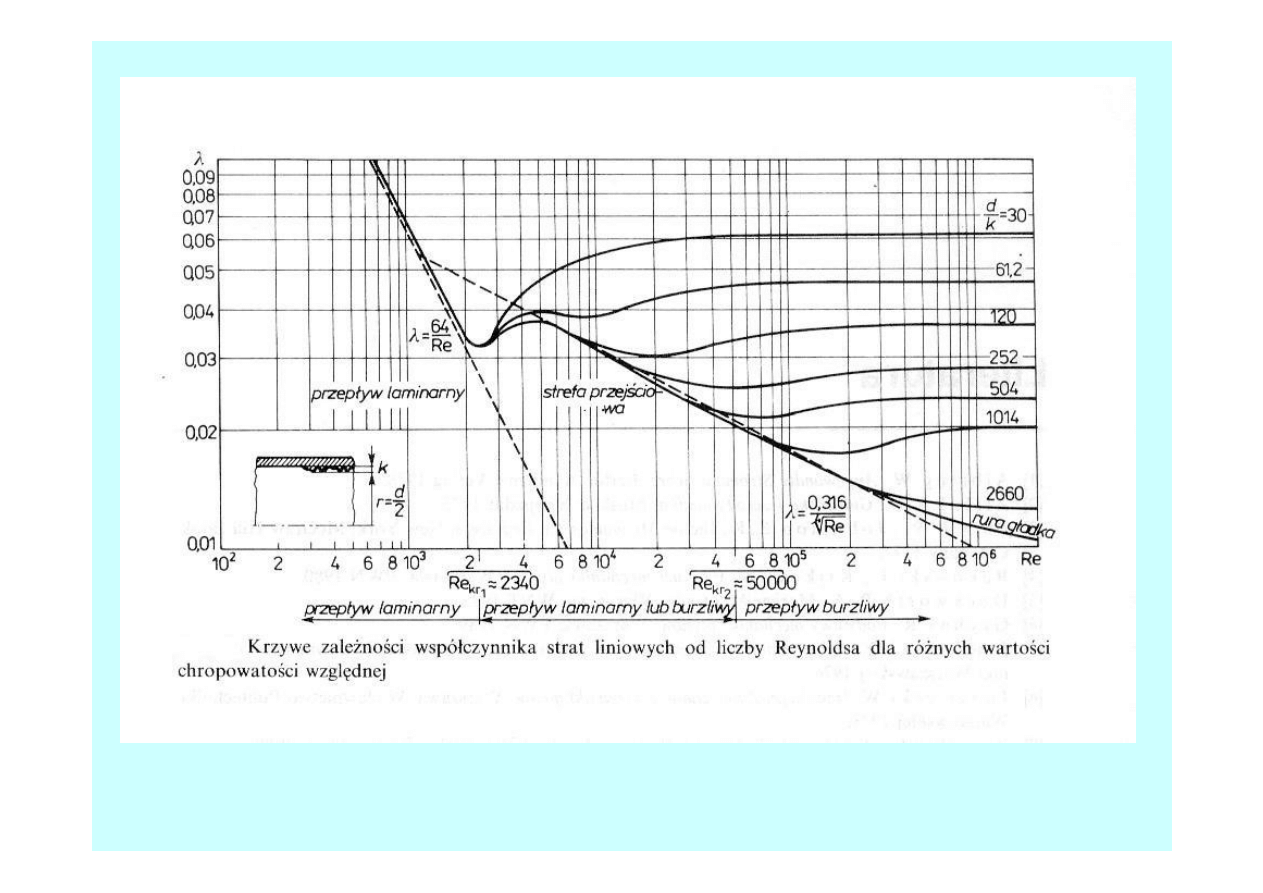
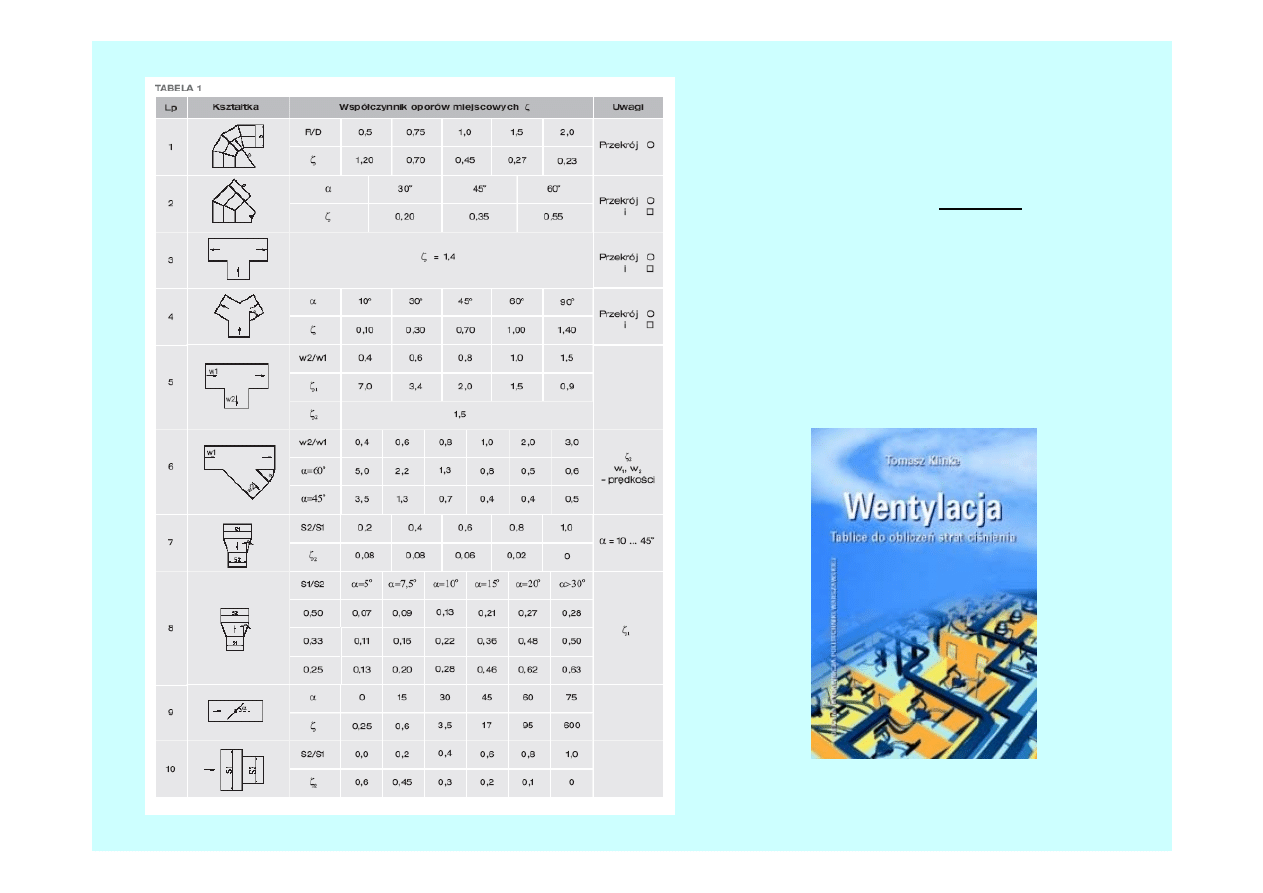
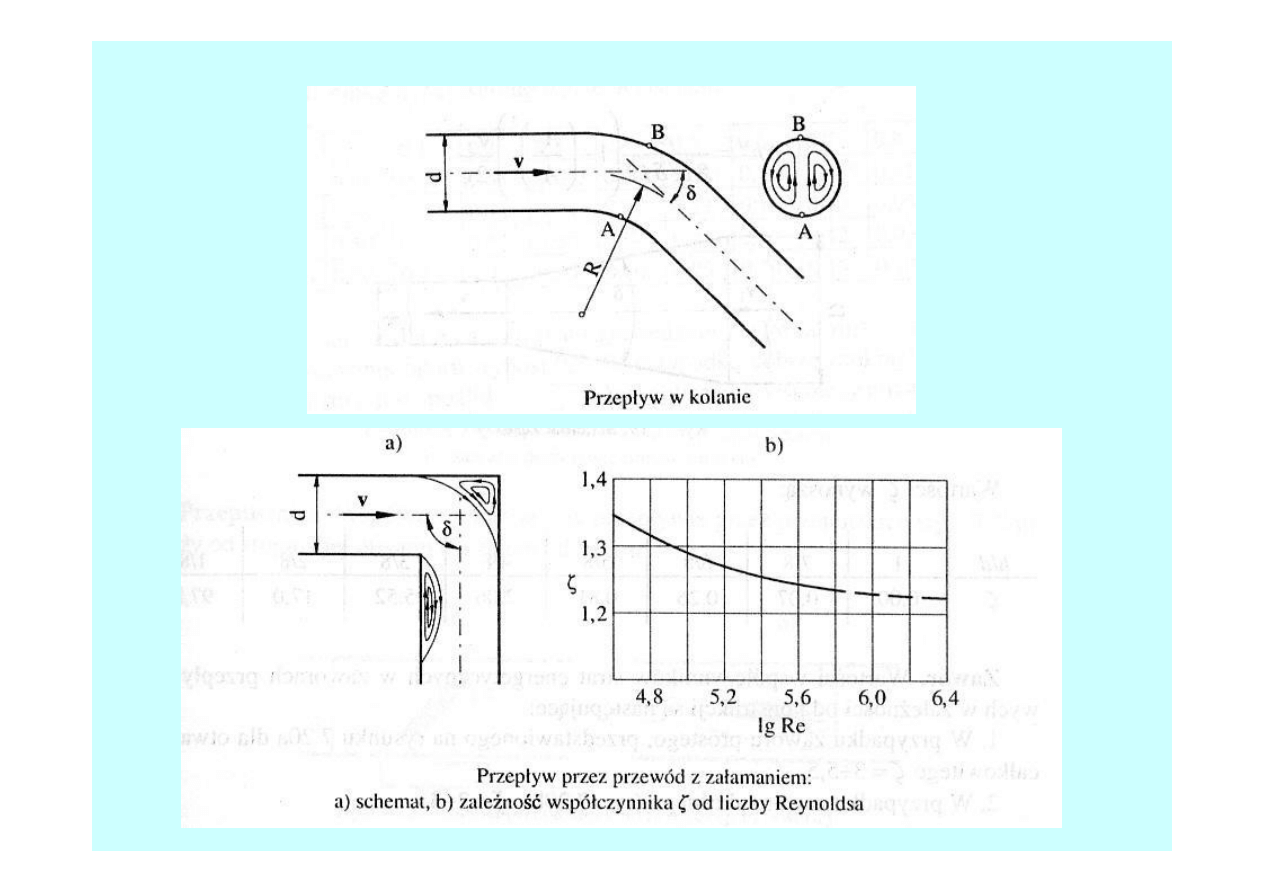
Straty miejscowe

-współczynnik oporów

miejscowych

ζ

2

2

ρυ

ζ

=

Δp

Gazy rzeczywiste

T

R

z

p

′

=

ρ

Równanie stanu gazu rzeczywistego

ρ

d

dp

a

=

T

R

k

p

k

a

′

=

=

ρ

Prędkość dźwięku

z

– współczynnik ściśliwości

Prędkość rozchodzenia się dźwięku dla różnych ośrodków:

•lód - 3300 m/s

•beton - 3800 m/s

•stal - 5100 m/s - 6000 m/s

•szkło - 6000 m/s

•powietrze - 340 m/s

•hel – 965 m/s

•woda - 1500 m/s

•rtęć - 1500 m/s

Ciepło właściwie

Ze względu na liczbę Macha można podzielić rodzaje przepływu na:

•nieściśliwy: Ma << 1
•poddźwiękowy: Ma < 1
•dźwiękowy: Ma = 1
•okołodźwiękowy: 0.8 < Ma < 1.2
•naddźwiękowy: Ma > 1
• hiperdźwiękowy: Ma >> 1

a

Ma

υ

=

Liczba Macha

v

v

c

v

T

u

T

q

c

⎟

⎠

⎞

⎜

⎝

⎛

∂

∂

=

⎟

⎠

⎞

⎜

⎝

⎛

∂

∂

=

p

p

c

p

T

i

T

q

c

⎟

⎠

⎞

⎜

⎝

⎛

∂

∂

=

⎟

⎠

⎞

⎜

⎝

⎛

∂

∂

=

R

c

c

v

p

′

=

−

κ

=

v

p

c

c

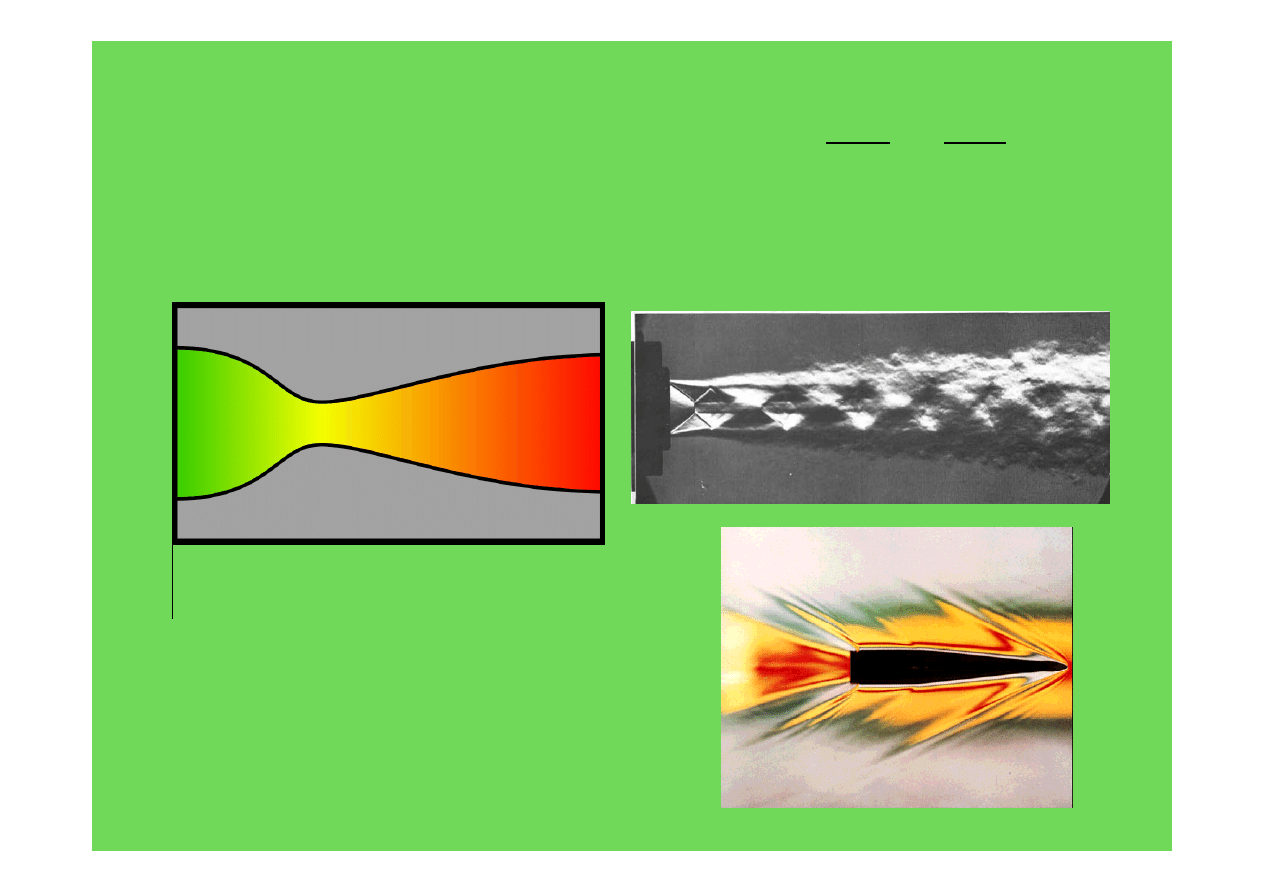
Równanie Hugoniota

(

)

A

dA

d

Ma

=

−

υ

υ

1

2

Fale uderzeniowe

Dysza de Lavala

1

<

Ma

1

=

Ma

1

>

Ma

Przepływy w ośrodkach porowatych

Porowatość powierzchniowa.
Porowatość objętościowa.
(0,259 ÷0,476)

p

rz

A

Q

=

υ

A

Q

=

υ

prędkość filtracji

A

A

m

p

A

=

V

V

m

p

V

=

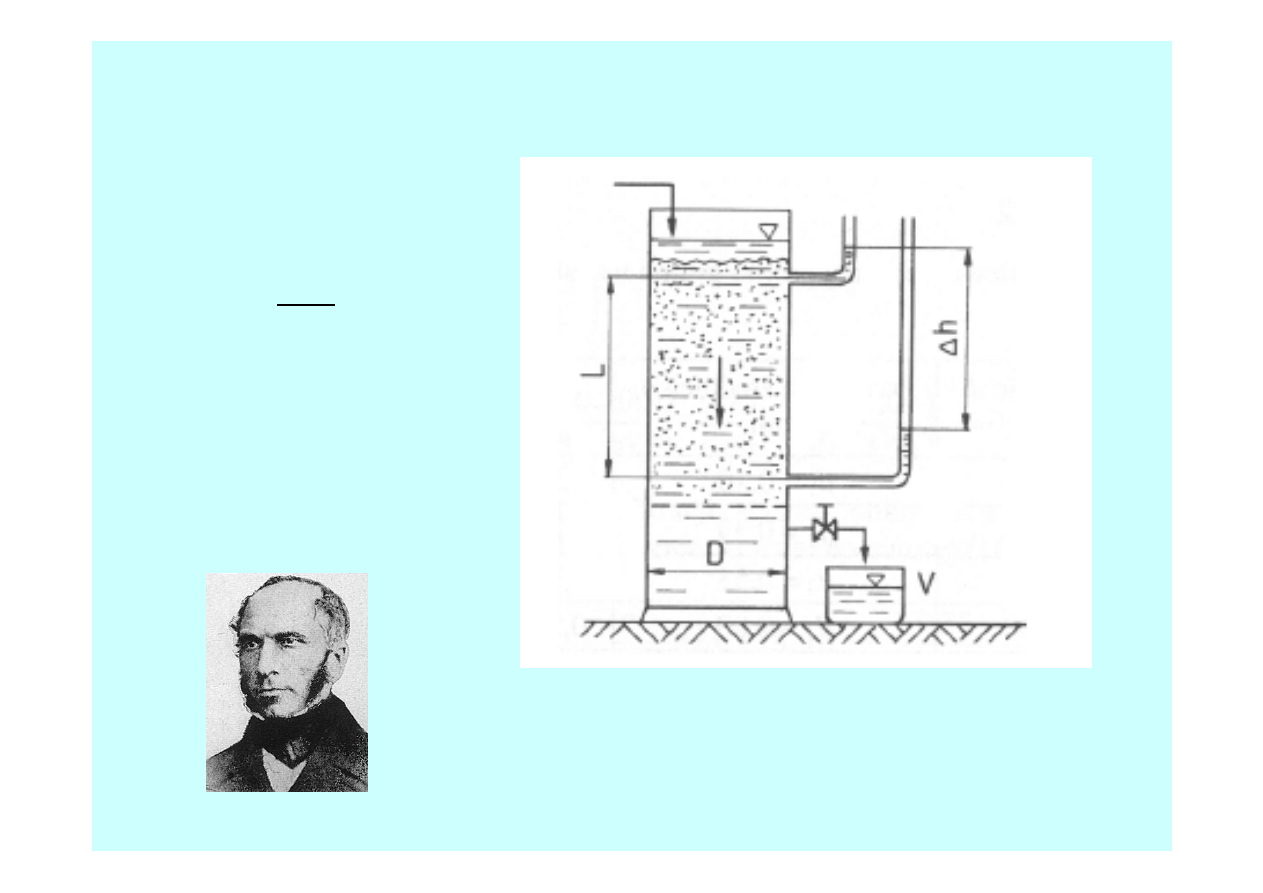
Henry Philibert Gaspard Darcy
(1803 - 1858) – francuski naukowiec.

k

- współczynnik filtracji

I

- spadek hydrauliczny

L

- droga filtracji

Prawo Darcy’ego

I

k

⋅

=

υ

dL

dh

I

=

Przepuszczalność

p

k

gradp

k

p

p

∇

−

=

−

=

μ

μ

υ

r

h

k

gradh

k

∇

−

=

⋅

−

=

υ

r

p

k

g

k

μ

ρ

=

0

=

∂

∂

+

x

h

k

x

x

υ

0

=

∂

∂

+

y

h

k

y

y

υ

0

=

∂

∂

+

z

h

k

z

z

υ

Równania Darcy’ego dla ośrodka niejednorodnego

.

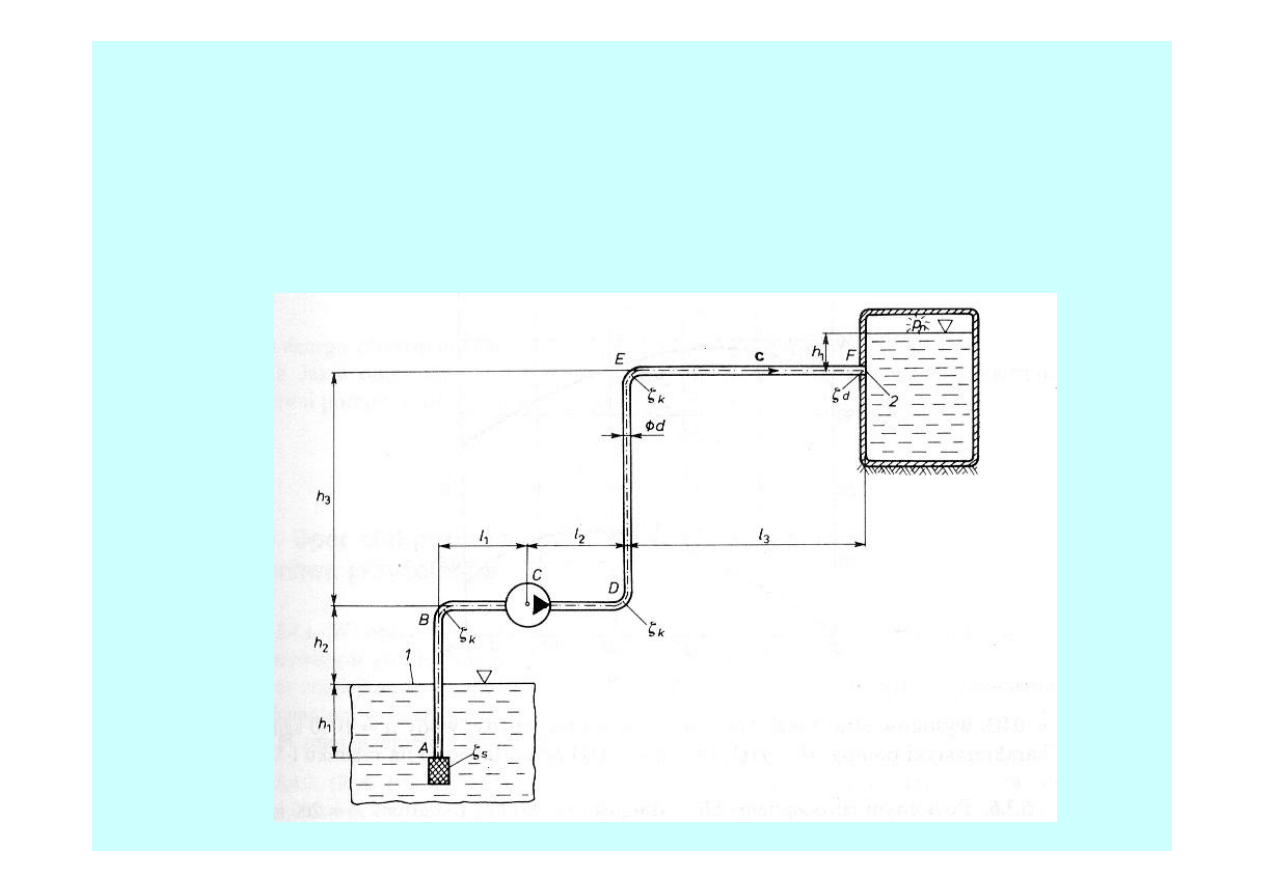
1. Obliczyć minimalną moc silnika

, niezbędnego do napędu pompy

przetłaczającej wodę w ilości Q = 300 l/min ze studni na głębokości

do

zbiornika, znajdującego się na wysokości od pompy. Długość rurociągu
ssawnego a rurociągu tłocznego . Przyjąć
współczynniki oporów miejscowych

, ,

, sprawność

pompy , ciśnienie , wysokość

.

e

N

m

h

6

2

=

m

h

18

3

=

m

l

h

h

12

1

2

1

=

+

+

m

l

h

l

24

3

3

2

=

+

+

3

,

9

=

s

ζ

3

,

0

=

k

ζ

0

,

1

=

d

ζ

76

0,

=

η

bar

p

g

5

,

1

=

m

h

2

4

=