Z. Kąkol-Notatki do Wykładu z Fizyki

14-1

Wykład 14

14. Statyka i dynamika płynów

Z makroskopowego punktu widzenia powszechnie przyjęty jest podział materii na

ciała stałe i płyny. Pod pojęciem substancji, która może płynąć rozumiemy ciecze i gazy.
Dla ciał sztywnych, mających określony rozmiar i kształt, sformułowaliśmy mechanikę
ciał sztywnych. Do rozwiązywania zagadnień z mechaniki płynów musimy wprowadzić
nowy formalizm ponieważ płyny łatwo zmieniają kształt, a w przypadku gazów przyj-
mują objętość równą objętości naczynia. Wygodnym jest w związku z tym sformułowa-
nie zasad dynamiki Newtona wraz z prawami opisującymi siły w szczególny sposób.

14.1

Ciśnienie i gęstość

Różnica w działaniu siły powierzchniowej na płyn i na ciało stałe polega na tym,

że dla cieczy siła powierzchniowa musi być zawsze prostopadła do powierzchni płynu
podczas gdy w ciele stałym może mieć dowolny kierunek. Spoczywający płyn nie może
równoważyć sił stycznych (warstwy płynu ślizgałyby się po sobie) i dlatego może zmie-
niać kształt i płynąć. Wygodnie jest więc opisywać siłę działającą na płyn za pomocą

ciśnienia p

zdefiniowanego jako wartość siły prostopadłej działającej na jednostkę po-

wierzchni

. Ciśnienie jest przekazywane na sztywne ścianki naczynia, a także na dowol-

ne przekroje płynów

prostopadle

do tych ścianek i przekrojów w każdym punkcie. Ci-

śnienie jest wielkością skalarną.
W układzie SI jednostką jest (pascal), 1 Pa = 1 N/m

2

. Innymi jednostkami są bar (1 bar

= 10

5

Pa), atmosfera (1 atm = 101325 Pa), mm Hg (760 mm Hg = 1 atm).

Płyn znajdujący się pod ciśnieniem wywiera siłę

na każdą powierzchnię będącą z nim w kontakcie.
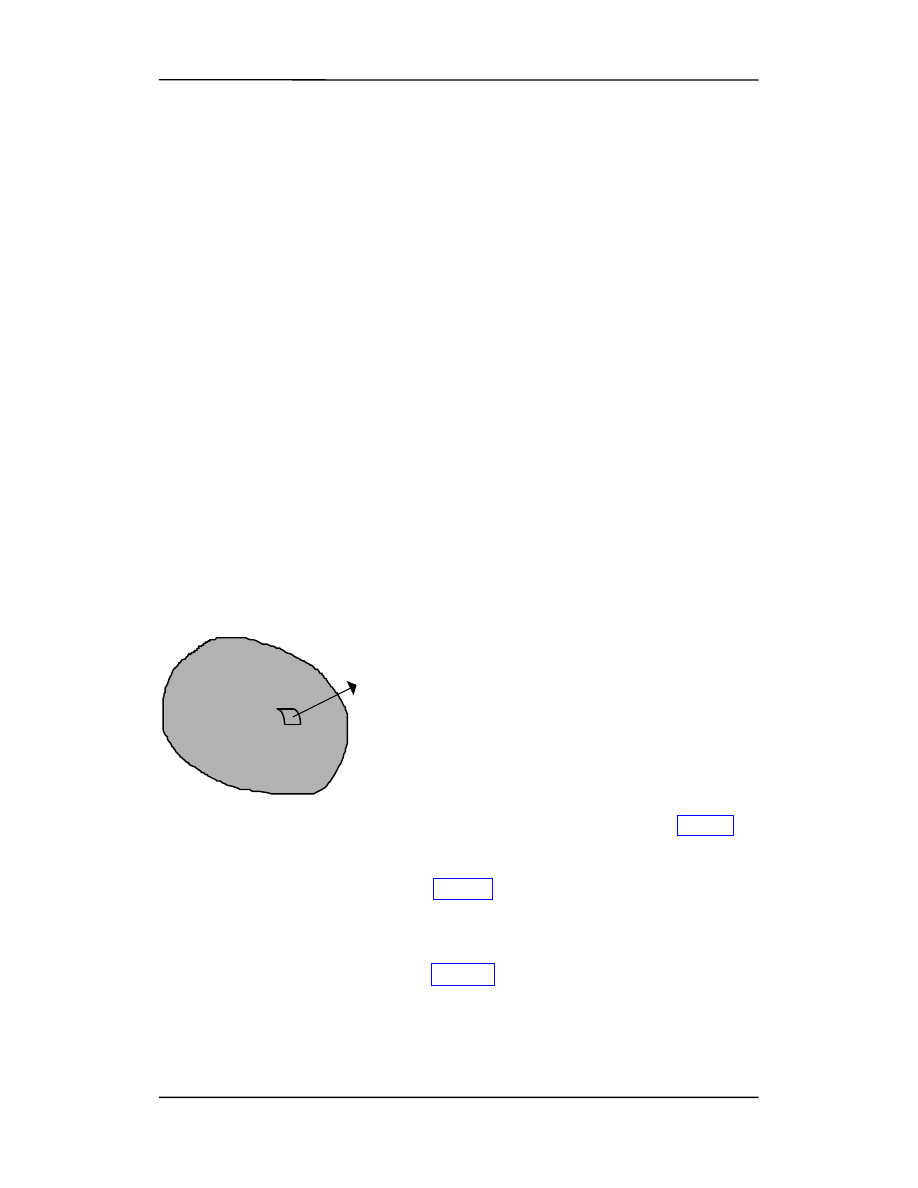
Rozważmy zamkniętą powierzchnię zawierającą
płyn (rysunek). Dowolny element powierzchni jest
reprezentowany przez wektor S (długość równa po-
wierzchni, kierunek prostopadły, zwrot na ze-
wnątrz). Wtedy siła F wywierana przez płyn na ten
element powierzchni wynosi

F = pS

(14.1a)

Ponieważ F i S mają ten sam kierunek więc ciśnienie p można zapisać

p = F/S

(14.1b)

Do opisu płynów stosujemy pojęcie

gęstości

ρ

:

ρ = m/V

(14.2)

Gęstość zależy od wielu czynników takich jak temperatura, ciśnienie. W tabeli przed-
stawiony jest zakres wartości gęstości spotykanych w przyrodzie.

S

S

Z. Kąkol-Notatki do Wykładu z Fizyki

14-2

Materiał

ρ

(kg/m

3

)

przestrzeń międzygwiezdna
najlepsza próżnia laboratoryjna
powietrze (1 atm 0

°

C)

powietrze (50 atm 0

°

C)

Ziemia:

wartość średnia

rdzeń

skorupa

Białe karły
jądro uranu

10

-18

- 10

-21

10

-17

1.3
6.5

5.52·10

3

9.5·10

3

2.8·10

3

10

8

- 10

15

10

17

14.2

Zmiany ciśnienia wewnątrz nieruchomego płynu

Gdy płyn znajduje się w równowadze to jego każda część jest w równowadze.

Rozpatrzmy element w kształcie cienkiego dysku znajdującego się w odległości y od
poziomu odniesienia. Grubość dysku wynosi dy, a powierzchnia każdej strony wynosi S.
Masa takiego elementu wynosi

ρSdy, a jego ciężar ρgSdy. Przypominam, że siły działa-

jące na element są w każdym punkcie prostopadłe do powierzchni (rysunek).

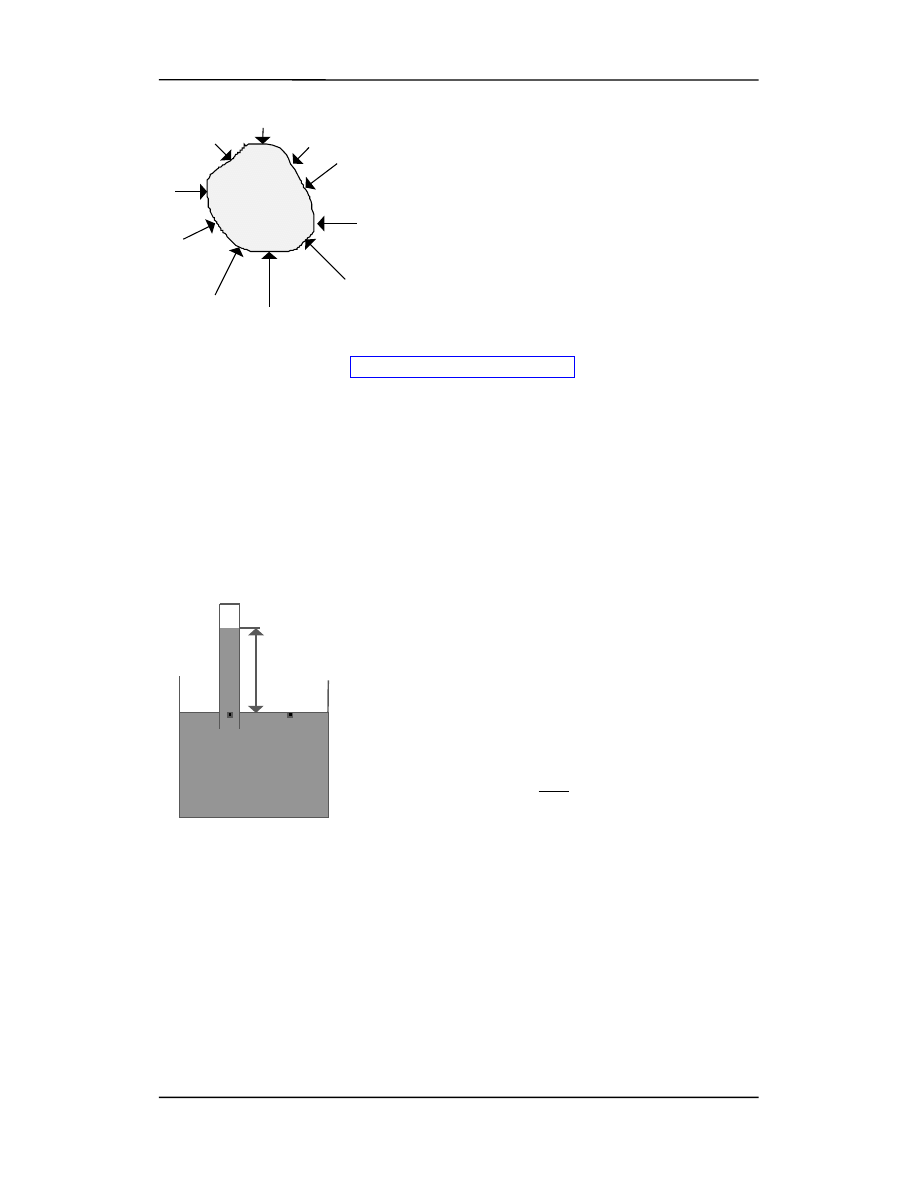
Siły poziome wywołane jedynie przez
ciśnienie płynu równoważą się. Siły
pionowe są wywoływane nie tylko
przez ciśnienie płynu ale też przez je-
go ciężar. Element płynu nie jest przy-
spieszany więc wypadkowa siła dzia-
łająca nań musi być zerem. Dla za-
chowania równowagi w pionie trzeba
więc by:

pS = (p+dp)S +

ρgSdy

a stąd

g

y

p

ρ

−

=

d

d

Równanie to pokazuje, że ciśnienie zmienia się ze zmianą wysokości ponad pewien po-
ziom odniesienia. Gdy wysokość rośnie tzn. dy > 0 wtedy dp < 0 tzn. ciśnienie maleje.
Powodem jest ciężar warstwy płynu leżącej pomiędzy punktami, dla których mierzymy
różnicę ciśnień. Dla cieczy zazwyczaj

ρ jest stałe (ciecze są praktycznie nieściśliwe),

różnice w wysokości nie są na tyle duże żeby uwzględniać zmiany g więc możemy dla
jednorodnej cieczy zapisać powyższe równanie w postaci:

g

y

p

ρ

−

=

∆

∆

(p+dp)S

pS

poziom odniesienia y=0

y

Z. Kąkol-Notatki do Wykładu z Fizyki

14-3

stąd

(p

2

- p

1

) = -

ρg(y

2

- y

1

)

Jeżeli powierzchnia cieczy jest swobodna to stanowi naturalny poziom odniesienia. Aby
przenieść poziom odniesienia na powierzchnię przyjmujemy y

2

równe wzniesieniu tej

powierzchni. Wtedy ciśnienie p

2

(na powierzchni) jest równe ciśnieniu atmosferyczne-

mu p

0

. Teraz y

1

opisuje położenie (wysokość) pewnego poziomu w cieczy. Ciśnienie na

tym poziomie oznaczmy p. Wtedy

p

0

- p = -

ρg(y

2

- y

1

)

Ponieważ y

2

- y

1

jest głębokością h poniżej poziomu cieczy więc

p = p

0

+

ρgh

(14.3)

Związek ten nie tylko pokazuje, że ciśnienie rośnie wraz z głębokością ale też, że jest
jednakowe dla punktów o tej samej głębokości.
Dla gazów

ρ jest małe i różnica ciśnień w dwóch punktach jest zazwyczaj do pominię-

cia i dlatego można przyjmować, że ciśnienie gazu w naczyniu jest wszędzie jednako-
we. Nie jest to jednak prawdziwe, gdy mamy do czynienia ze znaczną różnicą wysoko-
ści (gdy wznosimy się w atmosferze). Ciśnienie zmienia się wtedy znacznie, zmienia się
też

ρ. Np. na wysokości około 6 km ciśnienie wynosi 0.5 atm. Dla porównania 6 km w

głąb morza wynosi 600 atm.

14.3

Prawo Pascala i prawo Archimedesa

Na rysunku widzimy ciecz w naczyniu zamkniętym tłokiem, na który możemy

działać ciśnieniem zewnętrznym p

0

. W każdym punkcie A znajdującym się na głęboko-

ści h od górnej powierzchni cieczy, ciśnienie jest dane wyrażeniem

p = p

0

+

ρgh

Możemy powiększyć ciśnienie zewnętrzne o wartość

∆

p

0

. Po-

nieważ ciecze są nieściśliwe więc gęstość pozostaje praktycznie
bez zmian i dlatego ciśnienie teraz wynosi

p = p

0

+

∆

p

0

+

ρgh

Wynik ten został sformułowany przez Blaise Pascala i nazywa
się

prawem Pascala

. Prawo to formułuje się następująco:

ciśnie-

nie wywierane na zamknięty płyn jest przekazywane niezmienio-

ne na każdą część płynu oraz na ścianki naczynia

.

Prawo to jest konsekwencją praw mechaniki płynów podobnie jak

prawo Archimedesa

.

Kiedy ciało jest zanurzone w całości lub częściowo w spoczywającym płynie (cieczy lub
gazie) to płyn ten wywiera ciśnienie na każdą, będącą z nim w kontakcie, część po-
wierzchni ciała. Wypadkowa siła jest skierowana ku górze i zwie się

siłą wyporu

.

p

0

A

h

Z. Kąkol-Notatki do Wykładu z Fizyki

14-4

Ponieważ ciśnienie wywierane na ciało nie zależy od
materiału, z którego zrobiono ciało więc zastąpmy
w naszym rozumowaniu rozpatrywane ciało przez ten
sam płyn co płyn otoczenia. Na ten płyn będzie działa-
ło to samo ciśnienie co na ciało, które zastąpił. Poza
tym płyn będzie nieruchomy. Stąd działająca nań siła
będzie równa ciężarowi płynu i skierowana ku górze
tak, żeby ten ciężar zrównoważyć. Otrzymujemy

pra-

wo Archimedesa:

ciało w całości lub częściowo zanu-

rzone w płynie jest wypierane ku górze siłą równą cię-

żarowi wypartego przez to ciało płynu

. Tak więc

F

wyporu

= m

wypartego płynu

g =

ρVg

(14.4)

gdzie

ρ jest gęstością płynu, a V objętością części zanurzonej ciała.

14.4

Pomiar ciśnienia (barometr)

Evangelista Torricelli wynalazł w 1643 r barometr rtęciowy i tym samym podał spo-

sób pomiaru ciśnienia atmosferycznego. Barometr Torricellego składa się z rurki wypeł-
nionej rtęcią (

ρ = 13.6*10

3

kg/m

3

), którą odwracamy nad naczyniem z rtęcią tak jak na

rysunku. Ciśnienia w punktach A i B muszą być jednakowe bo punkty te są na jednako-
wej wysokości. Zgodnie z naszymi uprzednimi rozważaniami

p

A

=

ρgh

podczas gdy

p

B

= p

atm

Ponieważ p

A

= p

B

więc

ρgh = p

atm

g

p

h

atm

ρ

=

= 0.76 m

Mierząc wysokość słupa rtęci mierzymy wielkość ciśnienia atmosferycznego.
Przejdziemy teraz do opisu ruchu płynu (dynamika płynów).

14.5

Ogólny opis przepływu płynów

Znane są dwa podejścia do opisu ruchu płynu. Pierwsze wymaga "podzielenia" pły-

nu na nieskończenie małe cząstki (elementy objętości) i śledzenie tych elementów.
Oznacza to, że dla każdej cząstki mamy współrzędne x, y, z i ich zależność od czasu. W
ten sposób skonstruować można opis ruchu płynu (Joseph Louis Lagrange koniec XVIII
w).

Drugie podejście zaproponowane przez Leonharda Eulera jest bardziej wygodne.

Zamiast opisywać historię każdej z cząstek określamy gęstość płynu i jego prędkość

pró

żnia, p=0

B

A

h

Z. Kąkol-Notatki do Wykładu z Fizyki

14-5

w każdym punkcie przestrzeni i w każdej chwili czasu. Czyli podajemy

ρ(x,y,z,t) oraz

v

(x,y,z,t). Oznacza to, że koncentrujemy się na wybranym punkcie przestrzeni w pew-

nym czasie.
Na wstępie rozpatrzmy pewne ogólne właściwości charakteryzujące przepływ.

•

Przepływ może być

ustalony

(laminarny) lub

nieustalony

. Ruch płynu jest ustalony,

kiedy prędkość płynu v jest w dowolnie wybranym punkcie stała w czasie tzn. każda
cząstka przechodząca przez dany punkt zachowuje się tak samo. Warunki takie osiąga
się przy niskich prędkościach.

•

Przepływ może być

wirowy

lub

bezwirowy

. Przepływ jest bezwirowy, gdy w żadnym

punkcie cząstka nie ma wypadkowej prędkości kątowej względem tego punktu. Można
sobie wyobrazić małe kółko z łopatkami zanurzone w przepływającym płynie. Jeżeli
kółko nie obraca się to przepływ jest bezwirowy, w przeciwnym razie ruch jest wirowy.

•

Przepływ może być

ściśliwy

lub

nieściśliwy

. Zazwyczaj przepływ cieczy jest nieści-

śliwy (stała

ρ). Przepływ gazu też może być nieściśliwy tzn. zmiany gęstości są nie-

znaczne. Np. ruch powietrza względem skrzydeł samolotu podczas lotu z prędkością
mniejszą od prędkości głosu.

•

Przepływ może być

lepki

lub

nielepki

. Lepkość w ruchu płynów jest odpowiednikiem

tarcia w ruchu ciał stałych (lepkość smarów).

W naszych rozważaniach ograniczymy się do przepływów ustalonych, bezwirowych,

nieściśliwych i nielepkich. To znacznie upraszcza matematykę.

Nasze rozważania rozpoczniemy od wprowa-
dzenia pojęcia

linii prądu

.

W przepływie ustalonym

v jest stała w

czasie w danym punkcie. Rozważmy punkt P
wewnątrz płynu. Każda cząstka ma tam taką
samą prędkość. To samo dla punktów Q i R.
Jeżeli prześledzimy tor jednej cząstki to prze-
śledziliśmy zarazem tor każdej cząstki prze-
chodzącej przez P. Tor tej cząstki nazywamy

linią prądu. Linia prądu jest równoległa do prędkości płynu. Żadne linie prądu nie mogą
się przecinać bo istniała by niejednoznaczność w wyborze drogi przez cząstkę (a prze-
pływ jest ustalony).
Jeżeli wybierzemy pewną skończoną liczbę linii prądu to taką wiązkę nazywamy

strugą

prądu

. Brzegi składają się z linii

prądu więc płyn nie może przepły-
wać przez brzegi strugi. Płyn wcho-
dzący jednym końcem strugi musi
opuścić ją drugim.
Na rysunku obok prędkość cząstek
w punkcie P wynosi v

1

a pole prze-

kroju strugi A

1

. W punkcie Q odpo-

wiednio v

2

i

A

2

. W czasie

∆

t ele-

ment płynu prze-bywa odległość
v

∆

t. Masa płynu przechodzącego

przez A

1

w czasie

∆

t wynosi

v

P

P

Q

R

V

Q

v

R

A

1

P, v

1

A

2

Q, v

2

Z. Kąkol-Notatki do Wykładu z Fizyki

14-6

∆

m

1

=

ρ

1

A

1

v

1

∆

t

bo A

1

v

1

∆

t stanowi objętość elementu płynu. Wprowadzamy strumień masy jako

∆

m/

∆

t.

Wtedy otrzymujemy dla punktów P i Q odpowiednio

∆

m

1

/

∆

t =

ρ

1

A

1

v

1

oraz

∆

m

2

/

∆

t =

ρ

2

A

2

v

2

Ponieważ nie ma po drodze (między P i Q) żadnych "źródeł" ani "ścieków" więc stru-
mienie mas muszą być sobie równe.

ρ

1

A

1

v

1

=

ρ

2

A

2

v

2

Jeżeli płyn jest nieściśliwy to

ρ

1

=

ρ

2

i wtedy

A

1

v

1

= A

2

v

2

czyli

Av = const.

Z równania powyższego wynika, że prędkość płynu nieściśliwego przy ustalonym prze-
pływie jest odwrotnie proporcjonalna do pola przekroju. Linie prądu muszą się zagęsz-
czać w węższej części, a rozrzedzać w szerszej. Tzn. rzadko rozmieszczone linie ozna-
czają obszary niskiej prędkości, linie rozmieszczone gęsto obszary wysokiej prędkości.
Ponadto warto zauważyć, że skoro cząstki zwalniają przepływając z P do Q (v

1

> v

2

) to

poruszają się ruchem jednostajnie opóźnionym. Opóźnienie to może być wywołane gra-
witacją lub różnicą ciśnień, ale wystarczy wziąć jako przykład strugę poziomą, w której
grawitacja się nie zmienia, aby dojść do wniosku, że ciśnienie jest największe tam gdzie
prędkość najmniejsza (w przepływie ustalonym).

14.6

Równanie Bernoulliego

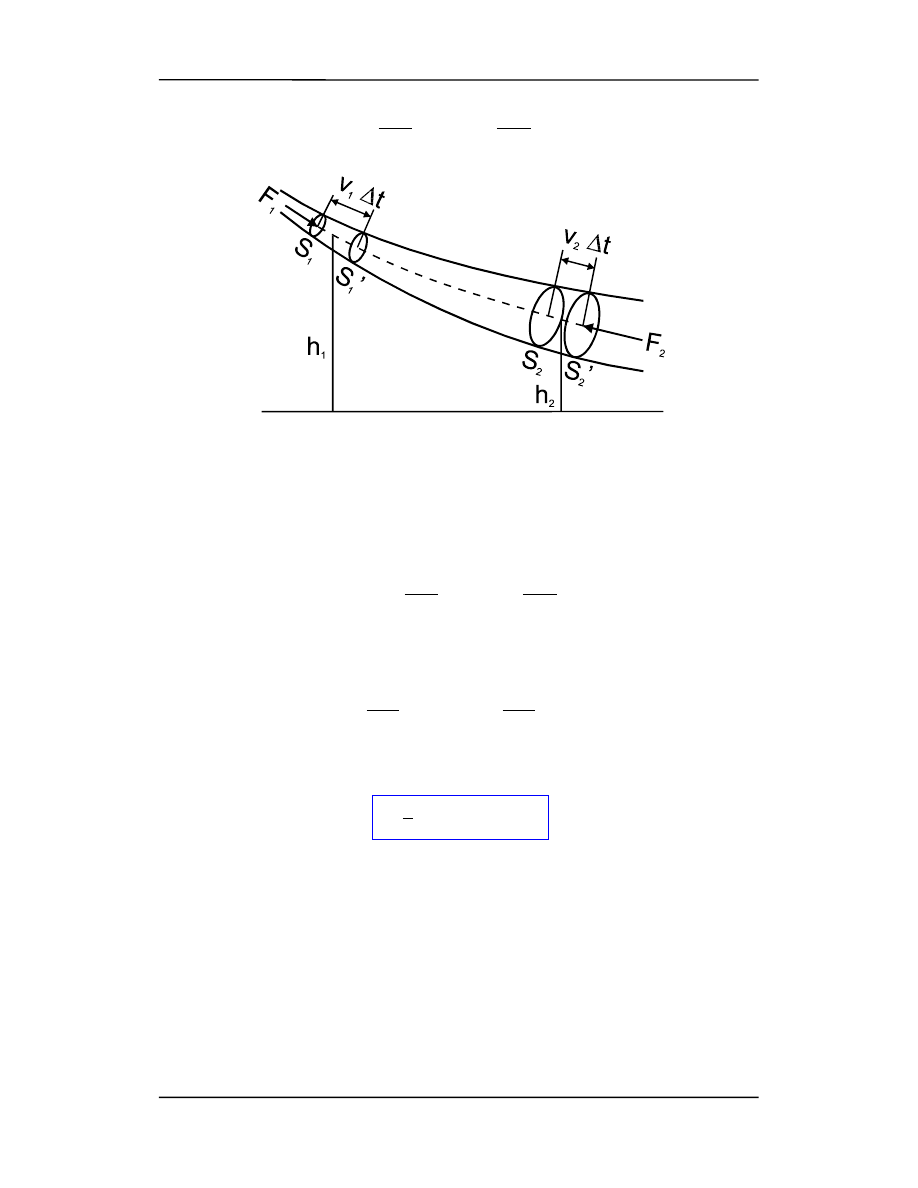
Rozważmy nielepki, ustalony, nieściśliwy przepływ płynu przez rurę (rysunek na na-

stępnej stronie). Ciecz na rysunku płynie w stronę prawą. W czasie

∆

t powierzchnia S

1

przemieszcza się o odcinek v

1

∆

t do położenia S

1

'. Analogicznie powierzchnia S

2

prze-

mieszcza się o odcinek v

2

∆

t do położenia S

2

'. Na powierzchnię S

1

działa siła F

1

= p

1

S

1

a

na powierzchnię S

2

siła F

2

= p

2

S

2

. Zwróćmy uwagę, że efekt sumaryczny przepływu

płynu przez rurkę polega na przeniesieniu pewnej objętości V płynu ograniczonej po-
wierzchniami S

1

S

1

' do położenia S

2

S

2

'. Twierdzenie o pracy i energii mówi, że praca

wykonana przez wypadkową siłę jest równa zmianie energii układu. Siłami, które wy-
konują pracę są F

1

i F

2

. Obliczamy więc pracę

V

p

p

t

S

p

t

S

p

t

F

t

F

W

)

(

1

2

1

1

1

2

2

2

1

1

2

2

−

=

∆

−

∆

=

∆

−

∆

=

v

v

v

v

oraz zmianę energii strugii

Z. Kąkol-Notatki do Wykładu z Fizyki

14-7









+

−









+

=

∆

1

2

1

2

2

2

2

2

mgh

m

mgh

m

E

v

v

Ponieważ

W =

∆E

to przy założeniu nieściśliwości płynu (

ρ = const)









+

−









+

=

−

1

2

1

2

2

2

1

2

2

2

)

(

mgh

m

mgh

m

V

p

p

v

v

Związek ten można przekształcić do postaci

2

2

2

2

1

2

1

1

2

2

gh

p

gh

p

ρ

ρ

ρ

ρ

+

+

=

+

+

v

v

czyli

const.

=

+

+

gy

p

ρ

ρ

2

2

1

v

(14.5)

Równanie to nosi nazwę

równania Bernoulliego

dla przepływu ustalonego, nielepkiego

i nieściśliwego. Jest to podstawowe równanie mechaniki płynów. Może być stosowane
do wyznaczenia prędkości płynu na podstawie pomiarów ciśnienia (rurka Venturiego,
rurka Pitota). Można też w oparciu o nie wyznaczyć dynamiczną siłę nośną.

14.6.1 Dynamiczna siła nośna

Dynamiczna siła nośna

jest to siła jaka działa na np. skrzydło samolotu, nartę wod-

ną, śmigło helikoptera, i wywołana jest ruchem tych ciał w płynie w odróżnieniu od sta-
tycznej siły nośnej, która jest siła wyporu działającą np. na balon czy statek zgodnie z

Z. Kąkol-Notatki do Wykładu z Fizyki

14-8

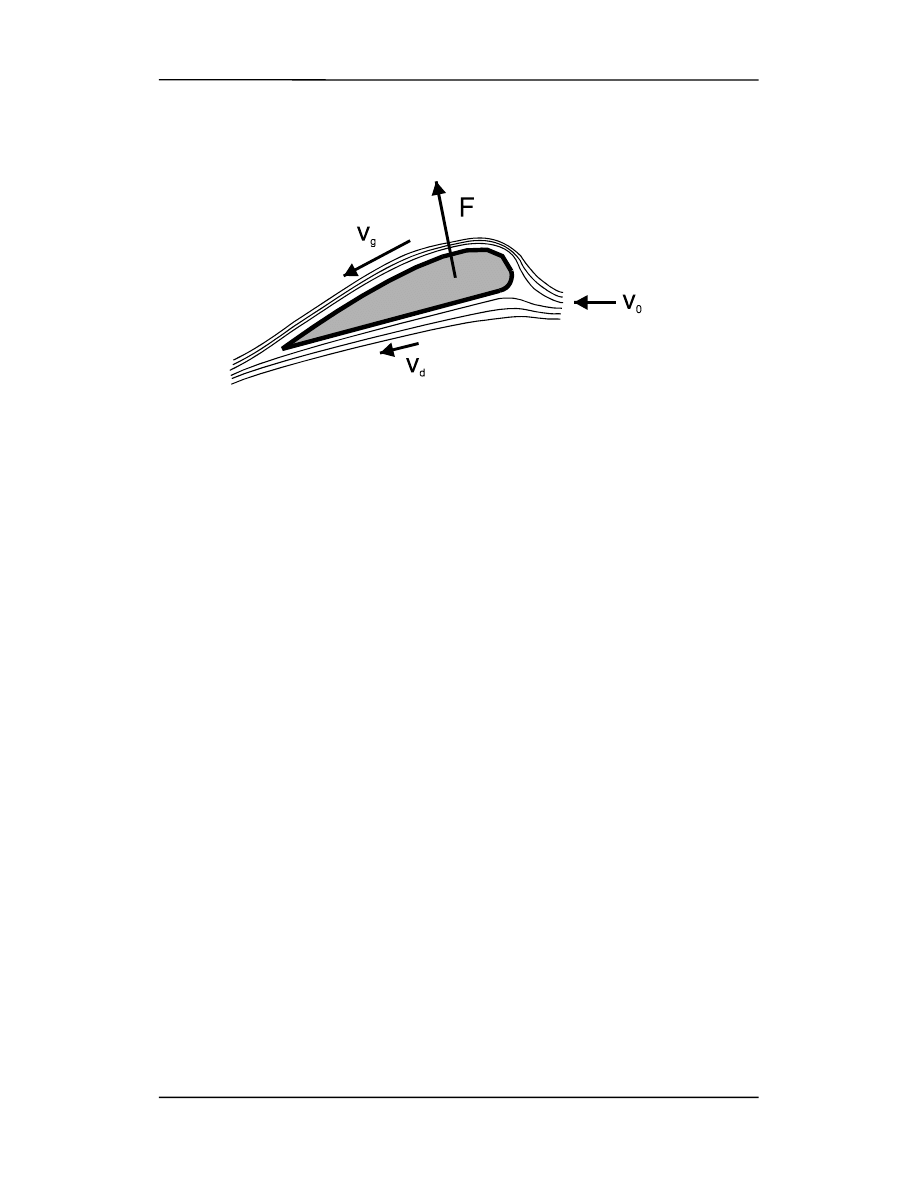
prawem Archimedesa. Na rysunku poniżej pokazane są schematycznie linie prądu wo-
kół skrzydła samolotu.

Analizując te linie prądu zauważymy, że ze względu na ustawienie skrzydła (kąt natar-
cia) linie prądu nad skrzydłem są rozmieszczone gęściej niż pod skrzydłem. Tak więc v

g

ponad skrzydłem jest większa niż pod skrzydłem v

d

a to oznacza zgodnie z prawem

Bernoulliego, że ciśnienie nad skrzydłem jest mniejsze od ciśnienia pod skrzydłem i
otrzymujemy wypadkową siłę nośną F skierowaną ku górze. Wynika to również z trze-
ciej zasady dynamiki Newtona. Prędkość v

0

powietrza zbliżającego się do skrzydła jest

pozioma podczas gdy powietrze za skrzydłem jest skierowane na ukos w dół (składowa
pionowa). Oznacza to, że skrzydło pchnęło powietrze w dół więc w reakcji powietrze
pchnęło skrzydło do góry.