STATYKA I DYNAMIKA

PŁYNÓW

Nazwa

płyny

obejmuje substancje

nie wykazujące

sprężystości kształtu:

ciecze i gazy

.

W przypadku brył, a więc ciał o jednoznacznie
określonych rozmiarach i kształcie, stosowaliśmy
mechanikę bryły sztywnej.

Opis mechaniki płynów musi być sformułowany w
inny sposób, ze względu na to, że nie mają one
zdefiniowanego kształtu. Oczywiście również w
mechanice płynów będziemy korzystać z zasad
dynamiki

Newtona,

chociaż

w

odpowiednio

zmodyfikowanej postaci.

Tradycyjnie odpowiednie działy fizyki noszą nazwę

hydrostatyka

(mechanika płynów nieruchomych

względem

przyjętego

układu

odniesienia)

i

hydrodynamika

(mechanika płynów poruszających

się w danym układzie odniesienia).

Ciśnienie i gęstość

Siła powierzchniowa

działająca na płyn musi być

zawsze prostopadła do jego powierzchni płynu,
podczas gdy w przypadku bryły może mieć dowolny
kierunek.

Płyn w spoczynku nie równoważy sił stycznych
(warstwy płynu ślizgałyby się po sobie), a więc może
zmieniać kształt.

Zatem siłę działającą na płyn będziemy opisywać za
pomocą ciśnienia p. Jest to, jak pamiętamy, wartość
siły

prostopadłej

działającej

na

jednostkę

powierzchni.

Ciśnienie działa na sztywne ścianki naczynia, a także
na dowolne przekroje płynów

prostopadle

do tych

ścianek i przekrojów w każdym punkcie.

Ciśnienie

jest wielkością skalarną wyrażaną w

układzie SI w

paskalach

(Pa) = (N/m

2

).

Jednostki pozaukładowe to

bar

(atmosfera fizyczna =

10

5

Pa),

atm

= 101325 Pa,

mm Hg

(760 mm Hg = 1

atm).

Płyn pod ciśnieniem działa siłą na każdą powierzchnię
będącą z nim w kontakcie.

Rozważmy zamkniętą powierzchnię zawierającą płyn i
wprowadźmy wektorowy element powierzchni dS =
ndS, podobnie, jak to robiliśmy w przypadku pola
grawitacyjnego.

Siła F wywierana przez płyn na ten element
powierzchni wynosi:

F = pS

Gęstość 

, jak wiemy, jest stosunkiem masy do

objętości płynu m/V (kg/m

3

). Zależy ona od

temperatury

i

ciśnienia

oraz

właściwości

materiałowych płynu.

Ponieważ F i S mają ten sam kierunek to:

p = F/S

Materiał

 (kg/m

3

)

przestrzeń międzygwiezdna

najlepsza próżnia laboratoryjna
powietrze (1 atm 0  C)
powietrze (50 atm 0  C)

Ziemia:

wartość średnia

rdzeń

skorupa

Białe karły

jądro uranu

10

-18

- 10

-21

10

-17

1.3

6.5

5.52·10

3

9.5·10

3

2.8·10

3

10

8

- 10

15

10

17

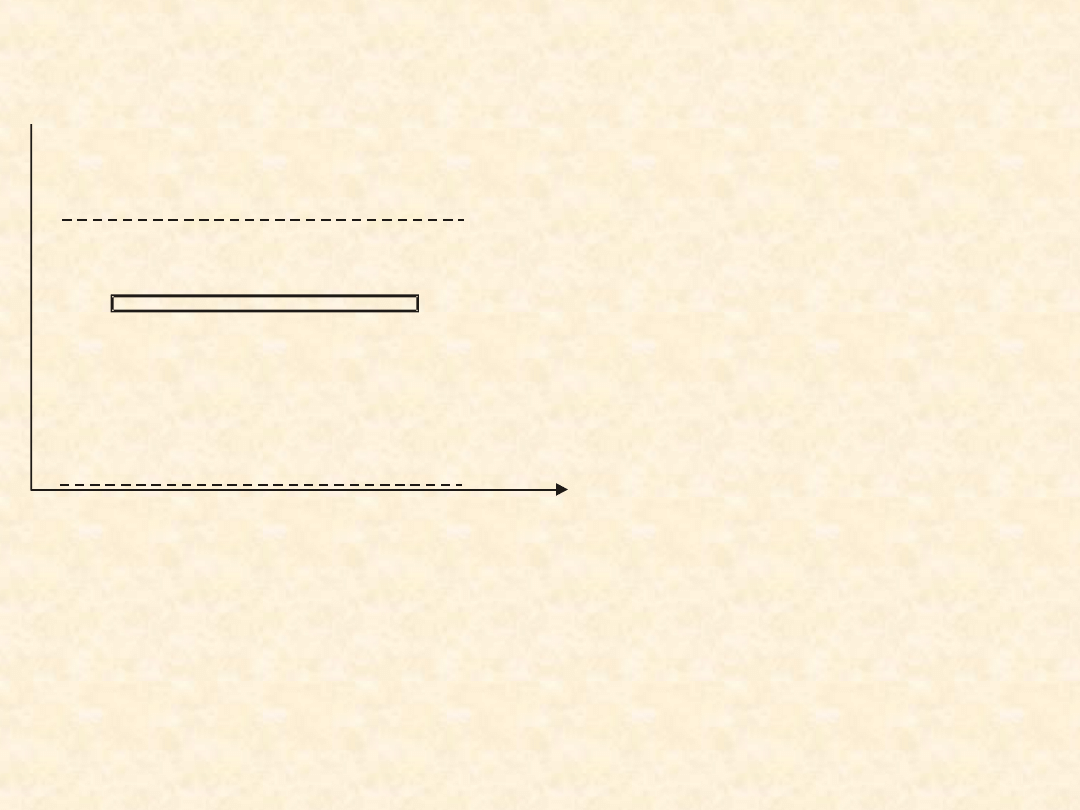
Hydrostatyczne zmiany ciśnienia

y

x

( p + d p ) S

p S

Gdy płyn znajduje się
w

równowadze,

to

każda

część

jego

objętości

jest

w

równowadze.

Rozpatrzmy

cienką

warstwę

płynu

o

grubości dy i polu
powierzchni

S,

znajdującą

się

w

odległości

y

od

poziomu odniesienia.

Masa takiego elementu wynosi Sdy, a jego ciężar
gSdy. Siły działające na warstwę są w każdym
punkcie prostopadłe do jej powierzchni. Zatem siły
równoległe do płaszczyzny warstwy się równoważą.

Natomiast siły działające prostopadle do warstwy są
wywoływane nie tylko przez ciśnienie płynu, ale też
przez

jego

ciężar.

Element

płynu

nie

jest

przyspieszany, więc wypadkowa siła działająca nań
musi być zerem. Warunek równowagi warstwy
przyjmuje zatem postać:

pS = (p+dp)S +
gSdy

ρg

dy

dp





Ciśnienie zmienia się więc ze zmianą wysokości. Gdy
wysokość rośnie, to ciśnienie maleje. Powodem jest
ciężar warstwy płynu leżącej pomiędzy punktami, dla
których mierzymy różnicę ciśnień.

Dla cieczy  jest stałe (ciecze są praktycznie
nieściśliwe), a zmiany g z wysokością na ogół można
pominąć, więc dla cieczy jednorodnej powyższe
równanie przyjmuje postać:

 (p

2

- p

1

) = -g(y

2

- y

1

)

Swobodna powierzchnia cieczy stanowi naturalny
poziom odniesienia, oznaczony tu jako y

2

, dla którego

ciśnienie wynosi p

2 i

jest równe atmosferycznemu p

0

.

Położenie pewnego poziomu wewnątrz cieczy
oznaczyliśmy przez y

1

. Niech ciśnienie na tym

poziomie wynosi p, zatem:

p

0

- p = -g(y

2

- y

1

)

Ponieważ y

2

- y

1

jest głębokością h poniżej poziomu

cieczy, to:

 

p = p

0

+gh

Ciśnienie rośnie wraz z głębokością i jest jednakowe
dla punktów leżących na tej samej głębokości.

Dla gazów  jest małe i różnica ciśnień w dwóch
punktach jest zazwyczaj do pominięcia, dlatego
można przyjąć, że ciśnienie gazu w naczyniu jest
wszędzie jednakowe.

Nie jest to jednak prawdą dla znacznej różnicy
wysokości. Np. na wysokości 6 km nad powierzchnia
Ziemi ciśnienie wynosi ok. 5x10

4

Pa, dla porównania

w morzu na głębokości 6 km ciśnienie wynosi 6x10

7

Pa.

Prędkość nieruchomego płynu jest równa zeru v = 0.
Założymy ponadto, że omawiane zjawiska są
niezależne od czasu, co umożliwia pominięcie
przenoszenia ciepła :

0

t

/

F







gdzie F jest dowolnym parametrem opisującym ruch
płynu. Podstawowe równanie

opisujące parametr F

płynu w stanie równowagi ma postać:

p

grad

z)

y,

(x,

ρ



F

z

p

ρF

;

y

p

ρF

;

x

p

ρF

z

y

x



















a w postaci
skalarnej

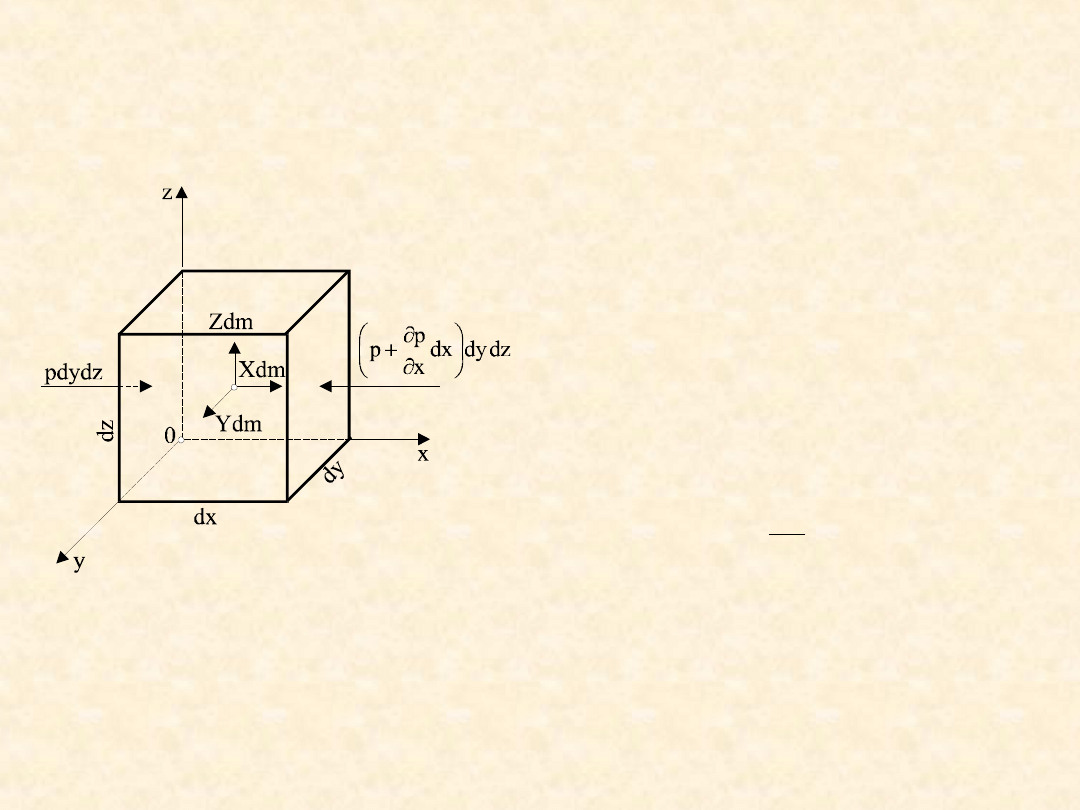
Równanie

równowagi

płynu

wyprowadzimy,

rozpatrując różniczkowy sześcian dx dy dz.

dz

dy

dx

x

p

p



















Rozpatrzmy równowagę
sił

działających

w

kierunku osi x. Siła
powierzchniowa,
będąca

iloczynem

ciśnienia i powierzchni
na odcinku dx rośnie od
wielkości p dydz do

Te siły są zwrócone ku
powierzchni

Element płynu dV = dx dy dz jest w równowadze,
jeżeli rzuty sił na osie układu są równe zeru, zatem dla
kierunków x, y, z możemy odpowiednio napisać
wyrażenia:

dz

dy

x

p

p

dx

dy

p

dm

F

x























dz

dx

y

p

p

dz

dx

p

dm

F

y























dy

dx

z

p

p

dy

dx

p

dm

F

z























Masa elementu płynnego o objętości dV wynosi

dm =

 dx dy dz

dodając stronami trzy składowe dostajemy:





dp

dz

z

p

dy

y

p

dx

x

p

dz

F

dy

F

dx

F

ρ

z

y

x

























środkowe wyrażenie jest różniczką zupełną ciśnienia
dp, co możemy również zapisać w postaci iloczynu
skalarnego:









p

grad

dz

dy

dx

z

p

y

p

x

p

dz

dy

dx

dp

k

j

i

k

j

i

k

j

i











































Ponieważ

F = F

x

+F

y

+

F

z

, to:

p

grad



F

Ten wynik słownie wyraża

prawo równowagi Eulera

:

Jeżeli na ciecz znajdującą się w spoczynku
działają siły powierzchniowe i masowe, to
wielkość ciśnienia wywieranego na element
powierzchniowy

umieszczony

w

dowolnym

punkcie cieczy nie zależy od orientacji tego
elementu.

Siły powierzchniowe

występują na powierzchniach

ograniczających

ciecz.

Ich

wielkość

jest

proporcjonalna do elementu pola powierzchni i nie
zależy od masy cieczy. Wektor każdej siły
powierzchniowej można rozłożyć na dwie składowe:
prostopadłą do elementu powierzchni – parcie P i
styczną do powierzchni – tarcie T.

Stosunek siły parcia (P) do powierzchni nacisku (S) to

ciśnienie

p, a stosunek T/S –

naprężenie styczne

.

Siły masowe są związane z masą cieczy, np. ciężar
ciała, siła bezwładności czy siła odśrodkowa.

W przypadku Ziemi rozważany przez nas wektor F ma
składowe:

F

x

= 0, F

y

= 0, F

z

= -g

Jesli na płyn nie działają żadne siły masowe, czyli

F =

0,

to na podstawie równania równowagi Eulera

otrzymujemy

prawo Pascala

:

grad p = 0

Jeżeli siły masowe działające na płyn są
pomijalnie małe (mogą działać siły powierzchniowe),
to płyn pozostaje w spoczynku, a ciśnienie
hydrostatyczne jest stałe w całej masie płynu.

Parcie hydrostatyczne

Parcie hydrostatyczne jest siłą powierzchniową, z jaką
płyn będący w spoczynku oddziałuje prostopadle na
powierzchnię S ściany naczynia lub ciała zanurzonego
w płynie lub na inny płyn. W przypadku, gdy działa
jedynie siła ciężkości:

p = dp/ds

gdzie p nazywamy

nadciśnieniem.

Ponieważ

to





dS

h

ρg

p

ρg

dS

ρgh

p

dS

p

dp

1

1

2























ρgh

p

p

1

2





Całkując to równanie po powierzchni S dostajemy:





S

ρgh

p

S

p

1

2





Zauważmy, że siła parcia P działająca na dno
zbiornika

nie zależy od kształtu zbiornika

. Dlatego

w zbiornikach ciśnieniowych dno jest wklęsłe (patrząc
z zewnątrz), co zwiększa wytrzymałość mechaniczną
zbiornika.

Zależność parcia od powierzchni w przypadku stałego
ciśnienia jest podstawą działania pras hydraulicznych.

Siły wyporu i równowaga ciał pływających

Rozpatrując parcie działające na ciało zanurzone w
płynie, łatwo stwierdzić, że:

Siły poziome

znoszą się wzajemnie (P

h

= 0) wobec

równości poziomych składowych parcia z każdej
strony bryły,

Siły pionowe

parcia działają ku górze, a składowa

parcia pionowego jest proporcjonalna do objętości
zanurzonej części ciała V.

Siła

wypadkowa,

zwana

siłą

wyporu

hydrostatycznego

(skierowana pionowo w górę i

zaczepiona w środku wyporu, czyli w geometrycznym
środku zanurzonej części ciała), jest równa iloczynowi
objętości zanurzonej części ciała i ciężaru właściwego
cieczy, w której to ciało jest zanurzone czyli

g

Vρ

Siła wyporu hydrostatycznego jest siłą, z jaką ciecz
działa na ciało w niej zanurzone, co opisuje

prawo

Archimedesa:

Wersja pierwotna

: Ciało zanurzone w cieczy traci

pozornie tyle na wadze, ile waży ciecz wyparta
przez to ciało.

Wersja współczesna

: Na ciało zanurzone w cieczy

działa siła wyporu skierowana pionowo w górę
i liczbowo równa ciężarowi cieczy wypartej
przez to ciało.

Stateczność

ciał pływających tylko pośrednio zależy

od wzajemnego położenia środków ciężkości i
wyporu. Ciało częściowo zanurzone może mieć trwałą
stateczność nawet w przypadkach, gdy środek
ciężkości znajduje się ponad środkiem wyporu. Miarą
stateczności ciała pływającego jest tzw.

wysokość

metacentryczna

m.

Metacentrum

(M)

jest punktem przecięcia osi

pływania z kierunkiem siły wyporu, po małym
wychyleniu ciała ze stanu równowagi.

W

przypadku

ciała

całkowicie

zanurzonego

metacentrum pokrywa się ze środkiem wyporu, a
więc o równowadze takiego ciała decyduje jedynie
wzajemne położenie środków: wyporu B i ciężkości G.

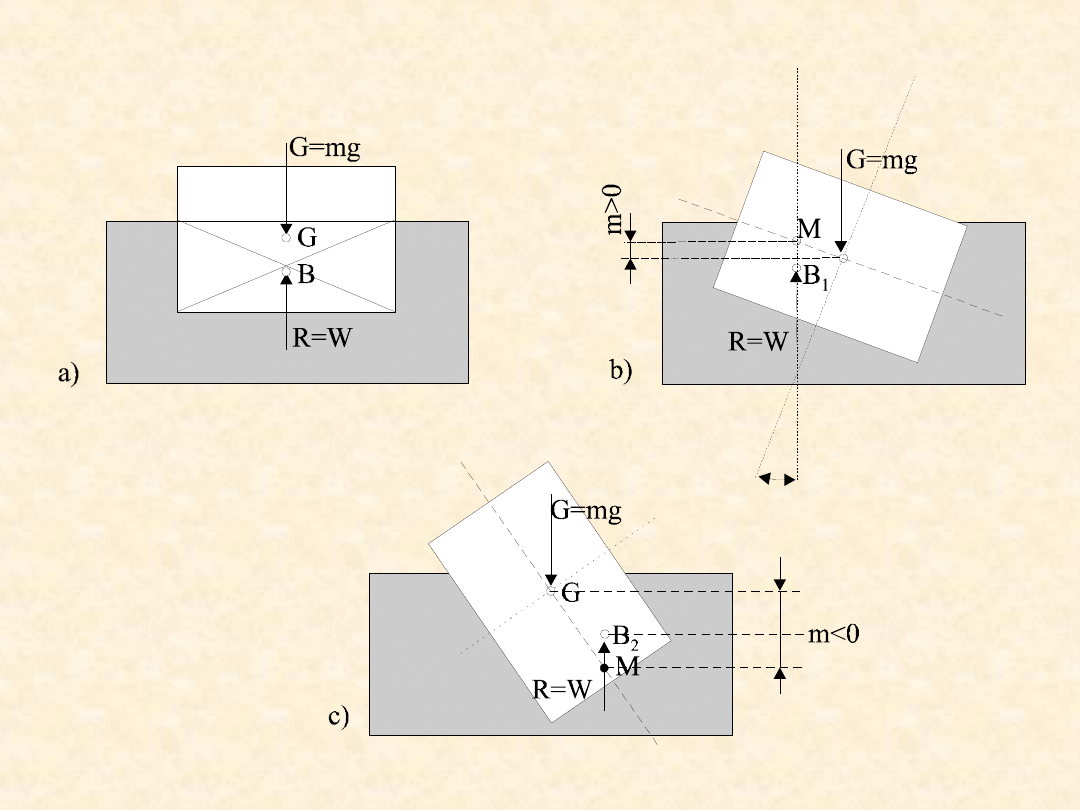
Dla ciała częściowo zanurzonego po wychyleniu
następuje zmiana kształtu bryły wyporu, a więc jej
środek wyporu ulega przesunięciu.

Metacentrum leży powyżej środka wyporu a jego
położenie zależy od kształtu i wielkości bryły.
Odległość środka ciężkości G do metacentrum M
nazywa się

wysokością metacentryczną m

, a jej

znak decyduje o stanie równowagi ciała pływającego:

m > 0 - równowaga stała (stabilna)

m = 0 - równowaga obojętna

m < 0 - równowaga chwiejna

Wysokość metacentryczna m, stanowiąca kryterium
stateczności nie zależy od kąta pochylenia  lecz od
kształtu i wielkości płaszczyzny pływania, położenia
środka ciężkości i środka wyporu oraz objętości
części zanurzonej ciała pływającego.