

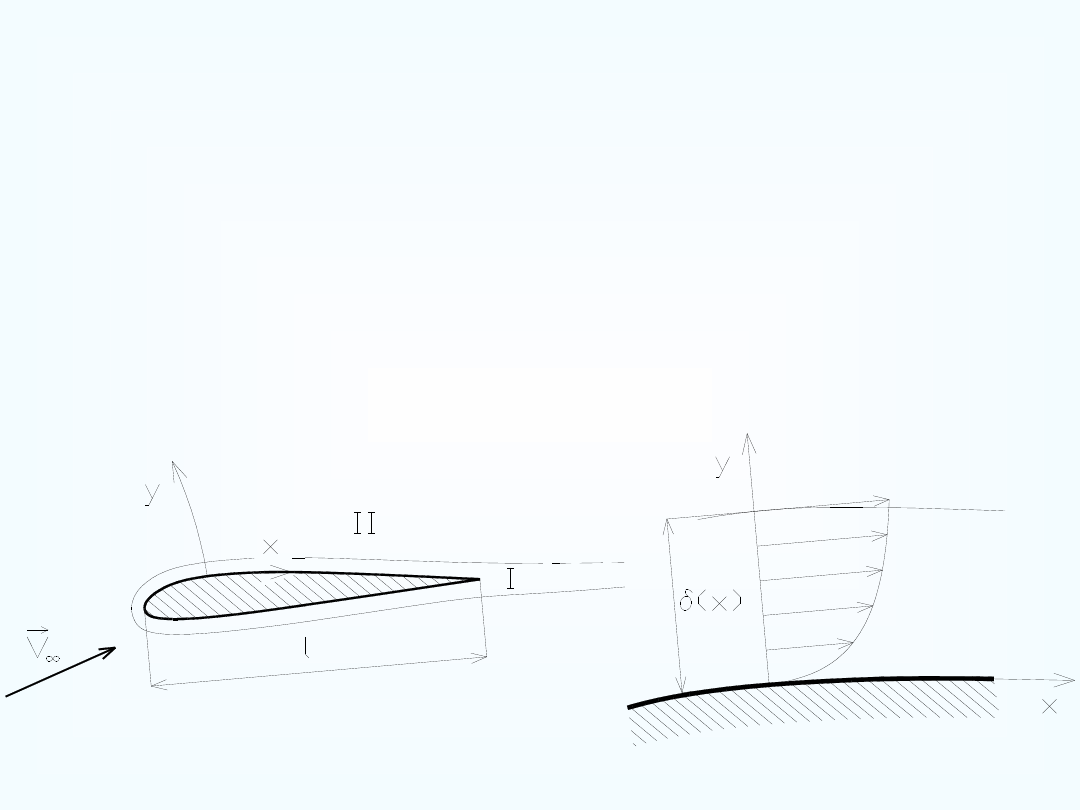
Płyn nielepki jest uproszczonym modelem płynu rzeczywistego, w
którym zakładamy występowanie wyłącznie naprężeń normalnych
(pochodzących od ciśnienia) i pomijamy wpływ sił pochodzących od
naprężeń stycznych.
Zakładamy, że ruch płynu został określony za pomocą pola
prędkości, pola gęstości oraz pola ciśnienia:
,
)
,
,
,
(
t
z
y
x
V
V
),
,
,
,
(
t
z
y
x
).
,
,
,
(
t
z
y
x
p
p
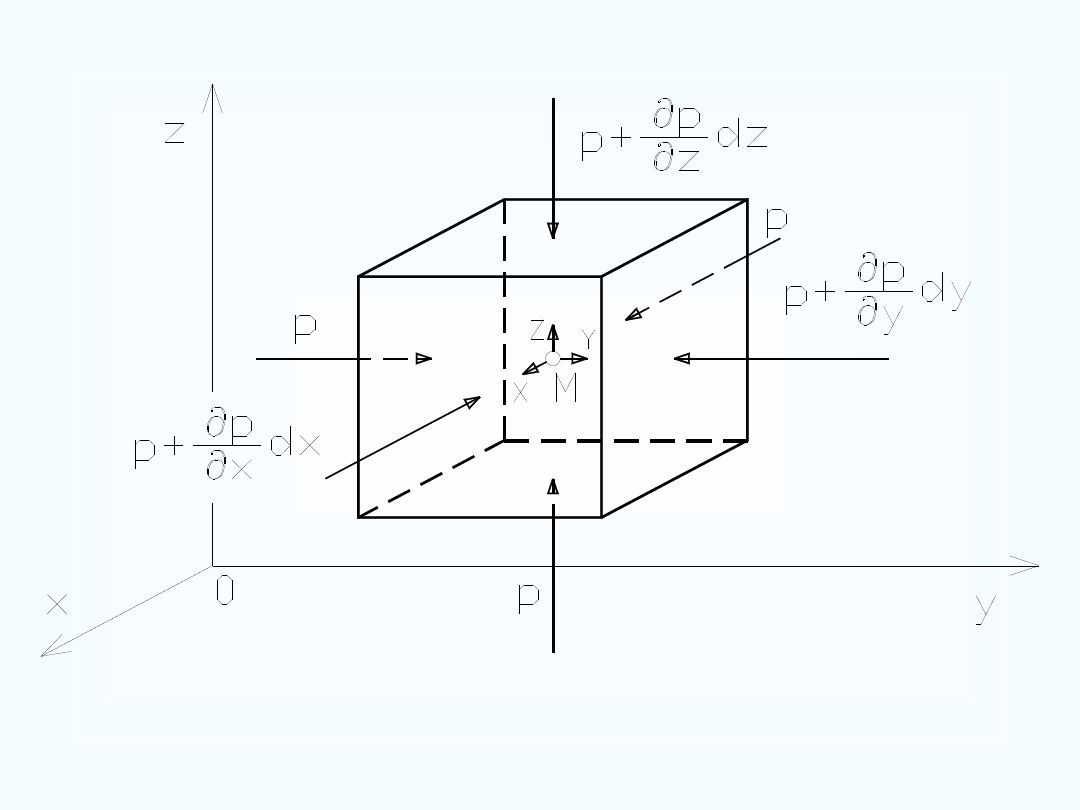

– siły masowe:
;
,
,
d
Z
d
Y
d
X
– siły powierzchniowe spowodowane działaniem ciśnienia
statycznego:
,
z
d
y
d
x
d
x
p
p
z
d
y
d
p
,
x
d
z
d
y
d
y
p
p
x
d
z
d
p
;
y
d
x
d
z
d
z
p
p
y
d
x
d
p
– siły bezwładności:
.
,
,
d
t
d
V
d
d
t
d
V
d
d
t
d
V
d
z
y
x
Siły działające na element płynu:

Zasada d’Alemberta: suma wszystkich sił rzeczywistych i
bezwładności na dowolny kierunek jest równa zeru:
.
1
,
1
,
1
z
p
Z
t
d
V
d
y
p
Y
t
d
V
d
x
p
X
t
d
V
d
z
y
x
Postaci wektorowe:
,
grad
1
p
t
d
d
F
V
.
grad
1
p
t
F
V
V
V
Równanie Eulera w formie Lamba i Gromeki
.
grad
1
rot
2
grad
2
p
V
t
F
V
V
V


Zapisując równania Eulera w postaci przekształconych równań:
,
0
1
,
0
1
,
0
1
t
d
V
d
z
p
Z
t
d
V
d
y
p
Y
t
d
V
d
x
p
X
z
y
x
po pomnożeniu ich, odpowiednio, przez
d
x
,
d
y
,
d
z
oraz dodaniu
stronami otrzymamy
0
1
z
z
y
y
x
x
V
d
V
V
d
V
V
d
V
z
d
z
p
y
d
y
p
x
d
x
p
z
d
Z
y
d
Y
x
d
X
Założenie upraszczające: stacjonarność ruchu.
.
,
,
z
V
V
y
V
V
x
V
V
t
d
V
d
z
V
V
y
V
V
x
V
V
t
d
V
d
z
V
V
y
V
V
x
V
V
t
d
V
d
z
z
z
y
z
x
z
y
z
y
y
y
x
y
x
z
x
y
x
x
x

ponieważ:
,
p
d
z
d
z
p
y
d
y
p
x
d
x
p
.
,
,
z
y
x
V
t
d
z
d
V
t
d
y
d
V
t
d
x
d
Zamieniając:
)
(
2
1
,
)
(
2
1
,
)
(
2
1
2
2
2
z
z
z
y
y
y
x
x
x
V
d
V
d
V
V
d
V
d
V
V
d
V
d
V
oraz pamiętając, że
2
2
2
2
V
V
V
V
z
y
x
można napisać
.
0
)
(
2
1
2
V
d
p
d
z
d
Z
y
d
Y
x
d
X

Dla pola sił ciężkości:
g
Z
Y
X
,
0
,
0
.
0
2
2
z
d
g
p
d
V
d
Dla cieczy jest:
;
.
const
2
0
2
2
2
B
C
z
g
p
V
z
g
p
V
d
ostatecznie dostajemy
B
C
d
d
0
grad
grad
V
s
- niezmienna wzdłuż linii prądu.
Document Outline
Wyszukiwarka
Podobne podstrony:
4 Podstawowe równwnia dynamiki płynów nielepkich 5
4 Podstawowe rownwnia dynamiki plynow nielepkich
4 Podstawowe równwnia dynamiki płynów nielepkich
4 Podstawowe równwnia dynamiki płynów nielepkich 3
4 Podstawowe równwnia dynamiki płynów nielepkich (1)
Projekt podstawowe człony dynamiczne
dynamika plynow poziomo
Charakterystyki częstotliwościowe podstawowych członów dynamicznych v4
Elementy statyki i dynamiki płynów
Dynamika plynow doskonałych i rzeczywistych
Wykł 09 Statyka i dynamika płynów
statyka i dynamika plynow(1)
Dynamika plynow 13 14
wyklad5, DYNAMIKA PŁYNÓW RZECZYWISTYCH
cw7 podstawowe człony dynamiczne
więcej podobnych podstron