
Grafika wektorowa
dr inż. Piotr Steć
Instytut Sterowania i Systemów Informatycznych
12 kwietnia 2005
2
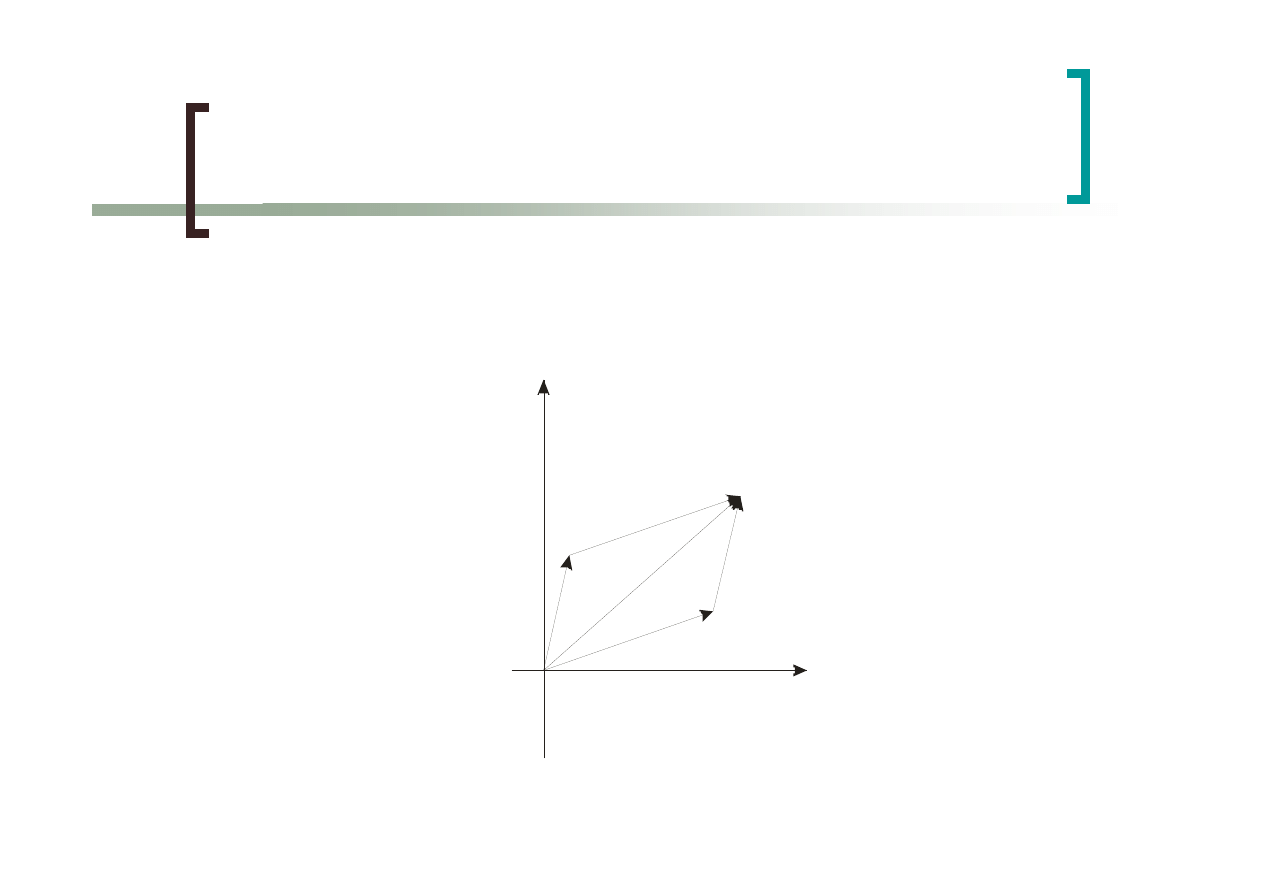
Operacje na wektorach
Dodawanie wektorów
v
w
v+w
X
Y
3
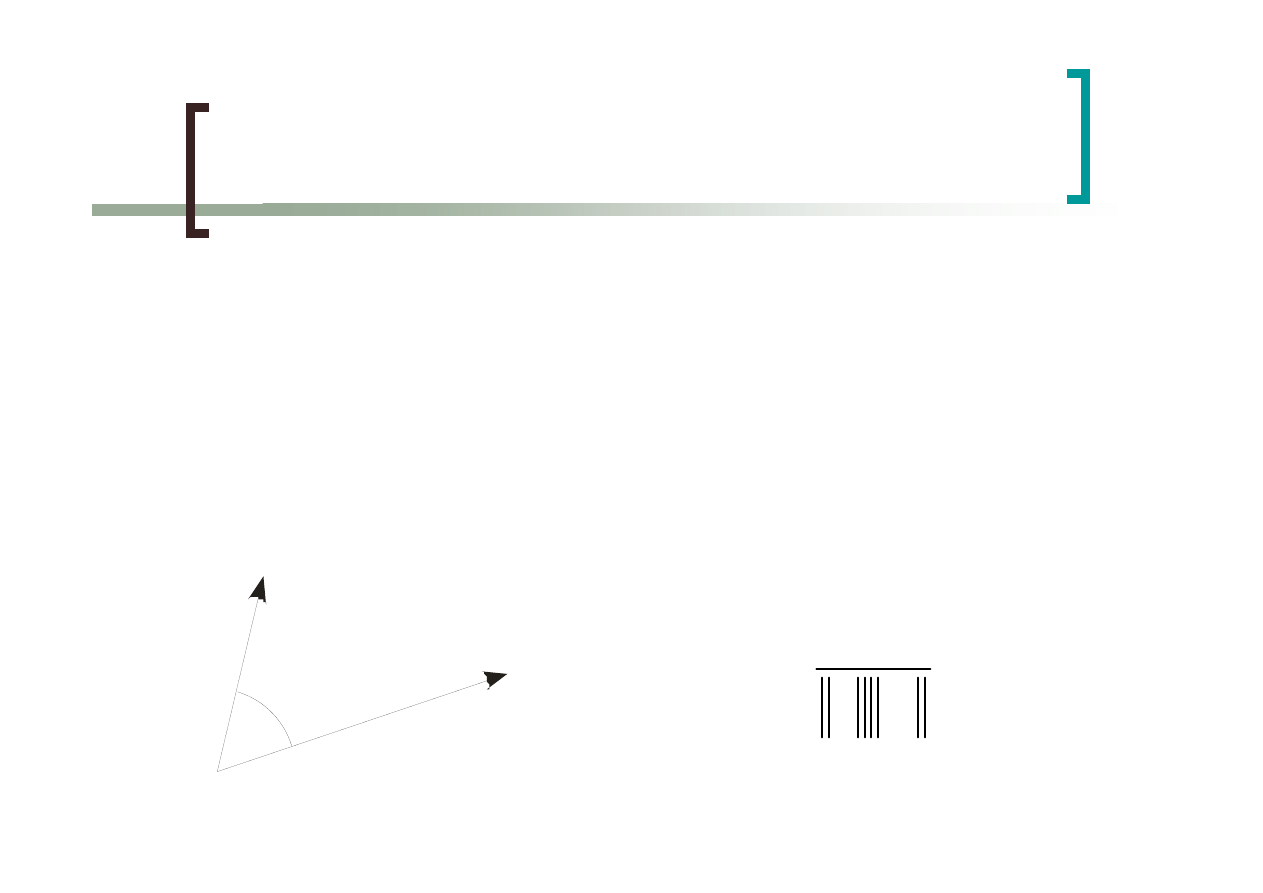
Operacje na wektorach
Iloczyn skalarny
n
n
n
n
x
x
y
x
x
y
x
x
w
v
+
+
=
⎥
⎥
⎥
⎦
⎤
⎢
⎢
⎢
⎣
⎡
⋅
⎥
⎥
⎥
⎦
⎤
⎢
⎢
⎢
⎣
⎡
=
⋅
K
M
M
1
1
1
1
w
v
w
v
⋅
=
α
cos
v
w
α
4
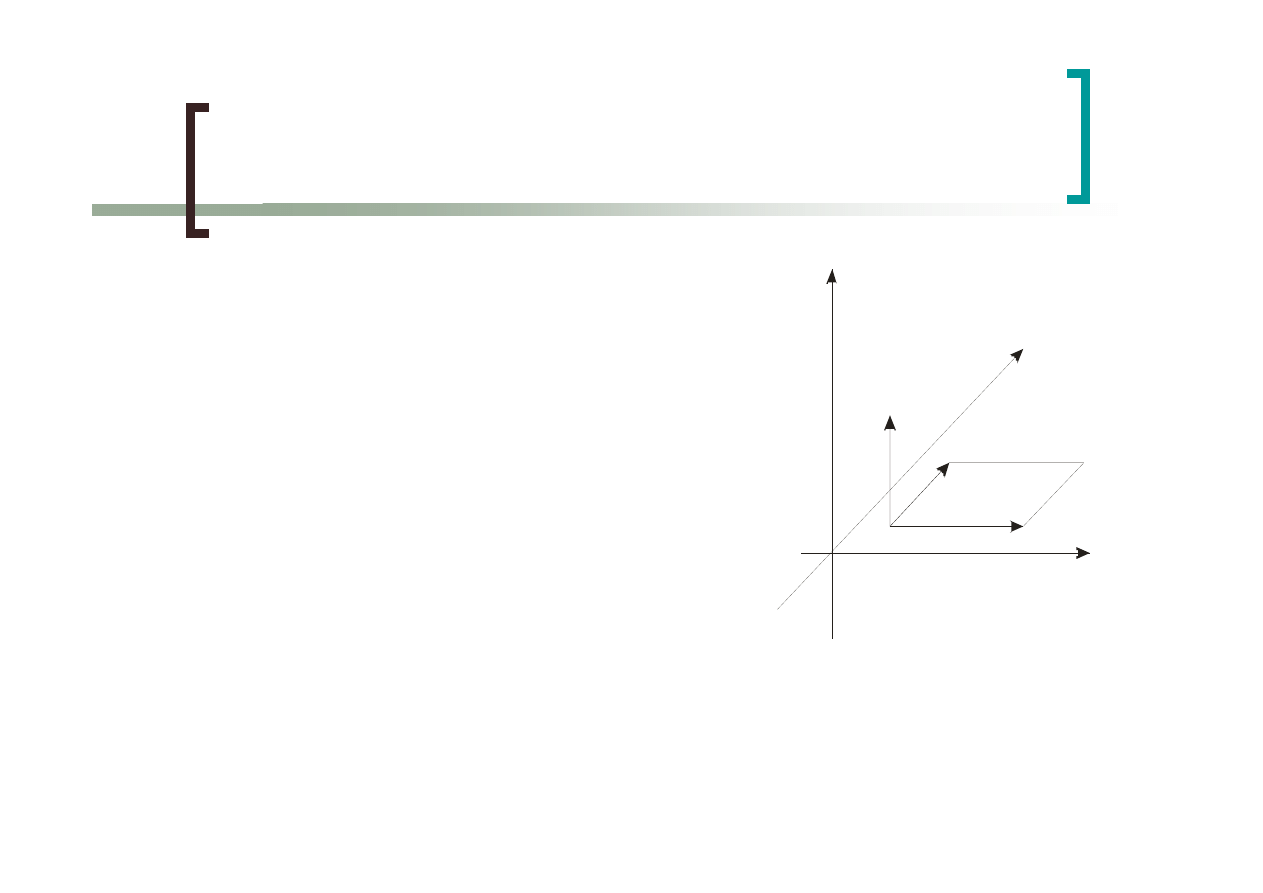
Operacje na wektorach
Iloczyn wektorowy
⎥
⎥
⎥
⎦
⎤
⎢
⎢
⎢
⎣
⎡
−
−
−
=
⎥
⎥
⎥
⎦
⎤
⎢
⎢
⎢
⎣
⎡
×
⎥
⎥
⎥
⎦
⎤
⎢
⎢
⎢
⎣
⎡
=
×
1
2
2
1
2
1
1
2
1
2
2
1
2
3
2
1
1
1
y
x
y
x
z
x
z
x
z
y
z
y
z
y
x
z
y
x
w
v
Wektor wynikowy jest prostopadły do płaszczyzny utworzonej
przez wektory źródłowe. Iloczyn wektorowy może być użyty do
obliczania wektorów normalnych do powierzchni.
v
w
X
Y
v w
x
Z
5
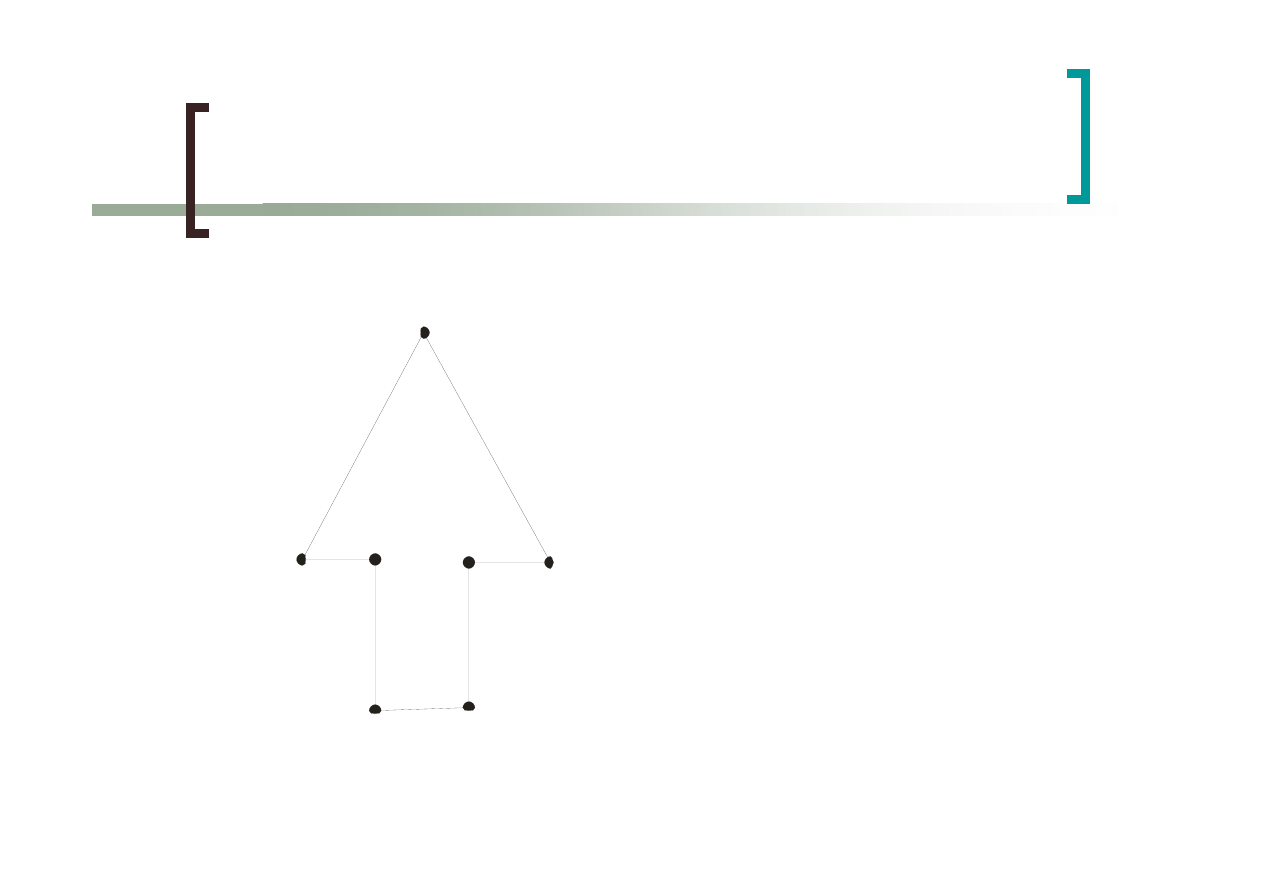
Reprezentacja obiektów
wektorowych
1
2
3
4
5
6
7
a
b
c
d
e
f
g
Lista współrzędnych
wierzchołków
1=[3,8]
2=[6,4]
3=[4,4], itd.
Lista krawędzi
a=[1,2]
b=[2,3]
c=[3,4], itd.
6
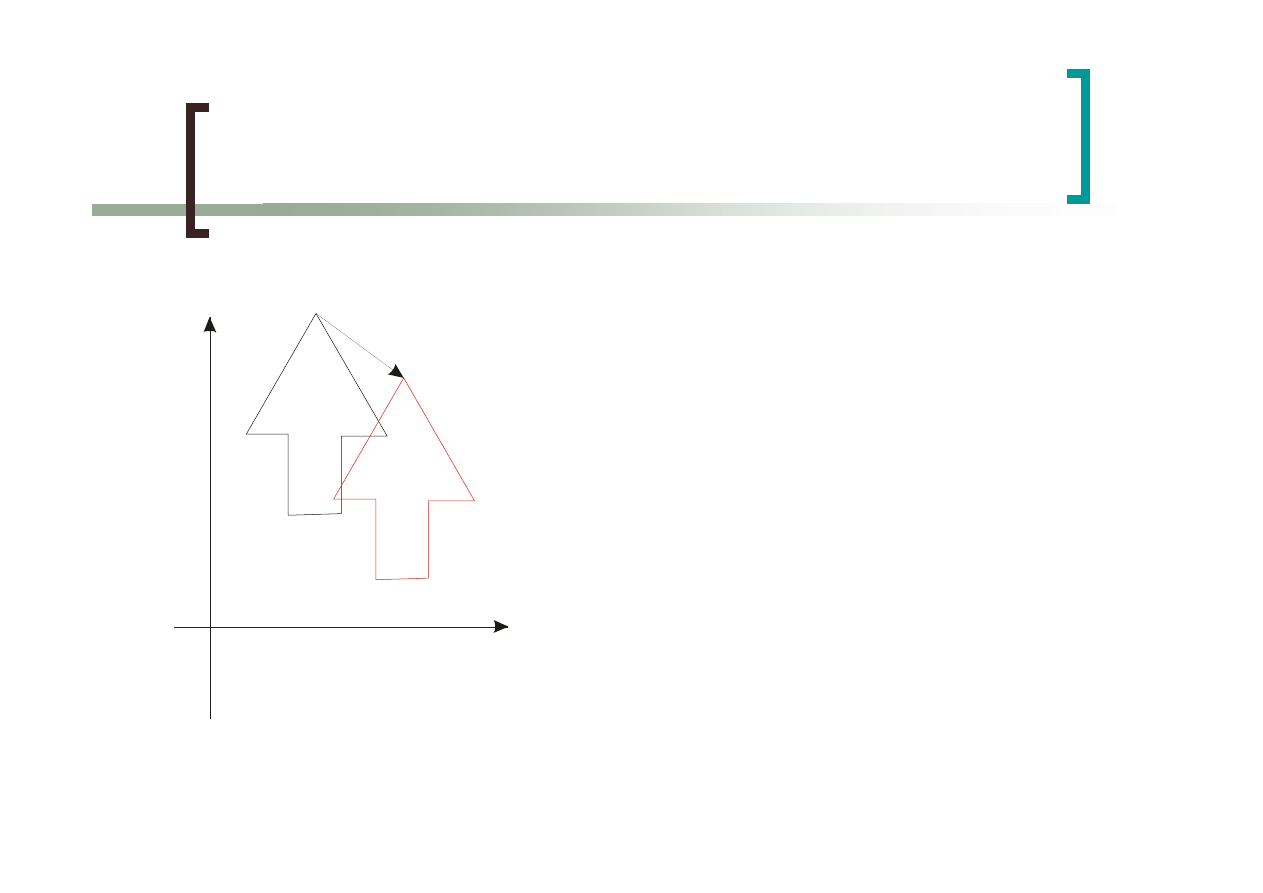
Przekształcenia 2D
Przekształcenia afiniczne to takie
przekształcenia, które zachowują
równoległość krawędzi, np.
{
Translacja (przesunięcie)
{
Skalowanie
{
Obrót
Aby przekształcić cały obiekt, należy poddać
przekształceniu wszystkie jego punkty
7
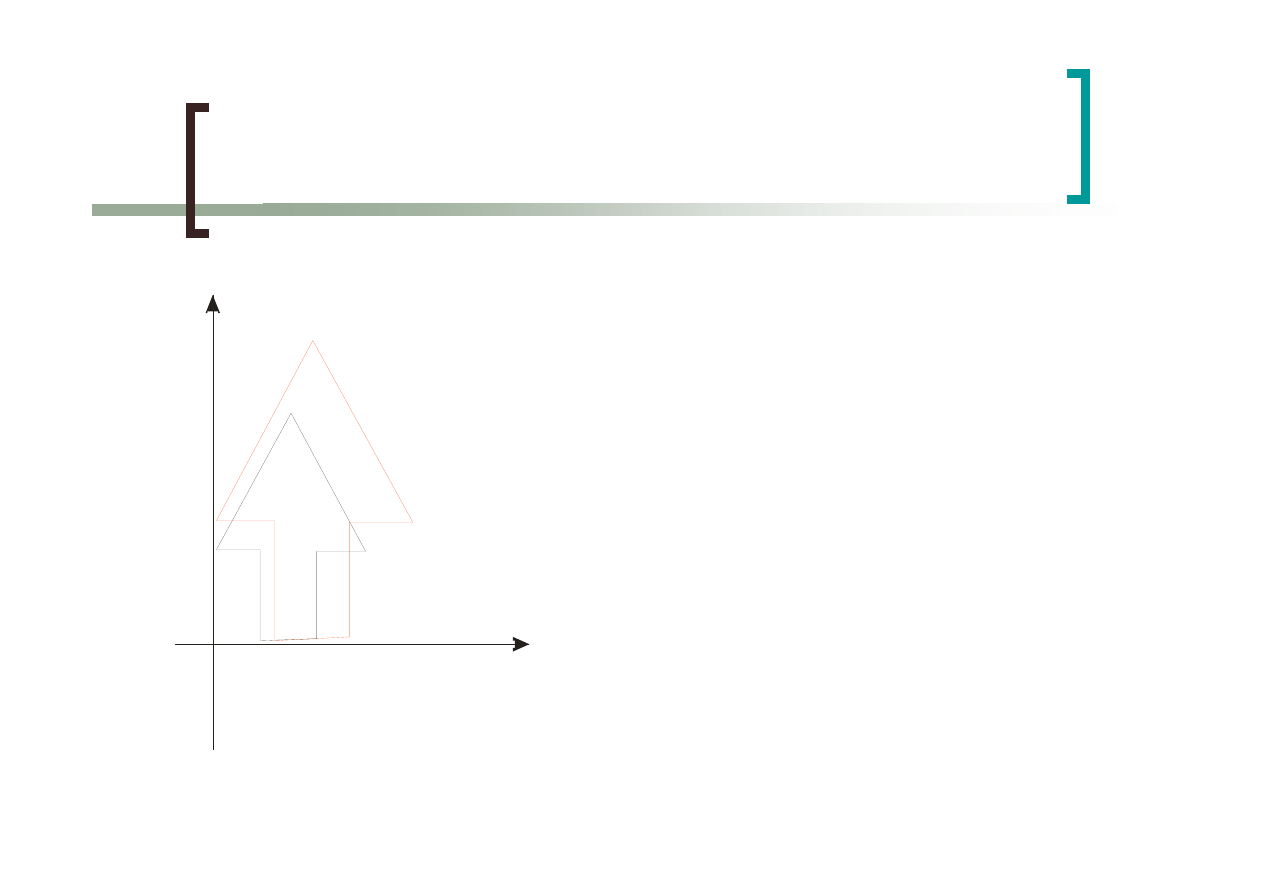
Translacja
X
Y
P
P’
Punkt można przesunąć
dodając do jego
współrzędnych wielkość
przesunięcia
⎥
⎦
⎤
⎢
⎣
⎡
+
⎥
⎦
⎤
⎢
⎣
⎡
=
+
=
′
y
x
d
d
y
x
T
P
P
8
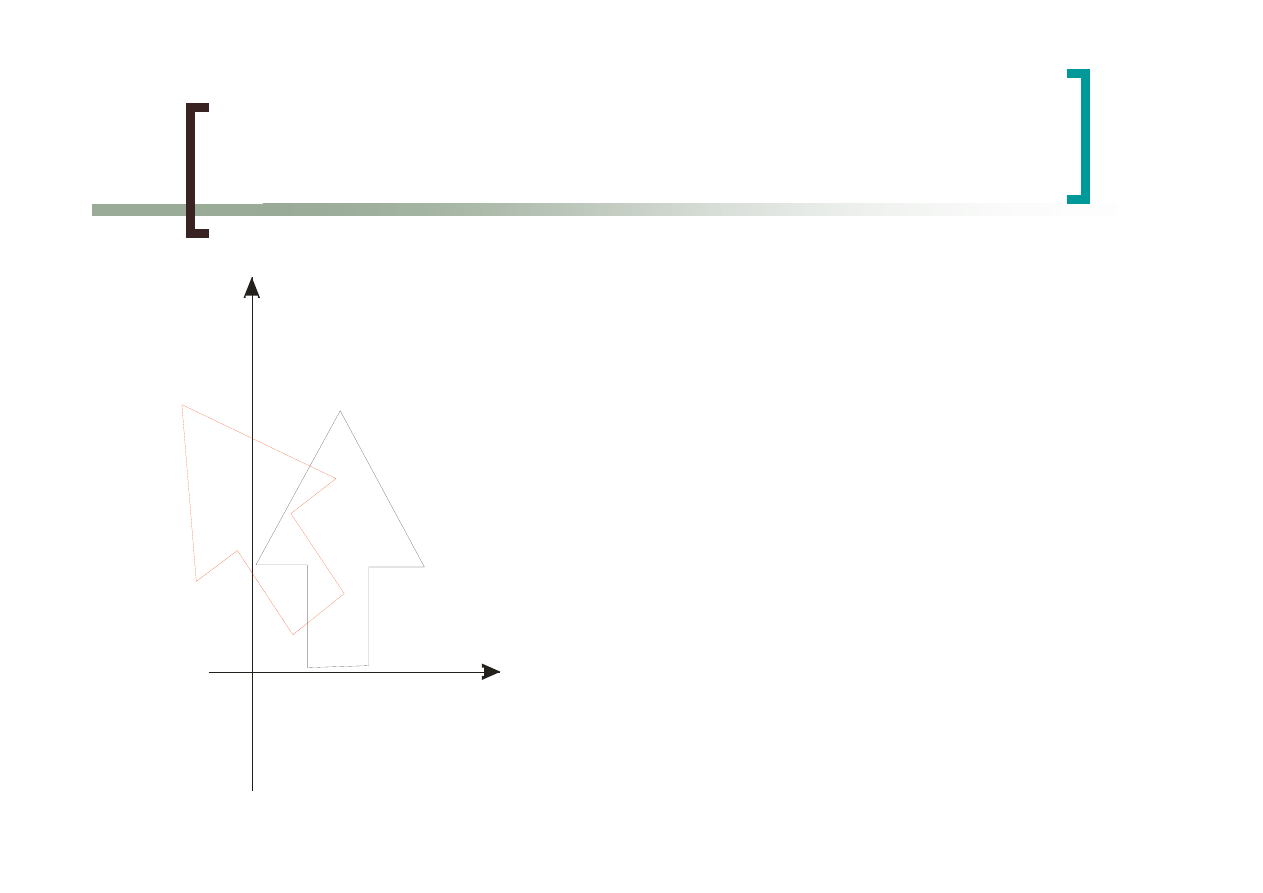
Skalowanie
Skalowanie odbywa się
względem środka układu
współrzędnych
Skalowanie może być
niejednorodne s
x
≠s
y
⎥
⎦
⎤
⎢
⎣
⎡
⋅
⎥
⎦
⎤
⎢
⎣
⎡
=
⋅
=
′
y
x
s
s
P
S
P
y
x
0
0
X
Y
P
P’
9
Obrót
Obrót odbywa się względem
środka układu współrzędnych
Skalowanie może być
niejednorodne s
x
≠s
y
⎥
⎦
⎤
⎢
⎣
⎡
⋅
⎥
⎦
⎤
⎢
⎣
⎡
−
=
⋅
=
′
y
x
P
R
P
α
α
α
α
cos
sin
sin
cos
X
Y
P
P’
10
Składanie przekształceń 2D
Obrót i skalowanie punktu
Rozwiązanie efektywniejsze – macierz złożona
Problem z włączeniem translacji do
przekształcenia złożonego
P
S
P
P
R
P
′
⋅
=
′′
⋅
=
′
P
M
P
R
S
M
⋅
=
′
⋅
=
11
Współrzędne jednorodne
Punkt na płaszczyźnie reprezentowany jest
przez trzy współrzędne (x,y,w)
Wsp. jednorodne reprezentują ten sam punkt
wtedy, gdy jeden zestaw jest wielokrotnością
drugiego, np. (2,1,4) i (4,2,8)
Przynajmniej jedna ze współrzędnych musi
być różna od zera (
(0,0,0) – niedopuszczalne
)
12
Translacja we współrzędnych
jednorodnych
⎥
⎥
⎥
⎦
⎤
⎢
⎢
⎢
⎣
⎡
⋅
⎥
⎥
⎥
⎦
⎤
⎢
⎢
⎢
⎣
⎡
=
⋅
=
′
1
1
0
0
1
0
0
1
y
x
d
d
P
T
P
y
x
⎥
⎥
⎥
⎦
⎤
⎢
⎢
⎢
⎣
⎡
+
+
=
⎥
⎥
⎥
⎦
⎤
⎢
⎢
⎢
⎣
⎡
⋅
⎥
⎥
⎥
⎦
⎤
⎢
⎢
⎢
⎣
⎡
=
⋅
=
′
1
0
0
1
0
0
1
1
0
0
1
0
0
1
1
0
0
1
0
0
1
2
1
2
1
1
2
1
1
2
1
y
y
x
x
y
x
y
x
d
d
d
d
d
d
d
d
T
T
T
13
Skalowanie we współrzędnych
jednorodnych
⎥
⎥
⎥
⎦
⎤
⎢
⎢
⎢
⎣
⎡
⋅
⎥
⎥
⎥
⎦
⎤
⎢
⎢
⎢
⎣
⎡
=
⋅
=
′
1
1
0
0
0
0
0
0
y
x
s
s
P
T
P
y
x
⎥
⎥
⎥
⎦
⎤
⎢
⎢
⎢
⎣
⎡
=
⎥
⎥
⎥
⎦
⎤
⎢
⎢
⎢
⎣
⎡
⋅
⎥
⎥
⎥
⎦
⎤
⎢
⎢
⎢
⎣
⎡
=
⋅
=
′
1
0
0
0
0
0
0
1
0
0
0
0
0
0
1
0
0
0
0
0
0
2
1
2
1
2
2
1
1
2
1
y
y
x
x
y
x
y
x
s
s
s
s
s
s
s
s
S
S
S
14
Obrót we współrzędnych
jednorodnych
⎥
⎥
⎥
⎦
⎤
⎢
⎢
⎢
⎣
⎡
⋅
⎥
⎥
⎥
⎦
⎤
⎢
⎢
⎢
⎣
⎡
−
=
⋅
=
′
1
1
0
0
0
cos
sin
0
sin
cos
y
x
P
R
P
α
α
α
α
⎥
⎥
⎥
⎦
⎤
⎢
⎢
⎢
⎣
⎡
−
⋅
⎥
⎥
⎥
⎦
⎤
⎢
⎢
⎢
⎣
⎡
−
=
⋅
=
′
1
0
0
0
cos
sin
0
sin
cos
1
0
0
0
cos
sin
0
sin
cos
2
1
β
β
β
β
α
α
α
α
R
R
R
15
Pochylenia we współrzędnych
jednorodnych
X
Y
⎥
⎥
⎥
⎦
⎤
⎢
⎢
⎢
⎣
⎡
=
1
0
0
0
1
0
0
1 a
SH
x
X
Y
⎥
⎥
⎥
⎦
⎤
⎢
⎢
⎢
⎣
⎡
=
1
0
0
0
1
0
0
1
b
SH
y
16
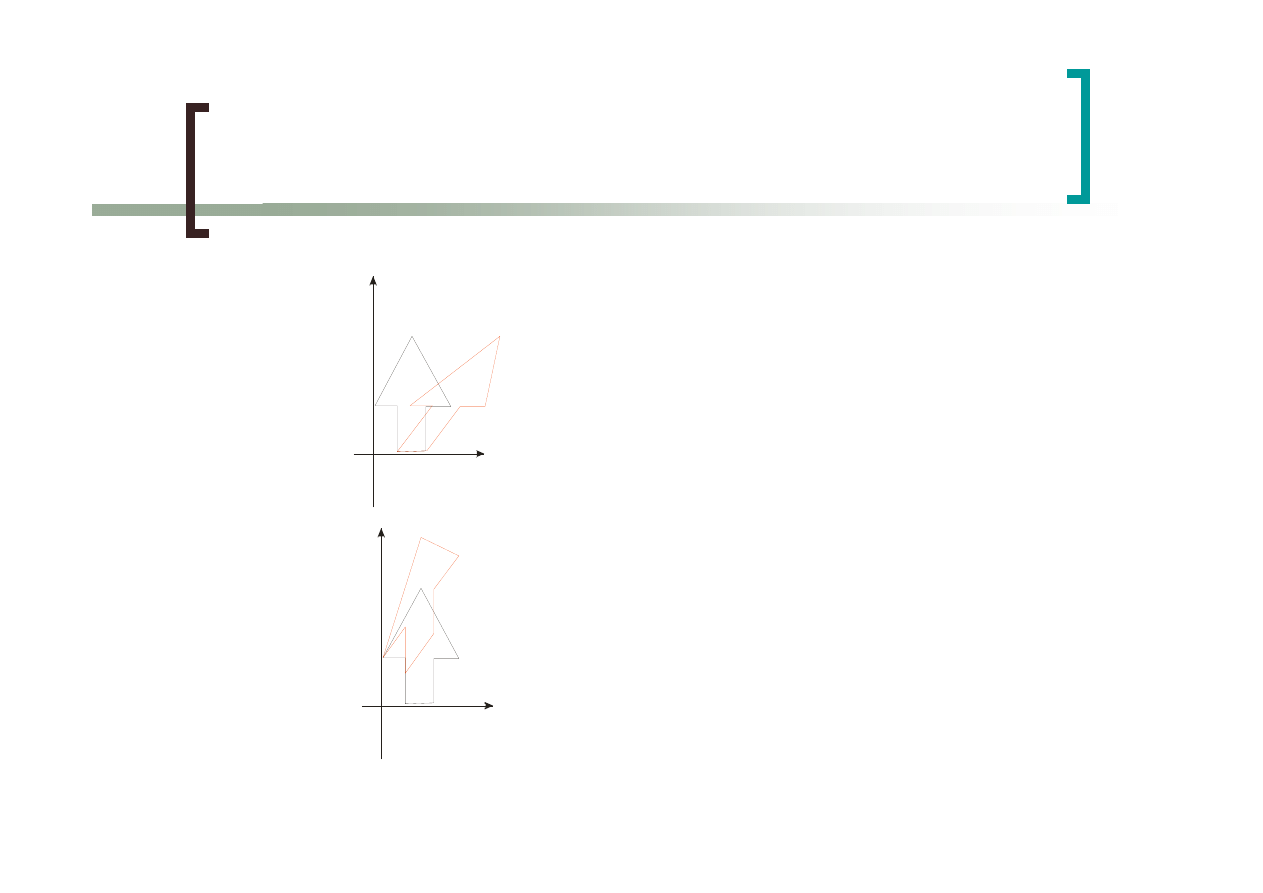
Składanie przekształceń 2D
Obrót wokół środka obiektu
{
Przesunięcie do środka układu współrzędnych
{
Obrót o zadany kąt
{
Przesunięcie na poprzednią pozycję
⎥
⎥
⎥
⎦
⎤
⎢
⎢
⎢
⎣
⎡
+
−
+
−
−
=
=
⎥
⎥
⎥
⎦
⎤
⎢
⎢
⎢
⎣
⎡
⋅
⎥
⎥
⎥
⎦
⎤
⎢
⎢
⎢
⎣
⎡
−
⋅
⎥
⎥
⎥
⎦
⎤
⎢
⎢
⎢
⎣
⎡
=
−
−
⋅
⋅
=
′
1
0
0
sin
)
cos
1
(
cos
sin
sin
)
cos
1
(
sin
cos
1
0
0
1
0
0
1
1
0
0
0
cos
sin
0
sin
cos
1
0
0
1
0
0
1
)
,
(
)
(
)
,
(
1
1
1
1
1
1
1
1
1
1
1
1
α
α
α
α
α
α
α
α
α
α
α
α
α
x
y
y
x
y
x
y
x
y
x
T
R
y
x
T
P
17
Składanie przekształceń 2D
Macierz wynikowa może być wynikiem mnożenia
dowolnej liczby macierzy podstawowych
Mnożenie jest zamienne w następujących
przypadkach:
M
1
M
2
Przesunięcie
Przesunięcie
Skalowanie
Skalowanie
Obrót
Obrót
Skalowanie (s
x
=s
y
)
Obrót
18
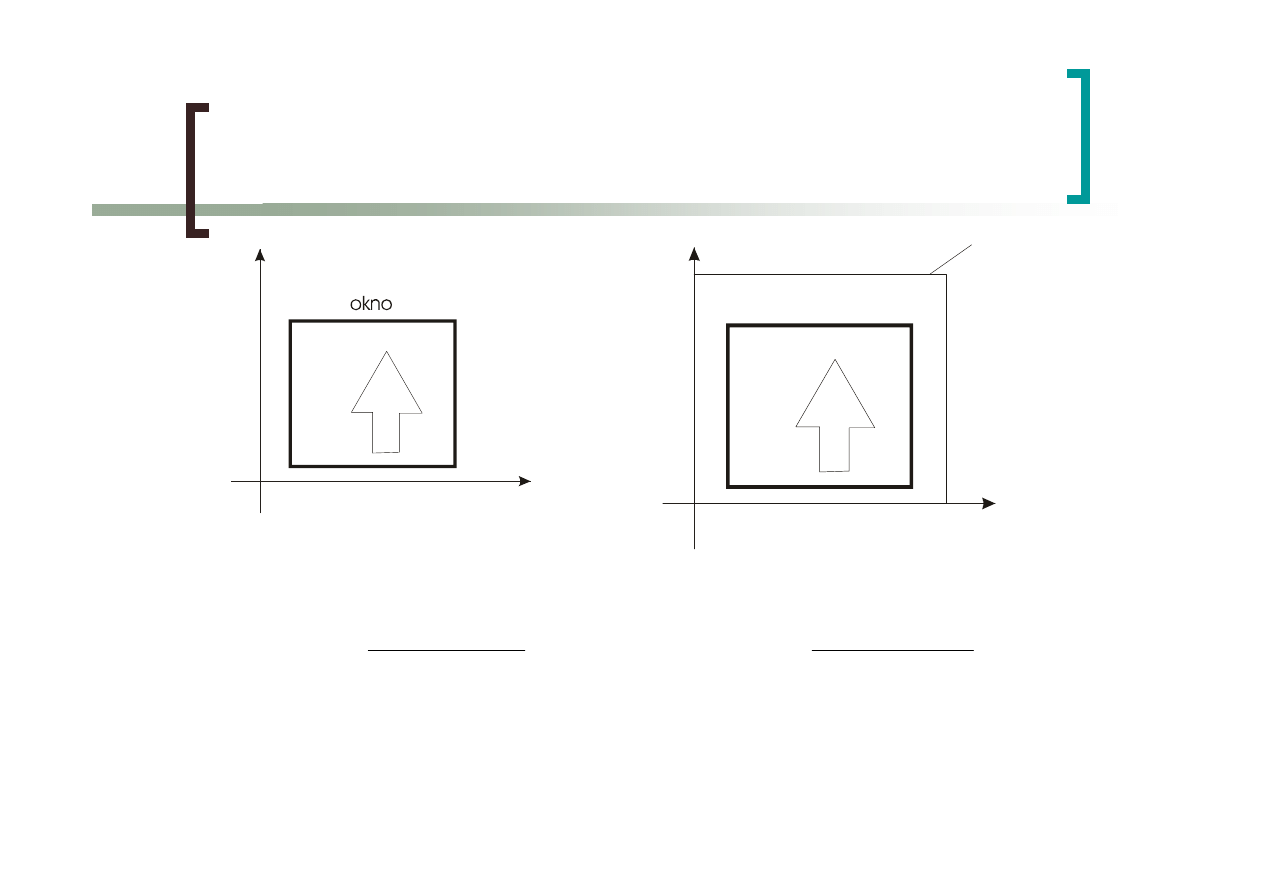
Przekształcenie okna w pole
wizualizacji
X
Y
u
v
obszar ekranu
pole wizualizacji
⎥
⎦
⎤
⎢
⎣
⎡
+
−
−
⋅
−
+
−
−
⋅
−
=
′
1
)
(
)
(
min
min
max
min
max
min
min
min
max
min
max
min
v
y
y
v
v
y
y
u
x
x
u
u
x
x
P
19
Przekształcenia 3D
Translacja
Skalowanie
⎥
⎥
⎥
⎥
⎦
⎤
⎢
⎢
⎢
⎢
⎣
⎡
=
1
0
0
0
1
0
0
0
1
0
0
0
1
z
y
x
d
d
d
T
⎥
⎥
⎥
⎥
⎦
⎤
⎢
⎢
⎢
⎢
⎣
⎡
=
1
0
0
0
0
0
0
0
0
0
0
0
0
z
y
x
s
s
s
S
20
Obroty 3D
⎥
⎥
⎥
⎥
⎦
⎤
⎢
⎢
⎢
⎢
⎣
⎡
−
=
1
0
0
0
0
cos
sin
0
0
sin
cos
0
0
0
0
1
α
α
α
α
x
R
⎥
⎥
⎥
⎥
⎦
⎤
⎢
⎢
⎢
⎢
⎣
⎡
−
=
1
0
0
0
0
cos
0
sin
0
0
1
0
0
sin
0
cos
α
α
α
α
y
R
⎥
⎥
⎥
⎥
⎦
⎤
⎢
⎢
⎢
⎢
⎣
⎡
−
=
1
0
0
0
0
1
0
0
0
0
cos
sin
0
0
sin
cos
α
α
α
α
x
R
21
Rzuty
Przekształcenie reprezentacji 3D na 2D
Rzuty równoległe – promienie rzutujące
są równoległe
Rzuty perspektywiczne – promienie
rzutujące zbiegają się w środku
rzutowania
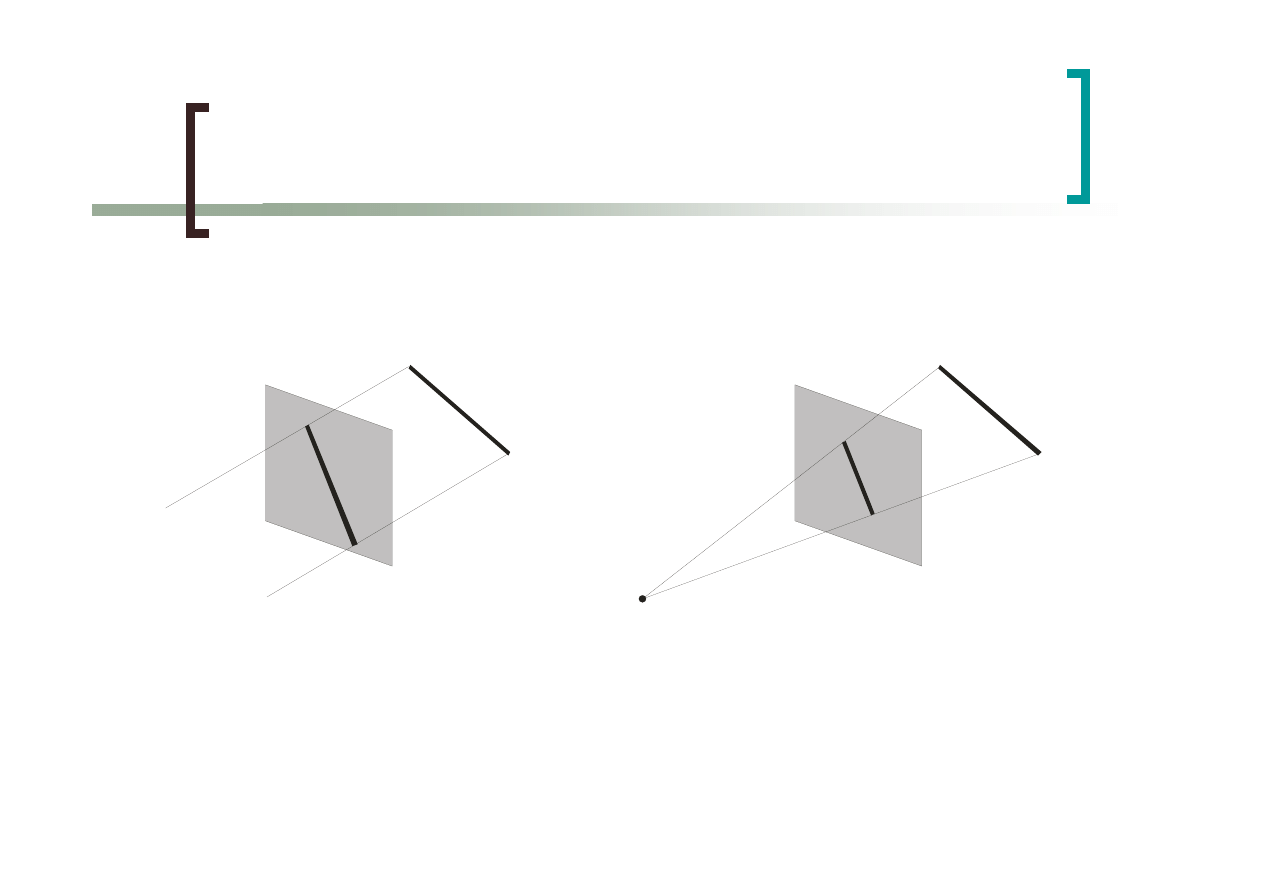
22
Rzuty
A
B
A’
B’
A
B
A’
B’
rzutnia
rzutnia
rzut równoległy
rzut perspektywiczny
23
Rzuty równoległe
Rzuty prostokątne – rzutnie równoległe
do osi układu współrzędnych
Rzut izometryczny – rzutnia tworzy
równe kąty z osiami układu
współrzędnych
Rzuty ukośne – normalna rzutni nie jest
równoległą z kierunkiem rzutowania
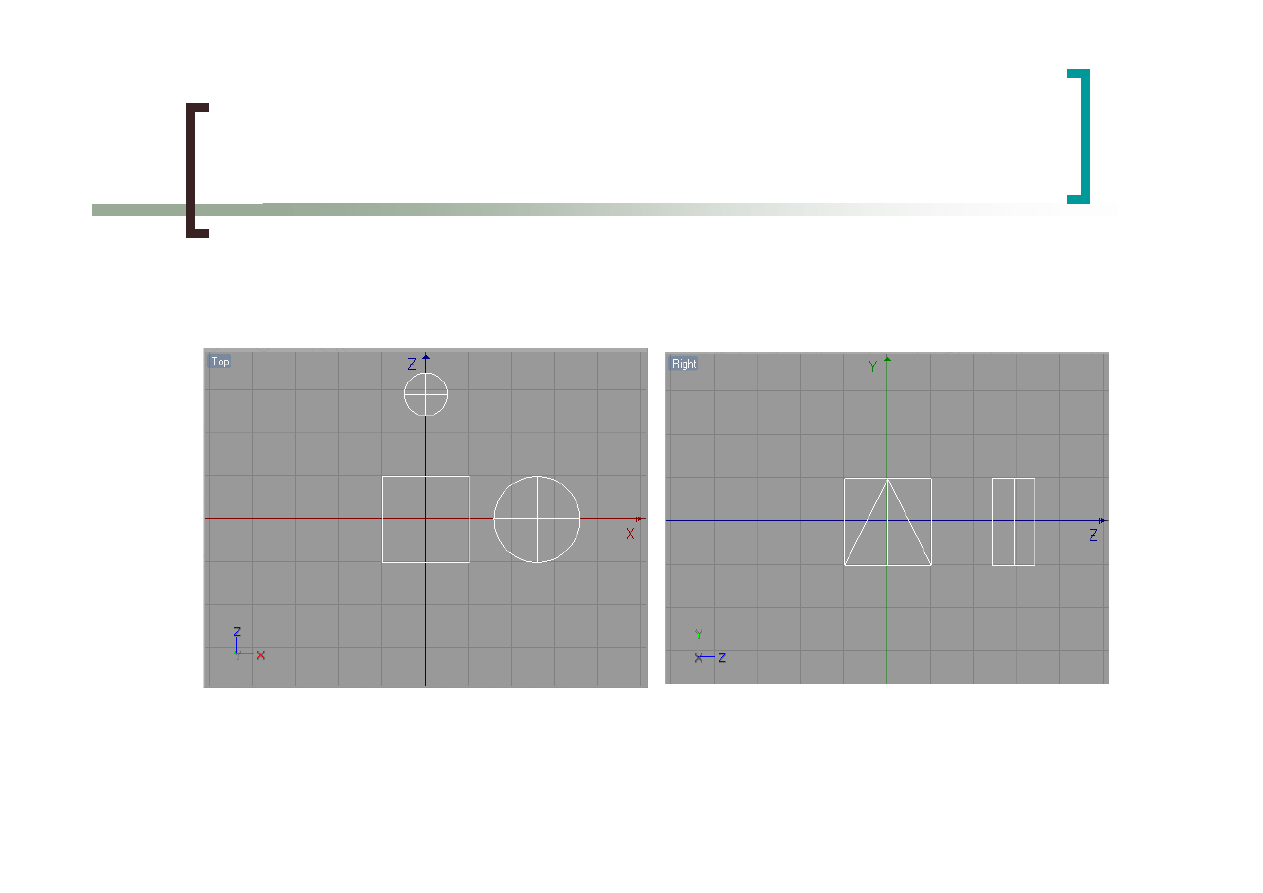
24
Rzuty prostokątne
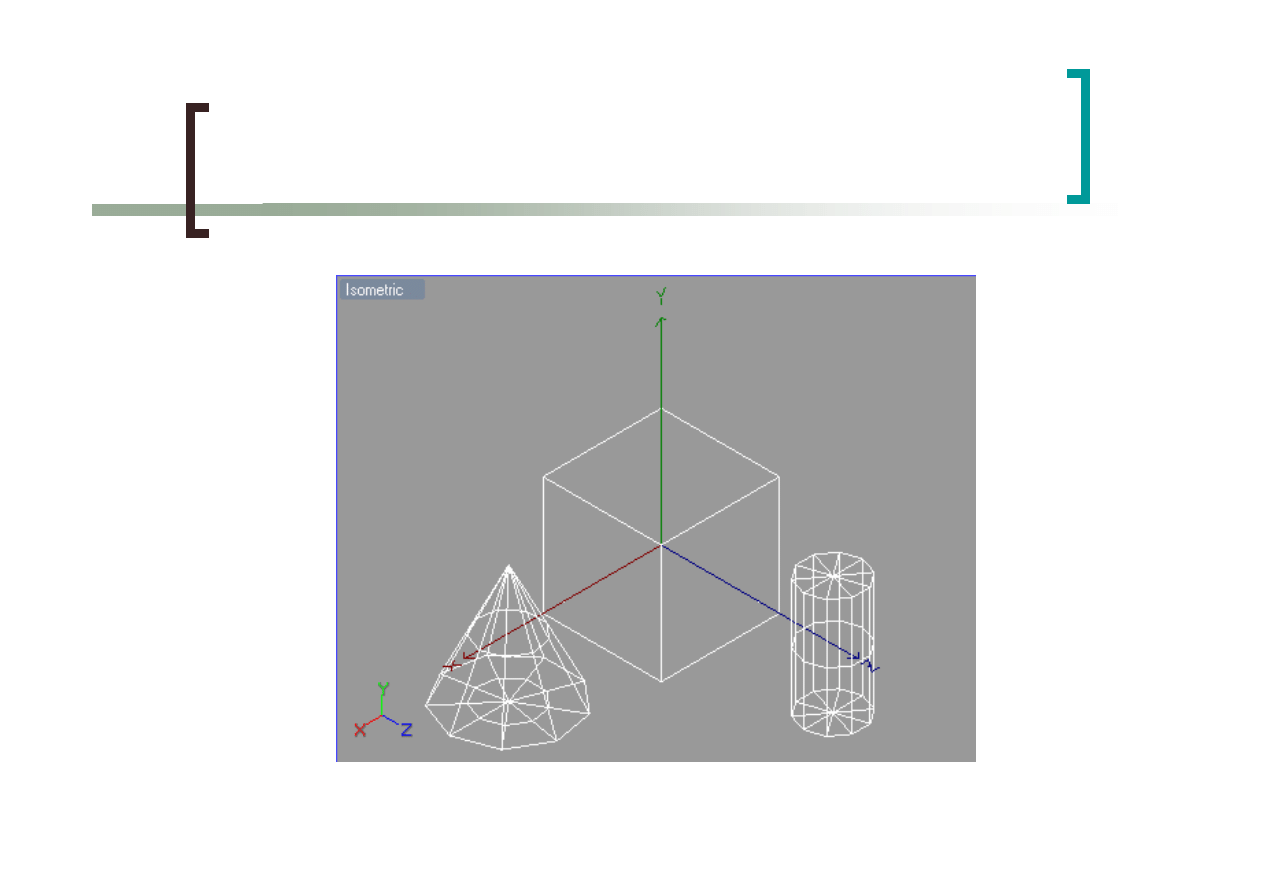
25
Rzut izometryczny
26
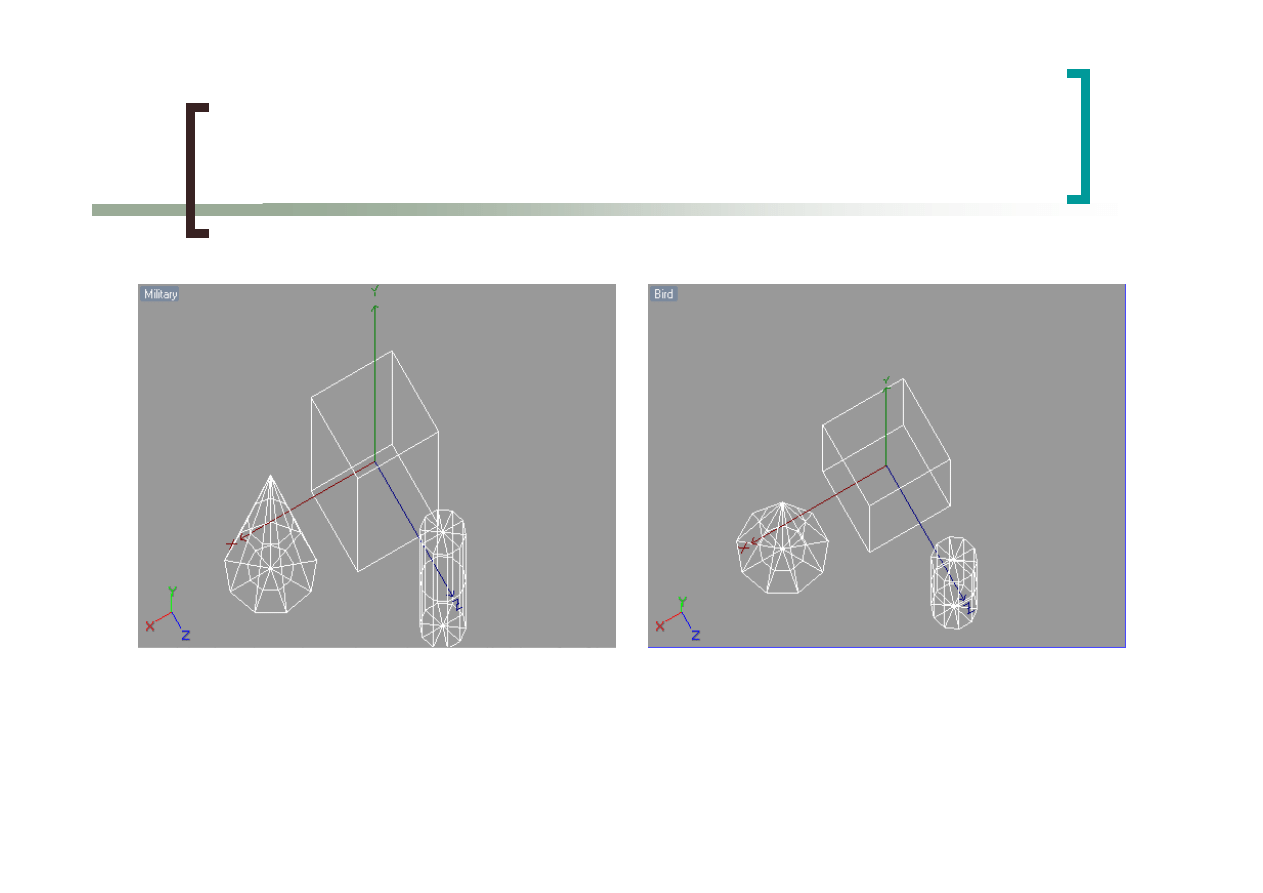
Rzuty ukośne
wojskowy
ptasi
27
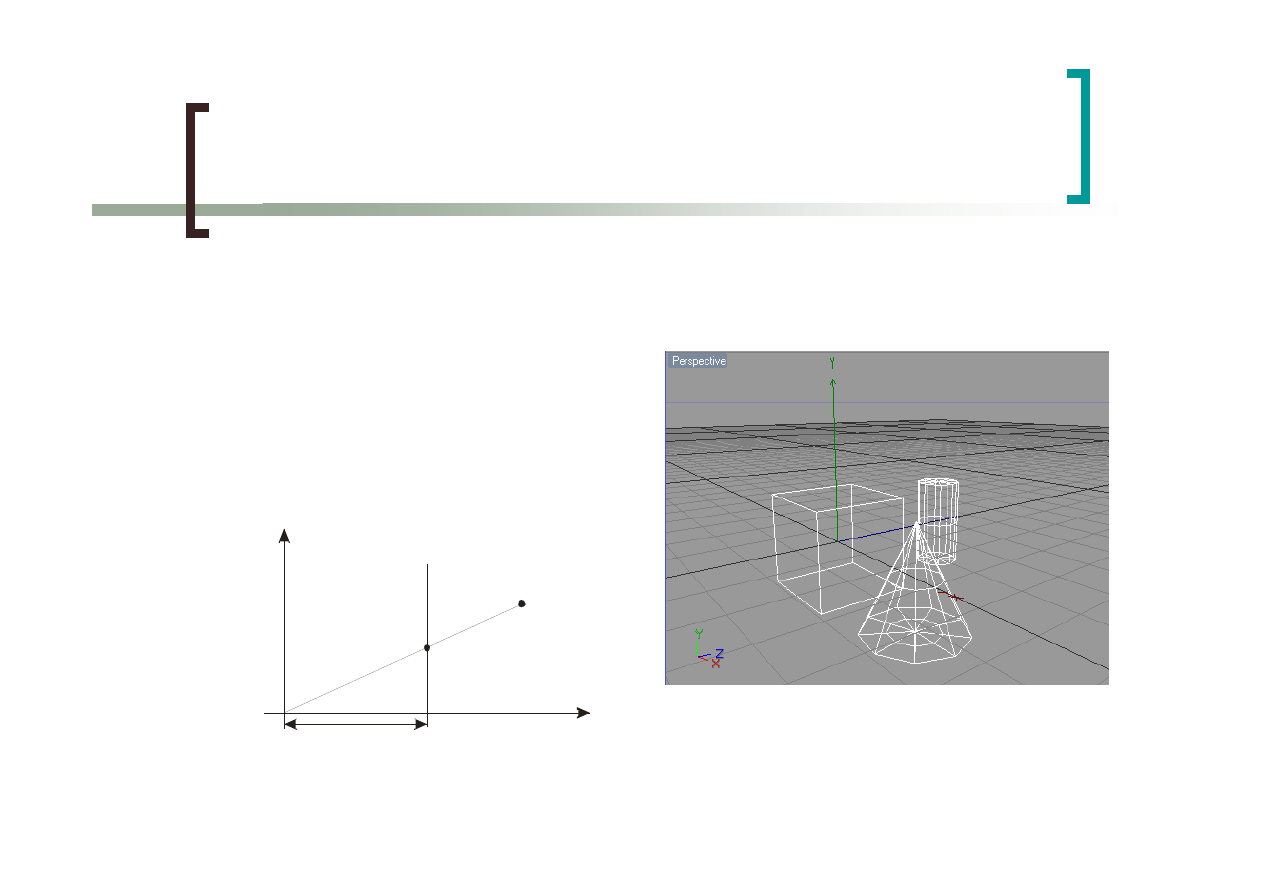
Rzut perspektywiczny
⎥
⎥
⎥
⎥
⎦
⎤
⎢
⎢
⎢
⎢
⎣
⎡
=
0
/
1
0
0
0
1
0
0
0
0
1
0
0
0
0
1
d
M
per
Z
X
d
rzutnia
P
P’
28
Reprezentacja krzywych
Krzywe reprezentowane parametrycznie
x=x(t), y=y(t), z=z(t)
Krzywe aproksymowane kawałkami
Najczęściej używane wielomiany
trzeciego stopnia
29
Wielomiany określające
segment krzywej
1
0
)
(
)
(
)
(
2
3
2
3
2
3
≤
≤
+
+
+
=
+
+
+
=
+
+
+
=
t
d
t
c
t
b
t
a
t
x
d
t
c
t
b
t
a
t
y
d
t
c
t
b
t
a
t
x
z
z
z
z
y
y
y
y
x
x
x
x
T
C
t
x
t
y
t
x
t
Q
t
t
t
T
d
c
b
a
d
c
b
a
d
c
b
a
C
z
z
z
z
y
y
y
y
x
x
x
x
⋅
=
⎥
⎥
⎥
⎦
⎤
⎢
⎢
⎢
⎣
⎡
=
⎥
⎥
⎥
⎥
⎥
⎦
⎤
⎢
⎢
⎢
⎢
⎢
⎣
⎡
=
⎥
⎥
⎥
⎦
⎤
⎢
⎢
⎢
⎣
⎡
=
)
(
)
(
)
(
)
(
1
2
3
Reprezentacja prosta
Reprezentacja macierzowa
30
Pochodna Q(t)
⎥
⎥
⎥
⎦
⎤
⎢
⎢
⎢
⎣
⎡
+
+
+
+
+
+
=
⎥
⎥
⎥
⎥
⎥
⎦
⎤
⎢
⎢
⎢
⎢
⎢
⎣
⎡
⋅
=
⋅
=
⎥
⎥
⎥
⎥
⎥
⎥
⎦
⎤
⎢
⎢
⎢
⎢
⎢
⎢
⎣
⎡
=
′
=
z
z
z
y
y
y
x
x
x
c
t
b
t
a
c
t
b
t
a
c
t
b
t
a
t
t
C
T
C
dt
d
t
z
dt
d
t
y
dt
d
t
x
dt
d
t
Q
t
Q
dt
d
2
3
2
3
2
3
0
1
2
3
)
(
)
(
)
(
)
(
)
(
2
2
2
2
Wektor styczny na początku segmentu t=0
Wektor styczny na końcu segmentu t=1
31
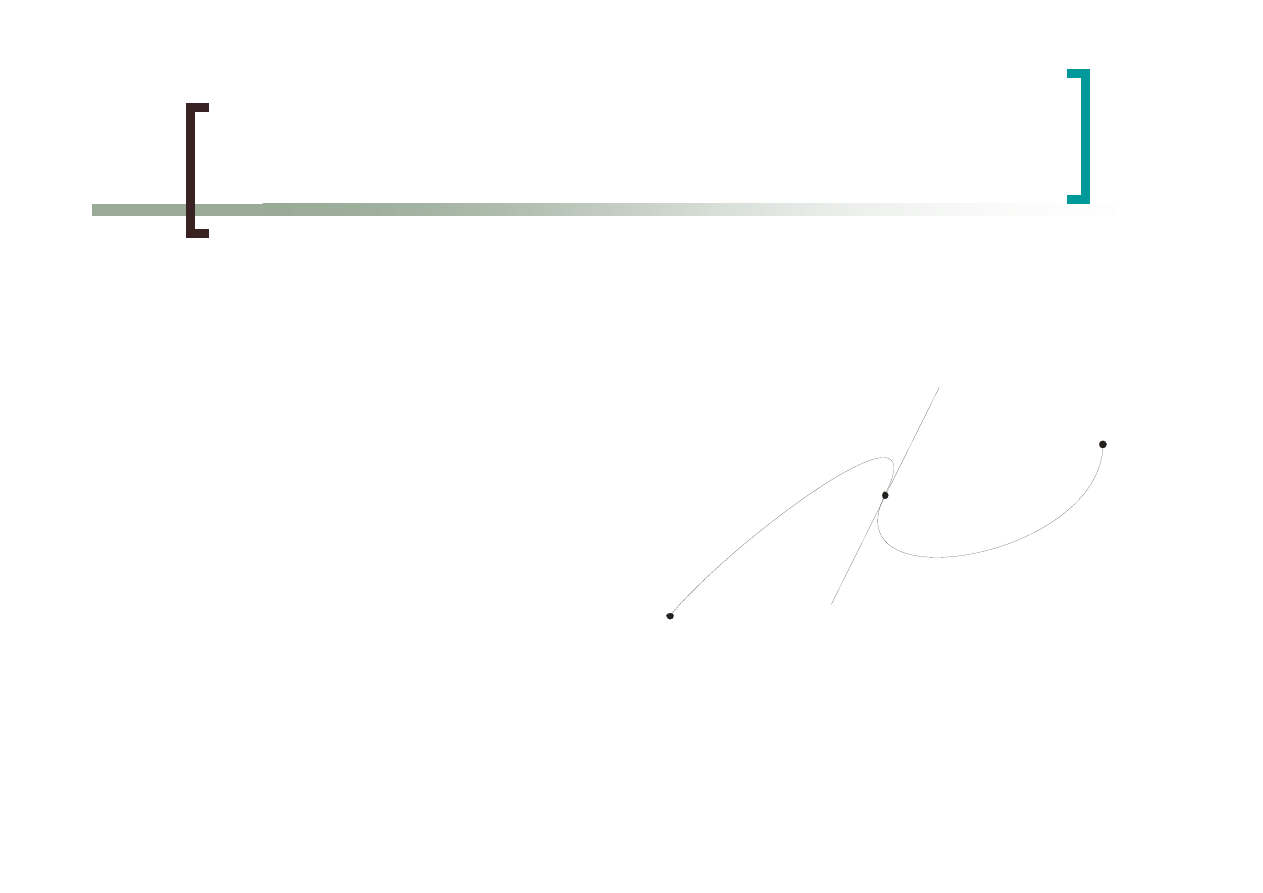
Ciągłość geometryczna
G
0
– segmenty łączą
się ze sobą
G
1
– styczne w
punkcie połączenia
mają ten sam
kierunek
Q
1
Q
2
Q
1
Q
2
S
1
S
2
32
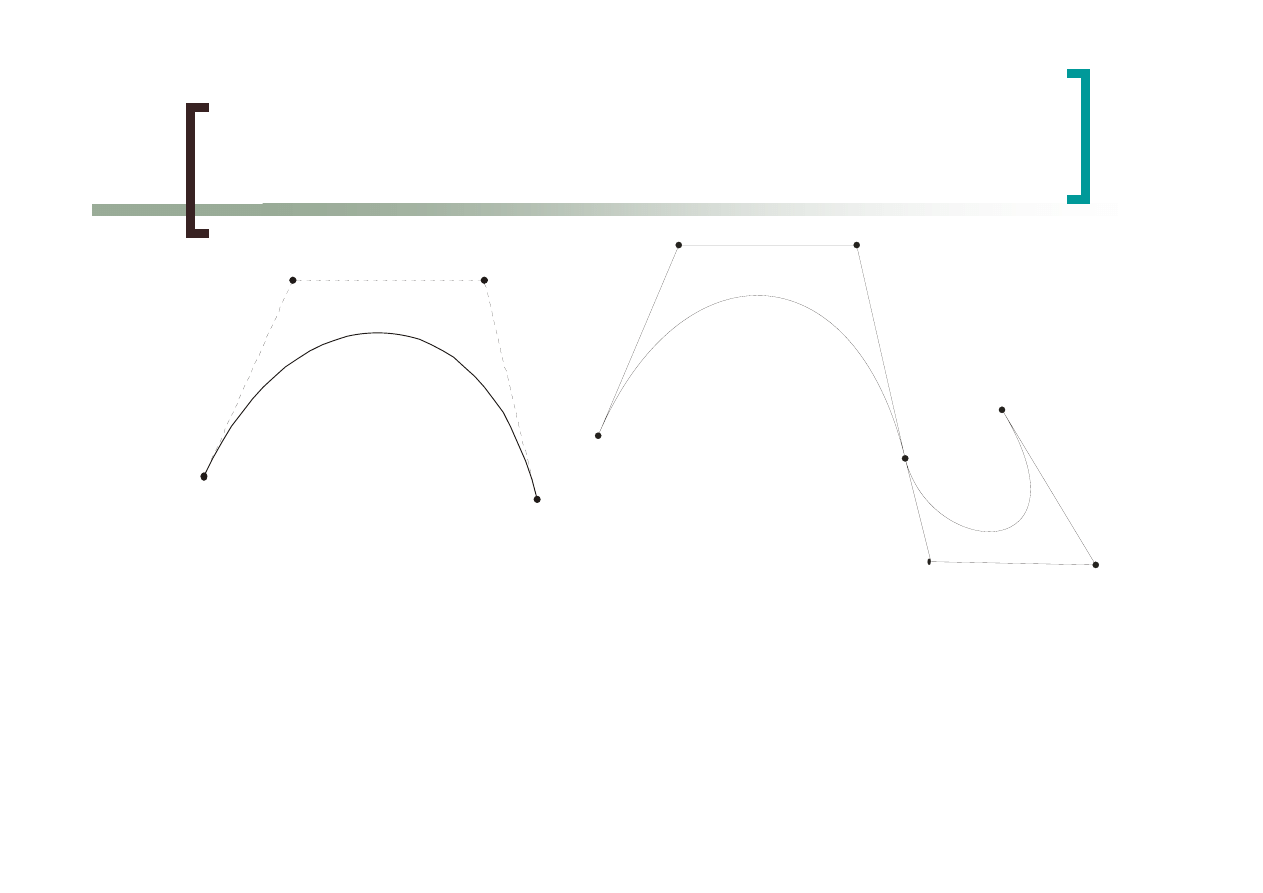
Ciągłość parametryczna
C1 – pierwsze
pochodne
segmentów w
punkcie połączenia
są identyczne
C2 – drugie
pochodne
segmentów w
punkcie połączenia
są identyczne
Q
1
Q
2
S
1
S
2
33
Krzywe Béziera
4
3
3
2
2
2
1
3
)
1
(
3
)
1
(
3
)
1
(
)
(
P
t
P
t
t
P
t
t
P
t
t
Q
+
−
+
−
+
−
=
Równanie opisujące krzywą:
Aby krzywa byłą ciągła, punkty P
3
, P
4
i P
5
muszą być
współliniowe
P
1
P
2
P
3
P
4
P
1
P
2
P
3
P
4
P
5
P
6
P
7
34
Jednorodne krzywe B-sklejane
1
0
6
6
1
3
3
3
6
4
6
3
6
)
1
(
)
(
3
1
2
3
2
2
3
3
3
≤
≤
+
+
+
+
−
+
+
−
+
−
=
−
−
−
−
t
P
t
P
t
t
t
P
t
t
P
t
t
t
Q
i
i
i
i
i
i
Krzywa aproksymuje m+1 punktów
kontrolnych P
0
, P
1
, …, P
m
, dla m ≥ 3
Węzły krzywej mają jednakową odległość ze
względu na parametr t
35
Niejednorodne krzywe
B-sklejane
Odstępy pomiędzy węzłami nie muszą być
jednakowe
Można określać stopień ciągłości w węzłach
Co najmniej 4 punkty kontrolne
Liczba węzłów m+4, gdzie m to liczba
punktów kontrolnych
Sekwencja węzłów musi być niemalejąca
np. (0, 0, 0, 1, 2, 2, 3, 4)
36
Niejednorodne krzywe
B-sklejane
Segment Q
i
jest określony przez punkty
kontrolne P
i-3
, P
i-2
, P
i-1
, P
i
i funkcje bazowe
B
i-3,4
(t), B
i-2,4
(t), B
i-1,4
(t), B
i,4
(t)
1
4
,
4
,
1
1
4
,
2
2
4
,
3
3
3
)
(
)
(
)
(
)
(
)
(
+
−
−
−
−
−
−
<
≤
≤
≤
⋅
+
⋅
+
⋅
+
⋅
=
i
i
i
i
i
i
i
i
i
i
i
t
t
t
m
i
t
B
P
t
B
P
t
B
P
t
B
P
t
Q
37
Funkcje bazowe dla krzywych
B-sklejanych
)
(
)
(
)
(
)
(
)
(
)
(
)
(
)
(
)
(
przypadku
przeciwnym
w
,
0
,
1
)
(
3
,
1
1
4
4
3
,
3
4
,
2
,
1
1
3
3
2
,
2
3
,
1
,
1
1
2
2
1
,
1
2
,
1
1
,
t
B
t
t
t
t
t
B
t
t
t
t
t
B
t
B
t
t
t
t
t
B
t
t
t
t
t
B
t
B
t
t
t
t
t
B
t
t
t
t
t
B
t
t
t
t
B
i
i
i
i
i
i
i
i
i
i
i
i
i
i
i
i
i
i
i
i
i
i
i
i
i
i
i
i
i
i
+
+
+
+
+
+
+
+
+
+
+
+
+
+
+
+
−
−
+
−
−
=
−
−
+
−
−
=
−
−
+
−
−
=
⎩
⎨
⎧
<
≤
=
38
Niejednorodne ułamkowe
krzywe B-sklejane (NURBS)
Postać ogólna
Są one niezmiennicze względem
przekształceń afinicznych i
perspektywicznego
Mogą dokładnie definiować dowolny
przekrój stożka
)
(
)
(
)
(
,
)
(
)
(
)
(
,
)
(
)
(
)
(
t
W
t
Z
t
z
t
W
t
Y
t
y
t
W
t
X
t
x
=
=
=
39
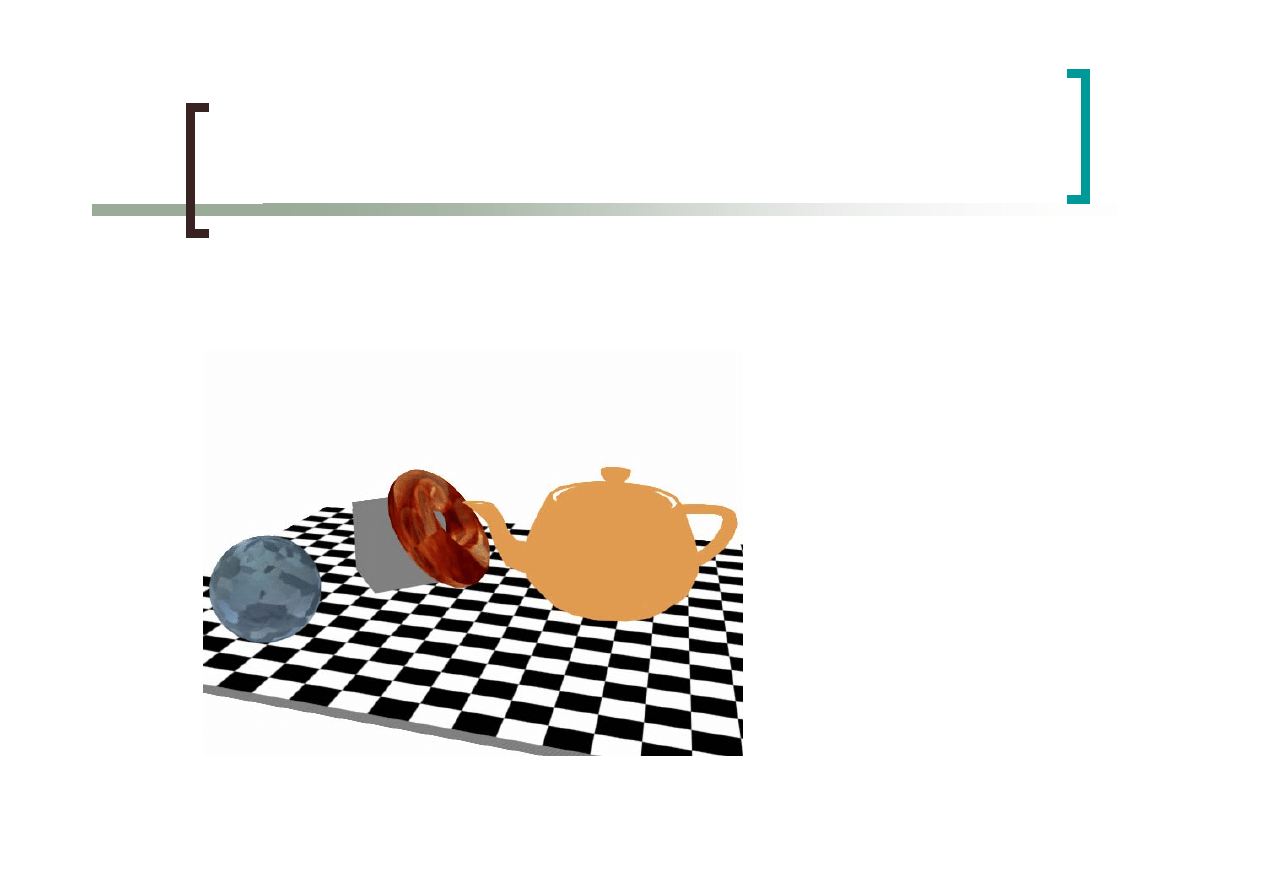
Oświetlenie i cieniowanie
powierzchni
Modele oświetlenia
Modele cieniowania
40
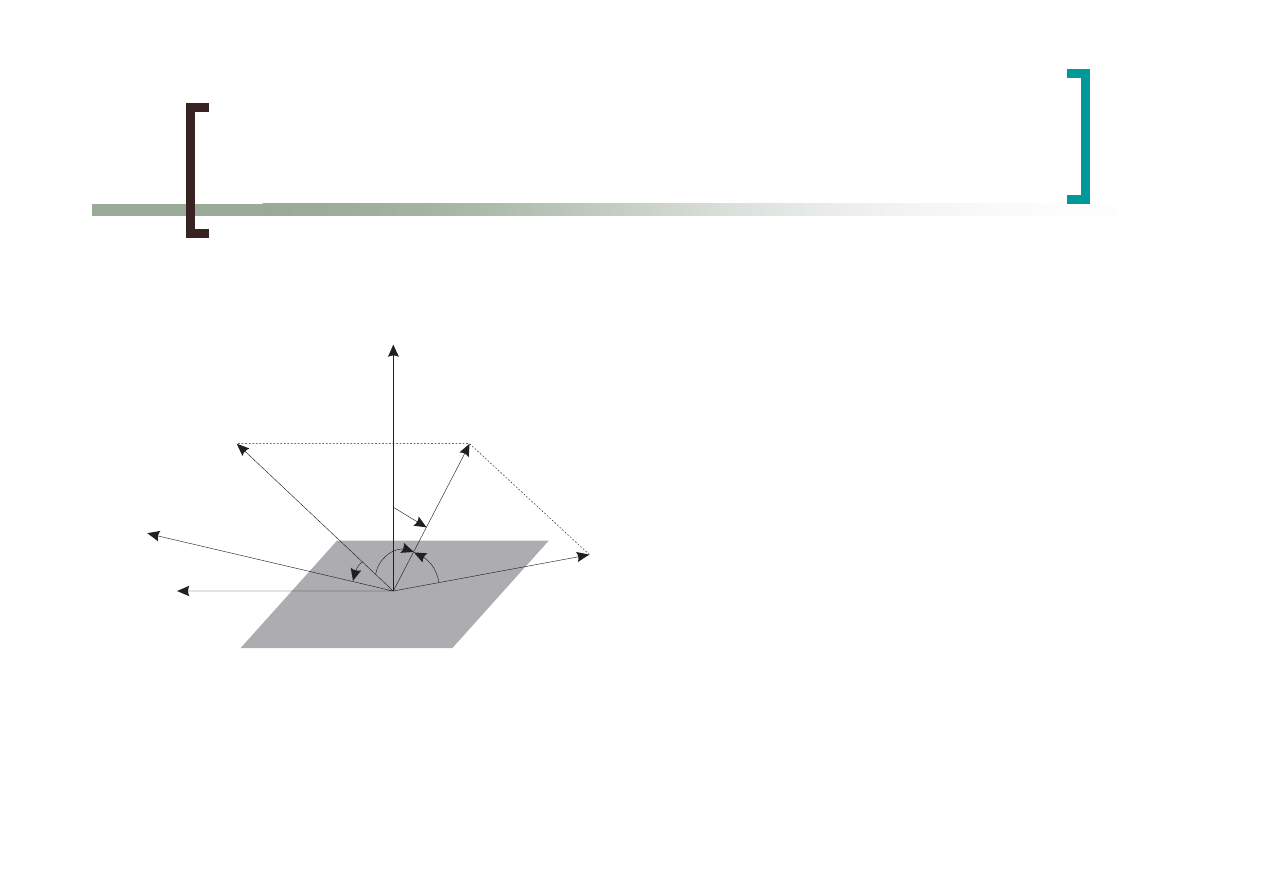
Wektory używane w
obliczeniach
n
v
l
h
t
r
l
n – wektor normalny
v – kierunek patrzenia
l – kierunek światła
h – wektor połowiczny
r
l
=2(l·n)n-l
t – wektor styczny do
powierzchni
41
Światło otoczenia
a
a
k
I
I
=
42
Odbicie rozproszone
(Lambertowskie)
)
( n
l
k
I
I
d
p
⋅
=
43
Odbicie zwierciadlane
(Model Phonga)
i
n
l
s
i
n
l
s
L
v
r
k
L
v
r
k
I
)
(
)
,
cos(
⋅
=
⋅
⋅
=
Parametr n
decyduje o wielkości
rozbłysku, im jest
większy, tym
rozbłysk jest węższy
i ostrzejszy
44
Model Blinn’a
i
n
s
L
h
n
k
I
)
(
⋅
=
Bardziej zbliżony do
rzeczywistości od
Phonga
Dobrze symuluje
matowe metaliczne
materiały
45
Przezroczystość
Przezroczystość interpolowana
Przezroczystość filtrowana
2
1
)
1
(
kI
I
k
I
+
−
=
2
1
I
kO
I
I
t
+
=
46
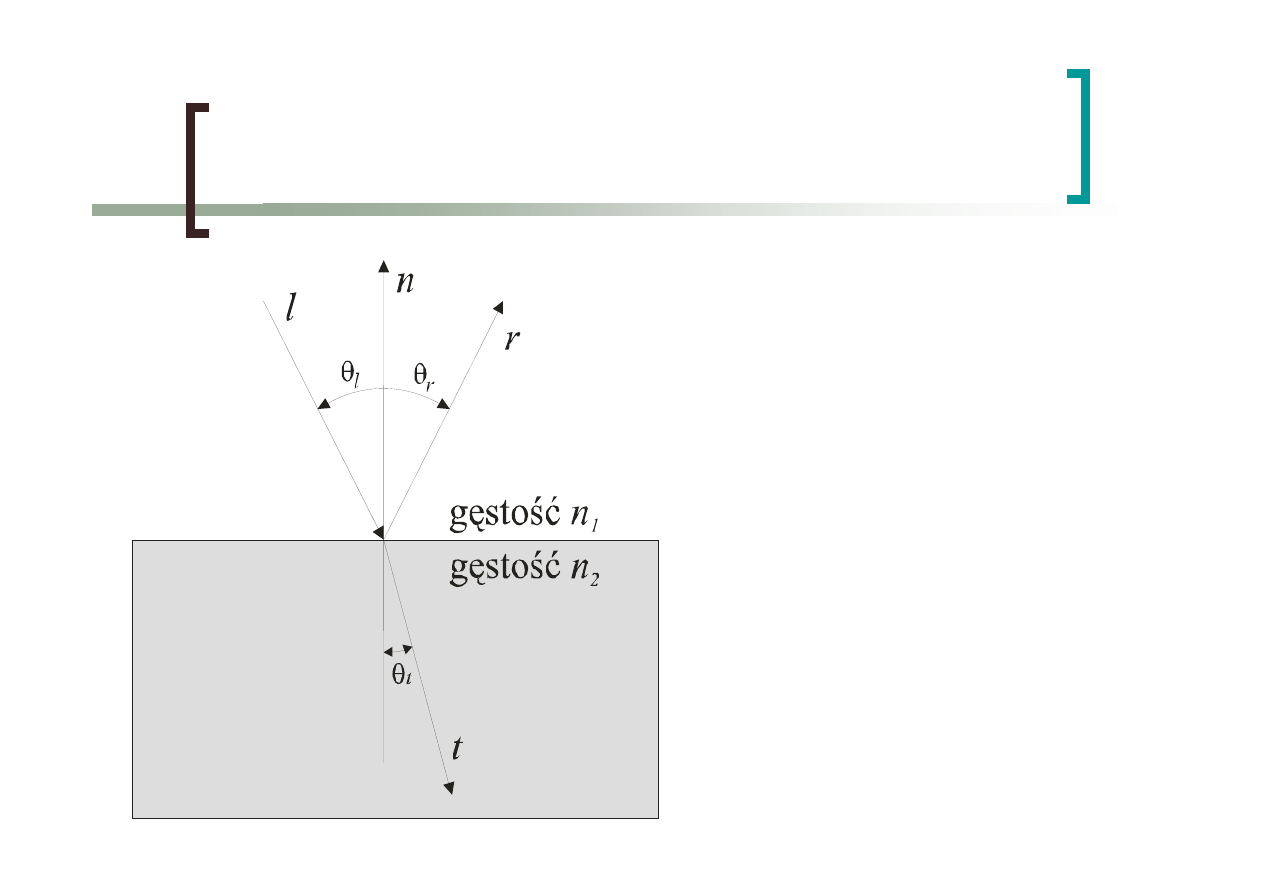
Załamanie światła
Prawo odbicia
światła
Prawo Snell’a
t
l
n
n
θ
θ
sin
sin
2
1
=
l
r
θ
θ
=
47
Reguła Fresnela
Stosunek ilości światła odbitego do
załamanego zależy od kąta padania
światła
Istnieje pewien graniczny kąt, powyżej
którego światło ulega całkowitemu
odbiciu
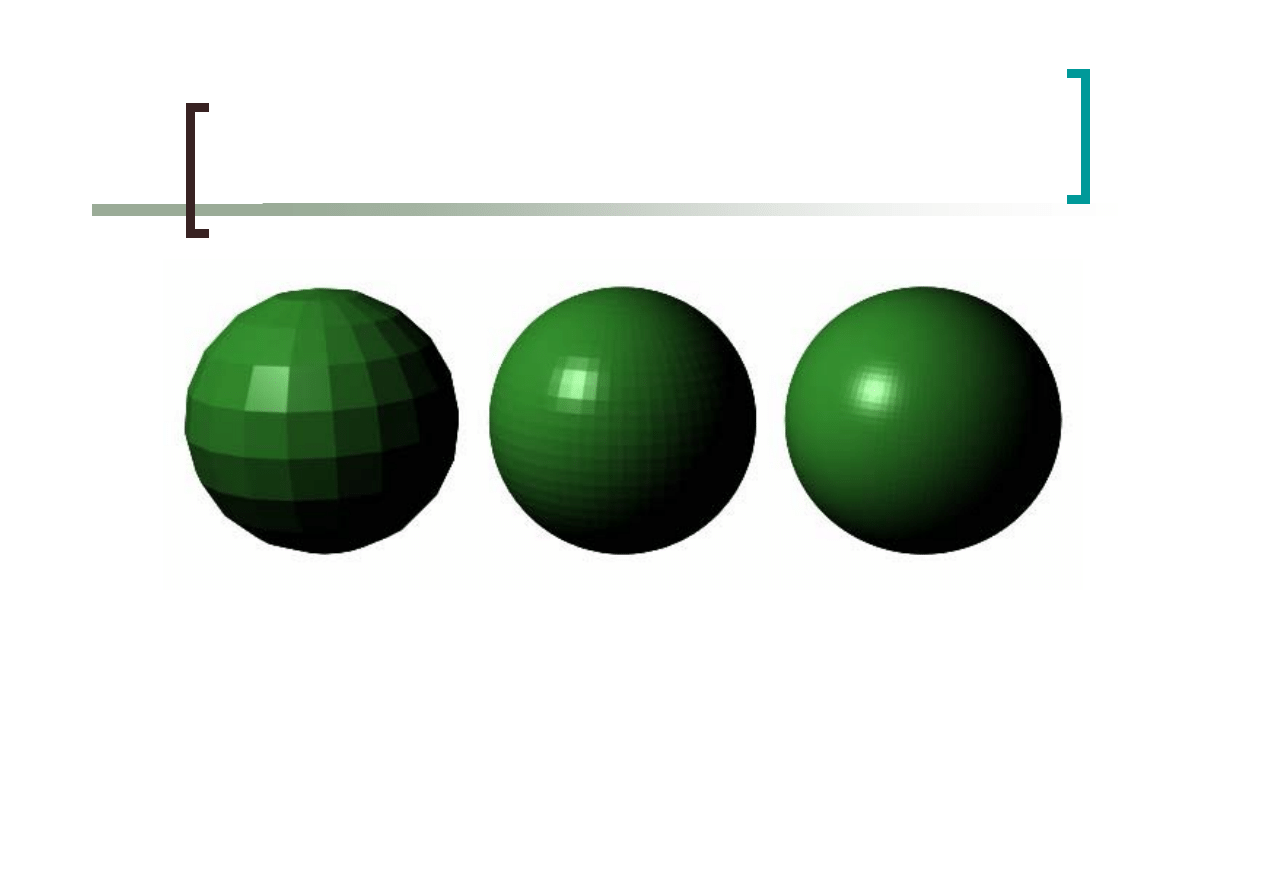
48
Cieniowanie płaskie
Wektory normalne obliczane dla wielokątów
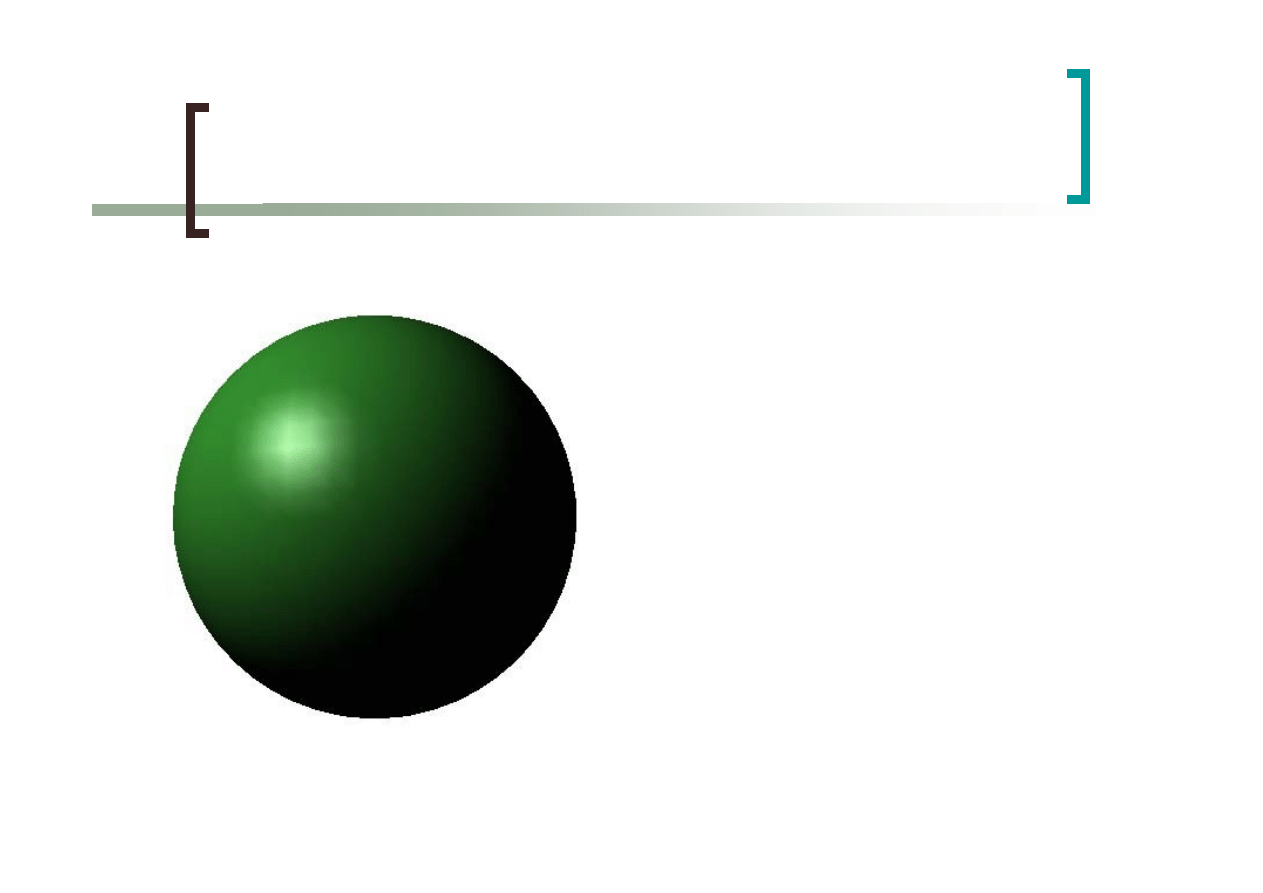
49
Cieniowanie Gourauda
Wektory normalne
określone dla wierzchołków
poprzez uśrednienie
wektorów sąsiednich
płaszczyzn
Oświetlenie liczone dla
wierzchołków
Obliczona wartość
interpolowana pomiędzy
wierzchołkami
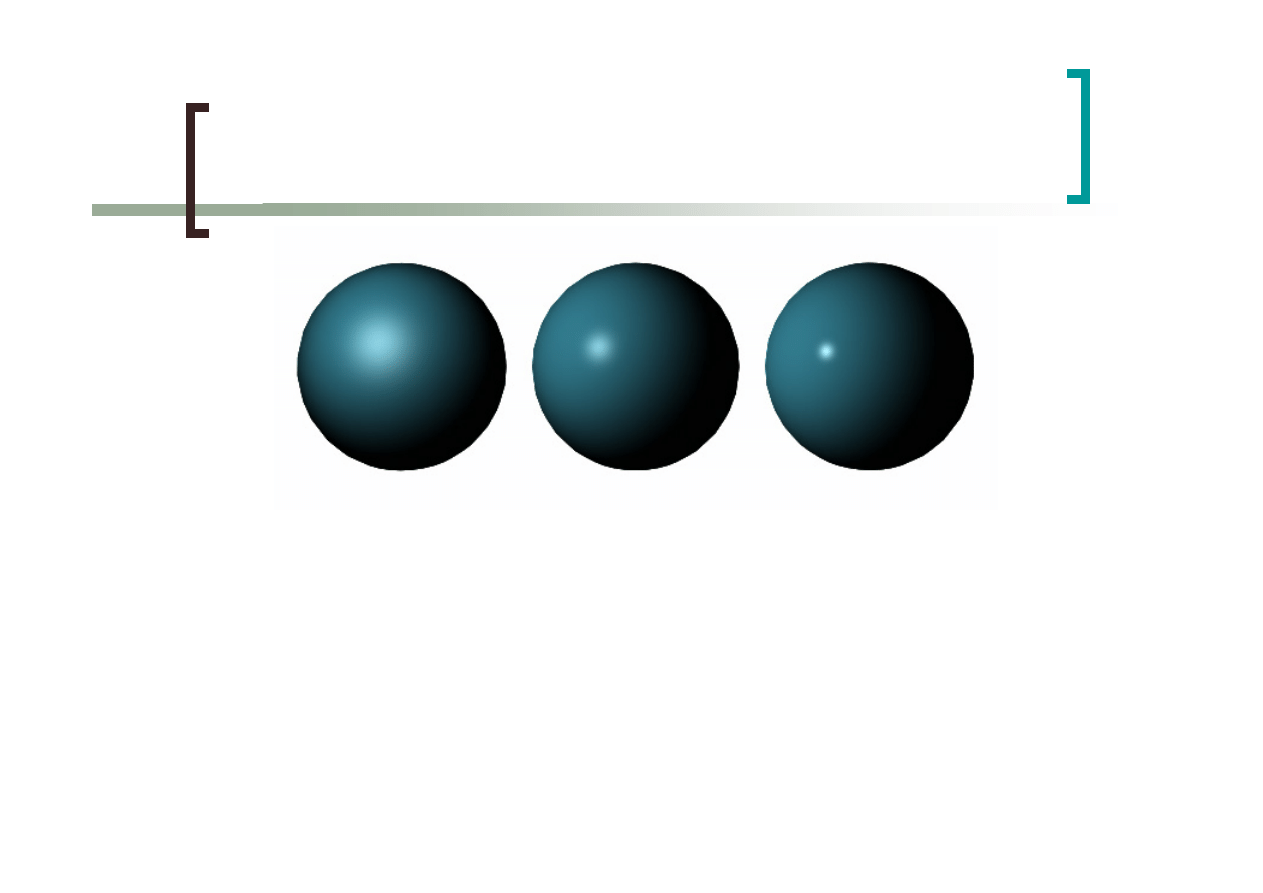
50
Cieniowanie Phong’a
Cieniowanie z interpolacją wektorów
normalnych
Oświetlenie obliczane dla każdego punktu
powierzchni
51
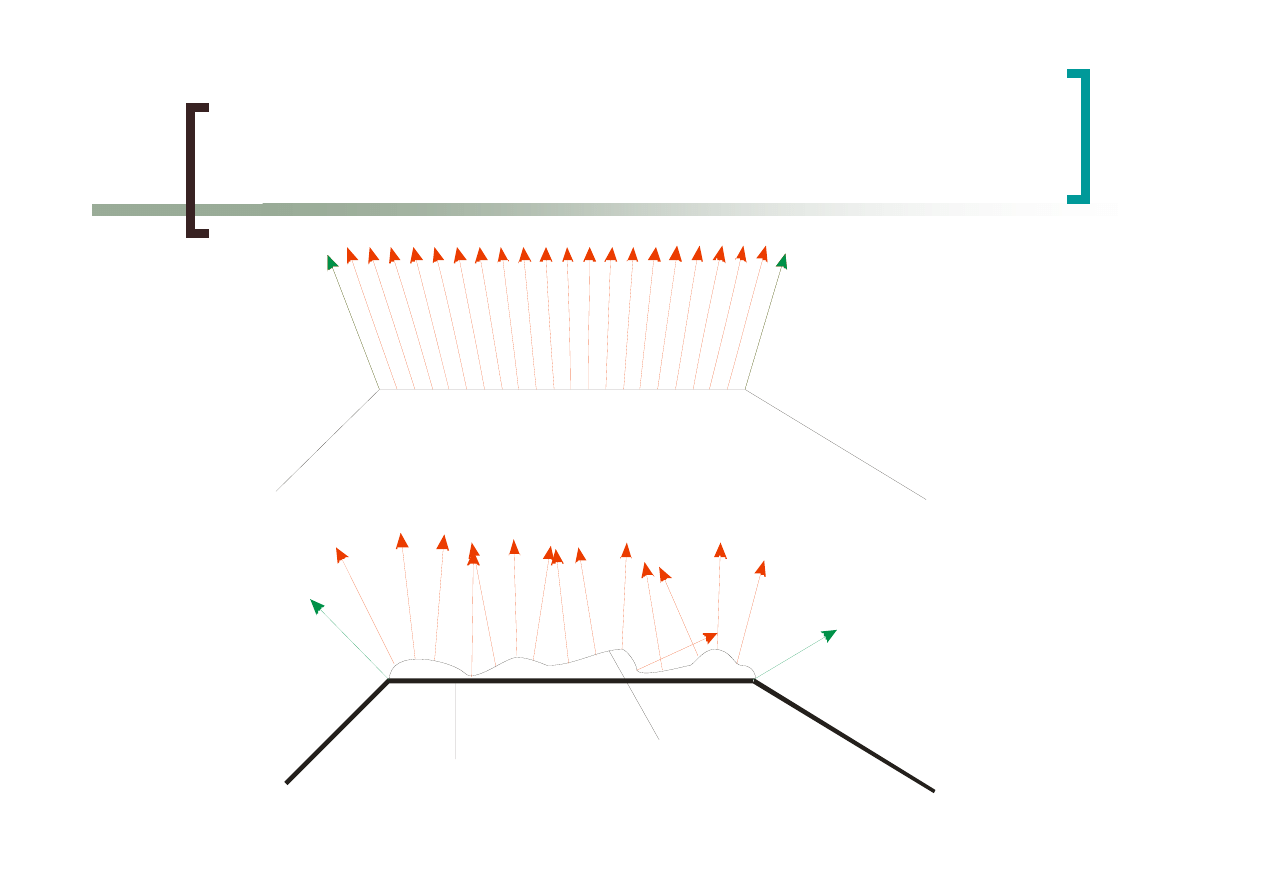
Interpolacja wektorów
normalnych
powierzchnia
mapa
wybrzuszeń

52
Parametryczne mapowanie
tekstury (UVW)
53
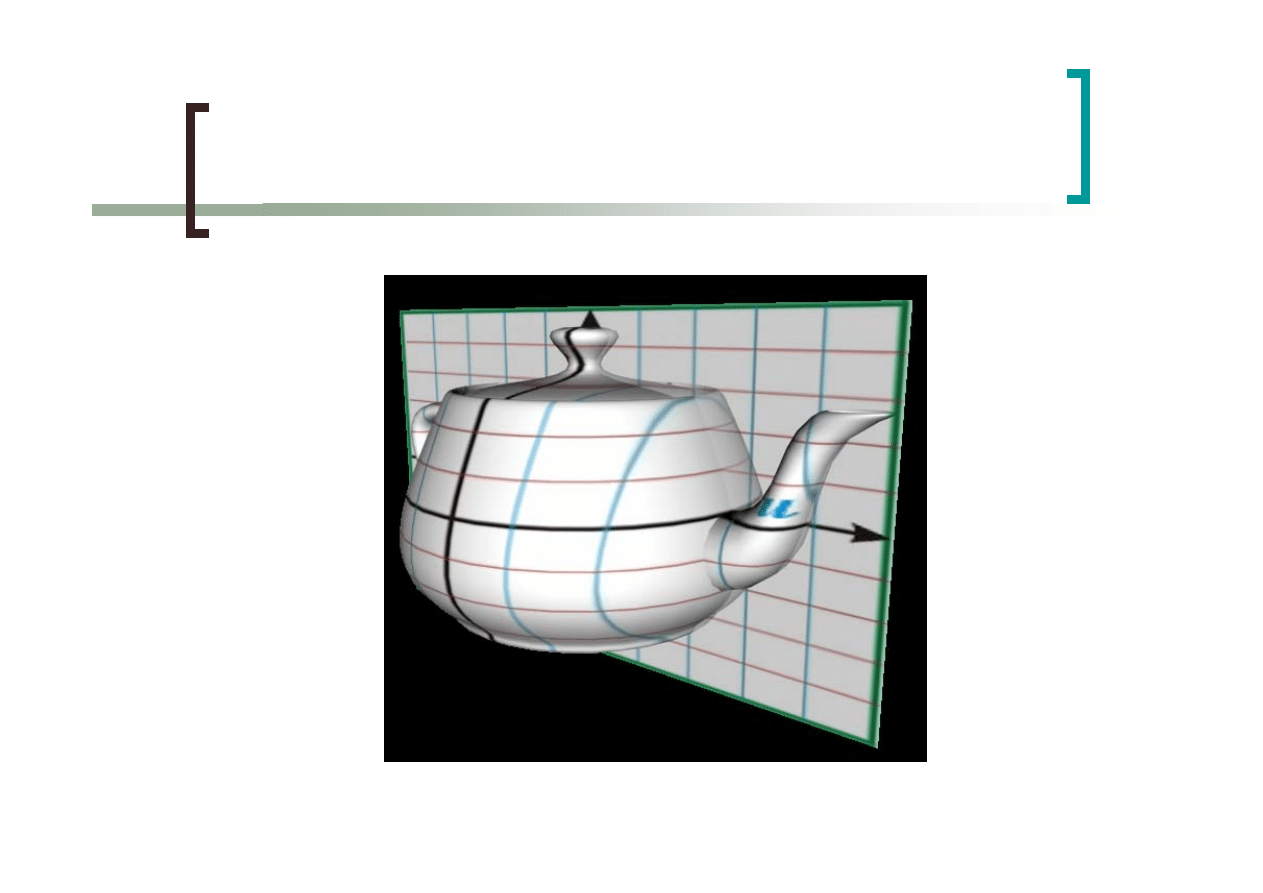
Mapowanie planarne
54
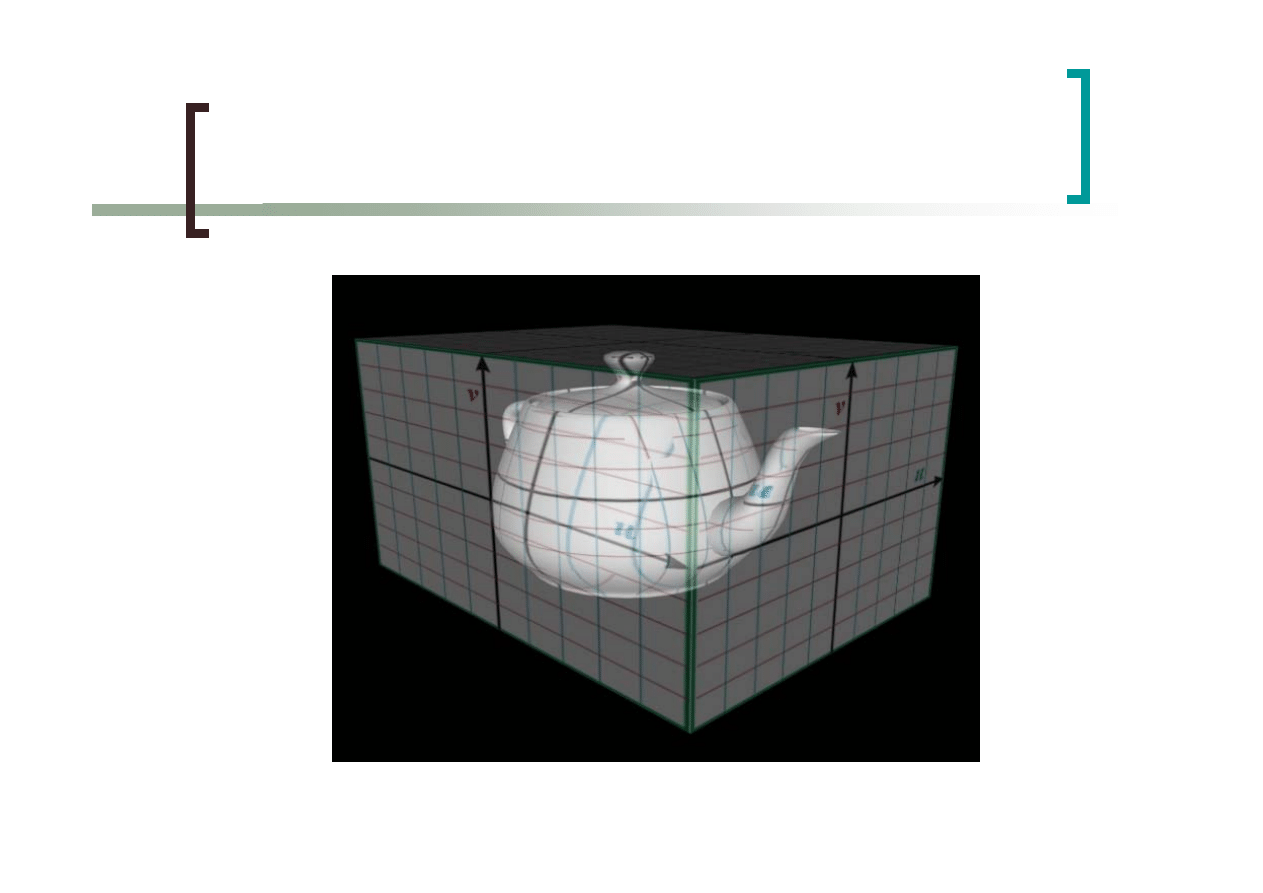
Mapowanie prostopadłościenne
55
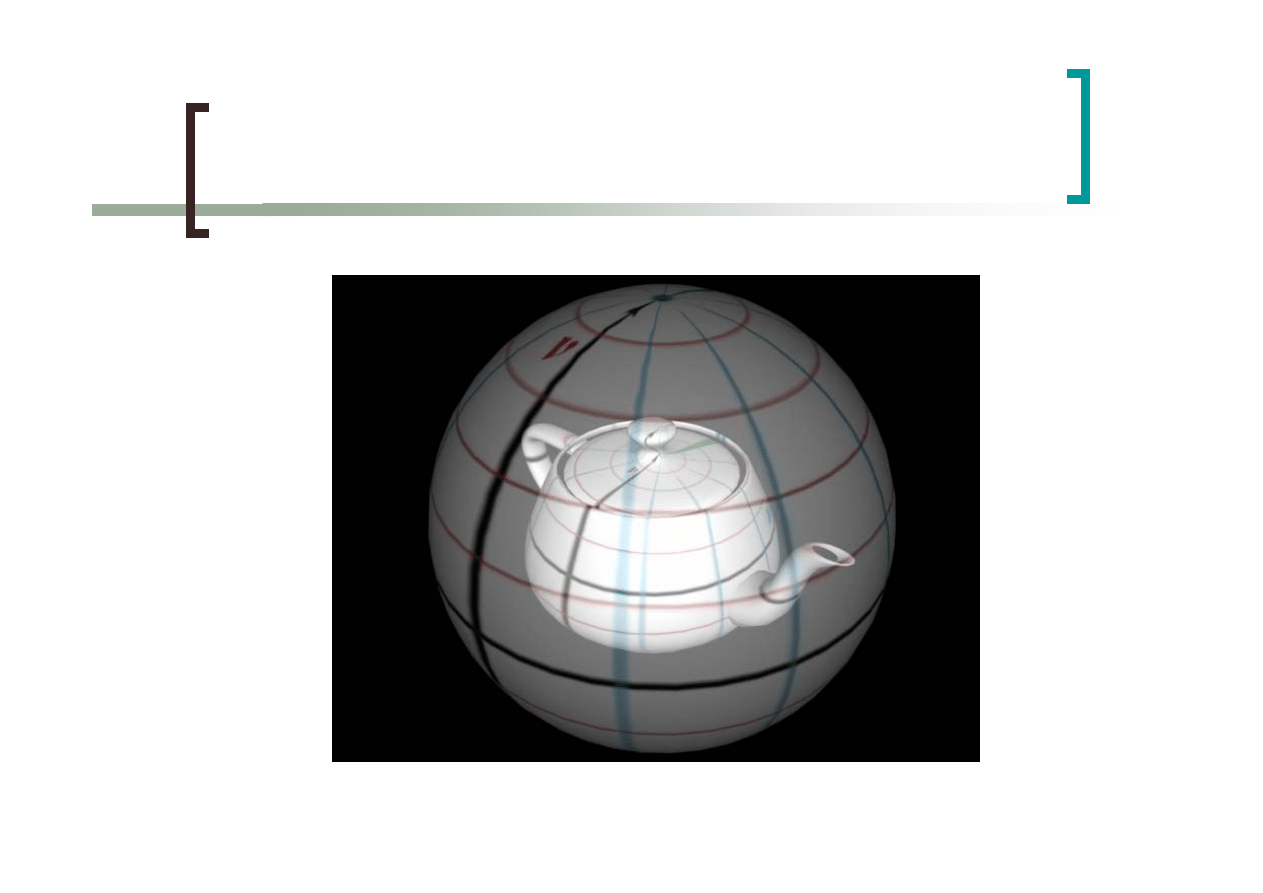
Mapowanie sferyczne
56
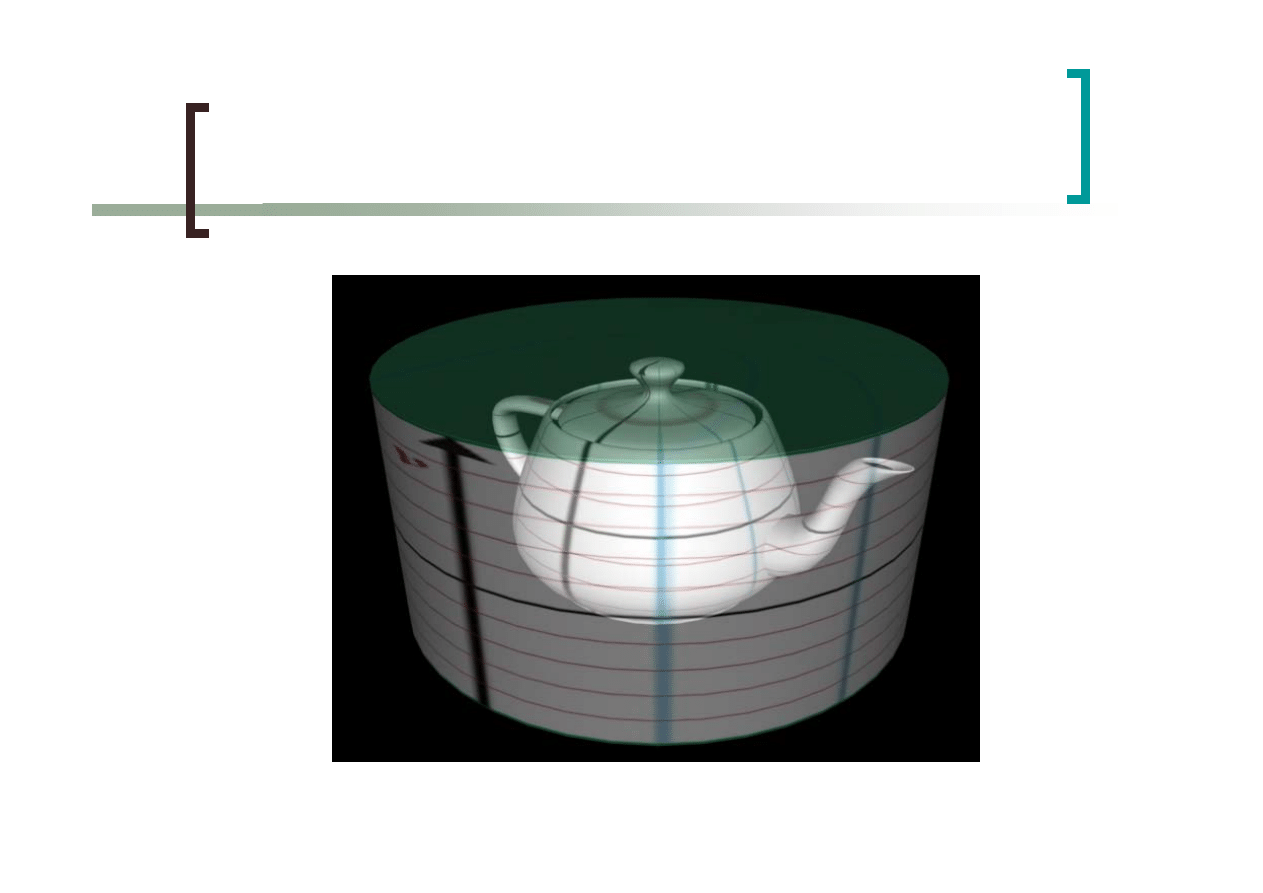
Mapowanie cylindryczne bez
podstawy
57
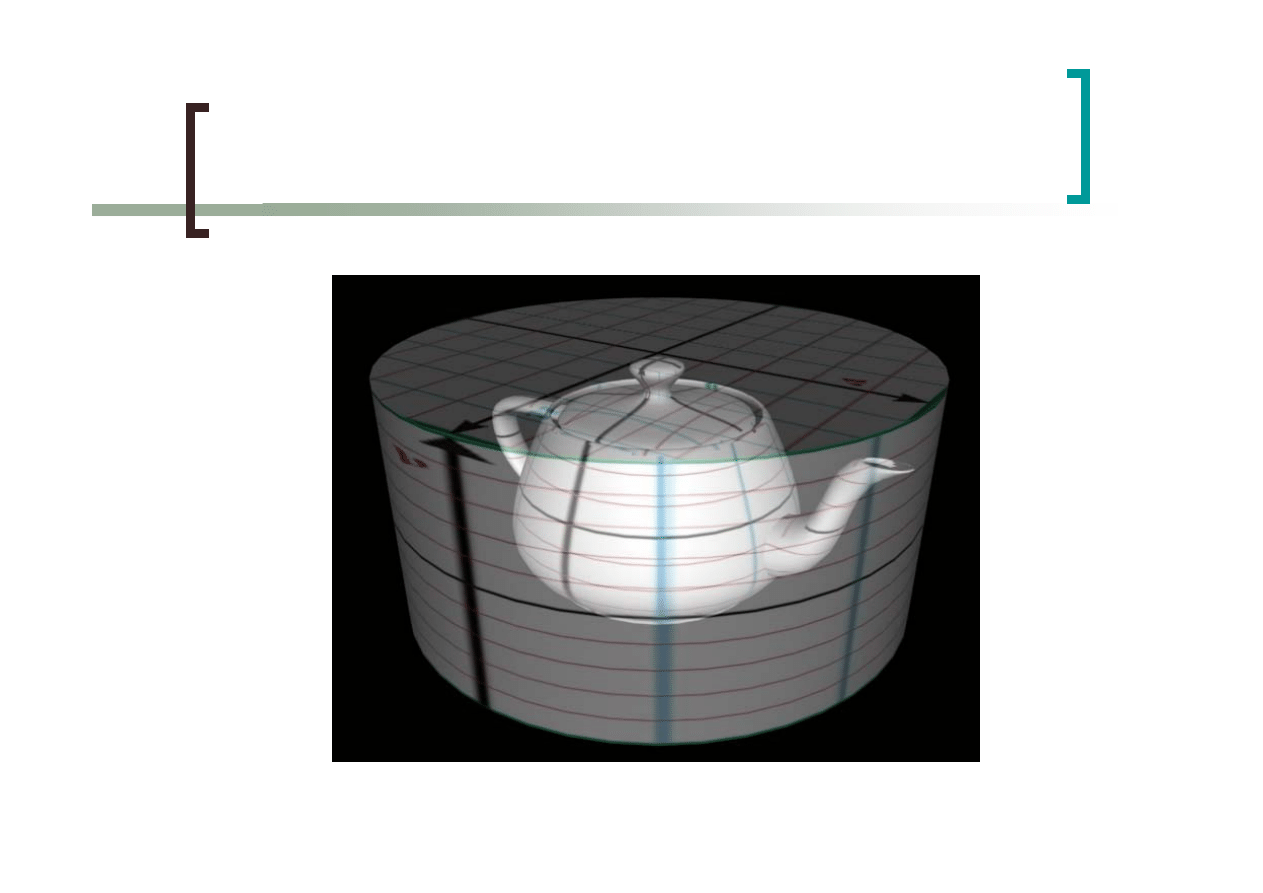
Mapowanie cylindryczne
z podstawą

58
Mapowanie środowiska

59
Mapowanie wybrzuszeń

60
Tekstury proceduralne
Document Outline
- Grafika wektorowa
- Operacje na wektorach
- Operacje na wektorach
- Operacje na wektorach
- Reprezentacja obiektów wektorowych
- Przekształcenia 2D
- Translacja
- Skalowanie
- Obrót
- Składanie przekształceń 2D
- Współrzędne jednorodne
- Translacja we współrzędnych jednorodnych
- Skalowanie we współrzędnych jednorodnych
- Obrót we współrzędnych jednorodnych
- Pochylenia we współrzędnych jednorodnych
- Składanie przekształceń 2D
- Składanie przekształceń 2D
- Przekształcenie okna w pole wizualizacji
- Przekształcenia 3D
- Obroty 3D
- Rzuty
- Rzuty
- Rzuty równoległe
- Rzuty prostokątne
- Rzut izometryczny
- Rzuty ukośne
- Rzut perspektywiczny
- Reprezentacja krzywych
- Wielomiany określające segment krzywej
- Pochodna Q(t)
- Ciągłość geometryczna
- Ciągłość parametryczna
- Krzywe Béziera
- Jednorodne krzywe B-sklejane
- Niejednorodne krzywe B-sklejane
- Niejednorodne krzywe B-sklejane
- Funkcje bazowe dla krzywych B-sklejanych
- Niejednorodne ułamkowe krzywe B-sklejane (NURBS)
- Oświetlenie i cieniowanie powierzchni
- Wektory używane w obliczeniach
- Światło otoczenia
- Odbicie rozproszone (Lambertowskie)
- Odbicie zwierciadlane (Model Phonga)
- Model Blinn’a
- Przezroczystość
- Załamanie światła
- Reguła Fresnela
- Cieniowanie płaskie
- Cieniowanie Gourauda
- Cieniowanie Phong’a
- Interpolacja wektorów normalnych
- Parametryczne mapowanie tekstury (UVW)
- Mapowanie planarne
- Mapowanie prostopadłościenne
- Mapowanie sferyczne
- Mapowanie cylindryczne bez podstawy
- Mapowanie cylindryczne z podstawą
- Mapowanie środowiska
- Mapowanie wybrzuszeń
- Tekstury proceduralne
Wyszukiwarka
Podobne podstrony:
2008 06 Edytor grafiki wektorowej Inkscape [Grafika]
3 Grafika wektorowa i bitmapowa
Grafika wektorowa(1)
Grafika wektorowa, edukacja i nauka, Informatyka
GRAFIKA WEKTOROWA I RASTROWA
Grafika rastrowa a grafika wektorowa
tutorial Pac-Men, Informatyka, grafika wektorowa
GRAFIKA WEKTOROWA
GRAFIKA WEKTOROWA I RASTROWA2
Grafika wektorowa
Grafika wektorowa
Grafika wektorowa, KOMPUTERY, Komputerowe!!!
Dodatek3 Grafika wektorowa id Nieznany
Konkrety grafiki wektorowej
Edytory grafiki wektorowej
GM 4 Grafika rastrowa grafika wektorowa
Grafika wektorowa
GK 5 Grafika wektorowa i rastrowa
Konkrety grafiki wektorowej
więcej podobnych podstron