Ćwiczenia z przedmiotu Technika Analogowa
Analiza wskazowa Dodatek
© C. Stefański
0_01_Zestawienie zaleznosci dla obwodow rezonansowych.doc
1/8
Zauważone błędy i usterki proszę zgłaszać autorowi na adres cestef@o2.pl
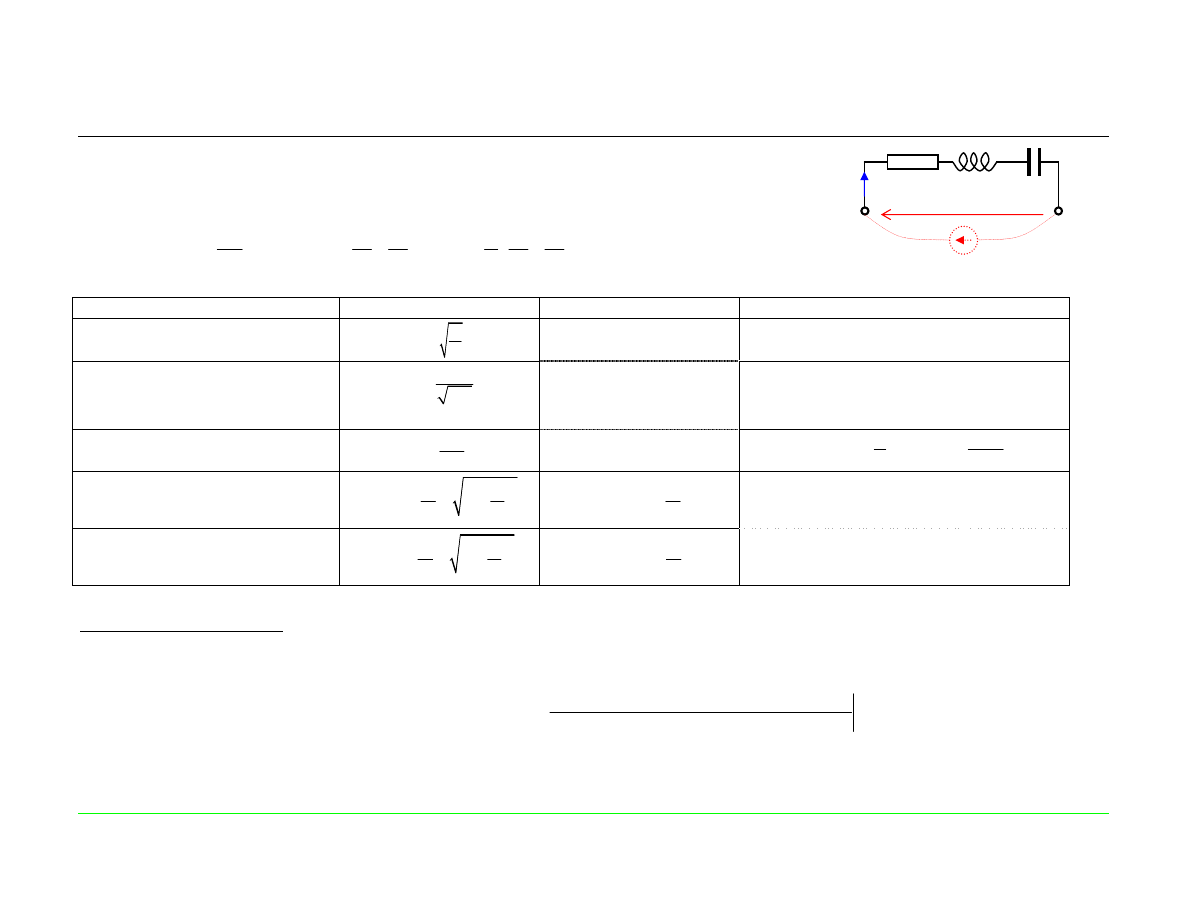
Zestawienie zależności dla szeregowego obwodu rezonansowego RLC
(współpracującego ze źródłem idealnym)
Impedancja
1
1
(1
)
(1
)
o
o
o
o
Z
R
L
Z
R
R
R
Q
R
C
R
ω
ω
ρ ω
ω
ω
ρ
ν
ξ
ω
ω
ω
ω
ω
=
+
−
=
=
+
−
=
+
−
=
+
=
+
j
j
j
j
j
Nazwa parametru i oznaczenie
Zależność
Zależność przybliżona
1
Uwagi
Opór charakterystyczny
ρ
L
C
ρ =
Pulsacja rezonansowa
ω
r
,
ω
o
Pulsacja
2
charakterystyczna
ω
o
1
o
LC
ω
=
,
ω
r
=
ω
o
Dla szeregowego obwodu rezonansowego RLC
ω
o
najczęściej nazywa się pulsacją rezonansową, bo za-
chodzi
ω
r
=
ω
o
, ale w przypadku ogólniejszym tak nie
jest i trzeba odróżniać
ω
r
od
ω
o
Dobroć
3
obwodu rezonansowego Q
o
L
Q
R
ω
=
Równoważnie
Q
R
ρ
=
,
a także
o
Q
RC
ω
1
=
Pulsacja graniczna dolna
ω
1
,
ω
d
2
1
1
1
2
2
1
o
Q
Q
ω
ω
−
=
+
+
(
)
1
1
1
2
o
Q
ω
ω
−
≈
Pulsacja graniczna górna
ω
2
,
ω
g
2
1
1
2
2
2
1
o
Q
Q
ω
ω
=
+
+
(
)
1
1
2
2
o
Q
ω
ω
+
≈
1
Przy założeniu, że Q>>1 (praktycznie Q>5) i
ω∼ω
o
(czytaj:
ω jest tego samego rzędu, co ω
o
)
2
W nieco bardziej skomplikowanych obwodach rezonansowych pulsacje
ω
o
i
ω
r
mają różne wartości, ale w zależnościach
ω
r
bywa wyrażane poprzez
ω
o
, które nie jest już pulsacją
rezonansową, ale nadal jest pewną wygodną wartością charakterystyczną pulsacji.
3
Ogólna definicja dobroci Q liniowego dwójnika D jest następująca:
( )
2
przy pobudzaniu
przebiegiem sinuso-
idalnym o pulsacji
maksymalna energia zmagazynowana w dwójniku D
Q
energia tracona w dwójniku D w jednym okresie
ω
ω
π
=
.
Dobroć obwodu rezonanso-
wego to policzona dla pulsacji rezonansowej wartość dobroci dwójnika D tworzącego obwód rezonansowy.
R
L
C
E
m
cos(
ωt)
I
m
co
s
(ω
t+
ϕ
)
Ćwiczenia z przedmiotu Technika Analogowa
Analiza wskazowa Dodatek
© C. Stefański
0_01_Zestawienie zaleznosci dla obwodow rezonansowych.doc
2/8
Zauważone błędy i usterki proszę zgłaszać autorowi na adres cestef@o2.pl
Pulsacja
ω
Lmax
maksymalnej ampli-
tudy napięcia na cewce
2
max
1
1
2
o
L
Q
ω
ω
−
=
max
L
o
ω
ω
>
Pulsacja
ω
Cmax
maksymalnej ampli-
tudy napięcia na kondensatorze
2
1
max
2
1
C
o
Q
ω
ω
=
−
max
C
o
ω
ω
<
Pasmo trzydecybelowe B
3dB
,B
3
2
1
o
dB
B
Q
ω
ω
ω
=
=
−
Jeżeli do zależności dokładnej na pasmo wstawimy
wartości przybliżone pulsacji granicznych to pasmo
zastanie wyznaczone, jak łatwo sprawdzić, dokładnie.
Wartość amplitudy napięcia na cew-
ce w rezonansie U
Lrez
U
Lrez
= QE
m
Wartość amplitudy napięcia na kon-
densatorze w rezonansie U
Crez
U
Crez
=QE
m
U
Lrez
= U
Crez
Wartość maksymalnej amplitudy
napięcia na cewce U
Lmax
( )
2
1
2
1
m
Lmax
Q
E Q
U
=
−
U
Lmax
> U
Lrez
= QE
m
Wartość maksymalnej amplitudy
napięcia na kondensatorze U
Cmax
( )
2
1
2
1
m
Cmax
Q
E Q
U
=
−
U
Cmax
> U
Crez
= QE
m
Rozstrojenie względne obwodu
ν
o
o
ω
ω
ν
ω
ω
=
−
2(
)
2
o
o
o
ω ω
ω
ν
ω
ω
−
∆
≈
=
Rozstrojenie to jest zdefiniowane jako stosunek roz-
strojenia bezwzględnego
ξ do dobroci obwodu; ∆ω jest
nazywane odchyłką pulsacji
Rozstrojenie bezwzględne obwodu
ξ
=
X
R
ξ
,
Q
ξ
ν
=
⋅
2(
)
2
o
o
o
Q
Q
ω ω
ω
ξ
ω
ω
−
∆
≈
=
Tu
1
rozstrojenie to jest zdefiniowane jako stosunek
reaktancji X do rezystancji R obwodu
=
X
R
ξ
Względna wartość amplitudy prą-
du
m
rez
I
I
2
1
1
m
rez
I
I
ξ
=
+
Dokładniej: względna wartość amplitudy prądu na
pulsacji
ω względem amplitudy prądu obwodu w rezo-
nansie przy pobudzeniu napięciowym
Kąt przesunięcia
ϕ
ϕ
=-arctg(ξ
)
Dokładniej: kąt przesunięcia prądu na pulsacji
ω
względem prądu w rezonansie przy pobudzeniu napię-
ciowym
1
Zachodzi
.
Z
Z
df
B
G
ξ
ζ
=
= −
, gdzie G
Z
jest konduktancją, a B
Z
susceptancją dwójnika o impedancji Z (admitancji 1/Z); porównaj – równoległy obwód rezonansowy RLC
Ćwiczenia z przedmiotu Technika Analogowa
Analiza wskazowa Dodatek
© C. Stefański
0_01_Zestawienie zaleznosci dla obwodow rezonansowych.doc
3/8
Zauważone błędy i usterki proszę zgłaszać autorowi na adres cestef@o2.pl
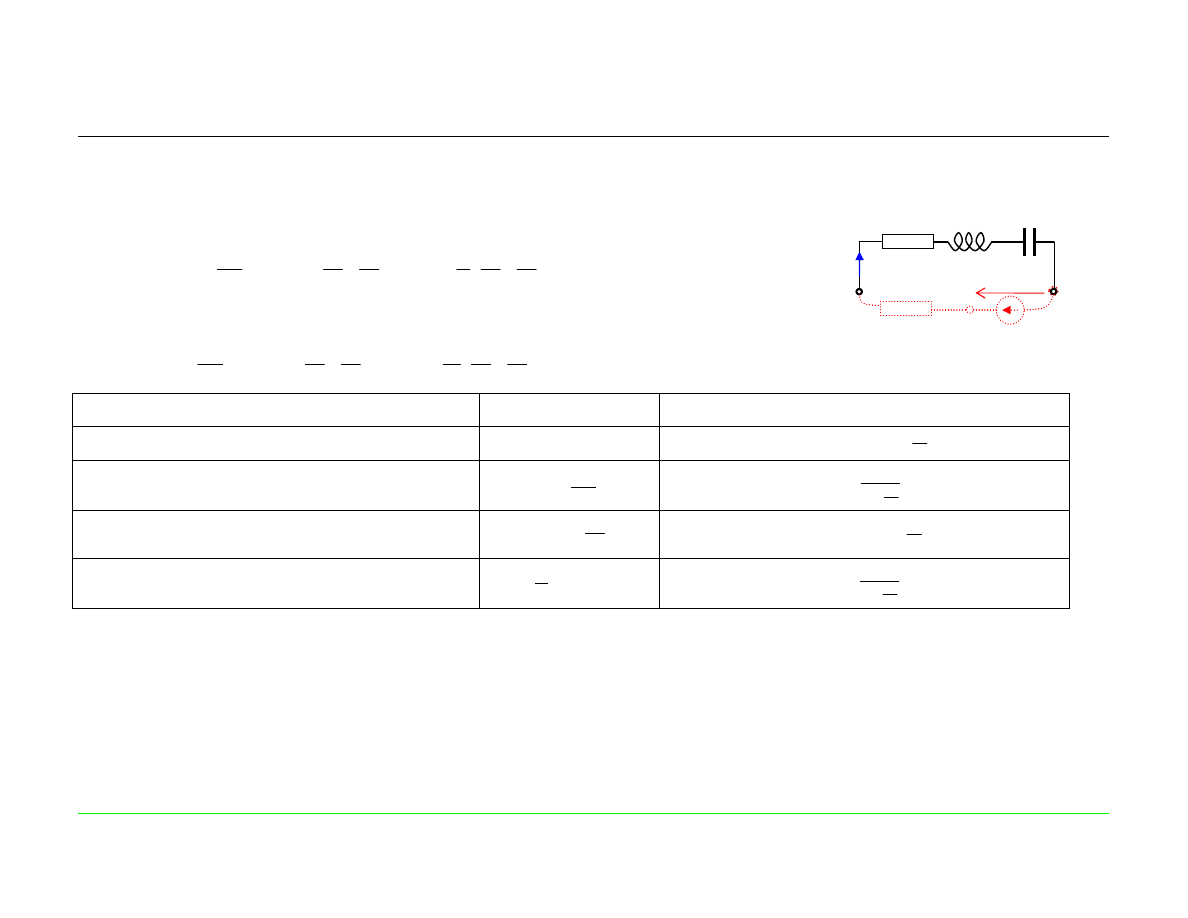
Współpraca szeregowego obwodu rezonansowego ze źródłem rzeczywistym
(‘)
Impedancja widziana z zacisków źródła rzeczywistego
1
o
o
Z
R
L
R
C
ω
ω
ω
ρ
ω
ω
ω
=
+
−
=
+
−
=
j
j
1
(1
)
(1
)
o
o
R
R
Q
R
R
ρ ω
ω
ν
ξ
ω
ω
+
−
=
+
=
+
j
j
j
Impedancja widziana z zacisków źródła idealnego (obwód rezonansowy to R’LC, gdzie R’=R+R
w
)
1
'
'
'
o
o
Z
R
L
R
C
ω
ω
ω
ρ
ω
ω
ω
=
+
−
=
+
−
=
j
j
' 1
'(1
' )
'(1
')
'
o
o
R
R
Q
R
R
ρ
ω
ω
ν
ξ
ω
ω
+
−
=
+
=
+
j
j
j
Nazwa parametru i oznaczenie
Zależność
Związek z parametrem nieprimowanym
(czyli z odpowiednim parametrem z sytuacji współpracy ze źródłem idealnym)
Rezystancja R’
(szeregowego obwodu rezonansowego współpracującego ze źródłem rzeczywistym)
R’
=ReZ’
R’=R+R
w
=
(
)
1
w
R
R
R
+
Dobroć Q’
(szeregowego obwodu rezonansowego współpracującego ze źródłem rzeczywistym)
'
'
o
L
Q
R
ω
=
'
1
w
R
R
Q
Q
=
+
Pasmo trzydecybelowe B’
3dB
(szeregowego obwodu rezonansowego współpracującego ze źródłem rzeczywistym)
3
'
'
o
dB
B
Q
ω
=
(
)
3
3
'
1
w
R
dB
dB
R
B
B
=
+
Rozstrojenie bezwzględne
ξ
’
(szeregowego obwodu rezonansowego współpracującego ze źródłem rzeczywistym)
'
=
X
R
ξ
,
'
'
Q
ξ
ν
=
⋅
'
1
w
R
R
ξ
ξ
=
+
Wyrażenia na opór charakterystyczny, pulsację rezonansową (i pulsację charakterystyczną) oraz rozstrojenie względne szeregowego obwodu rezo-
nansowego współpracującego ze źródłem rzeczywistym są identyczne jak dla szeregowego obwodu rezonansowego współpracującego ze źródłem ide-
alnym. Pozostałe parametry opisane w przedostatniej dotąd tabeli można wyznaczyć zastępując, stosownie do sytuacji, R przez R’, Q przez Q’,
ξ
przez
ξ
‘.
R
L
C
E
m
cos(
ω
t
)
I
m
co
s(
ω
t+
ϕ
)
R
w
Ćwiczenia z przedmiotu Technika Analogowa
Analiza wskazowa Dodatek
© C. Stefański
0_01_Zestawienie zaleznosci dla obwodow rezonansowych.doc
4/8
Zauważone błędy i usterki proszę zgłaszać autorowi na adres cestef@o2.pl
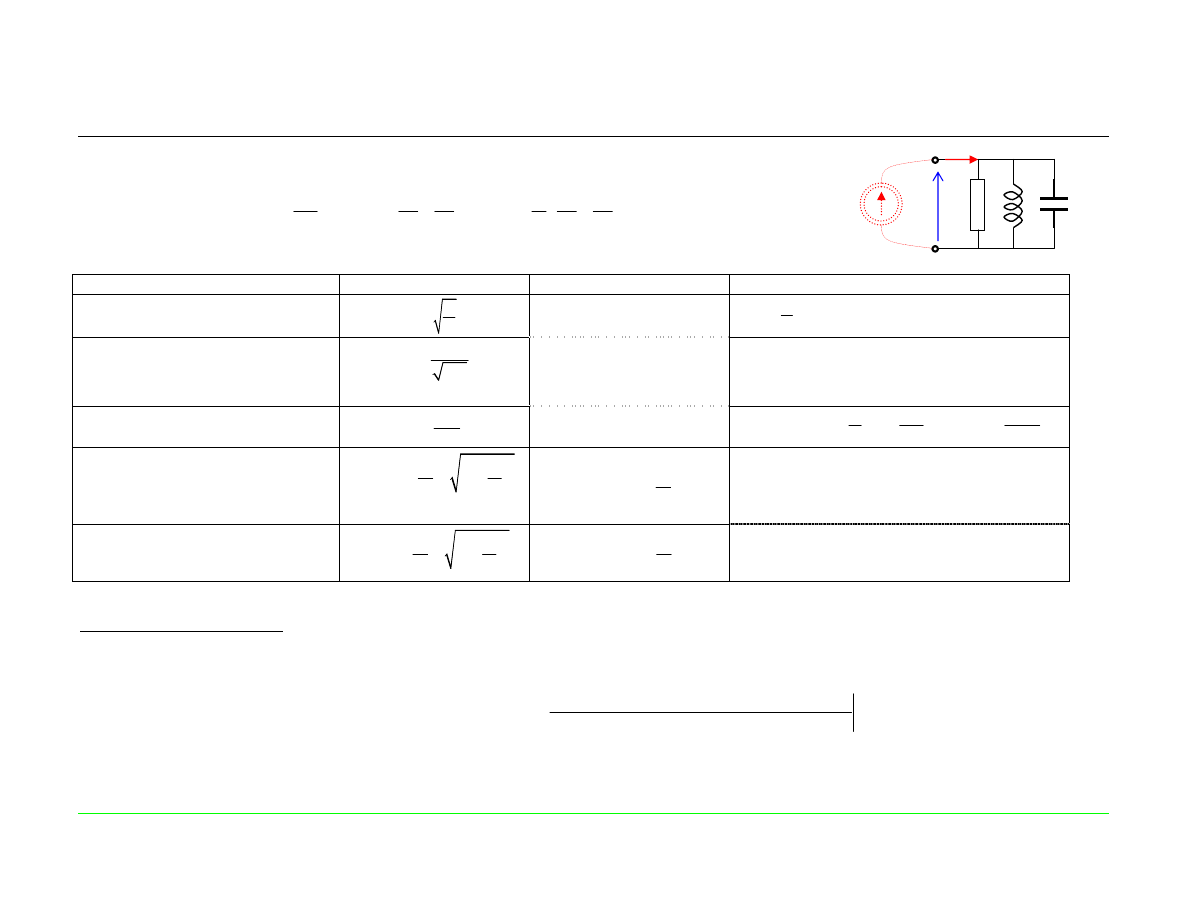
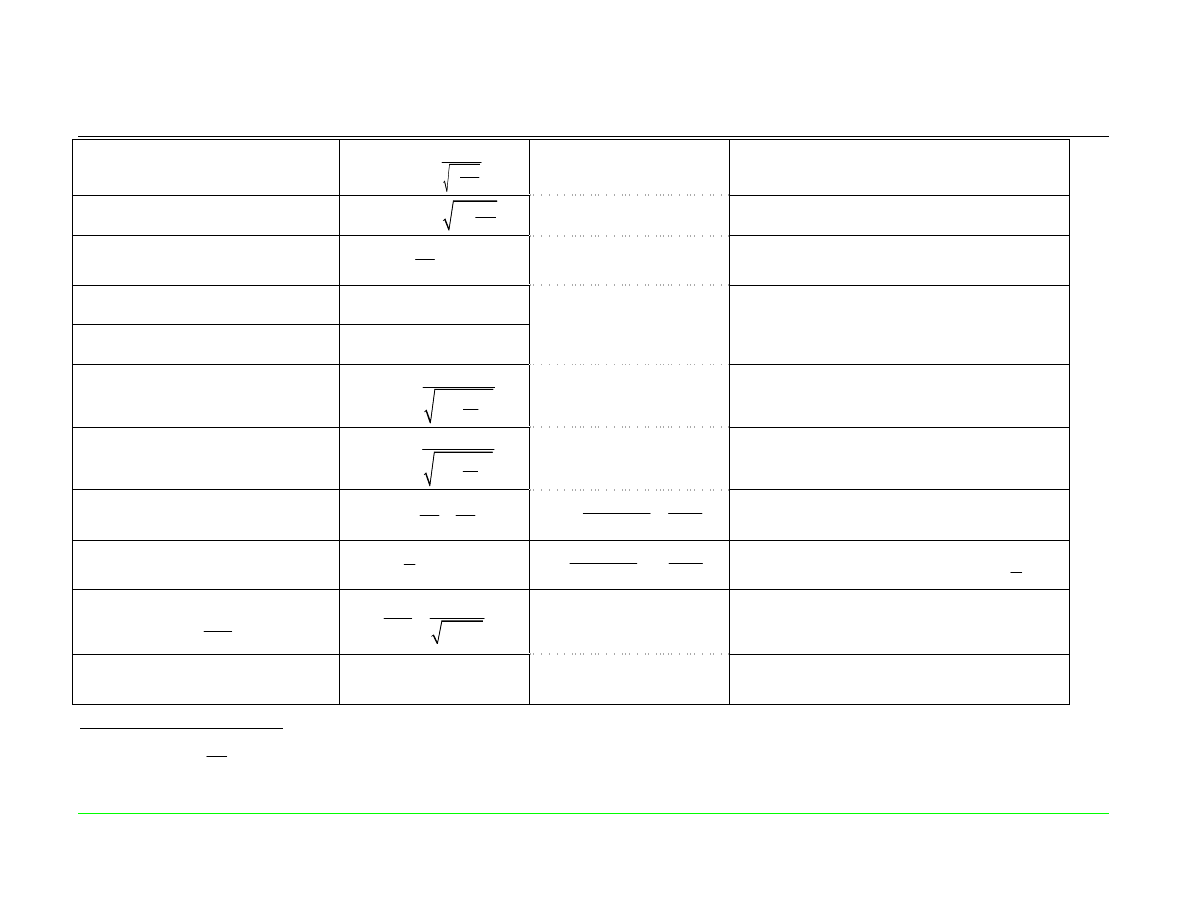
Zestawienie zależności dla równoległego obwodu rezonansowego RLC
(współpracującego ze źródłem idealnym)
Admitancja
1
1
(1
)
(1
)
o
o
o
o
Y
G
C
G
G
G
Q
G
L
G
ω
ω
γ
ω
ω
ω
γ
ν
ξ
ω
ω
ω
ω
ω
=
+
−
=
+
−
=
+
−
=
+
=
+
j
j
j
j
j
,
Nazwa parametru i oznaczenie
Zależność
Zależność przybliżona
1
Uwagi
Przewodność charakterystyczna
γ
C
L
γ =
1
γ
ρ
=
,
gdzie
ρ jest opornością charakterystyczną
Pulsacja rezonansowa
ω
r
,
ω
o
Pulsacja
2
charakterystyczna
ω
o
1
o
LC
ω
=
,
ω
r
=
ω
o
Dla równoległego obwodu rezonansowego RLC
ω
o
naj-
częściej nazywa się pulsacją rezonansową, bo zachodzi
ω
r
=
ω
o
, ale w przypadku ogólniejszym tak nie jest i trze-
ba odróżniać
ω
r
od
ω
o
Dobroć
3
obwodu rezonansowego Q
o
C
Q
G
ω
=
Równoważnie Q
G
γ
=
,
1
Q
G
ρ
=
, a także
o
Q
LG
ω
1
=
Pulsacja graniczna dolna
ω
1
,
ω
d
2
1
1
1
2
2
1
o
Q
Q
ω
ω
−
=
+
+
(
)
1
1
1
2
o
Q
ω
ω
−
≈
Pulsacja graniczna górna
ω
2
,
ω
g
2
1
1
2
2
2
1
o
Q
Q
ω
ω
=
+
+
(
)
1
1
2
2
o
Q
ω
ω
+
≈
1
Przy założeniu, że Q>>1 (praktycznie Q>5) i
ω∼ω
o
(czytaj:
ω jest tego samego rzędu, co ω
o
)
2
W nieco bardziej skomplikowanych obwodach rezonansowych pulsacje
ω
o
i
ω
r
mają różne wartości, ale w zależnościach
ω
r
bywa wyrażane poprzez
ω
o
, które nie jest już pulsacją
rezonansową, ale nadal jest pewną wygodną wartością charakterystyczną pulsacji.
3
Ogólna definicja dobroci Q liniowego dwójnika D jest następująca:
( )
2
przy pobudzaniu
przebiegiem sinuso-
idalnym o pulsacji
maksymalna energia zmagazynowana w dwójniku D
Q
energia tracona w dwójniku D w jednym okresie
ω
ω
π
=
.
Dobroć obwodu rezonanso-
wego to policzona dla pulsacji rezonansowej wartość dobroci dwójnika D tworzącego obwód rezonansowy.
R
L
C
J
m
cos(
ωt)
G=
1/R
U
m
co
s(
ω
t+
ϕ
)
Ćwiczenia z przedmiotu Technika Analogowa
Analiza wskazowa Dodatek
© C. Stefański
0_01_Zestawienie zaleznosci dla obwodow rezonansowych.doc
5/8
Zauważone błędy i usterki proszę zgłaszać autorowi na adres cestef@o2.pl
Pulsacja
ω
Cmax
maksymalnej ampli-
tudy prądu na kondensatorze
2
max
1
1
2
o
C
Q
ω
ω
−
=
max
C
o
ω
ω
>
Pulsacja
ω
Lmax
maksymalnej ampli-
tudy prądu na cewce
2
1
max
2
1
L
o
Q
ω
ω
=
−
max
L
o
ω
ω
<
Pasmo trzydecybelowe B
3dB
,B
3
2
1
o
dB
B
Q
ω
ω
ω
=
=
−
Jeżeli do zależności dokładnej na pasmo wstawimy
wartości przybliżone pulsacji granicznych to pasmo
zastanie wyznaczone, jak łatwo sprawdzić, dokładnie.
Wartość amplitudy prądu na kon-
densatorze w rezonansie I
Crez
I
Crez
= QJ
m
Wartość amplitudy prądu na cewce
w rezonansie I
Lrez
I
Lrez
=QJ
m
I
Crez
= I
Lrez
Wartość maksymalnej amplitudy
prądu kondensatora I
Cmax
( )
2
1
2
1
m
Cmax
Q
J Q
I
=
−
I
Cmax
> I
Crez
= QJ
m
Wartość maksymalnej amplitudy
prądu cewki I
Lmax
( )
2
1
2
1
m
Lmax
Q
J Q
I
=
−
I
Lmax
> I
Lrez
= QJ
m
Rozstrojenie względne obwodu
ν
o
o
ω
ω
ν
ω
ω
=
−
2(
)
2
o
o
o
ω ω
ω
ν
ω
ω
−
∆
≈
=
Rozstrojenie to jest zdefiniowane jako stosunek rozstro-
jenia bezwzględnego
ζ do dobroci obwodu; ∆ω jest
nazywane odchyłką pulsacji
Rozstrojenie bezwzględne obwodu
ζ
=
B
G
ζ
,
Q
ζ
ν
=
⋅
2(
)
2
o
o
o
Q
Q
ω ω
ω
ζ
ω
ω
−
∆
≈
=
Tu
1
rozstrojenie to jest zdefiniowane jako stosunek
susceptancji B do konduktancji G obwodu
=
B
G
ζ
Względna wartość amplitudy napię-
cia
m
rez
U
U
2
1
1
m
rez
U
U
ζ
=
+
Dokładniej: względna wartość amplitudy napięcia na
pulsacji
ω względem amplitudy napięcia obwodu w
rezonansie przy pobudzeniu prądowym
Kąt przesunięcia
ϕ
ϕ
=-arctg(ζ
)
Dokładniej: kąt przesunięcia napięcia na pulsacji
ω
względem napięcia w rezonansie przy pobudzeniu prą-
dowym
1
Zachodzi
.
df
Y
Y
X
R
ζ
ξ
= −
=
, gdzie R
Y
jest rezystancją, a X
Y
reaktancją dwójnika o admitancji Y (impedancji 1/Y); porównaj – szeregowy obwód rezonansowy RLC

Ćwiczenia z przedmiotu Technika Analogowa
Analiza wskazowa Dodatek
© C. Stefański
0_01_Zestawienie zaleznosci dla obwodow rezonansowych.doc
6/8
Zauważone błędy i usterki proszę zgłaszać autorowi na adres cestef@o2.pl
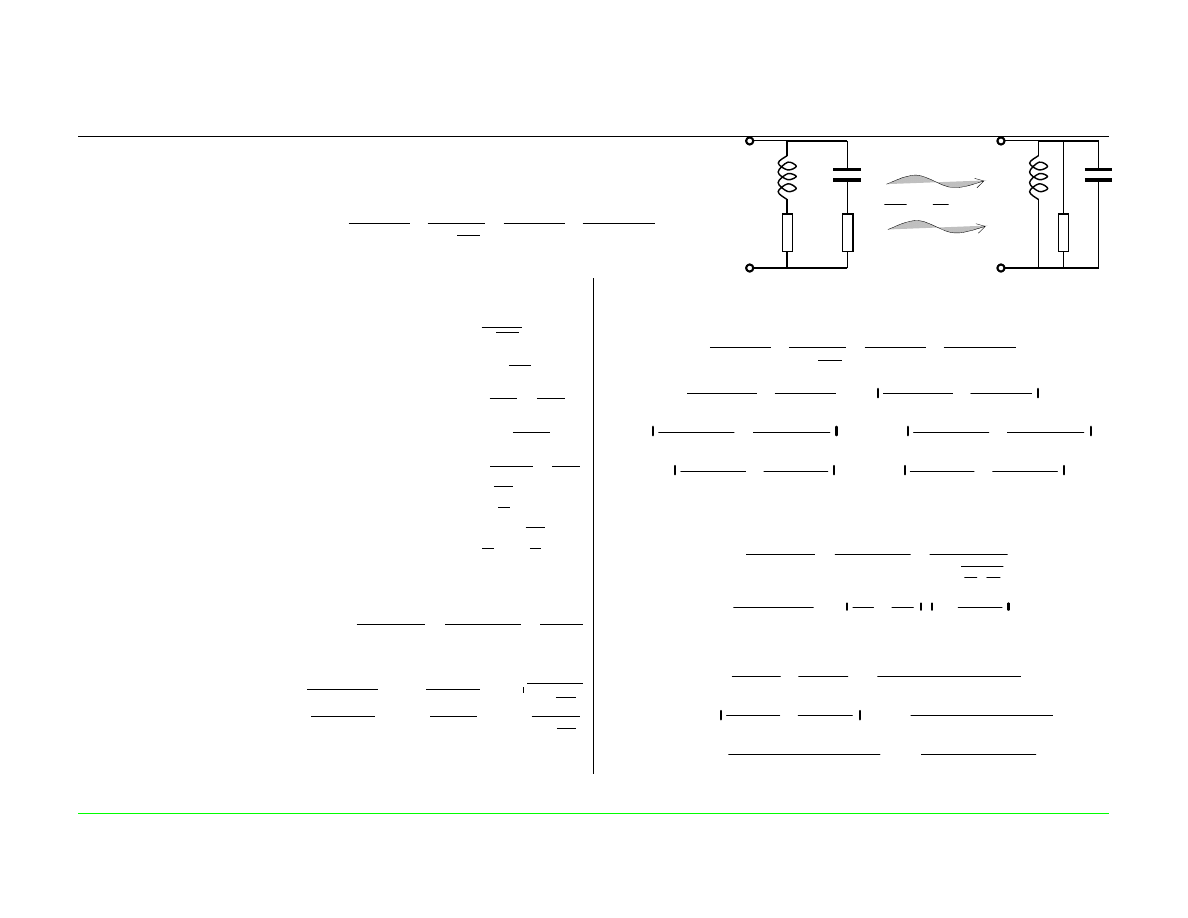
Współpraca równoległego obwodu rezonansowego ze źródłem rzeczywistym
(‘)
Admitancja widziana z zacisków źródła rzeczywistego
1
o
o
Y
G
C
G
L
ω
ω
ω
γ
ω
ω
ω
=
+
−
=
+
−
=
j
j
1
(1
)
(1
)
o
o
G
G
Q
G
G
γ
ω
ω
ν
ζ
ω
ω
+
−
=
+
=
+
j
j
j
Admitancja widziana z zacisków źródła idealnego (obwód rezonansowy to R’LC, gdzie R’=R||R
w
)
1
'
'
'
o
o
Y
G
C
G
L
ω
ω
ω
γ
ω
ω
ω
=
+
−
=
+
−
=
j
j
' 1
'(1
' )
'(1
')
'
o
o
G
G
Q
G
G
γ
ω
ω
ν
ζ
ω
ω
+
−
=
+
=
+
j
j
j
Nazwa parametru i oznaczenie
Zależność
Związek z parametrem nieprimowanym
(czyli z odpowiednim parametrem z sytuacji współpracy ze źródłem idealnym)
Konduktancja G’
(równoległego obwodu rezonansowego współpracującego ze źródłem rzeczywistym)
G’
=ReY’
G’=G+G
w
=
(
)
1
w
G
G
G
+
Dobroć Q’
(równoległego obwodu rezonansowego współpracującego ze źródłem rzeczywistym)
'
'
o
C
Q
G
ω
=
'
1
w
G
G
Q
Q
=
+
Pasmo trzydecybelowe B’
3dB
(równoległego obwodu rezonansowego współpracującego ze źródłem rzeczywistym)
3
'
'
o
dB
B
Q
ω
=
(
)
3
3
'
1
w
G
dB
dB
G
B
B
=
+
Rozstrojenie bezwzględne
ζ
(równoległego obwodu rezonansowego współpracującego ze źródłem rzeczywistym)
'
=
B
G
ζ
,
'
'
Q
ζ
ν
=
⋅
'
1
w
G
G
ζ
ζ
=
+
Wyrażenia na przewodność charakterystyczną, pulsację rezonansową (i pulsację charakterystyczną) oraz rozstrojenie względne równoległego ob-
wodu rezonansowego współpracującego ze źródłem rzeczywistym są identyczne jak dla równoległego obwodu rezonansowego współpracującego ze
ź
ródłem idealnym. Pozostałe parametry opisane w przedostatniej dotąd tabeli można wyznaczyć zastępując, stosownie do sytuacji, G przez G’,
Q
przez Q’,
ζ
przez
ζ
‘.
R
L
C
J
m
cos(
ωt)
G=
1/R
U
m
co
s
(ω
t+
ϕ
)
R
w
G
w
=
1/R
w
Ćwiczenia z przedmiotu Technika Analogowa
Analiza wskazowa Dodatek
© C. Stefański
0_01_Zestawienie zaleznosci dla obwodow rezonansowych.doc
7/8
Zauważone błędy i usterki proszę zgłaszać autorowi na adres cestef@o2.pl
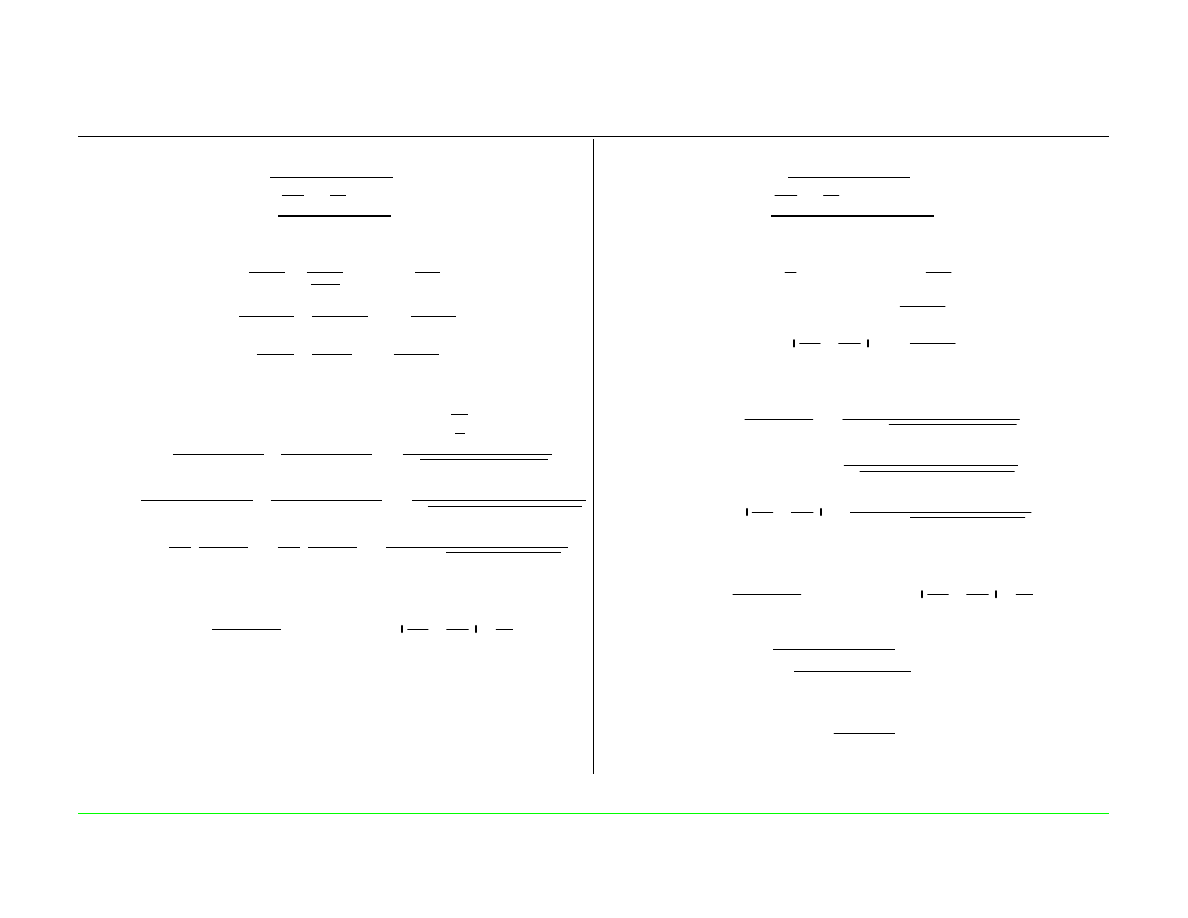
Zestawienie zależności dla równoległego dwugałęźnego obwodu
rezonansowego
Admitancja
Y
=
1
r
L
+ ¸ ω
L
+
1
r
C
+
1
¸ ω
C
=
1
r
L
+ ¸ ω
L
+
¸ ω
C
1
+ ¸ ω
C r
C
Pulsacja charakterystyczna -------------------------------
ω
o
=
1
è
L C
Dobroć (gałęzi) cewki ------------------------------------
Q
L
H
ω
L
=
ω
L
r
L
„Charakterystyczna” dobroć (gałęzi) cewki -----------
Q
Lo
=
ω
o
L
r
L
=
1
γ
r
L
Dobroć (gałęzi) kondensatora ----------------------------
Q
C
H
ω
L
=
1
ω
C r
C
„Charakterystyczna” dobroć (gałęzi) kondensatora ----
Q
Co
=
1
ω
o
C r
C
=
1
γ
r
C
Przewodność charakterystyczna obwodu ----------------
γ =
$
C
L
Oporność charakterystyczna obwodu --------------------
ρ =
1
γ
=
$
L
C
Oporność dynamiczna obwodu
R
d
=
L
C
H
r
L
+
r
C
L
=
1
γ
2
H
r
L
+
r
C
L
=
ρ
2
r
L
+
r
C
Pulsacja rezonansowa obwodu
ω
r
= ω
o
&
−
1
+ γ
2
r
L
2
−
1
+ γ
2
r
C
2
= ω
o
&
ρ
2
−
r
L
2
ρ
2
−
r
C
2
= ω
o
*
(
1
−
1
QLo
2
1
−
1
QCo
2
Wyrażenia dokładne
- na admitancję obwodu
Y
=
1
r
L
+
¸ ω
L
+
1
r
C
+
1
¸ ω
C
=
1
r
L
+
¸ ω
L
+
¸ ω
C
1
+
¸ ω
C r
C
Y
=
C
2
ω
2
r
C
1
+
C
2
ω
2
r
C
2
+
r
L
L
2
ω
2
+
r
L
2
+ ¸ ω
i
k
C
1
+
C
2
ω
2
r
C
2
−
L
L
2
ω
2
+
r
L
2
y
{
Y
= γ
2
i
k
ω
2
r
C
γ
2
ω
2
r
C
2
+ ω
o
2
+
r
L
ω
o
2
ω
2
+ γ
2
r
L
2
ω
o
2
y
{
+ ¸ γ ω ω
o
i
k
1
γ
2
ω
2
r
C
2
+ ω
o
2
−
1
ω
2
+ γ
2
r
L
2
ω
o
2
y
{
Y
= γ
i
k
Q
Lo
ω
o
2
ω
2
Q
Lo
2
+ ω
o
2
+
ω
2
Q
Co
ω
2
+
Q
Co
2
ω
o
2
y
{
+ ¸ γ ω ω
o
i
k
Q
Co
2
ω
2
+
Q
Co
2
ω
o
2
−
Q
Lo
2
ω
2
Q
Lo
2
+ ω
o
2
y
{
- na admitancję w rezonansie
Y
@
ω
r
D
=
C
H
r
C
+
r
L
L
L
+
C r
C
r
L
=
γ
2
H
r
C
+
r
L
L
1
+ γ
2
r
C
r
L
=
1
R
d
+
1
1
rC
+
1
rL
Y
@
ω
r
D
=
γ
H
Q
Co
+
Q
Lo
L
1
+
Q
Co
Q
Lo
= γ
i
k
1
Q
Co
+
1
Q
Lo
y
{
i
k
1
+
1
Q
Co
Q
Lo
y
{
−
1
- na admitancję na pulsacji charakterystycznej
Y
@
ω
o
D
=
C r
C
L
+
C r
C
2
+
C r
L
L
+
C r
L
2
+ ¸
C
H
r
L
2
−
r
C
2
L
ω
o
H
L
+
C r
C
2
L H
L
+
C r
L
2
L
Y
@
ω
o
D
= γ
2
i
k
r
C
1
+ γ
2
r
C
2
+
r
L
1
+ γ
2
r
L
2
y
{
+ ¸ γ
3
r
L
2
−
r
C
2
H
1
+ γ
2
r
C
2
L H
1
+ γ
2
r
L
2
L
Y
@
ω
o
D
= γ
H
Q
Co
+
Q
Lo
L H
1
+
Q
Co
Q
Lo
L
H
1
+
Q
Co
2
L H
1
+
Q
Lo
2
L
+ ¸ γ
Q
Co
2
−
Q
Lo
2
H
1
+
Q
Co
2
L H
1
+
Q
Lo
2
L
L
C
r
L
r
C
L
C
R
d
1
Q
Lo
<<
ω
ω
o
<<
Q
Co
Ćwiczenia z przedmiotu Technika Analogowa
Analiza wskazowa Dodatek
© C. Stefański
0_01_Zestawienie zaleznosci dla obwodow rezonansowych.doc
8/8
Zauważone błędy i usterki proszę zgłaszać autorowi na adres cestef@o2.pl
Wyrażenia przybliżone
, przy założeniu, że
1
Q
Lo
<<
ω
ω
o
<<
Q
Co
- na admitancję
Y
∼
=
r
L
ω
2
L
2
+
r
C
1
ω
2
C2
+ ¸
J
ω
C
−
1
ω
L
N
Y
∼
=
γ
2
ω
2
r
C1
ω
o
2
+
γ
2
r
L1
ω
o
2
ω
2
+ γ
ω
2
− ω
o
2
ω ω
o
Y
∼
=
γ ω
2
Q
Co
ω
o
2
+
γ ω
o
2
ω
2
Q
Lo
+ γ
ω
2
− ω
o
2
ω ω
o
- na admitancję na pulsacji rezonansowej
Y
∼
@
ω
r
D
=
C
H
L
−
C r
C
2
L
r
L
L
H
L
−
C r
L
2
L
+
C r
C
H
L
−
C r
L
2
L
L
H
L
−
C r
C
2
L
+ ¸
C
$
C
L
H
r
C
2
−
r
L
2
L
" H
L
−
C r
C
2
L H
L
−
C r
L
2
L
Y
∼
@
ω
r
D
=
γ
2
H
−
1
+ γ
2
r
C
2
L
r
L
−
1
+ γ
2
r
L
2
+
γ
2
r
C
H
−
1
+ γ
2
r
L
2
L
−
1
+ γ
2
r
C
2
+ ¸
γ
3
H
r
C
2
−
r
L
2
L
" H
−
1
+ γ
2
r
C
2
L H
−
1
+ γ
2
r
L
2
L
Y
∼
@
ω
r
D
= γ
Q
Co
Q
Lo
2
Q
Lo
2
−
1
Q
Co
2
−
1
+ γ
Q
Lo
Q
Co
2
Q
Co
2
−
1
Q
Lo
2
−
1
+ ¸
γ
H
Q
Lo
2
−
Q
Co
2
L
Q
Lo
Q
Co
"H
Q
Co
2
−
1
L H
Q
Lo
2
−
1
L
- na admitancję na pulsacji charakterystycznej
Y
∼
@
ω
o
D
=
C
H
r
C
+
r
L
L
L
= γ
2
H
r
C
+
r
L
L
= γ
i
k
1
Q
Co
+
1
Q
Lo
y
{
=
1
R
d
Wyrażenia przybliżone
, przy założeniu, że
1
Q
Lo
<<
ω
ω
o
<<
Q
Co
i
ω∼ω
o
- na admitancję
Y
∼∼
=
C
L
H
r
C
+
r
L
L
+ ¸
J
ω
C
−
1
ω
L
N
Y
∼∼
= γ
2
H
r
C
+
r
L
L
+ ¸ γ
ω
2
− ω
o
2
ω ω
o
Y
∼∼
= γ
i
k
1
Q
Co
+
1
Q
Lo
y
{
+ ¸ γ
ω
2
− ω
o
2
ω ω
o
- na admitancję na pulsacji rezonansowej
Y
∼∼
@
ω
r
D
=
C
H
r
C
+
r
L
L
L
+ ¸
C
H
r
C
2
−
r
L
2
L
ω
o
L
" H
L
−
C r
C
2
L H
L
−
C r
L
2
L
Y
∼∼
@
ω
r
D
= γ
2
H
r
C
+
r
L
L
+ ¸
γ
3
H
r
C
2
−
r
L
2
L
" H
−
1
+ γ
2
r
C
2
L H
−
1
+ γ
2
r
L
2
L
Y
∼∼
@
ω
r
D
= γ
i
k
1
Q
Co
+
1
Q
Lo
y
{
+ ¸
γ
H
Q
Lo
2
−
Q
Co
2
L
Q
Lo
Q
Co
" H
Q
Co
2
−
1
L H
Q
Lo
2
−
1
L
- na admitancję na pulsacji charakterystycznej
Y
∼∼
@
ω
o
D
=
C
H
r
C
+
r
L
L
L
= γ
2
H
r
C
+
r
L
L
= γ
i
k
1
Q
Co
+
1
Q
Lo
y
{
=
1
R
d
Wyrażenie przybliżone, przy założeniu, że
Q
Lo
>>
1, Q
Co
>>
1
- na dobroć obwodu dwugałęźnego
⋅
≈
Lo
Co
Lo
Co
Q
Q
Q
Q
+ Q
Wyszukiwarka
Podobne podstrony:
ZiIP Mat2 01 kol Zestaw id 5903 Nieznany
zapotrzebowanie ustroju na skladniki odzywcze 12 01 2009 kurs dla pielegniarek (2)
312[01] 01 122 Arkusz egzaminac Nieznany (2)
13 Modelowanie form odziezy dla Nieznany (2)
01 Przygotowanie produkcji piek Nieznany (2)
72 Nw 01 Zestawy glosnikowe
22 01 2011 TEST B PSYCHOLOGIA S Nieznany
zestaw8 id 588882 Nieznany
01 Thermoregulation, Fever PLid Nieznany (2)
MTA Zestaw3 id 310157 Nieznany
01 Konspekt STRESid 2838 Nieznany (2)
22 01 2011 TEST B PSYCHOLOGIA S Nieznany (2)
01 wstepny elektrycznyid 3080 Nieznany
01, PR, arkuszid 2747 Nieznany (2)
zestaw id 587883 Nieznany
01 roztwory buforoweid 2924 Nieznany
więcej podobnych podstron