Z. Kąkol-Notatki do Wykładu z Fizyki

31-1

Wykład 31

31. Polaryzacja

Teoria przewiduje, że światło podobnie jak każda fala elektromagnetyczna jest falą

poprzeczną. Kierunki drgań wektorów E i B są prostopadłe do kierunku rozchodzenia
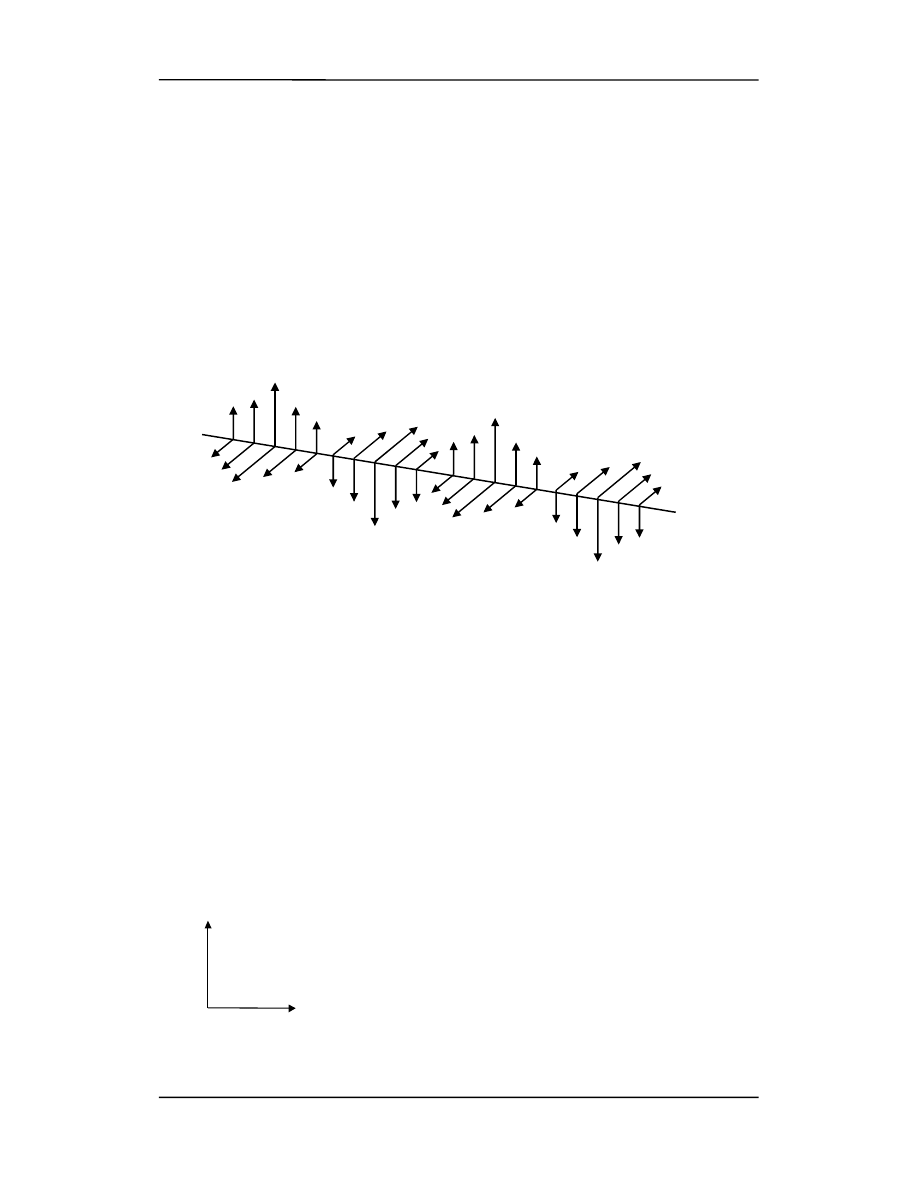
się fali. Na rysunku poniżej przedstawione falę elektromagnetyczną, która ma jeszcze
dodatkowo pewną charakterystyczną własność:
wektory E są do siebie równoległe we wszystkich punktach fali. Podobnie wektory B.
Mówimy, że ta fala jest

płasko spolaryzowana

(spolaryzowana liniowo).

Drgający wektor E tworzy z kierunkiem ruchu fali płaszczyznę zwaną

płaszczyzną

drgań

.

W fali spolaryzowanej liniowo wszystkie takie płaszczyzny są równoległe.
Z dotychczas opisanych doświadczeń z interferencją i dyfrakcją nie można wydeduko-
wać poprzecznej natury fal świetlnych ponieważ fale podłużne też interferują i ulegają
dyfrakcji.
Podstawy doświadczalne przyniosło następujące doświadczenie.

•

W wyniku oświetlenia kryształu kalcytu (CaCO

3

) z wiązki padającej można uzyskać

dwie oddzielne wiązki (omówione w dalszej części wykładu).

•

Wiązki te chociaż oczywiście są spójne nie dają prążków interferencyjnych ale rów-
nomierne oświetlenie ekranu.

Young wywnioskował z tego faktu, że światło jest falą poprzeczną i że płaszczyzny
drgań w tych falach są prostopadłe względem siebie.

Zauważmy, że chcemy dodać dwa zaburzenia falowe ta-
kie jak w doświadczeniu Younga tj. ale prostopadłe do
siebie. Można udowodnić, że fale świetlne spolaryzowane
liniowo o równych amplitudach i prostopadłych kierun-
kach drgań nie interferują ze sobą dając jednakowe (nie-
zależnie od różnicy faz) natężenie światła na ekranie. Tu
tylko zauważmy, że te dwie fale nigdy się nie wygaszają.

B

E

E

2

E

1

Z. Kąkol-Notatki do Wykładu z Fizyki

31-2

W fali poprzecznej, spolaryzowanej liniowo, należy określić dwa kierunki:

•

kierunek drgania (np. wektora E),

•

kierunek rozchodzenia się fali.

(Zauważmy, że w fali podłużnej te dwa kierunki się pokrywają.)
Przykładem fal spolaryzowanych liniowo są fale elektromagnetyczne radiowe (oraz mi-
krofale) emitowane przez antenę dipolową.
W antenie takiej fale wytwarzane są przez ładunek elektryczny drgający w górę i w dół
anteny. Taka fala w dużej odległości od dipola, na osi prostopadłej, ma wektor pola
elektrycznego równoległy do osi dipola (anteny) jest więc spolaryzowana liniowo. Kie-
dy taka fala pada na drugi dipol wówczas zmienne pole elektryczne (zmienny wektor E
fali) wywołuje w antenie odbiorczej drgania elektronów do góry i w dół (prąd zmienny).
Jeżeli jednak obrócimy antenę o 90° wokół kierunku padania fali, to wektor E będzie
prostopadły do anteny i nie wywoła ruchu elektronów (antena nie odbiera sygnału).
Źródła światła widzialnego różnią się od źródeł fal radiowych i mikrofal min. tym, że
atomy (cząsteczki) emitujące światło działają niezależnie.
W konsekwencji światło rozchodzące się w danym kierunku składa się z niezależnych
ciągów fal, których płaszczyzny drgań zorientowane są przypadkowo wokół kierunku
ruchu fali (rysunek poniżej). Takie światło chociaż jest falą poprzeczną jest niespolary-
zowane.
Rysunek poniżej pokazuje różnicę między falą poprzeczną spolaryzowaną liniowo (a)
i falą poprzeczną niespolaryzowaną (b). Rysunek (c) przedstawia inny równoważny opis
niespolaryzowanej fali poprzecznej; tutaj traktujemy ją jako złożenie dwóch spolaryzo-
wanych liniowo fal o przypadkowo zmiennej różnicy faz. Orientacja kierunków drgań
pól E względem kierunku rozchodzenia się fali jest też przypadkowa (ale prostopadła).

Dla zbadania fal świetlnych niespolaryzowanych potrzeba znaleźć metodę, która pozwo-
liłaby rozdzielić fale o różnych płaszczyznach drgań.

31.1 Płytki polaryzujące

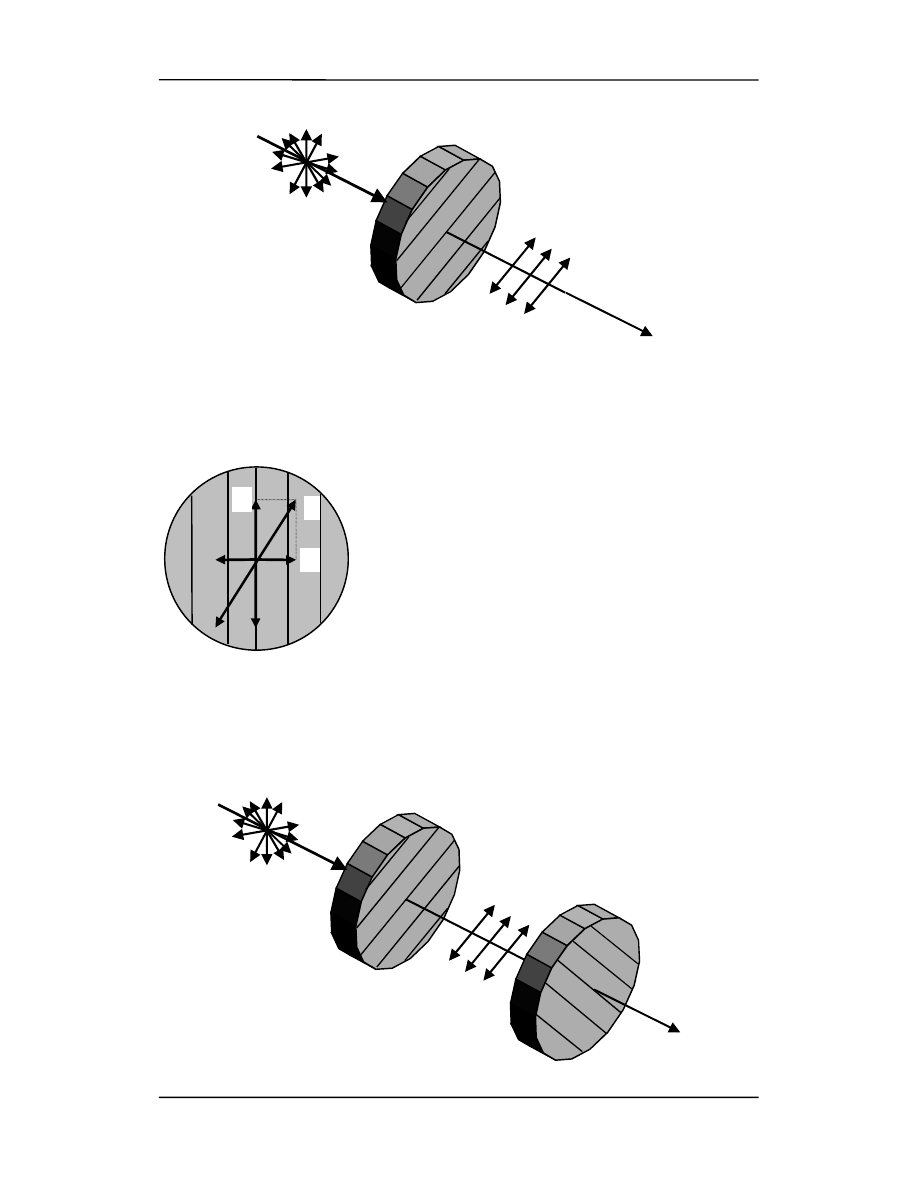
Na rysunku (na następnej stronie) światło niespolaryzowane pada na płytkę z

materiału polaryzującego, zwanego polaroidem.
W płytce istnieje pewien charakterystyczny kierunek polaryzacji zaznaczony liniami
równoległymi. Płytka przepuszcza tylko te fale, dla których kierunki drgań wektora
elektrycznego są równoległe do kierunku polaryzacji, a pochłania te fale, w których są
one prostopadłe.

c)
_

b)
_

a)
_

Z. Kąkol-Notatki do Wykładu z Fizyki

31-3

Kierunek polaryzacji ustala się w procesie produkcji:

•

cząsteczki o strukturze łańcuchowej osadza się na elastycznej warstwie plastycznej,

•

warstwę rozciąga się co powoduje równoległe ułożenie cząsteczek.

Żeby zanalizować natężenie światła przechodzącego
przez polaryzator rozpatrzmy ciąg fal padający na pola-
roid tak, że wektor E wyznaczający płaszczyznę drgań
tworzy kąt

θ z kierunkiem polaryzacji płytki (rysunek

obok).
Ten ciąg fal jest równoważny ciągom fal o składowych
E

x

i E

y

(składowe wektora E).

Składowa równoległa E

y

= Ecos

θ jest przepuszczana

podczas gdy składowa prostopadła E

x

= Esin

θ jest po-

chłaniana.

Postawmy teraz na drodze światła drugą płytkę polaryzującą (tak zastosowaną płytkę
nazywamy analizatorem). Jeżeli płytkę drugą (analizator) będziemy obracać wokół kie-
runku padania światła to natężenie światła przechodzącego przez obie płytki będzie się
zmieniać osiągając minimum dla położeń różniących się o 180° tj. przy prostopadłych
kierunkach polaryzacji obu płytek.

p

łytka

polaryzuj

ąca

E

y

E

E

x

θ

p

łytka

polaryzuj

ąca

Z. Kąkol-Notatki do Wykładu z Fizyki

31-4

Jeżeli amplituda pola elektrycznego fali padającej na analizator jest równa E

m

to ampli-

tuda fali wychodzącej z analizatora wynosi E

m

cos

θ, gdzie θ jest kątem pomiędzy kie-

runkami polaryzacji obu płytek. Ponieważ natężenie światła jest proporcjonalne do
kwadratu amplitudy więc otrzymujemy

I = I

m

cos

2

θ

(30.1)

Zauważmy, że I ma maksimum dla

θ = 0° lub θ = 180° a minimum dla θ = 90° lub

θ = 270°. Powyższe równanie zwane jest

prawem Malusa

.

Znane są jeszcze inne sposoby otrzymywania światła spolaryzowanego. Niektóre omó-
wione są poniżej.

31.2 Polaryzacja przez odbicie

W 1809 r. Malus odkrył, że światło może być częściowo lub całkowicie spolary-

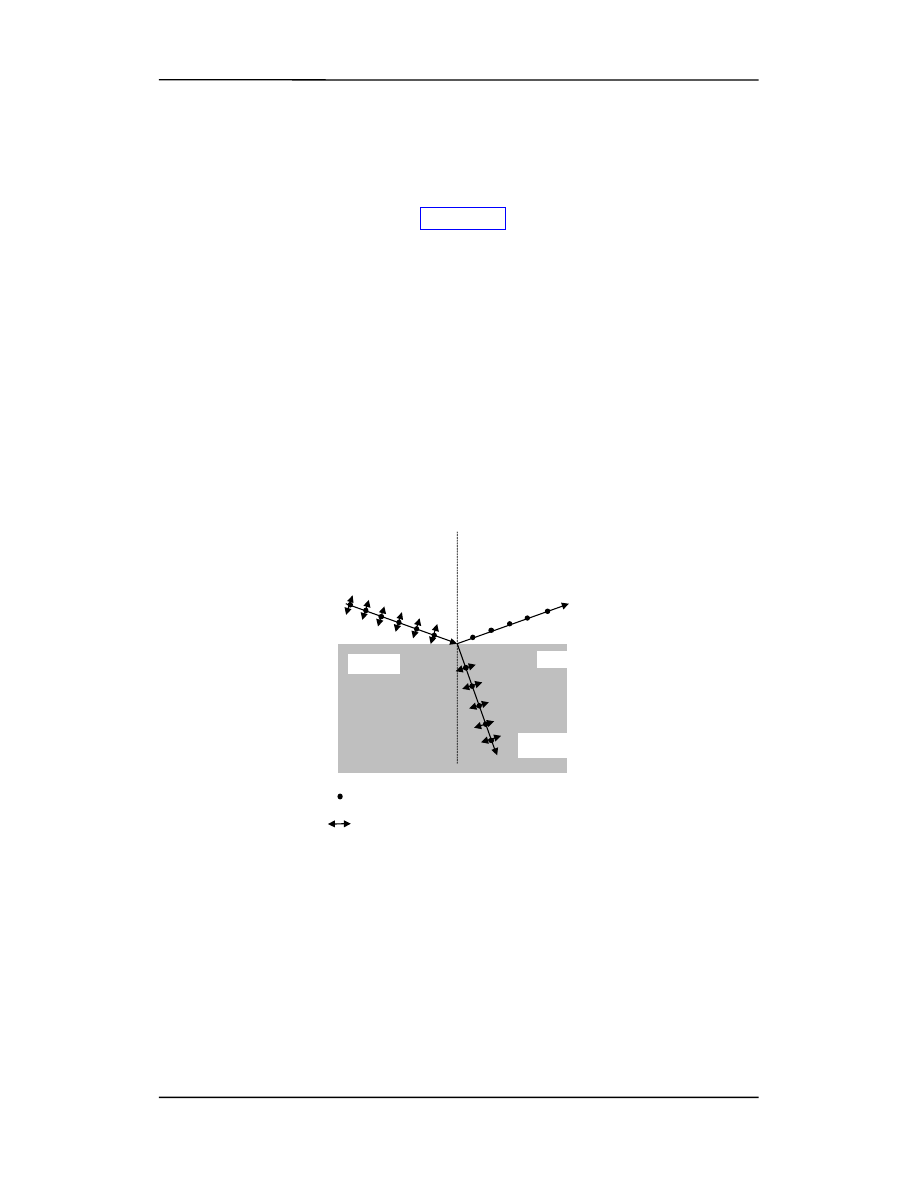
zowane przez odbicie. Rysunek przedstawia wiązkę niespolaryzowaną padającą na po-
wierzchnię szkła. Wektor E można rozłożyć na dwie składowe:

•

składową

σ prostopadłą do płaszczyzny padania (płaszczyzna rysunku),

•

składową

π leżącą w płaszczyźnie padania.

Dla światła całkowicie niespolaryzowanego obie składowe maja jednakowe amplitudy.
Stwierdzono doświadczalnie, że dla szkła (i innych materiałów dielektrycznych) istnieje
pewien kąt padania, nazywany

kątem całkowitej polaryzacji

α

p

, dla którego współczyn-

nik odbicia składowej

π jest równy zero. Wtedy wiązka odbita jest spolaryzowana li-

niowo prostopadle do płaszczyzny padania. Wiązka przechodząca jest tylko częściowo
spolaryzowana (składowa

π jest całkowicie załamana, a składowa σ tylko częściowo).

Zwróćmy uwagę, że wiązka załamana ma większe natężenie od wiązki odbitej.
Doświadczalnie stwierdzono, że gdy kąt padania jest równy kątowi całkowitej polaryza-
cji to wówczas wiązka odbita i załamana tworzą kąt prosty co oznacza że

α + β = 90°

α

α

β

padaj

ące światło

niespolaryzowane

fala odbita

fala za

łamana

sk

ładowa

π

sk

ładowa

σ

powietrze

szk

ło

n = 1.5

Z. Kąkol-Notatki do Wykładu z Fizyki

31-5

Natomiast z prawa załamania mamy

β

α

sin

sin

2

1

n

n

=

Z obu tych równań otrzymujemy

α

α

α

cos

)

90

sin(

sin

2

2

1

n

n

n

=

−

=

o

albo

n

n

n

=

=

1

2

tg

α

(30.2)

przy czym promień pada z ośrodka 1 i załamuje się w ośrodku 2.
To ostatnie równanie jest nazywane

prawem Brewstera

.

Prawo to zostało znalezione doświadczalnie ale oczywiście można je wyprowadzić ści-
śle przy pomocy równań Maxwella.

31.3 Załamanie podwójne

Dotychczas milcząco zakładaliśmy, że prędkość światła, a więc i współczynnik za-

łamania, nie zależą od kierunku rozchodzenia się światła w ośrodku ani od jego polary-
zacji. Ciała spełniające te warunki nazywamy

ciałami optycznie izotropowymi

. Istnieje

jednak szereg ciał

anizotropowych

(nie izotropowych).

Dotyczy to nie tylko własności optycznych ale wielu innych. Np. pewne kryształy łamią
się łatwo tylko w jednej płaszczyźnie, opór elektryczny mierzony w różnych kierunkach
jest różny. Kryształy łatwiej magnesuje się w jednym kierunku niż innych itd.
Uwaga: Ciała polikrystaliczne (złożone z wielu małych kryształków) z powodu przy-
padkowej orientacji kryształków mogą wydawać się izotropowymi.
Na początku wykładu wspomniany został eksperyment z kryształem kalcytu.
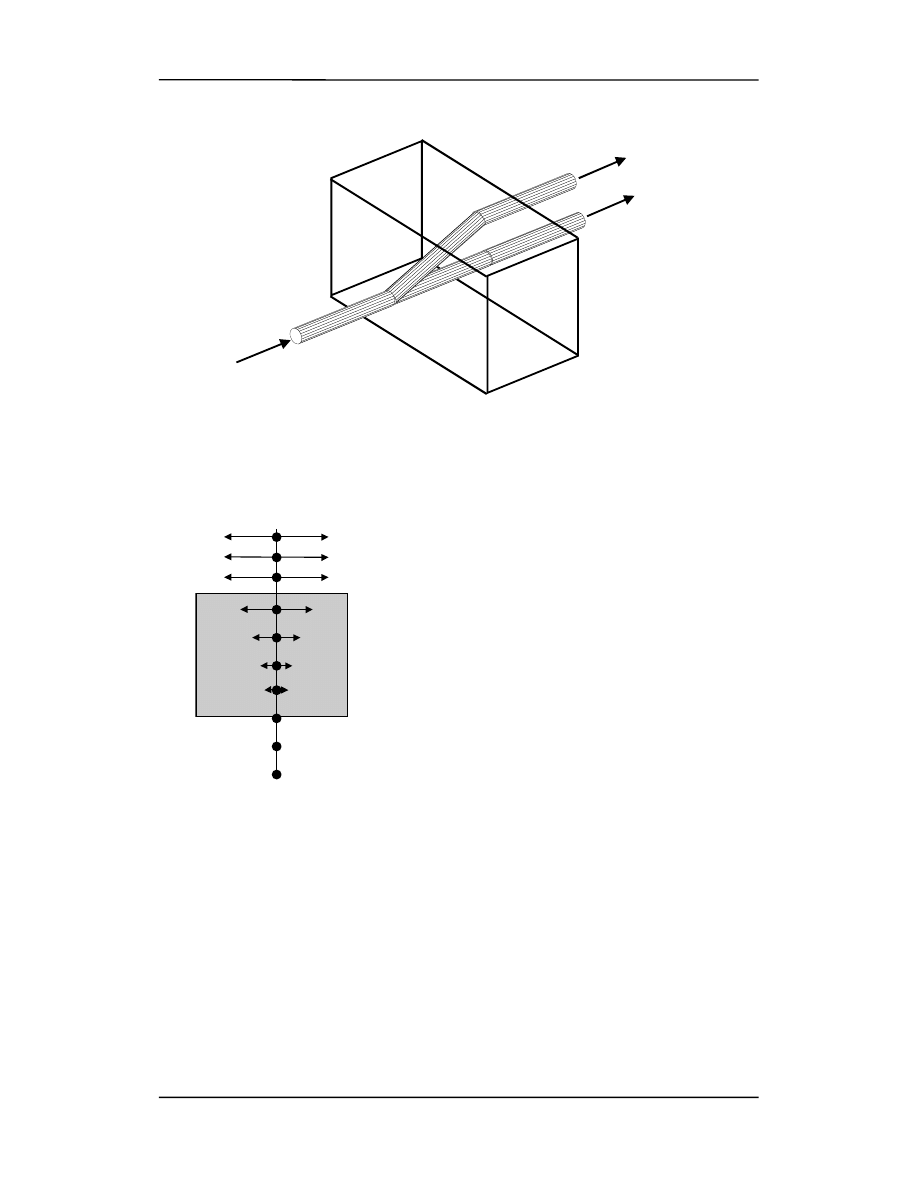
Na rysunku poniżej niespolaryzowana wiązka światła pada na kryształ kalcytu prosto-
padle do jednej z jego ścian.
Pojedyncza wiązka rozszczepia się na powierzchni kryształu na dwie.
Mamy do czynienia z

podwójnym załamaniem

.

Możemy zanalizować obie wychodzące wiązki za pomocą płytki polaryzującej.
Okazuje się, że obie wiązki są spolaryzowane liniowo, przy czym ich płaszczyzny drgań
są wzajemnie prostopadłe. Wiązki te są oznaczone przez o i e.
Jeżeli zmienimy kąt padania to okaże się, że jedna z wiązek tzw.

promień zwyczajny o

spełnia prawo załamania (tak jak dla ośrodka izotropowego) a druga wiązka tzw.

pro-

mień nadzwyczajny

e nie spełnia tego prawa.

Na rysunku (na następnej stronie) kąt padania jest równy zeru więc i kąt załamania też
powinien być zerowy i tak jest dla promienia o ale nie dla promienia e.

Różnicę tę można wyjaśnić następująco:

•

promień o przechodzi przez kryształ z jednakową prędkością we wszystkich kierun-
kach tzn. ma jeden współczynnik załamania n

0

tak jak izotropowe ciało stałe.

Z. Kąkol-Notatki do Wykładu z Fizyki

31-6

•

promień e ma prędkość w krysztale zależna od kierunku tzn. prędkość zmienia się

od

v

0

do

v

e

a współczynnik załamania od n

o

do n

e

. Dla

kalcytu n

e

= 1.658, n

o

= 1.486.

Wielkości n

e

i n

0

nazywamy

głównymi współczynnikami

załamania kryształu

.

Niektóre podwójnie załamujące kryształy mają interesują-
cą własność nazywaną

dichroizmem

, polegającą na tym, że

jedna ze składowych polaryzacji jest pochłaniana silniej
niż druga. Własność ta jest pokazana na rysunku obok. Na
tej zasadzie opiera się działanie szeroko stosowanych po-
laroidów.
Zamiast dużej płytki wyciętej z kryształu można zastoso-
wać wiele małych kryształów o osiach optycznych usta-
wionych równolegle do siebie.

Niektóre przezroczyste ciała bezpostaciowe jak szkła czy

tworzywa sztuczne optycznie izotropowe pod wpływem przyłożonych naprężeń mecha-
nicznych stają się optycznie anizotropowe.

Fakt ten jest szeroko wykorzystywany w technice do badania naprężeń w różnych kon-
strukcjach i mechanizmach.
Naprężenia można wyznaczyć ilościowo, budując model plastyczny urządzenia, które
poddaje się działaniu różnych sił. Anizotropię optyczną, jaka przy tym powstaje w mo-
delu, bada się przy pomocy polaryzacji.

wi

ązka

padaj

ąca

kryszta

ł

CaCO

3

e

o

światło
niespolaryzowane