INSTYTUT KONSTRUKCJI MASZYN

Katedra Maszyn Roboczych i Transportu Bliskiego

LABORATORIUM

NAP

Ę

D I STEROWANIE

HYDRAULICZNE I PNEUMATYCZNE

Temat: Wyznaczanie sprawno

ś

ci pompy wyporowej

Grupa: ........................ Zespół: .........................

Lp

Nazwisko i Imię

Ocena

Data

Parametry pracy pomp wyporowych

Głównymi jednostkami napędu hydrostatycznego są pompy i silniki hydrauliczne. Wspólną

ich funkcją jest zmiana rodzaju energii. Pompy zamieniają energię mechaniczną w energię hydrau-
liczną magazynowaną pod postacią ciśnienia przepływającego czynnika roboczego (cieczy hydrau-
licznej), silniki natomiast zamieniają energię hydrauliczną w energię mechaniczną. Bardzo istotne
jest przy tym, by zamiana energii odbywała się przy minimalnych jej stratach. W układach napędo-
wych i sterujących maszyn i urządzeń, ze względu na relatywnie wysoką sprawność energetyczną,
zastosowanie znajdują głównie pompy i silniki wyporowe.

Pompy wyporowe charakteryzują się tym, że przestrzeń ssawna oddzielona jest w nich szczel-

nie od przestrzeni tłocznej przez odpowiednio ukształtowany element, którego ruch wypiera ciecz z
jednej przestrzeni do drugiej, wymuszając odpowiednio ruch cieczy. Zasada działania silników wy-
porowych jest odwróceniem działania pomp wyporowych, stąd wiele pomp wyporowych jest jed-
nostkami odwracalnymi, czyli może pracować jako silniki wyporowe.

W zależności od kształtu i rozmieszczenia elementów wyporowych wyróżnia się następujące

rodzaje jednostek:
- pompy i silniki zębate o zazębieniu zewnętrznym i wewnętrznym,
- pompy i silniki wielotłoczkowe osiowe lub promieniowe,
- pompy i silniki łopatkowe,
- silniki o ruchu postępowym (cylindry hydrauliczne),
oraz inne o mniejszym zakresie zastosowań jak np.: pompy i silniki gerotorowe, pompy membra-
nowe, itp. Największe zastosowanie w hydraulicznych układach napędowych maszyn, mają pompy i
silniki wielotłokowe osiowe, pompy i silniki zębate oraz cylindry hydrauliczne.

Parametrem charakterystycznym pomp i silników wyporowych jest objętość skokowa q (teo-

retyczna objętość przypadająca na jeden obrót wału maszyny) lub objętość jednostkowa

ϕ

V

(objętość

przypadająca na jeden radian obrotu wału maszyny). Poprzez ten parametr wyznacza się wydajność
teoretyczną lub chłonność teoretyczną (idealną, geometryczną) pomp i silników Q

t

:

n

q

Q

t

⋅

=

lub

ω

⋅

=

t

t

V

Q

(1)

gdzie:

ω

.

n

- odpowiednio, prędkość obrotowa i prędkość kątowa,

przy czym objętość skokowa i objętość jednostkowa związane są zależnością:

π

ϕ

2

q

V

=

.

Objętość skokowa nazywana jest także w literaturze fachowej geometryczną objętością robo-

czą, czy też wydajnością jednostkową lub właściwą w przypadku pomp i chłonnością jednostkową
lub właściwą w przypadku silników. Objętość skokowa określona jest na podstawie parametrów
geometrycznych elementu wypierającego.

Wyróżnia się pompy o stałej wydajności i pompy o zmiennej wydajności oraz silniki o stałej

chłonności i o zmiennej chłonności. W przypadku pomp i silników o zmiennej objętości (chłonno-
ś

ci), zależność na wydajność teoretyczną lub chłonność teoretyczną (1), przyjmuje postać:

n

q

Q

t

⋅

⋅

=

ε

lub

ω

ε

ϕ

⋅

⋅

=

V

Q

t

(1')

gdzie:

ε

- jest parametrem nastawy (regulacji) określającym stosunek danej (bieżącej) wartości na-

stawy, do maksymalnej nastawy przewidywanej dla danej konstrukcji. Wartość parametru
nastawy może się zatem zmieniać od 0 do 1.

Moc teoretyczną pompy lub silnika N

t

określa związek w postaci:

p

Q

N

t

t

∆

⋅

=

(2)

przy czym uwzględnienie parametru nastawy prowadzi do zależności:

p

n

q

N

t

∆

⋅

⋅

⋅

=

ε

lub

p

V

N

p

t

∆

⋅

⋅

⋅

=

ω

ε

ϕ

(2')

Moment teoretyczny (idealny) M

t

pompy lub silnika dla

ε

= 1 bez uwzględnienia strat, wyznacza się

z równania mocy dla stanu ustalonego:

p

Q

M

t

t

∆

⋅

=

⋅

ω

zatem:

p

V

p

Q

M

t

t

∆

⋅

=

∆

⋅

=

ϕ

ω

(3)

Wynika stąd, że moment teoretyczny zależny jest jedynie od objętości jednostkowej (skokowej)
i różnicy ciśnień na wejściu i wyjściu pompy lub silnika hydraulicznego. Dla jednostek o zmiennej
wydajności (chłonności) moment teoretyczny wyraża się zależnością:

p

V

M

t

∆

⋅

⋅

=

ϕ

ε

lub

p

q

M

t

∆

⋅

⋅

=

π

ε

2

(3')

Przedstawione zależności (1), (2), (3) dotyczą jednostek idealnych, nie uwzględniają bowiem

strat występujących w rzeczywistych pompach i silnikach. Straty te dzieli się zwykle na straty obję-
tościowe i straty hydrauliczno-mechaniczne.

Straty objętościowe wpływające na wydajność teoretyczną pomp i chłonność silników są

związane przede wszystkim z przeciekami czynnika z komór wyporowych. Straty te określa się za
pomocą sprawności objętościowej (volumetrycznej).
Straty hydrauliczno-mechaniczne są związane z oporami przepływu oleju we wszystkich kana-
łach wewnętrznych jednostki oraz ze stratami tarcia na powierzchniach elementów będących w ru-
chu względnym, w czasie pracy jednostki. Straty te wyrażające się momentem strat są ujmowane
łącznie
i określane za pomocą sprawności hydrauliczno -mechanicznej.

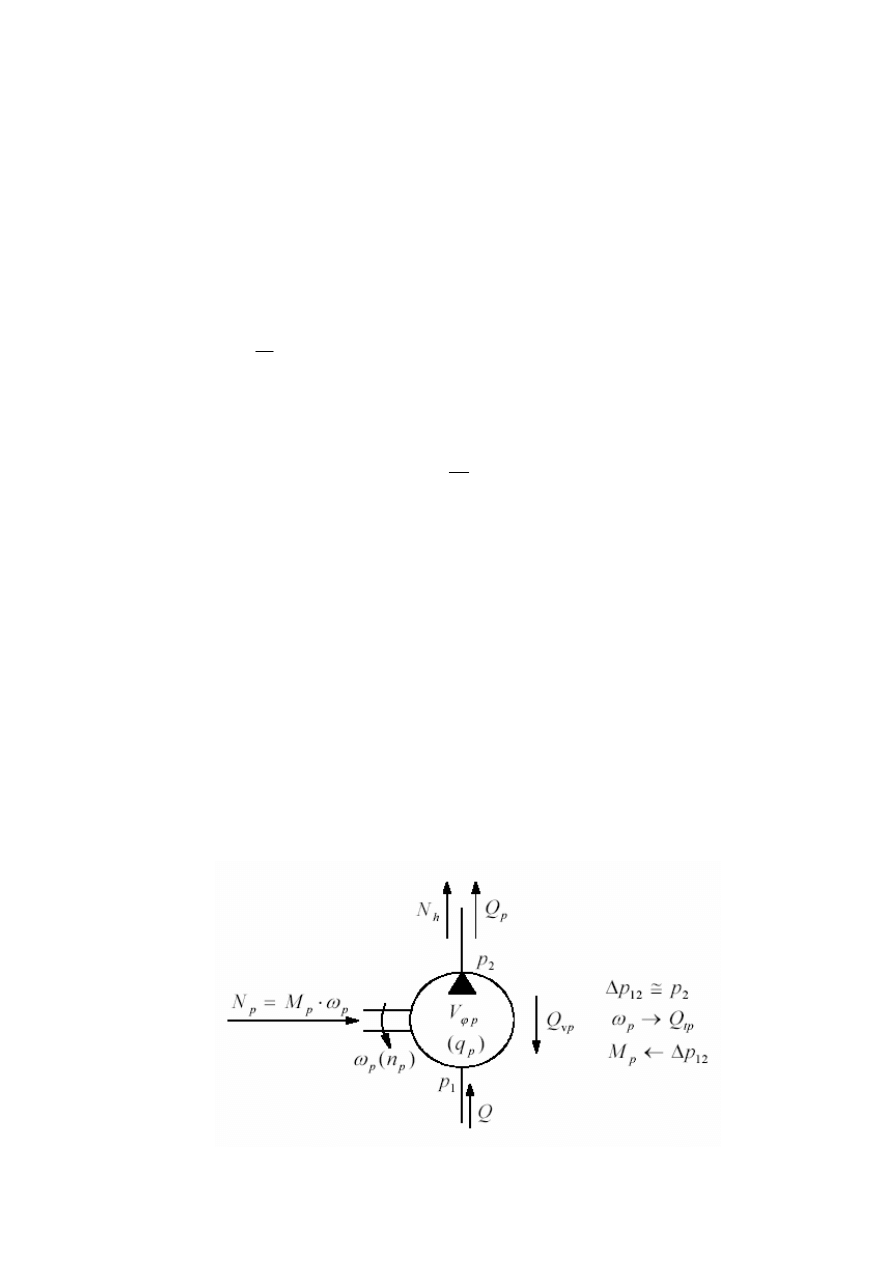
Zadanie pomp wyporowych polega na zasilaniu układu hydraulicznego cieczą roboczą pod

odpowiednim ciśnieniem. Stanowią one zatem źródło natężenia przepływu (wydatku) w układzie
hydraulicznym, toteż nazywane są niekiedy generatorami wydatku.

Podstawowymi parametrami pracy pompy są: wydajność pompy Q

p

przy ustalonej prędkości

obrotowej n

p

oraz ciśnienie na wyjściu pompy (ciśnienie tłoczenia) p

2

.

Rys. 1. Symbol graficzny pompy wyporowej wraz z oznaczeniem parametrów pracy

Sprawność objętościowa

Teoretycznie wydajność pompy nie zależy od ciśnienia tłoczenia a wynika jedynie z geome-

trycznych wymiarów elementów pompy. Wskutek istnienia technologicznych luzów pomiędzy ru-
chomymi elementami pompy oraz wskutek warunków na ssaniu (tj. niecałkowitego napełnienia
komory ssawnej), wydajność rzeczywista Q

p

jest mniejsza od teoretycznej Q

tp

o wartość strat obję-

tościowych Q

vp

. Znając straty objętościowe można wyznaczyć sprawność objętościową pompy defi-

niowaną jako stosunek wydajności rzeczywistej Q

p

do wydajności teoretycznej Q

tp

, czyli:

p

p

vp

tp

vp

tp

tp

p

vp

n

q

Q

Q

Q

Q

Q

Q

⋅

−

=

−

=

=

1

η

(4)

Ze związku (2.4) wynika, że wydajność rzeczywistą pompy można określić na podstawie znajomo-
ś

ci wydajności teoretycznej i sprawności objętościowej:

vp

p

p

vp

p

p

vp

tp

p

V

n

q

Q

Q

η

ω

η

η

ϕ

⋅

⋅

=

⋅

⋅

=

⋅

=

(4')

Ponieważ Q

vp

, a zatem

vp

η

zależy od różnicy ciśnień

12

p

∆

, straty objętościowe można wyznaczyć z

zależności:

p

C

Q

vp

vp

∆

⋅

=

(5)

gdzie:

C

vp

- współczynnik przecieku pompy określony dla danego typu pompy i danej lepkości cie-

czy roboczej.

Uwzględniając powyższą zależność w wyrażeniu (4) widać, że wydajność rzeczywista pompy jest
funkcją ciśnienia. Należy podkreślić, że zależność (5) jest konsekwencją założenia, że wielkość
przecieków w pompie sprowadzić można do przepływu cieczy przez szczeliny. Uwzględniając pa-
rametry geometryczne szczeliny (przepływ laminarny), straty objętościowe (przecieki) można okre-
ś

lić również z zależności:

µ

µ

ϕ

µ

12

12

3

12

p

V

C

p

l

b

c

Q

p

v

vp

∆

⋅

⋅

=

∆

⋅

⋅

⋅

=

(5')

gdzie:

µ

v

C

- stała związana z określoną konstrukcją pompy,

c

b

l ,

,

- odpowiednio długość, szerokość i grubość szczeliny,

µ

- współczynnik lepkości dynamicznej.

Stąd straty objętościowe są proporcjonalne do różnicy ciśnień i do trzeciej potęgi grubości

szczeliny, a więc do luzów między współpracującymi elementami oddzielającymi przestrzenie o
różnych ciśnieniach. Na wydajność pompy mają również wpływ straty wywołane nie całkowitym
napełnieniem komór roboczych pomp w czasie ssania (spowodowane np. zapowietrzeniem lub zbyt
dużymi oporami przepływu cieczy), a także straty związane ze ściśliwością cieczy i odkształceniem
elementów konstrukcyjnych pompy. Straty te przy prawidłowo zaprojektowanych jednostkach są
małe i mogą być często pominięte przy obliczeniach. Stąd też korzystając z zależności (4) i (5) moż-
na zapisać:

dla

const

n

p

=

const

p

vp

12

1

∆

−

=

η

dla

const

p

=

∆

12

p

vp

n

const

−

=

1

η

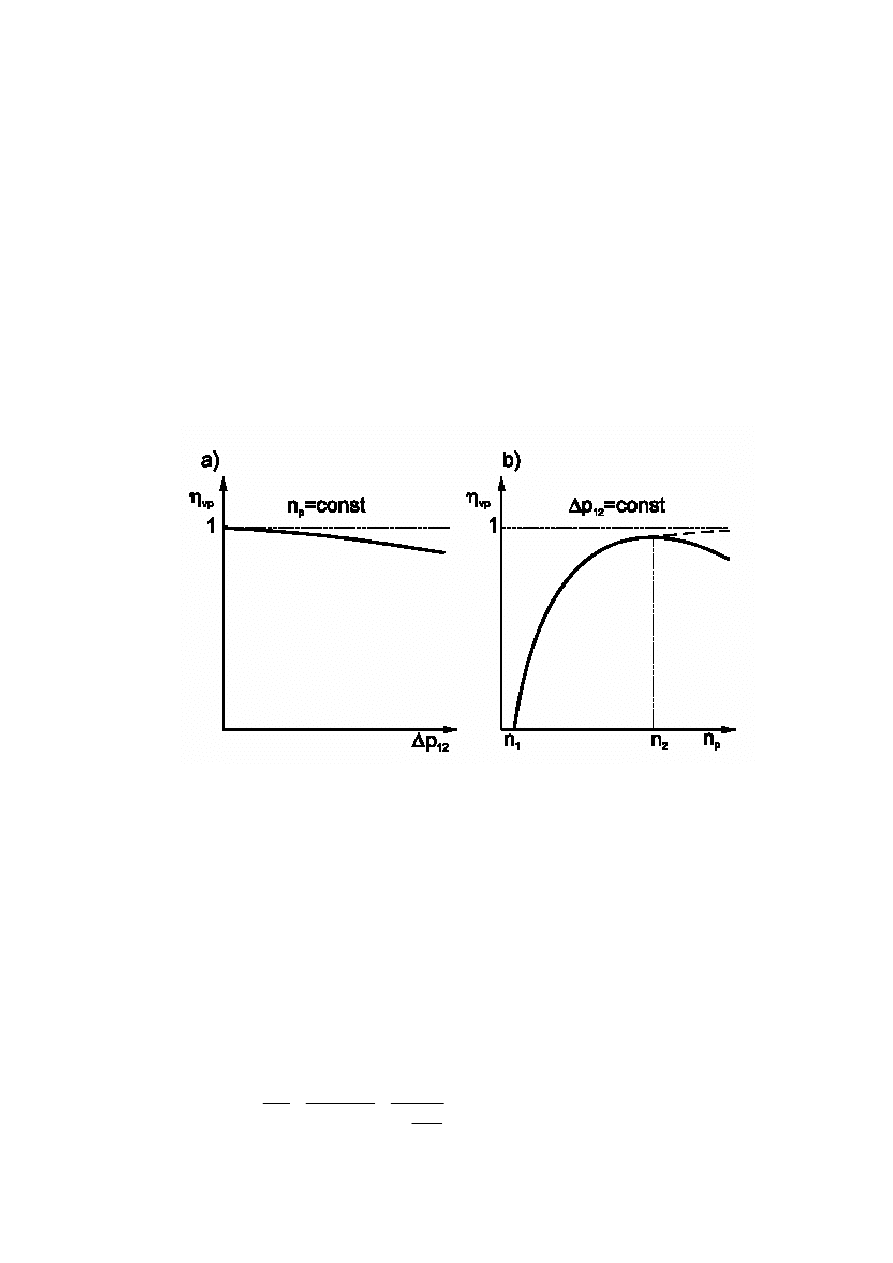
zatem charakter zmian sprawności objętościowej pompy w funkcji ciśnienia i prędkości obrotowej
można przedstawić jak na wykresach rys. 2 a,b.

Z przedstawionych wykresów wynika, że sprawność objętościowa maleje liniowo ze wzro-

stem ciśnienia. Rzeczywisty przebieg

)

( p

f

vp

∆

=

η

będzie nieco różnił się od przebiegu przedstawio-

nego na rys. 2a, ze względu na wpływ wcześniej wspomnianych innych strat objętościowych. Łatwo
zauważyć, że wykres przedstawiony na rys. 2a jest także, w innej skali, obrazem zmian wydajności
rzeczywistej Q

p

w funkcji obciążenia, czyli

)

( p

f

Q

p

∆

=

. Na rys. 2b przedstawiono przebieg zależno-

ś

ci objętościowej sprawności pompy przy zmianie prędkości obrotowej dla ustalonej wartości ci-

ś

nienia. W zakresie bardzo małych prędkości tj. n < n

1

sprawność

0

=

vp

η

. Jest to spowodowane

tym, że przy małych prędkościach wydajność pompy jest tak bardzo mała, iż nie pokrywa we-
wnętrznych strat objętościowych. W miarę zwiększania prędkości obrotowej od n

1

, sprawność obję-

tościowa gwałtownie rośnie i osiąga swoje maksimum przy wartości n

2

, a następnie maleje wskutek

niecałkowitego wypełnienia komór roboczych pompy w czasie ssania.

Rys. 2. Teoretyczny przebieg obj

ę

to

ś

ciowej sprawno

ś

ci pompy wyporowej:

a)

)

(

12

p

f

vp

∆

=

η

b)

)

(

p

vp

n

f

=

η

Oprócz opisanych strat objętościowych w pompach wyporowych występują straty hydrauliczno-
mechaniczne. Obejmują one straty związane z oporami przepływu czynnika w kanałach wewnętrz-
nych pompy (straty hydrauliczne) oraz straty wywołane oporami tarcia (straty mechaniczne). Straty
te wyrażone są sumarycznym momentem strat i określane za pomocą sprawności hydrauliczno-
mechanicznej.


Sprawność hydrauliczno-mechaniczna pompy

Sprawność hydrauliczno-mechaniczna pompy

hmp

η

jest to stosunek momentu teoretycznego

pompy

tp

M

do momentu rzeczywistego pompy

p

M

, czyli:

tp

str

str

tp

tp

p

tp

hmp

M

M

M

M

M

M

M

+

=

−

=

=

1

1

η

(6)

przy czym:
M

tp

- moment teoretyczny (idealny) jest to moment, jaki byłby potrzebny do napędu pompy gdyby

nie istniały w pompie żadne opory tarcia ani opory przepływu cieczy w pompie, zgodne z za-
leżnością (3):

π

ϕ

2

12

12

p

q

p

V

M

p

p

tp

∆

⋅

=

∆

⋅

=

(7)

M

p

- moment rzeczywisty jest to moment obrotowy, jaki trzeba doprowadzić do wału pompy, aby

otrzymać jej pracę, czyli:

str

tp

p

M

M

M

+

=

(8)

M

str

- moment strat hydrauliczno-mechanicznych jest sumą momentu strat tarcia lepkiego

µ

M

zależ-

nego od prędkości i lepkości, momentu strat tarcia mechanicznego (kulombowskiego)

f

M

,

które zależne jest od obciążenia, momentu strat hydraulicznych

h

M

(proporcjonalnego do kwa-

dratu prędkości) i momentu strat stałych

0

M

niezależnego od parametrów ruchowych, czyli:

0

M

M

M

M

M

h

f

str

+

+

+

=

µ

(9)

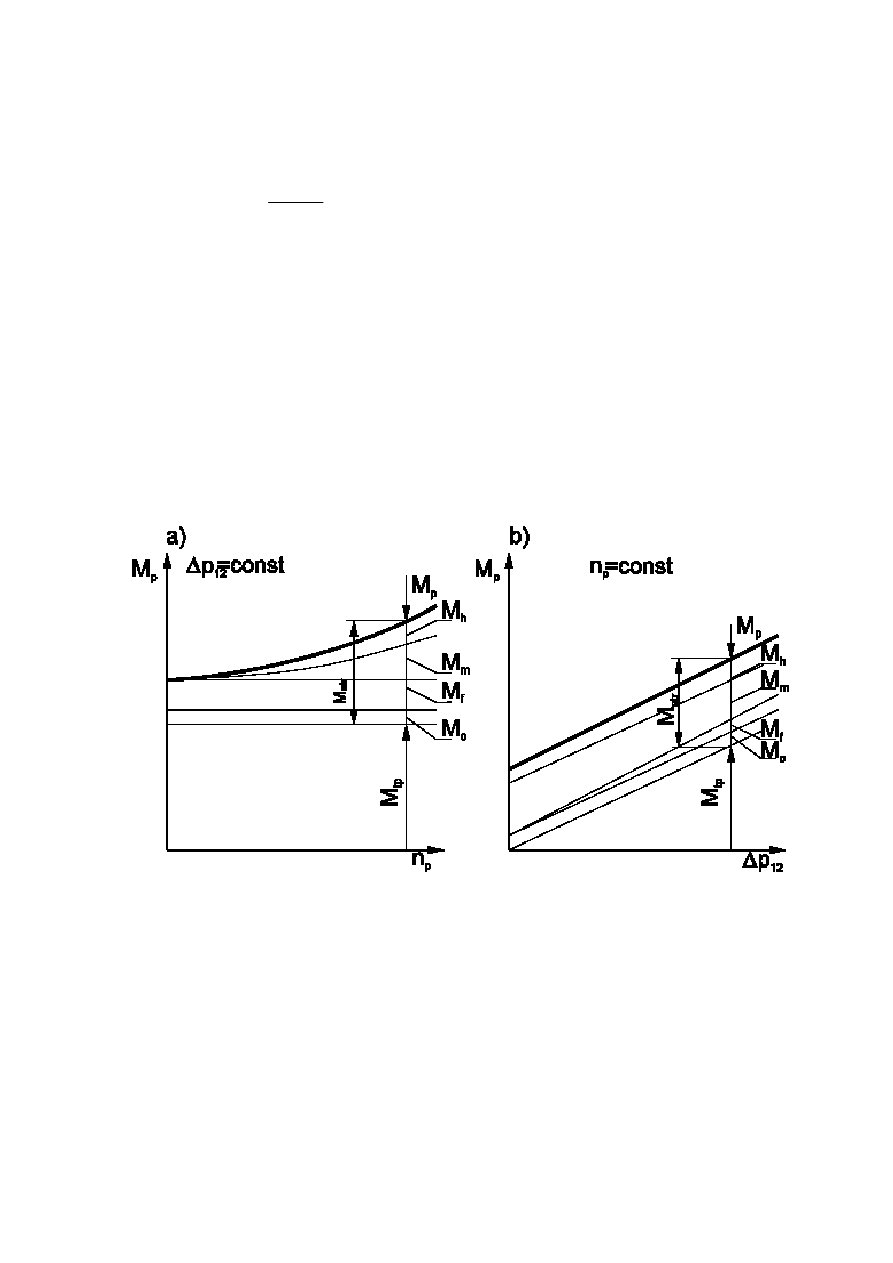
Rys. 3. Przebieg momentu rzeczywistego pompy

p

M

w zale

ż

no

ś

ci od:

a) pr

ę

dko

ś

ci obrotowej wałka pompy

p

n

, b) ró

ż

nicy ci

ś

nie

ń

12

p

∆

(obci

ąż

enia)

Teoretyczny przebieg momentu rzeczywistego

p

M

dla pompy wyporowej przedstawiono na

rys. 3. W nowoczesnych jednostkach wyporowych dominujące znaczenie posiadają: moment strat
tarcia lepkiego

µ

M

(zależny od prędkości i lepkości) oraz moment strat tarcia suchego

f

M

(zależny

od obciążenia). Dla zobrazowania charakteru zmian sprawności hydrauliczno -mechanicznej w
funkcji prędkości oraz w funkcji ciśnienia przyjąć można zgodnie z wyżej przedstawionym podzia-
łem momentów strat następujące związki:

2

)

(

n

C

n

B

A

n

f

M

str

⋅

+

⋅

+

=

=

E

p

D

p

f

M

str

+

∆

⋅

=

∆

=

)

(

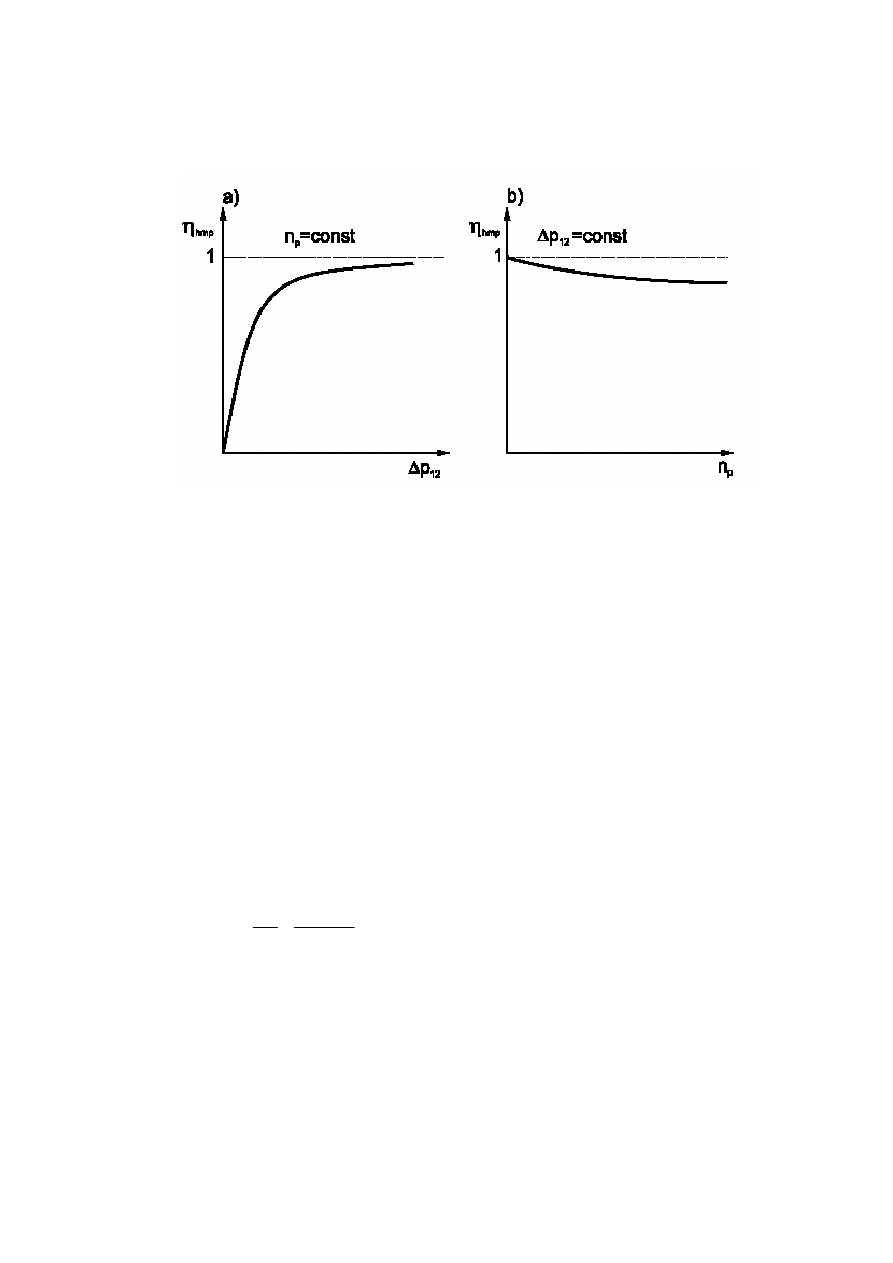
Związki te przy wykorzystaniu zależności (6) pozwalają przedstawić teoretyczny przebieg sprawno-
ś

ci hydrauliczno-mechanicznej pompy wyporowej w postaci jak na rys. 4.

Rys. 4. Teoretyczny przebieg sprawno

ś

ci hydrauliczno-mechanicznej pompy wyporowej

hmp

η

;

a) w funkcji ci

ś

nienia

12

p

∆

,

b) w funkcji pr

ę

dko

ś

ci obrotowej

p

n

Moc oddawana przez pompę, czyli moc efektywna, którą można wykorzystać w układzie na-

pędowym jest równa iloczynowi wydajności rzeczywistej pompy Q

p

i różnicy ciśnień na pom-

pie

12

p

∆

tak więc:

12

12

12

p

n

q

p

Q

p

Q

N

vp

p

p

vp

tp

p

h

∆

⋅

⋅

⋅

=

∆

⋅

⋅

=

∆

⋅

=

η

η

(10)

Natomiast moc pobierana przez pompę, czyli moc, którą należy doprowadzić do silnika na-

pędowego, nazywa się mocą napędową pompy, która wynosi:

p

p

p

p

p

M

M

n

N

⋅

=

⋅

⋅

=

ω

π

2

(11)

Stosunek mocy oddanej przez pompę, czyli mocy efektywnej (hydraulicznej) N

h

uzyskiwanej

z pompy, do mocy doprowadzonej do pompy N

p

określa sprawność ogólna (całkowita) pompy

p

η

stąd:

p

p

p

p

h

p

M

p

Q

N

N

n

ω

⋅

∆

⋅

=

=

12

(12)

Można wykazać, że sprawność ogólna pompy

p

η

jest iloczynem jej sprawności objętościo-

wej

vp

η

i hydrauliczno-mechanicznej

hmp

η

:

hmp

vp

p

η

η

η

⋅

=

(13)

Charakterystyczne parametry pompy można przedstawić w postaci wykresów, które pozwala-

ją na dobór właściwej pompy. Istnieje wiele rodzajów tych wykresów, przy czym uwzględniają one
takie wielkości charakteryzujące pracę pompy, jak: ciśnienie

p

∆

, wydajność Q

p

, sprawności

vp

p

η

η

,

,

moc na wale pompy N

p

, prędkość obrotowa pompy n

p

, a dla pomp o zmiennej wydajności również

wielkość regulowaną np. kąt pochylenia tarczy

δ

. Najczęściej w katalogach pomp spotyka się wy-

kresy zależności:

)

( p

f

Q

p

∆

=

,

)

( p

f

p

∆

=

η

,

)

( p

f

vp

∆

=

η

oraz

)

( p

f

N

p

∆

=

dla

const

n

=

, oraz

)

(

n

f

N

p

=

i

)

(

n

f

M

p

=

dla

const

p

=

∆

.

Dogodną formę, przedstawienia parametrów eksploatacyjnych pomp uzyskuje się stosując

charakterystyki uniwersalne, które przedstawiają wykres wydajności pomp Q

p

w funkcji ciśnienia,

z naniesionymi krzywymi prędkości obrotowej i mocy pobieranej oraz sprawności. Pozwalają one
na szybki dobór odpowiednich pomp dla projektowanego układu.

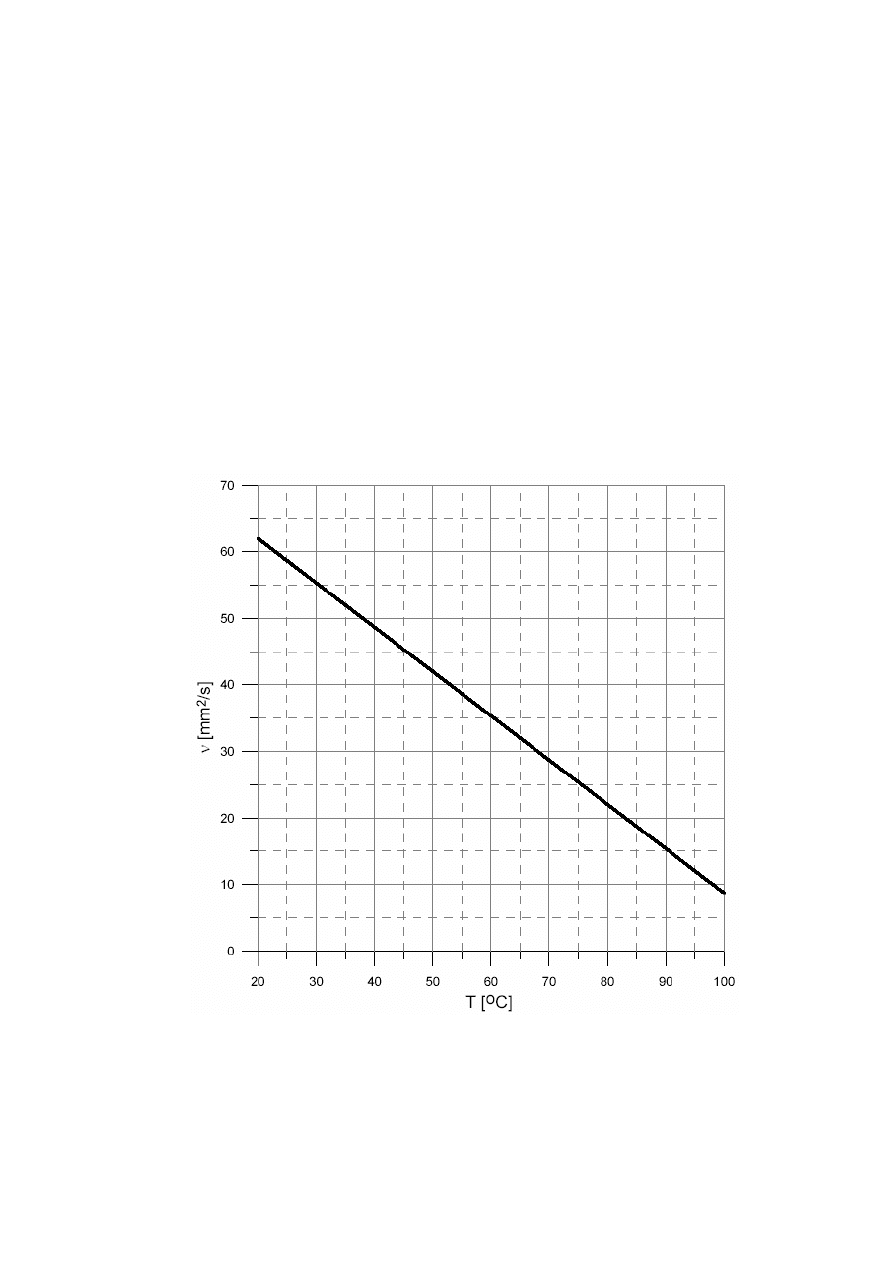
Lepko

ść

oleju

Ponieważ jednym z najistotniejszych parametrów mających wpływ na charakterystyki

sprawności pompy jest lepkość, na opracowanych wykresach sprawności w funkcji ciśnienia należy
podać wartość współczynnika lepkości cieczy roboczej, przy jakim przeprowadzona była próba.
W stanowisku zastosowano olej biodegradalny typu HEES firmy Caterpillar, dla którego przybliżo-
na charakterystyka współczynnika lepkości kinematycznej w funkcji temperatury zamieszczona jest
na rys. 5.

Rys. 5. Charakterystyka współczynnika lepko

ś

ci kinematycznej oleju HEES firmy Caterpillar

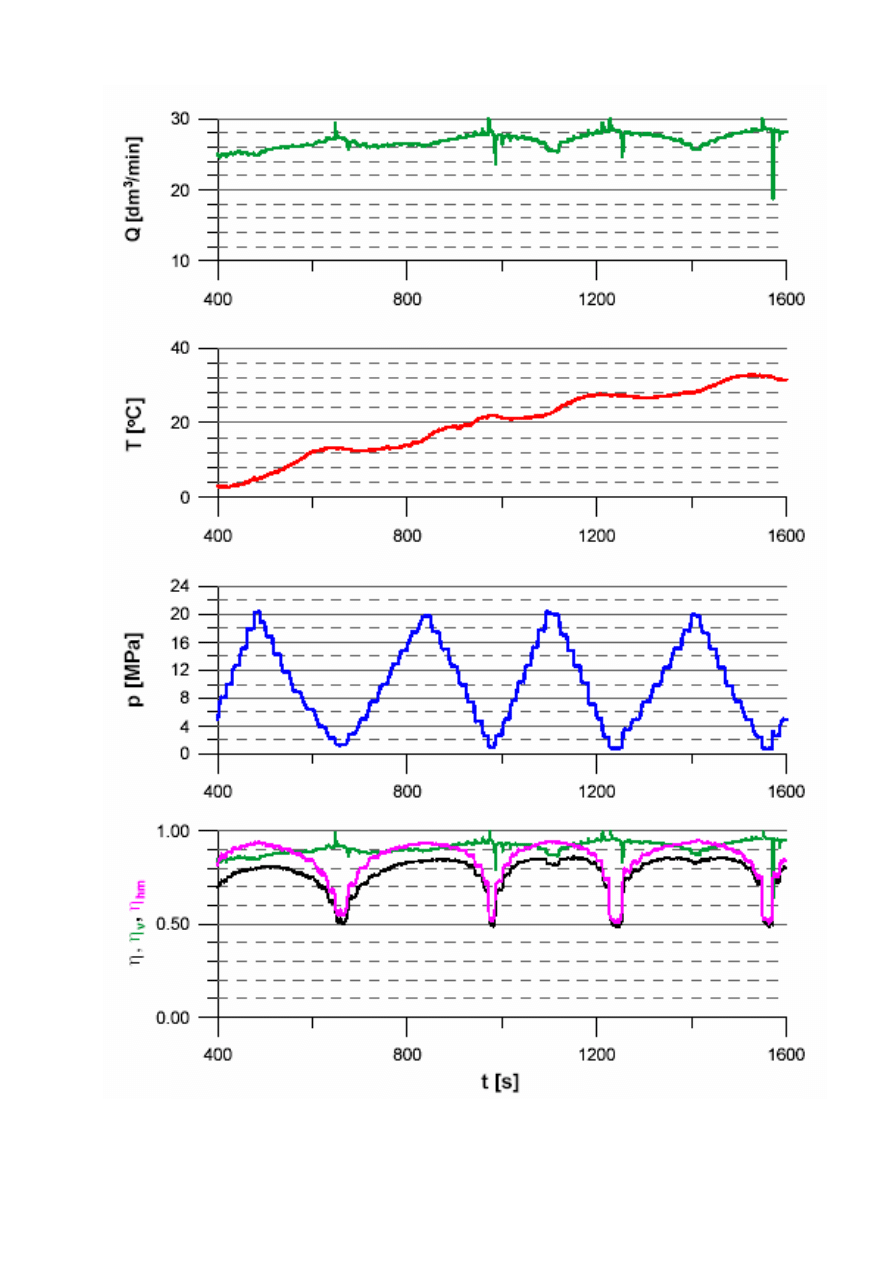
Rys. 8. Przykładowe przebiegi parametrów przy wyznaczeniu sprawno

ś

ci pompy

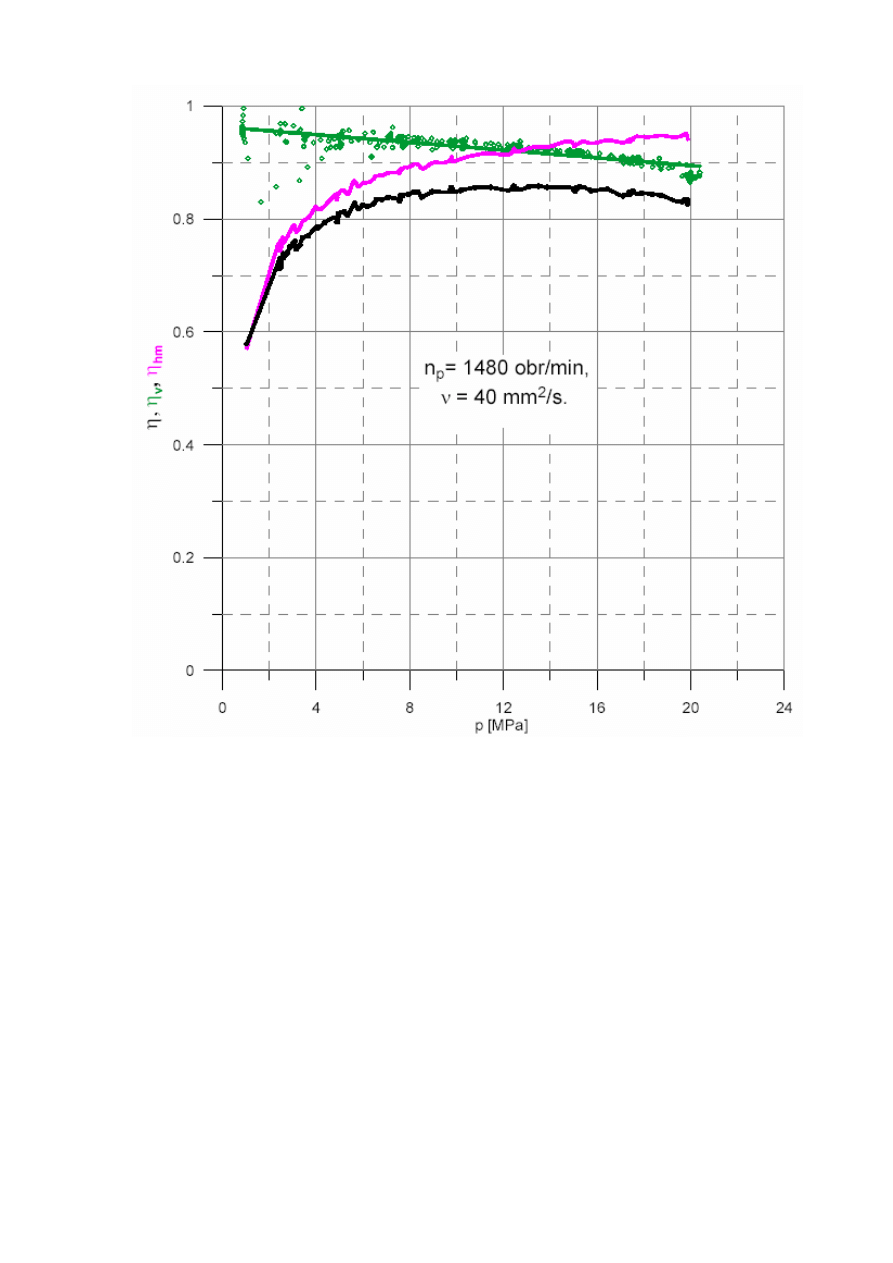
Rys. 7. Przykładowe charakterystyki wyznaczonej sprawno

ś

ci pompy w funkcji ci

ś

nienia

Wymagania do sprawozdania:

1.

sprawozdanie studenci wykonują dwójkami,

2.

sprawozdanie powinno zawierać:

−

krótki opis wykonywanego ćwiczenia,

−

schemat ideowy stanowiska badawczego wraz z czujnikami pomiarowymi,

−

wykaz (tabela) mierzonych parametrów oraz procedurę obliczania sprawności obj.,
hydr.mech. i ogólnej,

−

przebiegi parametrów mierzonych i obliczonych,

−

charakterystyki sprawności w funkcji ciśnienia z podanie parametrów, przy jakich zostały
wyznaczone ( prędkość obrotowa, współczynnik lepkości, temperatura, typ oleju),

−

wnioski,

3.

nie należy do sprawozdania dołączać kserowanych i skanowanych materiałów,

4.

nie będą przyjmowane sprawozdania będące wielokrotnym wydrukiem tego samego pliku,

5.

oszczędzać papier – optymalnie dobierać wielkość rysunków, stronę tytułową ograniczyć do kil-

ku centymetrów nagłówka itp.