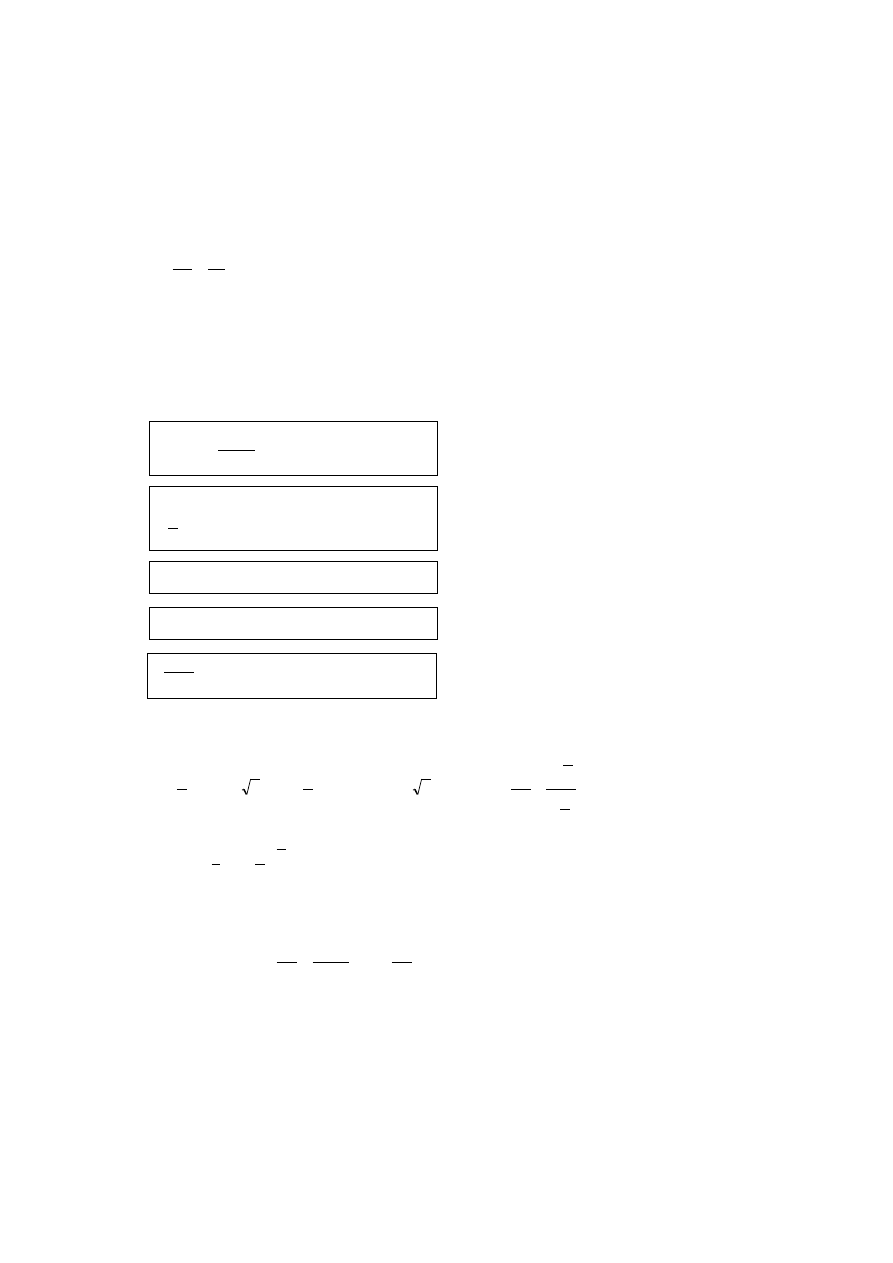
Pojęcia całki - jest to działanie odwrotne do pochodnej.
f x
x
x
F x
F x
x
x
C
( )
( ) ?
( )
5 2
6
5
3
3
6
2
Obliczyć całkę to odpowiedzieć na pytanie jak wyglądała funkcja która ma taką pochodną.
gdzie stała C może byc dowolną liczbą
f x dx
F x
C
F x
f x
( )
( )
( )
( )
Wzory:
1.
xndx
xn
n
C
n
1
1
1
dla
2.
gdy x = -1 to
1
x
dx
x C
ln| |
3. Cf x dx
C f x dx
( )
( )
4.
f x
g x dx
f x dx
g x dx
( )
( )
( )
( )
5.
1
1
1
x
dx
x
dx C
ln(
)
Przykład:
1
5 2
1
5 2
5
3
3
1
1
2
1
1
2
5
3
3
3
2
3
2
x
x
x dx
x
dx
x dx
xdx
x
x
x
C
x
x
x
C
ln| |
ln| |
Przykład:
(
)
x
dx
xdx
dx
x
x
C
x
x C
1
1
2
2
0 1
0 1
2
2
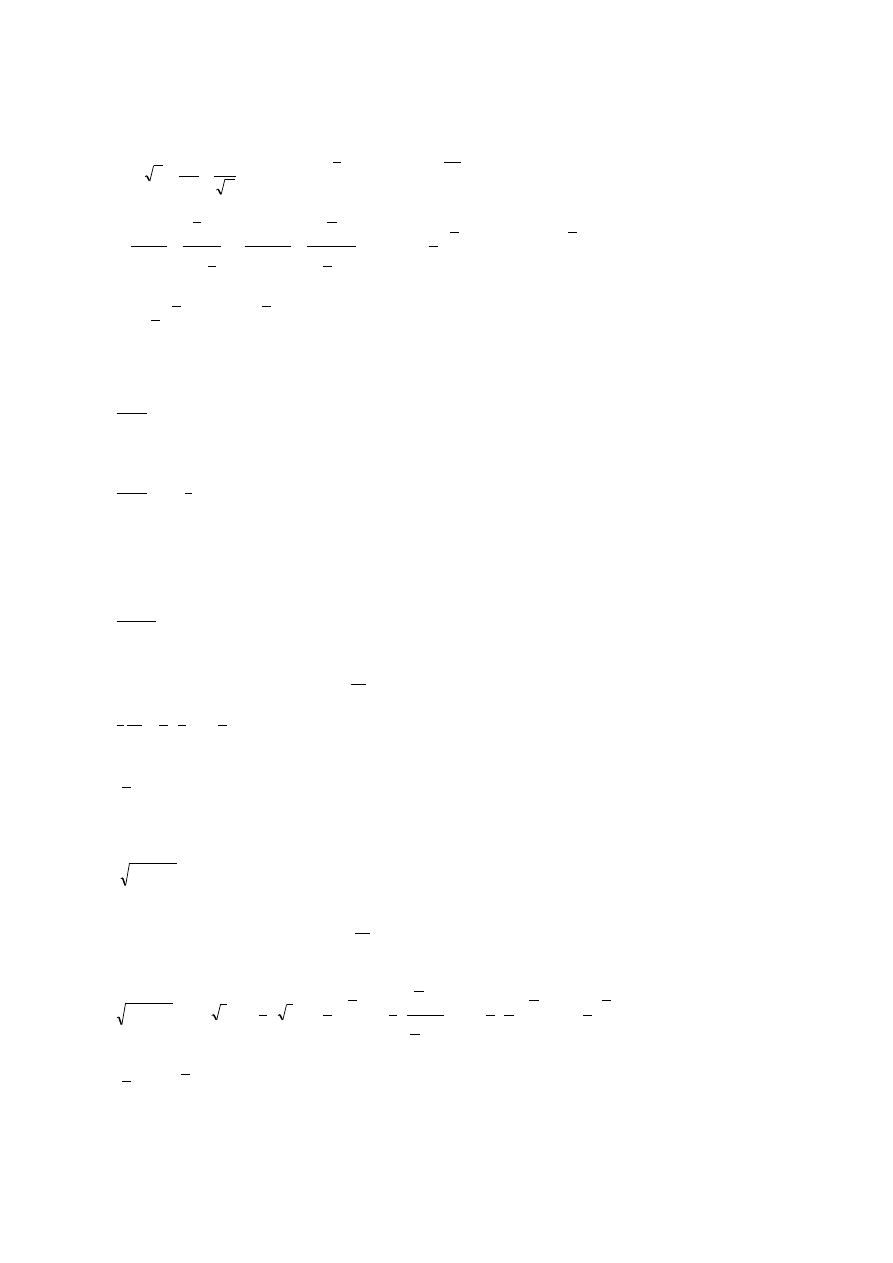
Przykład:
3 5
5
2
1
3
1
5
5
2
1
2
x
x
x
dx
dx
x dx
x
x
3
0 1
0 1
1
5
1
1
1
5
5
2 1
2 1
1
2
1
1
2
1
3
5
6
6
5
5 1
1 2
1
2
x
x
x
x
C
x
x
x
x
C
(
)
3
5
6
6
5 5 1 2
1
2
x
x
x
x
C
Przykład:
1
1
1
1
1
x
dx
x
t
x
dx
dx
dt
podstawiamy
liczymy pochodną stronami:
(
)
(
)
1
1
1
x
dx
dt
t C
x
dx C
1
t
ln| |
ln(
)
Przykład:
1
3
2
3
2
3
3
x
dx
x
t
dx
dt
dx
dt
podstawiamy
liczymy pochodną stronami:
(
)
1
3
1
3
1
1
3
1
3
3
2
t
dt
t
dt
t C
x
C
ln| |
ln|
|
Przykład:
3
5
3
5
3
3
x
dx
x
t
dx
dt
dx
dt
podstawiamy
liczymy pochodną stronami:
(
)
3
5
1
3
1
3
1
2
1
3
1
2
1
1
2
1
1
3
2
3
3
2
2
9
3
2
2
9
3
5
3
2
x
dx
dx
tdt
t dt
t
C
t
C
t
C
x
C
t
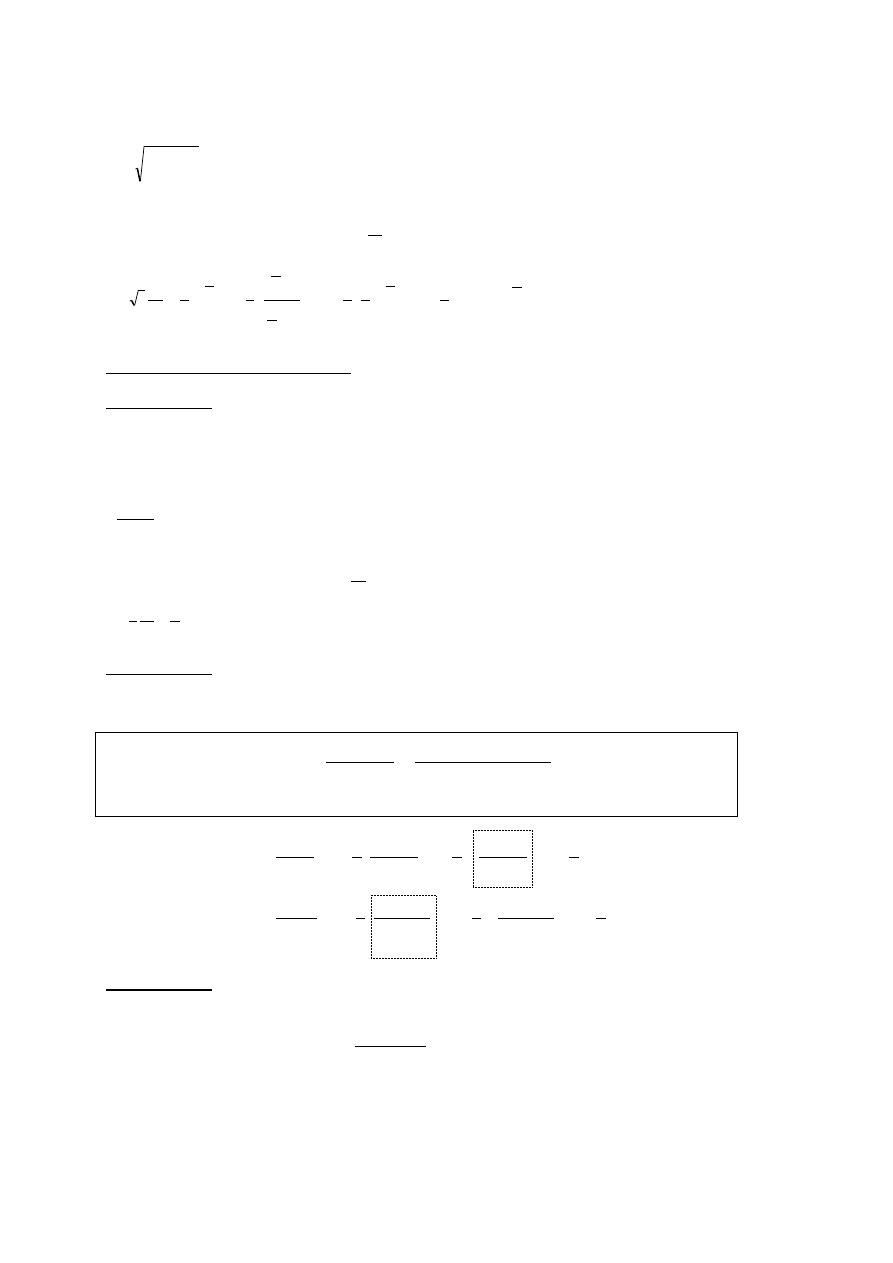
Przykład:
x
x
dx
x
t
x dx
dt
dx
dt
2
3 5
3 5
3 2
3
podstawiamy
liczymy pochodną stronami:
x2
(
)
t
dt
t
t dt
t
C
t
C
x
C
1
3
1
2
1
3
1
2
1
1
2
1
1
3
2
3
2
3
2
9
3 5
3
2
Uproszczenia możliwe w obliczeniach:
Uproszczenie 1.
Wyprowadzenie:
Rozwiążmy poniższy przykład:
1
2
1
2
1
2
2
x
dx
x
t
dx
dt
dx
dt
podstawiamy
liczymy pochodną stronami:
(
)
1
2
1
2
2
1
t
dt
x
C
ln|
|
Uproszczenie 1.
Końcowy wzór:
Jeżeli w mianowniku jest funkcja a w liczniku jest pochodna tej funkcji to całka jest równa:
ln| ( )|
f x
C
Przykład1:
1
2
1
1
2
2
2
1
1
2
2
2
1
1
2
2
1
x
dx
x
dx
x
dx
x
C
ln|
|
Przykład2:
1
2 5
1
2
2
2 5
1
2
2
2 5
1
2
2 5
x
dx
x
x
dx
x
x
dx
x
C
ln|
|
Uproszczenie 2.
Wyprowadzenie:
Rozwiążmy następujący przykład:
dx
x
x
2 5 6
Nie możemy zastosować poznanych wcześniej wzorów. Stosujemy metodę rozkładu na ułamki proste.
Sprowadzamy mianownik do postaci rozłożonej.

b
ac
2 4
25 24 1
1
x1
5 1
2
3
x1
5 1
2
2
dx
x
x
dx
dx
x x
x x
dx
dx
x
x
dx
2 5 6
1
2
3
2
(
)(
)
(
)(
)
Gdyby wyrażenie:
1
3
2
(
)(
)
x
x
można było przedstawić jako sumę dwu wyrażeń
A
x
B
x
(
) (
)
3
2
to można by było zastosować znane już wzory.
Zakładamy, że są takie wartości A i B które spełniają te wyrażenia. Dokonajmy więc przekształcenia takiej sumy
wyrażeń:
1
3
2
3
2
2
3
3
2
2
3
3
2
2
3
3
2
(
)(
)
(
) (
)
(
)
)
(
)(
)
(
)(
)
(
)
(
)(
)
x
x
A
x
B
x
A x
B( x
x
x
Ax
A Bx
B
x
x
x A B
A
B
x
x
czyli:
1
3
2
2
3
3
2
(
)(
)
(
)
(
)(
)
x
x
x A B
A
B
x
x
Jeżeli strony równania są równe przy jednakowych mianownikach, więc liczniki są też równe. Możemy więc
napisać:
1
2
3
x A B
A
B
(
)
Obliczamy wartość A i B dla których równanie będzie prawdziwe. Aby „x” nie miał wpływu na wyrażenie musi
być spełniony warunek :
x(A+B) = 0
będzie to zawsze spełnione gdy: A + B = 0
Przy takim warunku całe wyrażenie
1
2
3
x A B
A
B
(
)
będzie prawdziwe gdy 2A+3B = 1
Możemy napisać układ równań z których wyliczymy wartość A i B :
A B
A
B
0
2
3
1
| (-2)
2
2
0
2
3
1
0
1
1
A
A
B
B
B
A B
A
A
0
1 0
1
Całe nasze wyrażenie przybierze postać:
dx
x
x
dx
x
dx
x
dx
x
dx
x
dx
x
x
C
(
)(
)
ln|
| ln|
|
3
2
1
3
1
2
1
3
1
2
3
2
Uproszczenie 2.
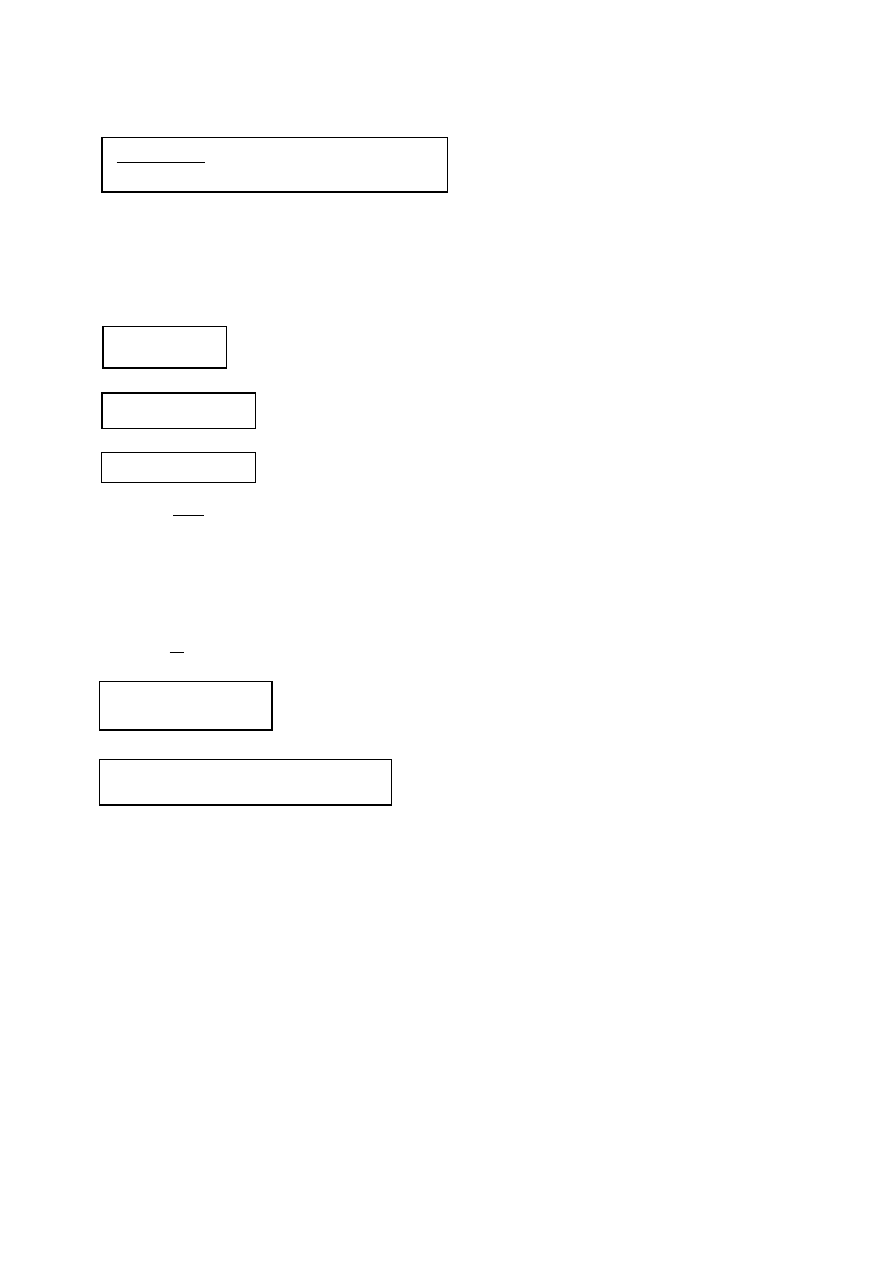
Końcowy wzór:
dx
x
x
dx
x
x
C
(
)(
)
ln|
| ln|
|
3
2
3
2
Temat:
Pojęcia całki - część dalsza
Wzory:
e xdx
e x
C
sin
cos
xdx
x C
cos
sin
xdx
x C
tgxdx
x
x
dx
sin
cos
cos
sin
sin
x
t
xdx
dt
xdx
dt
obl. pochodną z obu stron
dt
t
x C
tgxdx
x C
ln|cos |
ln|cos |
f x g x dx
g x F x
F x g x dx
( ) ( )
( ) ( )
( ) ( )
Przykład:
x e xdx
f x
e x
F x
e x
g x
x
g x
x
x e xdx
x e x
xe xdx
2
2
2
2
2
2
- mamy tu całkę z mnożenia
- mamy tu następną całkę z mnożenia, postępujemy podobnie
( )
( )
( )
( )
f x
e x
F x
e x
g x
x
g x
( )
( )
( )
( )
1
x ex
xe xdx
x ex
xex
exdx
x ex
xex
ex
C
2
2
2
2
2
2
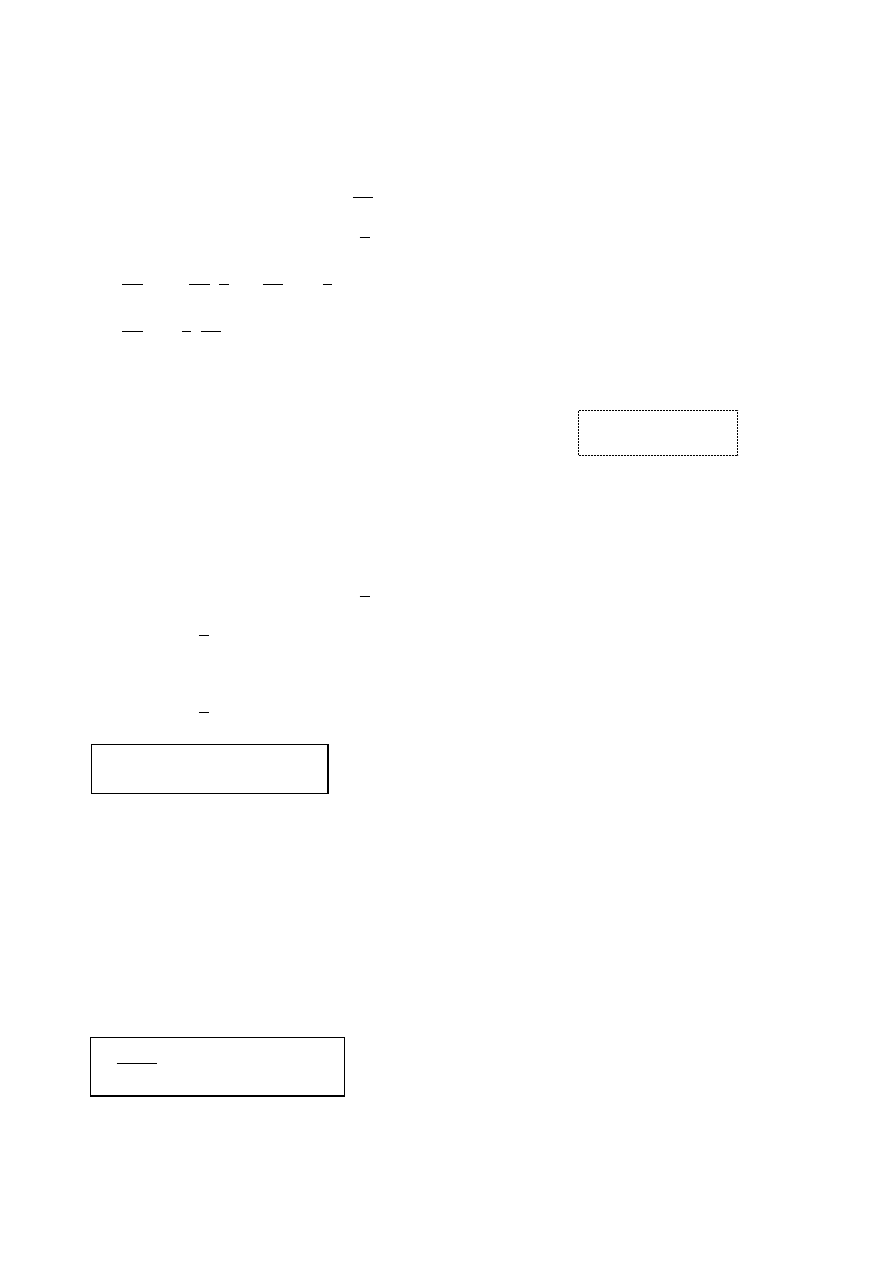
Przykład:
x
x dx
f x
x
F x
x
g x
x
g x
x
3
3
4
4
1
ln
( )
( )
( ) ln
( )
- mamy tu całkę z mnożenia
x
x
x
x
dx
x
x
x dx
x
x
x
C
4
4
4
4
1
4
4
1
4
3
4
4
1
4
4
4
ln
ln
ln
=
Przykład:
ln
ln
ln
x dx
x dx
x dx
- nie mamy wzoru na taką całkę, ale możemy ją zapisać jako:
=
1
mamy więc całkę z mnożenia :
Rozwiązujemy ją w znany sposób:
1
1
1
1
ln
ln
( )
( )
( ) ln
( )
x dx
x dx
f x
F x
x
g x
x
g x
x
x
x
x
x
dx
x
x
dx
x
x x C
ln
ln
ln
1
=
x
x
x
x
dx
x
x
dx
x dx
x
x x C
ln
ln
ln
ln
1
=
Przykład:
x
x dx
f x
x
F x
x
g x
x
g x
sin
( ) sin
( )
cos
( )
( )
- mamy tu całkę z mnożenia
1
x
x
x dx
x
x
xdx
x
x
x C
cos
( cos )
cos
cos
cos
sin
1
=
1
1
2
x
dx
arctgx C
Wzór do zapamiętania!

Co to jest arctg?
tg
arctg
300
3
3
3
3
300
tg
arctg
450
1
1 450
Przykład:
dx
x2 4
dx - wykorzystamy powyższy wzór:
dx
x
dx
x
dx
x
x
t
x= t
dx= dt
2
4
4
2
4
1
1
4
2
2
1
2
2
2
dx
dx
dx
| 2
1
4
2
2 1
1
2
2 1
1
2
2
dt
t
dt
t
arctg
x
C
dx
dx
Przykład:
dx
x
dx
x
dx
x
x
t
dx
dt
dt
dt
t
arctg
x
C
2 2 5
2 2
5
1
2
5
2
1
2
5
2
5
5
2
5
2
2 1
5
2
2
5
dx =
1
5
dx =
1
5
dx
dx =
1
5
dx
1
5
Matematyka.
Ćwiczenia - Rozwiązywanie całek..
Przykład:
3 2 5
7
1
3 2 5
7
1
1
x
x
x
x dx
x
xdx
dx
x
dx
x x dx
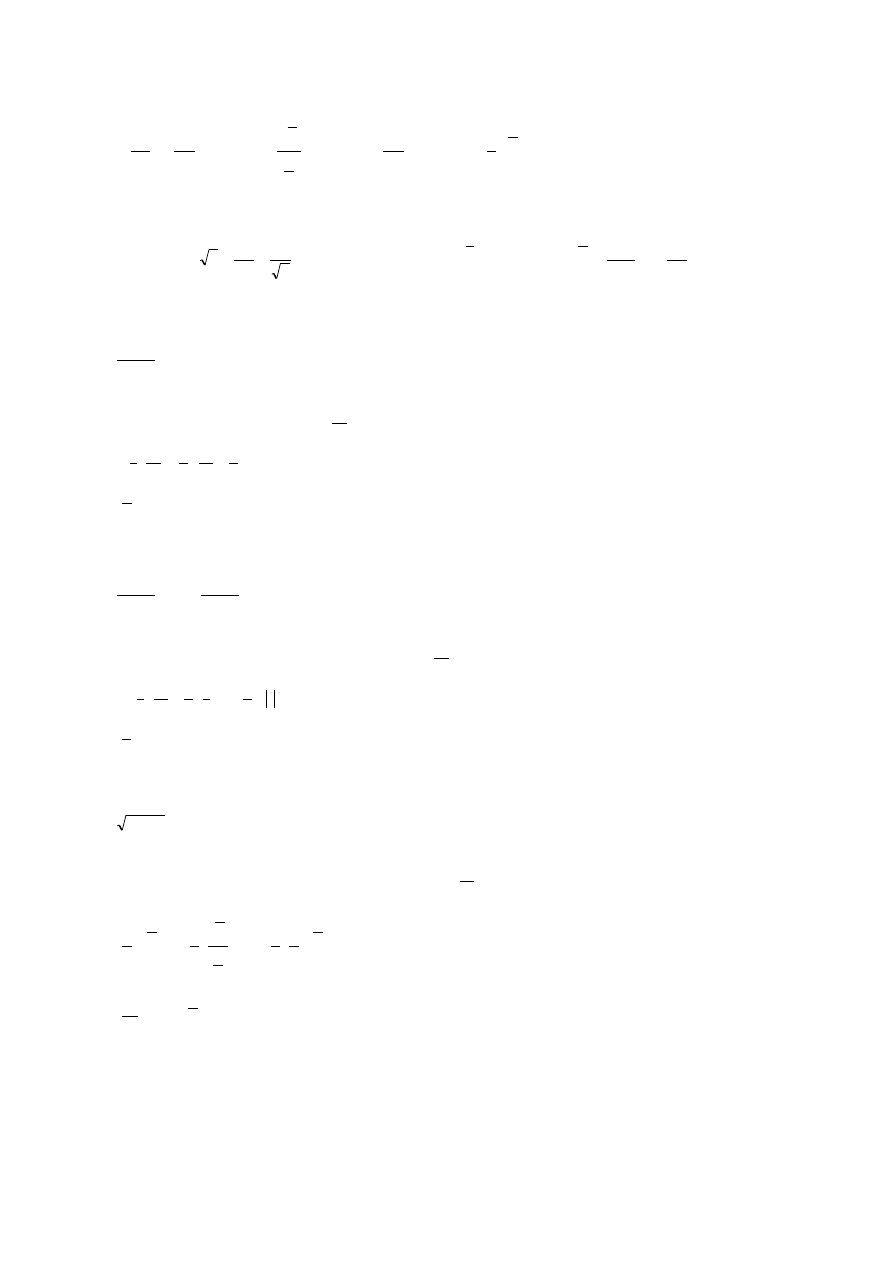
3
3
3
5
2
2
7
3
2
3
2
3 5
2
2
7
2
3
3
2
x
x
x
x
x
C
x
x
x
x
x
C
ln| |
ln| |
Przykład:
7 3 21
5
1
2
5
7 3
21
1
5
2 5
1
2
7 4
4
21
2
2
x
x
x
x
x
dx
x dx
xdx
x dx
x
x
x
x
C
Przykład:
1
2
1
2
1
2
2
1
2
1
2
1
2
1
2
2
1
x
dx
x
t
dx
dt
dx
dt
t
dt
dt
t
t C
x
C
.
(
)
ln| |
ln|
|
podstawiamy
liczymy pochodną stronami:
Przykład:
6
5
7
6
6
5
7
5
7
5
6
1
5
6
5
1
6
5
6
5
5
7
x
dx
x
dx
x
t
dx
dt
t
dt
t
dt
t
C
x
C
podstawiamy
liczymy pochodną stronami:
5dx = dt
ln
ln|
|
Przykład:
7
9
7
9
7
7
1
7
1
2
1
7
3
2
3
2
1
7
2
3
3
2
2
21
7
9
3
2
x
x
t
dx
dt
dx
dt
t dx
t
C
t
C
x
C
podstawiamy
liczymy pochodną stronami
Przykład:

1
2 3
9
1
2
1
3
9
1
2
3
9
3
3
x
dx
x
dx
x
t
dx
dt
dx
dt
podstawiamy
liczymy pochodną stronami:
1
2
1
1
2
3
1
2
1
2
1
2
1
3
1
2
1
1
2
1
1
2
1
3
1
2
1
2
1
2
1
3
2
1
1
2
1
3
3
9
1
2
t
dt
t
dt
t
C
t
C
t
C
x
C
Przykład:
1
1
2
(
)(
)
..............................
x
x
dx
??????????????????????????????????
1
3
1
1
1
3
1
2
(
)
(
)
x
dx
x
dx
1
3
1
1
3
2
ln|
|
ln|
|
x
x
C
Przykład:
2
1
2
6
5
36 20 16
4
1
6 4
2
1
2
6 4
2
5
2
1
2
6
5
2
1
1
5
2
1
1
5
2
1
5
2
5
1
1
5
x
x
x
dx
x
x
x
x
dx
x
x
x
dx
A x
x
dx
B
x
Ax
x
dx
B
x
Ax x
B x
x
x
dx
x
(
)(
)
( )
(
)
(
)
(
)
(
)
(
)
(
)
(
)(
)
A x
Ax Bx B
x
x
B
A B
A
A
dx
x
dx
dx
x
dx
2 2 10
1
5
2
5
1
4
1
1
4
2
1
4
2
1
4
5
2
1
4
1
5
(
)(
)
??????????????????
............................................
A
dodajemy stronami
_ _ _ _ _ _ _ _ _ _
B
-
1
4
x - 1
-
1
4
1
x - 1
= -
1
4
ln|
|
ln|
|
x
x
C
1 2
1
4
5

Przykład:
dx
x
x
x
x
x
x
A
x
B
x
C
x
A x
x
B( x
x
C x
x
x
x
x
(
)(
)(
)
(
)(
)(
)
(
)(
)
)(
)
(
)(
)
(
)(
)(
)
1
1
2
1
1
1
2
1
1
2
1
2
1
2
1
1
1
1
2
A(x
x x
B( x
x x
C x
(x
)(x
)(x
)
(Ax
Ax
A
Bx
Bx
B
Cx
C
(x
)(x
)(x
)
Ax
Ax
A Bx
Bx
B Cx
C
(x
)(x
)(x
)
x
A B C
x A B
A
B C
(x
)(x
)(x
)
2
2
2
2
2
2
2 1
1
1
2
2
3
2
2
2
2
1
1
2
2
3
2
2
2
2
1
1
2
2
3
2
2
1
1
2
)
)
(
)
) (
) (
)
(
)
(
)
Jeżeli ułamki:
1
1
1
2
2
3
2
2
1
1
2
(
)(
)(
)
(
)
(
)
x
x
x
x A B C
x A B
A
B C
(x
)(x
)(x
)
są równe to i liczniki tych ułamków są równe. Możemy więc napisać:
x A B C
x A B
A
B C
2
3
2
2
1
(
)
(
)
Obliczamy wartość A, B, C
A + B + C = 0
3A + B + 0 = 0
2A - 2B - C = 1
______________
Z drugiego równania obliczamy B:
B = -3A
A - 3A + C = 0
2A - 2(-3A) - C = 1
__________________
-2A +C = 0
8A - C = 1
_______________
6A = 1
A = 1/6
B = -3A = - 3(1/6) = - 1/2
B = - 1/2
A + B + C = 0
A + B = - C
1
6
1
2
1 3
6
C
C

1
3
1
3
C
C
A
1
6
1
2
1
3
B
C
Nasze równanie przybierze więc postać:
dx
x
x
x
x
dx
x
dx
x
dx
x
x
x
C
(
)(
)(
)
(
)
(
)
(
)
ln|
|
ln|
|
ln|
|
1
1
2
1
6
1
1
2
1
1
3
2
1
6
1
1
2
1
1
3
2
Przykład:
5
7
4 256
5
7
2 16 2 16
5
7
4
4
2 16
x
x
dx
x
x
x
dx
x
x
x
x
dx
A
x
B
x
Cx D
x
dx
A x
x
B x
x
Cx D x
x
x
x
x
dx
4
4
2 16
4
2 16
4
2 16
4
4
4
4
2 16
(
)(
)
(
)
4
2 16
64
3 4 2 16
64
3 16
2 16
4
4
2 16
Ax
A
A Bx
Bx
Bx
B Cx
Cx Cx
D
x
x
x
dx
x A B C
x
A
B D
x
A
B
C
A
B
D
x
x
x
dx
3
2 4
4
16
16
16
64
64
16
4
4
2 16
(
)
(
)
(
)
Aby obliczyć wartości A, B, C, D, piszemy układy równań:
A B C
A
B D
A
B
C
A
B
D
0
4
4
0
16
16
16
5
64
64
16
7
16
16
Dodajemy pierwsze i trzecie równanie :
16
16
16
0
16
16
16
5
32
32
5
A
B
C
A
B
C
A
B
Dodajemy drugie i czwarte równanie :
64
64
16
0
64
64
16
7
128
128
7
A
B
D
A
B
D
A
B
W wyniku tych działań otrzymujemy dwa równania:

32
32
5
128
128
7
128
128
20
128
128
7
256
13
13
256
A
B
A
B
A
B
A
B
A
A
4
Z równania 32
32
5
A
B
obliczamy B
32
13
256
32
5
13
8
32
5
5
13
8
32
40 13
8
32
27
8 32
27
256
27
256
B
B
B
B
Z równania A + B + C = 0 obliczamy C
C
A B
C
13
256
27
256
13 27
276
40
256
40
256
Z równania 4A - 4B + D = 0 obliczamy D
4
13
256
4
27
256
0
13
64
27
64
0
13
64
27
64
14
64
7
32
7
32
D
D
D
D
Podstawiamy obliczone wartości A, B, C, D do równania:
A
x
B
x
Cx
D
x
dx
x
dx
x
dx
x
x
dx
x
dx
x
dx
x
x
dx
4
4
2
16
13
256
4
27
256
4
40
256
7
32
2
16
13
256
1
4
27
256
1
4
40
256
7
32
2
16
13
256
4
27
256
4
40
256
7
32
2
16
ln|
|
ln|
|
x
x
x
x
dx
a
b
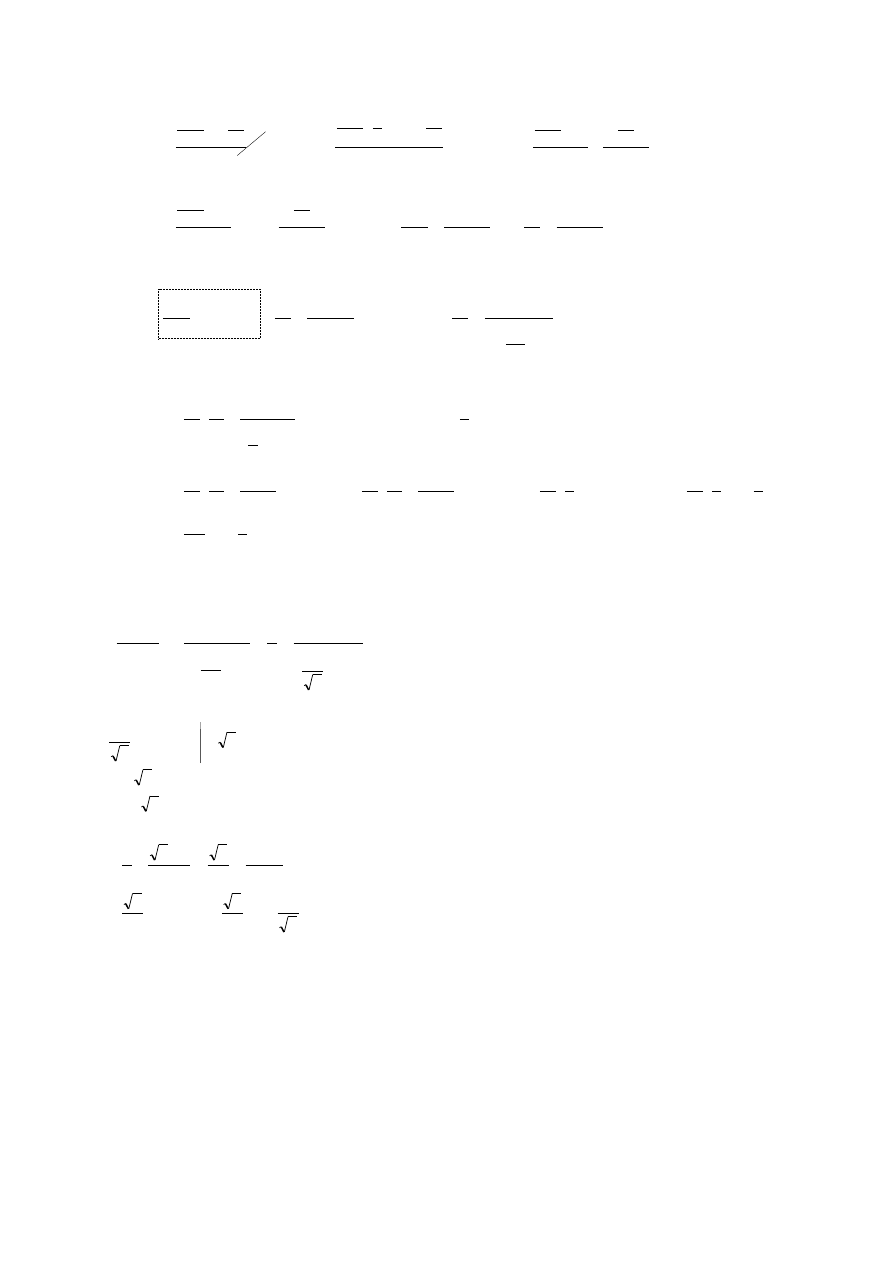
a b
x
x
dx a b
x
x
dx a b
x
x
x
dx
a b
x
x
dx
x
40
256
7
32
2 16
40
256
1
2
2
7
32
2 16
40
512
2
2 16
7
32
2 16
40
512
2
2 16
7
32
2 16
dx a b
x
x
dx
x
dx
40
512
2
2 16
7
32
1
2 16
a b
x
x
dx a b c
x
dx
a b c
dx
x
x
t x
t dx
dt
a b c
dt
t
40
512
2
16
7
32
1
2
16
7
32
1
16
2
16
1
7
32
1
16
4
2
1
4
4
4
7
32
1
16
4
2
1
ln|
|
podstawiamy
a b c
dt
t
a b c
arctgt a b c
arctg
x
a b c
arctg
x
7
32
4
16
2
1
7
32
1
4
7
32
1
4
4
7
128
4
Przykład:
dx
x
dx
x
dx
x
x
t
x
t
dx
dt
dt
t
dt
t
arctgt C
arctg
x
C
2
7
7
2
7
1
1
7
7
2
1
7
7
7
7
1
7
7
2 1
7
7
2 1
7
7
7
7
7
c
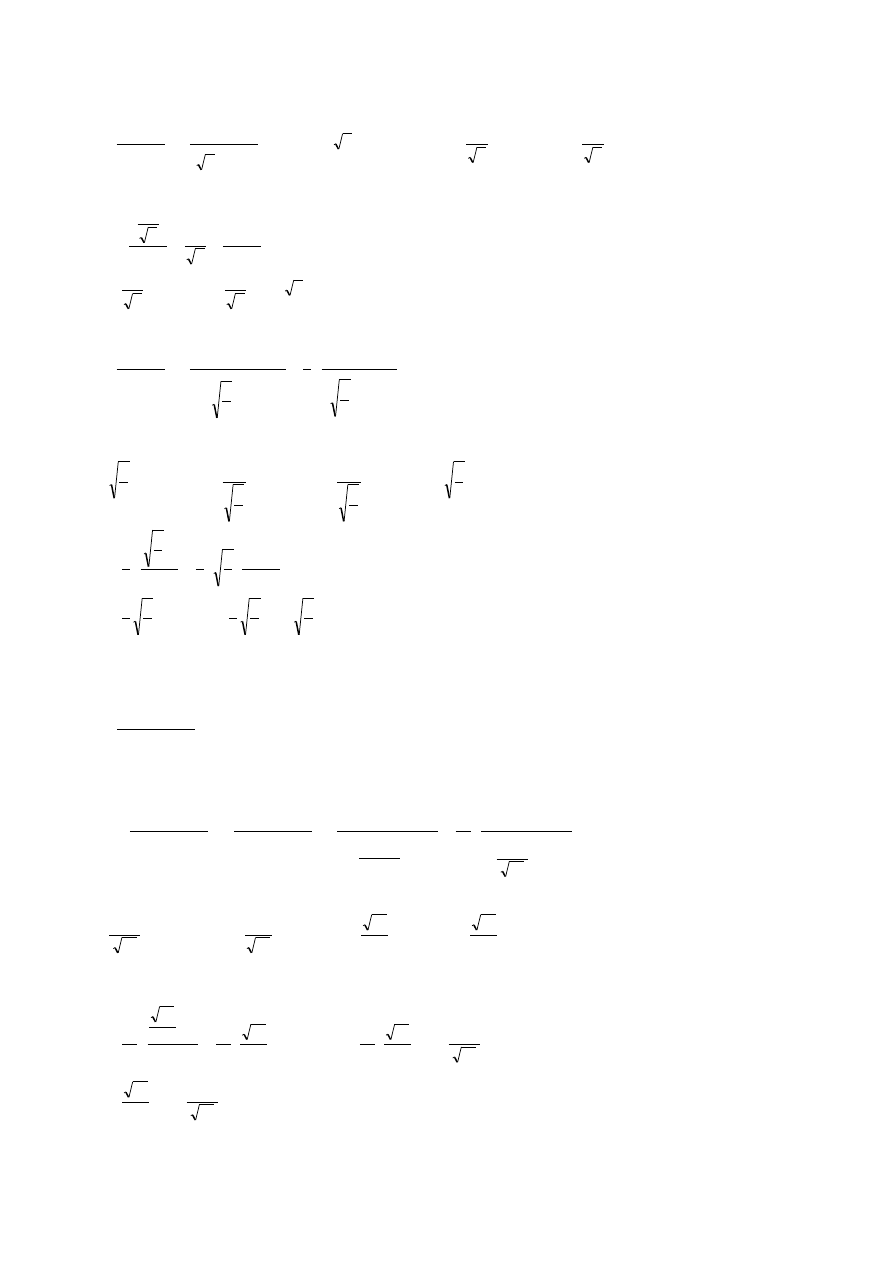
Przykład:
dx
x
dx
x
x
t
x
t
dx
dt
dt
t
dt
t
arctgt C
arctg
x
C
2 2 1
2
2
1
2
2
2
2
2 1
1
2
2 1
1
2
1
2
2
|
|
Przykład:
dx
x
dx
x
dx
x
x
t x
t
dt
dt
dt
t
dt
t
arctgt C
arctg
x
C
3 2 5
5
3
5
2
1
1
5
3
5
2
1
3
5
3
5
3
5
5
3
1
5
5
3
2 1
1
5
5
3
2 1
1
5
5
3
1
5
5
3
5
3
dx
dx
|
|
Przykład:
dx
x
x
a
ab b
x
x
x
x
x
x
x
dx
x
x
dx
x
dx
x
dx
x
x
t
x
t
x
2 6 24
2
2 2
2
2 6 24
2 6 9 15
2 6 9 15
3 2 15
2 6 24
3 2 15
15
3
15
2
1
1
15
3
15
2
1
3
15
3
15
3
15
15
a + b
t
x
dt
dt
t
arctg t
C
arctg
x
C
arctg
x
C
d
+
15
15
1
15
15
15
2 1
1
15
15
15
1
15
15
15
3
15
15
15
3
15
.........................
| |
|
|
|
|

Temat:
cd całki.
Powtórka:
1
1
2
x
dx
arctgx C
Przykład:
dx
x
x
2 3 7
9 28
19
delta ujemna, do rozwiązania należy wykorzystać inną metodę.
Wykorzystać można wzór:
a b
a
ab b
2
2 2
2
dx
x
x
dx
x
x
dx
x
x
dx
dx
x
dx
x
x
t
x
2
3
7
2
2
3
2
9
4
9
4
7
3
2
2
19
4
4
19
3
2
2
19
4
19
4
4
19
3
2
2
19
4
1
4
19
3
2
19
2
2
1
3
2
19
2
3
2
19
2
=
podstawiamy za
t
dx
dt
19
2
4
19
19
2
2 1
4
19
19
2
2 1
2 19
19
2
3
2
19
2
dt
t
dt
t
arctg
x
C
Przykład:
5
7
2
7
20
x
x
x
dx
Przypomnienie wzoru:
f x
f x
f x
C
( )
( )
ln| ( )|
pochodna z mianownika naszego przykładu była by:
x
x
x
2 7 20
2
7
licznik z naszego przykładu jest : 5
7
x
aby doprowadzić go do postaci:
2
7
x
należy dokonać przekształcenia:
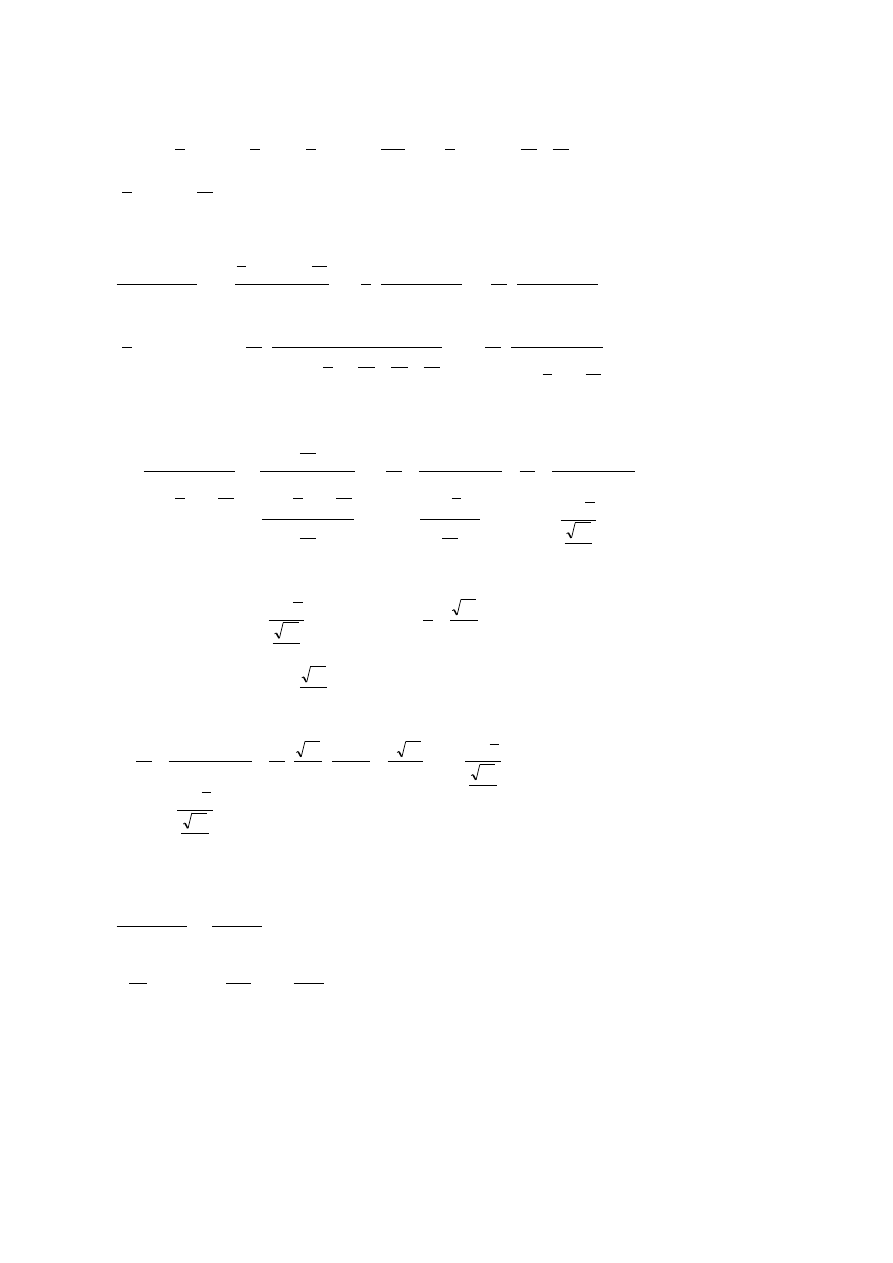
5
7 5
1
2
2
7
7
2
7
5
2
2
7
5 7
2
7
5
2
2
7
35
2
14
2
5
2
2
7
21
2
x
x
x
x
x
x
Wracamy do naszej całki:
5
7
2
7
20
5
2
2
7
21
2
2
7
20
5
2
2
7
2
7
20
21
2
2
7
20
x
x
x
dx
x
x
x
dx
x
x
x
dx
dx
x
x
5
2
2 7 20 21
2
2 2 7
2
49
4
49
4
80
4
21
2
7
2
2
31
4
ln|
|
x
x
K
dx
x
x
B
K
dx
x
B
B
dx
x
x
dx
dx
x
dx
x
7
2
2
31
4
4
31
7
2
2
31
4
31
4
4
31
7
2
2
31
4
1
4
31
7
2
31
2
2
1
x
t
x
t
dx
dt
7
2
31
2
7
2
31
2
31
2
| całkujemy stronami
B
dx
x
dt
t
arctg
x
C
4
31
7
2
31
2
2
1
4
31
31
2
2 1
2 31
31
7
2
31
2
|
|
Przykład:
dx
x
x
dx
x
x
t
dx
dt
2
2
1
1 2
1
dt
t
t
dt
t
C
x
C
2
2
1
1
1
1
Temat2: Całki oznaczone.
Wszystkie poznane do tej pory całki to całki nieoznaczone.
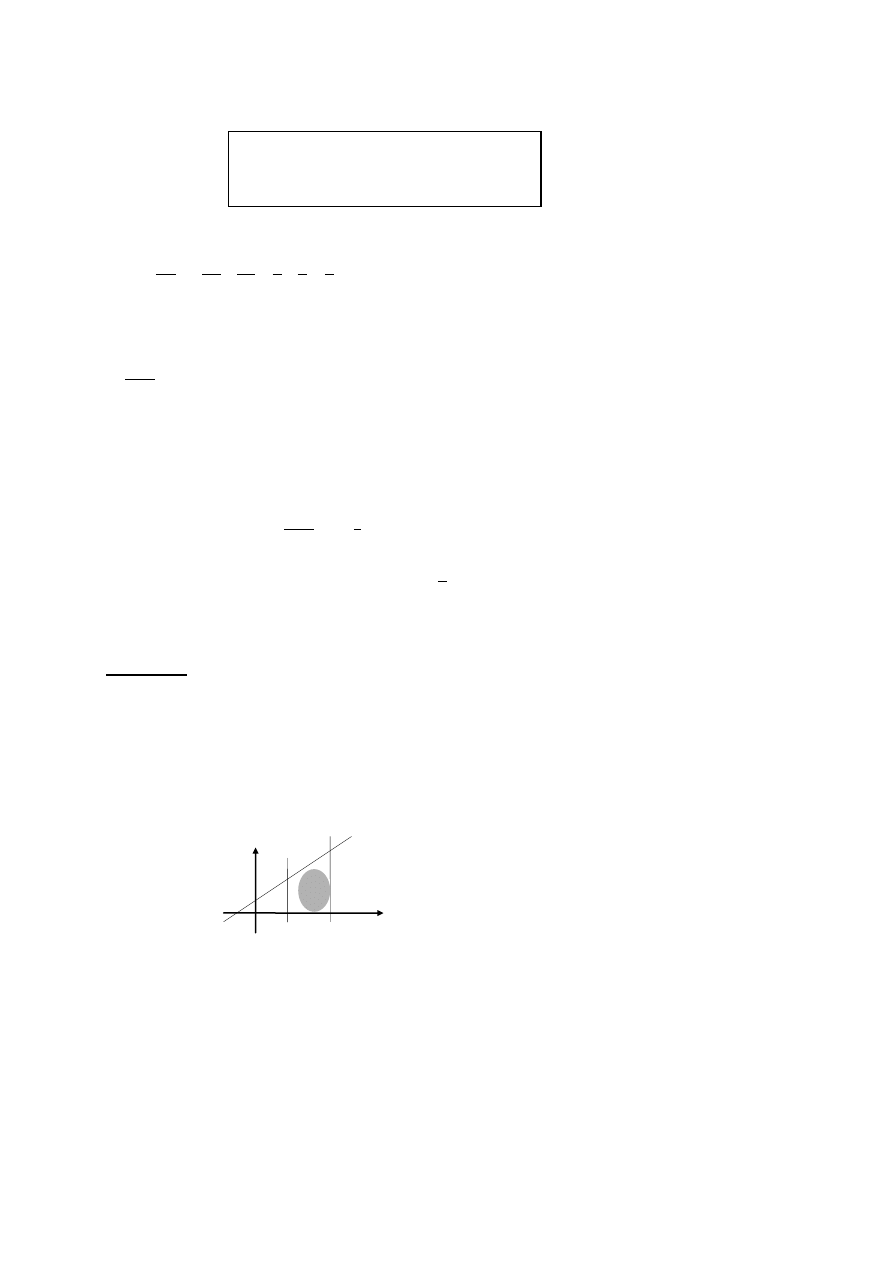
Całka oznaczona to całka dla której określa się przedział. Musi być różniczkowalna.
f x dx
a
b
F b
F a
( )
( )
( )
Przykład:
xdx
x
1
3
2
2 1
3
32
2
12
2
9
2
1
2
8
2
4
|
Przykład:
1
1
5
10
x
dx
podstawiamy:
x
t
dx
dt
1
dla
x
x
5
10
t
t
( )
(
)
5
4
10
9
Przy metodzie podstawiania trzeba zmienić granice całkowania bo zmienia się zmienna.
Wracamy do przykładu:
1
1
5
10
1
4
9
4
9
9
4
9
4
x
dx
t
dt
ln
|
ln
ln
ln
| t |
Twierdzenia:
f x dx
f f dx
a
c
f f dx
c
b
a
b
c
a b
( )
( )
( )
( , )
f x dx
a
a
( )
0
f x
a b
( )
( , )
0
P
a b
| |
( )
P
f x dx
a
b
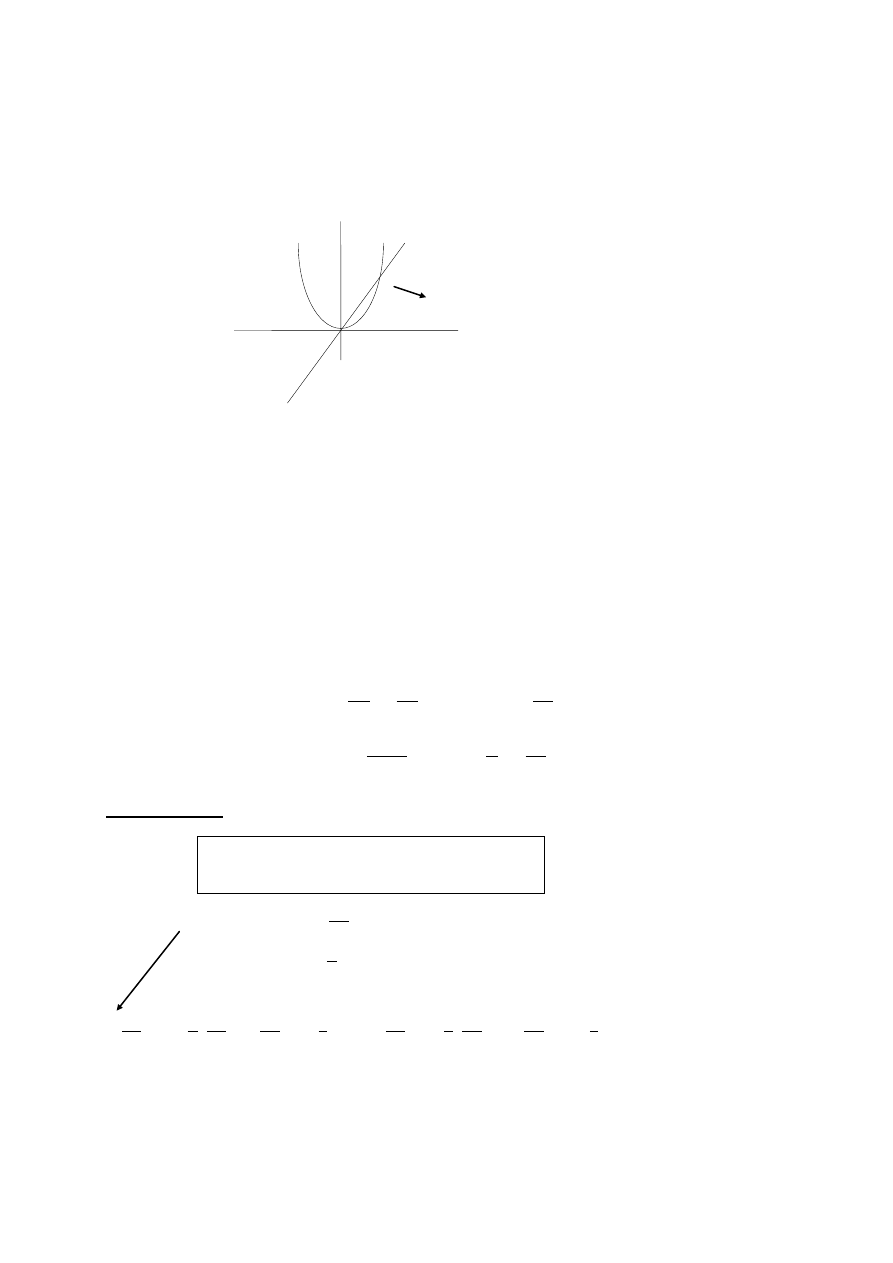
Przykład:
Mamy dwie funkcje:
f x
x
g x
x
( )
( )
2
4
x
2
4x
Obliczyć pole zawarte między jednym a drugim wykresem w obszarze między przecięciami się tych wykresów.
Wykresy przecinają się dla x który jest równy:
x
x
2
4
x
x
x x
x
x
2
4
0
4
0
0
4
(
)
Pole będzie równe różnicy :
Pole
xdx
x dx
x
x
4
4
2
3
4 8 0
64
3
0
32
32 2
3
32 1
2
3
32
3
2
0
4
0
4
2
0
4
3
0
4
|
|
(
)
25.04.98 ćwiczenia
Przykład:
f x g x
g x F x
F x g x dx C
( ) ( )
( )
( )
( )
( )
x
xdx
f
x
F
x
g
x
g
x
x
x
x
x
dx
x
x
x dx
x
x
x
C
x
x
C
2
2
3
3
1
3
3
1
3
3
3
3
1
3
2
3
3
1
3
3
3
3
3
1
3
ln
ln
ln
ln
ln
ln
Miejsce przecięcia się obu wykresów

Przykład:
x
xdx
f
x
F
x
g
x
g
x
x
xdx
x
x
x C
sin
sin
cos
cos
cos
cos
sin
1
Przykład:
1
1
1
1
1
x
x
dx
x
t
x
dx
dt
dt
x
x
dx
dx
x
x
dx
x t
dt
t
dt
t
t C
x
C
ln
ln
ln
ln
ln
ln(ln )
dx
x
Przykład:
1
2
2
2
1
1
1
1
x
x
dx
x
t
dx
dx
dt
t
t
dt
t
C
t
C
x
C
ln
ln
ln
1
x
Przykład:
dx
x
x
x
x
A
x
B
x
A x
B( x
x
x
Ax
A Bx
x
x
x A B
A
B
x
x
x
t
x
z
x
dt
(
)(
)
(
)(
)
(
) (
)
(
)
)
(
)(
)
(
)(
)
(
)
(
)(
)
5
1
1
5
1
5
1
1
5
5
1
5
5
1
5
5
1
5
1
d
dx
dz
A B
A
B
0
5
1
(-1)
A B
A
B
0
5
1
6
1
1
6
B
B
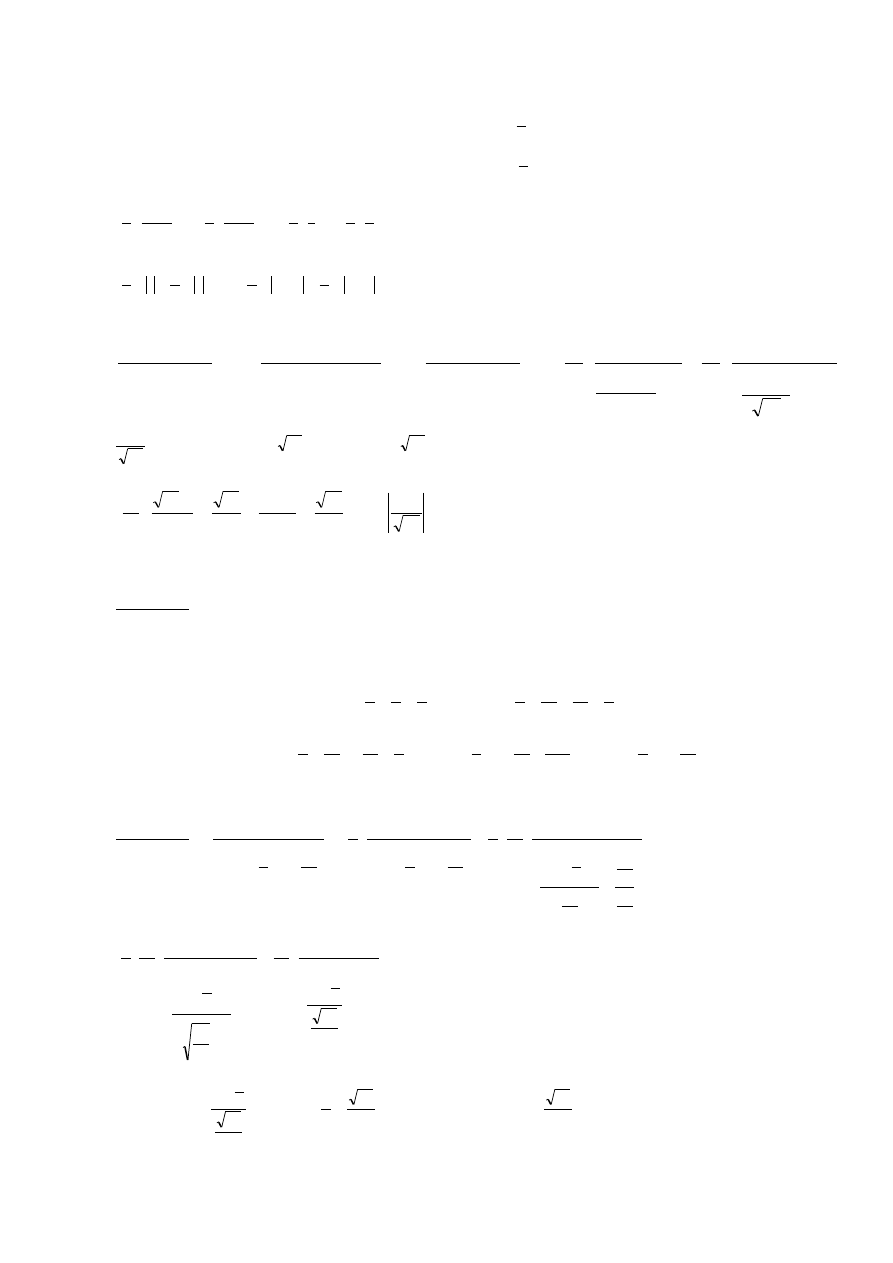
A
A
1
6
0
1
6
1
6
1
5
1
6
1
1
1
6
1
1
6
1
x
dx
x
dx
t
dt
z
dz
1
6
1
6
1
6
5
1
6
1
ln
ln
ln
ln
t
z
C
x
x
C
Przykład:
1
2
11
1
2
1 10
1
1
10
1
10
1
10
1
1
10
1
10
1
2
2
2
2
2
x
x
dx
x
x
dx
x
dx
dx
x
dx
x
x
t
x
t
dx
dt
1
10
1
10
10
1
10
10
1
10
10
1
10
10
1
10
2
2
dt
t
dt
t
arctg
x
C
Przykład:
dx
x
x
x
x
x
x
x
x
2 2
7
2 2
7 2 2
2
2
2
7
2
2 2 2
4
1
16
1
16
7
2
wyciągnijmy przed mianownik 2 i przedstawmy go w postaci:
2
2 2
4
1
16
1
16
7
2
2
1
4
2
1
16
8 7
16
2
1
4
2
55
16
x
x
x
x
Podstawiamy do naszego przykładu:
dx
x
x
2 2
7
2
55
16
1
2
2
55
16
1
2
16
55
2
55
16
55
16
55
16
dx
2 x +
1
4
dx
x +
1
4
dx
x +
1
4
1
2
16
55
2
55
16
2
1
8
55
55
4
2
1
55
4
55
4
55
4
dx
x +
1
4
x +
1
4
podstawiamy:
x +
1
4
x +
1
4
różniczkujemy:
dx
t
t
dx
dt
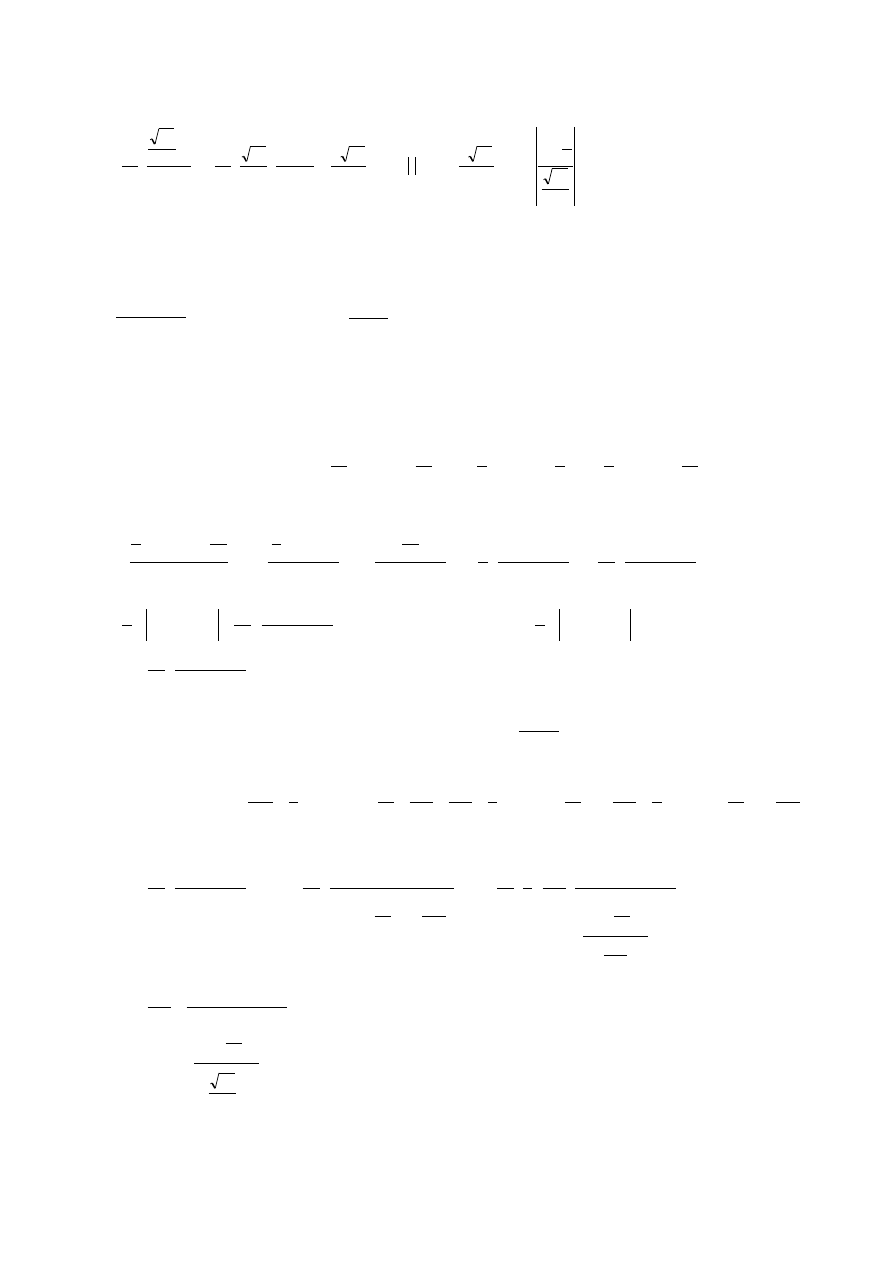
8
55
55
4
2 1
8
55
55
4
2 1
2 55
55
2 55
55
1
4
55
4
dt
t
dt
t
arctg t
C
arctg
x
C
Przykład:
3
7
6 2
4
x
x
x
zastosujemy wzór
f x
f x
f x
C
( )
( )
ln| ( )|
Obliczamy pochodną mianownika:
6 2
4
12
1
3
7 3
1
12
12
1
1
12
7
1
4
12
1
1
4
7
1
4
12
1
27
4
x
x
x
x
x
x
x
aby licznik doprowadzić do takiej wartości,
należy dokonać w nim następujących przekształceń:
Podstawiamy obliczoną wartość w miejsce licznika:
1
4
12
1
27
4
6 2
4
1
4
12
1
6 2
4
27
4
6 2
4
1
4
12
1
6 2
4
27
4 6 2
4
x
x
x
dx
x
x
x
dx
x
x
dx
x
x
x
dx
dx
x
x
dx
1
4
6 2
4
27
4 6 2
4
1
4
6 2
4
ln
ln
x
x
dx
x
x
dx
x
x
oznaczmy A =
A
dx
x
x
dx
27
4 6 2
4
Rozpisujemy mianownik aby można było zastosować wzór:
1
1
2
x
dx
arctgx C
6 2
4
6 2 2
2 6
4
6
6 2 2
12
1
144
1
144
2
3
6
1
12
2
1
144
2
3
6
1
12
2
95
144
x
x
x
x
x
x
x
x
Wracamy do obliczeń całki:
A
dx
x
x
dx
A
dx
x
A
dx
x
A
dx
x
27
4 6 2
4
27
4
6
1
12
2
95
144
27
4
1
6
144
95
1
12
2
95
144
1
162
95
1
12
2
95
12
2
1
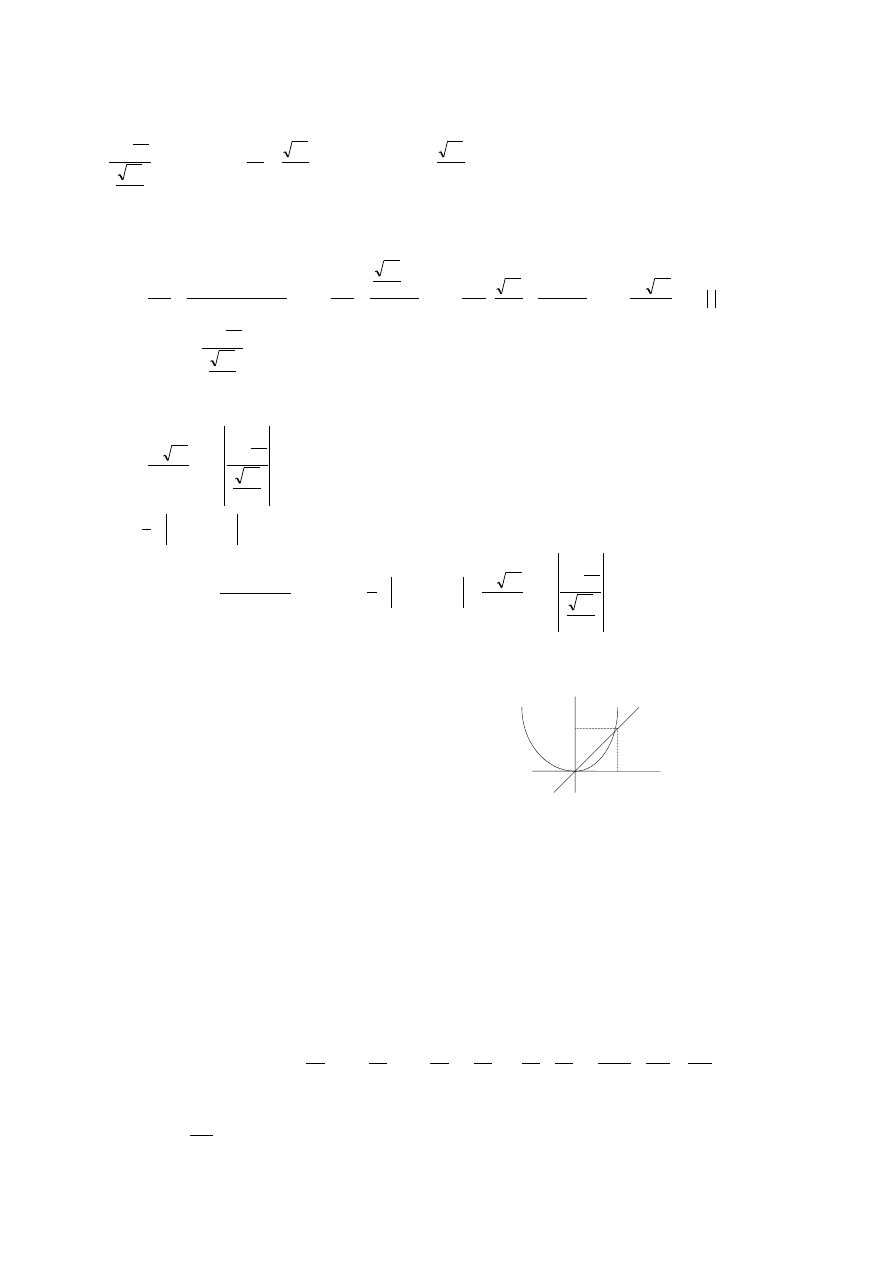
Podstawiamy:
x
t
x
t
dx
dt
1
12
95
12
1
12
95
12
95
12
Wstawiamy to do przykładu:
A
dx
x
A
dt
t
A
dt
t
A
arctg t
C
A
arctg
x
C
162
95
1
12
95
12
2
1
162
95
95
12
2 1
162
95
95
12
2 1
81 95
6 95
81 95
6 95
1
12
95
12
A =
1
4
6 2
4
ln x
x
Rozwiązaniem
3
7
6 2
4
x
x
x
jest: =
1
4
6 2
4
ln x
x
81 95
6 95
1
12
95
12
arctg
x
C
Przykład:
Obliczyć pole między wykresami funkcji: y
x
2
y
x
7
7
Obliczamy miejsca przecięcia się tych wykresów (wspólne wartości X dla obu wykresów):
x
x
x
x
x x
2
7
2 7
0
7
0
(
)
Dla
x1 0
oraz
x2 7
wykresy tych funkcji przecinają się.
Pole między wykresami tych funkcji będzie równe różnicy całek oznaczonych tych funkcji dla przedziału 0,7
P
xdx
x dx
x
x
P
7
0
7
2
0
7
7
2
2 0
7
3
3 0
7
7
72
2
7
02
2
73
3
03
3
7 49
2
343
3
343
6
343
6
|
|

Przykład:
Obliczyć pole między wykresami funkcji: y
x
y
x
2
1/4
Obliczamy miejsca przecięcia się tych wykresów (wspólne wartości X dla obu wykresów):
x
x
x
x
x
x
x x
2
4 2
4 2
0
4
1
0
(
)
Dla wartości:
wykresy przecinają się.
x
x
1
0
2
1
4
Pole między wykresami tych funkcji będzie równe różnicy całek oznaczonych tych funkcji dla przedziału 0
1
4
,
P
xdx
xdx
x dx
xdx
x
0
1
4
2
0
1
4
1
2
0
1
4
2
0
1
4
2
3
2
3
0
1
4
0
1
4
|
|
2
x2
2
2
3
1
64
1
16
2
3
1
8
1
16
1
12
1
16
4 3
48
1
48
1
48
P

Wzory na obliczanie całek:
1.
xndx
xn
n
C
n
1
1
1
dla
gdy x = -1 to
1
x
dx
x C
ln| |
2.
Cf x dx
C f x dx
( )
( )
3.
f x
g x dx
f x dx
g x dx
( )
( )
( )
( )
4.
1
1
1
x
dx
x
dx C
ln(
)
5.
Jeżeli w mianowniku jest funkcja a w liczniku jest pochodna tej funkcji to całka jest równa:
f x
f x
f x
C
( )
( )
ln| ( )|
6.
1
3
2
3
2
(
)(
)
ln|
| ln|
|
x
x
dx
x
x
C
7.
e xdx
e x
C
8.
sin
cos
xdx
x C
9.
cos
sin
xdx
x C
10.
tgxdx
x C
ln|cos |
11.
f x g x dx
g x F x
F x g x dx
( ) ( )
( ) ( )
( ) ( )
12.
ln
ln
x dx
x x x C
13.
1
2 1
x
dx
arctgx C
14.
f x dx
a
b
F b
F a
( )
( )
( )
15.
Twierdzenia:
1.
f x dx
f f dx
a
c
f f dx
c
b
a
b
c
a b
( )
( )
( )
( , )
2.
f x dx
a
a
( )
0
Wyszukiwarka
Podobne podstrony:
Matematyka (24 strony id 282823 Nieznany
Matematyka (24 strony)
Matematyka (24 strony)
matma Matematyka (24 strony)
Matematyka (24 strony) calki, pojecia calki
Magazyn - 24 strony tekstu, ABC Magazynu
Popyt a wielkość produkcji w gospodarce (24 strony) HJYY5KED42JOXKQMW7RSXZ5RJ4R5YGVETSQ6P3Q
od Elwiry, Spółka Z o.o. (24 strony), VII
Makroekonomia (24 strony) SQIWIV4IA7FNJZZWXNCAU4N3SKBRJXMEXAKQATA
Teorie?ektywności kierowania ludźmi (24 strony) LQBBVQDP2GQABUFQPAGYZYSCHG7J5YDKACUPZ3Q
Organizacja i zarządzanie (24 strony) 3U3GX2BGVCRNILB33XHMZ32ZXUUGAJNZ5K5INGQ
GPW (24 strony) D4PLANM73IV747E6YMELKV6SJZY4SXNXI4AGBCQ
Logistyka - projekt (24 strony)
więcej podobnych podstron