Barbara Wanik

Zakład Fizyki, Akademia Rolnicza

Kraków, 2000

Do u ytku wewn trznego

wiczenie 23

A. Wyznaczanie współczynnika lepko ci dynamicznej cieczy newtonowskiej metod

Poiseuille'a

B. Wyznaczanie współczynnika lepko ci dynamicznej cieczy newtonowskiej metod

wzgl dn Arrheniusa

SPIS TRE CI

I. CZ

TEORETYCZNA.................................................................................................................................. 2

1.

W

PROWADZENIE DO REOLOGII

,

MIKRO

-

I MAKROREOLOGIA

.

O

DKSZTAŁCENIA OBJ TO CI I POSTACI

..................... 2

1.1. cinanie proste, napr enie styczne............................................................................................................... 3

1.2. Przepływ lepki, poj cie płynu (równie cieczy) newtonowskiego. Krzywa płyni cia................................... 5

2.

B

URZLIWO

W PRZEPŁYWACH

.

L

ICZBA

R

EYNOLDSA

. .......................................................................................... 8

3.

W

ISKOZYMETRIA

.

R

ODZAJE PRZEPŁYWÓW CIECZY LEPKIEJ

................................................................................... 8

4.

P

ODSTAWY WISKOZYMETRII KAPILARNEJ CIECZY

................................................................................................ 11

4.1. Przepływ laminarny płynu newtonowskiego przez kapilary. Prawo Hagena-Poiseuille'a............................ 11

5.

E

FEKTY CIEPLNE PODCZAS PŁYNI CIA

................................................................................................................. 15

6.

P

ODSTAWY TEORETYCZNE REOMETRII ROTACYJNEJ

............................................................................................ 15

7.

W

PŁYW TEMPERATURY NA LEPKO

CIECZY

....................................................................................................... 15

II. CEL WICZENIA .......................................................................................................................................... 16

III. WYKONANIE WICZENIA....................................................................................................................... 16
III.A.

W

YZNACZANIE WSPÓŁCZYNNIKA LEPKO CI DYNAMICZNEJ CIECZY NEWTONOWSKIEJ METOD

P

OISEUILLE

'

A

16

III.A.1. Zasada pomiaru...................................................................................................................................... 16

III.A.2. Wykonanie wiczenia ............................................................................................................................ 18

III.A.3. Opracowanie wyników, dyskusja bł dów .............................................................................................. 19

III.B.

W

YZNACZANIE WSPÓŁCZYNNIKA LEPKO CI DYNAMICZNEJ CIECZY NEWTONOWSKIEJ METOD WZGL DN

A

RRHENIUSA

........................................................................................................................................................... 20

III.B.1. Zasada pomiaru:..................................................................................................................................... 20

III.B.2. Wykonanie wiczenia ............................................................................................................................ 21

III.B.3. Opracowanie wyników, dyskusja bł dów .............................................................................................. 22

IV. LITERATURA ............................................................................................................................................... 23

V. INDEKS............................................................................................................................................................ 23

2

Spis rysunków
Ryc. 1.1. cinanie proste - jest to rodzaj odkształcenia postaci ciała ...................................... 3

Ryc. 1.2. lizganie si warstewek ciała odkształcanego pod działaniem siły stycznej do górnej

powierzchni ciała .................................................................................................. 4

Ryc. 1.3. Rozkład wektorów pr dko ci warstw ciała odkształcanego sił F styczn do górnej

powierzchni .......................................................................................................... 5

Ryc. 1.4. Krzywa płyni cia płynu newtonowskiego ................................................................ 6

Ryc. 3.1. Przepływ Poiseuille'a .............................................................................................. 8

Ryc. 3.2. Inne rodzaje przepływów

a. Przepływ Couette'a

b. Przepływ skr tny mi dzy równoległymi płytkami

c. Przepływ skr tny mi dzy sto kiem i płytk ......................................................... 8

Ryc. 4.1. Rozkład napr e stycznych i profil pr dko ci cieczy newtonowskiej (przepływ

laminarny, przekrój kapilary jest kołowy),

τ

w

- napr enie styczne przy ciance

kapilary ................................................................................................................. 9

Ryc. 4.2. Walec cieczy o promieniu r i długo ci L oraz siły działaj ce na ten walec:

p

1

πr

2

, -p

2

πr

2

, -2

πrLτ ............................................................................................ 10

Ryc. III.A. Schemat aparatury do wyznaczania współczynnika lepko ci dynamicznej cieczy

metod Poiseuille'a ............................................................................................. 13

Ryc. III.A.1. Butla Mariotte'a ............................................................................................... 13

Ryc. III.A.2. Katetometr ...................................................................................................... 13

Ryc. III.B.1. Schemat aparatury z wiskozymetrem kapilarnym do wyznaczania wzgl dnego

współczynnika lepko ci dynamicznej metod wzgl dn Arrheniusa ..................

16

I. CZ

TEORETYCZNA

1. Wprowadzenie do reologii, mikro- i makroreologia. Odkształcenia obj to ci i postaci

Reologia (od gr. rheo - płyn oraz logos - słowo, nauka), której elementy zostan tu

przedstawione, zajmuje si odkształceniami i przepływem materii, przy czym przepływ jest
traktowany jako jedna z postaci odkształcenia. Odkształcenia s skutkiem działania sił
zewn trznych, st d reologia jako nauka jest dziedzin fizyki.

Reologi dzielimy na mikroreologi i makroreologi . Mikroreologia ujmuje zwi zki

mi dzy struktur ciał na poziomie cz steczkowym a wła ciwo ciami reologicznymi.
Makroreologia zaniedbuje struktur cz steczkow ciał traktuj c je jako o rodki ci głe, które
mo na scharakteryzowa przy pomocy reologicznych wielko ci fizycznych. Odkształcenia
dzielimy na:
- odkształcenia spr yste. Odkształcenie spr yste jest to odkształcenie, które jest samorzutnie

odwracalne, tzn. znika natychmiast i całkowicie po zaprzestaniu działania siły;

3

- odkształcenia plastyczne. Odkształcenie plastyczne jest to odkształcenie nieodwracalne.

Energia zu yta na odkształcenie zamienia si na ciepło;

- przepływy.

Przepływ w reologii jest to odkształcenie nieodwracalne, którego stopie ro nie w czasie i

które zachodzi, jak ka de odkształcenie, pod działaniem okre lonej siły. Przepływ jest
zjawiskiem wymuszonym - energia przepływu ulega zamianie na ciepło i rozprasza si
(mówimy, e ulega dysypacji).

W ród odkształce wyró nia si odkształcenia obj to ciowe (lub obj to ci) i postaciowe

(lub postaci).

Efektem odkształcenia obj to ciowego jest zmiana g sto ci ciała (nast puje bowiem

zmiana obj to ci przy stałej masie), której przyczyn jest działaj ce izotropowo ci nienie.
Je eli obj to ciała odkształcanego zmniejsza si - nast puje kompresja, przy zwi kszaniu
obj to ci - mówi si o dylatancji.

Efektem odkształcenia postaciowego jest zmiana kształtu ciała bez zmiany jego obj to ci

(g sto ciała nie zmienia si ).
Wi cej szczegółów na temat odkształce ciał mo na znale w pi miennictwie (3,4,6).
1.1. cinanie proste, napr enie styczne

cinanie proste jest to rodzaj odkształcenia postaci. Ten rodzaj odkształcenia tłumaczymy

wprowadzaj c płytkowy (warstwowy inaczej laminarny) model ciała odkształcanego, jak na
ryc. 1.1.

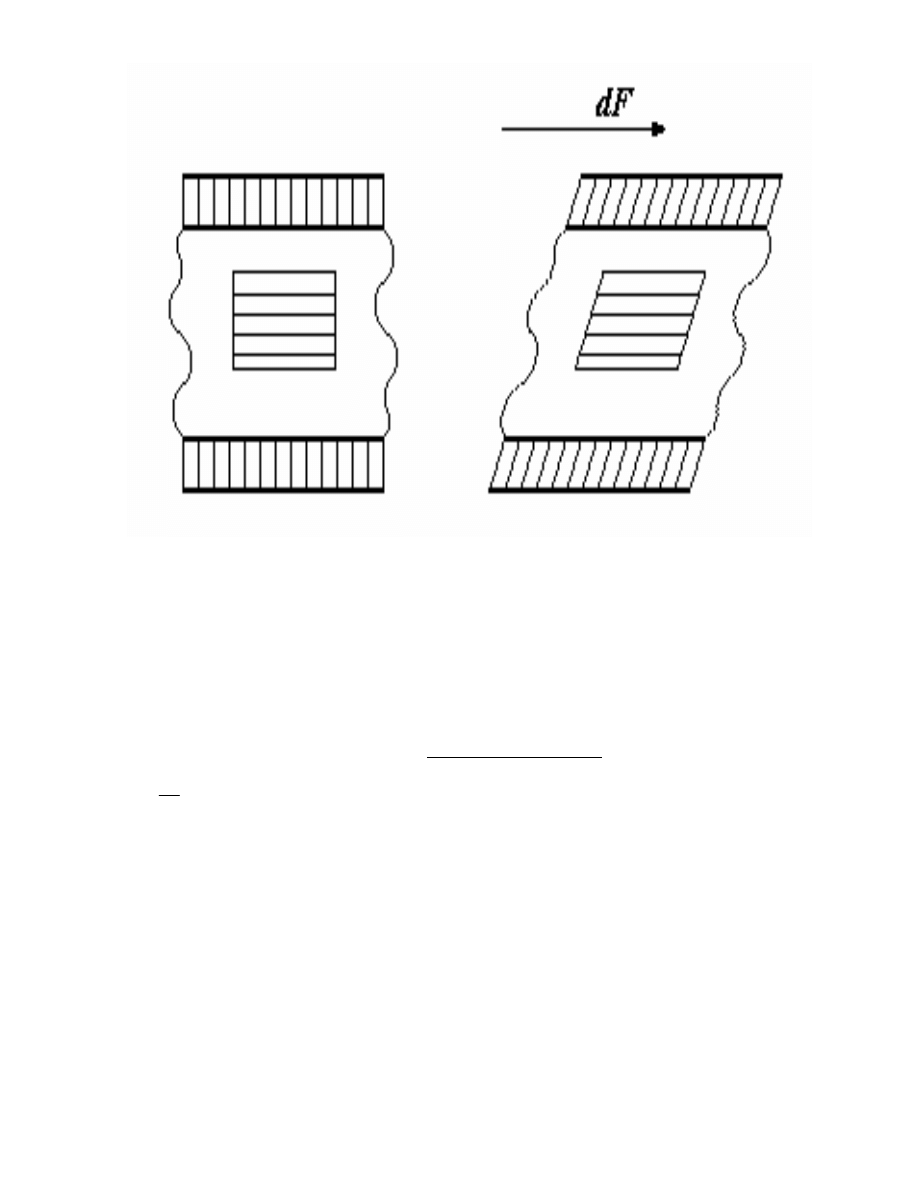
4

Ryc. 1.1. cinanie proste - jest to rodzaj odkształcenia postaci

Niech dolna płytka b dzie unieruchomiona a na górn niech działa stycznie pewna siła

dF. Ciało znajduj ce si mi dzy tymi płytkami ulega odkształceniu, które wytłumaczy mo na
zakładaj c jego warstwow (laminarn ) struktur . Warstwy o niesko czenie małej grubo ci
oddziałuj wzajemnie na siebie, przy czym lizgaj si po sobie przesuwaj c si w tym samym
kierunku. Miar szybko ci zmniejszania si pr dko ci kolejnych płytek lub inaczej miar

szybko ci cinania jest wielko

γ

γ γ

γ zwana gradientem przesuni cia (odkształcenia) (ryc.1.2.).

γ

α

=

=

dl

dh

tg

(1.1)

5

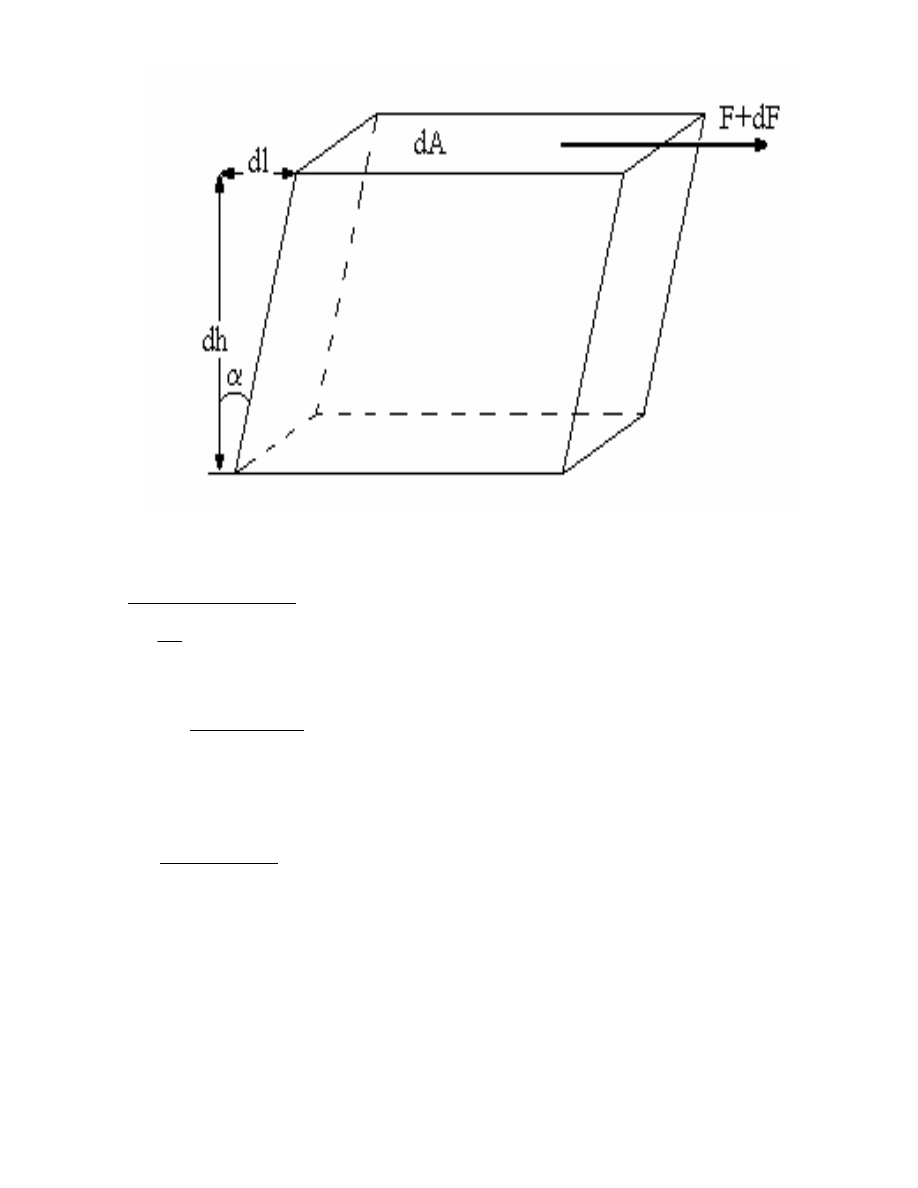
Ryc. 1.2. lizganie si warstewek ciała odkształcanego pod działaniem siły stycznej do górnej

powierzchni ciała

Napr eniem stycznym nazywa si wielko

τ

=

dF

dA

(1.2)

Jest to odpowiednik ci nienia stycznego w mechanice.

Dla ciał spr ystych Hooke,a zachodzi prosta proporcjonalno mi dzy napr eniem

stycznym i gradientem przesuni cia

τ = G γ

(1.3)

gdzie G - moduł spr ysto ci postaciowej w N/m2.

Ciała plastyczne rzeczywiste przy małych napr eniach stycznych zachowuj si jak ciała

spr yste. W tym zakresie napr e stycznych, a do pewnej granicznej warto ci

ττττ

g

obserwuje

si prost proporcjonalno mi dzy napr eniem stycznym i gradientem odkształcenia

γγγγ. Po

osi gni ciu warto ci napr enia stycznego

ττττ

g

zale no ta nie wyst puje.

1.2. Przepływ lepki, poj cie płynu (równie cieczy) newtonowskiego. Krzywa płyni cia

Płynem w dalszych rozwa aniach b dzie nazwany o rodek, który daje si przelewa . Płyn

lepki jest to płyn wykazuj cy tarcie wewn trzne czyli lepko .

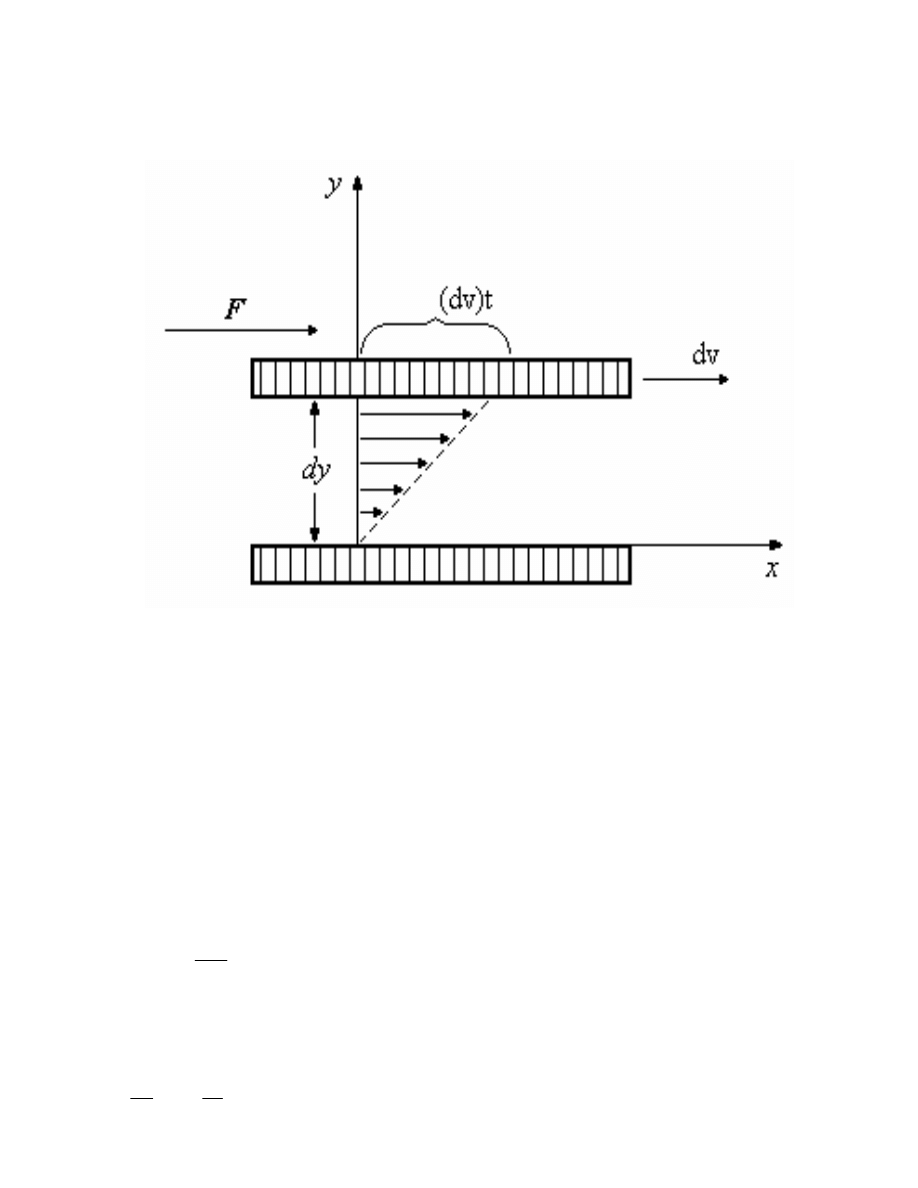
6

Niech mi dzy płytkami o bardzo du ej powierzchni odległymi od siebie o

dy znajduje si

warstwa płynu lepkiego. Dolna płytka jest nieruchoma a do górnej ruchomej przyłó my
stycznie sił

F (ryc. 1.3.).

Ryc. 1.3. Rozkład wektorów pr dko ci warstw ciała odkształcanego sił styczn do górnej

powierzchni ciała

Górna płytka b dzie porusza si z pr dko ci

dv wzgl dem płytki dolnej. Je eli ruch

płynu b dzie ustalony przyło ona siła

F b dzie zrównowa ona przez sił tarcia wewn trznego

płynu hamuj c przepływ. Siła

F jest to zatem siła, która równowa y tarcie wewn trzne w

cieczy, przeciwdziała wzajemnemu przesuwaniu si warstewek płynu po sobie. Siła ta jest tym
wi ksza im wi ksz warto ma szybko odkształcania, a wi c szybko płyni cia. Zało enie,

e cz steczki płynu w warstewkach bezpo rednio przyległych do płytek s nieruchome poci ga

za sob rozkład pr dko ci warstewek płynu w kierunku prostopadłym do kierunku płyni cia, a

wi c w kierunku dy jak na ryc. 1.3. Miar odkształcenia jest k t

α.

α.

α.

α. Przy napr eniu stycznym ττττ

( )

tg

d t

dy

α γ

= =

v

(

1.4)

gdzie

t - czas odkształcania.

Szybko odkształcania (

γ

•

) jest równa pierwszej pochodnej (

dγ/

γ/

γ/

γ/dt)

d

dt

d
dy

γ γ

= =

•

v

(

1.5)

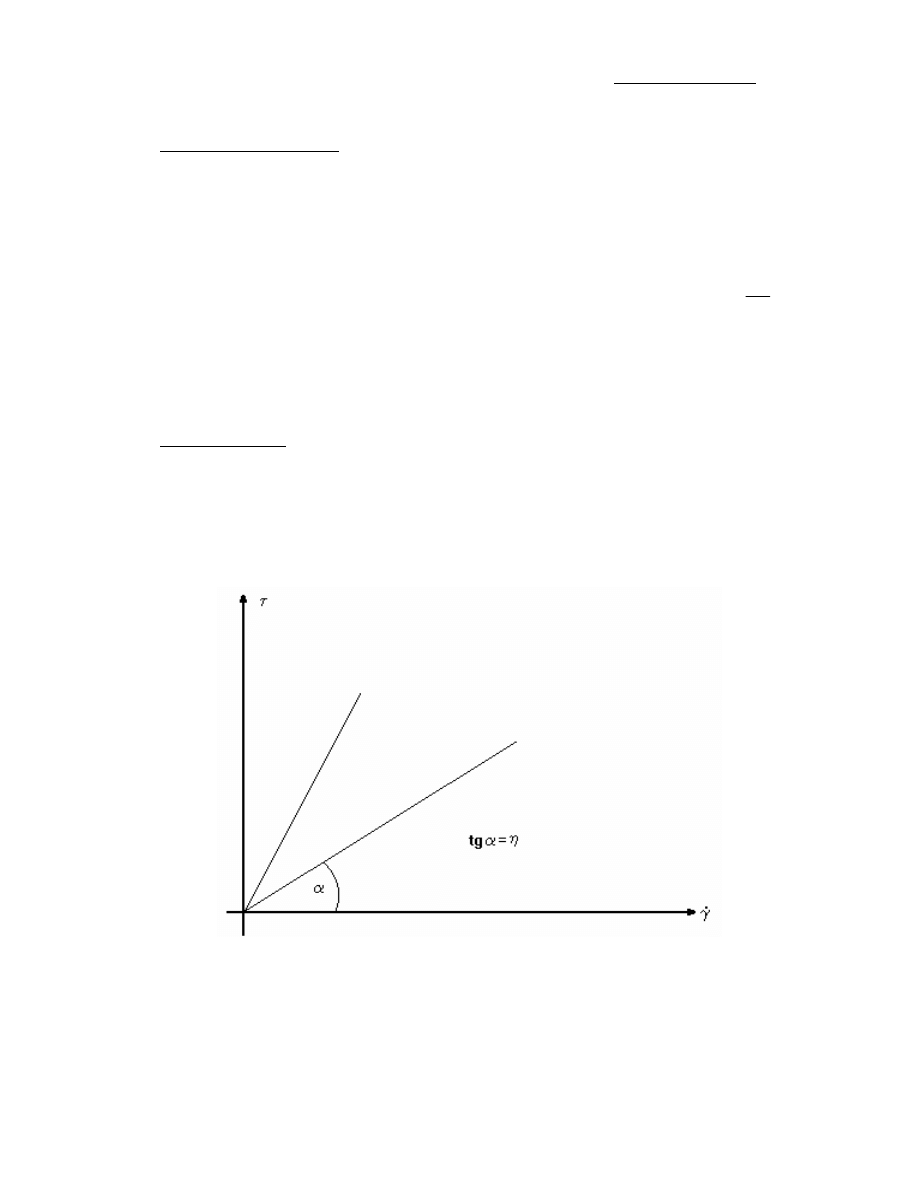
7

i jest to wielko zwana w reologii gradientem pr dko ci płynu lub szybko ci cinania.

Podaje si j w s

-1

.

Płynami newtonowskimi nazywamy te ciecze i gazy, dla których przy prostym cinaniu

warstewek płynu zachodzi prosta proporcjonalno mi dzy napr eniem stycznym i
szybko ci cinania

τ ηγ

=

⋅ •

(1.6)

gdzie

η −

η −

η −

η − współczynnik lepko ci dynamicznej lub lepko dynamiczna, podawana w

N

m

s

2

czyli w

Pas

(1 Pas czytaj jedna paskalosekunda).

Współczynnik

ηηηη lepko ci cieczy newtonowskiej jest funkcj temperatury i ci nienia, i jest

zupełnie niezale ny od szybko ci cinania.

Krzyw płyni cia nazywamy wykres zale no ci napr enia stycznego od szybko ci

cinania. Krzyw płyni cia cieczy newtonowskiej przedstawiono na ryc. 1.4. Jest to linia

prosta, nachylona do osi szybko ci cinania pod k tem zale nym od rodzaju cieczy. Tangens
k ta nachylenia wykresu do osi szybko ci cinania jest równy współczynnikowi lepko ci

dynamicznej

η.

Ryc. 1.4. Krzywa płyni cia płynu newtonowskiego

Do płynów newtonowskich nale ciecze, w których lepkie rozpraszanie energii zachodzi

wskutek zderze wzgl dnie małych cz steczek. Tu nale y zaliczy gazy i ciecze proste oraz
roztwory zwi zków o małym ci arze cz steczkowym. Koloidy, roztwory polimerów,

8

biopolimerów o du ych cz steczkach wykazuj na krzywej płyni cia odst pstwa od wykresu
dla cieczy newtonowskich.
2. Burzliwo w przepływach. Liczba Reynoldsa.

Ograniczymy si obecnie do omawiania cieczy. Je eli przepływ cieczy przez np. rurki o

małym przekroju jest warstwowy, wektory pr dko ci przepływu warstw układaj si
równolegle wzgl dem siebie tak, e najwi ksz pr dko maj warstwy przyosiowe,
najmniejsz (niemal równ zero) warstwy le ce przy ciankach rurki. Je eli ruch cieczy
przestaje by laminarny, czyli je eli warstewki cieczy przestaj si lizga po sobie, nast puje
powolne przekształcanie ruchu laminarnego cieczy w ruch burzliwy czyli turbulentny. Tory
cz steczek cieczy podobnie jak wektory pr dko ci warstw przestaj by równoległe do siebie.
Cz

energii płyn cej cieczy zostaje rozproszona podczas ruchów chaotycznych

poszczególnych jej elementów. Krzywa płyni cia cieczy w takim przypadku odchyla si od

półprostej dla cieczy newtonowskiej w kierunku osi napr enia stycznego

τ, które jest

proporcjonalne do kwadratu pr dko ci płyni cia (

τ ∼ v

2

). Aby bli ej okre li obserwowany

charakter ruchu cieczy newtonowskiej posługujemy si zwykł liczb Reynoldsa

Re

=

Dv

ρ

η

(2.1)

gdzie D - rednica rurki lub kapilary przez któr płynie ciecz, v -pr dko płyni cia,

ρ - g sto płynu, η - lepko dynamiczna płynu (okre lenie dalej).

Je eli liczba Re jest mniejsza od warto ci krytycznej Re

kryt

= 2100 ruch jest laminarny.

Powy ej Re

kryt

ruch przechodzi w burzliwy. Liczba Reynoldsa jest liczb niemianowan .

Dla płynów nienewtonowskich korzysta si z uogólnionej liczby Reynoldsa,

wyprowadzonej dla układów reostabilnych, nie wykazuj cych po lizgu przy ciance. Warto
uogólnionej liczby Reynoldsa poni ej której ruch płynu nienewtonowskiego jest laminarny,
jest w przybli eniu taka sama jak dla płynów newtonowskich (4).
3. Wiskozymetria. Rodzaje przepływów cieczy lepkiej.

W badaniach wiskozymetrycznych cieczy newtonowskich stosuje si najcz ciej

wiskozymetry punktowe, daj ce jedn warto napr enia stycznego i jedn warto szybko ci

cinania. Jest to wystarczaj co du o dla płynu newtonowskiego (krzywa płyni cia przechodzi

przez pocz tek układu i dany punkt - ryc.1.4) ale o wiele za mało dla okre lenia wła ciwo ci
reologicznych płynu nienewtonowskiego.

Do badania wła ciwo ci reologicznych płynów nienewtonowskich (tzw. reostabilnych i

reologicznie niestabilnych) stosuje si metody wiskozymetryczne. Metodami tymi ustala si

9

zale no mi dzy szybko ci cinania oraz napr eniem stycznym. Wiskozymetry stosowane
do bada wła ciwo ci reologicznych cieczy newtonowskich s na ogół nieprzydatne w
badaniach wła ciwo ci reologicznych cieczy nienewtonowskich. Przyczyn s przeszkody
natury technicznej szczególnie trudno ci równoczesnego oznaczenia napr enia stycznego i
szybko ci cinania. Stosowane przyrz dy pomiarowe wskazuj zwykle warto ci, które s
funkcj wielu, równie innych ni reologiczne, wła ciwo ci cieczy. Przyrz dy pomiarowe
takie jak wiskozymetr kulkowy Hoepplera, Englera i kilka innych s to przyrz dy
porównawcze - pozwalaj na porównanie lepko ci badanej cieczy z lepko ci cieczy
wzorcowej. Nie mo na przy ich zastosowaniu dokonywa pomiarów bezwzgl dnych.

Wi kszo płynów biologicznych s to płyny nienewtonowskie, dla których pomiarów

lepko ci dokonuje si za pomoc przyrz dów wielopunktowych absolutnych - badania nie s
w tym przypadku porównawcze. Przyrz dy te nazywa si reometrami. Ka dy reometr posiada
swoiste dostosowanie techniczne, które realizuje okre lony rodzaj przepływu płynu. Jest tak
zbudowany, by realizowa okre lone równanie przepływu płynu lub jego przybli enie (dla
okre lonego modelu mechanicznego cieczy). Pomiary lepko ci wykonuje si dla najprostszych
przypadków. Bada si te szczególnie proste przepływy, dla których mo na ci le okre li
zale no mi dzy napr eniem stycznym i szybko ci cinania. S to przepływy
wiskozymetryczne. Dla tych przepływów podstawowym zało eniem jest, e badany płyn jest
ci gły i nie ci liwy, co dla cieczy jest zachowane. S nast puj ce klasy przepływów
wiskozymetrycznych, poza omówionym wy ej przepływem w warunkach cinania prostego:
1. Przepływ Poiseuille'a czyli przepływ przez przewód o przekroju kołowym
2. Płaski przepływ Poiseuille'a czyli przepływ w szczelinie mi dzy płaskimi równoległymi
płytkami albo przepływ w kierunku osiowym przez szczelin w rodzaju pier cienia mi dzy
dwoma współosiowymi cylindrami
3. Przepływ Couette'a czyli przepływ mi dzy wiruj cymi wzgl dem siebie cylindrami.

W wymienionych przepływach s spełnione warunki ustalonego i uformowanego

przepływu laminarnego tj. przepływu ustalonego w rozumieniu Lagrange'a (7) - jak na ryc.3.1.

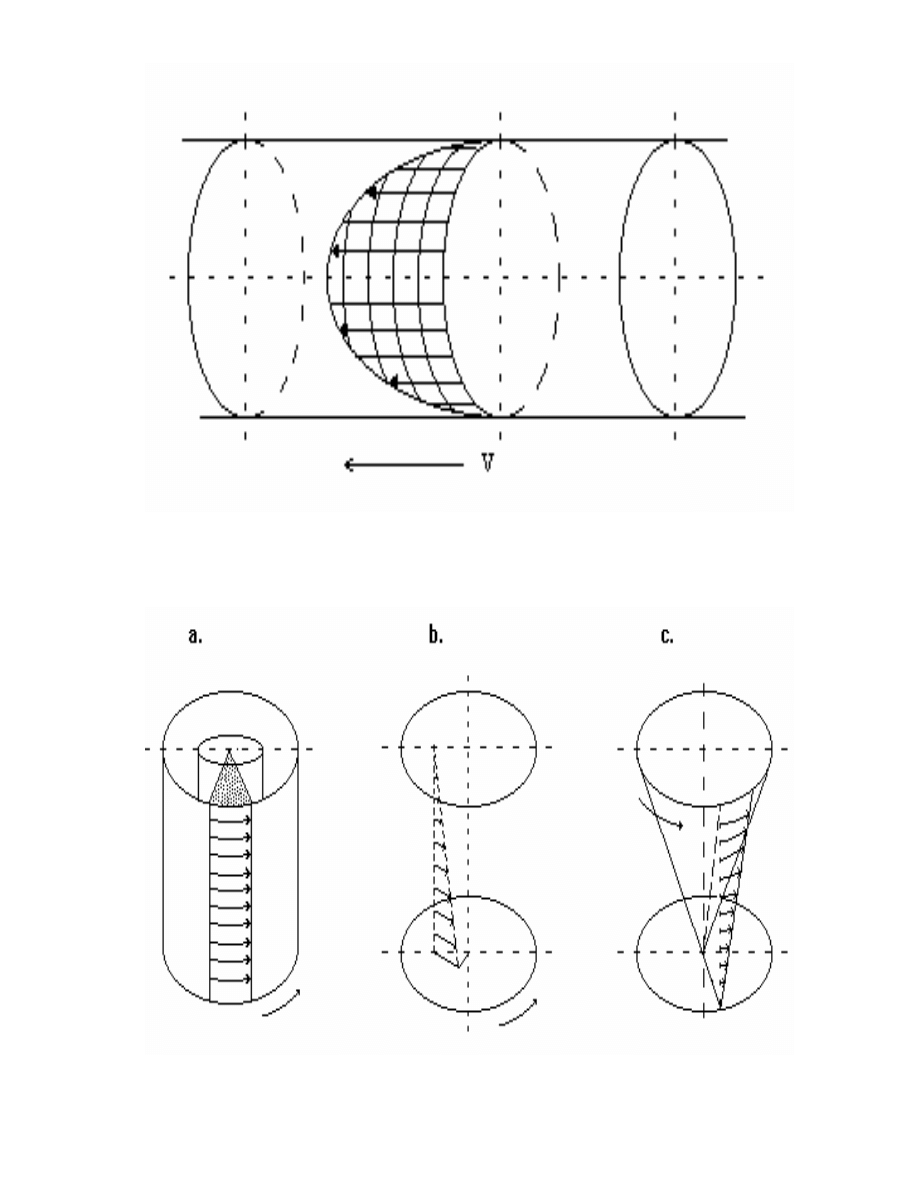
10

Ryc. 3.1. Przepływ Poiseuille'a

W stosowanych reometrach kapilarnych jest realizowany przepływ Poiseuille'a. W

reometrach rotacyjnych wyst puj inne rodzaje przepływów przedstawione na ryc. 3.2

Ryc. 3.2. Inne rodzaje przepływów
a. Przepływ Couette'a,

11

b. Przepływ skr tny mi dzy równoległymi płytkami,

c. Przepływ skr tny mi dzy sto kiem i płytk

Dane pomiarowe z wiskozymetrów kapilarnych i rotacyjnych s ze sob porównywalne,

dlatego cz sto wiskozymetry te s stosowane jako uzupełniaj ce si .
4. Podstawy wiskozymetrii kapilarnej cieczy

Zasada działania wiskozymetru kapilarnego polega na przetłaczaniu badanej cieczy przez

rurki o idealnie gładkiej powierzchni wewn trznej. Przepływ powinien odbywa si w stałej
temperaturze, z zasady powinien by ustalony i laminarny. Celem jest znalezienie zale no ci
mi dzy obj to ciowym nat eniem przepływu a spadkiem ci nienia w cieczy wywołanym
tarciem wewn trznym czyli lepko ci płyn cej cieczy.

W przypadku gdy mo liwe jest wyznaczenie tej zale no ci dla ró nych warto ci nat enia

przepływu (lub spadku ci nienia), mo na uzyska krzyw płyni cia.
Wiskozymetry kapilarne posiadaj wiele cennych zalet:
1) stosuj c zmienne rednice kapilar oraz zmienne ci nienia mo na uzyska szeroki zakres
pracy tych wiskozymetrów
2) nie wyst puj straty cieplne w przyrz dzie - ciecz przebywa w kapilarach bardzo krótko
(mo na stosowa termostatowanie)
3) s bardzo proste, mo liwe do skonstruowania w skromnych warunkach aparaturowych.
4.1. Przepływ laminarny płynu newtonowskiego przez kapilary. Prawo Hagena-

Poiseuille'a
Ciecz newtonowsk przepływaj c przez poziom cylindryczn kapilar mo na sobie

wyobrazi jako ruch warstewek tej cieczy w kształcie cylindrów o bardzo małej grubo ci,

lizgaj cych si po sobie. Pr dko ci tych warstewek s równoległe do osi cylindrów i s to

jedyne składowe pr dko ci w tym przepływie.

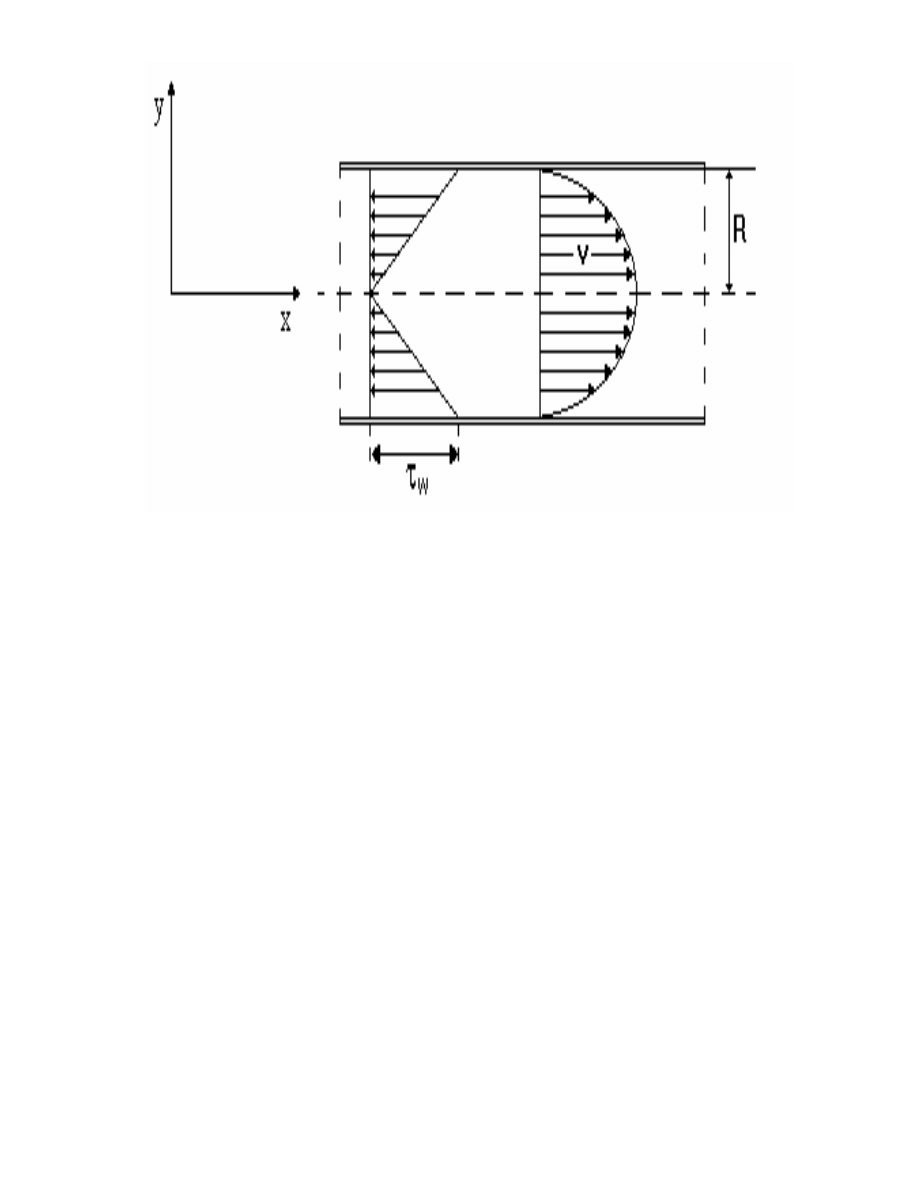
12

Ryc. 4.1. Rozkład napr e stycznych i profil pr dko ci cieczy newtonowskiej (przepływ

laminarny, przekrój kapilary jest kołowy),

τ

w

- napr enie styczne przy ciance

kapilary

Warto pr dko ci jest tu funkcj odległo ci od osi cylindra. Najwi ksz pr dko maj

warstwy przyosiowe, przy ciankach (warstwy praktycznie przylegaj do cianek kapilary),
ich pr dko jest równa zero. Je eli z osi kapilary lub rurki o przekroju kołowym i promieniu
r zwi za układ współrz dnych jak na rysunku, widzimy, e w kierunku wzrastaj cego y
maleje pr dko płyni cia warstw cieczy (ryc. 4.1).

W kierunku promienia kapilary wyst puje wi c ujemny gradient pr dko ci, mi dzy

warstewkami cieczy działaj napr enia styczne których rozkład przedstawia ryc. 4.1. Ruch
cieczy odbywa si pod wpływem ró nicy ci nie p

1

i p

2

, przyło onych w kierunku osi kapilary,

jak na ryc. 4.2.

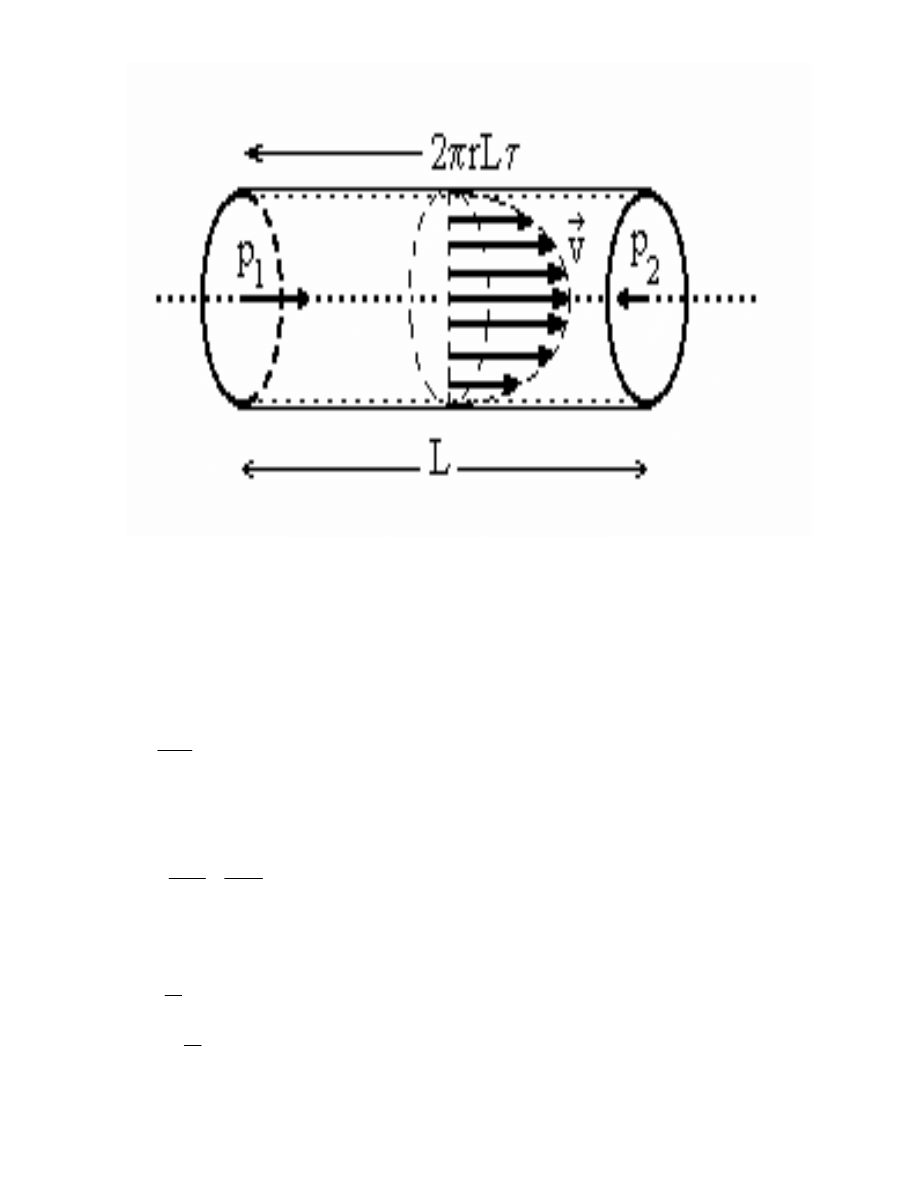
13

Ryc. 4.2. Walec cieczy o promieniu r i długo ci L oraz siły działaj ce na ten walec:

p

1

πr

2

, -p

2

πr

2

, -2

πrLτ

Równowag sił podczas przepływu cieczy mo na zapisa w nast puj cy sposób

p

1

πr

2

- p

2

πr

2

- 2

πrLt =0

(4.1)

sk d napr enie styczne, zale ne od odległo ci r od osi kapilary jest równe

τ

=

∆

p r

L

2

(4.2)

gdzie

∆p = p

2

-p

1

.

Dla r = R (czyli przy ciance kapilary)

τ

w

p R

L

p D

L

=

=

∆

∆

2

4

(4.3)

gdzie D=2R i oznacza rednic kapilary.
Dla cieczy płyn cych przez kapilary słuszna jest równo Newtona

τ η

=

d
dr

v

(4

.4)

gdzie

−

d
dr

v

ujemny gradient pr dko ci (7). Po porównaniu (4.4) i (4.2) i po scałkowaniu

otrzymuje si

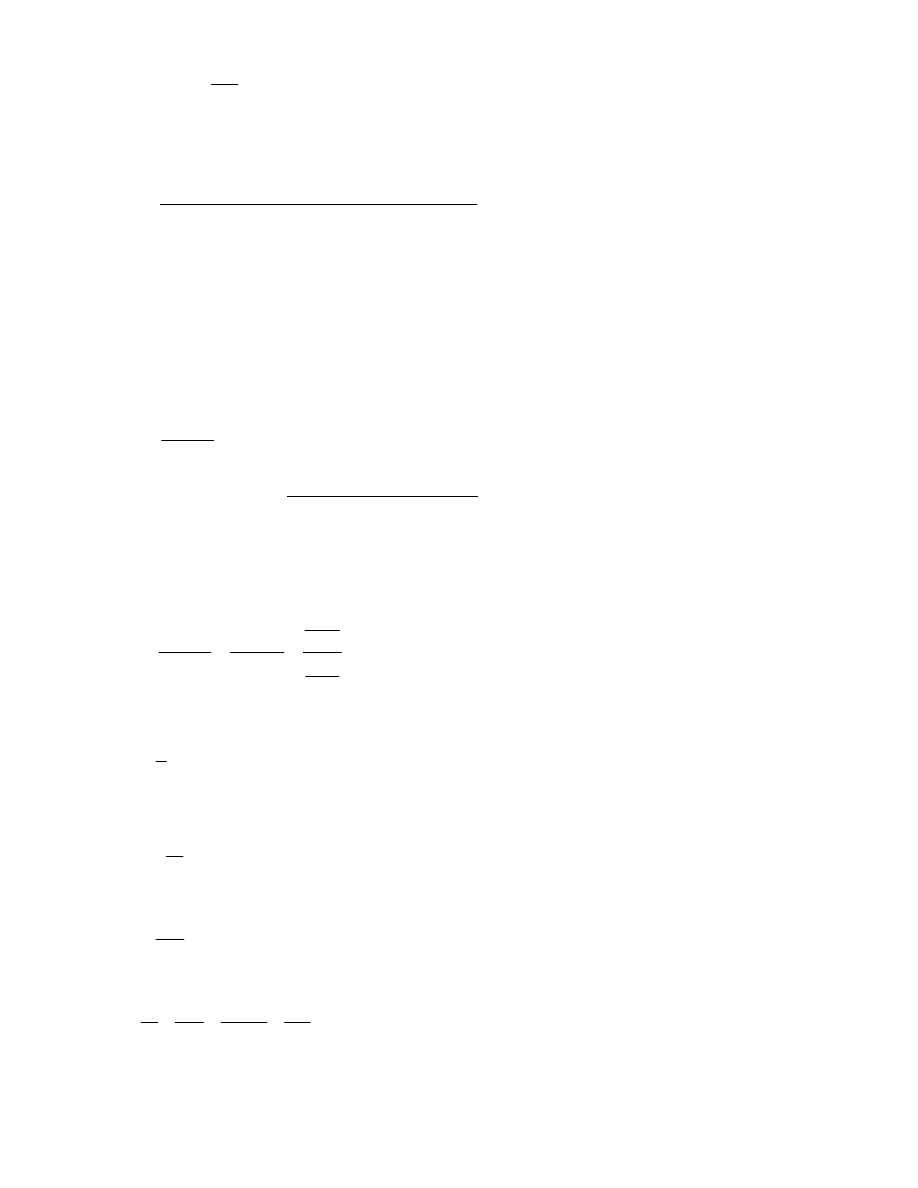
14

(

)

v

=

−

R

r

p

L

2

2

4

∆

η

(4.5)

gdzie r - promie bie cy kapilary, zmienny lub te inaczej odległo warstwy od osi kapilary,
jak wy ej. Pr dko warstw cieczy jest wi c funkcj kwadratow odległo ci od osi kapilary.

Obj to ciowe nat enie przepływu Q (m

3

/s) czyli obj to cieczy przepływaj ca przez

przekrój kapilary w jednostce czasu, b dzie obliczane jak nast puje:dla pier cienia cieczy o
grubo ci dr

dQ = 2

πr dr

v

(4.6)

i dla wszystkich warstw

Q

r d

R

= 2

0

π

v r

(4.7)

Q

pR

L

=

π∆

η

4

8

(4.8)

Wzór ten wyra a prawo Hagena-Poiseuille'a, które cz sto wykorzystuje si do

wyznaczania współczynnika lepko ci dynamicznej

η (patrz wzory III.A.2 i III.A.4).

Wzór powy szy mo na przekształci i zapisa tak, by wyst powało w nim napr enie

styczne w odległo ci równej promieniowi kapilary, a zatem przy ciance kapilary

η π∆

π∆

π

=

=

=

pR

LQ

pD

LQ

D p

L

Q

D

4

4

3

8

126

4

32

∆

(4

.9)

Sk din d

η τ

γ

=

•

(4.10)

gdzie

γ

•

= −

d
dr

v

(4.11)

Porównuj c ostatnie dwa wyra enia otrzymuje si

γ

π

•

=

32

2

Q

D

(4.12)

i

( )

−

=

=

=

d
dr

Q

D

Q

R

Q

R

v

32

32

2

4

3

3

3

π

π

π

(4.13)

sk d po scałkowaniu

15

v

= 4

2

Q

D

π

(4.14)

Jest to rednia liniowa pr dko przepływu laminarnego cieczy w kapilarze.

5. Efekty cieplne podczas płyni cia

Podczas płyni cia cieczy przy du ych napr eniach stycznych mog powstawa w płynie

wyra ne gradienty temperatury, temperatura cieczy wyra nie wzrasta. Wpływa to na
wła ciwo ci reologiczne płynu. Lepko pozorna płynu nienewtonowskiego podobnie jak
lepko dynamiczna płynu newtonowskiego maleje ze wzrostem temperatury, co dokładniej
wyja niono w pi miennictwie (4, 6, 7).

6. Podstawy teoretyczne reometrii rotacyjnej

W przyrz dach zwanych reometrami rotacyjnymi cinanie nast puje w wyniku obrotów

elementu układu pomiarowego najcz ciej mi dzy dwoma powierzchniami, z których jedna
jest ruchoma a druga jest nieruchoma. W szczelinie mi dzy nimi znajduje si badany płyn.
Zasada pomiaru polega na równoczesnym wyznaczeniu pr dko ci k towej wiruj cego
elementu oraz momentu skr caj cego zwi zanego z tym obrotem.

Zmieniaj c cz sto obrotów elementu wiruj cego mo na zebra dane do wykre lenia

krzywej płyni cia.

Reometry rotacyjne s przyrz dami o szerokich mo liwo ciach zmiany szybko ci cinania

i napr e stycznych, mog pracowa w długim czasie przy zmianach ci głych i skokowych.
[Mo na je produkowa nawet w skromnych warunkach warsztatowych.] Zasad działania i
oblicze dla tego rodzaju przepływu podał w 1881 roku Margules (6).

7. Wpływ temperatury na lepko cieczy

Lepko cieczy (traktowana jako tarcie wewn trzne) jest zjawiskiem

mi dzycz steczkowym (1) a przeto w du ym stopniu zale nym od temperatury. Zale no ta
zmienia si wraz z kształtem cz steczek b d te zmian konformacji, a wi c jest funkcj
rozmiarów i kształtów cz steczek cieczy. Wiadomo z do wiadcze , e je eli temperatura

wzrasta współczynnik lepko ci dynamicznej cieczy

η maleje i tak jest dla wi kszo ci cieczy.

Ale znane s ciecze, których lepko dla pewnych temperatur osi ga minimum lub maksimum.
Jest to zwi zane z ł czeniem si cz steczek w kompleksy b d te rozpadaniem si
kompleksów w odpowiedniej temperaturze. Dla wielu cieczy, głównie newtonowskich,
słuszna jest nast puj ca zale no współczynnika lepko ci od temperatury

η

=

Ae

W kT

/

16

gdzie k - stała Boltzmanna, e - podstawa logarytmu naturalnego, A, W - stałe dla cieczy,
wyznaczane w sposób indywidualny dla ka dej. W - jest to energia aktywacji lepko ci. Energi
aktywacji lepko ci W nazywamy energi potrzebn na pokonanie sił lepko ci działaj cych na
cz steczk cieczy. Warto W wyznacza si do wiadczalnie.

II. CEL WICZENIA

Celem wiczenia jest wyznaczenie współczynnika lepko ci dynamicznej cieczy

newtonowskiej, któr jest woda, (cz. A) w temperaturze otoczenia oraz wzgl dnego
współczynnika lepko ci dynamicznej badanej cieczy równie w temperaturze otoczenia.

III. WYKONANIE WICZENIA

III.A. Wyznaczanie współczynnika lepko ci dynamicznej cieczy newtonowskiej metod

Poiseuille'a

III.A.1. Zasada pomiaru

W wiczeniu do utrzymania stałego ci nienia, pod którym nast puje wypływ cieczy z

kapilary K wykorzystuje si butl Mariotte'a (ryc. III.A.1). Kapilar K i wylot rurki pionowej R
obserwuje si przez katetometr (ryc. III.A.2.) - patrz punkt 5.

Butla Mariotte'a jest to butla szklana zamkni ta szczelnie korkiem z pionow rurk

szklan R, wprowadzon do cieczy na pewn gł boko . Nad dnem butli znajduje si wylot,
przez który ciecz (najcz ciej woda) mo e wypływa .

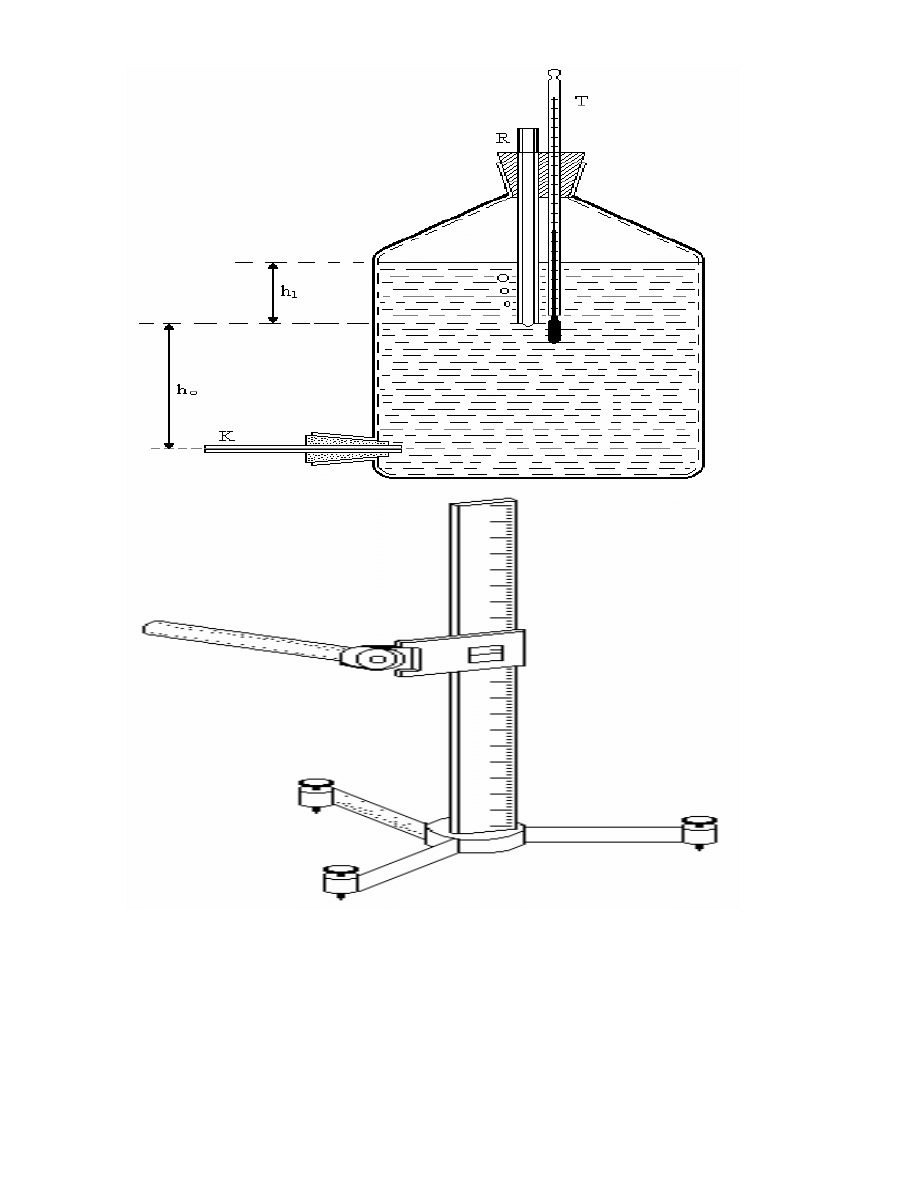
17

Ryc. III.A.1. Butla Mariotte'a ,

∆p = ρ g h

0

Ryc. III.A.2. Katetometr

Ryc. III.A. Schemat aparatury do wyznaczania współczynnika lepko ci dynamicznej cieczy

newtonowskiej metod Poiseuille'a

W miar wypływu cieczy ci nienie powietrza nad ciecz maleje i powietrze

atmosferyczne pod wpływem ró nicy ci nie zaczyna wchodzi do wn trza butli przez
pionow rurk R. Na poziomie wylotu rurki pionowej R pojawiaj si p cherzyki powietrza.
Ukazanie si pierwszych p cherzyków powietrza u wylotu rurki R oznacza, e na poziomie

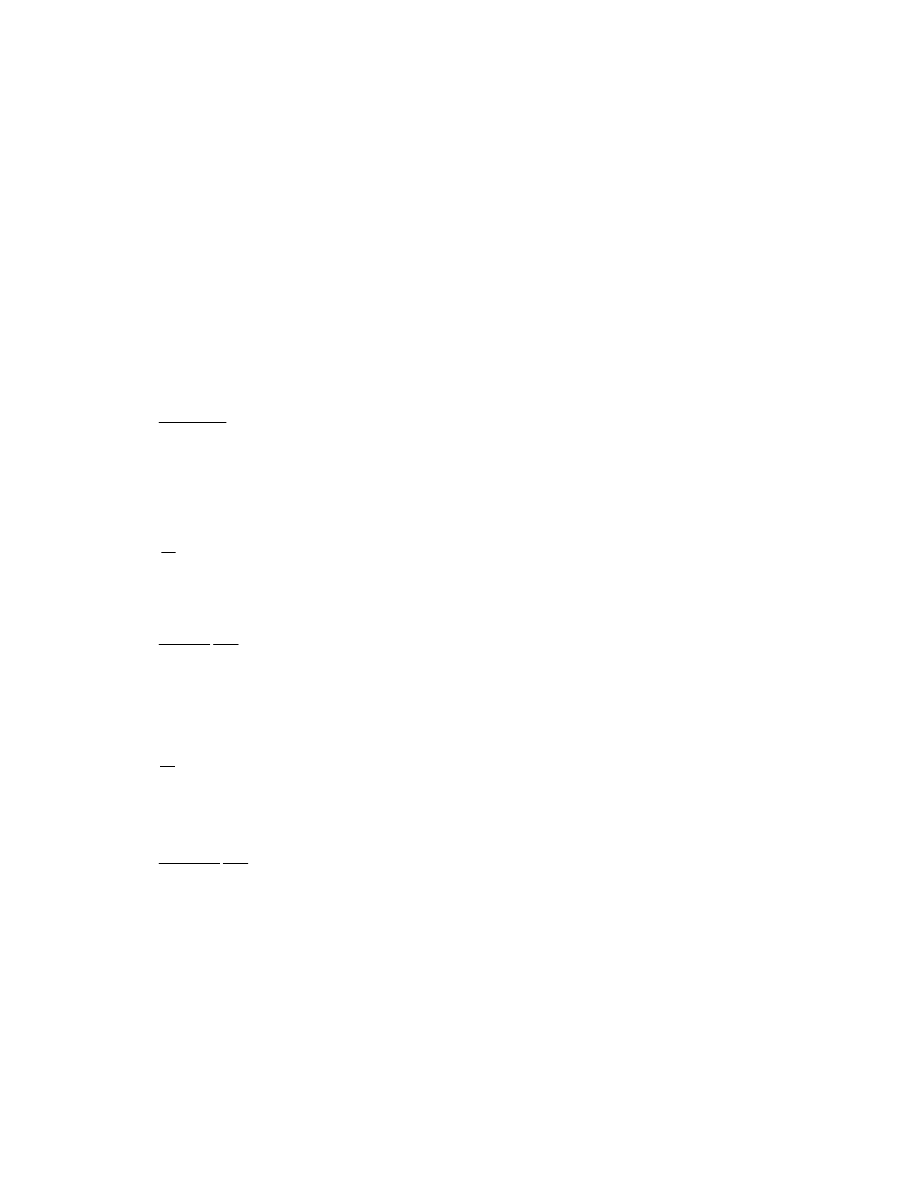
18

jej wylotu

panuje ci nienie równe ci nieniu atmosferycznemu. Ci nienie to utrzymuje si na

tym poziomie dopóty, dopóki poziom cieczy w naczyniu znajduje si powy ej wylotu rurki.
Ciecz wypływa z naczynia przez wylot dolny nad dnem butli, a wi c równie przez kapilar K

pod stałym ci nieniem równym ci nieniu hydrostatycznemu

∆p słupa cieczy o wysoko ci h

0

.

Warto tego ci nienia mo na zmienia , zmieniaj c gł boko na której znajduje si wylot
rurki pionowej R (ryc. III.A.1). Uwzgl dniaj c to mamy

∆p = ρ g h

0

(III.A.1)

gdzie

ρ - g sto cieczy znajduj cej si w butli (cieczy badanej), g - przyspieszenie ziemskie.

Współczynnik lepko ci dynamicznej wyznaczamy wykorzystuj c wzór (4.8), z którego po

przekształceniu otrzymuje si

η π ρ

=

R gh

Ql

4

0

8

(III.A.2)

gdzie - Q obj to ciowe nat enie przepływu w m

3

/s.

Je eli warto Q wyrazi si przez obj to cieczy, która wypłyn ła w czasie t

Q

V

t

=

(III.A.3)

powy szy wzór przyjmuje posta

η π ρ

=

R g

L

h t

V

4

0

8

(III.A.4)

Je eli nadto zauwa ymy, e obj to cieczy, która wypłyn ła mo na wyrazi poprzez jej

mas

V

m

=

ρ

(III.A.5)

wzór (III.A.4) przyjmuje posta

η π ρ

=

R

g

L

h t

m

4

2

0

8

(III.A.6)

Wielko ciami mierzonymi bezpo rednio s tu wysoko słupa cieczy (wody) h

0

, czas t

oraz masa cieczy (wody) m.

III.A.2. Wykonanie wiczenia

1. Zwa y mał (najlepiej 100 mililitrow ) zlewk , zapisa jej mas m

1

.

2. Odczyta temperatur wody w butli T (w stopniach Celsjusza), zapisa . Zdj kołpak z

poziomej kapilary i odczeka a z rurki pionowej zaczn wydobywa si p cherzyki

19

powietrza. Podstawi pod kapilar jak kolwiek zlewk , by woda wypływaj ca z kapilary
nie kapała na stół.

3. Podstawi teraz zwa on zlewk pod kapilar i pozwoli wypływa wodzie 5 - 8 minut.

Zmierzy stoperem czas wypływu wody t, zapisa .

4. Zwa y zlewk z wod , która wypłyn ła z kapilary - m

2

. Masa wody jest równa

m = m

2

- m

1

, zapisa warto m.

5. Przy pomocy katetometru zmierzy wysoko słupa wody h

0

(katetometr jest to liniał

ustawiony w pozycji pionowej, wzdłu którego przesuwa si lunetka pozwalaj ca dokładnie
zobaczy poło enie wylotu kapilary pionowej i kapilary poziomej - ryc. A.III.2).

III.A.3. Opracowanie wyników, dyskusja bł dów

1. Korzystaj c z danych: R = (4,4

± 0,1) 10

-4

m

L = (1,5

± 0,01) 10

-1

m

g = (9,81

± 0,01) m/s

2

ρ = (9,97 ± 0,01) 10

2

kg/m

3

oraz wyników własnych pomiarów (m, t, h

0

)

obliczy ze wzoru (III.A.6) współczynnik lepko ci dynamicznej wody

η

w

, wyra aj c go w

układzie jednostek SI (w Pa s).

2. Obliczy maksymaln warto bł du bezwzgl dnego stosuj c metod pochodnej

logarytmicznej.

3. Obliczon warto współczynnika

η

w

porówna z warto ci tablicow dla temperatury T.

Uwaga:

zasady oceny bł dów wielko ci fizycznych mierzonych jednorazowo podano w

broszurce "Bł dy pomiarów".

20

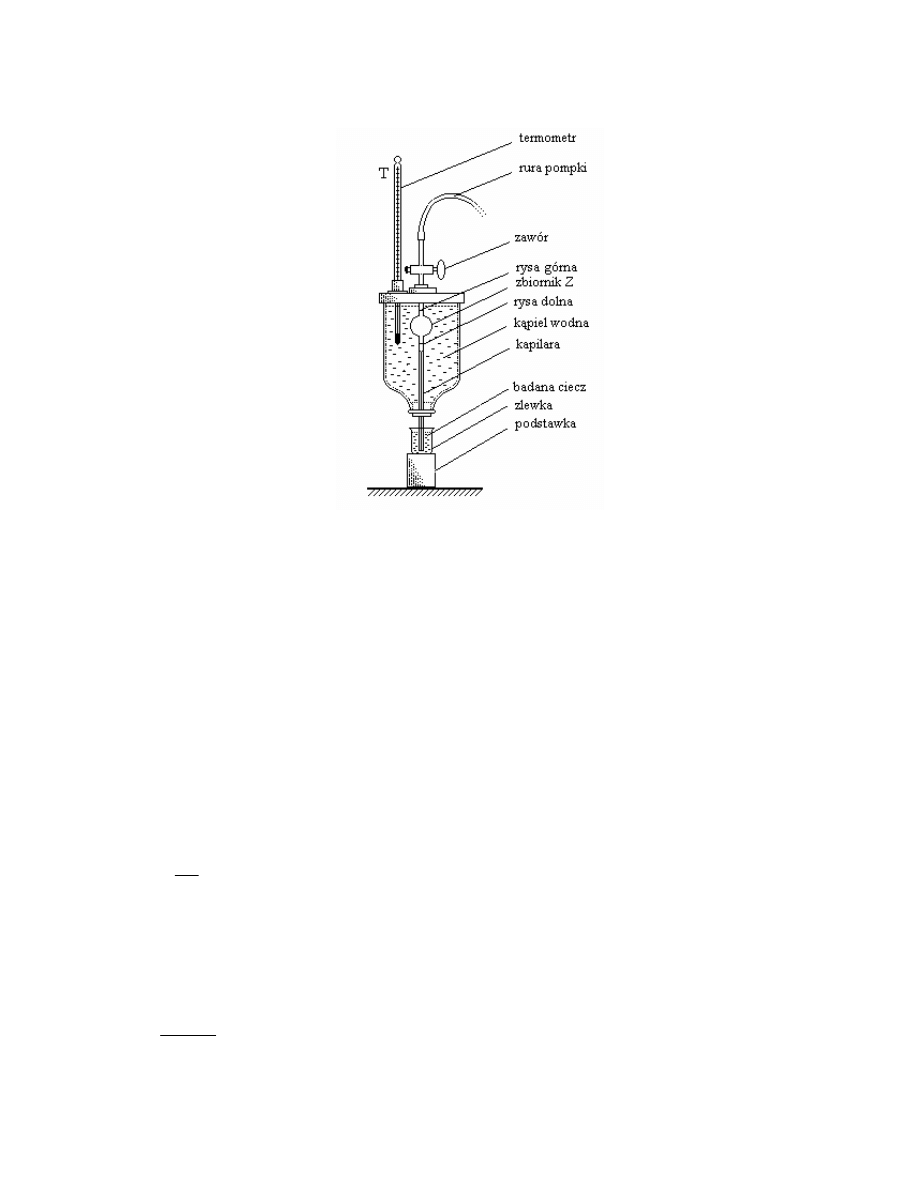
III.B. Wyznaczanie współczynnika lepko ci dynamicznej cieczy newtonowskiej metod

wzgl dn Arrheniusa

Ryc. III.B.1. Wiskozymetr kapilarny do wyznaczania współczynnika lepko ci dynamicznej

metod wzgl dn Arrheniusa

III.B.1. Zasada pomiaru:

Badamy przepływ dwóch cieczy newtonowskich wypływaj cych przez kapilar ze

zbiornika

Z

(ryc. III.B.1) o obj to ci V. Obj to t wyznaczaj dwie rysy poziome

zaznaczone na rurkach szklanych zbiornika

Z

(ryc. III.B.1). Zbiornik

Z

jest termostatowany

wod , której temperatur odczytuje si na termometrze T.

Współczynnik lepko ci dynamicznej badanej cieczy

η

c

(w naszym przypadku jest to 96%

wodny roztwór alkoholu etylowego) jest tu porównywany ze współczynnikiem lepko ci

dynamicznej

η

w

wody destylowanej, która jest ciecz wzorcow . Lepko wzgl dna jest równa

η

η

η

rel

c

w

=

(III.B.1)

Korzystaj c z wzoru Poiseuille’a (wzór 4.8) zastosowanego dwukrotnie: do cieczy

badanej i do cieczy wzorcowej otrzymujemy na t sam obj to wypływaj cej cieczy V
wyra enie

V

R p

L

t

c

c

=

π

η

4

8

∆

'

(III.B.2)

21

V

R p

L

t

w

w

=

π

η

4

8

∆

(III.B.3)

gdzie t

c

- czas wypływu cieczy badanej z obj to ci V, t

w

- czas wypływu wody z obj to ci V.

We wzorach tych ci nienia hydrostatyczne, które wymuszaj przepływ cieczy

∆p' i ∆p nie s

równe ze wzgl du na ró nic (tu nieznaczn ) g sto ci cieczy badanej

ρ

c

i cieczy wzorcowej

ρ

w

. Mamy wi c przy tej samej wysoko ci h słupów obydwóch cieczy ci nienia

∆p' = ρ

c

g h

(III.B.4)

∆p = ρ

w

g h

(III.B.5)

St d

V

R

gh

L

c

c

=

π ρ

η

4

8

(III.B.6)

oraz

V

R

gh

L

w

w

=

π ρ

η

4

8

(III.B.7)

Porównuj c prawe strony powy szych równo ci otrzymujemy

π

ρ

η

π

ρ

η

R gh

L

t

R gh

L

t

c

c

c

w

w

w

4

4

8

8

=

(III.B.8)

lub

ρ

η

ρ

η

c

c

c

w

w

w

t

t

=

(III.B.9)

albo

η

η

ρ

ρ

η

c

w

c

w

c

w

rel

t

t

=

=

(III.B.10)

Do wyznaczenia lepko ci wzgl dnej

η

rel

wystarczy wyznaczy do wiadczalnie czasy

wypływu z obj to ci V cieczy badanej (t

c

) i cieczy wzorcowej (t

w

) przy tej samej temperaturze

wypływu. G sto ci cieczy odczytuje si z tablic dla tej samej temperatury.

III.B.2. Wykonanie wiczenia

1. Do małej zlewki nala dokładnie odmierzonych 25 ml wody destylowanej.
2. Ustawi zlewk z wod na metalowej podstawce pod wylot kapilary K wiskozymetru.

22

3. Przy pomocy gruszki zassa wod do zbiornika Z wiskozymetru nieco powy ej górnej rysy

pomiarowej i zamkn zawór szklany S, ustawiaj c go w poło enie poziome.

4. Odczeka 3-5 minut, a temperatura wody w zbiorniku Z wiskozymetru zrówna si z

temperatur k pieli termostatuj ej. Odczyta temperatur (w stopniach Celsjusza) z
termometru T, zapisa .

5. Otworzy zawór szklany S ustawiaj c go w poło eniu pionowym. Stoperem zmierzy czas

przepływu wody destylowanej mi dzy górn i doln rys pomiarow wiskozymetru, czas t

w

, zapisa .

6. Przy pomocy gruszki opró ni dokładnie wn trze wiskozymetru z wody destylowanej.

Wyj zlewk spod kapilary.

7. Czynno ci od 1 - 6 powtórzy dla badanej cieczy (alkohol etylowy). Zapisa czas wypływu

cieczy tc.

III.B.3. Opracowanie wyników, dyskusja bł dów

1. Obliczy warto wzgl dnego współczynnika lepko ci dynamicznej

η

rel

według wzoru

(B.III.10) przyjmuj c

ρ

w

= (9,97

± 0,01) 10

2

kg/m

3

ρ

c

=

ρ

alkoholu

= (7,88

± 0,04) 10

2

kg/m

3

,

2. Wyznaczy graficznie lub metod interpolacji (analitycznie) współczynnik lepko ci wody

destylowanej

η

w

dla temperatury pomiaru T, korzystaj c z danych w poni szej tabeli 1.

Tabela 1

Współczynnik lepko ci dynamicznej wody

η

w

w funkcji temperatury podany w Pa

⋅s

(1 Pa

⋅s = 10 P (≡ 10 puazów) = 10

3

cP (

≡ 10

3

centypuazów)

T (

o

C)

10

15

20

25

30

η

w

(Pa

⋅s)

0,00131

0,001142

0,001060

0,000893

0,000800

3. Przekształcaj c wzór (B.III.10) obliczy warto współczynnika lepko ci dynamicznej

alkoholu etylowego

η

c

=

η

w

η

rel

(III.B.11)

Przyj , e

η

w

ma warto tablicow .

23

4. Obliczon warto

η

c

porówna z warto ci tablicow . Uzasadni mo liwe odchylenie

uzyskanego wyniku od warto ci tablicowej (dla alkoholu etylowego współczynnik lepko ci

dynamicznej w temperaturze 20

o

C wynosi

η

alkoholu

= 0,001190 Pa

⋅s.

5. Obliczy maksymaln warto bł du bezwzgl dnego stosuj c metod pochodnej

logarytmicznej.

IV. LITERATURA

1. Cwietkow W.M., Eskin W.Je., Frenkel S.Ja., Struktura makrocz steczek w roztworach,

WN-T, Warszawa,1968

2. Flory P.J., Principles of Polymer Chemistry, Cornell University Press, Ithaca, New York,

1953

3. Je ewski M., Fizyka, PWN, Warszawa, 1972
4. Kembłowski Z., Reometria płynów nienewtonowskich, WN-T, Warszawa, 1973
5. Reiner M., Reologia teoretyczna, PWN, Warszawa, 1958
6. Wilkinson W.L., Ciecze nienewtonowskie, WN-T, Warszawa, 1963
7. Wanik B.M., Wykłady z Fizyki, t. 1, Wyd. AR Kraków, 1998

V. INDEKS

butla Mariotte'a (13)

ciało spr yste Hooke'a (4)

dilatancja (3)

efekt cieplny podczas płyni cia (11)

energia aktywacji lepko ci (12)

gradient przesuni cia (4)

katetometr (13)

kompresja (3)

krzywa płyni cia (6)

lepko ci dynamicznej współczynnik (5)

liczba Reynoldsa

uogólniona (7)

zwykła (6)

makroreologia (3)

mikroreologia (3)

napr enie

styczne (4)

odkształcenie

obj to ci (3)

24

postaci (3)

paskalosekunda (5)

płyn

newtonowski (5)

nienewtonowski (7)

pomiary wiskozymetryczne bezwzgl dne (7)

prawo Hagena - Poiseuille'a (9)

przepływ (3)

Couette'a (8)

laminarny przez kapilary (9)

Poiseuille'a (8)

reometr (7)

rotacyjny (12)

ruch burzliwy (turbulentny) (6)

szybko

cinania (5)

cinanie proste (3)

wiskozymetria

metody (7)

kapilarna (8)