7.3.1. Definicja krętu i kręt układu materialnego

Krętem k

O

punktu materialnego o masie m względem punktu O nazywamy

moment pędu

v

p m

=

tego punktu materialnego względem punktu O:

v

r

p

r

k

m

O

×

=

×

=

. (7.56)

Z

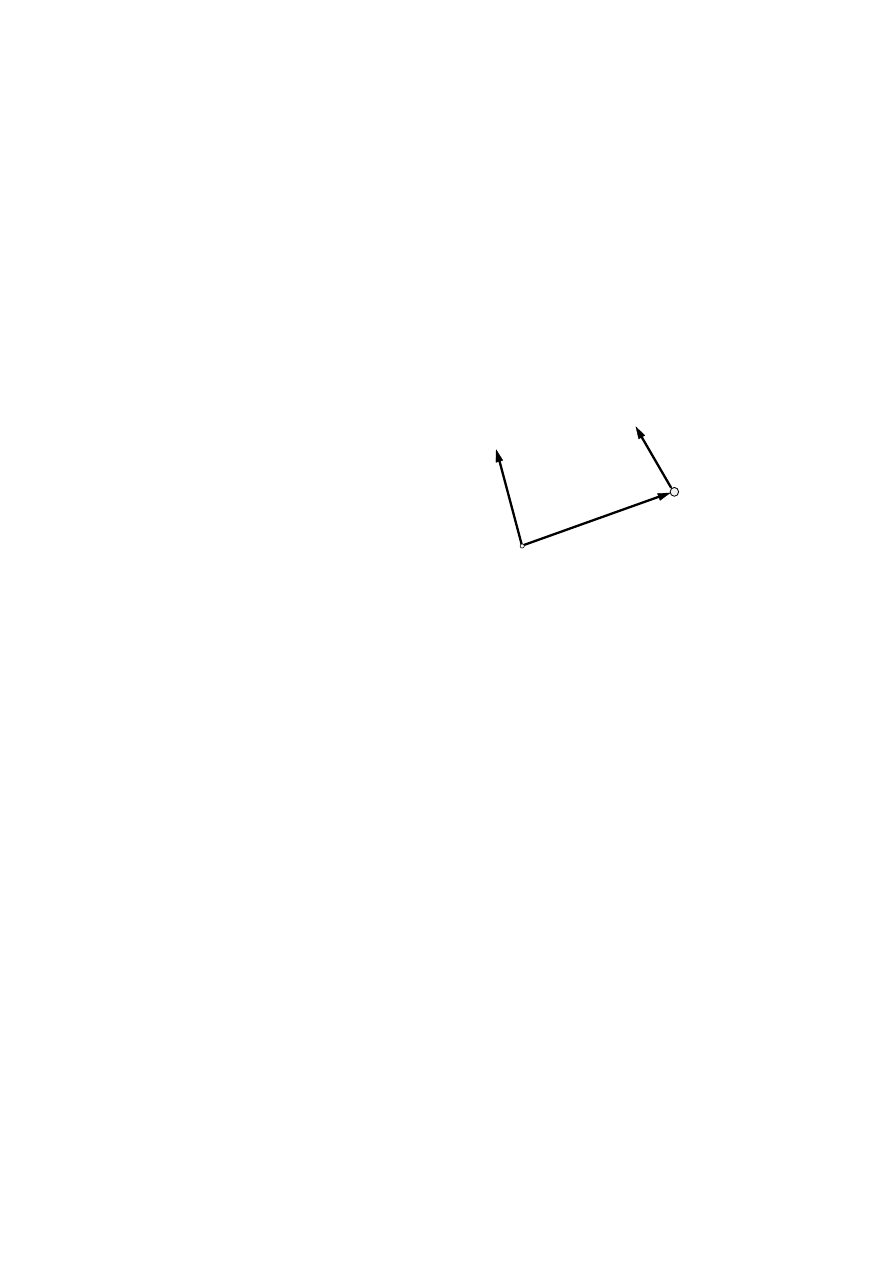
powyższej definicji wynika, że kręt

− zdefiniowany podobnie jak moment siły

względem punktu

− jest wektorem

prostopadłym do płaszczyzny
wyznaczonej przez punkt O i wektor
prędkości v (rys. 7.16).
Kręt punktu będzie równy zeru,
poza przypadkami trywialnymi (r = 0 i
v = 0), gdy wektory r i v będą
współliniowe.
Jeżeli będziemy mieli układ n
punktów materialnych o masach m

k

opisanych wektorami wodzącymi r

k

i

poruszających się z prędkością v

k

(rys. 7.17), to kręt tego układu materialnego

względem nieruchomego punktu O będzie równy sumie krętów (sumie momentów
pędów) nieruchomego punktu O będzie równy sumie krętów (sumie momentów
pędów)

k

o

m

mv

O

r

Rys. 7.16. Kręt (moment pędu) punktu

materialnego

∑

∑

=

=

×

=

×

=

n

1

k

k

k

k

n

1

k

k

k

O

m v

r

p

r

k

. (7.57)

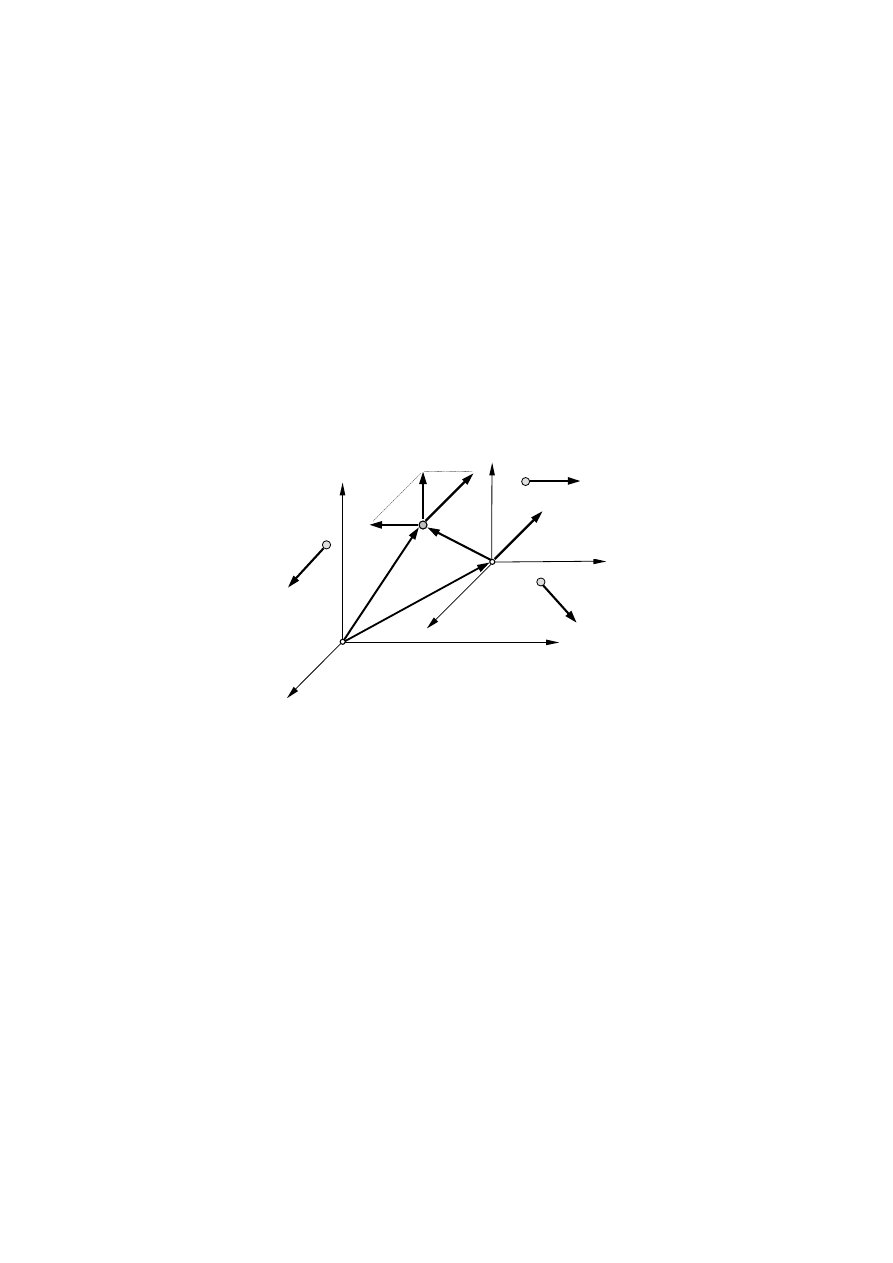
7.3.2. Redukcja krętu do środka masy

Wzór (7.57) opisuje kręt układu materialnego obliczony względem dowolnego
nieruchomego punktu O. Zadajmy sobie pytanie, jaki będzie kręt tego samego
układu materialnego względem środka masy C. W tym celu przyjmijmy w środku
masy C początek ruchomego układu współrzędnych o osiach

równoległych do odpowiednich osi nieruchomego układu współrzędnych x, y, z
(rys. 7.17). W tej sytuacji układ

′ ′ ′

x , y , z

′ ′ ′

x , y , z będzie się poruszał ruchem postępowym

względem układu nieruchomego x, y, z z prędkością środka masy v

C

.

v

1

v

2

r

C

r

Ck

m

k

z

x

′

z

′

y

′

y

x

r

k

C

O

m

1

v

k

m

2

m

n

v

n

v

C

v

C

v

Ck

Rys. 7.17. Rozkład prędkości układu punktów materialnych

Przy

takim

założeniu prędkość bezwzględna v

k

każdego punktu materialnego

względem układu nieruchomego x, y, z będzie sumą prędkości unoszenia równej
prędkości środka masy v

C

i prędkości względnej v

Ck

wzgędem układu ruchomego

, nazywanej dalej prędkością względem środka masy:

′ ′ ′

x , y , z

Ck

C

k

v

v

v

+

=

. (a)

Kręt rozpatrywanego układu punktów materialnych względem środka masy wyrazi
wzór:

∑

=

×

=

n

1

k

k

Ck

C

m

k

v

r

k

, (7.58)

gdzie r

Ck

jest promieniem wodzącym punkt materialny o masie m

k

w układzie

. Z rysunku 7.17 wynika, że promień wodzący r

′ ′ ′

x , y , z

k

jest równy sumie

promienia wodzącego środka masy r

C

i promienia r

Ck

:

Ck

C

k

r

r

r

+

=

.

Po wyznaczeniu z tej zależności

C

k

Ck

r

r

r

−

=

i podstawieniu do wzoru (7.58) otrzymamy:

(

)

∑

∑

∑

=

=

=

×

−

×

=

×

−

=

n

1

k

n

1

k

k

C

n

1

k

k

k

C

C

m

m

m

k

k

k

k

k

v

r

v

r

v

r

r

k

.

(b)

Pierwsza suma po prawej stronie tego wzoru, zgodnie ze wzorem (7.57), jest
krętem k

O

względem nieruchomego punktu O, druga zaś jest pędem omawianego

układu materialnego. Na podstawie wzoru (7.42) możemy zapisać:

C

n

1

k

k

m

m

v

v

p

k

=

=

∑

=

,

gdzie m jest masą całego układu. Zatem równanie (b) przyjmie postać:

C

C

O

C

mv

r

k

k

×

−

=

lub

C

C

C

O

mv

r

k

k

×

+

=

. (7.59)

Kręt k

O

układu punktów materialnych względem dowolnego nieruchomego

punktu O jest równy krętowi k

C

tego układu względem środka masy

powiększonemu o kręt

masy całkowitej skupionej w środku masy.

C

C

mv

r

×

Wzór (7.58) przedstawia kręt układu materialnego względem środka masy
obliczony dla ruchu bezwzględnego, ponieważ występująca w tym wzorze
prędkość v

k

jest prędkością względem nieruchomego układu odniesienia.

Zastanówmy się, czemu będzie równy kręt tego układu materialnego względem
środka masy wyznaczony dla ruchu względnego. W tym celu podstawmy do wzoru
(7.58) zależność (a).

(

)

.

m

m

m

m

m

m

m

m

n

1

k

Ck

k

Ck

n

1

k

k

Ck

C

n

1

k

Ck

k

Ck

C

n

1

k

k

Ck

n

1

k

n

1

k

Ck

k

Ck

C

k

Ck

n

1

k

Ck

C

k

Ck

n

1

k

k

k

Ck

C

∑

∑

∑

∑

∑

∑

∑

∑

=

=

=

=

=

=

=

=

×

+

×

−

=

×

+

×

⎟⎟

⎠

⎞

⎜⎜

⎝

⎛

=

=

×

+

×

=

+

×

=

×

=

v

r

r

v

v

r

v

r

v

r

v

r

v

v

r

v

r

k

Ale suma

∑

=

=

n

1

k

k

Ck

0

m

r

,

ponieważ moment statyczny układu względem środka masy jest równy zeru.
Ostatecznie mamy:

∑

∑

=

=

×

=

×

=

n

1

k

Ck

k

Ck

n

1

k

k

k

Ck

C

m

m

v

r

v

r

k

.

(7.60)

Z otrzymanej zależności wynika stwierdzenie:
Kręt układu punktów materialnych względem środka masy wyznaczony dla
ruchu bezwzględnego jest równy krętowi względem środka masy wyznaczonemu
dla ruchu względnego.

7.3.3. Kręt bryły

Wyznaczmy kręt bryły o masie m poruszającej się ruchem dowolnym, a więc

bryły swobodnej. Podobnie jak w kinematyce bryły (p. 5.3.2) przyjmiemy dwa
układy współrzędnych

− jeden nieruchomy o początku w nieruchomym punkcie

O i osiach x, y, z, a drugi ruchomy, sztywno związany z bryłą o osiach

(rys. 7.18) i początku nie w dowolnym punkcie

′ ′ ′

x , y , z

′

O , lecz w środku masy C. W

bryle wydzielmy myślowo element masy dm o wektorze wodzącym

r

r

r

′

+

=

C

, (c)

gdzie

.

z

y

x

,

z

y

x

C

C

C

C

k

j

i

r

k

j

i

r

′

′

+

′

′

+

′

′

=

′

+

+

=

Znając prędkość v

C

środka masy C i prędkość kątową

ω, możemy obliczyć

prędkość v dowolnego punktu bryły (wzór 5.32). Zatem prędkość elementarnej
masy dm

r

ω

v

v

′

×

+

=

C

. (d)

Zgodnie z definicją kręt elementu
masy dm względem nieruchomego
punktu O

d

dm

O

k

r v

= ×

∫

×

=

m

O

dm

v

r

k

.

Kręt bryły będzie równy całce z
powyższej zależności rozciągniętej
na całą masę m bryły:

.

Po podstawieniu do tego wzoru
zależności (c) i (d) otrzymamy:

(

) (

)

(

)

(

)

.

dm

dm

dm

dm

dm

m

C

m

C

m

m

C

C

C

C

∫

∫

∫

∫

′

×

ω

×

′

+

×

′

+

′

×

ω

×

+

×

=

′

×

ω

+

×

′

+

=

r

r

v

r

r

r

v

r

r

v

r

r

m

O

∫

+

k

v

x

z

x

′

z

′

y

′

y

r

C

r

′

r

dm

C

O

Rys. 7.18. Opis położenia dowolnego elementu

bryły sztywnej

Występujące pod całkami wielkości r

C

, v

C

i

ω nie podlegają całkowaniu i mogą

być wyciągnięte przed znaki całek:

(

)

.

dm

dm

dm

dm

m

m

C

m

C

m

C

C

O

∫

∫

∫

∫

′

×

×

′

+

′

×

−

⎟⎟

⎠

⎞

⎜⎜

⎝

⎛

′

×

×

+

×

=

r

ω

r

r

v

r

ω

r

v

r

k

Dwie środkowe całki są momentami statycznymi bryły względem środka masy,
a więc są równe zeru:

,

0

dm

m

∫

=

′

r

a pierwsza całka jest masą całkowitą bryły:

.

∫

=

m

dm

m

Ostatecznie kręt bryły możemy zapisać w postaci:

(

)

C

C

m

O

m

dm

v

r

r

ω

r

k

×

+

′

×

×

′

=

∫

. (7.61)

Całka występująca w tym wzorze jest krętem

bryły w jej ruchu względem

środka masy C z prędkością kątową

ω.

k

C

(

)

∫

′

×

×

′

=

m

C

dm

r

ω

r

k

. (7.62)

Zatem wzór (7.61) możemy zapisać w postaci:

C

C

C

O

m v

r

k

k

×

+

=

. (7.63)

Kręt k

O

bryły względem dowolnego nieruchomego punktu O jest równy krętowi

k

C

bryły względem środka masy C (w jej ruchu względem środka masy z

prędkością kątową

ω) powiększonemu o kręt r

v

C

m

C

×

masy m bryły

poruszającej się z prędkością v

C

środka masy.

Obecnie obliczymy współrzędne wektora k

C

w ruchomym układzie

współrzędnych

o początku w środku masy C (rys. 7.18). W tym układzie

współrzędnych wektory występujące we wzorze (7.62) mają następujące
współrzędne:

′ ′ ′

x , y , z

,

z

y

x

,

k

k

k

z

C

y

C

x

C

C

k

j

i

r

k

j

i

k

′

′

+

′

′

+

′

′

=

′

′

+

′

+

′

=

′

′

′

=

ω

.

z

y

x

k

j

i

′

ω

+

′

ω

+

′

ω

′

′

′

Po rozpisaniu podwójnego iloczynu wektorowego ze wzoru (7.62), zgodnie ze
wzorem (2.34) otrzymamy:

(

)

( )

(

)

.

dm

dm

r

dm

dm

m

2

m

m

C

∫

∫

∫

∫

′

⋅′

−

′

=

⋅′

′

−

′

⋅′

=

m

r

ω

r

ω

ω

r

r

r

r

ω

k

Pierwsza całka występująca po prawej stronie powyższego równania jest
biegunowym momentem bezwładności względem środka masy C:

( )

∫

′

=

m

2

C

dm

r

I

,

a więc

(

)

dm

I

m

C

C

∫

′

⋅′

−

=

r

ω

r

ω

k

. (7.64)

Współrzędne krętu k

C

otrzymamy po zrzutowaniu tego wektora na osie

:

′ ′ ′

x , y , z

−

ω

=

′

⋅

=

′

′

C

x

C

x

C

I

k

i

k

(

)

,

dm

x

m

∫

′

⋅′ ω

r

−

ω

=

′

⋅

=

′

′

C

y

C

y

C

I

k

j

k

(

)

,

dm

y

m

∫

′

⋅′ ω

r

−

ω

=

′

⋅

=

′

′

C

z

C

z

C

I

k

k

k

(

)

.

dm

z

m

∫

′

⋅′ ω

r

Po podstawieniu do tych wzorów iloczynu skalarnego:

=

⋅′ω

r

z

y

x

z

y

x

′

′

′

ω

′

+

ω

′

+

ω

′

oraz wyłączeniu przed całki współrzędnych prędkości kątowej otrzymujemy:

( )

( )

( )

.

dm

z

dm

z

y

dm

x

z

I

k

,

dm

z

y

dm

y

dm

y

x

I

k

,

dm

x

z

dm

y

x

dm

x

I

k

2

z

m

y

m

x

C

z

z

C

m

z

m

2

y

m

x

C

y

y

C

m

z

m

y

m

2

x

C

x

x

C

∫

∫

∫

∫

∫

∫

∫

∫

∫

′

ω

−

′

′

ω

−

′

′

ω

−

ω

=

′

′

ω

−

′

ω

−

′

′

ω

−

ω

=

′

′

ω

−

′

′

ω

−

′

ω

−

ω

=

′

′

′

′

′

′

′

′

′

′

′

′

′

′

′

Całki występujące w powyższych wzorach są zdefiniowanymi w p. 6.1.2
momentami bezwładności bryły względem odpowiednich płaszczyzn i momentami
dewiacyjnymi. Po wykorzystaniu zależności (6.7) i (6.9) między momentami

bezwładności względem bieguna, płaszczyzn i osi oraz odpowiednim
uporządkowaniu wyrazów współrzędne krętu k

C

bryły opisują wzory:

⎪

⎭

⎪

⎬

⎫

ω

+

ω

−

ω

−

=

ω

−

ω

+

ω

−

=

ω

−

ω

−

ω

=

′

′

′

′

′

′

′

′

′

′

′

′

′

′

′

′

′

′

′

′

′

′

′

′

′

′

′

.

I

D

D

k

,

D

I

D

k

,

D

D

I

k

z

z

z

y

y

x

z

x

z

C

z

y

z

y

y

y

x

x

y

C

x

z

z

y

x

y

x

x

x

C

(7.65)

Z

powyższych wzorów wynika, że do obliczenia krętu k

C

bryły swobodnej

względem środka masy C musimy znać wszystkie osiowe momenty bezwładności
i wszyskie momenty dewiacyjne, czyli tensor bezwładności. Wzory (7.65) znacznie
się upraszczają, gdy osie

′ ′ ′

x , y , z są głównymi centralnymi osiami bezwładności.

W tym przypadku, jak wiadomo z p. 6.5, wszystkie momenty dewiacyjne są równe
zeru i kręt

k

j

i

k

′

ω

+

′

ω

+

′

ω

=

′

′

′

′

′

′

z

z

y

y

x

x

C

I

I

I

. (7.66)

Jeżeli założymy, że osią obrotu bryły jest np. oś

z′ , to prędkość kątowa

ω pokryje

się z osią obrotu:

ω =

k

k

′

ω

=

′

ω

′

z

.

Wówczas kręt wyznaczony ze wzorów (7.65) ma postać:

k

j

i

k

′

ω

+

′

ω

−

′

ω

−

=

′

′

′

′

′

z

z

y

x

z

C

I

D

D

,

(7.67)

a na podstawie wzoru (7.66)

k

k

′

ω

=

′

z

z

C

I

. (7.68)

Z porównania wzorów (7.67) i (7.68) wynika, że jeżeli oś obrotu jest główną
centralną osią bezwładności, to wektor krętu leży na tej osi; gdy tak nie jest,
kierunek wektora krętu nie pokrywa się z osią obrotu.

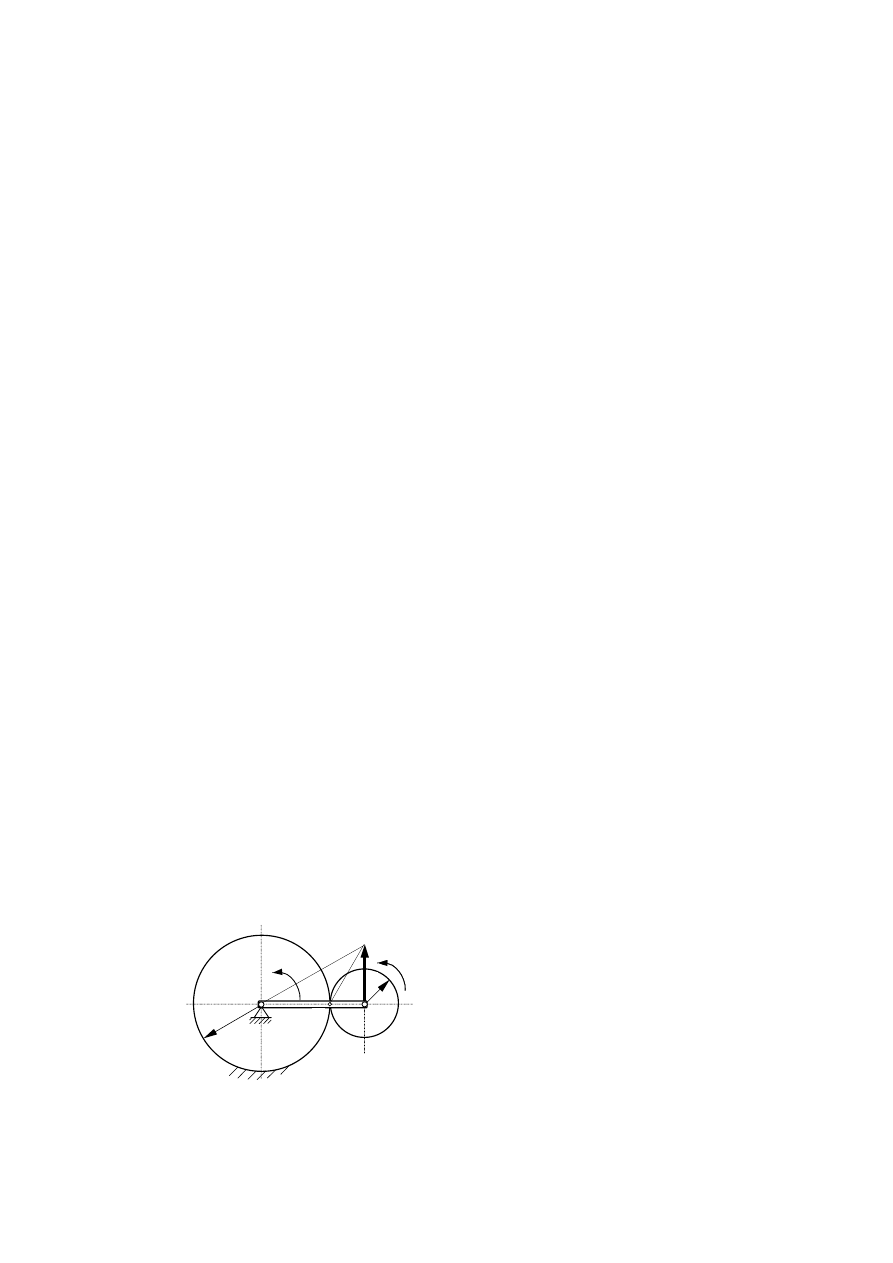
Przykład 7.9. Korba OA o masie m

m

1

=

obraca się z prędkością kątową

ω

0

wokół osi z przechodzącej przez punkt O i prostopadłej do płaszczyzny rys. 7.19.

Na końcu A korby jest osadzona cienka
jednorodna tarcza o masie

i

promieniu r, która toczy się bez poślizgu
po nieruchomym kole o promieniu R.
Wyznaczyć kręt układu względem osi z.
Korbę OA uważać za pręt jednorodny.

m

2

2

=

ω

2

O

A

r

ω

0

R

C

v

A

Rys. 7.19. Wyznaczenie krętu układu

m

Rozwiązanie

. Kręt układu względem osi z składa się z krętu

korby OA

poruszającej się ruchem obrotowym wokół osi z oraz krętu

tarczy poruszającej

się ruchem postępowym środka ciężkości A tarczy z prędkością

oraz ruchem

obrotowym z prędkością

względem osi

k

1z

k

z

2

v

A

ω

2

′

z równoległej do osi z i

przechodzącej przez środek tarczy:

z

2

z

1

z

k

k

k

+

=

. (a)

Kręt korby OA względem osi z

0

z

z

1

I

k

ω

=

. (b)

Kręt tarczy względem tej samej osi na podstawie wzoru (7.63) możemy wyrazić
zależnością:

(

)

A

2

2

z

z

2

v

m

r

R

I

k

+

+

ω

=

′

. (c)

We wzorach (b) i (c)

I i

są odpowiednio momentami bezwładności korby

względem osi z przechodzącej przez punkt O i tarczy względem osi
przechodzącej przez jej środek A. Zgodnie ze wzorami (f) i (a) z przykładu 6.2:

I

z

z

′

′

z

(

)

(

)

2

2

2

z

2

2

1

z

r

m

r

m

2

1

I

,

r

R

m

3

1

r

R

m

3

1

I

=

=

+

=

+

=

′

. (d)

Prędkość środka tarczy

(

)

0

A

r

R

v

ω

+

=

. (e)

Ponieważ punkt C (rys. 7.19) styku tarczy z nieruchomym kołem jest chwilowym
środkiem obrotu tarczy, mamy również:

,

r

v

2

A

ω

=

stąd

(

)

0

A

2

r

r

R

r

v

ω

+

=

=

ω

.

(f)

Po uwzględnieniu w związkach (b) i (c) wzorów (d), (e) i (f) oraz po ich
podstawieniu do równania (a) otrzymujemy kręt układu względem osi z.

(

)

(

)

(

)(

)

(

)(

)

.

r

10

R

7

r

R

m

3

1

r

R

r

R

m

2

r

r

R

r

m

r

R

m

3

1

k

0

0

0

2

0

2

z

ω

+

+

=

=

ω

+

+

+

ω

+

+

ω

+

=

7.3.4. Zasada krętu i pokrętu. Zasada zachowania krętu

Załóżmy, że mamy układ materialny składający się z n punktów materialnych
o masach m

k

poruszających się z prędkością v

k

(rys. 7.17). Na każdy punkt niech

działa siła zewnętrzna P

k

oraz siły wewnętrzne F

kl

. Zgodnie z drugim prawem

Newtona możemy dla dowolnego punktu rozważanego układu materialnego
napisać dynamiczne równanie ruchu:

wk

P

P

r

+

=

k

2

k

2

k

dt

d

m

lub

(

)

n

,

2

,

1

k

t

d

d

m

k

k

k

,

.

.

.

P

P

v

wk

=

+

=

W powyższym równaniu zgodnie ze wzorem (7.45) P

wk

jest wypadkową sił

wewnętrznych działających na punkt o masie m

k

. Pomnóżmy wektorowo każde z n

równań obustronnie przez wektor wodzący r

k

i dodajmy wszystkie równania

stronami. Otrzymamy:

(

)

∑

∑

∑

∑

=

=

=

×

+

×

=

+

×

=

×

n

1

k

wk

k

k

n

1

=

k

k

n

1

k

n

1

k

wk

k

k

k

k

k

t

d

d

m

P

r

P

r

P

P

r

v

r

. (e)

Druga suma po prawej stronie tego równania jest sumą momentów sił
wewnętrznych względem punktu O i jak wykazano w p. 7.1.4 (wzór 7.13), jest
równa zeru. Z kolei suma momentów sił zewnętrznych względem punktu O jest
równa momentowi głównemu (3.26):

k

n

1

=

k

k

o

P

r

M

×

=

∑

.

Sumę występującą po lewej stronie równania (e) możemy przekształcić:

(

)

(

)

.

dt

d

m

dt

d

m

dt

d

dt

d

m

dt

d

m

dt

d

m

O

n

1

k

n

1

k

k

k

k

k

k

k

k

k

n

1

k

k

n

1

k

n

1

=

k

k

k

k

k

k

k

k

k

k

v

r

v

r

v

r

v

r

v

v

v

r

=

×

=

×

=

=

×

=

⎟

⎠

⎞

⎜

⎝

⎛

×

+

×

=

×

∑

∑

∑

∑

∑

=

=

=

=

Wynika z tego, że lewa strona równania (e) jest pochodną krętu całego układu
materialnego względem nieruchomego punktu O. Ostatecznie otrzymujemy:

O

O

dt

d

M

k =

. (7.69)

Otrzymana zależność różniczkowa jest zasadą krętu.

Pochodna

względem czasu krętu układu punktów materialnych względem

dowolnego nieruchomego punktu jest równa momentowi głównemu wszystkich sił
zewnętrznych względem tego samego punktu.

Po obustronnym scałkowaniu równania (7.69) w granicach od 0 do t

otrzymamy:

( )

( )

∫

=

−

t

0

O

O

O

dt

0

t

M

k

k

. (7.70)

Całka występująca w tym równaniu nosi nazwę pokrętu momentu głównego, a
samo równanie jest zasadą krętu i pokrętu.
Przyrost

krętu układu materialnego względem dowolnego nieruchomego punktu

jest równy pokrętowi momentu głównego sił zewnętrznych względem tego samego
punktu.

Równania (7.69) i (7.70) są słuszne nie tylko dla układu punktów materialnych,
ale i dla bryły.
Często się zdarza, że moment główny układu sił zewnętrznych względem
obranego nieruchomego bieguna redukcji O jest stale równy zeru bądź jest
pomijalnie mały,

. Wtedy całka po prawej stronie równania (7.70) jest

równa zeru i zasada krętu i pokrętu przechodzi w zasadę zachowania krętu:

0

O

≡

M

( )

( )

( )

( )

const

0

t

czyli

0

0

t

O

O

O

O

=

=

=

−

k

k

,

k

k

lub

const

to

0

li

jeże

O

O

=

=

k

,

M

. (7.71)

Otrzymaną zasadę zachowania krętu można wyrazić słownie:

Jeżeli moment główny sił zewnętrznych względem nieruchomego punktu
redukcji O jest równy zeru, to kręt układu materialnego (bryły) względem tego
punktu jest wielkością stałą.

7.3.5. Redukcja zasady krętu i pokrętu do środka masy

Zastanówmy

się, jaką postać przyjmie zasada krętu i pokrętu (7.70), jeżeli za

biegun redukcji przyjmiemy nie dowolny punkt O, lecz środek masy układu
materialnego C. W celu udzielenia odpowiedzi na postawione pytanie podstawmy
do równania (7.69) wzór (7.59):

C

C

C

O

mv

r

k

k

×

+

=

oraz twierdzenie o momencie głównym (3.29):

W

r

M

M

×

+

=

C

C

O

i dokonajmy różniczkowania:

(

)

W

r

M

v

r

k

×

+

=

×

+

C

C

C

C

C

dt

m

d

dt

d

,

(

)

W

r

M

v

r

v

r

k

×

+

=

×

+

×

+

C

C

C

C

C

C

C

dt

m

d

m

dt

d

dt

d

.

(f)

Drugi wyraz po lewej stronie powyższego równania jest równy zeru, ponieważ jest
to iloczyn wektorowy wektorów równoległych:

0

m

m

dt

d

C

C

C

C

=

×

=

×

v

v

v

r

,

a pochodna występująca w trzecim wyrazie jest pochodną względem czasu pędu
układu materialnego, równą wektorowi głównemu układu sił zewnętrznych (7.48):

(

)

W

p

v

=

=

dt

d

dt

m

d

C

.

Po uwzględnieniu powyższych zależności w równaniu (f) i uproszczeniu
otrzymamy zasadę krętu przy redukcji do środka masy:

C

C

dt

d

M

k

=

. (7.72)

Z kolei po scałkowaniu tego równania od zera do t otrzymamy zasadę krętu
i pokrętu zredukowaną do środka masy układu:

( )

( )

∫

=

−

t

0

C

C

C

dt

0

t

M

k

k

. (7.73)

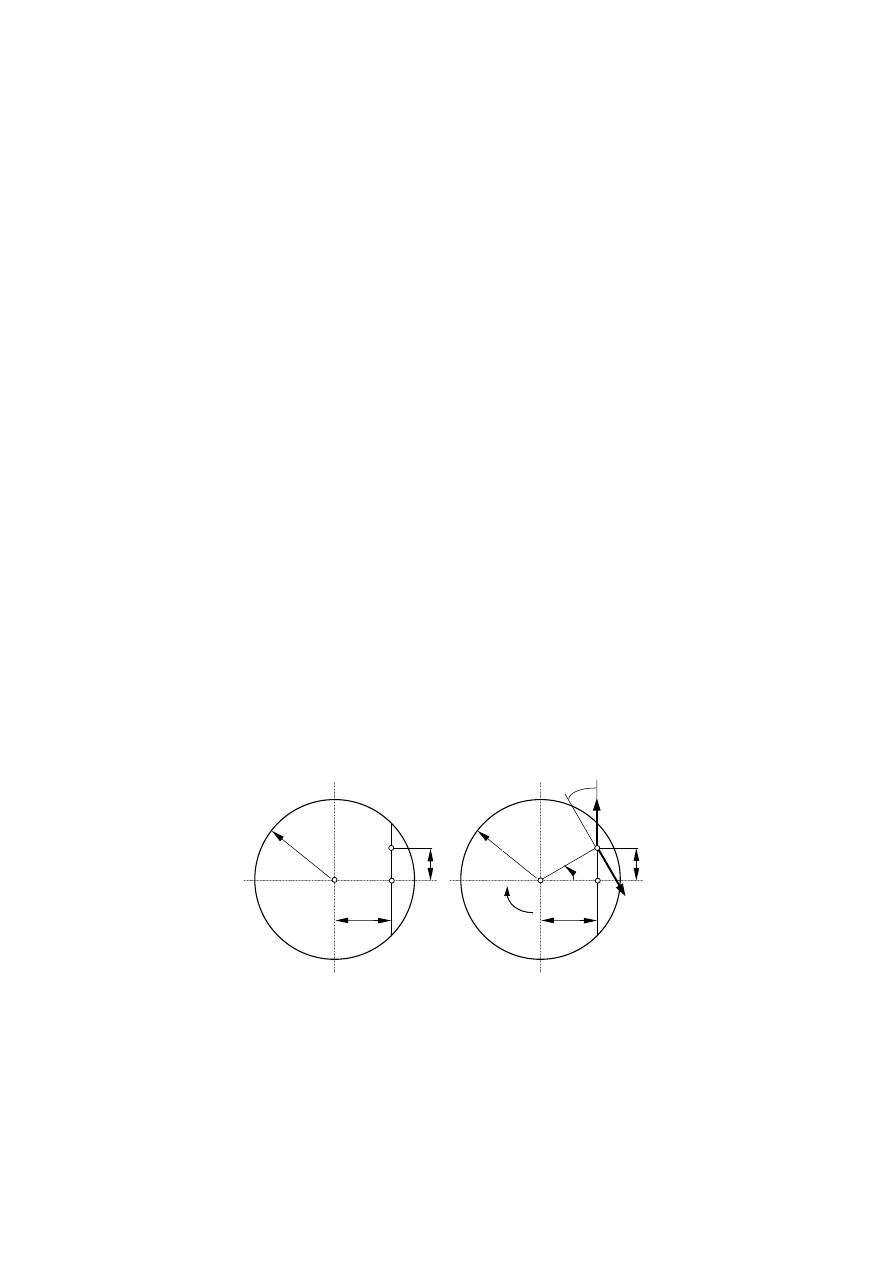
Widzimy,

że formalna postać otrzymanych równań (7.72) i (7.73) jest taka

sama jak równań (7.69) i (7.70), ale równania (7.72) i (7.73) nie opisują ruchu
środka masy C. Do opisu ruchu środka masy C należałoby zastosować zasadę pędu
(7.48).
Jeżeli założymy teraz, że moment sił zewnętrznych względem środka masy C
układu materialnego będzie stale równy zeru,

M

C

≡ 0 , to zasada krętu i pokrętu

(7.73) zredukowana do środka masy przejdzie w zasadę zachowania krętu
względem środka masy, co można zapisać w następujący sposób:

const

to

0

li

jeże

C

C

=

=

k

,

M

(7.74)

lub ująć słownie:

Jeżeli moment główny sił zewnętrznych względem środka masy układu
materialnego jest równy zeru, to kręt tego układu materialnego względem środka
masy jest wielkością stałą.

Przykład 7.10. Punkt materialny A o masie m

1

zaczął się poruszać wzdłuż

cięciwy BC (rys. 7.20a) poziomej jednorodnej tarczy kołowej o promieniu R i
masie m według równania:

sinkt

b

x

=

,

gdzie x oznacza współrzędną odmierzoną jak na rys. 7.20, k pewną stałą, a

2b BC

≤

. Tarcza może się obracać bez tarcia wokół osi pionowej z przechodzącej

przez środek tarczy O. Wyznaczyć prędkość kątową

ω tarczy w funkcji czasu t,

jeżeli odległość cięciwy od środka tarczy wynosi b, a tarcza w chwili początkowej

była nieruchoma.

t

= 0

O

A

R

O

A

R

v

w

r

ω

b

A

0

α

x

x

b

v

u

A

0

a)

b)

α

B

C

Rys. 7.20. Wyznaczenie prędkości kątowej tarczy

Rozwiązanie. Na układ działają siły zewnętrzne ciężkości tarczy i punktu
materialnego oraz reakcje w łożyskach osi obrotu tarczy. Siły ciężkości są
równoległe do osi obrotu, więc ich momenty względem osi obrotu są zawsze

równe zeru. Nie dają momentu względem tej osi również reakcje w łożyskach.
Zatem zgodnie z zasadą zachowania krętu (7.71) kręt układu względem osi nie
ulega zmianie. Ponieważ w chwili początkowej t

= 0 , gdy punkt A był jeszcze

nieruchomy, kręt układu był równy zeru, zatem w dowolnej chwili t kręt tego
układu również będzie równy zeru. Po rozpoczęciu ruchu punktu A tarcza zacznie
się poruszać ruchem obrotowym z prędkością kątową

do ruchu punktu (rys. 7.20b). Prędkość punktu tarczy, w którym w chwili t
znajduje się punkt A, czyli prędkość unoszenia punktu A

kt

sin

1

b

x

b

r

v

2

2

2

u

+

ω

=

+

ω

=

ω

=

.

Prędkość punktu A względem tarczy (prędkość względna)

coskt

bk

dt

dx

v

w

=

=

.

Z kolei prędkość bezwzględna punktu A jest równa sumie wektorowej prędkości
unoszenia i prędkości względnej:

w

u

A

v

v

v

+

=

.

Rzut wektora prędkości bezwzględnej punktu A na kierunek prostopadły do
promienia OA r

= jest równy

u

w

v

cos

v

−

α

.

Kręt układu w chwili t względem osi obrotu z składa się z krętu

punktu A

i krętu

tarczy względem tej osi. Kręt punktu A

k

1z

k

z

2

(

)

(

)

(

) (

)

(

)

[

]

,

kt

sin

1

b

coskt

k

b

m

x

b

kt

sin

1

b

coskt

k

b

m

r

kt

sin

1

b

b

v

m

r

v

cos

r

v

m

v

cos

v

r

m

k

2

2

2

1

2

2

2

2

1

2

w

1

u

w

1

u

w

1

z

1

+

ω

−

=

=

+

+

ω

−

=

+

ω

−

=

=

−

α

=

−

α

=

a kręt tarczy względem osi obrotu

ω

=

ω

=

2

z

z

2

mR

2

1

I

k

.

Ponieważ kręt całkowity układu jest w każdej chwili równy zeru, otrzymujemy:

(

)

[

]

0

mR

2

1

kt

sin

1

b

coskt

k

b

m

2

2

2

2

1

=

ω

−

+

ω

−

.

Z powyższego równania znajdujemy prędkość kątową tarczy:

(

)

2

2

2

1

2

1

mR

2

1

kt

sin

1

b

m

coskt

k

b

m

+

+

=

ω

.