Wykład z algebry - definicje i twierdzenia

Definicja (działanie wewnętrzne, struktura algebraiczna)

Działaniem wewnętrznym dwuargumentowym określonym (wykonalnym) w niepustym zbiorze A nazywamy każdą funkcję

Przyjmujemy oznaczenie:

Niepusty zbiór A z określonym działaniem wewnętrznym nazywamy strukturą algebraiczną i oznaczamy
.

Definicja (grupa)

Strukturę
nazywamy grupą jeśli jednocześnie zachodzą warunki:

1. 
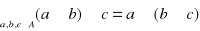
   - łączność

2. 
   
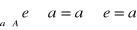
   - istnienie elementu neutralnego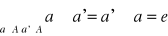

3. 
   - istnienie elementu symetrycznego (a')

Jeśli ponadto zachodzi

4. 
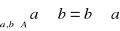
   - przemienność

to
nazywamy grupą przemienną (inaczej grupą abelową).

Definicja (pierścień)

Jeśli w zbiorze
są określone dwa dwuargumentowe działania
oraz
, ponadto
jest grupą przemienną i zachodzi

5. 
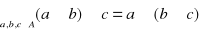
   - łączność działania
   

6. 
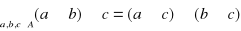
   - rozdzielność działania
   względem
   

to
nazywamy pierścieniem.

Definicja (ciało)

Ciałem nazywamy pierścień
w którym zachodzi ponadto

7. 
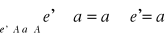
   - istnienie elementu neutralnego działania
   

8. 
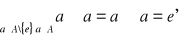
   - istnienie elementu symetrycznego (
   )

9. 
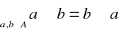
   - przemienność działania
   

Przyjęte są następujące oznaczenia i terminologia

Symbol	Oznaczenie	Określenie
	+	dodawanie
		mnożenie
e	0	element zerowy
e'	1	jedność
a'	-a	element przeciwny do a
		element odwrotny do a

Twierdzenie

Ciało zawiera co najmniej dwa elementy (
). W ciele

Rozważmy ciało
. Przyjmijmy, że
. Wtedy rozwiązaniem równania
są liczby urojone i oraz -i.

Definicja (ciało liczb zespolonych)

Ciałem liczb zespolonych nazywamy zbiór liczb postaci
z dodawaniem + i z mnożeniem
.

Uwaga

Twierdzenie

Ciało
jest to najmniejsze ciało (w sensie inkluzji) zawierające ciało
oraz liczbę urojoną i

Definicja (ciało liczbowe)

Ciało
oraz każdy podzbiór C, który ze względu na działania + i
jest ciałem (podciało) nazywamy ciałem liczbowym.

Twierdzenie

Najmniejszym ciałem liczbowym w sensie inkluzji jest ciało liczb wymiernych
.

Twierdzenie (zasadnicze twierdzenie algebry)

Każdy wielomian stopnia dodatniego o współczynnikach zespolonych rozkłada się w C na czynniki liniowe.

Definicja (struktury izomorficzne)

Dwie struktury algebraiczne nazywamy izomorficznymi jeśli istnieje funkcja odwzorowująca wzajemnie jednoznacznie jedną strukturę na drugą zachowująca wszystkie działania.

Definicja (przestrzeń liniowa)

Niech
będzie ciałem liczbowym oraz
będzie grupą przemienną z pewnym działaniem
. Określmy ponadto działanie zewnętrzne
takie, że:

1. 
   

2. 
   

3. 
   

4. 
   

Wówczas strukturę
nazywamy przestrzenią liniową (wektorową) nad ciałem K. Elementy zbioru V nazywamy wektorami a elementy zbioru K nazywamy skalarami.

Definicja (macierz)

Rozważmy dwa podzbiory zbioru N (liczb naturalnych):
,
oraz zbiór
. Macierzą o p wierszach oraz s kolumnach nazywamy funkcję
.

Dla
oraz
przyjmujemy
.

Macierz zapisujemy w postaci tabeli
.

Jeśli,
to macierz nazywamy kwadratową.

Liczby
nazywamy wyrazami macierzy
.

Macierz
nazywamy przeciwną do
.

Macierz dla której wszystkie wyrazy są zerami nazywamy zerową i oznaczamy
.

Macierz kwadratową dla której
oraz
dla
nazywamy diagonalną.

Jeśli
, to macierz nazywamy jednostkową i oznaczamy
.

Macierz
dla której
nazywamy symetryczną, a taką dla której
- antysymetryczną.

Zbiór wszystkich macierzy o p wierszach i s kolumnach oznaczamy
.

Niech
oraz
.

Definicja (suma macierzy)

Sumą macierzy
nazywamy macierz
taką, że
gdzie
,
.

Definicja (iloczyn macierzy przez skalar)

Iloczynem macierzy
przez skalar
(symbolicznie
) nazywamy macierz
taką, że
.

Twierdzenie

Struktura
jest przestrzenią liniową.

Definicja (macierz transponowana)

Macierzą transponowaną do macierzy
nazywamy macierz
taką, że
.

Definicja (iloczyn macierzy)

Niech
oraz
,
i
. Iloczynem
nazywamy macierz
taką, że
.

Twierdzenie

Struktura
jest pierścieniem nieprzemiennym
z jedynką.

Uwaga

Jedynką tego pierścienia jest macierz jednostkowa.

Twierdzenie

Iloczyn macierzy diagonalnych jest macierzą diagonalną.

Definicja (macierz odwracalna)

Macierz
(kwadratową) nazywamy odwracalną, jeśli istnieje macierz
taka, że
. Macierz
nazywamy odwrotną do
.

Uwaga

Macierz kwadratowa ma co najwyżej jedną macierz odwrotną.

Twierdzenie

Definicja (wyznacznik)

Wyznacznikiem macierzy kwadratowej
(oznaczenia detA lub |A|).

nazywamy dla

p=1

p>1

gdzie

- jest to algebraiczne dopełnienie
. Macierz
jest to macierz powstała z A przez skreślenie i-tego wiersza oraz j-tej kolumny. Wyznacznik
nazywamy minorem stopnia pierwszego macierzy A.

Twierdzenie Laplace'a: Niech A∈M_nn

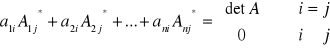
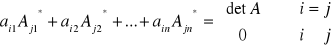
oraz

Własności wyznaczników

1. det A^T = det A.

2. Jeżeli w wyznaczniku zamienimy miejscami dwa dowolne wiersze (kolumny), to wartość wyznacznika zmieni się na przeciwną.

3. Aby wyznacznik pomnożyć przez liczbę należy wszystkie elementy dowolnego wiersza (kolumny) pomnożyć przez tę liczbę.

4. Jeżeli w wyznaczniku wszystkie elementy znajdujące się nad (lub pod) diagonalą są równe zeru, to wartość wyznacznika równa jest iloczynowi elementów diagonali. O takim wyznaczniku mówimy, że ma postać trójkątną.

5. Jeżeli w wyznaczniku
   a) wszystkie elementy pewnego wiersza (kolumny) są równe zeru lub
   b) dwa wiersze (kolumny) są identyczne lub
   c) wszystkie elementy pewnego wiersza ( kolumny ) są proporcjonalne do odpowiednich elementów innego wiersza (kolumny) lub
   d) pewien wiersz (kolumna) jest kombinacją liniową pozostałych wierszy (kolumn) , to wartość wyznacznika równa jest zeru.

6. Jeżeli w wyznaczniku do elementów pewnego wiersza (kolumny) dodamy odpowiednie elementy innego wiersza (kolumny) pomnożone przez jedną i tę samą liczbę, to wartość wyznacznika nie ulegnie zmianie.

7. Wyznacznik jest różny od zera wtedy i tylko wtedy, gdy jego wiersze (kolumny) są liniowo niezależne.

8. Twierdzenie Cauchy'ego. Jeżeli A i B są macierzami tego samego stopnia to
   
   det(A·B) = detA·detB

Definicja (macierz nieosobliwa)

Macierz A nazywamy nieosobliwą jeśli
.

Twierdzenie

Macierz jest odwracalna wtedy i tylko wtedy gdy jest nieosobliwa.

Definicja

Macierz A nazywamy ortogonalną jeśli
.

Twierdzenie

Jeśli A jest ortogonalna to
oraz
jest ortogonalna.

Definicja

Niech
,
,
,
,
,
.Wówczas układ równań AX=B nazywamy układem Cramera jeśli A jest nieosobliwa.

Twierdzenie Cramera

Jeżeli układ n równań liniowych o n niewiadomych, ma nieosobliwą macierz A współczynników przy niewiadomych, to układ ten ma jedyne rozwiązanie dane wzorami Cramera

gdzie A_i jest wyznacznikiem powstałym z wyznacznika macierzy A, przez zastąpienie w nim kolumny współczynników przy niewiadomej x_i kolumną wyrazów wolnych.

Układ równań Cramera jest oznaczony.

Definicja (liniowa kombinacja)

Jeśli V jest przestrzenią liniową nad ciałem liczbowym K oraz
to mówić będziemy, że
jest liniową kombinacją wektorów
jeśli istnieją skalary
takie, że
.

Definicja (wektory liniowo zależne)

Wektory
nazywamy liniowo zależnymi jeśli istnieje ich liniowa kombinacja o współczynnikach nie znikających jednocześnie, równa wektorowi zerowemu.

Wektory, które nie są liniowo zależne nazywamy liniowo niezależnymi.

Definicja

Zbiór wszystkich liniowych kombinacji wektorów
przestrzeni liniowej V jest przestrzenią liniową (podprzestrzenią liniową V), oznaczamy ją
.

Definicja (baza p-ni liniowej)

Bazą przestrzeni liniowej V nazywamy układ liniowo niezależnych wektorów
taki, że
.

Moc bazy nazywamy wymiarem V i oznaczamy dimV. Jeśli baza jest skończona (nieskończona) mówimy, że V jest skończenie (nieskończenie) wymiarowa.

--------------------------------------------------------------------------------------------------------------

Jeżeli
i jest zapisany w bazie kanonicznej oraz
oznacza ten sam wektor zapisany w nowej bazie
to zachodzi wzór:
, gdzie
.

Definicja (rząd macierzy)

Niech
mówimy, że rzędem macierzy A jest liczba t, rzA = t jeśli istnieje minor macierzy A stopnia t, różny od zera oraz każdy minor stopnia większego niż t jest równy zero.

Twierdzenie

Niech
oraz
oznaczają kolumny A
to

Własności rzędu macierzy

Poniższe operacje nie zmieniają rzędu macierzy (chociaż zmieniają samą macierz):

1. transpozycja

2. odrzucenie wiersza (kolumny) złożonego z samych zer

3. pomnożenie lub podzielenie wszystkich elementów pewnego wiersza (kolumny) przez tę samą liczbę różną od zera

4. dodanie do elementów pewnego wiersza (kolumny) odpowiednich elementów innego wiersza (kolumny) pomnożonych przez tę samą liczbę

5. dodanie do elementów pewnego wiersza (kolumny) kombinacji liniowej odpowiednich elementów pozostałych wierszy (kolumn)

6. odrzucenie jednego z dwóch wierszy (kolumn) o odpowiednich elementach proporcjonalnych

7. odrzucenie wiersza (kolumny) będącego kombinacją liniową pozostałych wierszy (kolumn).

Twierdzenie Kroneckera Capelliego

Niech
,
,
wówczas układ równań liniowych AX=B ma rozwiązanie wtedy i tylko wtedy gdy rzA=rz[A|B] gdzie [A|B] jest to macierz uzupełniona, powstała z A przez dopisanie do niej kolumny B (wyrazów wolnych) jako ostatniej.

Definicja (układ jednorodny)

Układ równań liniowych AX=
nazywamy jednorodnym.

Twierdzenie

Zbiór
jest przestrzenią liniową ( podprzestrzenią liniową
). Jej bazę nazywamy fundamentalnym układem rozwiązań równania jednorodnego AX=
.

Twierdzenie

Jeżeli
jest bazą przestrzeni liniowej V nad ciałem liczbowym K to dla każdego wektora
istnieje dokładnie jeden ciąg skalarów
taki, że
ciąg
nazywamy współrzędnymi
w bazie
.

Twierdzenie

Każda niezerowa przestrzeń liniowa ma co najmniej jedną bazę i jednoznacznie wyznaczony wymiar.

Każdy układ liniowo niezależny wektorów V można uzupełnić do bazy przestrzeni liniowej V.

Definicja

Rozważmy przestrzeń liniową
złożoną z n-elementowych ciągów o wyrazach z ciała liczbowego K. Układ wektorów
takich, że
(na i-tym miejscu jest 1) stanowi bazę
. Nazywamy ją bazą kanoniczną.

Twierdzenie

Wektory
stanowią bazę
wtedy i tylko wtedy gdy
.

Definicja

Macierzą przejścia od bazy kanonicznej
do nowej bazy
nazywamy macierz
, której kolumnami są wektory
. Macierz B jest nieosobliwa.

Definicja (przestrzeń afiniczna)

Niech dana będzie przestrzeń liniowa

nad ciałem liczbowym K, zbiór
oraz funkcja
taka, że

1. 
   

2. 
   

to strukturę
nazywamy przestrzenią afiniczną stowarzyszoną z przestrzenią liniową V. Elementy E nazywamy punktami .

Jeśli przyjąć oznaczenia
to warunki 1) i 2) można zapisać:

1. 
   

2. 
   .

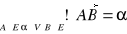
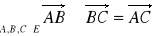
Własności:

Definicja (przesunięcie przestrzeni afinicznej)

Jeśli
to istnieje jeden
taki, że
. Punkt
nazywamy sumą punktu
i wektora
:
. Jeśli ustalimy
to odwzorowanie
takie, że
nazywamy przesunięciem przestrzeni afinicznej
o wektor
.

Twierdzenie

Jeśli dany jest układ równań liniowych

,
,
o wyrazach z ciała liczbowego K,
oraz stowarzyszony z nim układ jednorodny
oraz
,
,
, to
.

GEOMETRIA !!!

Wektory w przestrzeni Rⁿ.

Długość wektora a którą oznaczać będziemy  a  wyraża się wzorem

|a| =

Kątami kierunkowymi wektora a nazywamy kąty _i jakie wektor a tworzy z kolejnymi osiami układy współrzędnych, zaś kosinusy tych kątów nazywamy kosinusami kierunkowymi wektora a. Kosinusy kierunkowe wektora a określają wzory

Suma kwadratów kosinusów kierunkowych dowolnego wektora równa jest jedności.

Wektory w przestrzeni R³. W przestrzeni R³ wektor ma postać a = [a_x,a_y,a_z]^T, gdzie
.

ab = [a_x,a_y,a_z]^T  [b_x, b_y,b_z]^T =

Równoległość i prostopadłość wektorów

a  a₁b₁ + a₂b₂ + a₃b₃ = 0.

Iloczyn mieszany wektorów.

(ab)c =

Płaszczyzna i prosta.

Równania parametryczne płaszczyzny. Niech P(x,y,z) będzie dowolnym punktem płaszczyzny π,  Zatem wektory [x-x₀,y-y₀,z-z₀]^T oraz u i v są komplanarne, a to oznacza, że są liniowo zależne. Istnieją więc stałe t i s takie, że

tu + sv, gdzie t,sR.

gdzie t,sR.

Te równania skalarne nazywamy równaniami parametrycznymi płaszczyzny.

Równanie ogólne płaszczyzny.

Równaniu temu można nadać postać

A(x-x₀) + B(y-y₀) + C(z-z₀) = 0 (*)

lub Ax + By + Cz + D = 0.

Ostatnie równanie nazywamy równaniem ogólnym płaszczyzny.

Weźmy pod uwagę wektor n = [A,B,C]^T . Łatwo zauważyć, że jest on iloczynem wektorowym wektorów u i v :

n = u  v = = [A,B,C]^T

Wektor n = [A,B,C]^T nazywamy wektorem normalnym płaszczyzny π. .

L.p.	wektor n	równanie	położenie płaszczyzny
	A=0	By + Cz + D = 0	równoległa do osi Ox
	B=B=0	Ax + Cz + D = 0	równoległa do osi Oy
	C=0	Ax + By + D =0	równoległa do osi Oz
	D=0	Ax + By + Cz =0	zawiera początek układu współrzędnych
	A=B=0	Cz + D = 0 lub z=c	prostopadła do osi Oz, równoległa do plaszcz. Oxy
	A=C=0	By + D = 0 lub y=b	prostopadła do osi Oy, równoległa do plaszcz. Oxz
	B=C=0	Ax + D = 0 lub x=a	prostopadła do osi Ox, równoległa do plaszcz. Oyz
	A=D=0	By + Cz = 0	zawiera oś Ox
	B=D=0	Ax + Cz = 0	zawiera oś Oy
	C=D=0	Ax + By = 0	zawiera oś Oz
	A=B=D=0	z = 0	równanie płaszczyzny Oxy
	A=C=D=0	y = 0	równanie płaszczyzny Oxz
	B=C=D=0	x = 0	równanie płaszczyzny Oyz

,

Z równania normalnego łatwo można otrzymać wzór na odległość dowolnego punktu P₀(x₀,y ₀,z₀) od płaszczyzny określonej równaniem normalnym

lub od płaszczyzny określonej równaniem ogólnym

Jest to równanie odcinkowe płaszczyzny.

Wzajemne położenie dwóch płaszczyzn

Rząd macierzy	Układ równań, liczba param.	Położenie płaszczyzn
r(A)r(U)	Sprzeczny	płaszczyzny są równoległe
r(A)=r(U)=1	nieoznaczony, p = n-r = 2	płaszczyzny pokrywają się
r(A)=r(U)=2	nieoznaczony, p = n-r = 1	płaszczyzny mają wspólną prostą

Równania parametryczne prostej l.

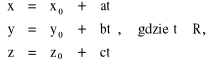
Równania kierunkowe prostej

Równania krawędziowe prostej.

jest ,

Wzajemne położenie dwóch prostych. Dane są dwie proste l₁ i l₂

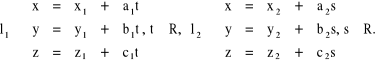
	wektory są równoległe	wektory nie są równoległe
proste mają punkt wspólny	proste pokrywają się	proste przecinają się
proste nie mają punktu wspólnego	proste równoległe	proste są skośne

Pęk płaszczyzn

_(A₁x+B₁y+C₁z+D₁)+_(A₂x+B₂y+C₂z+D₂)  

Definicja (przekształcenie liniowe)

Niech
,
będą przestrzeniami liniowymi nad ciałem liczbowym K. Przekształcenie
takie, że
nazywamy przekształceniem liniowym.

Jeśli
jest bazą
oraz
jest bazą
, to macierz
której kolumnami są odpowiednio współrzędne wektorów
w bazie
nazywamy macierzą przekształcenia
w ustalonych bazach. W zapisie macierzowym oznacza to że
.

Definicja (jądro i obraz przekształcenia g)

Jeśli
jest przekształceniem liniowym
, to zbiór
nazywamy jądrem
. Zbiór ten jest przestrzenią liniową (podprzestrzenią liniową
), a
nazywamy defektem i oznaczamy
.

Zbiór
nazywamy obrazem
. Ten zbiór również jest przestrzenią liniową (podprzestrzenią liniową
),
nazywamy rzędem przekształcenia
i oznaczamy
.

Twierdzenie

Odwzorowanie
jest różnowartościowe wtedy i tylko wtedy gdy
. Ponadto
oraz
, gdzie
jest macierzą
w dowolnych bazach.

Twierdzenie

Niech
oraz
będzie macierzą przekształcenia przy ustalonych bazach
oraz
. Jeśli
jest macierzą przejścia od bazy
do nowej bazy
natomiast
jest macierzą przejścia od
do nowej bazy
, to macierzą
w bazach
i
jest macierz
postaci:

.

Definicja (wyznacznik macierzy przekształcenia)

Jeśli przekształcenie liniowe
, to wyznacznikiem
,
nazywamy wyznacznik macierzy przekształcenia w dowolnych bazach.

Definicja (podprzestrzeń liniowa niezmiennicza)

Niech
. Podprzestrzeń liniową
nazywamy niezmienniczą względem odwzorowania liniowego
jeśli

Twierdzenie

Jeśli
jest niezmiennicza, to istnieje skalar
taki, że
.

Definicja (wektor własny , wartość własna)

Wektor
nazywamy wektorem własnym względem odwzorowania liniowego
jeśli
oraz
jest podprzestrzenią niezmienniczą względem
. Skalar
taki, że
nazywamy wartością własną.

Definicja (macierz charakterystyczna, wielomian charakterystyczny, równanie charakterystyczne)

Jeśli
jest macierzą przekształcenia liniowego
, to macierz
nazywamy macierzą charakterystyczną
, wielomian
nazywamy wielomianem charakterystycznym
, a równanie
nazywamy równaniem charakterystycznym
.

Twierdzenie

Wielomian charakterystyczny nie zależy od wyboru bazy.

Twierdzenie

Na to by liczba
była wartością własną przekształcenia liniowego
potrzeba i wystarcza by
.

Twierdzenie

Zbiór wektorów własnych
o wartości własnej
uzupełniony o wektor zerowy jest niezmienniczą przestrzenią liniową , oznaczamy ją
,
, gdzie
- macierz przekształcenia.

Twierdzenie

Jeśli
wektory własne przekształcenia liniowego
mają różne wartości własne, to są liniowo niezależne.

Twierdzenie

Jeśli
ma n różnych wartości własnych
oraz dla

jest wektorem własnym o wartości własnej
, to
tworzą bazę
. W bazie tej
ma macierz diagonalną , której główną przekątną (diagonalę) tworzą liczby
.

Twierdzenie. Jeśli
ma n liniowo niezależnych wektorów własnych, to macierz
której kolumnami są kolejne wektory własne
nazywamy diagonalizującą
. Macierz
jest diagonalna.

Twierdzenie Cayleye'a Hamiltona

Każda macierz kwadratowa spełnia swoje równanie charakterystyczne, traktowane jako równanie macierzowe.

Definicja (forma liniowa)

Niech
,
- ciało liczb rzeczywistych,
- baza
. Odwzorowanie
takie, że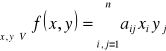
,
nazywamy formą liniową , gdzie
.

Macierz
nazywamy macierzą formy,
-rzędem formy,
- wyróżnikiem formy.

Jeśli
to mówimy, że
jest nieosobliwa.

Jeśli
to mówimy, że
jest symetryczna.

Definicja (forma kwadratowa)

Jeśli
jest dwuliniową symetryczną formą, to funkcję
nazywamy formą kwadratową formy dwuliniowej
. Jeśli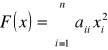
to mówimy, że
jest postaci kanonicznej.

Każdą formę kwadratową można sprowadzić do postaci kanonicznej. Ilość współczynników dodatnich w każdej postaci kanonicznej formy jest taka sama.

Definicja (forma dodatnio określona)

Formę
nazywamy dodatnio (ujemnie, niedodatnio, nieujemnie) określoną jeśli
(
).

Twierdzenie

Na to by
była dodatnio określona potrzeba i wystarcza by

1. minory główne macierzy formy
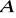
   były dodatnie lub

2. wszystkie wartości własne macierzy formy były dodatnie lub

3. 
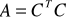
   , gdzie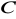
   - jest pewną nieosobliwą macierzą.

Definicja (iloczyn skalarny, przestrzeń euklidesowa)

Formę dwuliniową symetryczną dodatnio określoną
(
- przestrzeń liniowa nad
) nazywamy iloczynem skalarnym , a strukturę
nazywamy przestrzenią euklidesową.

Twierdzenie

W każdej skończenie wymiarowej przestrzeni euklidesowej
można utworzyć bazę ortonormalną.

2

9

---