KOD
ZDAJÑCEGO
Miejsce na naklejk´ z kodem
LISTOPAD
ROK 2009
Za rozwiàzanie
wszystkich zadaƒ
mo˝na otrzymaç
∏àcznie 50 punktów.
PESEL ZDAJÑCEGO
Wpisuje zdajàcy przed rozpocz´ciem pracy
ARKUSZ PRÓBNEJ
MATURY Z OPERONEM
MATEMATYKA
POZIOM PODSTAWOWY
Czas pracy 170 minut
Instrukcja dla zdajàcego
1.
Sprawdê, czy arkusz zawiera 15 stron.
2.
W zadaniach od 1. do 20. sà podane 4 odpowiedzi:
A, B, C, D, z których tylko jedna jest prawdziwa. Wy-
bierz tylko jednà odpowiedê.
3.
Rozwiàzania zadaƒ od 21. do 31. zapisz starannie i czy-
telnie w wyznaczonych miejscach. Przedstaw swój tok
rozumowania prowadzàcy do ostatecznego wyniku.
4.
Pisz czytelnie. U˝ywaj d∏ugopisu/pióra tylko z czarnym
tuszem/atramentem.
5.
Nie u˝ywaj korektora. B∏´dne zapisy przekreÊl.
6.
Pami´taj, ˝e zapisy w brudnopisie nie podlegajà ocenie.
7.
Obok numeru ka˝dego zadania podana jest maksymal-
na liczba punktów mo˝liwych do uzyskania.
8.
Mo˝esz korzystaç z zestawu wzorów matematycznych,
cyrkla i linijki oraz kalkulatora.
˚yczymy powodzenia!
Arkusz opracowany przez Wydawnictwo Pedagogiczne OPERON.
Kopiowanie w ca∏oÊci lub we fragmentach bez zgody wydawcy zabronione. Wydawca zezwala na kopiowanie zadaƒ
przez dyrektorów szkó∏ bioràcych udzia∏ w programie Próbna Matura z OPERONEM.
2
Matematyka. Poziom podstawowy
Próbna Matura z OPERONEM i „Gazetà Wyborczà”
ZADANIA ZAMKNI¢TE
W zadaniach od 1. do 20. wybierz i zaznacz na karcie odpowiedzi jednà poprawnà odpowiedê.
Zadanie 1. (1 pkt)
Liczba 27
9
2
6
$
-
jest równa:
A. 9
5
B. 3
16
C. 6
4
D. 3
6
Zadanie 2. (1 pkt)
Kàt
a jest ostry i sin
7
2
=
a
. Wtedy cos
a jest równy:
A.
49
45
B.
7
3 5
C.
7
5
D.
7
5 3
Zadanie 3. (1 pkt)
Zaznacz, na którym rysunku jest przedstawiony zbiór rozwiàzaƒ nierównoÊci
<
x
2
4
-
.
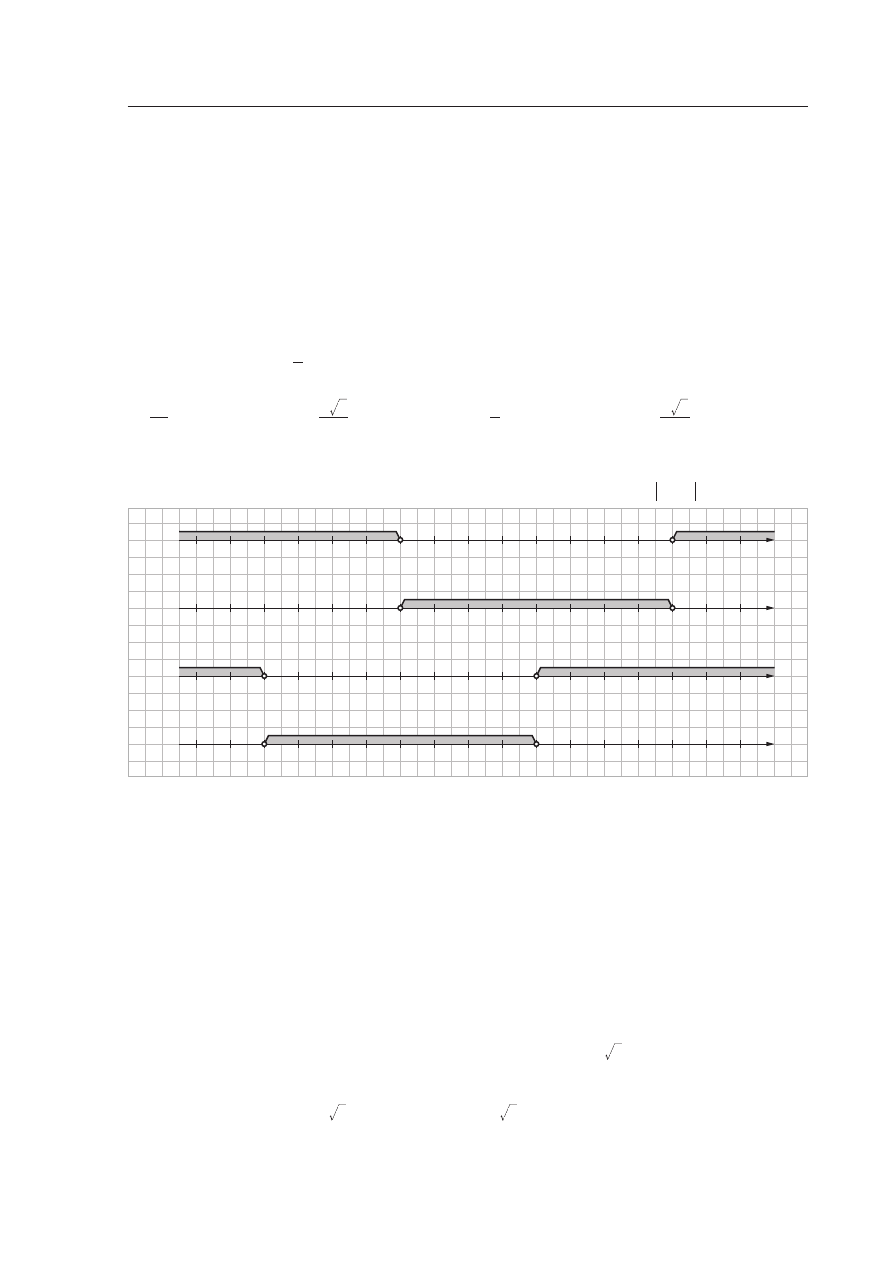
Zadanie 4. (1 pkt)
Dany jest okràg o równaniu (
)
(
)
x
y
3
2
16
2
2
+
+
+
=
. D∏ugoÊç tego okr´gu jest równa:
A. 16
r
B. 8
r
C. 4
r
D. 6
r
Zadanie 5. (1 pkt)
Obj´toÊç szeÊcianu jest równa 125. Pole powierzchni ca∏kowitej tego szeÊcianu jest równe:
A. 25
B. 100
C. 250
D. 150
Zadanie 6. (1 pkt)
WysokoÊç trójkàta równobocznego wpisanego w okràg jest równa 6 3. Promieƒ tego okr´gu jest
równy:
A. 4
B. 2 3
C. 4 3
D. 6
X
– 6
– 7
– 8
A.
– 5
– 4
– 3
– 2
– 1
2
1
0
3
4
5
6
7
8
X
– 6
– 7
– 8
B.
– 5
– 4
– 3
– 2
– 1
2
1
0
3
4
5
6
7
8
X
– 6
– 7
– 8
C.
– 5
– 4
– 3
– 2
– 1
2
1
0
3
4
5
6
7
8
X
– 6
– 7
– 8
D.
– 5
– 4
– 3
– 2
– 1
2
1
0
3
4
5
6
7
8

3
Matematyka. Poziom podstawowy
Próbna Matura z OPERONEM i „Gazetà Wyborczà”
BRUDNOPIS
4
Matematyka. Poziom podstawowy
Próbna Matura z OPERONEM i „Gazetà Wyborczà”
Zadanie 7. (1 pkt)
Najmniejsza wartoÊç funkcji kwadratowej ( )
(
)
f x
x
3
4
5
2
=
-
+
to:
A. 4
-
B. 3
C. 1
D. 5
Zadanie 8. (1 pkt)
Zbiorem rozwiàzaƒ nierównoÊci (
)(
)
x
x
1
3
0
G
-
+
-
jest:
A. (
, )
1 3
-
B. (
,
,
)
3
1
,
3
3
-
-
C. (
,
,
)
1
3
,
3
3
-
-
D.
,
1 3
-
Zadanie 9. (1 pkt)
Liczba
,
log
log
0 1
16
2
+
jest równa:
A. 6
B. 5
-
C. 3
D. 7
Zadanie 10. (1 pkt)
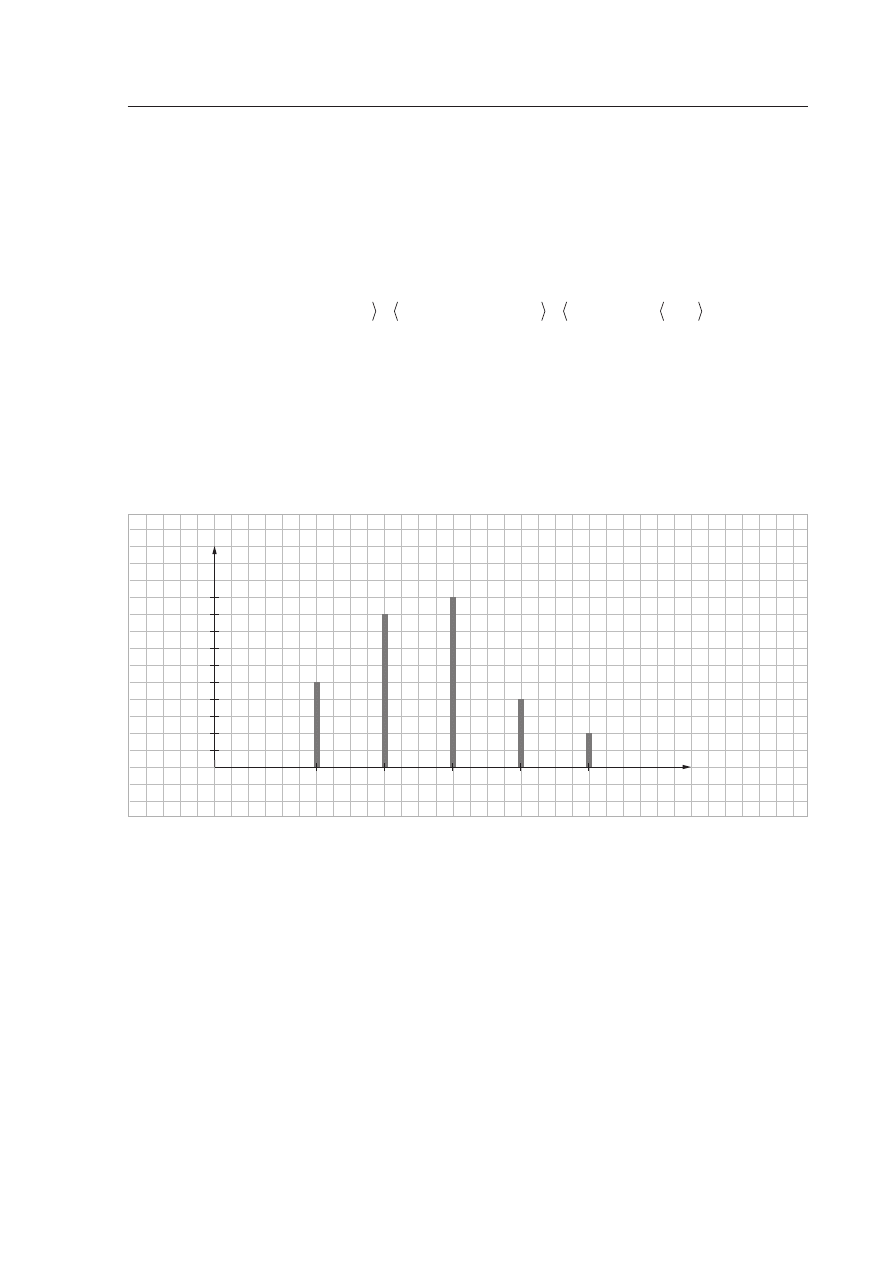
Na diagramie sà przedstawione wyniki pomiaru wzrostu uczniów klasy 3d.
Ile osób w tej klasie ma wzrost powy˝ej Êredniego?
A. 6
B. 14
C. 21
D. 16
Zadanie 11. (1 pkt)
Prosta o równaniu y
mx
6
=
+
przechodzi przez punkt
( ,
)
A
2
4
=
-
, gdy:
A. m
5
=
B. m
5
= -
C. m
1
=
D. m
4
= -
Zadanie 12. (1 pkt)
Torba kosztowa∏a 40 z∏, a po podwy˝ce 50 z∏. O ile procent podwy˝szono cen´ tej torby?
A. %
10
B.
%
25
C.
%
75
D.
%
20
wzrost w cm
liczba
uczniów
1
2
3
4
5
6
7
8
9
10
160
165
170
175
180

5
Matematyka. Poziom podstawowy
Próbna Matura z OPERONEM i „Gazetà Wyborczà”
BRUDNOPIS
6
Matematyka. Poziom podstawowy
Próbna Matura z OPERONEM i „Gazetà Wyborczà”
Zadanie 13. (1 pkt)
Dane sà wielomiany ( )
W x
x
4
=
-
i
( )
M x
x
x
2
2
=
-
. Wielomian ( )
( )
W x
M x
$
jest równy:
A. x
x
x
2
8
3
2
-
-
B. x
x
x
6
8
3
2
-
+
C. x
x
x
4
10
3
2
-
-
D. x
x
x
4
6
3
2
-
+
Zadanie 14. (1 pkt)
Punkty
(
, )
P
1 2
= -
i
( ,
)
R
3
1
=
-
sà sàsiednimi wierzcho∏kami kwadratu. Obwód tego kwadratu jest
równy:
A. 20
B. 5
C. 10
D. 25
Zadanie 15. (1 pkt)
Liczby 5, x
4
+
, 1 w podanej kolejnoÊci tworzà ciàg arytmetyczny. Zatem liczba x jest równa:
A. 5
-
B. ,
0 5
C. 2
D. 1
-
Zadanie 16. (1 pkt)
Wykres funkcji ( )
f x
k
4
x
=
+
przechodzi przez punkt ( ,
)
2
1
-
, gdy liczba k jest równa:
A. 17
B. 9
C. 17
-
D. 9
-
Zadanie 17. (1 pkt)
W ciàgu geometrycznym pierwszy wyraz jest równy 1, a iloraz czwartego wyrazu przez trzeci jest
równy
2
1. Drugi wyraz tego ciàgu jest równy:
A.
2
1
B. 2
C.
4
1
D. 4
Zadanie 18. (1 pkt)
Podstawa trójkàta równoramiennego ma d∏ugoÊç 24, a wysokoÊç opuszczona na t´ podstaw´ jest
równa 5. Rami´ tego trójkàta ma d∏ugoÊç:
A. 13
B. 26
C. 3
D. 5 2
Zadanie 19. (1 pkt)
Kàt Êrodkowy
a jest oparty na ∏uku wyznaczonym przez
9
1 okr´gu. Kàt wpisany, oparty na tym
samym ∏uku, co kàt
a ma miar´:
A. 80c
B. 40c
C. 20c
D. 45c
Zadanie 20. (1 pkt)
Funkcja liniowa ( )
f x
x
3
2
4
= -
+
przyjmuje wartoÊci ujemne dla:
A. <
x
6
B. >
x
6
C. >
x
6
-
D. <
x
6
-

7
Matematyka. Poziom podstawowy
Próbna Matura z OPERONEM i „Gazetà Wyborczà”
BRUDNOPIS

8
Matematyka. Poziom podstawowy
Próbna Matura z OPERONEM i „Gazetà Wyborczà”
ZADANIA OTWARTE
Rozwiàzania zadaƒ o numerach od 21. do 31. nale˝y zapisaç w wyznaczonych miejscach pod
treÊcià zadaƒ.
Zadanie 21. (2 pkt)
Rozwià˝ równanie x
x
x
1
0
3
2
+
+
+
=
.
Odpowiedê: ............................................................................................................................................
Zadanie 22. (2 pkt)
Rozwià˝ graficznie nierównoÊç
>
x
x
2
2
+
.

9
Zadanie 23. (2 pkt)
Wyznacz równania stycznych do okr´gu x
x
y
y
4
2
4
0
2
2
-
+
-
-
=
równoleg∏ych do osi
.
OY
Odpowiedê: ............................................................................................................................................
Zadanie 24. (2 pkt)
Podstawy trapezu równoramiennego majà d∏ugoÊci 4 cm i 6 cm, a cosinus kàta ostrego trapezu jest
równy
2
1. Oblicz obwód trapezu.
Odpowiedê: ............................................................................................................................................
Matematyka. Poziom podstawowy
Próbna Matura z OPERONEM i „Gazetà Wyborczà”
10
Matematyka. Poziom podstawowy
Próbna Matura z OPERONEM i „Gazetà Wyborczà”
Zadanie 25. (2 pkt)
Suma n poczàtkowych wyrazów ciàgu arytmetycznego wyra˝a si´ wzorem
(
)
S
n n
2
n
=
-
. Oblicz
pierwszy wyraz ciàgu i jego ró˝nic´.
Odpowiedê: ............................................................................................................................................
Zadanie 26. (2 pkt)
Sprowadê wyra˝enie x
x
x
1
1
-
+
- - +
do najprostszej postaci, gdy
( , )
x
0 1
!
.
Odpowiedê: ............................................................................................................................................
11
Zadanie 27. (2 pkt)
Za dwa lata Julka b´dzie dwa razy starsza ni˝ by∏a osiem lat temu. Ile lat ma Julka?
Odpowiedê: ............................................................................................................................................
Zadanie 28. (2 pkt)
W prostokàcie przekàtna d∏ugoÊci d dzieli kàt prostokàta na dwie równe cz´Êci. Wyka˝, ˝e pole
kwadratu zbudowanego na tej przekàtnej jest dwa razy wi´ksze od pola prostokàta.
Matematyka. Poziom podstawowy
Próbna Matura z OPERONEM i „Gazetà Wyborczà”

12
Matematyka. Poziom podstawowy
Próbna Matura z OPERONEM i „Gazetà Wyborczà”
Zadanie 29. (5 pkt)
Ciàg ( , , )
x y
4
jest ciàgiem geometrycznym malejàcym. Ciàg ( ,
, )
y x
1 5
+
jest ciàgiem arytmetycznym.
Wyznacz x.
Odpowiedê: ............................................................................................................................................

13
Zadanie 30. (5 pkt)
Samochód przejecha∏ 180 km, jadàc ze sta∏à pr´dkoÊcià. Gdyby jecha∏ z pr´dkoÊcià o 30 km/h
wi´kszà, to czas przejazdu skróci∏by si´ o godzin´. Z jakà pr´dkoÊcià jecha∏ samochód?
Odpowiedê: ............................................................................................................................................
Matematyka. Poziom podstawowy
Próbna Matura z OPERONEM i „Gazetà Wyborczà”

14
Matematyka. Poziom podstawowy
Próbna Matura z OPERONEM i „Gazetà Wyborczà”
Zadanie 31. (4 pkt)
Punkty
(
, )
A
2 4
= -
,
(
,
)
B
2
2
= -
-
,
( ,
)
C
5
3
=
-
,
( , )
D
1 4
=
sà wierzcho∏kami czworokàta. Oblicz wspó∏-
rz´dne punktu przeci´cia przekàtnych tego czworokàta.
Odpowiedê: ............................................................................................................................................

15
Matematyka. Poziom podstawowy
Próbna Matura z OPERONEM i „Gazetà Wyborczà”
BRUDNOPIS

Wyszukiwarka
Podobne podstrony:
Matematyka próbna OPERON 2009
Matematyka próbna OPERON 2008
Matura próbna z Operonem 2009 odpowiedzi
Matura próbna z Operonem 2009 teksty
Matura próbna z Operonem 2009 teksty
Matematyka próbna OPERON 2008 odpowiedzi
Matematyka próbna OPERON 2008
probna matura 2009 arkusz matematyka KLUCZ
probna matura 2009 arkusz matematyka-KLUCZ
2011 matematyka listopad EGZAMIN próbna Operon
2011 matematyka listopad EGZAMIN próbna Operon
probna matura 2009 arkusz matematyka KLUCZ
więcej podobnych podstron