1

Rok akademicki 2010/2011

Program zajęć

Technologia informacyjna i statystyka

wykład - 15 godzin, semestr zimowy, studia stacjonarne I stopnia

Technologia informacyjna

1. Podstawowe pojęcia i terminologia technologii informacyjnej
2. Systemy liczbowe binarny i heksadecymalny i zapis informacji w mikrokomputerze
3. Budowa i funkcje zestawu komputerowego oraz urządzeń współpracujących:

-mikroprocesor, pamięci ROM i RAM, magistrala systemowa, program BIOS

-dysk twardy, napęd dysków elastycznych, karta graficzna i monitor, mysz

-urządzenia peryferyjne w szczególności w zakresie potrzeb edukacyjnych

4. Oprogramowanie i jego podział
5. Systemy operacyjne znakowe i graficzne

-struktura i elementy systemu (foldery systemowe i plików, pliki, atrybuty plików)

6. Sieć komputerowa Internet do realizacji celów edukacyjnych:

-definicja sieci i usługi sieciowe

-korzystanie ze źródeł informacji i baz danych oraz wzajemne komunikowanie się

-bazy danych chemicznych, fizykochemicznych i bibliograficznych

-podstawy języka HTML

7. Zastosowania informatyki i technologii informacyjnej w chemii i jej nauczaniu:

-arkusz kalkulacyjny EXCEL

-edytor tekstowy WORD

-edytory wzorów chemicznych IsisDraw i ChemSketch

-program do tworzenia prezentacji multimedialnych PowerPoint

-specjalistyczne oprogramowanie w chemii

8. Wstęp do zastosowania informatyki we wspomaganiu pomiarów chemicznych:

-struktura stanowiska pomiarowego

-typy systemów pomiarowych

9. Wybrane zagadnienia technologii informacyjnej - zagrożenia komputerowe

Uwaga:

1. Zakres Informatyki zgodny jest ze standardami przedmiotu Technologia Informacyjna -

obowiązkowego przedmiotu nauczania na pierwszych 3.latach studiów wyższych prowadzonych
w bolońskim systemie kształcenia.

2. Na wykładzie przekazane będą wybrane elementy w/w programu - cały obowiązujący materiał,

a w szczególności zagadnienia na poziomie podstawowym, należy przygotować w oparciu o plik
2010_TB_wyklady_informatyka.pdf

Statystyka

1. Podstawowe pojęcia statystyki:

- podział statystyki

- populacja a próba, podział populacji i prób

- cechy (zmienne) skokowe i ciągłe, ilościowe i jakościowe

2. Podstawy techniki eksperymentu:

- definicja pomiaru, dokładność i czułość, powtarzalność i odtwarzalność pomiaru

3. Podział błędów i niepewności w zależności od źródeł ich powstania. Źródła błędów i

niepewności w pomiarach chemicznych

4. Wstęp do rozkładów statystycznych wyników pomiarów i niepewności:

2

- funkcje gęstości rozkładu prawdopodobieństwa dla zmiennych skokowych i ciągłych,
dystrybuanta rozkładu, momenty rozkładu

- parametry rozkładu: wartość oczekiwana, wariancja, odchylenie standardowe

5. Rozkłady statystyczne zmiennych skokowych:

- zerojedynkowy, dwumianowy, Poissone'a

6. Rozkłady statystyczne zmiennych ciągłych:

- równomierny, Gaussa, t-Studenta,

χ

2

- estymatory parametrów rozkładu: średnia, średnia niepewność pojedynczego pomiaru i średnia
niepewność średniej

- pojęcie przedziału ufności

- estymacja parametrów rozkładu z dużej próby - szereg rozdzielczy

7. Hipotezy i testowanie hipotez:

- podział hipotez i testów, hipoteza H

0

- testy parametryczne i nieparametryczne. Test

χ

2

8. Analiza wyników wątpliwych - kryteria odrzucania wyników w pomiarach chemicznych

w oparciu o test Dixona i test Grubbsa

9. Dwuwymiarowe zmienne losowe:

- korelacja, analiza współczynnika korelacji
- regresja liniowa - metoda najmniejszych kwadratów
- linearyzacja zależności nieliniowych

10. Elementy walidacji metod analitycznych

LITERATURA do technologii informacyjnej

1.

P. Fulmański, Ś. Sobieski - Wstęp do informatyki - podręcznik, Wydawnictwo Uniwersytetu
Łódzkiego, 2005

2.

A. Kisielewicz - Wprowadzenie do informatyki, Helion, 2002

3.

P. Wróblewski - ABC Komputera, Helion, 2002

4.

M. Sokół - Windows XP PL. Kurs, Helion, 2003

5.

B. Krzymowski - Microsoft Office 2003 PL. Poradnik HELP dla nieinformatyków, Help, 2004

6.

Steve Sagman - Po prostu Office 2003 PL, Helion, 2004

7.

R. Zimek - PowerPoint 2003 PL. Ćwiczenia, Helion, 2004

8.

A. Obecny – Statystyka opisowa w Excelu dla szkół - Ćwiczenia praktyczne, Helion, 2002

9.

B. Krzymowski - Strony WWW bez programowania czyli Word jako edytor stron
internetowych, Help, 2005

10.

W. Ufnalski, K. Mądry - Excel dla chemików i nie tylko, WNT, Warszawa 2000

11.

instrukcje do ćwiczeń

12.

wykład z informatyki - plik 2010_TB_wyklady_informatyka.pdf

specjalność nauczycielska: S. Juszczyk, J. Janczyk, D. Morańska, M. Musioł - Dydaktyka

informatyki i technologii informacyjnej, Wydawnictwo A.Marszałek, Toruń, 2004

3

LITERATURA do statystyki

1.

wykłady ze statystyki - pliki 2010_TB_statystyka_moduł_xx.pdf

2.

Ć

wiczenia rachunkowe z chemii analitycznej - praca zbiorowa pod redakcją Zbigniewa Galusa,

PWN Warszawa 1972 i nowe wydanie IV, PWN, Warszawa, 1993, 1998

3.

Ocena i kontrola jakości wyników pomiarów analitycznych - praca zbiorowa pod redakcją
P.Konieczki i J.Namieśnika, WNT, Warszawa 2007

4.

R.Gondko, A.Zgirski, M.Adamska - Biostatystyka w zadaniach, Wyd. II, Wydawnictwo UŁ,
Łódź 2001

5.

John R.Taylor -Wstęp do analizy błędu pomiarowego, PWN, Warszawa, 1995

6.

W. Hyk, Z. Stojek - Analiza statystyczna w laboratorium analitycznym, Komitet Chemii
Analitycznej PAN, Warszawa 2000

7.

K. Eckschlager - Błędy w analizie chemicznej, PWN, 1974

8.

J. Czermiński, A. Iwasiewicz, Z. Paszek, A. Sikorski - Metody statystyczne dla chemików,
PWN, Warszawa,1992

9.

autorzy jak wyżej - Metody statystyczne w doświadczalnictwie chemicznym, PWN, 1974

10.

H. Szydłowski - Teoria pomiarów, PWN, Warszawa, 1978

Cel zajęć

1. umieć zdefiniować niepewności (błędy, nieokreśloności, nieoznaczoności) pomiarów, poznać ich

ź

ródła w eksperymentach chemicznych i fizycznych

2. nauczyć się poprawnie przeprowadzać obliczenia na liczbach przybliżonych, które otrzymuje się

w wyniku wykonania pomiarów chemicznych lub fizycznych oraz w wyniku wykonania innych
obliczeń

3. nauczyć się poprawnie przeprowadzać analizę statystyczną elementów małej i średniej próby

(zbiór do 30 elementów); obliczać wartość najlepszą i granice w jakich znaleźć się powinna
z określonym prawdopodobieństwem "wartość prawdziwa"

4. nauczyć się opracowywać statystycznie zbiory duże
5. umieć postawić hipotezę statystyczną i przetestować jej prawdziwość
6. nauczyć się opracowywania zbiorów zmiennych zależnych, znalezienia korelacji między tymi

zmiennymi i obliczania parametrów regresji (z ograniczeniem do regresji liniowej)

7. nauczyć się statystycznych metod weryfikacji wyników wątpliwych

Gdzie to będzie miało zastosowanie

1. na innych zajęciach obliczeniowych z chemii, gdzie na ogół nie jest przeprowadzany rachunek

błędów i analiza statystyczna

2. na pracowniach chemicznych do poprawnego opracowywania ćwiczeń
3. na pracowni informatycznej jako teoretyczne podstawy do ćwiczeń
4. jest wstępem do walidacji metod analitycznych i do chemometrii

4

Uwagi wstępne na I. wykładzie

- przedmiot Technologia informacyjna i statystyka trwa 1 semestr i kończy się zaliczeniem

wykładu i konwersatorium ze statystyki oraz laboratorium informatycznego

- wykłady z informatyki są do skopiowania z serwera sieciowego chemii
- wykłady ze statystyki dokładnie notować - będą sukcesywnie w trakcie semestru pojawiać się na

serwerze sieciowym chemii - o każdej zmianie będę sygnalizował na wykładzie (materiał
wykładów jest dynamiczny i bardziej wskazane jest przechowywać go w plikach niż drukować)

- wykłady w czwartki przez 1/2 semestru - start o 8.15, przerwa 10 min.

Zaliczenie przedmiotu

- przy zaliczeniu do indeksu wpisać nazwy przedmiotów dokładnie takie, jakie będą na karcie

egzaminacyjnej (zaliczeniowej):

•

Technologia informacyjna i statystyka - wykład: daję wpis po uzyskaniu zaliczeń

z konwersatorium i laboratorium. UWAGA: ocena z wykładu jest średnią z ocen
z konwersatorium i z laboratorium. Ocena z wykładu brana jest do obliczenia ogólnej średniej

•

Technologia informacyjna i statystyka - konwersatorium: zaliczenie wpisuje osoba prowadząca

zajęcia - jej nazwisko będzie w karcie i należy je wpisać do indeksu

•

Technologia informacyjna i statystyka - laboratorium: zaliczenie wpisuje osoba prowadząca

pracownię - jej nazwisko będzie w karcie i należy je wpisać do indeksu

- szczegółowe zasady uzyskania zaliczenia podane będą na zajęciach konwersatoryjnych i

laboratoryjnych z informatyki

- przepisanie zaliczenia (dotyczy studentów powtarzających rok i tych, którzy przenieśli się

z innych uczelni lub kierunków lub też studiują równolegle na jeszcze jednym kierunku):
- przepisanie uzgodnić na początku zajęć
- przepisanie jest na podstawie indeksu z poprzednich lat (2 lata):

- ze statystyki - indywidualna rozmowa ze mną
- pracowni - decyzję podejmuje prowadzący pracownię i on przepisuje zaliczenie
- "fizyczny" wpis zaliczenia jest pod koniec semestru
Przepisanie zaliczenia może zrobić Dziekan dr A. Bieniek - wtedy w/w zasady nie mają
zastosowania.

Sprawy inne

- przenoszenie się między grupami informatycznymi - po uzgodnieniu z prowadzącymi zajęcia
- maksymalnie 15 - 16 osób w jednej grupie informatycznej
- przenoszenie się między grupami konwersatoryjnymi - jedynie w wyjątkowo uzasadnionych

przypadkach - uzgodnić z prowadzącymi zajęcia

- po 2. tygodniach wszystkie grupy powinny już być ustabilizowane
- konsultacje - terminy będą podane po ustabilizowaniu się wszystkich zajęć
- program zajęć z informatyki, warunki zaliczenia, siatka zajęć na pracowni - są wywieszone na

tablicy informacyjnej przy pracowni komputerowej

- wszystkie programy przedmiotu "Technologia informacyjna i statystyka", literatura, warunki

zaliczeń, wykłady i instrukcje do ćwiczeń dostępne są w Internecie pod adresem:

www.chemia.uni.lodz.pl/kchogin/pracownia

- Pracownia komputerowa, sala 125 ul. Tamka 12, I p. budynek 1

Kontakt do mnie

dr Tadeusz Błaszczyk

Katedra Chemii Nieorganicznej i Analitycznej

Tamka 12 pok. 121 (I p.) budynek 1

e-mail: [e-mail]

5

CYFRY ZNACZĄCE LICZBY PRZYBLIśONEJ, ZASADY ZAOKRĄGLANIA
I POPRAWNOŚĆ PRZEPROWADZANIA OBLICZEŃ

Pozycyjny system zapisu liczby - rozwinięcie dziesiętne liczby

Każdą liczbę dziesiętną można rozwinąć do postaci

a = a

n

⋅

10

n

+a

n-1

⋅

10

n-1

+...+a

1

⋅

10

1

+a

0

⋅

10

0

+a

-1

⋅

10

-1

+a

-2

⋅

10

-2

+...+a

-k

⋅

10

-k

podstawa systemu p = 10

znaki do zapisu liczby (cyfry) a

i

= 0, 1, 2, 3, 4, 5, 6, 7, 8, 9

Przykład:

a = 3734,037 = 3·10

3

+7·10

2

+3·10

1

+4·10

0

+0·10

-1

+3·10

-2

+7·10

-3

Pozycja, czyli miejsce na którym znajduje się dana cyfra w zapisie dziesiętnym określa jej
ważność (wagę) w danej liczbie

Inne systemy pozycyjne

system dwójkowy (binarny, binarny naturalny)

podstawa systemu p = 2

znaki do zapisu liczby a

i

= 0, 1

Przykłady:

L

2

=1 1011

→

L

2

=1

⋅

2

4

+1

⋅

2

3

+0

⋅

2

2

+1

⋅

2+1=27

10

L

2

= 1 1010 0100 0111 = 6727

10

system szesnastkowy (heksadecymalny)

podstawa systemu p = 16

znaki do zapisu liczby a

i

= 0, 1, 2, 3, 4, 5, 6, 7, 8, 9, A, B, C, D, E, F

Przykłady:

L

16

=11011

→

L

16

=1

⋅

16

4

+1

⋅

16

3

+0

⋅

16

2

+1

⋅

16+1= 69649

10

= 1 0001 0000 0001 0001

2

L

16

=A09F

→

L

16

=10

⋅

16

3

+0

⋅

16

2

+9

⋅

16+15= 41119

10

= 1010 0000 1001 1111

2

Podział liczb:

całkowite, rzeczywiste, dodatnie, ujemne, naturalne, pierwsze itd. oraz dokładne i przybliżone

Przykłady liczb dokładnych: liczba studentów w sali, mnożnik 2 we wzorze na długość okręgu
l = 2

π

r, dwie cząsteczki 2H

2

w równaniu reakcji spalania 2H

2

+ O

2

→

2H

2

O, itp.

Przykłady liczb przybliżonych: wysokość lub masa studenta, zmierzony promień
r okręgu, ilość moli (cząsteczek) H

2

przy wykonaniu doświadczeniu spalania, itp.

Wyniki pomiarów są praktycznie zawsze liczbami przybliżonymi

Liczby przybliżone mogą być również efektem operacji matematycznych na liczbach
(zarówno przybliżonych jak i dokładnych)

Podstawowe pojecie - cyfry znaczące liczby w zapisie dziesiętnym

Jeżeli nie mamy żadnych dodatkowych informacji o liczbie, to cyfrą znaczącą tej liczby jest
każda cyfra oprócz zer napisanych na początku liczby

Przykłady:

cyfry znaczące są podkreślone: 10201, 12,501, -0,0156, -10000, 100,0, -0,1010

MSB

LSB

6

Zmiennoprzecinkowy system zapisu liczby (naukowy, półlogarytmiczny) - inaczej notacja
(reprezentacja) zmiennoprzecinkowa liczby

a = M

⋅

10

C

M - mantysa - liczba rzeczywista od 1,000... do 9,999..., C - cecha - liczba całkowita; zarówno
mantysa jak i cecha mogą być poprzedzone znakiem -(minus)

Przykłady: a = 2,305

⋅

10

4

, -2,500

⋅

10

-3

,6,023

⋅

10

2

3, -5,000

⋅

10

0

- komentarz do ostatniej liczby:

podając liczbę w takiej postaci jednoznacznie informujemy, że wszystkie napisane cyfry mantysy są
cyframi znaczącymi,

Czytanie liczby w notacji zmiennoprzecinkowej w kalkulatorach i programach komputerowych
(Excel):

a = 2,345E-2 = 2,345

⋅

10

-2

a = -7,2541E0004 = -7,2541

⋅

10

4

a = 6,02E23 = 6,02

⋅

10

23

Uwaga: gdy w notacji zmiennoprzecinkowej wyrażona jest niepewność pomiaru (inne nazwy to
nieoznaczoność, nieokreśloność, błąd pomiaru), to mantysa M może być liczbą mniejszą od 1,00...

Poprawny zapis wyników pomiarów i obliczeń

W obliczeniach chemicznych bardzo ważnym zagadnieniem jest poprawny zapis liczb w
działaniach arytmetycznych oraz zapis otrzymanego wyniku końcowego.

Głównym problemem (zmorą wszystkich zajęć!!!) jest pisanie przez studentów wyniku
końcowego z użyciem wszystkich cyfr wyświetlanych na kalkulatorze!

Szczególnie jest ważne - jak poprawnie zapisać wynik końcowy tak, żeby podać właściwą liczbę
cyfr znaczących? Poprzednio przedstawione przykłady dają jedynie informacje, co to są cyfry
znaczące, ale nic nie mówią o ich ilości jaka powinna być zapisana w wyniku.

Jednoznaczny i najbardziej poprawny jest zapis wyniku w postaci liczby wraz z jej niepewnością
(nieoznaczonością, nieokreślonością, błędem). Formalnie wygląda to tak:

a = a

obl

±

∆∆∆∆

a

obl

Proste zasady wykonywania działań arytmetycznych

Jeżeli dodajemy lub odejmujemy liczby o różnej ilości cyfr znaczących, to w wyniku
końcowym zostawiamy taką ilość cyfr znaczących, żeby ostatnia cyfra tego wyniku
znajdowała się na takiej pozycji dziesiętnej na której była ostatnia cyfra najmniej dokładnej
liczby.

(Analiza przykładów na konwersatorium)

Uwaga: nie powinno się zaokrąglać liczb przed ich dodawaniem / odejmowaniem (takie wskazówki
wstępnego zaokrąglania liczb można spotkać w niektórych opracowaniach). Działania dodawania /
odejmowania należy wykonać na pełnym formacie każdej liczby, a zaokrągla się dopiero
otrzymany wynik końcowy.

Jeżeli mnożymy lub dzielimy liczby o różnej ilości cyfr znaczących, to w wyniku końcowym
zostawiamy taką ilość cyfr znaczących ile cyfr znaczących ma liczba najkrótsza (o
najmniejszej ilości cyfr znaczących). Inaczej można powiedzieć, że w wyniku końcowym
zostawiamy taką ilość cyfr znaczących jaka jest w liczbie najmniej dokładnej (inaczej: w
liczbie o największym błędzie względnym).

(Analiza przykładów na konwersatorium)

7

Niepewności liczb przybliżonych

Niepewność bezwzględna liczby przybliżonej

jest to bezwzględna wartość różnicy między liczbą

przybliżoną a i dokładną A

∆

(a) = |a - A|

Kres górny niepewności bezwzględnej

jest to każda liczba nie mniejsza od niepewności

bezwzględnej liczby przybliżonej

∆

a

≥

∆

(a)

Uwaga: niepewność bezwzględna

∆

(a) i kres górny niepewności bezwzględnej

∆

a wyrażane muszą

być w takich samych jednostkach jak wielkość a (mówiąc inaczej - wszystkie mają takie same
miana)

Dokładne cyfry znaczące liczby przybliżonej

jeżeli ostatnia cyfra dokładna liczby przybliżonej znajduje się na n-tej pozycji rozwinięcia
dziesiętnego tej liczby, to kres górny niepewności bezwzględnej liczby przybliżonej nie przekracza
połowy jednostki n-tej pozycji dziesiętnej

n

10

2

1

a

⋅

=

∆

Niepewność względna liczby przybliżonej

jest to stosunek niepewności bezwzględnej liczby

przybliżonej do wartości bezwzględnej liczby dokładnej

( ) ( )

A

a

a

∆

δ

=

Kres górny niepewności względnej

jest to każda liczba

δ

a nie mniejsza od niepewności względnej

tej liczby

( )

a

a

δ

δ

≥

Jako kres górny niepewności względnej przyjmuje się wartość wyrażenia

a

a

a

a

∆

∆

δ

−

=

lub przy założeniu, że |a|>>

∆

a ostatni wzór upraszcza się do postaci

a

a

a

∆

δ

=

Uwaga: niepewność względna i kres górny niepewności względnej nie mają jednostek (inaczej
mówiąc - są liczbami niemianowanymi). Po pomnożeniu

δ

a przez 100% niepewność względna

wyrażona będzie w procentach - jest to często spotykane w chemii

8

Niepewności działań arytmetycznych na liczbach przybliżonych

Niepewność sumy i różnicy

Jeżeli dodajemy lub odejmujemy liczby przybliżone, to kres górny niepewności bezwzględnej sumy
lub różnicy tych liczb nie przekracza sumy kresów górnych niepewności bezwzględnych
dodawanych lub odejmowanych liczb. Czyli jeżeli

a = a

1

+ a

2

+ a

3

+...+a

n

lub a = a

1

- a

2

- a

3

-....-a

n

to

∆

a

≤

∆

a

1

+

∆

a

2

+

∆

a

3

+....+

∆

a

n

Niepewność iloczynu i ilorazu

Jeżeli mnożymy lub dzielimy liczby przybliżone, to kres górny niepewności względnej iloczynu lub
ilorazu tych liczb przybliżonych nie przekracza sumy kresów górnych niepewności względnych
mnożonych lub dzielonych liczb. Czyli jeżeli

a = a

1

⋅

a

2

⋅

a

3

⋅

...

⋅

a

n

lub

a

....

a

a

a

a

n

3

2

1

⋅

⋅

⋅

=

to

δ

a

≤

δ

a

1

+

δ

a

2

+

δ

a

3

...+

δ

a

n

Niepewność potęgi

Jeżeli potęgujemy liczbę przybliżoną a, to kres górny niepewności względnej m-tej potęgi tej liczby
jest |m| razy większy niż kres górny niepewności względnej liczby potęgowanej

u = a

m

to

δ

u = |m|

⋅δ

a

Podstawowe zasady prowadzenie obliczeń i zaokrąglania wyników

1. Obliczenia niepewności (również i pomiarowych) powinny być prowadzone z dokładnością co

najmniej trzech cyfr znaczących

2. Obliczona niepewność końcowa powinna być zaokrąglana do dwóch cyfr znaczących

lub do jednej cyfry znaczącej

3. Obliczenia wyniku (również wyniku pomiaru) należy prowadzić z taką dokładnością, aby

pozycja ostatniej cyfry dziesiętnej wyniku przekraczała pozycję ostatniej cyfry dziesiętnej
niepewności końcowej

4. Wynik końcowy zaokrągla się na tej samej pozycji dziesiętnej co niepewność końcową

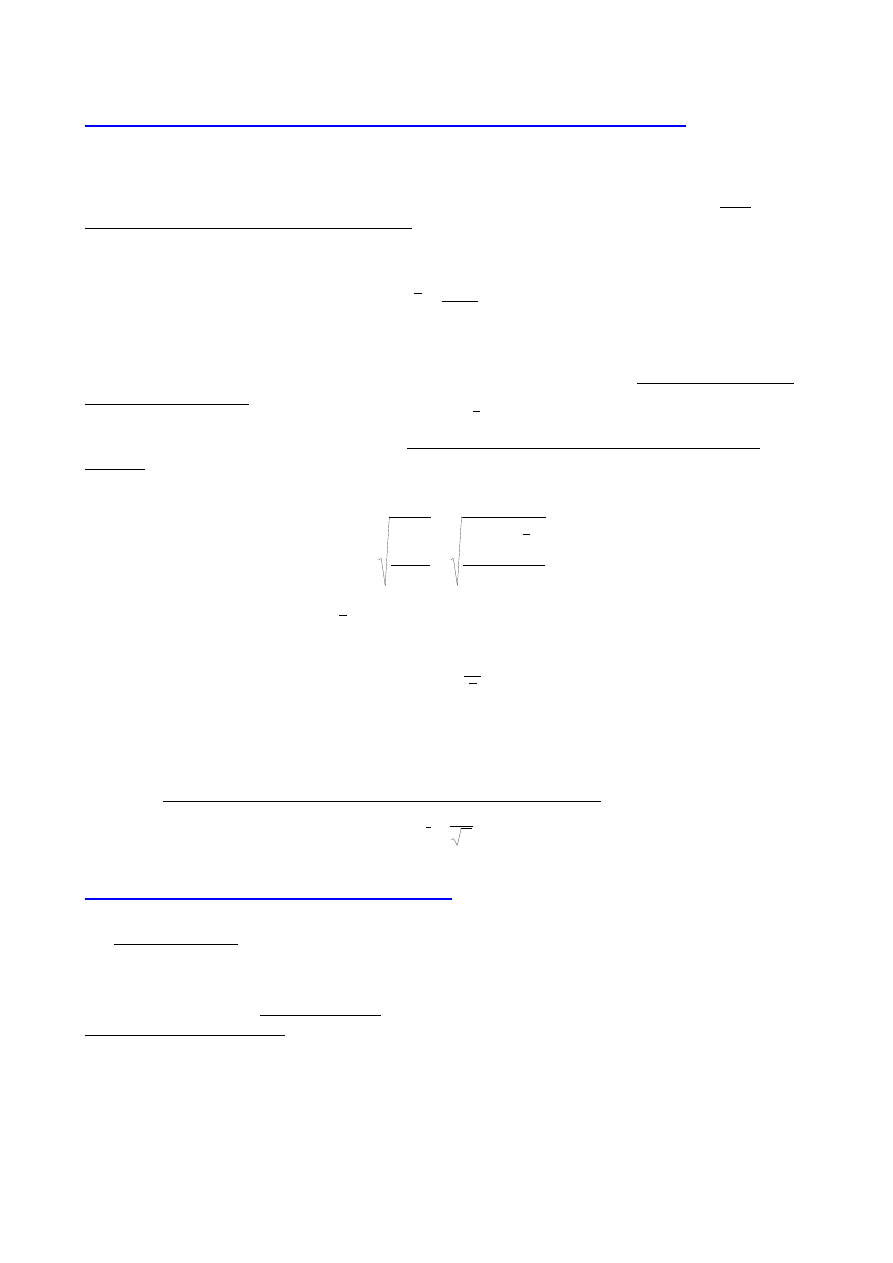
9

OPRACOWANIE WYNIKÓW POMIARÓW POJEDYNCZEJ WIELKOŚCI

Jeżeli wykonuje się n-krotnie pomiar pojedynczej wielkości X, to przy stosowaniu dostatecznie
precyzyjnej i czułej metody pomiarowej, dostaje się w wyniku z reguły n różnych wartości
liczbowych. Jeżeli ilość pomiarów jest niewielka (do 30) i nie ma innych przesłanek, to jako
najlepszą przyjmuje się średnią arytmetyczną z uzyskanych wyników eksperymentalnych
(w sensie statystycznym jest to estymator wartości oczekiwanej wielkości X)

n

x

x

n

1

i

i

∑

=

=

gdzie i - numer pomiaru, n - ilość wszystkich pomiarów, x

i

- wartość i -tego pomiaru

Każdy pomiar obarczony jest indywidualną niepewnością, która nosi nazwę niepewności pozornej
pojedynczego pomiaru

x

x

v

i

i

−

=

Do oceny niepewności pomiarów używa się średniej kwadratowej niepewności pojedynczego
pomiaru, która jest miarą rozproszenia wyników względem wartości średniej i jest definiowana
wzorem (w sensie statystycznym jest to estymator odchylenia standardowego)

(

)

1

n

x

x

1

n

v

s

n

1

i

2

i

n

1

i

2

i

x

−

−

=

−

=

∑

∑

=

=

Używana jest również wielkość nazywana względnym odchyleniem standardowym (skrót RSD),
określona równaniem (oczywiście

0

x

≠

)

x

s

RSD

x

=

oraz współczynnik zmienności CV

CV = RSD

⋅

100%

Również i obliczona średnia arytmetyczna obarczona jest niepewnością

n

s

s

x

x

=

Statystyczne opracowanie niepewności pomiaru

W sensie statystycznym bardziej poprawną wielkością niż obliczona niepewność wartości średniej
jest przedział ufności.

Przedziałem ufności nazywa się taki symetryczny przedział wokół wartości średniej, że
powinien się w nim znaleźć określony ułamek wyników (określona część wyników).

Ten ułamek nosi nazwę poziomu ufności i oznaczany jest symbolem 1-α. Samo α nazywa się
współczynnikiem istotności.

10

Obliczanie przedziału ufności dla małych i średnich prób - zastosowanie rozkładu Studenta
(t-Studenta)

W przypadku małej ilości wyników (do 30) do obliczenia szerokości przedziału ufności najczęściej
używany jest rozkład Studenta. Obliczenie przedziału ufności składa się z następujących kroków:

1. założenie określonego poziomu ufności 1-α (lub współczynnika istotności α)

2. określenia ilości stopni swobody rozkładu Studenta (przy opracowaniu pomiarów pojedynczej

wielkości ilość stopni swobody rozkładu Studenta wynosi k = n - 1)

3. odczytanie z tablic rozkładu Studenta wartości standaryzowanej funkcji t

k,α

(inne określenia: współczynnik rozkładu Studenta, funkcja Studenta, współczynnik Studenta)

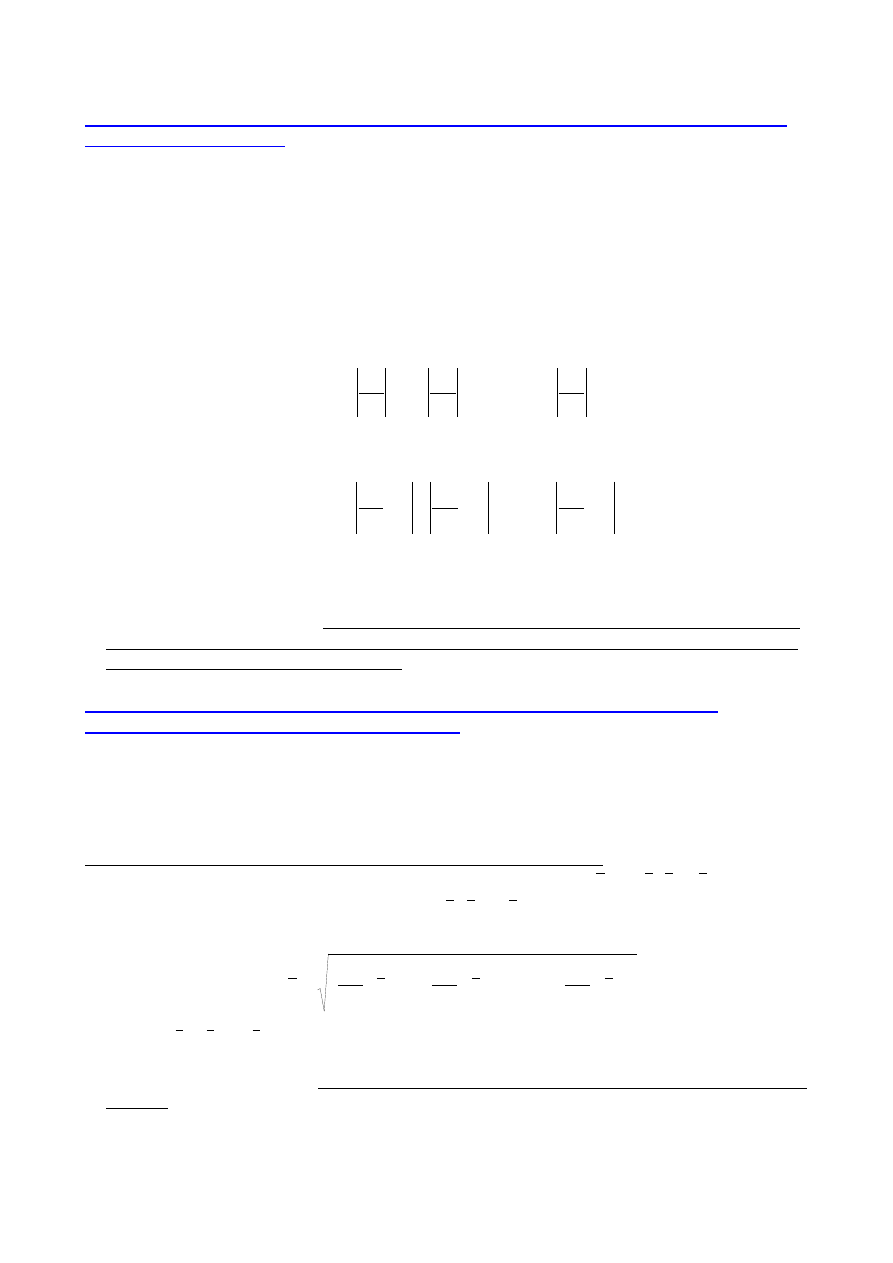
4. obliczenie wartość przedziału ufności

α

⋅

=

,

k

x

St

x

t

s

s

Ostateczna odpowiedź ma postać

St

x

s

x

X

±

=

11

OBLICZANIE NIEPEWNOŚCI MAKSYMALNYCH WIELKOŚCI ZŁOśONEJ - metoda
różniczki zupełnej funkcji

Metoda ta stosuje się do takich sytuacji, gdy praktycznie wyniki pojedynczych pomiarów wielkości
są jednakowe i o dokładności pomiaru decyduje dokładność stosowanego przyrządu i metody
pomiarowej

Wielkość złożona u określona jest następująco

)

x

,...

x

,

x

(

f

u

n

2

1

=

gdzie funkcja f jest funkcją ciągłą i różniczkowalną zmiennych niezależnych

n

2

1

x

,...

x

,

x

.

Można wykazać, korzystając z rozwinięcia Taylora funkcji f, że maksymalny bezwzględny przyrost

wartości funkcji f jest wyrażony wzorem:

n

n

2

2

1

1

x

x

f

.........

x

x

f

x

x

f

f

u

∆

∆

∆

∆

∆

∂

∂

+

+

∂

∂

+

∂

∂

=

=

lub w innej postaci

n

n

2

2

1

1

x

x

f

........

x

x

f

x

x

f

f

u

∆

∆

∆

∆

∆

∂

∂

+

+

∂

∂

+

∂

∂

=

=

Wielkości

n

2

1

x

.....

,

x

,

x

,

u

∆

∆

∆

∆

interpretujemy jako niepewności maksymalne odpowiednio

wielkości złożonej u i zmiennych niezależnych

n

2

1

x

,...

x

,

x

Zastosowany sposób nazywa się obliczaniem niepewności maksymalnej metodą różniczki zupełnej

funkcji. Wzór ten w teorii rachunku błędów nosi też nazwę prawa przenoszenia się niepewności
maksymalnych (błędów maksymalnych).

OBLICZANIE NIEPEWNOŚCI ŚREDNICH KWADRATOWYCH WIELKOŚCI
ZŁOśONEJ - metoda różniczki zupełnej funkcji

Metoda ta z kolei stosuje się do takich sytuacji, gdy wyniki pojedynczych pomiarów wielkości są
zróżnicowane, a dla wyników tych wyznaczyć można wartości najlepsze i średnie odchylenia
(są to z reguły średnie arytmetyczne i przedziały ufności)

Założenia wstępne do analizy są takie same jak w przypadku błędu maksymalnego.
Niepewność średnia kwadratowa wartości średniej wielkości złożonej u obliczana jest jako średnia

miara kwadratów odchyleń wielkości złożonej w otoczeniu punktu

)

,...

,

(

2

1

n

x

x

x

f

u

=

, tzn.

punktu odpowiadającego średnim wartościom

n

2

1

x

......

x

,

x

.

Niepewność tę (dokładniej kres górny niepewności) określa wyrażenie

2

n

n

2

2

2

2

1

1

x

x

f

.....

x

x

f

x

x

f

u













∂

∂

+

+













∂

∂

+













∂

∂

=

∆

∆

∆

∆

Wielkości

n

2

1

x

,....

x

,

x

∆

∆

∆

są niepewnościami (przedziałami ufności) odpowiednio zmiennych

x

1

, x

2

....x

n

.

Zastosowany sposób nazywa się metodą różniczki zupełnej funkcji obliczania niepewności wartości

ś

redniej.

12

Uwagi:

1. metoda obliczeniowa jest uniwersalna dla wszystkich wielkości złożonych spełniających

założenia wstępne

2. metoda może być stosowana dla "mieszanych" niepewności, np. z wielu pomiarów średnie

wartości masy i objętości z ich przedziałami ufności i pojedynczy pomiar temperatury z
niepewnością maksymalną

3. obliczona niepewność

u

∆

nie podlega dalszej "obróbce" z zastosowaniem np. rozkładu Studenta.

Niepewność ta ma sens statystyczny przedziału ufności, jeżeli do obliczeń były użyte przedziały
ufności.

13

WSTĘP DO STATYSTYKI

Statystyka jest to dziedzina nauki obejmująca metody analizy danych

Podział statystyki

Statystykę dzieli się na statystykę opisową oraz statystykę matematyczną, którą inaczej nazywa się
wnioskowaniem statystycznym

Statystyka opisowa

jest to opis, uporządkowanie, zestawienie danych liczbowych

i ich prezentacja w postaci tabel, szeregów i wykresów. Zestawienia takie mogą zawierać
dodatkowe informacje, takie jak wartości średnie, rozproszenie, itp.
Metodami statystyki opisowej posługujemy się przy opracowaniu danych doświadczalnych.
Dane uzyskane metodą statystyki opisowej dotyczą zdarzeń mających miejsce w przeszłości lub
teraźniejszości, nigdy zaś w przyszłości (Zgirski)

Statystyka matematyczna

zajmuje się analizą, interpretacją i planowaniem wszelkiego rodzaju

eksperymentów w oparciu o teorie statystyki i dane statystyki opisowej. Statystyka matematyczna,
czyli wnioskowanie statystyczne, pozwala na wykrycie ogólnych prawidłowości, czyli na
uogólnienie wyników badań.
Wnioskowanie statystyczne pozwala też na podejmowanie najwłaściwszej decyzji,
a także w niektórych przypadkach przewidywanie zdarzeń w przyszłości (Zgirski)

Podstawowe pojęcia statystyki

Populacja

(inaczej zbiorowość statystyczna, zbiorowość generalna) jest to zbiór zdarzeń,

przedmiotów, osób, liczb, który może być logicznie zdefiniowany i posiada określoną treść
merytoryczną. W języku statystycznym nazywa się je jednostkami statystycznymi. Liczba jednostek
statystycznych stanowi liczność (inaczej liczebność) danej populacji

Populacja skończona

jest to zbiorowość o ustalonej lub możliwej do ustalenia liczbie elementów.

Przykładem populacji skończonej może być liczba np. studentów przyjętych w danym roku na
studia w Polsce

Populacja nieskończona

jest wtedy, gdy zbiór elementów jest nieograniczony lub niemożliwy do

ustalenia. Przykładem populacji nieskończonej może być liczba możliwych do uzyskania związków
węgla

Badania kompletne

(inaczej stuprocentowe, całkowite, wyczerpujące) są to badania obejmujące

całą populację. W praktyce w wielu przypadkach badania kompletne są niewykonalne ze względu
na czas bądź koszty lub też niecelowe

Badania częściowe

są to badania które obejmują tylko część populacji. Ta część populacji, która

pobrana jest do badań częściowych nazywa się

próbą

lub

próbką

Losowość i reprezentatywność próby

Próba jest losowa

(inaczej randomizowana) wtedy, gdy z populacji w sposób przypadkowy czyli

losowy zostaje wybrana określona liczba jednostek

Próba jest reprezentatywna

wtedy, gdy jej struktura i własności są jak najbardziej zbliżone do

struktury i własności całej populacji

14

Parametry populacji i estymatory parametrów populacji

Parametry populacji

są to liczby charakteryzujące populację. Bardzo rzadko możliwe jest

bezpośrednie wyznaczenie tych parametrów. Parametry populacji najczęściej oznaczane są literami
greckimi

Estymatory parametrów populacji

(inaczej oszacowania parametrów lub statystyki)

są to liczbowe charakterystyki prób pobranych z badanej populacji. Estymatory mogą przyjmować
różne wartości dla poszczególnych (kolejnych) prób. Estymatory najczęściej oznaczane są
symbolami alfabetu łacińskiego
Przykłady

µ

- wartość oczekiwana

x

- estymator wartości oczekiwanej

σ

- dyspersja

x

s

- estymator dyspersji

Podział cech

Cechy ilościowe

(inaczej mierzalne) są to wielkości które można wyznaczyć liczbowo poprzez

pomiar np. masa ciała, stężenie związku, itp.

Cechy jakościowe

to te, których nie można zmierzyć

Cechy ciągłe

to te, które przyjmują dowolne wartości liczbowe w określonym przedziale, np.

wzrost, masa, czas itp.

Cechy skokowe

(inaczej dyskretne) to te, które przyjmują tylko określone wartości liczbowe ze

zbioru skończonego

Zmienna

- określenie używane zamiast pojęcia cecha, szczególnie w statystyce matematycznej.

Stąd zmienna ilościowa, jakościowa, ciągła i skokowa.

Podsumowując - zadaniem statystyki jest:

1) określenie sposobu zbierania danych zależnie od rodzaju mierzonej cechy
2) określenie sposobu analizy zebranych danych liczbowych
3) estymacja parametrów danej populacji na podstawie próby
4) stawianie hipotez dotyczących badanej cechy i testowanie hipotez
5) wysnuwanie właściwych wniosków z obserwacji poczynionych na próbie i przenoszenie ich
na populacje skończone lub na populacje nieskończone
6) planowania doświadczeń

15

PODSTAWY TECHNIKI EKSPERYMENTU - POMIARY, NIEPEWNOŚCI I BŁĘDY
POMIARÓW, METODY POMIAROWE

Definicja pomiaru

Pomiarem nazywamy operację przyporządkowania wartości liczbowej do wielkości fizycznej,
chemicznej lub innej. Inaczej można powiedzieć, że dana wielkość będzie wyrażona poprzez liczbę.
Liczba ta wyraża wynik porównania mierzonej wielkości z odpowiednią jednostką

Cechy (atrybuty) pomiaru

Metoda pomiaru jest to zespół czynności i rozumowań pozwalający wnioskować o wartości
mierzonej wielkości
Aparatura pomiarowa jest to pewien system oddziaływujący z mierzonym obiektem
Jednostki podstawowych wielkości określa się za pomocą umownie przyjętych wzorców
Wprowadzonych i legalnych jest 9 jednostek układu SI
Jednostki wielkości pochodnych definiuje się w oparciu o jednostki podstawowe i zależności
funkcyjne między nimi

Niepewności (błędy, nieoznaczoności, nieokreśloności) pomiarów

Wielokrotne wykonywanie pomiarów jednej wielkości prowadzi do uzyskania szeregu różnych
wyników, które nie są powtarzalne. Przyczyna tego tkwi w niepewnościach (błędach,
nieoznaczonościach, nieokreślonościach) pomiaru.
Przyczyną niepowtarzalności wyników pomiaru są między innymi: dynamiczna( fluktuacyjna)
natura badanych zjawisk, oddziaływanie między urządzeniem a obiektem mierzonym, niemożliwy do
uniknięcia wpływ otoczenia prowadzący do zmian warunków przeprowadzania pomiaru, itp.

Niepewności pomiaru powstają tym samym wskutek nakładania się na siebie wielu bardzo
drobnych czynników o charakterze losowym.

Wszystkie te czynniki powodują, że wyniki pomiaru mają charakter przypadkowy, a zatem
stanowią w sensie statystycznym zdarzenie losowe.
Wyniki pomiaru należy traktować jako zmienną losową.
Jeżeli poszczególnym wynikom pomiaru przypiszemy prawdopodobieństwa ich występowania,
to otrzymamy funkcję charakteryzującą rozkład prawdopodobieństw wyników.
Funkcja rozkładu prawdopodobieństw charakteryzuje pewne statystyczne prawidłowości
występujące w danym pomiarze.

Podział niepewności i błędów pomiarowych

Błędy systematyczne

są to błędy, które zniekształcają wynik w określoną stronę, np. wszystkie

wyniki są mniejsze od wartości rzeczywistej. Zaliczamy do nich błędy związane z przyrządami
pomiarowymi i niewłaściwą metodyką pomiarową (np. efekt paralaksy, przesunięty punkt zerowy
skali termometru, menisk roztworu zawsze poniżej kreski miarowej, itp.).
Błędy systematyczne są często trudne do wykrycia. Błędy te są w wielu przypadkach możliwe do
weryfikacji poprzez wykonanie pomiarów testowych i porównaniu wyników z wzorcem.
Błędy systematyczne nie podlegają analizie statystycznej.

Niepewności przypadkowe (losowe, dawne określenie: błędy losowe pomiarów)

są to

niepewności, które spełniają następujące warunki:
1) niepewności równe co do modułu są jednakowo prawdopodobne, tzn. równie prawdopodobne
jest otrzymanie wyniku z niedomiarem jak i z nadmiarem względem wartości rzeczywistej
2) niepewności małe co do modułu są bardziej prawdopodobne niż duże

16

3) prawdopodobieństwo niepewności przekraczającej pewną określoną liczbę E, nazywaną granicą
możliwych niepewności (błędów), jest praktycznie równe zeru:

P(|x

i

-x

0

|>E)=0

gdzie x

i

-wartość otrzymana z pomiaru, x

0

- wartość rzeczywista

Niepewności przypadkowe subiektywne

są to niepewności uzyskiwane przez eksperymentatora

np. efekt paralaksy przy odczycie wartości z przyrządu pomiarowego (w innym sensie niż przy
błędzie systematycznym), niedokładne przyłożenie linijki

Niepewności przypadkowe obiektywne

są to niepewności uzależnione od wpływu zewnętrznych

czynników, często niemożliwych do przewidzenia przez eksperymentatora (np. zmiana temperatury
przy otwarciu drzwi, fluktuacje napięcia zasilającego)

Błędy grube (pomyłki, niepewności grube)

powodują, że wyniki obarczone takimi błędami mają

charakter wyników odskakujących lub wątpliwych, czyli pojedynczych wartości istotnie różniących
się od pozostałych. Są łatwe do wyeliminowania na drodze weryfikacji statystycznej lub
posiadanego doświadczenia

Wstępne szacowanie niepewności i błędów:

celowym jest przeprowadzenie szacunkowej oceny

niepewności i błędów przed wykonaniem doświadczenia po to, aby wielkości decydujące o błędzie
końcowym wyznaczyć z dużą uwagą i dokładnością. Przy okazji wstępnego szacowania błędów
powstaje też obraz dokładności obliczeń - kontroli ilości miejsc znaczących w wynikach pośrednich
i w wyniku końcowym

Parametry metrologiczne metod pomiarowych

Dokładność metody

związana jest z odległością wyników pomiaru od wartości rzeczywistej

(prawdziwej)
Metoda dokładna to taka, której wyniki leżą blisko wartości rzeczywistej.
Przy stosowaniu wielokrotnym metody dokładnej największe skupienie wyników jest wokół
wartości rzeczywistej, zaś wyniki obarczone błędami przypadkowymi rozłożone będą
równomiernie po obu stronach tej wartości

Precyzja metody

związana jest z rozrzutem (inaczej rozproszeniem) wyników pomiaru

Metoda precyzyjna to taka, przy stosowaniu której rozrzut wyników jest bardzo mały (inaczej
- wyniki są skupione)

Powtarzalność

charakteryzuje precyzję metody w odniesieniu do jednego laboratorium

Odtwarzalność

charakteryzuje precyzję metody w odniesieniu do wielu laboratoriów

Czułość metody

jest to najmniejsza różnica w wynikach, jaką można określić za pomocą danej

metody pomiarowej. Czułość głównie związana jest z precyzją metody pomiarowej

17

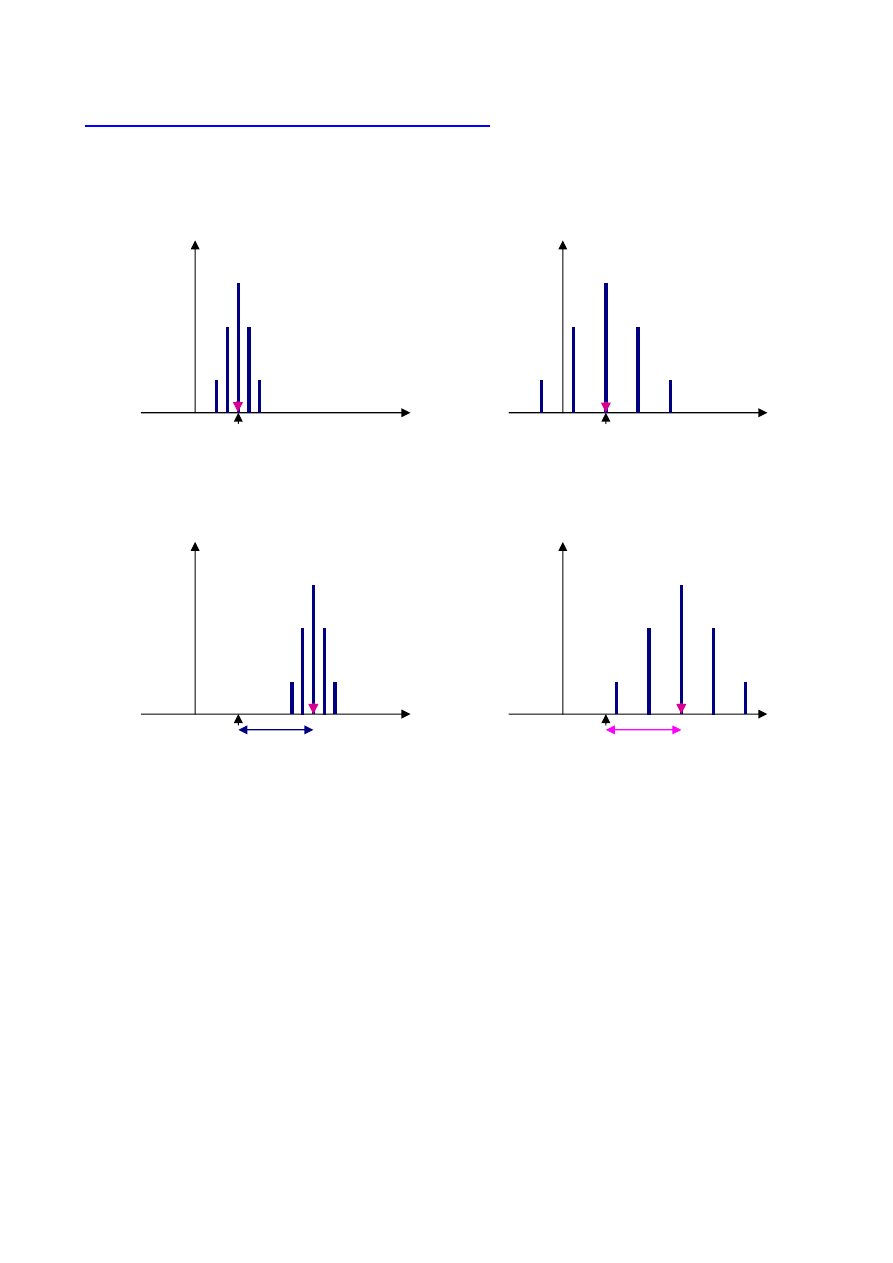
Graficzna prezentacja dokładności i precyzji metody

x

0

- wartość rzeczywista (prawdziwa)

x

ś

r

- wartość średnia z prób uzyskanych z zastosowaniem danej metody pomiarowej

n

i

x

i

n

i

n

i

n

i

x

i

x

i

x

i

x

0

x

0

x

ś

r

≈

x

0

x

ś

r

≈

x

0

x

ś

r

≠

x

0

x

ś

r

x

ś

r

x

ś

r

≠

x

0

metoda dokładna
i precyzyjna

metoda dokładna
i nieprecyzyjna

metoda niedokładna
i precyzyjna

metoda niedokładna
i nieprecyzyjna

18

ZMIENNE LOSOWE JEDNOWYMIAROWE - PARAMETRY ROZKŁADÓW

Każdemu zdarzeniu X należącemu do populacji generalnej przyporządkowujemy liczbę x, będącą

wynikiem doświadczenia. Liczby tej nie można przewidzieć przed wykonaniem doświadczenia. W

wyniku doświadczenia zmienna losowa przyjmuje tylko jedną wartość liczbową spośród wszystkich,

które może przyjąć.

Zbiór zdarzeń zastępuje się zbiorem liczb.

Twierdzenie o zmiennej losowej:

jeżeli x jest zmienną losową, to zmienną losową jest też

|x|, x+C, C x, x

2

.

Zmiennym losowym można przypisać prawdopodobieństwo ich występowania.

Efektem tego jest

otrzymanie rozkładu prawdopodobieństw zmiennej losowej, lub krócej - rozkładu zmiennej losowej.

Zmienna losowa skokowa

Jest to zmienna, której zbiór wartości jest przeliczalny.

Prawdopodobieństwo, że X = x

i

oznacza się

P

(X=x

i

) = p(x

i

)

Prawdopodobieństwo to spełnia warunek normalizacji

( )

1

x

p

n

1

i

i

=

∑

=

gdzie n określa wszystkie wartości zmiennej X

Zmienna losowa ciągła

Wartości zmiennej tworzą liczby z pewnego przedziału. Zbiór tych liczb jest nieprzeliczalny.

Prawdopodobieństwo wystąpienia wartości zmiennej zawartej w przedziale

x, x+dx

oznacza się

(

) ( )

dx

x

f

dx

x

X

x

P

=

+

≤

<

i spełnia warunek normalizacji w postaci

( )

1

dx

x

f

x

=

∫

gdzie całka rozciągnięta jest na cały obszar zmienności zmiennej.

Funkcje p(x

i

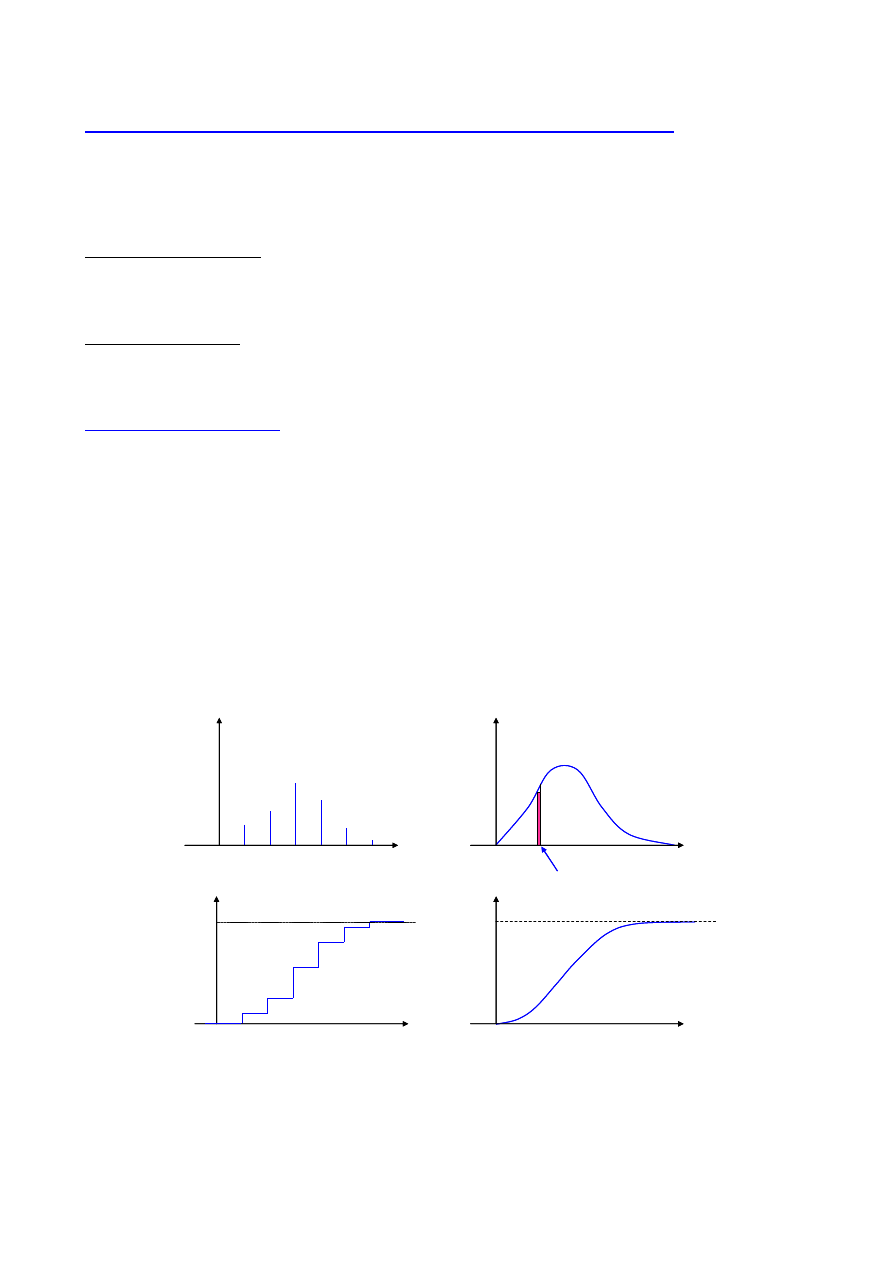
) i f(x) są to funkcje rozkładu zmiennej losowej.

Funkcję f(x) nazywa się też funkcją gęstości zmiennej losowej, funkcją gęstości

prawdopodobieństwa lub gęstością prawdopodobieństwa.

19

Dystrybuanta zmiennej losowej lub dystrybuanta rozkładu zmiennej losowej

Dystrybuanta zmiennej losowej jest to funkcja podająca prawdopodobieństwo wystąpienia zmiennej

X

nie większej od konkretnej, zadanej wartości x

j

, czyli prawdopodobieństwo wystąpienia wartości

x

≤

x

j

:

- dla zmiennej skokowej

( )

(

)

j

j

1

i

i

j

x

x

P

x

p

F

≤

=

=

∑

=

- dla zmiennej ciągłej

( )

( )

(

)

j

x

j

x

x

P

dx

x

f

x

F

j

≤

<

∞

−

=

=

∫

∞

−

Właściwości dystrybuanty:

1. funkcja F(x) jest funkcją niemalejącą, tzn. jeżeli x

1

< x

2

, to F(x

1

)

≤

F

(x

2

)

2. F(-

∞

)=0 i F(+

∞

)=1, czyli wykres dystrybuanty zawarty jest między wartościami 0 i 1 oraz

posiada dwie asymptoty poziome

3. różnica F(x

2

) - F(x

1

) określa prawdopodobieństwo występowania zmiennej losowej X w przedziale

(x

1

,x

2

>

4. prawdopodobieństwo wystąpienia zmiennej w przedziale (x

j

,∞

) wynosi

P

(x>x

j

) = 1 - F(x

j

)

x

i

p(x

i

)

x

1

x

2

x

3

x

4

x

5

x

6

x

i

F(x

i

)

1

0

x

x+dx

x

f(x)

F(x)

zmienna skokowa

zmienna ciągła

1

0

x

x

1

x

2

x

3

x

4

x

5

x

6

x

i

p(x

i

)

x

1

x

2

x

3

x

4

x

5

x

6

x

i

F(x

i

)

1

0

x

x+dx

x

f(x)

F(x)

zmienna skokowa

zmienna ciągła

1

0

x

x

1

x

2

x

3

x

4

x

5

x

6

20

PARAMETRY ROZKŁADU

Parametr rozkładu jest liczba dająca scharakteryzowanie zbioru wartości, jakie może przyjmować
zmienna losowa

Wartość oczekiwana zmiennej losowej

oznaczana jako E(X), określona jest:

- dla zmiennej skokowej

( )

( )

∑

=

⋅

=

n

1

i

i

i

x

p

x

X

E

sumowanie rozciągnięte jest na wszystkie wartości zmiennej skokowej

- dla zmiennej ciągłej

( )

( )

∫

∞

∞

−

⋅

=

dx

x

f

x

X

E

całkowanie rozciągnięte jest na cały obszar zmienności zmiennej losowej

Przykład zastosowania:

Zmienna skokowa jako wynik doświadczenia

Wykonano k serii pomiarów; każda seria posiada m

i

wyników. Całkowita ilość wyników wynosi

tym samym

∑

=

=

k

1

i

i

m

n

Prawdopodobieństwo wystąpienia wartości x

i

z serii określa wyrażenie

( )

n

m

x

p

i

i

=

Wartość oczekiwana:

( )

n

x

m

X

E

k

1

i

i

i

∑

=

=

Jeżeli serie składają się z pojedynczych pomiarów wykonywanych w identycznych warunkach,
czyli dla każdego i jest m

i

=1

, to wartość oczekiwana jest zwykłą średnią arytmetyczną

( )

x

n

x

X

E

n

i

i

=

=

∑

=

1

Ś

rednia ważona

stosowana jest wtedy, gdy są różnice w warunkach wykonywania pomiarów. Dla

każdego pomiaru lub serii pomiarów wprowadza się wagę w

i

. Średnia ważona opisana jest wzorem:

∑

∑

=

=

=

k

1

i

i

k

1

i

i

i

w

x

w

x

w

i

- waga pomiaru lub serii pomiarowej, x

i

- wartość pomiaru lub serii pomiarowej

21

Wariancja rozkładu zmiennej losowej

oznaczana jako D

2

(X), określana jest jako wartość

oczekiwana kwadratu odchylenia zmiennej losowej X od wartości oczekiwanej E(X)

( )

( )

(

)

[

]

2

2

X

E

x

E

X

D

−

=

- dla zmiennej skokowej

( )

( )

[

]

( )

∑

=

⋅

−

=

n

1

i

i

2

i

2

x

p

X

E

x

X

D

- dla zmiennej ciągłej

( )

( )

[

]

( )

∫

∞

∞

−

⋅

−

=

dx

x

f

X

E

x

X

D

2

2

Odchylenie standardowe (dyspersja) rozkładu

( )

( )

X

D

X

2

=

σ

Uwaga: odchylenie standardowe używane jest w praktyce częściej niż wariancja

Uogólnienie
momentem rzędu k zmiennej losowej

nazywa się wartość oczekiwaną k-tej potęgi odchyleń

poszczególnych wartości zmiennej losowej od wartości c (c - pewna stała)

- dla zmiennej skokowej

(

) ( )

i

n

1

i

k

i

k

x

p

c

x

⋅

−

=

µ

∑

=

- dla zmiennej ciągłej

(

) ( )

∫

∞

∞

−

⋅

−

=

µ

dx

x

f

c

x

k

k

- jeżeli c = 0 - momenty zwykłe

→

wartość oczekiwana E(X) jest momentem zwykłym rozkładu

1-go

rzędu

- jeżeli c=E(X) (wartością oczekiwaną) - moment centralny

→

wariancja D

2

(X)

jest momentem

centralnym rozkładu 2-go rzędu

Zastosowanie momentu centralnego - miara asymetrii rozkładu - znormalizowana wielkość

3

3

1

σ

µ

γ

=

- gdy

γ

1

= 0

to rozkład jest rozkładem symetrycznym

- gdy

γ

1

≠

0

to rozkład jest rozkładem asymetrycznym; wartość

γ

1

jest miarą skośności rozkładu

22

Inne miary położenia
Ś

rednia geometryczna

stosowana wtedy, gdy zmienne x

1

, x

2

, ....x

n

zachowują się jak wyrazy szeregu

geometrycznego

n

n

2

1

g

x

...

x

x

x

=

Ś

rednia harmoniczna

stosowana m. in. wtedy, gdy n zmiennych ma silnie zróżnicowane wartości

∑

=

=

n

1

i

i

h

x

1

n

x

Kwantyle

są to wartości cechy badanej próby, które dzielą tę próbę na określone części pod

względem liczby pomiarów. Wyniki tworzące próbę muszą być uporządkowane rosnąco.
Najczęściej stosowane kwantyle:

kwartyle - podział na 4 części

decyle - podział na 10 części

percentyle - podział na 100 części

Kwartyle

kwartyl pierwszy Q

1

- to taka wartość, która dzieli próbę w ten sposób, że ¼ (25%) ilości pomiarów

ma od niej wartości nie większe, a ¾ (75%) nie mniejsze.
kwartyl drugi Q

2

(inaczej mediana) - jest to wartość znajdującą się w środku próby

- jeżeli ilość wyników n w próbie jest nieparzysta:

( )

1

n

2

1

2

x

Q

+

=

- jeżeli ilość wyników jest parzysta:

2

x

x

Q

1

n

2

1

n

2

1

2

+

+

=

kwartyl trzeci Q

3

- to taka wartość, która dzieli próbę w ten sposób, że ¾ (75%) ilości pomiarów ma

od niej wartości nie większe, a ¼ (25%) nie mniejsze.

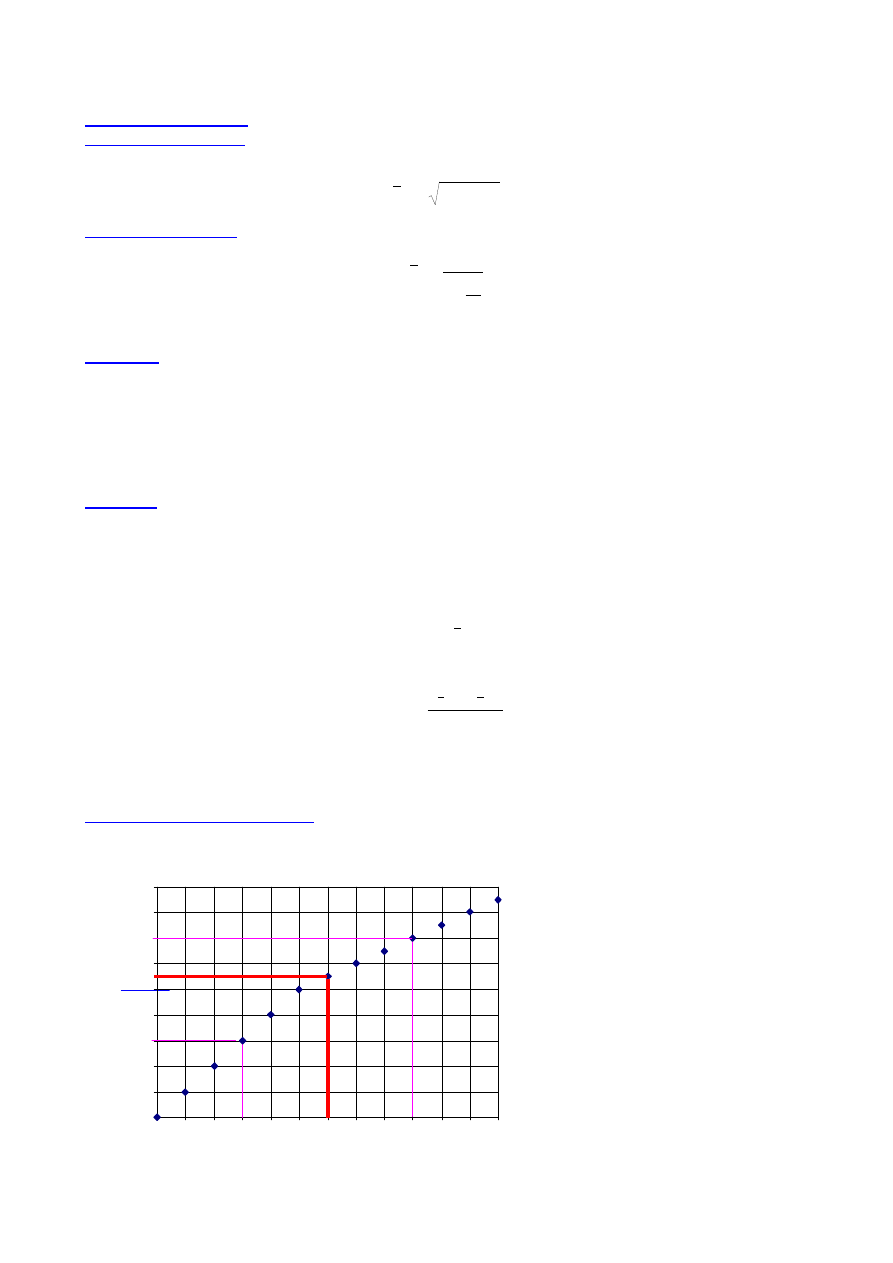
Przykład zastosowania kwartyli

Uzyskano n = 13 wyników zmiennej X. Wyznaczyć parametry charakteryzujące próbę

x

ś

r

Q

2

Q

3

Q

1

10

20

30

40

50

60

70

80

90

0

0

1

2

3

4

5

6

7

8

9

10

11

12

i

x

i

średnia arytmetyczna

49.23

rozstęp R = x

12

- x

0

85

kwartyl 1 - Q

1

30

kwartyl 2 - Q

2

(mediana)

55

kwartyl 3 - Q

3

70

rozstęp kwartylny Q

3

- Q

1

40

23

Wartość modalna

(wartość najczęstsza, moda, dominanta) jest to wartość występująca najczęściej

w badanym zbiorze z wykluczeniem wartości skrajnych x

min

i x

max

, np. dla zbioru:

11, 13, 14, 10, 13, 14, 16, 15, 14

- dominanta równa jest 14.
W przypadku szeregu rozdzielczego dominanta wyznaczana jest dla przedziału klasowego,
w którym występuje największa liczba obserwacji

24

PRZYKŁADY TYPÓW ROZKŁADÓW ZMIENNYCH LOSOWYCH

WYBRANE ROZKŁADY ZMIENNYCH LOSOWYCH

rozkłady zmiennych losowych skokowych

- rozkład zero - jedynkowy
- rozkład dwumianowy (Bernoulliego)
- rozkład Poissona

rozkłady zmiennych losowych ciągłych

- rozkład równomierny (prostokątny)
- rozkład normalny (Gaussa)
- rozkład

χ

2

- rozkład t-Studenta

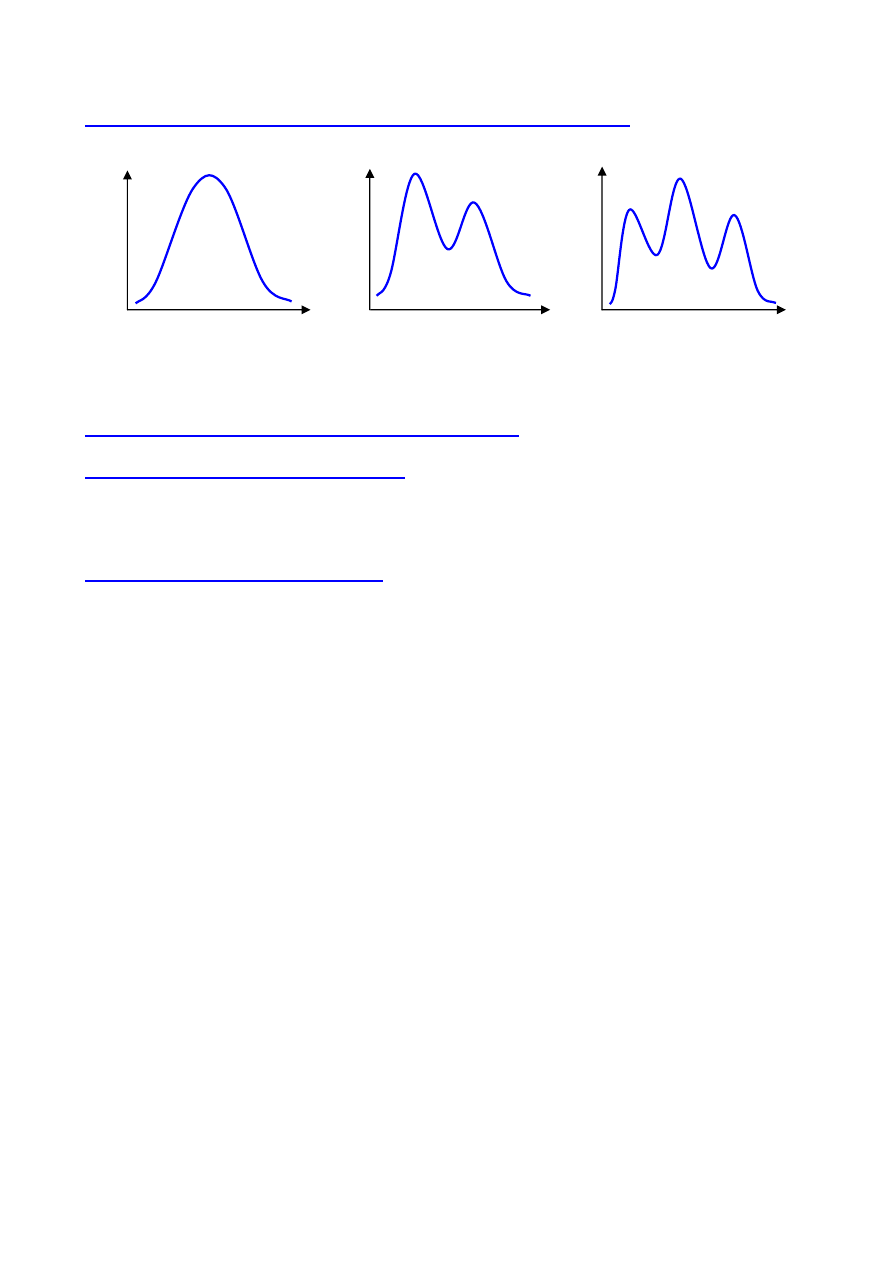
f(x)

x

rozkład jednomodalny

f(x)

x

rozkład bimodalny

f(x)

x

rozkład wielomodalny

25

ROZKŁAD zero - jedynkowy

opisuje zmienną losową X, która może przyjmować tylko dwie wartości x

1

= 1

i x

2

= 0.

Prawdopodobieństwo wystąpienia x

1

=1

wynosi p, a prawdopodobieństwo wystąpienia x

2

= 0

wynosi q:

p(x

1

) = p,

p(x

2

) = q = 1 - p

Dystrybuantę rozkładu określa jest funkcja











≥

<

≤

<

=

1

1

2

2

x

x

dla

1

x

x

x

dla

q

x

x

dla

0

)

x

(

F

Wartość oczekiwana rozkładu

E(X) = 1

⋅

p +0

⋅

q = p

Wariancja rozkładu

D

2

(X) = (1-p)

2

⋅

p + (0-p)

2

⋅

q = q

⋅

p

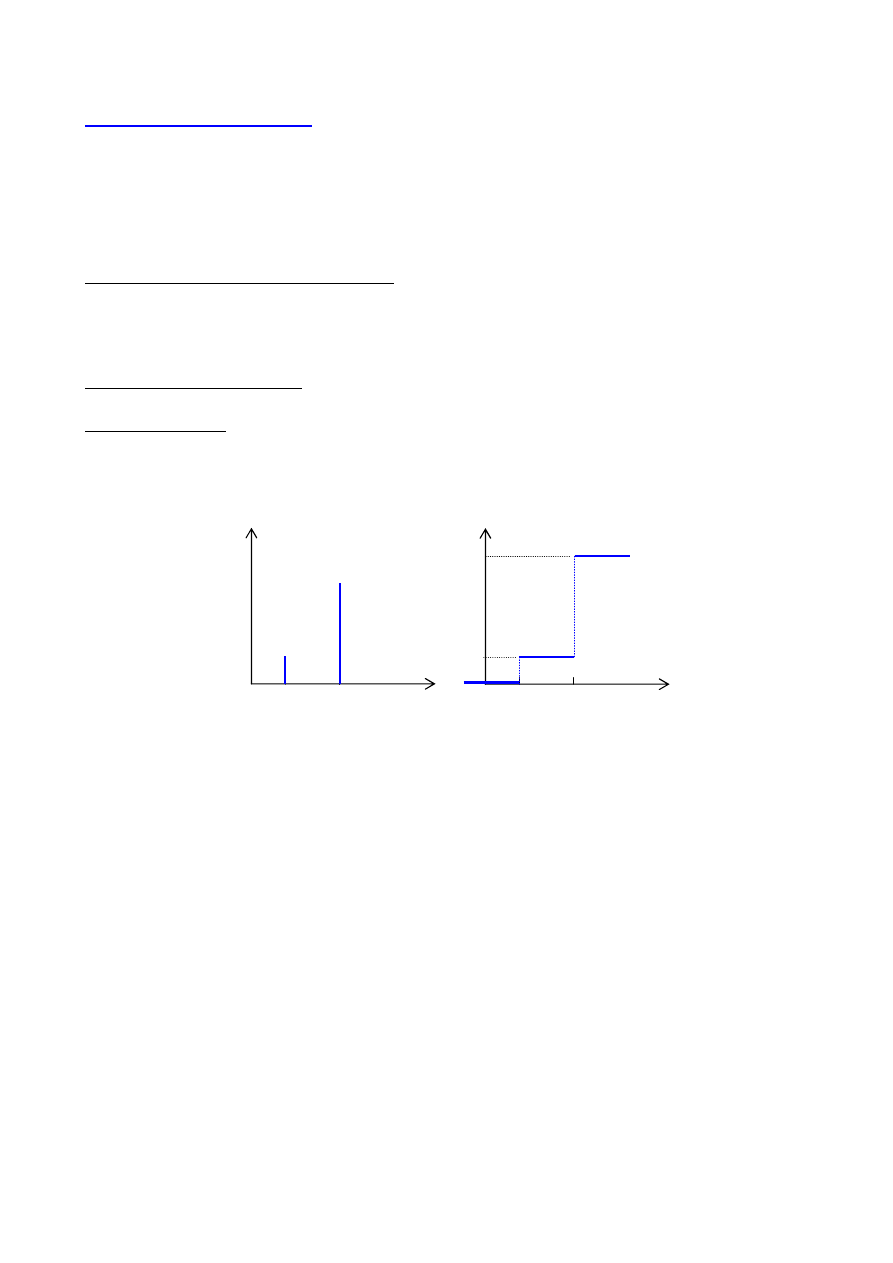
0 1

x

p(x)

0 1

x

F(x)

q

p

q

p

1

0

26

Rozkład dwumianowy (Bernoulliego)

opisuje rozkład zmiennej losowej X uzyskiwanej w wyniku realizacji n doświadczeń, w których
pojawia się zdarzenie określane jako sukces lub nie pojawia się takie zdarzenie i wtedy określane
jest jako porażka. Prawdopodobieństwo sukcesu wynosi p, prawdopodobieństwo porażki wynosi
q = 1 - p

. Jak widać sukces i porażka są to zdarzenia wzajemnie się wykluczające.

Przy wykonaniu n doświadczeń uzyskać można liczbę k sukcesów. Prawdopodobieństwo
wystąpienia k sukcesów opisywane jest wzorem - rozkład dwumianowy:

( )

k

n

k

k

n

k

n
k

)

p

1

(

p

)!

k

n

(

!

k

!

n

)

p

1

(

p

)

k

X

(

p

−

−

−

−

=

−

=

=

k = 1, 2, 3 ... n -

liczba wystąpienia sukcesów

n

– liczba doświadczeń

p

– prawdopodobieństwo wystąpienia sukcesu

Dystrybuantę rozkładu dwumianowego przedstawia wzór

( )

∑

=

−

−

=

≤

=

1

k

1

k

k

n

k

n
k

1

1

)

p

1

(

p

)

k

X

(

P

)

k

(

F

Wartość oczekiwana rozkładu

p

n

)

k

X

(

p

k

)

X

(

E

n

1

k

⋅

=

=

⋅

=

∑

=

Wariancja rozkładu

[

]

)

p

1

(

p

n

)

k

X

(

p

)

X

(

E

k

)

X

(

D

n

1

k

2

2

−

⋅

⋅

=

=

−

=

∑

=

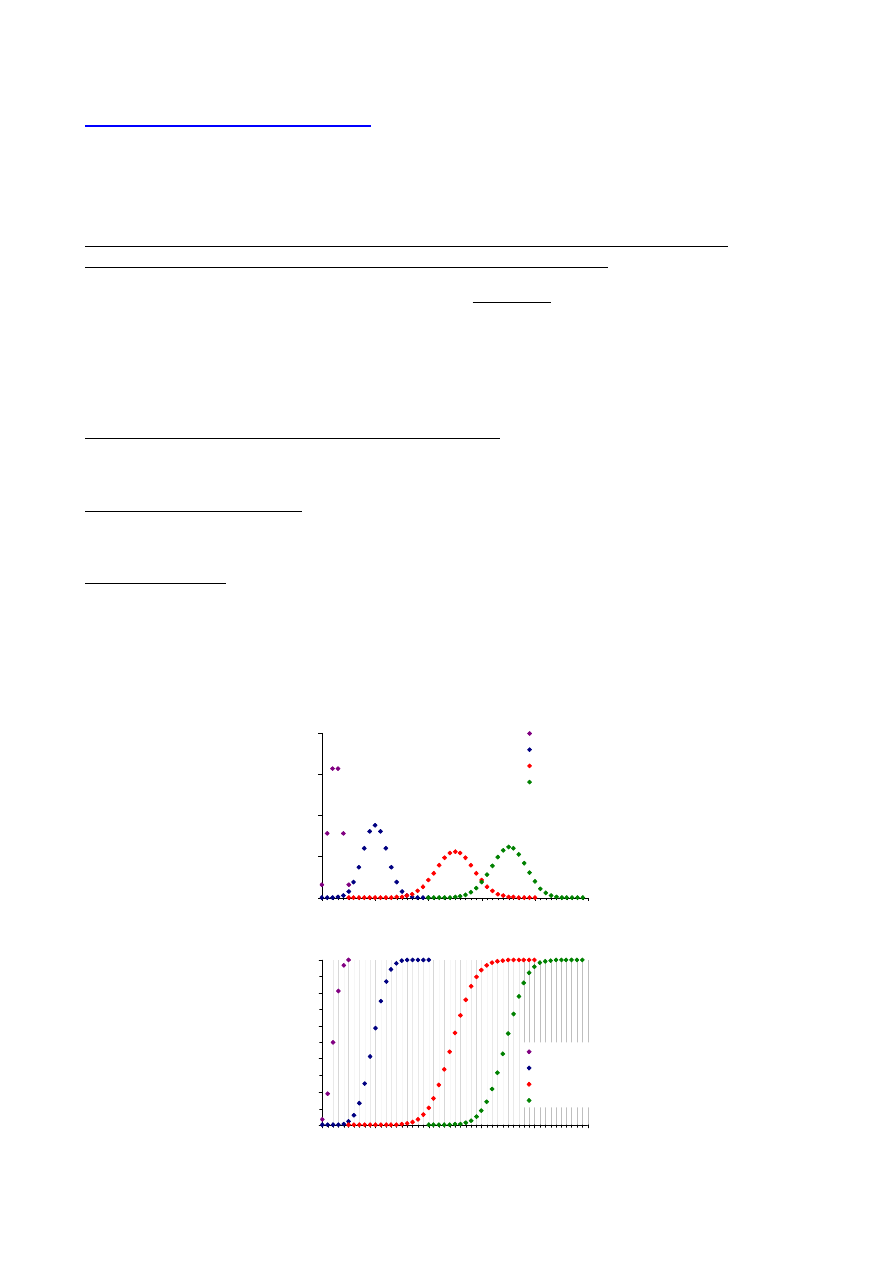
Rozkład dwumianowy znajduje duże zastosowanie w statystycznej analizie w biologii np. przy
badaniu jakości roślin pod katem ich zdolności do wykiełkowania.
.

0.0

0.1

0.2

0.3

0.4

0

10

20

30

40

50

n=5, p=0.5

n=20, p=0.5

n=50, p=0.5

n=50, p=0.7

p(k)

k

0.0

0.2

0.4

0.6

0.8

1.0

0

10

20

30

40

50

n=5, p=0.5

n=20, p=0.5

n=50, p=0.5

n=40, p=0.7

F(k)

k

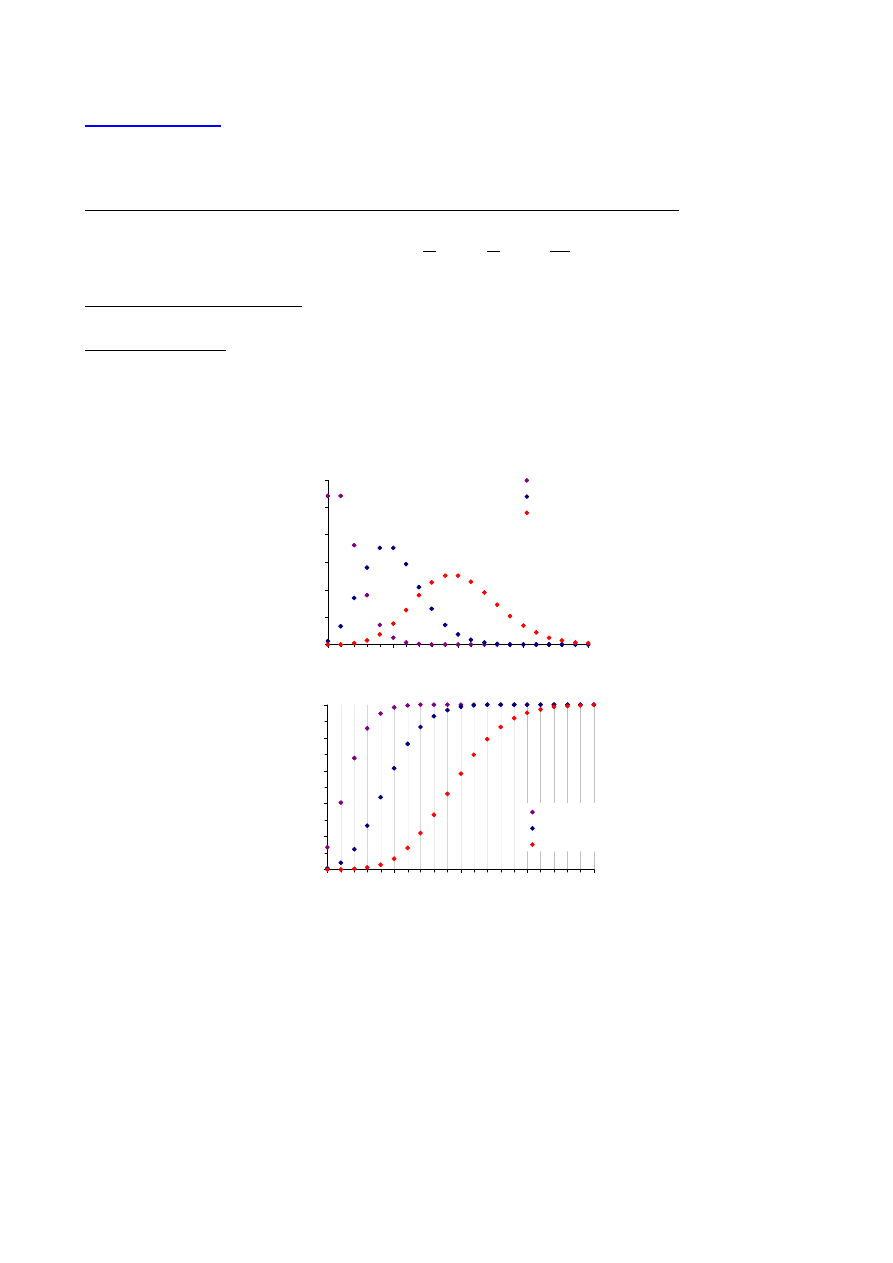
27

Rozkład Poissona

jest szczególnym przypadkiem rozkładu dwumianowego, w którym prawdopodobieństwo p sukcesu
jest bardzo małe, a liczba doświadczeń n bardzo duża. Wprowadza się wielkość

λ

określoną

wzorem

λ

= n

⋅

p

. Wielkość

λ

dla analizowanych doświadczeń jest stała i niezbyt duża.

Prawdopodobieństwo uzyskania k sukcesów przedstawia wzór - rozkład Poissona:

λ

λ

λ

λ

−

−

=













−

























=

=

e

!

k

n

1

n

k

n

)

k

X

(

P

k

k

n

k

Wartość oczekiwana rozkładu

λ

=

)

X

(

E

Wariancja rozkładu

λ

=

)

X

(

D

2

Rozkład Poissona znajduje zastosowanie np. w statystycznej kontroli jakości produktów, gdzie
liczba produktów sprawdzanych jest duża, a ilość produktów wadliwych jest bardzo mała. Znajduje
również zastosowanie w fizyce w analizie zjawiska rozpadu promieniotwórczego.

0.00

0.05

0.10

0.15

0.20

0.25

0.30

0

5

10

15

20

lambda = 2

lambda = 5

lambda = 10

k

p(k)

k

F(k)

0.0

0.2

0.4

0.6

0.8

1.0

0

5

10

15

20

lambda = 2

lambda = 5

lambda = 10

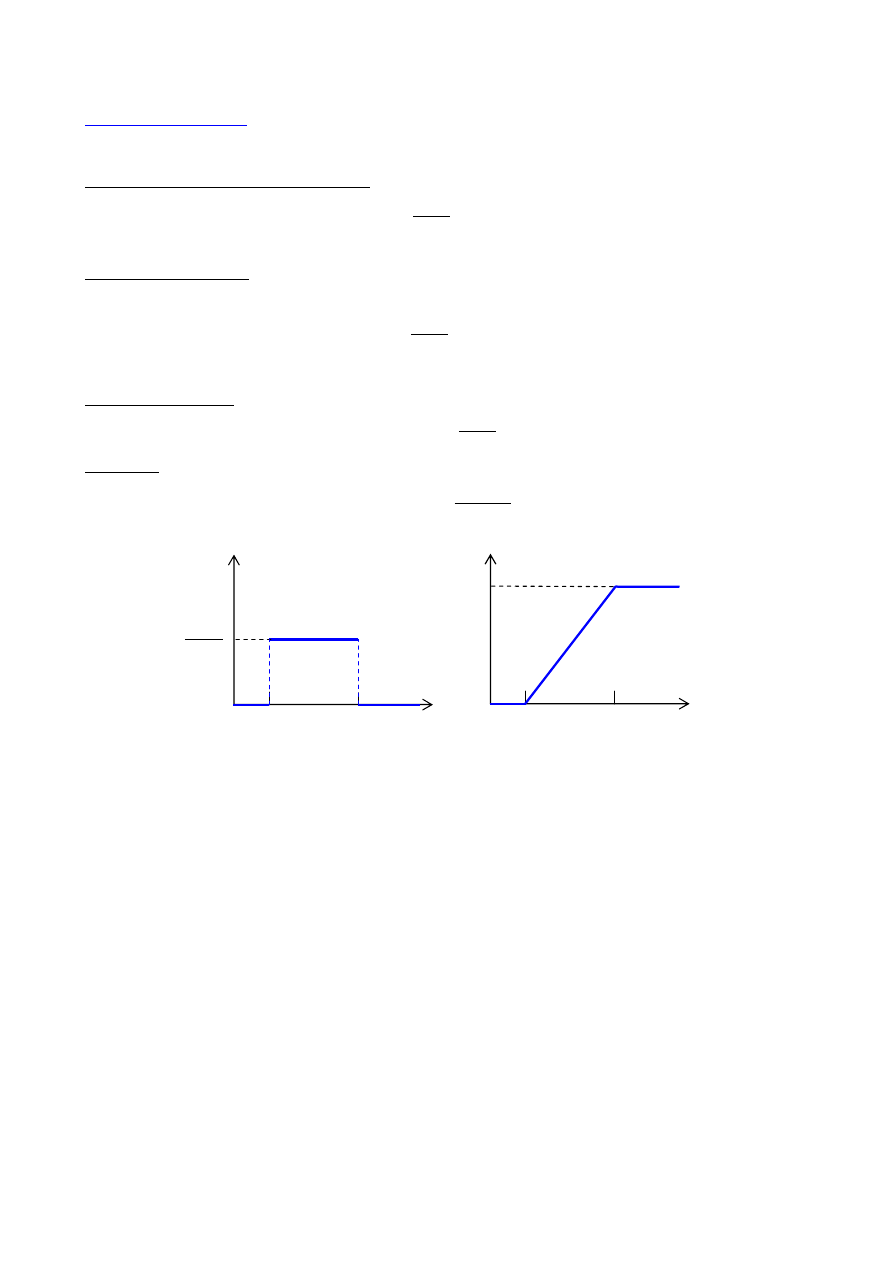
28

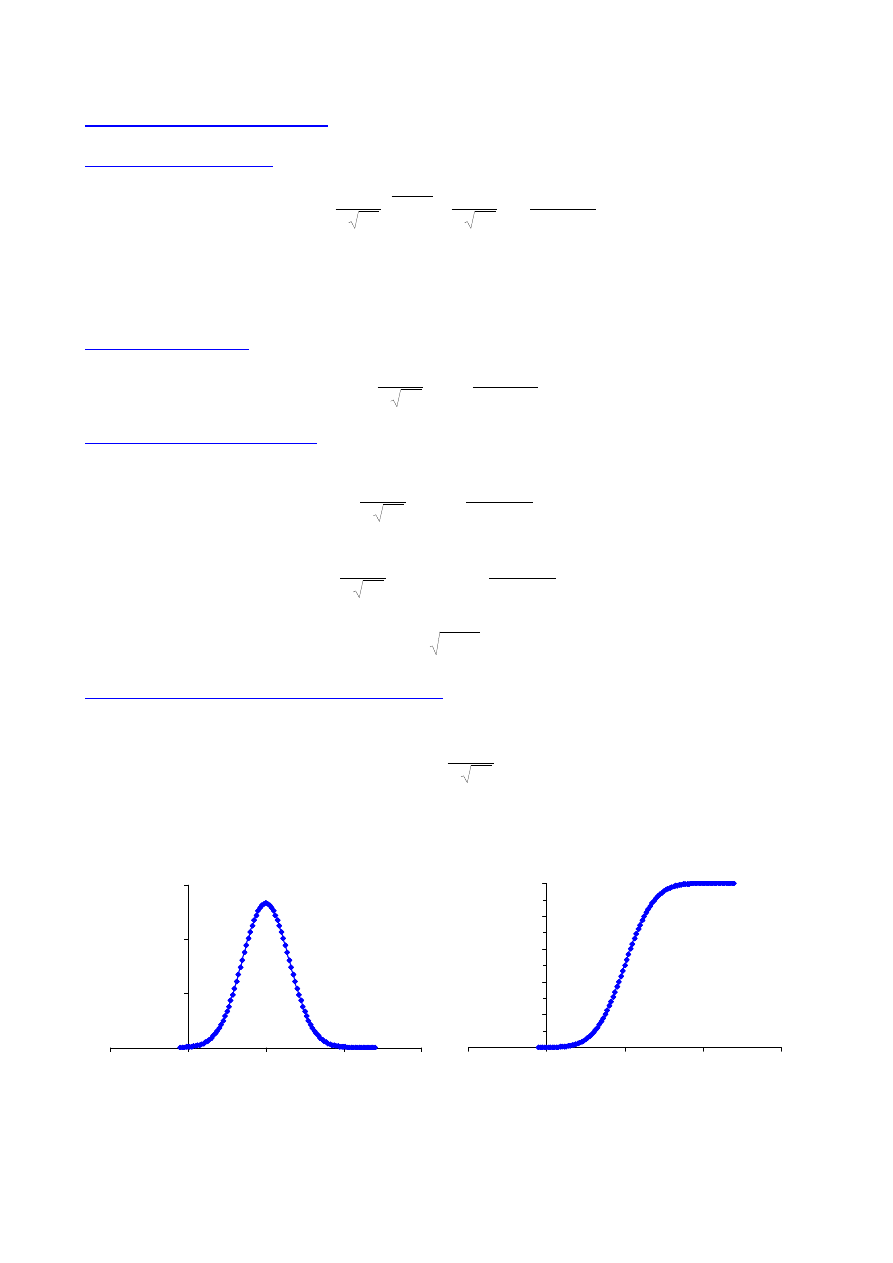
Rozkład prostokątny:

jest stosowany tam, gdzie w pewnym przedziale <a, b> prawdopodobieństwo zajścia zdarzenia jest
stałe, a poza tym przedziałem równe jest 0.
Funkcję gęstości rozkładu opisuje wzór









>

<

≤

≤

−

=

b

x

i

a

x

dla

0

b

x

a

dla

a

b

1

)

x

(

f

Dystrybuanta rozkładu













>

≤

≤

−

−

<

=

b

x

dla

1

b

x

a

dla

a

b

a

x

a

x

dla

0

)

x

(

F

Wartość oczekiwana

2

a

b

)

X

(

E

+

=

Wariancja

(

)

12

a

b

)

X

(

D

2

2

−

=

F(x)

a b x

1

0

f(x)

a b x

0

a

b

1

−−−−

29

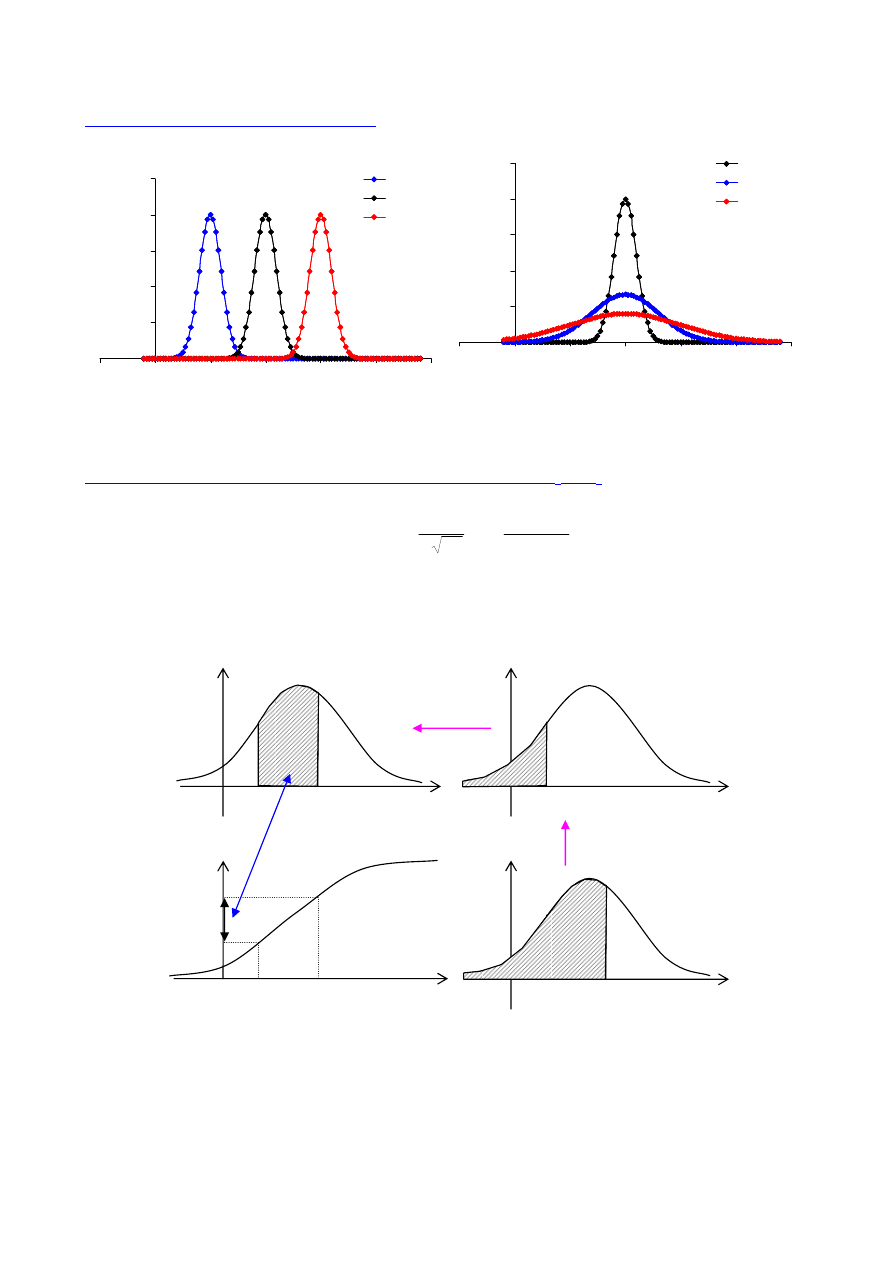
ROZKŁAD normalny (Gaussa)

Funkcja gęstości rozkładu

( )

(

)

(

)

















−

−

=

=

−

−

2

2

2

2

2

1

2

1

2

2

σ

µ

π

σ

π

σ

σ

µ

x

exp

e

x

f

x

gdzie:

µ

-

wartość oczekiwana rozkładu,

σ

- odchylenie standardowe rozkładu inaczej dyspersja

rozkładu

Przy analizie właściwości rozkładu zakłada się, że wartości te są znane.

Dystrybuanta rozkładu

( )

(

)

∫

∞

−

















−

−

=

x

dx

x

exp

x

F

2

2

2

2

1

σ

µ

π

σ

Parametry rozkładu normalnego

- wartość oczekiwana rozkładu

( )

(

)

µ

σ

µ

π

σ

=

















−

−

=

∫

∞

∞

−

dx

x

exp

x

X

E

2

2

2

2

1

- wariancja rozkładu

( )

(

)

(

)

2

2

2

2

2

2

2

1

σ

σ

µ

µ

π

σ

=

















−

−

−

=

∫

∞

∞

−

dx

x

exp

x

X

D

- dyspersja rozkładu

( )

( )

σ

σ

=

=

x

D

x

2

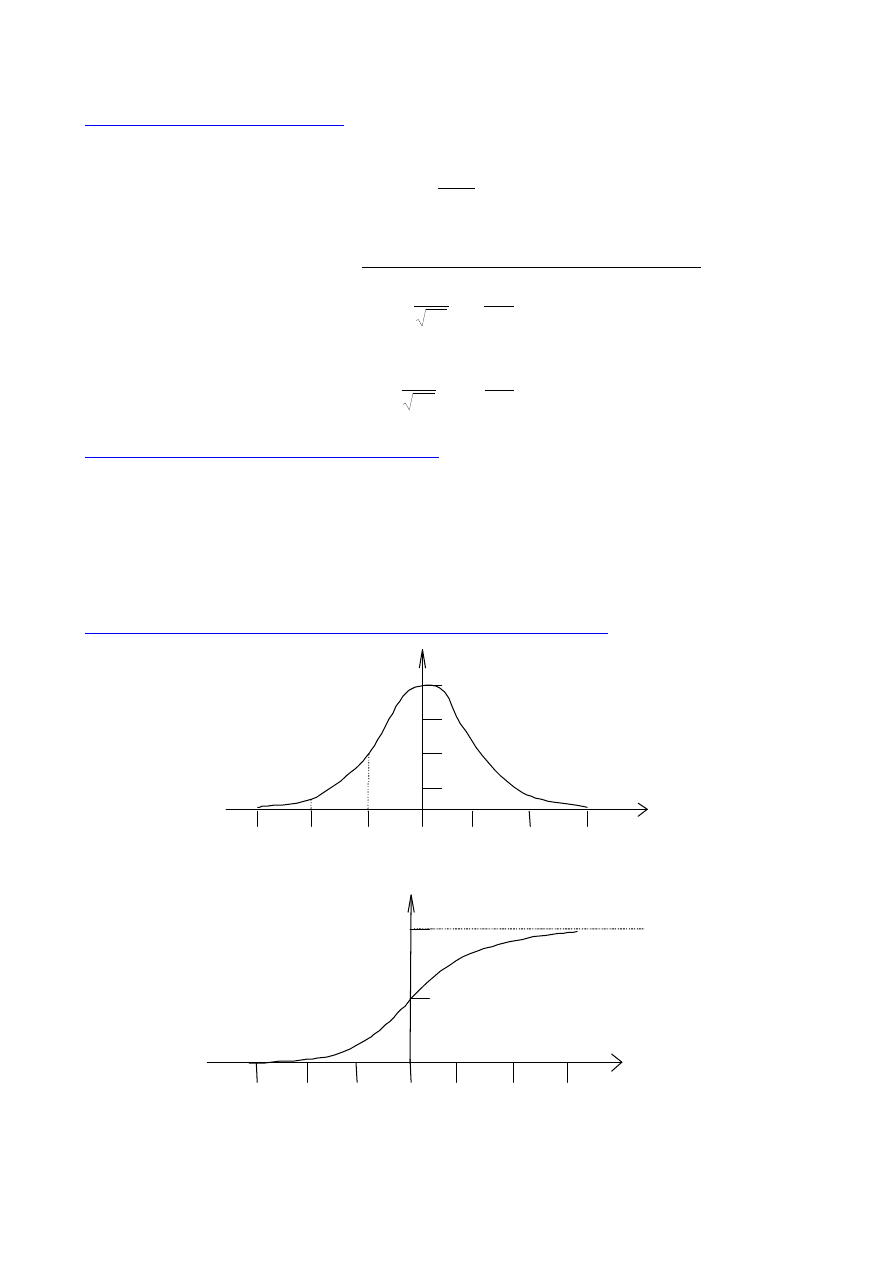
Własności krzywej gęstości rozkładu normalnego

- krzywa posiada maksimum dla x=

µ

; wartość maksymalna wynosi

( )

π

σ

µ

2

1

=

f

- krzywa jest symetryczna względem

µ

; ma kształt dzwonu

- punkty przegięcia krzywej:

µ

-

σ

i

µ

+

σ

x

f(x)

0.00

0.05

0.10

0.15

-10

0

10

20

30

x

f(x)

0.00

0.05

0.10

0.15

-10

0

10

20

30

x

F(x)

0.0

0.2

0.4

0.6

0.8

1.0

-10

0

10

20

30

x

F(x)

0.0

0.2

0.4

0.6

0.8

1.0

-10

0

10

20

30

30

Wpływ µ i

σ

na kształt krzywej gęstości

0.0

0.1

0.2

0.3

0.4

0.5

-5

0

5

10

15

20

25

mi = 5

mi = 10

mi = 15

f(x)

x

0.0

0.1

0.2

0.3

0.4

0.5

-5

0

5

10

15

20

25

mi = 5

mi = 10

mi = 15

f(x)

x

0.0

0.1

0.2

0.3

0.4

0.5

-5

0

5

10

15

20

25

sigma = 1

sigma = 3

sigma = 5

f(x)

µµµµ

σσσσ

1

σσσσ

2

σσσσ

3

x

0.0

0.1

0.2

0.3

0.4

0.5

-5

0

5

10

15

20

25

sigma = 1

sigma = 3

sigma = 5

f(x)

µµµµ

σσσσ

1

σσσσ

2

σσσσ

3

x

µµµµ

1

<

µµµµ

2

<

µµµµ

3

σσσσ

1

=

σσσσ

2

=

σσσσ

3

=

σσσσ

µµµµ

1

=

µµµµ

2

=

µµµµ

3

=

µµµµ

σσσσ

1

<

σσσσ

2

<

σσσσ

3

Obliczanie prawdopodobieństwa wystąpienia x w przedziale od x

1

do x

2

(

)

(

)













−

−

−

=

≤

<

∫

)

x

(

F

)

x

(

F

dx

x

exp

x

x

x

P

x

x

1

2

2

2

2

1

2

1

2

2

1

σ

µ

π

σ

-interpretacja graficzna:

f(x)

x

x

1

x

2

F(x)

x

x

1

x

2

F

x1

F

x2

P(x)

f(x)

x

x

1

x

2

F

x1

f(x)

x

x

1

x

2

F

x2

31

Standaryzacja rozkładu normalnego

- wprowadza się zmienną standaryzowaną

σ

µ

−

=

x

t

dx =

σ

dt

po podstawieniu do f(x) otrzymuje się funkcję gęstości dla zmiennej standaryzowanej

( )















−

=

2

t

exp

2

1

t

f

2

π

- dystrybuanta

( )

dt

2

t

exp

2

1

t

F

t

2

∫

∞

−















−

=

π

Parametry rozkładu normalnego po standaryzacji

- wartość oczekiwana

E(t) = 0

- wariancja

D

2

(t) = 1

- dyspersja

σ

t

= 1

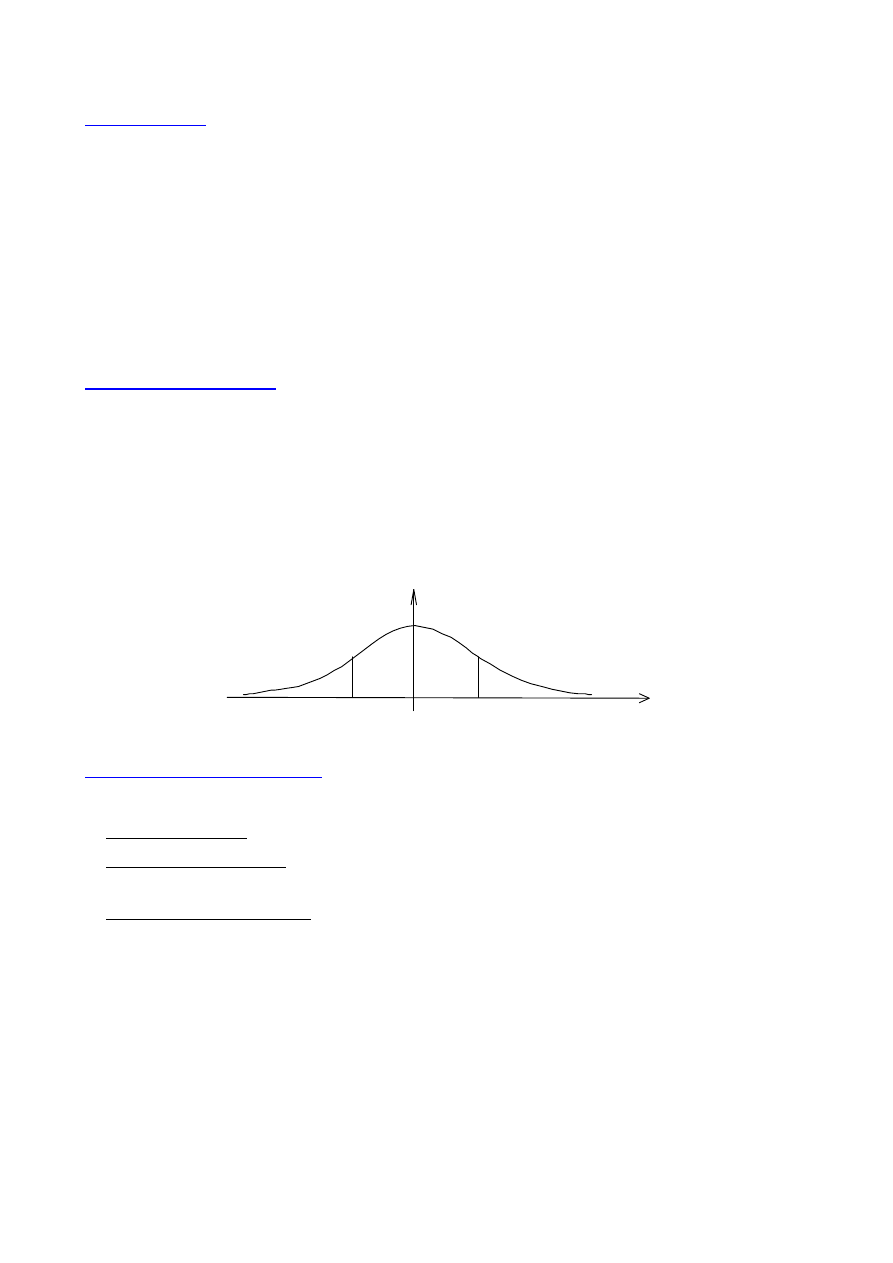
Krzywa gęstości i dystrybuanta standaryzowanego rozkładu normalnego

f(t)

0.24

0.05

0.0044

-3 -2 -1 0 1 2 3

0.40

t

-3 -2 -1 0 1 2 3

0.0014

0.023

0.159

0.5

0.841

0.977

0.9987

F(t)

t

32

Prawo "3 sigma"

- w przedziale od -3

⋅σ

do +3

⋅σ

wokół wartości oczekiwanej znajdują się prawie wszystkie wartości

zmiennej losowej

P(µ - 3

σ

< x

≤

µ + 3

σ

)

= 0.997 lub P(-3 < t

≤

3)

= 0.997

- w przedziale od -2

⋅σ

do +2

⋅σ

wokół wartości oczekiwanej znajduje się ok. 95% wszystkich

wartości zmiennej

P(µ - 2

σ

< x

≤

µ + 2

σ

)

= 0.954 lub P(-2 < t

≤

2)

= 0.954

- w przedziale od -1

⋅σ

do +1

⋅σ

wokół wartości oczekiwanej znajduje się ok. 68% wszystkich

wartości zmiennej

P(µ-

σ

< x

≤

µ+

σ

)

= 0.682 lub P(-1 < t

≤

1)

= 0.682

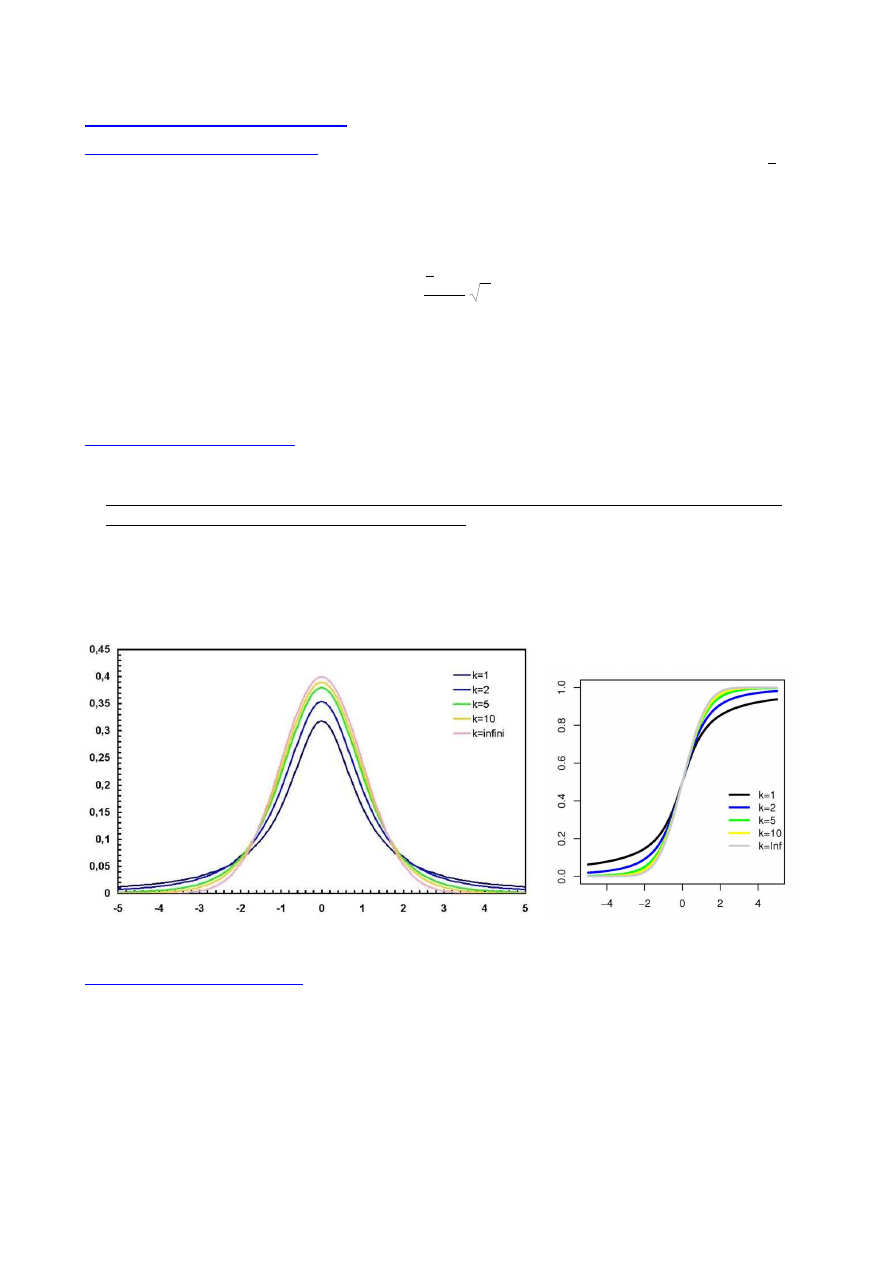
PRZEDZIAŁ UFNOŚCI jest to symetryczny przedział wokół wartości oczekiwanej, wewnątrz

którego prawdopodobieństwo wystąpienia zmiennej losowej określane jest jako poziom
ufności i oznaczane 1-

αααα

1-

α

= P(-t

α

/2

< t

≤

t

α

/2

)

- sens statystyczny: wewnątrz tego przedziału znajdzie się (1-

α

)

⋅

100%

wyników pomiarowych

(przy wykonywaniu w identycznych warunkach danego doświadczenia)

- obszar zewnętrzny nazywa się przedziałem krytycznym, zaś

α

- współczynnikiem istotności

f

-t

α

/2

t

α

/2

t

α/2

α/2

1−α

Przedział ufności a błąd pomiaru

przedziały ufności związane są z błędami (niepewnościami) pomiarowymi:

- niepewność średnia (błąd średni) równa jest odchyleniu standardowemu

σ

(ok. 68% wyników)

- niepewność maksymalna (błąd maksymalny) równa jest potrójnemu odchyleniu standardowemu

3

σ

(ok. 99.7% wyników)

- niepewność prawdopodobna (błąd prawdopodobny) jest to niepewność, dla której poziom

ufności 1-

α

wynosi 0.5 (wewnątrz przedziału znajdzie się 50% wyników).

Niepewność ta równa jest

t

1-

α

=0.5

= 0.6745

czyli 0.6745

⋅σ

i jest mniejsza od niepewności średniej. Uważa się, że określanie

niepewności pomiaru poprzez niepewność prawdopodobną jest zbyt optymistyczne.

Jako najpoprawniejszą interpretację niepewności w sensie statystycznym przyjmuje się
wartość odchylenia standardowego.

33

ROZKŁAD Studenta (t-Studenta)

Założenia do rozkładu Studenta:

- jeżeli zmienna losowa X ma rozkład normalny o parametrach

µ

i

σ

, to średnia arytmetyczna x

obliczona z n-elementowej próby ma również rozkład normalny

- rozkład tej średniej może być określony dopiero wtedy, gdy znane są dokładne wartości obydwu

parametrów w populacji generalnej

- jeżeli próba pochodzi z populacji generalnej, to zmienna określona równaniem

n

s

x

t

x

µ

−

=

ma rozkład niezależny od parametru

σ

- rozkład tak zdefiniowanej zmiennej nazywa się rozkładem Studenta
- funkcje gęstości i dystrybuanty rozkładu Studenta są bardzo skomplikowane - znaleźć je można w

podręcznikach

Własności rozkładu Studenta

- jest symetryczny, jego kształt zależy od ilości stopni swobody

Stopień swobody rozkładu to liczba niezależnych wyników obserwacji pomniejszona o liczbę
związków, które łączą wyniki obserwacji ze sobą.

- jest szerszy od rozkładu normalnego

- pokrywa się z rozkładem normalnym przy n

→∝

( w praktyce różnice stają się pomijalne przy n

równym ok. 30)

- krzywa gęstości i dystrybuanta rozkładu Studenta:

(wykresy: http://pl.wikipedia.org/wiki/Rozk%C5%82ad_Studenta)

Stosowanie rozkładu Studenta

-stosowane są tablice określone zależnością:

P(|t|) > t

k,

α

) =

α

czyli P(t < -t

k,α

i t > t

k,α

) = α

α

- współczynnik istotności, t

k,

α

- wartość krytyczna zmiennej t

oraz tablice

P(|t|) < t

k,

α

) = 1-

α

czyli P(-t

k,

α

< t < t

k,

α

) = 1-

α

1-

α

- poziom ufności

34

ESTYMATORY ROZKŁADU

Analiza rozkładu normalnego oparta była na założeniu, że znane są parametry rozkładu

µ

i

σ

, tzn.

ż

e znana jest cała populacja generalna. W praktyce wykonuje się skończoną ilość pomiarów

(przypomnienie: próba jest przeliczalnym i skończonym podzbiorem całej populacji; pobierana
powinna być losowo i powinna być reprezentatywna dla całej populacji)

Wnioski wyciągane na podstawie próby określa się estymacją, a uzyskane parametry

z próby nazywa się estymatorami, czyli oszacowaniami bądź ocenami parametrów
populacji

Wartość estymatora parametru zależy oczywiście od wartości elementów próby i od jej liczebności

- gdybyśmy próbę wykonywali wielokrotnie, to otrzymalibyśmy różne wartości zmiennej
losowej oraz różne wartości estymatora.

Nazwijmy ogólnie parametr populacji generalnej jako Q (Q może być wartością oczekiwaną,

odchyleniem standardowym itp.), a estymator tego parametru jako Q

n

Estymator Q

n

tym lepiej przybliża parametr Q im większa jest liczebność próby

Uwaga: na ogół istnieje kilka możliwych estymatorów tego samego parametru, np. wartość
oczekiwaną można estymować średnią arytmetyczną, medianą, średnią geometryczną, itp.

Właściwości estymatorów:

zgodność, nieobciążalność, największa efektywność, niezmienniczość

Zajmiemy się jedynie nieobciążalnością estymatora

Estymatorem nieobciążonym nazywa się taki estymator Q

n

, którego wartość oczekiwana jest równa

prawdziwej wartości Q parametru populacji:

E(Q

n

) = Q

W przypadku wykonywania dużej ilości prób różnica między otrzymywanymi wartościami Q

n

a

wartością Q powinna dążyć do zera.

Estymatorem obciążonym jest taki estymator Q

n

, dla którego różnica ta jest różna od zera.

Błąd systematyczny

B

n

= E(Q

n

) - Q

nazywa się obciążeniem estymatora.

Np. nieobciążonym estymatorem odchylenia standardowego jest wyrażenie

1

n

)

x

x

(

2

i

−

−

∑

,

zaś obciążonym jest

n

)

x

x

(

2

i

∑

−

.

Estymatory są również zmiennymi losowymi i podlegają rozkładom statystycznym

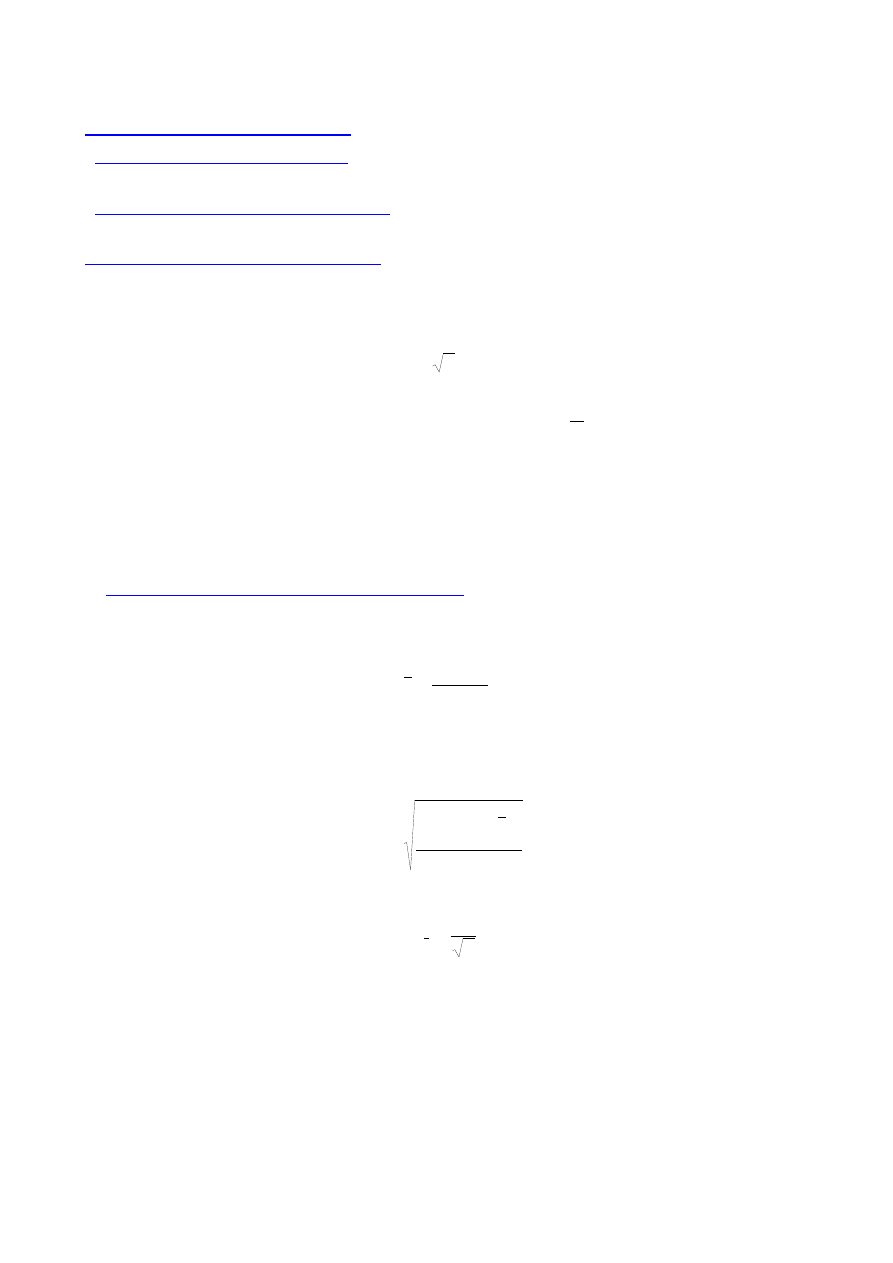
35

Estymatory rozkładu normalnego:

- dla próby małej (do 30 pomiarów):

estymatory wyrażone są wzorami określającymi wartość

ś

rednią, błąd średni pojedynczego pomiaru i błąd średni wartości średniej

- dla próby dużej (powyżej 30 pomiarów):

tworzy się szereg rozdzielczy i estymatory oblicza się

jako parametry szeregu rozdzielczego

Zasady tworzenia szeregu rozdzielczego:

- uporządkować wyniki w określony sposób np. w kierunku wzrastającej wartości zmiennej

losowej

- utworzyć przedziały klasowe:

- znaleźć rozstęp R = x

max

- x

min

- określić ilość przedziałów klasowych

n

k

≅

k

; k powinno być nie mniejsze od 5 i raczej nie

większe od 20

- określić szerokość pojedynczego przedziału klasowego

k

R

dx

≅

- określić kres dolny, wartość środkową i kres górny dla każdego przedziału klasowego

- każdy wynik wpisać do określonego przedziału klasowego - rzeczywista wartość będzie

reprezentowana środkową wartością przedziału

- w przypadku gdy liczności skrajnych przedziałów są b. małe zalecane jest łączenie ich w jeden

przedział (zlewanie przedziałów)

- narysować histogram doświadczalny, zaznaczyć wielobok częstości

Opracowanie wyników dla szeregu rozdzielczego

- estymator wartości oczekiwanej (średnia ważona):

n

x

m

x

k

1

i

i

i

∑

=

=

i

- numer przedziału klasowego, m

i

- ilość wyników w i-tym przedziale klasowym,

x

i

-wartość środkowa i-tego przedziału klasowego

- estymator odchylenia standardowego:

(

)

1

n

x

x

m

s

k

1

i

2

i

i

x

−

−

=

∑

=

- estymator odchylenia standardowego rozkładu średnich

n

s

s

x

x

====

PODSUMOWANIE ROZKŁADU NORMALNEGO - CENTRALNE TWIERDZENIE

GRANICZNE

Rozkład każdej zmiennej losowej X dąży do rozkładu normalnego, gdy liczebność próby dąży
do nieskończoności.

36

HIPOTEZY I TESTOWANIE HIPOTEZ (WNIOSKOWANIE STATYSTYCZNE)

Hipoteza statystyczna jest to każde takie przypuszczenie, które dotyczy:

- wartości parametrów rozkładu zmiennej losowej

lub

- postaci (typu) rozkładu zmiennej losowej,

i które może być weryfikowane statystycznie, tzn. w oparciu o wyniki zaobserwowane

w próbie losowej

Weryfikacja hipotezy

odbywa się przez zastosowanie testu statystycznego.

Test statystyczny

to każda jednoznacznie zdefiniowana reguła postępowania określająca warunki,

przy których należy sprawdzaną hipotezę przyjąć lub odrzucić.

Podział hipotez i testów statystycznych:
- parametryczne

- dotyczą parametrów rozkładu zmiennej losowej, np. wartości oczekiwanej i

wariancji

- nieparametryczne

- dotyczą innych cech nie związanych z parametrami, np. typu rozkładu

Hipoteza H

0

jest to hipoteza statystyczna stawiana w oparciu o przeprowadzoną próbę, związana

z wyznaczeniem wielkości nazywanych funkcjami testowymi, sprawdzianami hipotezy lub
statystyką

Jako hipotezę H

0

wybiera się z reguły hipotezą łatwiejszą do weryfikacji, np:

H

0

:

µµµµ

= x

sr

H

0

: rozkład jest rozkładem normalnym

Uwagi ogólne:

- nie można udzielić absolutnie pewnej odpowiedzi co do słuszności postawionej hipotezy

- w praktyce określa się wielkość obszaru, wewnątrz którego z określonym prawdopodobieństwem

powinna się znaleźć weryfikowana wielkość uzyskana z próby, aby można ją było uznać za
reprezentatywną dla populacji generalnej

- hipotezę H

0

się przyjmuje

, jeżeli wartość testu trafi do obszaru przyjęcia hipotezy,

hipotezę H

0

się odrzuca

, jeżeli wartość testu trafi do obszaru krytycznego

f(

χ

2

)

χ

2

χ

2

kr

1-

α

=0.95

α

=0.05

ilość stopni swobody k=6

obszar przyjęcia

hipotezy H

0

obszar odrzucenia

hipotezy H

0

(krytyczny)

37

Konsekwencje weryfikacji hipotezy:

H

0

słuszna

H

0

fałszywa

przyjęcie H

0

+

błąd drugiego rodzaju

odrzucenie H

0

błąd pierwszego rodzaju

+

- popełnienie błędu pierwszego rodzaju - silnie uwarunkowane jest wartością poziomu ufności 1-

α

(zbyt wysoki poziom powodować może odrzucenie hipotezy mimo tego, że hipoteza jest
prawdziwa)

W celu uniknięcia błędów lub w przypadku odrzucenia hipotezy H

0

formułuje się często hipotezę

alternatywną H

1

, która jest konkurencyjna względem hipotezy H

0

, np:

H

1

:

µµµµ

<x

sr

lub H

1

:

µµµµ

>x

sr

lub H

1

:

µµµµ≠≠≠≠

x

sr

H

1

: rozkład nie jest normalnym

Wikipedia:

Czasami nazwą błąd trzeciego rodzaju określa się też wszelkie inne błędy, które mogą

wyniknąć przy testowaniu hipotez, np. błąd wynikający z zaokrąglenia wartości statystyki testowej
podczas obliczeń komputerowych.

38

TEST

χχχχ

2

(chi kwadrat)

- test nieparametryczny wprowadzony w 1900 r. przez Pearsona

- test daje w wyniku jedną ilościową miarę zgodności częstości doświadczalnych m

i

i teoretycznych

(modelowych) m

it

w całym badanym przedziale zmienności

- test może być stosowany do wszystkich rozkładów zmiennych losowych

- hipoteza H

0

: rozkład wyników uzyskany z próby jest rozkładem określonego typu, np. rozkładem

normalnym, czyli:
H

0

: rozkład wyników = rozkład N

- hipoteza alternatywna H

1

: rozkład wyników jest rozkładem innego typu, czyli:

H

1

: rozkład wyników

≠

rozkład N

- postać funkcji testowej (statystyki)

∑

=

−

=

k

1

i

it

2

it

i

2

m

)

m

m

(

χ

k

- ilość przedziałów klasowych (k

≥

5)

, m

i

- ilość wyników w i-tym przedziale klasowym

(m

i

≥

5)

, m

it

-ilość teoretyczna wyników w i-tym przedziale klasowym uzyskana przy założeniu

prawdziwości hipotezy H

0

o określonym typie rozkładu zmiennej losowej, np. że rozkład jest

rozkładem normalnym

- statystyka opisana jest rozkładem

χ

2

; przy ilości stopni swobody równej k

sw

=k-L-1

(L

-liczba wielkości określanych z próby x

sr

i s

x

: L=2):

k

sw

=k-3

- uzyskaną wartość

χ

2

porównuje się z wartością

χ

2

k,

α

odczytaną z tablic rozkładu

χ

2

przy założeniu

określonego poziomu ufności 1-

α

;

- hipotezy H

0

nie powinno się odrzucać, jeżeli

χχχχ

2

≤≤≤≤χχχχ

2

k,

αααα

- gdy

χχχχ

2

>

χχχχ

2

k,

αααα

należy hipotezę H

0

odrzucić

; prawdopodobieństwo tego, że decyzja jest błędna nie

przekracza wartości

α

- zalecane jest sformułowanie hipotezy alternatywnej

- wartość

χ

2

zależy silnie od sposobu grupowania wyników - ważną rolę odgrywa opracowanie

szeregu rozdzielczego; opracowanie to może wpływać na powstanie błędów I i II rodzaju

39

TESTY NA WYKRYCIE BŁĘDU GRUBEGO

Wynik odskakujący nie zawsze musi świadczyć o tym, że wynik ten jest obarczony błędem
grubym. Odrzucenie lub pozostawienie takiego wyniku powinno oparte być na ocenie statystycznej
- należy zastosować odpowiedni test na błąd gruby

Test Dixona - oparty jest na wyznaczaniu rozrzutu wyników

Procedura testowa

- należy uporządkować wyniki w określony sposób np. od najmniejszej do największej wartości

x

1

, x

2

,.....x

n-1

, x

n

. Błędem grubym może być obarczona najmniejsza wartość x

1

lub największa x

n

- należy obliczyć wartości parametrów definiowanych następująco:

- dla ilości wyników z zakresu od 3 do 7 (zależność podstawowa):

1

n

1

2

min

x

x

x

x

Q

−

−

=

1

n

1

n

n

max

x

x

x

x

Q

−

−

=

−

- dla ilości wyników z zakresu od 8 do 12:

1

1

n

1

2

min

x

x

x

x

Q

−

−

=

−

2

n

1

n

n

max

x

x

x

x

Q

−

−

=

−

- dla ilości wyników z zakresu od 13 do 40:

1

2

n

1

3

min

x

x

x

x

Q

−

−

=

−

3

n

2

n

n

max

x

x

x

x

Q

−

−

=

−

- z obliczonych Q

min

i Q

max

wybrać wartość większą i porównać ją z wartością krytyczną Q

kryt

odczytaną przy założonym poziomie ufności z tabeli testu Dixona (z reguły poziom ufności
0.95). Jeżeli wybrana wartość spełnia warunek

Q

wybrane

≤

Q

kryt

to nie ma podstaw do odrzucenia wątpliwego wyniku (z prawdopodobieństwem 95% lub inaczej
- z prawdopodobieństwem 5% podjęcia błędnej decyzji). Jeżeli warunek nie jest spełniony z
takimi samymi prawdopodobieństwami należy wynik wątpliwy odrzucić

40

Test Grubbsa - oparty jest na wyznaczaniu odchylenia wątpliwego wyniku od średniej

względem odchylenia standardowego

Procedura testowa

- należy uporządkować wyniki w określony sposób np. od najmniejszej do największej wartości

x

1

, x

2

,.....x

n-1

, x

n

.

- należy obliczyć wartość parametru T z wzoru

x

watpl

s

x

x

T

−

=

gdzie x

watpl

- wynik odskakujący, x - średnia arytmetyczna i s

x

- estymator odchylenia

standardowego (błąd średni pojedynczego pomiaru) wyznaczony z wszystkich wyników

- obliczoną wartość T porównać z wartością krytyczną T

kryt

odczytaną przy założonym poziomie

ufności z tabeli testu Grubbsa (z reguły poziom ufności 0.95). Jeżeli wybrana wartość spełnia
warunek

T

≤

T

kryt

to nie ma podstaw do odrzucenia wątpliwego wyniku (z prawdopodobieństwem 95% lub inaczej
- prawdopodobieństwem 5% podjęcia błędnej decyzji). Jeżeli warunek nie jest spełniony z takimi
samymi prawdopodobieństwami należy wynik wątpliwy odrzucić

41

TEST t-Studenta różnic dwóch średnich

Test stosowany w celu porównania różnic dwóch wartości średnich z dwóch serii pomiarowych

(wyniki pochodzą z populacji generalnych o rozkładzie normalnym)

Procedura testowa

- należy obliczyć średnie arytmetyczne x

1śr

i x

2śr

estymatory odchyleń standardowych (błędy średnie

pojedynczych pomiarów) s

x1

i s

x2

dla dwóch serii pomiarowych

- obliczyć wartość parametru t z wzoru

(

) (

)

(

)

2

1

2

1

2

1

2

2

2

2

1

1

ś

r

2

ś

r

1

n

n

2

n

n

n

n

s

1

n

s

1

n

x

x

t

+

−

+

−

+

−

−

=

gdy obydwie serie są równoliczne tzn. n

1

= n

2

wzór upraszcza się do postaci

n

s

s

x

x

t

2

2

2

1

ś

r

2

ś

r

1

+

−

=

- obliczoną wartość t porównać z wartością krytyczną t

kryt

odczytaną przy założonym poziomie

ufności z tablic rozkładu t-Studenta (z reguły poziom ufności 0.95) dla liczby stopni swobody
równej

2

-

n

n

k

2

1

+

=

. Jeżeli obliczona wartość spełnia warunek

t

≤

t

kryt

to obydwie średnie nie różnią się w sposób statystycznie istotny (z prawdopodobieństwem 95%)

- inaczej obydwie poprawnie reprezentują tę samą wielkość. Jeżeli warunek nie jest spełniony to
różnią się w sposób statystycznie istotny.

TEST F-Snedecora (Fishera-Snedecora)

Test ten stosowany jest do porównania wartości odchyleń standardowych (lub wariancji) dla dwóch

serii wyników (wyniki pochodzą z populacji generalnych o rozkładzie normalnym).

Procedura testowa

- obliczyć wartości odchylenia standardowego dla dwóch serii wyników

- obliczyć wartość parametry testu F-Snedecora wg wzoru

2

2

2

2

2

1

1

1

s

1

n

n

s

1

n

n

F

−

−

=

gdy n

1

= n

2

wzór przyjmuje postać

2

2

2

1

s

s

F

=

Uwaga: wzór należy tak skonstruować, żeby wartość F była zawsze większa od 1

- obliczoną wartość należy porównać z wartością krytyczną F

kr

znalezioną w tablicach rozkładu

testu F-Snedecora dla założonego poziomu istotności

α

(najczęściej 0,05) i ilości stopni

swobody f

1

= n

1

- 1

i f

2

= n

2

- 1

- jeżeli spełniony jest warunek

F

≤

F

kr

42

to odchylenia standardowe nie różnią się między sobą w sposób statystycznie istotny. W praktyce

oznacza to, że obydwie serie wyznaczone zostały metodami o tej samej precyzji. W przeciwnym
przypadku różnica jest istotna i precyzje metod są różne.

Inne testy

parametryczne:

- test różnicy dwóch średnich (test Cochrana - Coxa i test Aspina - Welcha))

- test t-Studenta istotności różnicy wartości średniej z założoną wartością

nieparametryczne:

- test Smirnowa - Kołmogorowa

- test Shapiro - Wilka

Podsumowanie - ogólna metodyka testów statystycznych:

- postawienie hipotezy H

0

w oparciu o wyniki z próby (lub z prób)

- wybranie odpowiedniej funkcji testowej

- obliczenia wartości funkcji testowej

- porównanie wartości obliczonej z wartością krytyczną dla wybranej funkcji testowej przy

założonym poziomie ufności lub współczynniku istotności

43

DWUWYMIAROWE ZMIENNE LOSOWE - KORELACJA I REGRESJA

W wielu doświadczeniach należy ustalić i ocenić powiązanie (inaczej zależność) badanej zmiennej

losowej Y od jednej lub kilku zmiennych X, np. pojemności kolb są zależne od ich wymiarów
ocenianych optycznie, natężenie prądu zależy od przyłożonego napięcia itp.

Dwie zmienne X i Y mogą być ze sobą powiązane zależnością funkcyjną, zależnością statystyczną

(inaczej korelacyjną) lub mogą być niezależne

Zależność funkcyjna

to jest taka zależność, że każdej wartości jednej zmiennej X odpowiada tylko

jedna, jednoznacznie określona wartość zmiennej zależnej Y

Zależność korelacyjną

mamy wtedy, gdy zmiennymi są zmienne losowe, a zmiana jednej ze

zmiennych pociąga zmianę drugiej zmiennej. Np. konkretnym wartościom zmiennej X
odpowiadają wskutek czynników losowych różne wartości zmiennej Y. Zależność statystyczna
istnieje wtedy, gdy poszczególnym wartościom x

i

można przyporządkować średnią wartość

drugiej zmiennej y

ś

r

(x

i

)

.

Zależność tę zapisać można w postaci funkcyjnej

y

ś

r

(x) = f(x)

Równanie to w ogólnej postaci nazywa się równaniem regresji zmiennej Y względem
zmiennej X, funkcję f(x) - regresją, a jej wykres - prostą regresji zmiennej Y względem X

Typy (modele) regresji zależą od funkcji f(x):

f(x) = a + bx

- regresja prostoliniowa

f(x) = a + bx +cx

2

- regresja kwadratowa

f(x) = a + bx +cx

2

+dx

3

- regresja sześcienna (inaczej 3.stopnia)

f(x) = a + bx +cx

2

+dx

3

+ .....+kx

n

- regresja wielomianowa n.stopnia

f(x) = a x

b

- regresja potęgowa

f(x) = a b

x

- regresja wykładnicza

f(x) = a/x + b

- regresja hiperboliczna

Na wykresie korelacyjnym zależności y = f(x) każdemu pomiarowi odpowiada punkt określony

współrzędnymi (x

i

,y

i

)

Zadaniem statystyki należy ustalenie czy między wielkościami X i Y istnieje korelacja, określenie

rodzaju zależności korelacyjnej i znalezienie postaci funkcji regresji.

UWAGA:
Współzależność między obydwiema wielkościami Y i X może być silna, słaba lub może jej w
ogóle nie być. Często istnieje teoretyczna zależność funkcyjna między nimi, której w
eksperymencie w wyniku czynników zakłócających (ogólnie niepewności pomiarów) możemy
nie znaleźć. I odwrotnie - znaleziona zależność korelacyjna może mieć charakter przypadkowy i
nie znajduje potwierdzenia w wyniku innych badań naukowych. Również związek przyczynowo
- skutkowy między wielkościami X i Y może być odwrotny niż to było zakładane. Stwierdzenie
korelacji między wielkościami X i Y nie zawsze odpowie na pytanie, która wielkość jest
przyczyną a która skutkiem.

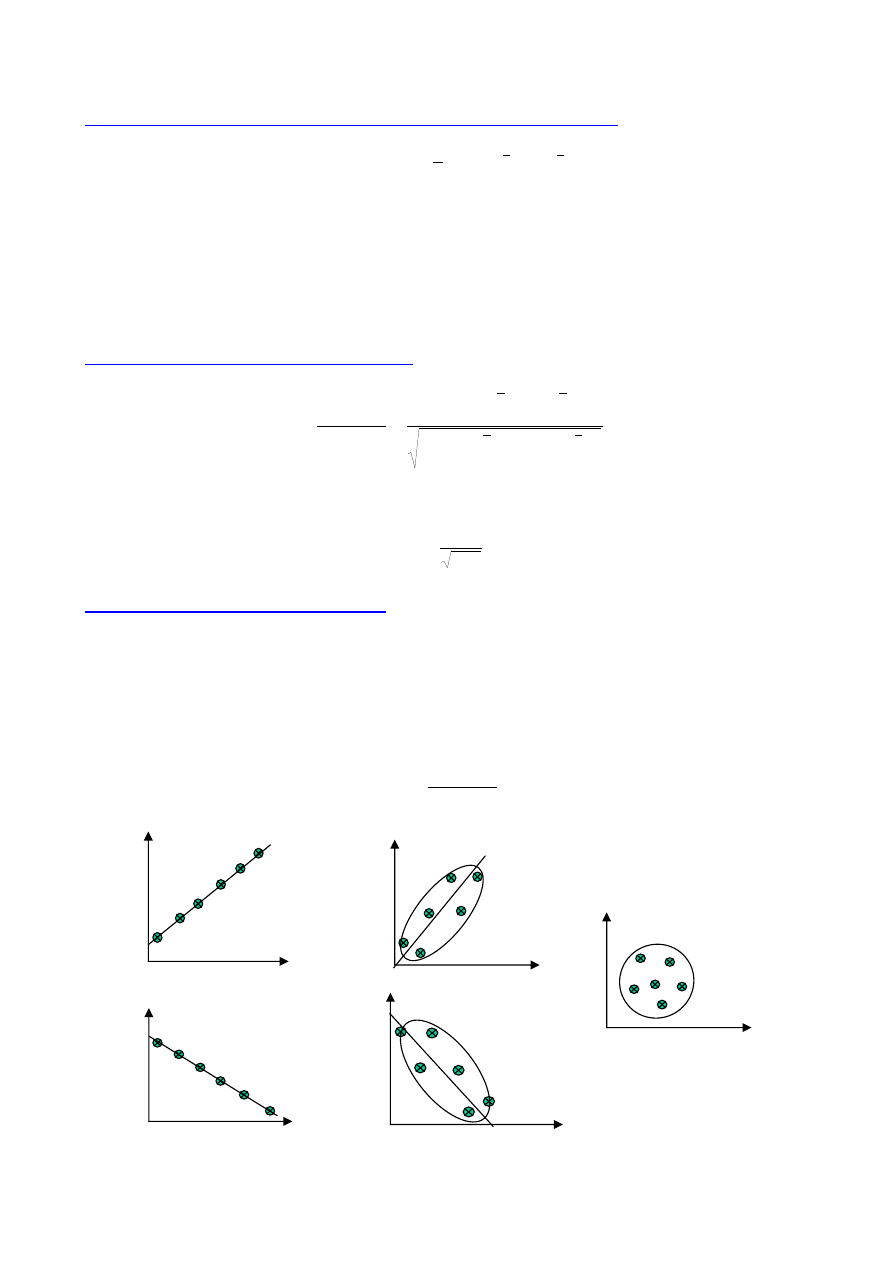
44

Miarą współzależności między zmiennymi X i Y jest kowariancja cov(x,y)

∑

=

−

−

=

=

n

i

i

i

xy

)

y

y

)(

x

x

(

n

s

)

y

,

x

cov(

1

1

n

- ilość punktów pomiarowych, x

i

y

i

-wartości par zmiennych X i Y, x

sr

i y

sr

- wartości średnie

zmiennych X i Y

cov(x,y)

jest liczbą mianowaną i przez to rzadko stosowaną do oceny współzależności między

zmiennymi X i Y
jeżeli cov(x,y) = 0 - między zmiennymi X i Y nie ma zależności, w przeciwnym przypadku
zależność między nimi istnieje

Współczynnik korelacji liniowej (Pearsona) r

,

częściej używany zamiast kowariancji, definiowany

jest wzorem

∑

∑

∑

−

−

−

−

=

⋅

=

i

2

i

i

2

i

i

i

i

y

x

)

y

y

(

)

x

x

(

)

y

y

)(

x

x

(

s

s

)

y

,

x

cov(

r

s

x

s

y

- dyspersje zmiennych X i Y

Odchylenie standardowe (dyspersja) współczynnika korelacji:

1

1

2

−

−

=

n

r

s

r

Właściwości współczynnika korelacji r:

- r jest wielkością bezwymiarową

- interpretacja współczynnika korelacji r (zależności między zmiennymi X i Y mają charakter

liniowy):
1. r = 1 lub r = -1 - idealna korelacja (punkty leżą na prostej); odpowiednio:

gdy

∆

x > 0

to

∆

y > 0

i gdy

∆

x > 0

to

∆

y < 0

2. 0 < r < 1 i -1 < r < 0 - istnieje korelacja (punkty leżą wewnątrz figury o wyróżnionym

kierunku symetrii)

3. r = 0 - brak korelacji między zmiennymi; UWAGA: nie musi to oznaczać, że zmienne te są

niezależne

y

i

x

i

r =1

∆

x>0

to

∆

y>0

y

i

x

i

r=-1

∆

x>0

to

∆

y<0

y

i

x

i

0<r<1

y

i

x

i

-1<r<0

y

i

x

i

r=0

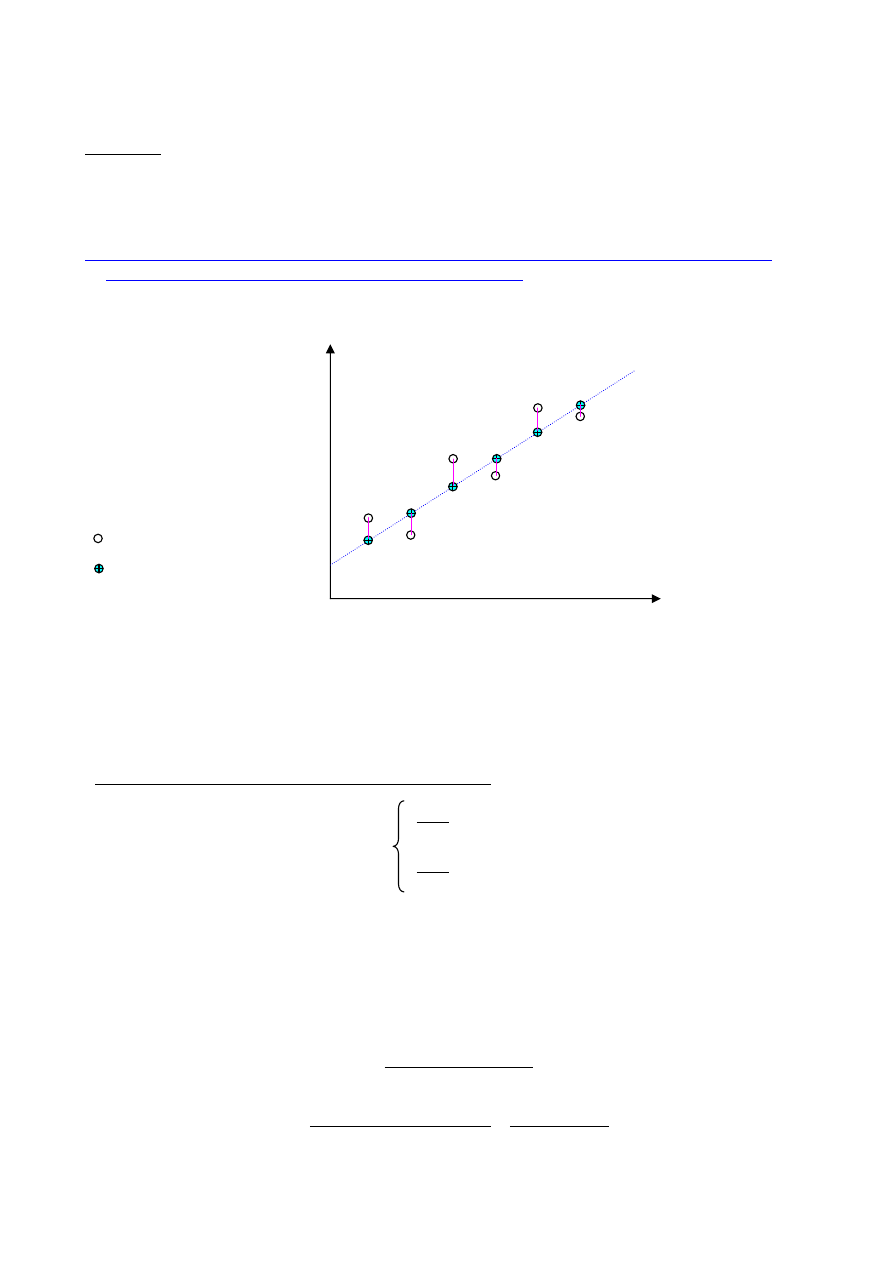
45

REGRESJA LINIOWA typu y = b x + a (metoda najmniejszych kwadratów)

Założenia:

- wynikiem pomiarów jest zbiór n punktów x

i

i y

i

- zależność teoretyczna jest postaci y

it

= b x

i

+ a

- współczynnik korelacji r jest różny od zera

Celem regresji jest przeprowadzenie optymalnej prostej przez zbiór punktów doświadczalnych,

z których każdy obarczony jest niepewnością pomiarową:

1. regresja ortogonalna - gdy

∆

x

jest porównywalne z

∆

y

2. regresja nieortogonalna, zwykle gdy

∆

x <<

∆

y (dla takiej regresji dalej jest robiona analiza)

- punkt eksperymentalny

- punkt teoretyczny

Obliczenie optymalnych współczynników a i b:

- tworzona jest funkcja określająca sumę kwadratów odchyleń między wartościami

doświadczalnymi a teoretycznymi:

∑

=

−

=

n

i

it

i

)

y

y

(

D

1

2

2

funkcja D

2

dla określonego zbioru x

i

i y

i

zależy od a i b

- minimum funkcji D

2

odpowiada spełnieniu warunków:

0

2

=

∂

∂

a

D

0

2

=

∂

∂

b

D

daje to układ równań liniowych

0

2

1

∑

=

=

−

−

−

n

i

i

i

)

bx

a

y

(

0

)

bx

a

y

(

x

2

n

1

i

i

i

i

∑

=

=

−

−

−

współczynniki a i b wyrażają równania:

∑

∑

∑

∑

∑

−

−

=

2

2

)

x

(

x

n

y

x

y

x

n

b

i

i

i

i

i

i

n

x

b

y

)

x

(

x

n

y

x

x

y

x

a

i

i

i

i

i

i

i

i

i

∑

∑

∑

∑

∑

∑ ∑

∑

−

=

−

−

=

2

2

2

y

i

x

i

46

Rozrzut statystyczny wielkości mierzonych y

i

względem teoretycznych y

it

określa wyrażenie

2

)

(

2

−

−

=

∑

n

y

y

s

it

i

y

- wielkość (s

y

)

2

- wariancja resztowa - średnia suma kwadratów odchyleń rzędnych

empirycznych i teoretycznych

- średnie błędy kwadratowe współczynników a i b:

∑

∑

∑

−

=

2

2

2

)

(

i

i

i

y

b

x

x

n

x

s

s

∑

∑

−

=

2

2

)

(

i

i

y

a

x

x

n

n

s

s

W przypadku małej ilości punktów statystyczny rozrzut opisany jest rozkładem Studenta

(ilość stopni swobody k = n - 2)

∆

b=t

k,

α

s

b

∆

a= t

k,

α

s

a

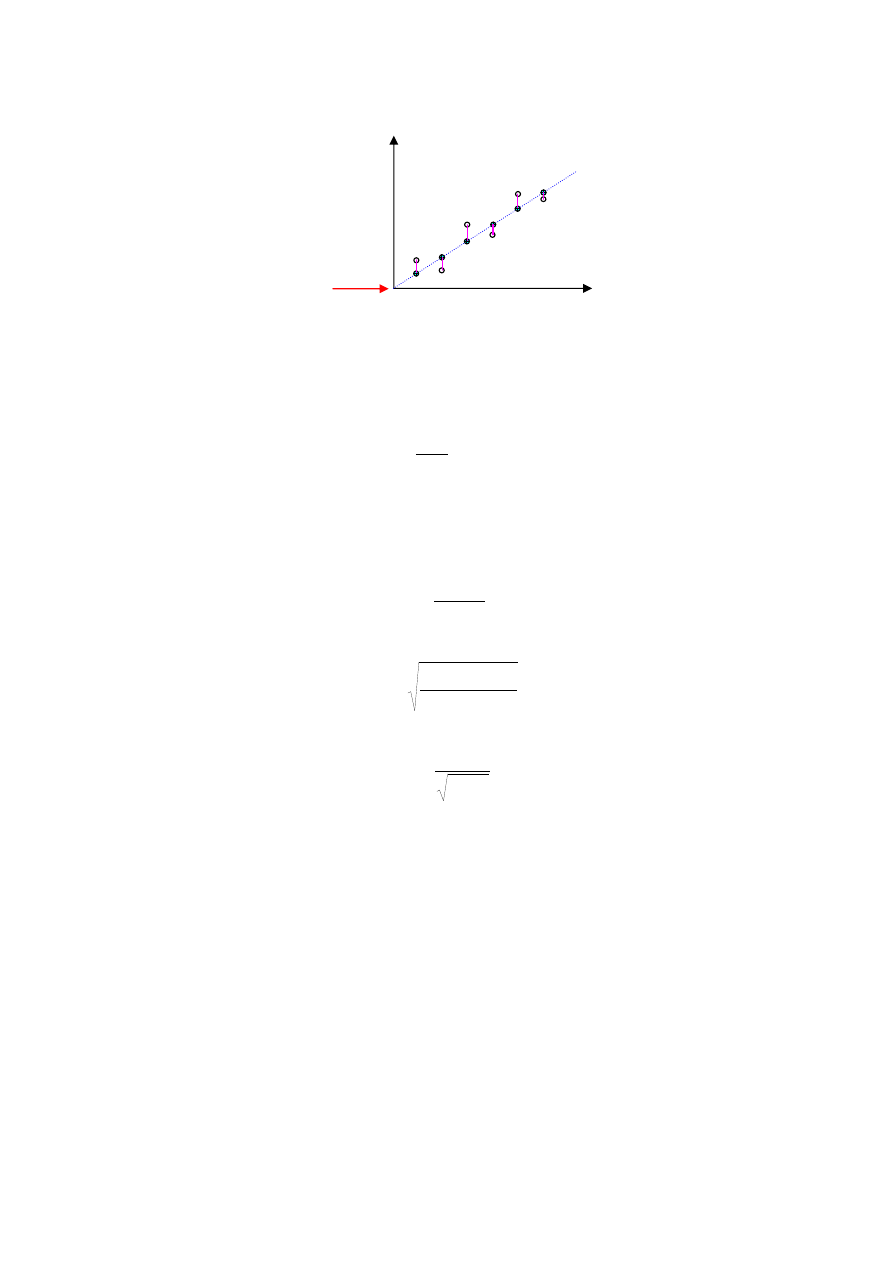
47

REGRESJA LINIOWA typu y = b x

tworzona jest identyczna jak wyżej funkcja określająca sumę kwadratów odchyleń między

wartościami doświadczalnymi a teoretycznymi:

∑

=

−

=

n

i

it

i

)

y

y

(

D

1

2

2

- warunek minimum

0

db

dD

2

=

co daje

∑

=

−

−

0

)

(

2

i

i

i

bx

y

x

a z tego

∑

∑

=

2

i

i

i

x

y

x

b

- rozrzut wielkości mierzonych względem teoretycznych

1

)

(

2

−

−

=

∑

n

y

y

s

it

i

y

- błąd średni kwadratowy współczynnika b

∑

=

2

i

y

b

x

s

s

Uwzględniając rozkład Studenta (ilość stopni swobody

k = n - 1)

α

⋅

=

k

b

t

s

b

∆

y

i

x

i

z założenia a = 0

48

LINEARYZACJA ZALEśNOŚCI NIELINIOWYCH

W wielu przypadkach teoretyczne zależności mają postać pozwalającą na ich linearyzację poprzez
odpowiednie podstawienie.

Przykłady:

1.

w

b

y

=

podstawienie

w

x

1

=

daje zależność

x

b

y

⋅

=

2.

w

z

v

t

⋅

=

po zlogarytmowaniu

z

lg

w

v

lg

t

lg

+

=

i po podstawieniu

t

lg

y

=

i

z

lg

x

=

otrzyma się liniową zależność

x

w

v

lg

y

⋅

+

=

czyli

x

b

a

y

⋅

+

=

3.

x

w

v

t

⋅

=

po zlogarytmowaniu

w

lg

x

v

lg

t

lg

+

=

i po podstawieniu

t

lg

y

=

otrzyma się liniową zależność

w

lg

x

v

lg

y

+

=

REGRESJA KRZYWOLINIOWA

- teoretyczna zależność nie jest liniowa - może być wielomianem stopnia n, krzywą wykładniczą,

logarytmiczną itp.

- przykładowo dla zależności postaci (regresja kwadratowa)

c

x

b

x

a

y

i

2

i

it

+

⋅

+

⋅

=

- funkcja kwadratów odchyleń

(

)

∑

−

=

2

it

i

2

y

y

D

ma minimum przy spełnieniu układu równań:

0

c

D

;

0

b

D

;

0

a

D

2

2

2

=

∂

∂

=

∂

∂

=

∂

∂

Prowadzi to do skomplikowanego układu równań, z którego można wyznaczyć optymalne

współczynniki a, b i c.

UWAGI nt. WYKONYWANIA WYKRESÓW:

- osie wykresów dobiera się tak, aby zawierały cały zakres mierzonych wielkości; opis w przypadku

dużych lub małych liczb w postaci zmiennoprzecinkowej, opis osi zaokrąglony do pełnych
wartości
(Uwaga: koniecznie należy usunąć niepotrzebne zera opisów osi)

- punkty pomiarowe zaznaczone wyraźnie z naniesionymi niepewnościami w postaci prostokątów

lub elipsy niepewności (błędów)

- gdy zależność prowadzona jest w sposób przybliżony („na oko”), prosta lub krzywa powinna

przechodzić przez 2/3 prostokątów lub elips niepewności; krzywa powinna prowadzona być w
postaci możliwie gładkiej

49

ELEMENTY WALIDACJI METOD ANALITYCZNYCH

(główne źródło do wykładu "Ocena i kontrola jakości wyników pomiarów analitycznych"
- praca zbiorowa pod redakcją P.Konieczki i J.Namieśnika, WNT, Warszawa 2007)

Definicja walidacji

(wg P.Konieczki i J.Namieśnika):

Walidacja metody to proces oceny metody analitycznej prowadzony w celu zapewnienia zgodności
ze stawianymi jej wymogami, umożliwiający opis tej metody oraz pozwalający określić jej
przydatność.
Walidacja metody analitycznej obejmuje sprawdzenie jej ważnych cech charakterystycznych.
Ostatecznym jej celem jest pewność, że proces analizy przebiega w sposób rzetelny i precyzyjny
oraz daje miarodajne wyniki.

Inna definicja walidacji

(wg ISO = International Organization for Standardization)

:

Walidacja metod analitycznych to proces ustalania parametrów charakteryzujących sprawność
działania i ograniczeń metody oraz sprawdzenie jej przydatności do określonych celów.

Walidacja wykonywana jest najczęściej wtedy, gdy:

- opracowywana jest nowa metoda analityczna

- prowadzi się próby rozszerzenia zakresu stosowalności znanej metody analitycznej, np.

oznaczania danego analitu, ale w innej matrycy (Matryca analityczna: w chemii analitycznej
składniki głównej próbki, inne niż składnik wykrywany lub oznaczany

)

- kontrola jakości stosowanej metody wykazała zmienność jej parametrów w czasie

- dana metoda analityczna ma być wykorzystywana w innym laboratorium (innym od tego, w

którym była już poddana procesowi walidacji) bądź z zastosowaniem innej aparatury, czy też
oznaczenia mają być wykonywane przez innego analityka

- przeprowadza się porównanie nowej metody analitycznej ze znaną metodą odniesienia.

Przeprowadzenie procesu walidacji wymaga zastosowania:

- ślepych próbek

- roztworów wzorcowych (roztworów kalibracyjnych, próbek testowych)

- próbek ze znaną ilością dodanego analitu (wzbogaconych w analit)

- certyfikowanych materiałów odniesienia

- powtórzeń

- obróbki statystycznej zbiorów wyników

Podstawowa klasyfikacja metod analizy chemicznej:

1.

metody pierwotne

2.

metody stosunków

3.

metody wtórne

4.

metody bezwzględne

5.

metody względne

6.

metody bezpośrednie

7.

metody pośrednie

8.

metody do określania stężenia chwilowego analitów

50

9.

metody do określania stężenia ważonego w czasie

10.

metody prowadzenia pomiarów in situ

11.

metody laboratoryjne

12.

metody z zastosowaniem urządzeń z bezpośrednim odczytem stężenia analitu

13.

metody z wstępnym przygotowaniem próbki i obliczeniem stężenia analitu na podstawie

wyników pomiarów przeprowadzonych w laboratorium

14.

metody sedymentacyjne

15.

metody izolacyjne

16.

metody aspiracyjne

17.

metody manualne

18.

metody automatyczne

19.

metody monitoringowe

Jakość wyników analitycznych

Wyniki pomiarów analitycznych muszą być miarodajne (inaczej wiarygodne), tzn. muszą
odzwierciedlać w sposób dokładny rzeczywistą ilość analitów w próbce stanowiącej
reprezentatywną część badanego obiektu materialnego.

System zapewnienia jakości

Podstawowy kierunek rozwoju chemii analitycznej to dążenie do oznaczania coraz mniejszych
stężeń analitów w próbkach o złożonej matrycy.

Systemy zapewnienia jakości pracy laboratoriów analitycznych:

- dobra praktyka laboratoryjna (GLP - Good Laboratory Practice)

- akredytacja laboratorium wg EN 45001 lub PN-EN ISO/IEC 17025:2005

- certyfikacja wg ISO serii 9000

Istotną rolę w zapewnieniu jakości laboratoriów analitycznych odgrywają audit wewnętrzny i audit
zewnętrzny.

Podstawowym warunkiem zapewnienia właściwej jakości wyników analitycznych jest:

- weryfikacja rzetelności stosowanych przyrządów pomiarowych poprzez okresowe sprawdzania

rzetelności przyrządów za pomocą mieszanin wzorcowych, w szczególności mieszaniny
"zerowe" do sprawdzania położenia punktu zerowego na skali pomiarowej przyrządu,
rozcieńczanie mieszanin wzorcowych

- sprawdzanie zakresu stosowalności i kalibracji stosowanych metod analitycznych poprzez dodatek

wzorca do analizowanej próbki i wykorzystanie materiałów odniesienia.

Szczególną rolę odgrywają:

- wybór materiału z którego próbki mają być pobrane

- przygotowanie planu pobierania próbek

- wybranie i użycie technik i urządzeń do pobrania próbek, transport, konserwacja i

przechowywanie próbek

51

Niepewność pomiaru w analityce chemicznej

Wielkości stosowane do obliczenia niepewności pomiarów analitycznych:

- standardowa niepewność pomiaru

i

x

u - niepewność pomiaru przedstawiona i obliczona jako

odchylenie standardowe

- złożona standardowa niepewność wyniku oznaczenia

y

c

u - standardowa niepewność wyniku

oznaczenia y, której wartość jest obliczona na podstawie niepewności parametrów wpływających
na wartość wyniku analizy z zastosowaniem prawa propagacji niepewności

- niepewność względna

i

x

r

u

- stosunek niepewności do wielkości mierzonej

- rozszerzona niepewność U - wielkość określająca przedział wokół uzyskanego wyniku analizy, w

którym można, na odpowiednim przyjętym poziomie istotności (prawdopodobieństwa),
spodziewać się wystąpienia wartości oczekiwanej

- współczynnik rozszerzenia k - wartość liczbowa użyta do pomnożenia złożonej standardowej

niepewności wyniku oznaczenia w celu uzyskania rozszerzonej niepewności, np. k = 2 dla 95%.
Wartość współczynnika rozszerzenia wybierana jest najczęściej z przedziału 2 - 3

-

niepewność typu A - metoda szacowania niepewności na podstawie pomiarów statystycznych

(oparta na wartości odchylenia standardowego serii pomiarów)

-

niepewność typu B - metoda szacowania niepewności wykorzystująca inne sposoby niż

statystyczne metody obróbki zbiorów wyników:

- wcześniejsze doświadczenia

- wcześniejsze wyniki podobnych badań

- dostarczone przez producenta specyfikacje

- wyniki zaczerpnięte z wcześniejszych raportów np. dotyczące kalibracji

-niepewność odniesiona na podstawie wyników badań dla materiału odniesienia

Podstawowymi źródłami niepewności w trakcie badania próbek z wykorzystaniem odpowiedniej

procedury analitycznej mogą być:

-błędnie lub nieprecyzyjnie zdefiniowana wielkość oznaczana

- niespełnienie wymogu reprezentatywności dla pobranej próbki

- nieprawidłowo zastosowana metoda oznaczeń

- osobowe błędy systematyczne w odczytach sygnałów analogowych

- nieznajomość wpływu wszystkich warunków zewnętrznych na wynik pomiaru analitycznego

- niepewność związana z kalibracją stosowanego przyrządu pomiarowego

- niepewności związane ze stosowanymi wzorcami i/lub materiałami odniesienia

- niepewność parametrów wyznaczonych w osobnych pomiarach

- przybliżenia i założenia związane ze stosowaniem danego przyrządu pomiarowego

- wahania w trakcie powtórzeń pomiarów w przypadku zdawałoby się identycznych warunkach

zewnętrznych

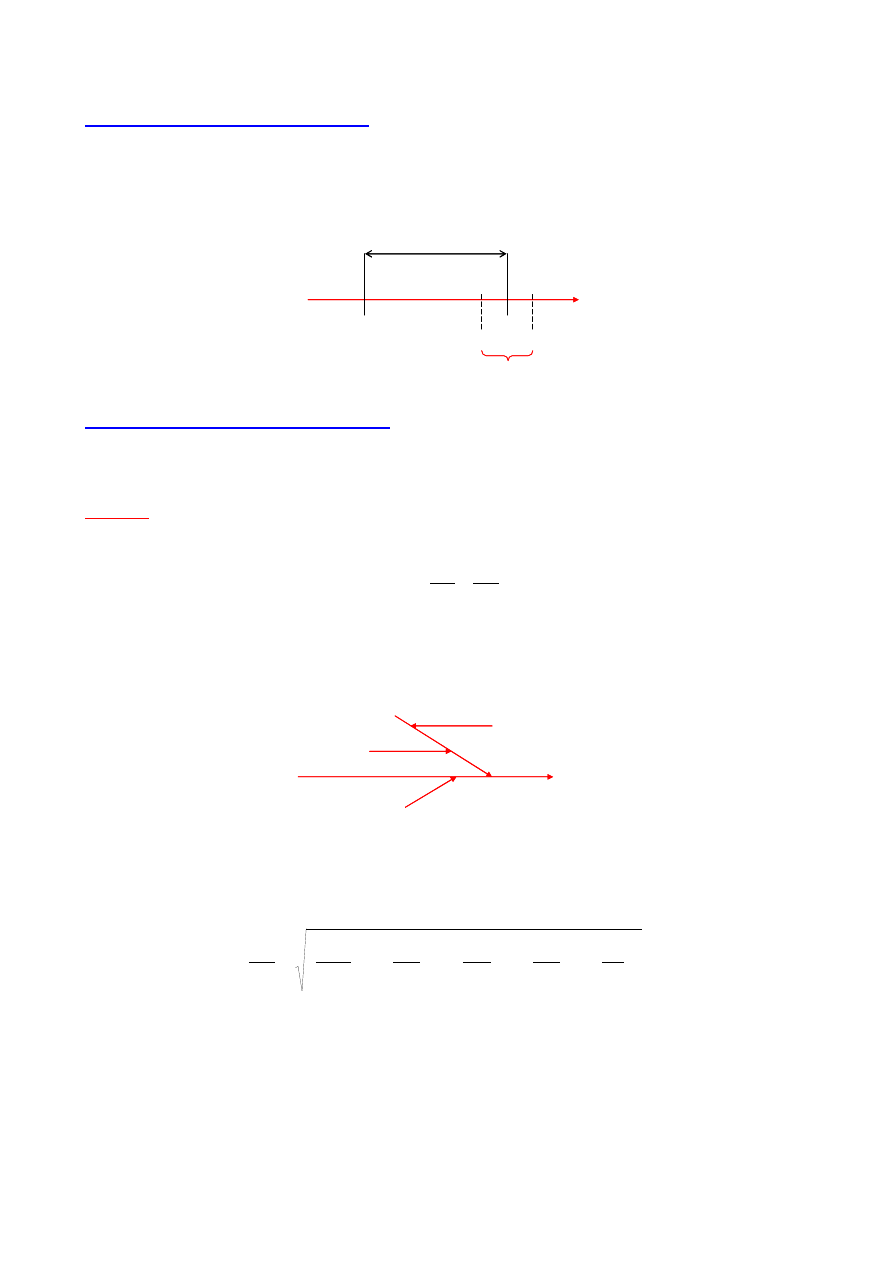
52

Niepewność pomiaru a błąd pomiaru

Błąd to różnica między wartością oznaczaną a oczekiwaną, natomiast niepewność to zakres

przedziału, w którym znaleźć się może z danym prawdopodobieństwem wartość oczekiwana.
Wartość niepewności nie może zatem służyć do skorygowania uzyskanego wyniku pomiaru.

Graficzna interpretacja różnicy między błędem pomiaru a niepewnością pomiaru:

µµµµ

x

x

ś

r

-u

c

+u

c

niepewność pomiaru

błąd pomiaru

µµµµ

x

x

ś

r

-u

c

+u

c

niepewność pomiaru

błąd pomiaru

Diagramy Ishikawy (fish-bone diagram)

Jest to graficzne przedstawianie wpływu niepewności poszczególnych parametrów procesu
analitycznego na wartość złożonej niepewności końcowego wyniku

Przykład

Sporządzanie roztworu wzorcowego przez rozcieńczanie roztworu podstawowego

1000

V

V

V

V

c

c

2

k

2

p

1

k

1

p

NIST

wz

























=

gdzie:
c

wz

- stężenie otrzymanego roztworu wzorcowego, c

NIST

- stężenie roztworu podstawowego,

V

p1

, V

p2

- pojemności pipet stosowanych w rozcieńczaniu, V

k1

, V

k2

- pojemności kolb stosowanych

w rozcieńczania

c

NIST

ΣΣΣΣ

V

k

ΣΣΣΣ

V

k

Rozcieńczanie

c

wz

c

NIST

ΣΣΣΣ

V

k

ΣΣΣΣ

V

k

Rozcieńczanie

c

wz

Diagram Ishikawy

Wyrażenie do obliczenia złożonej standardowej niepewności stężenia wzorcowego (prawo

propagacji (przenoszenia się) błędów):

2

k

k

2

k

V

2

2

p

V

2

1

p

V

2

NIST

c

wz

c

2

2

1

1

k

2

p

1

p

NIST

wz

V

u

V

u

V

u

V

u

c

u

c

u















+















+















+















+













=

53

Zestawienie parametrów metody analitycznej podlegających procesowi walidacji

zalecane przez ICH (The International Conference on Harmonization) i USP (The United States
Pharmacopoeia)

1. Precyzja

powtarzalność

precyzja pośrednia

odtwarzalność

2. Dokładność

3. Granica wykrywalności

4. Granica oznaczalności

5. Specyficzność / selektywność

6. Liniowość

7. Zakres pomiarowy

8. Odporność

9. Elastyczność

Raport z walidacji metody analitycznej

Raport powinien zawierać:

- przedmiot i zakres walidacji

- rodzaj oznaczanych związków i matrycy

- opis metody

- kryteria akceptacji

- stosowane odczynniki, substancje porównawcze i wzorce

- opis aparatury (producent, typ)

- względy bezpieczeństwa

- parametry pomiaru

- opis przeprowadzonego eksperymentu

- postępowanie statystyczne i obliczenia

- reprezentatywne wykresy

- kryteria rewalidacji

- podsumowanie i wnioski

54

Polskie Centrum Akredytacji

(http://www.pca.gov.pl/)

Polskie Centrum Akredytacji (PCA) jest krajową jednostką akredytującą upoważnioną do

akredytacji jednostek certyfikujących, kontrolujących, laboratoriów badawczych i wzorcujących
oraz innych podmiotów prowadzących oceny zgodności i weryfikacje na podstawie ustawy z
dnia 30 sierpnia 2002 r. o systemie oceny zgodności (tekst jednolity Dz.U. 2004 r. Nr 204, poz.
2087 z późniejszymi zmianami)

.

PCA posiada status państwowej osoby prawnej i jest nadzorowane przez Ministerstwo Gospodarki.

PCA obecnie prowadzi procesy akredytacji i sprawuje nadzór nad:

- laboratoriami badawczymi wg DAB-07;

- laboratoriami wzorcującymi wg DAP-04;

- laboratoriami medycznymi wg DAM-01;

- jednostkami inspekcyjnymi wg DAK-07;

- jednostkami certyfikującymi wyroby, systemy zarządzania i osoby wg DAC-08;

- weryfikatorami EMAS (System Ekozarządzania i Audytu) wg DAC-09;

- weryfikatorami GHG (Emisja Gazów Cieplarnianych) wg DAC-10;
- organizatorami badań biegłości wg DAPT-01.