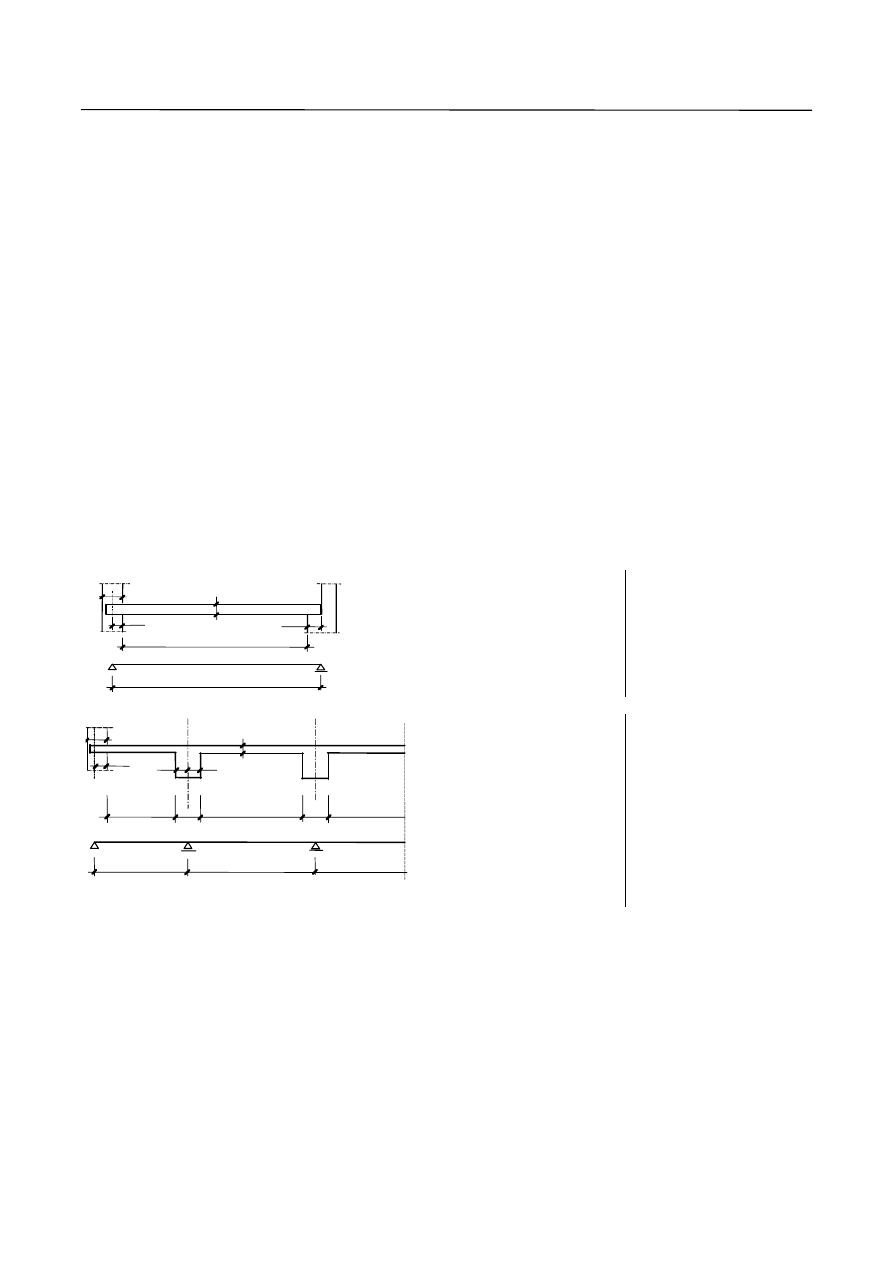
Budynek o konstrukcji mieszanej – wersja 2007

Dr inż. Maria WŁODARCZYK

Projekt techniczny STUDENT

Dr inż. Barbara GOSZCZYŃSKA

Do użytku wewnętrznego. Na prawach rękopisu.

35

3. PROJEKT TECHNICZNY

3.1. Analiza konstrukcji

Podstawowym celem analizy konstrukcji jest określenie rozkładu sił wewnętrznych (siły normalne, siły
tnące, momenty zginające i skręcające) oraz naprężeń, odkształceń i przemieszczeń całej konstrukcji lub jej
części pod wpływem przyłożonych obciążeń zewnętrznych. Tam gdzie jest to konieczne należy
przeprowadzić analizę lokalną części konstrukcji (przy podporach, w węzłach ram, w miejscach przyłożenia
obciążeń itp.), która umożliwi poprawne zaprojektowanie obszarów, w których występują odstępstwa od
wartości otrzymanych w modelu podstawowym.
W celu przeprowadzenia analizy konstrukcji należy przyjąć odpowiadający rzeczywistości model
obliczeniowy, stosując przy tym odpowiednie uproszczenia dotyczące geometrii, obciążeń oraz właściwości
materiałowych betonu i stali.
Idealizacja geometryczna polega na zastąpieniu rzeczywistej konstrukcji układem prętów (belki, słupy)
modelami jednowymiarowymi, ustrojami powierzchniowymi (płyty, tarcze, ściany) modelami
dwuwymiarowymi a w przypadku fundamentów – trójwymiarowymi. Przyjęcie odpowiedniego modelu
odpowiadającego rzeczywistości i ustalenie dla niego warunków brzegowych jest podstawowym zadaniem
projektanta. Dla ustalenia modelu geometrii konieczne jest także przyjęcie obliczeniowych wymiarów
elementu.

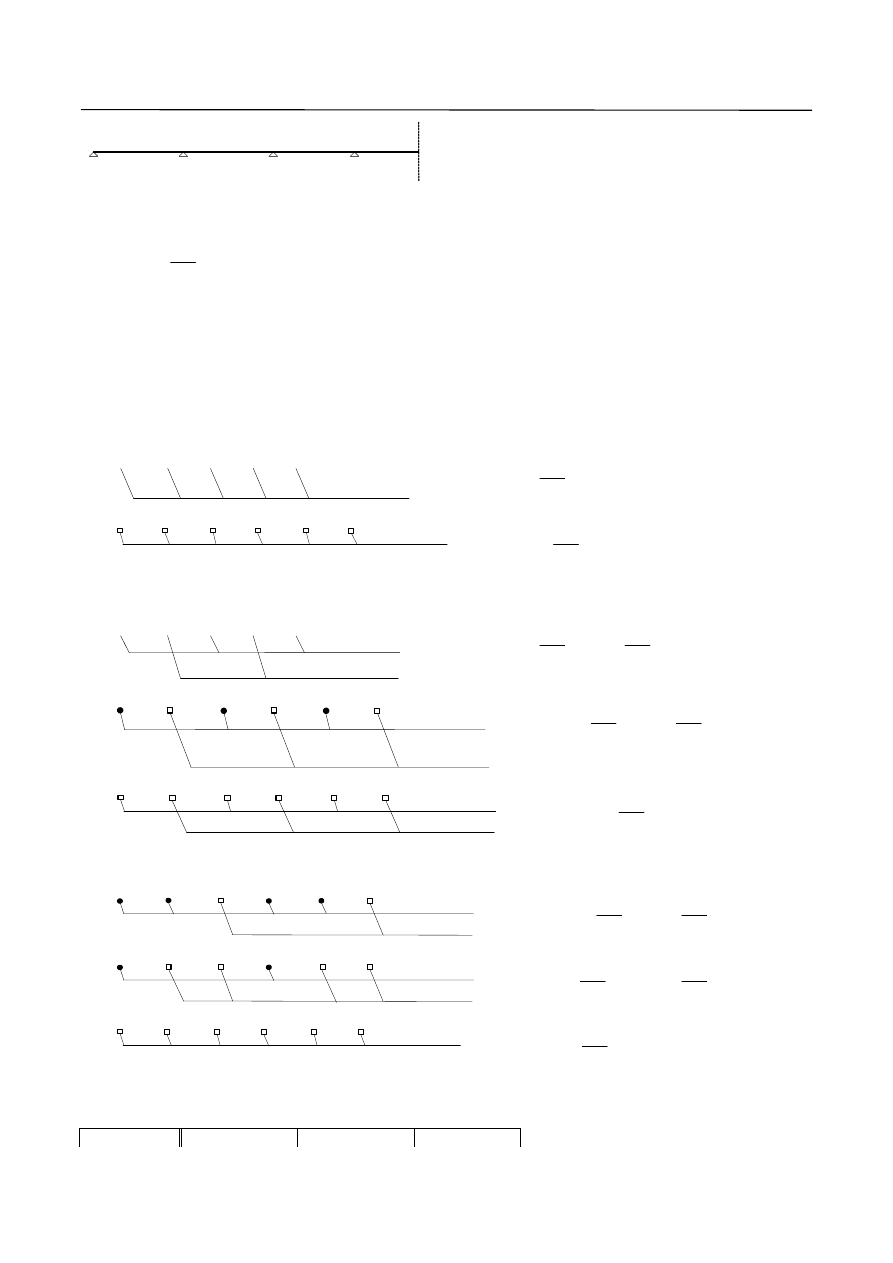
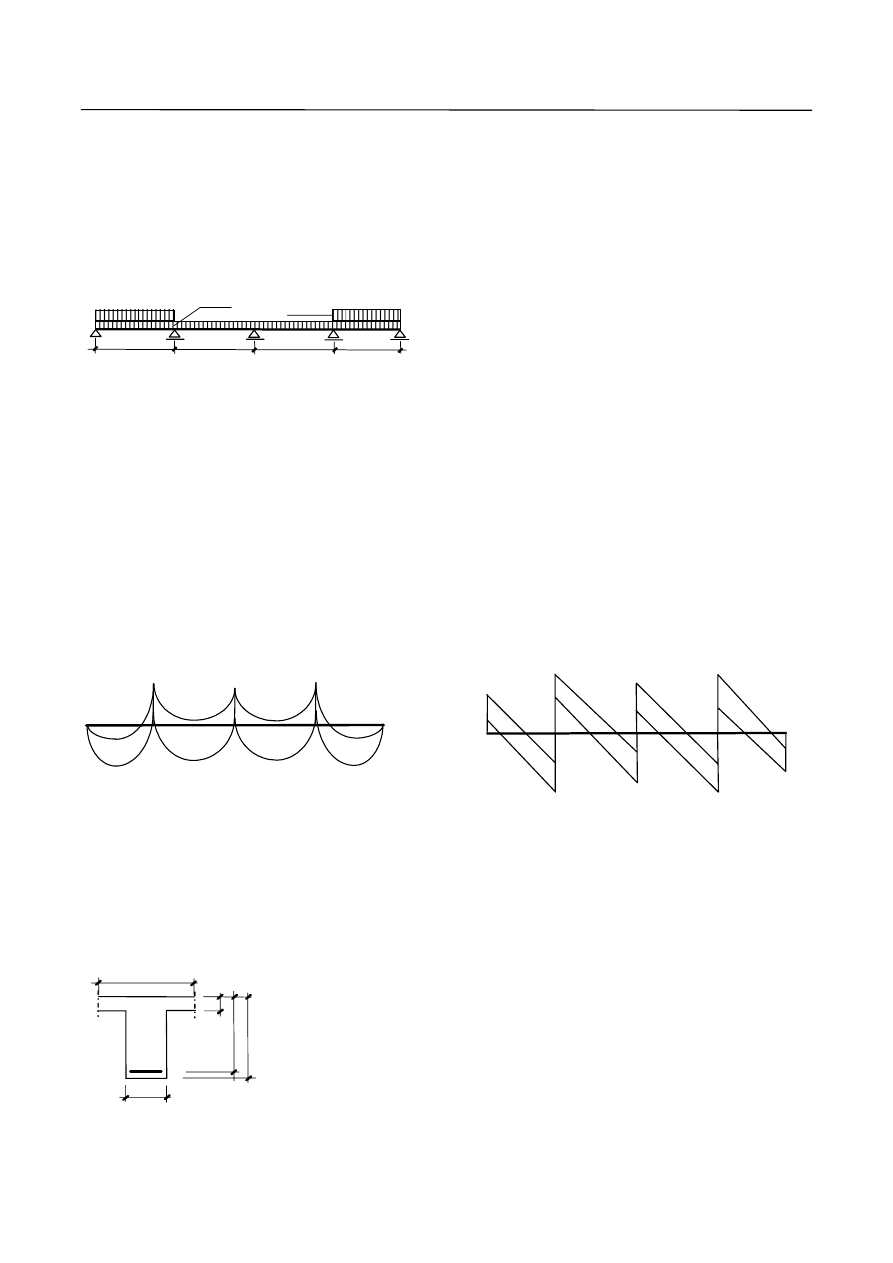
3.2. Rozpiętości obliczeniowe

Schemat statyczny

Teoria sprężystości

Metoda plastycznego

wyrównania momentów

a) belka jednoprzęsłowa

1

2

n

n

eff

a

l

l

+

=

(

)

h

t

a

n

5

.

0

;

5

.

0

min

1

=

gdzie: t – szerokość podpory

h

l

l

n

eff

5

.

0

+

=

b) belka ciągła

2

1

1

1

n

n

n

eff

a

a

l

l

+

+

=

2

2

2

2

n

n

eff

a

l

l

+

=

(

)

h

t

a

n

5

.

0

;

5

.

0

min

1

=

(

)

h

t

a

n

5

.

0

;

5

.

0

min

2

=

1

1

n

eff

l

l

=

2

2

n

eff

l

l

=

Rys. 5. Rozpiętości obliczeniowe przyjmowane do wyznaczenia wielkości sił przekrojowych: a) dla belki swobodnie

podpartej; b) dla belki ciągłej.

W innych przypadkach można przyjmować

n

n

n

n

l

a

a

a

025

.

0

2

1

=

=

=

.

Rozpiętość obliczeniowa:

n

eff

l

l

05

.

1

=

.

3.3. Tablice Winklera

Tablice Winklera można stosować do wyznaczenia wielkości sił przekrojowych jeżeli rozpiętości przęseł są
równe lub niewiele się różnią miedzy sobą (

max

min

8

.

0 l

l

≥

). Tablice Winklera opracowane są dla kilku

najczęściej występujących rodzajów obciążenia. Są to:

a

n1

h

l

eff

a

n1

t

l

n

a

n2

a

n2

t

l

n1

a

n1

h

t

l

n2

t

l

n2

l

eff1

l

eff2

l

eff2

Budynek o konstrukcji mieszanej – wersja 2007

Dr inż. Maria WŁODARCZYK

Projekt techniczny STUDENT

Dr inż. Barbara GOSZCZYŃSKA

Do użytku wewnętrznego. Na prawach rękopisu.

36

- obciążenie ciągłe rozłożone równomiernie na elemencie,
- obciążenie siłami skupionymi: jedną siłą w środku rozpiętości, dwoma siłami w 1/3 rozpiętości

i trzema w 1/4 rozpiętości elementu.

Tablice Winklera przewidziane są dla belek 2–, 3–, 4–, i 5–przęsłowych. Przy większej liczbie przęseł
obliczenie przeprowadza się jak dla belki 5–przęsłowej, przyjmując, że środkowe przęsła 3 i podpory
środkowe C powtarzają się kilkakrotnie (rys. 6).

Rys. 6. Sprowadzenie belki wieloprzęsłowej do belki pięcioprzęsłowej.

Posługując się tablicami Winklera wartości momentów

Sd

M i sił poprzecznych

Sd

V określa się ze wzorów:

- przy obciążeniu równomiernie rozłożonym

(

)

2

'

1

1

eff

Sd

Sd

Sd

l

p

k

g

k

M

+

=

(

)

eff

Sd

Sd

Sd

l

p

k

g

k

V

'

2

2

+

=

- przy obciążeniu siłami skupionymi

(

)

eff

Sd

Sd

Sd

l

P

k

G

k

M

'

3

3

+

=

Sd

Sd

Sd

P

k

G

k

V

'

4

4

+

=

gdzie:

i

k ,

'

i

k – współczynniki (dla

4

,

3

,

2

,

1

=

i

) odczytane z tablic Winklera dla rozpatrywanych schematów

obciążeń (przyjęte z odpowiednim znakiem) w odpowiednich przekrojach belki,

Sd

g ,

Sd

G – obciążenie stałe obliczeniowe (lub wyznaczone dla współczynnika obciążenia 0

.

1

=

f

γ

)

odpowiednio równomiernie rozłożone i siły skupione,

Sd

p ,

Sd

P , – obciążenie zmienne obliczeniowe (lub wyznaczone dla współczynnika obciążenia

0

.

1

=

f

γ

) odpowiednio równomiernie rozłożone i siły skupione.

W przypadku przęseł nierównych, lecz nie różniących się między sobą więcej niż 20%, do obliczania
momentów przęsłowych i sił poprzecznych miarodajna jest rozpiętość rozpatrywanego przęsła, a dla
momentów podporowych – średnia rozpiętość przyległych przęseł.
Obliczanie sił przekrojowych przy wykorzystaniu tablic Winklera jest obliczeniem uproszczonym, gdyż przy
zastosowaniu wyżej podanych wzorów, przy wyznaczaniu momentów przęsłowych dodaje się wartości
momentów:

2

,

eff

Sd

g

Sd

l

kg

M

=

i

2

'

,

eff

Sd

p

Sd

l

p

k

M

=

,

występujące w dwóch różnych punktach elementu. Różnice wynikające z tej nieścisłości można zazwyczaj
pominąć gdyż są one niewielkie i nie mają zbyt wielkiego wpływu na bezpieczeństwo konstrukcji.

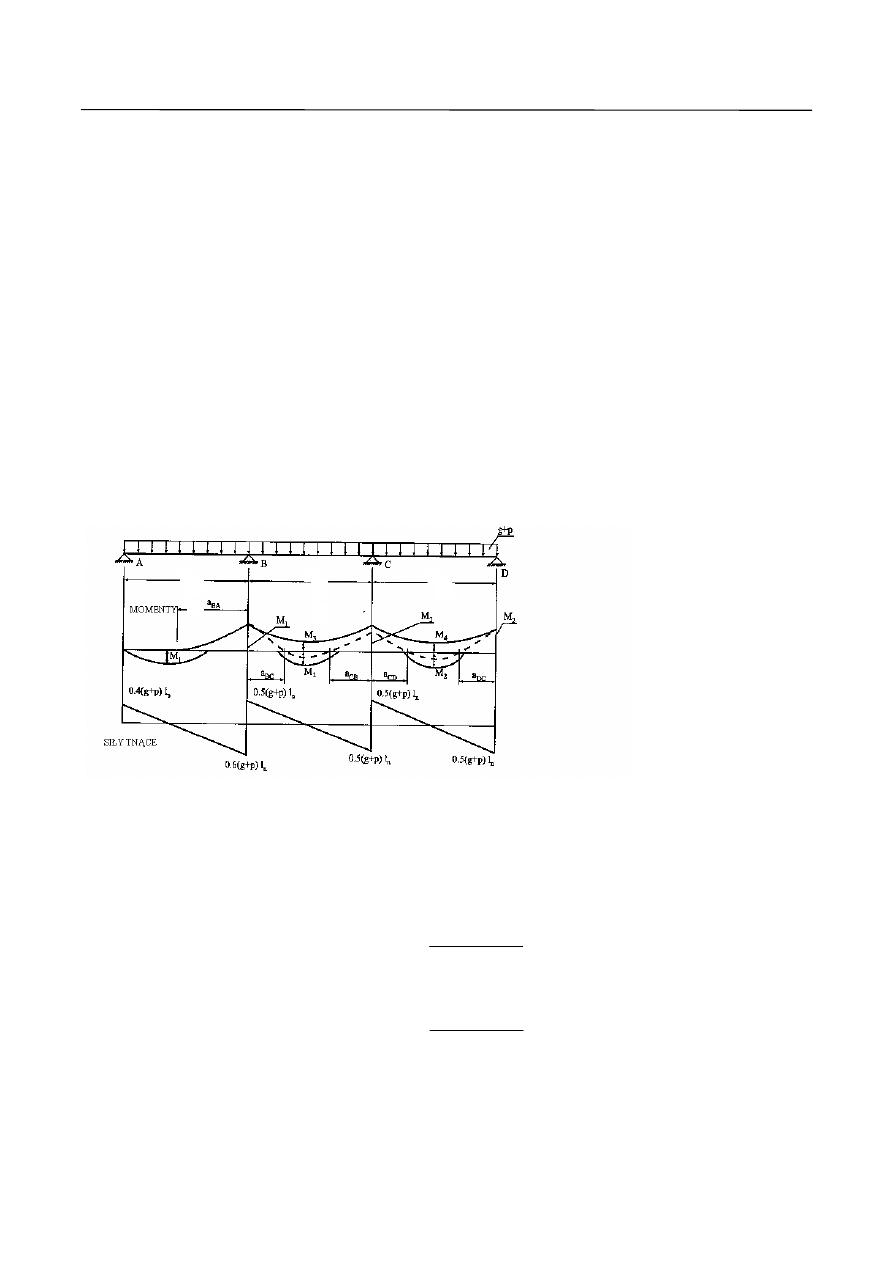
3.4. Metoda plastycznego wyrównania momentów

Założenia metody plastycznego wyrównania momentów uwzględniające specyfikę pracy konstrukcji
żelbetowych podane w odniesieniu do płyt ciągłych.

Płyty ciągłe mogą być obliczane metodą plastycznego wyrównania momentów, gdy spełnione są warunki:
1. Zbrojenie płyty wykonane jest ze stali o wysokiej ciągliwości czyli ze stali klasy A0 do AIII. Nie może

być zastosowana stal klasy AIIIN, ponieważ wykres

ε

σ

− ma zbyt krótką półkę plastyczną nie

pozwalającą na dostateczny obrót przegubu plastycznego. Stal klasy AIIIN charakteryzuje się średnią
ciągliwością.

A

B

C

C

C

C

B

A

2

3

3

1

3

2

1

A

B

C

C

B

A

2

3

2

1

1

Budynek o konstrukcji mieszanej – wersja 2007

Dr inż. Maria WŁODARCZYK

Projekt techniczny STUDENT

Dr inż. Barbara GOSZCZYŃSKA

Do użytku wewnętrznego. Na prawach rękopisu.

37

2. Wymiary przekroju betonowego są tak dobrane, że wysokość strefy ciskanej w przekrojach krytycznych

w stanie granicznym nośności nie przekraczała wartości:

d

x

25

.

0

=

gdzie: d – wysokość użyteczna przekroju.

3. Płyty ciągłe są monolitycznie połączone z belkami spełniającymi rolę podpór tak, że wpływ obciążenia

w dowolnym przęśle na sąsiednie przęsło jest ograniczony przez opór belek na skręcanie.

4. Stosunek wartości momentów w przęśle i na podporze zawiera się w przedziale od 0.5 do 2.0.

Istotą metody plastycznego wyrównania momentów jest założenie, że w wyniku utworzenia się przegubów
plastycznych na podporze lub na obu podporach rozpatrywanego przęsła następuje redukcja do 1/3 momentu
podporowego lub obu momentów w stosunku do wartości wyznaczonej dla układu sprężystego, co prowadzi
do odpowiedniego zwiększenia momentu przęsłowego.
Ze względu na możliwość nadmiernej szerokości rys i zbyt dużych ugięć przyjmowany do obliczeń rozkład
momentów nie może wyraźnie odbiegać od rozkładu momentów ustalonego na podstawie pracy sprężystej.
Dla płyt zalecana różnica momentów między rozkładem sprężystym a plastycznym nie powinna przekraczać
±30%. Im ta różnica jest większa, tym większych odkształceń plastycznych należy oczekiwać przy
redystrybucji momentów. Nie można także dopuścić, by powstanie przegubów plastycznych miało miejsce w
stadium użytkowania.

l

eff

l

eff

l

eff

Oznaczenia przyjęte na rysunku:

l

eff

= l

n

g

Sd

= g

p

sd

= p

M

Sd

= M

Rys. 7. Rozkład sił wewnętrznych dla płyty ciągłej wg metody plastycznego wyrównania momentów.

Dla płyt ciągłych o równych rozpiętościach przęseł lub jeśli rozpiętości różnią się od siebie nie więcej niż
20%, oraz jeżeli obciążenie jest rozłożone równomiernie, momenty wyznaczamy wg następujących wzorów:
- moment w przęśle skrajnym oraz moment krawędziowy na podporze przedskrajnej (środkowej

w przypadku płyty dwuprzęsłowej:

(

)

11

2

1

eff

Sd

Sd

Sd

l

p

g

M

+

±

=

- moment w przęsłach pośrednich oraz momenty krawędziowe na podporach pośrednich:

(

)

16

2

2

eff

Sd

Sd

Sd

l

p

g

M

+

±

=

gdzie: g

Sd

, p

Sd

– obliczeniowe obciążenie stałe i zmienne,

l

eff

– rozpiętość obliczeniowa wyznaczona zgodnie z pkt. 3.1.

Budynek o konstrukcji mieszanej – wersja 2007

Dr inż. Maria WŁODARCZYK

Projekt techniczny STUDENT

Dr inż. Barbara GOSZCZYŃSKA

Do użytku wewnętrznego. Na prawach rękopisu.

38

W przypadku nierównych rozpiętości przęseł (przy

max

,

min

,

8

.

0

eff

eff

l

l

≥

) moment podporowy należy obliczać

przyjmując we wzorach do wyznaczania wielkości momentów zginających większą z rozpiętości l

eff

obu

przyległych przęseł do podpory na której wyznaczamy moment.

Wartości momentów minimalnych w przęsłach pośrednich należy obliczać przy przyjęciu wartości
momentów podporowych wyznaczonych jak wyżej zakładając, że przęsła obciążone są zastępczym
obciążeniem o wartości:

4

Sd

Sd

p

p

g

q

+

=

.

Natomiast zasięg w przęśle skrajnym momentu podporowego na podporze przedskrajnej należy wyznaczyć
ze wzoru:

(

)

p

eff

Sd

Sd

BA

q

l

p

g

a

8

+

=

.

Zastosowanie tej metody pozwala zaoszczędzić 15

÷ 20% zbrojenia.

Zaletą metody jest ujednolicenie zbrojenia w przęsłach i na podporach (jest to istotne przy zastosowaniu
siatek zbrojeniowych).
Wadą – należy się liczyć z większymi ugięciami.

3.5. Projekt techniczny stropu międzykondagnycyjnego

Uwaga

: W projekcie technicznym wymiarowane elementy budynku oznaczamy tym samym numerem

pozycji co w projekcie wstępnym.

Poz. 2. Strop międzykondygnacyjny

Poz. 2.1. Płyta stropu

A. Obciążenia działające na płytę

Obciążenia stałe i zmienne, charakterystyczne i obliczeniowe według poz. 2.1. projektu wstępnego.

B. Obliczenia statyczne
- Rozpiętości obliczeniowe należy wyznaczyć zgodnie z zasadami podanymi w

2002

:

03264

B

PN

−

−

i opisanymi w punkcie 3.2.

- Obwiednie momentów i sił tnących.

Siły wewnętrzne w konstrukcji oblicza się przyjmując modele obliczeniowe odwzorowujące warunki pracy
konstrukcji w rozpatrywanych stanach granicznych. Analiza konstrukcji poprzedzona jest przyjęciem
odpowiedniego modelu konstrukcji i podstawowych danych geometrycznych.

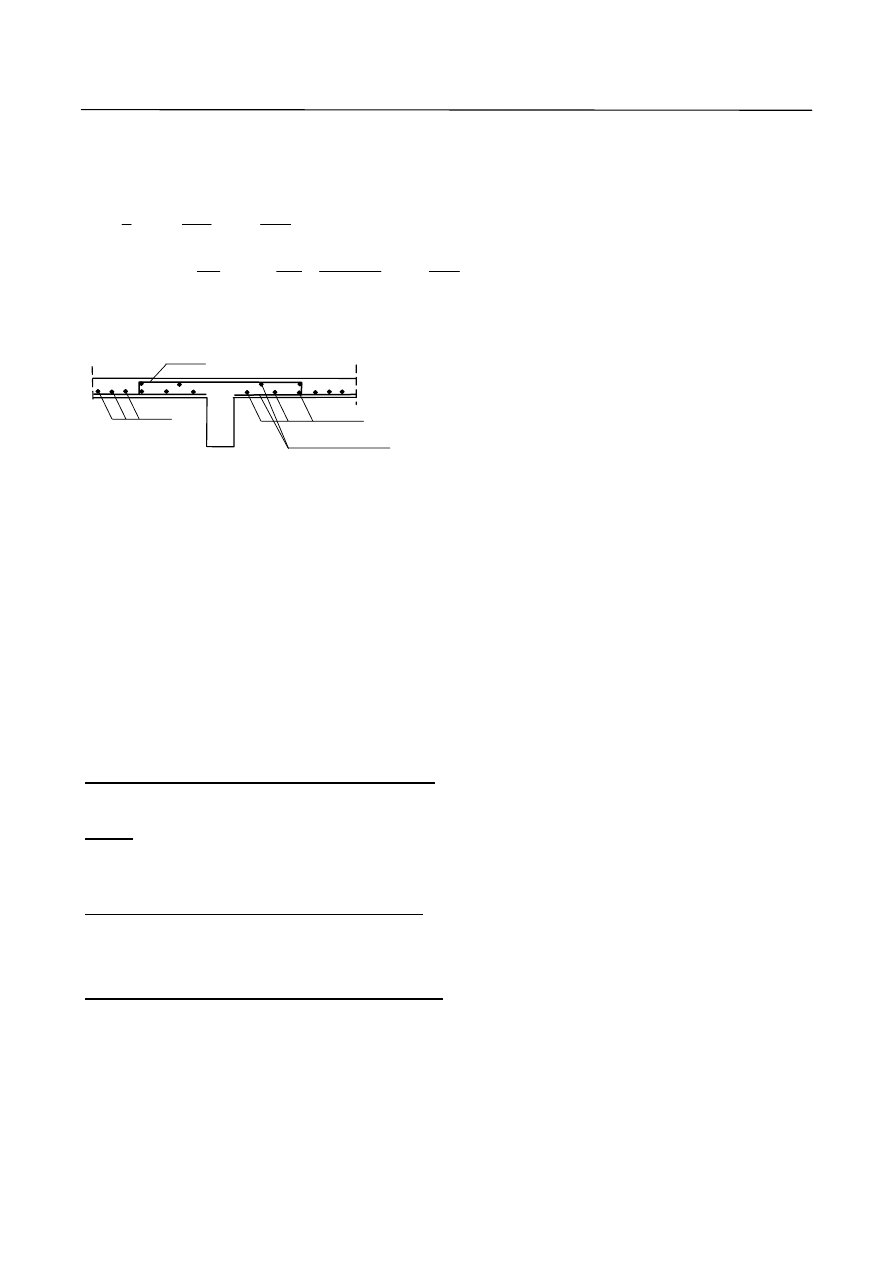
Do obliczania płyt można zastosować następujące metody analizy konstrukcji:
- liniowo sprężystą bez redystrybucji i z ograniczoną redystrybucją momentów,
- plastyczną – bez bezpośredniego sprawdzania zdolności obrotu przekroju lub w oparciu o modele

kratownicowe,

- nieliniową.

Płyty traktowane są jako jednokierunkowo zbrojone gdy są podparte na dwóch przeciwległych krawędziach,
lub gdy oparte są na obwodzie i stosunek większej rozpiętości do mniejszej jest większy od 2.

Obwiednie momentów i sił tnących można wykonać przy wykorzystaniu tablic Winklera lub metody
plastycznego wyrównania momentów.

C. Wymiarowanie na zginanie

Wymiarowanie na maksymalne momenty przęsłowe

max

,

Sd

M

[kNm/m]

Beton C

→ f

cd

, f

ck

, f

ctm

Stal A

→ f

yd

, f

yk

,

ξ

eff,lim

Budynek o konstrukcji mieszanej – wersja 2007

Dr inż. Maria WŁODARCZYK

Projekt techniczny STUDENT

Dr inż. Barbara GOSZCZYŃSKA

Do użytku wewnętrznego. Na prawach rękopisu.

39

Zbrojenie płyty obliczamy dla pasma płytowego o szerokości m

0

.

1

=

b

.

1

a

h

d

f

−

=

wysokość użyteczna płyty

gdzie: h

f

– grubość płyty

φ

5

.

0

min

1

+

= c

a

w którym:

(

)

mm

12

5

.

4

÷

∈

φ

–

średnica prętów zbrojeniowych stosowanych przy zbrojeniu płyt,

min

c

– minimalna grubość otulenia przyjmowana w zależności od klasy środowiska

zgodnie z punktem 8.1.1.2,

2002

:

03264

B

PN

−

−

, (str. 89).

Uwaga

: Zbrojenie płyty wyznaczamy dla trzech przęseł skrajnego, przedskarajnego i środkowego. Zbrojenie

we wszystkich przęsłach środkowych płyty ciągłej przyjmujemy takie samo jak zbrojenie wyznaczone dla
przęsła środkowego płyty 5

–

przęsłowej.

Wymiarowanie na minimalne momenty przęsłowe

Jeżeli w rozpatrywanym przęśle płyty maksymalny i minimalny moment są przeciwnego znaku, to zachodzi
konieczność wymiarowania zbrojenia na minimalny moment przęsłowy. Jednak zbrojenie na momenty
ujemne w przęśle należy stosować większe niż wynika to z wartości

min

,

Sd

M

, ponieważ jest to najmniejsza

co do wartości bezwzględnej wartość momentu w przęśle.
Potrzebne zbrojenie na moment ujemny w przęśle można obliczać przyjmując moment zastępczy, który nie
może być mniejszy od minimalnej wartości momentu przęsłowego.

(

)

min

min

max

3

1

prz

Sd

prz

Sd

pod

Sd

zast

Sd

M

M

M

M

≥

+

=

gdzie:

min

prz

Sd

M

– minimalny moment ujemny w rozpatrywanym przęśle,

max

pod

Sd

M

– maksymalny moment podporowy z dwóch sąsiednich podpór przylegających do

rozpatrywanego przęsła.

Wymiarowanie na maksymalne momenty podporowe

Zbrojenie płyty, dla maksymalnych momentów podporowych, wyznaczamy dla podpory przedskrajnej
i środkowej. Dla wszystkich podpór środkowych przyjmujemy takie samo zbrojenie jak wyznaczone dla
podpory środkowej belki pięcioprzęsłowej.

D. Sprawdzenie stanów granicznych użytkowalności

Sprawdzenie stanu granicznego zarysowania

Szerokość rys prostopadłych w elementach zginanych o przekroju prostokątnym, zbrojonych stalą
żebrowaną, przy wartości stosunku

95

.

0

85

.

0

/

÷

=

h

d

uważać można za ograniczoną do wartości

mm

0.3

lim

=

w

, jeśli maksymalna średnica prętów zbrojenia jest nie większa niż podano w tablicy D.1,

2002

:

03264

B

PN

−

−

, str. 141.

Uwaga:

Obliczenie szerokości rys można pominąć.

Sprawdzenie stanu granicznego ugięć

Stanu granicznego użytkowania można nie sprawdzać jeżeli

max













≤

d

l

d

l

eff

eff

,

Budynek o konstrukcji mieszanej – wersja 2007

Dr inż. Maria WŁODARCZYK

Projekt techniczny STUDENT

Dr inż. Barbara GOSZCZYŃSKA

Do użytku wewnętrznego. Na prawach rękopisu.

40

przy czym

max













d

l

eff

jest wielkością odczytaną z tab. 13, str. 68,

2002

:

03264

B

PN

−

−

w zależności od

procentu zbrojenia –

ρ

, naprężeń w stali

σ

s

i klasy betonu. Dla wartości pośrednich graniczne wartości

z tabeli można interpolować liniowo.

Wartość naprężeń w zbrojeniu rozciąganym

σ

s

wyznaczamy ze wzoru:

1

S

Sd

s

zA

M

σ

=

gdzie: M

Sd

– moment wyznaczony dla kombinacji obciążeń długotrwałych (

0

.

1

=

f

γ

),

d

z

9

.

0

≈

.

E. Dobór zbrojenia dla płyty

Zbrojenie główne

płyt jest to zbrojenie, które wymagane jest obliczeniowo dla przejęcia momentów

zginających, niezależnie od kierunku ich działania. Zbrojenie to w płytach jednokierunkowo zbrojonych
przyjmowane jest w kierunku mniejszej rozpiętości i kształtowane w oparciu o uzyskane obwiednie
momentów.

Zbrojenie rozdzielcze

(drugorzędne) jest to zbrojenie poprzeczne, prostopadłe do głównego, które wymagane

jest w celu przejęcia efektów nie uwzględnianych w obliczeniach (skurcz, temperatura, lokalne momenty
poprzeczne). Zbrojenie rozdzielcze przyjmowane jest konstrukcyjnie na podstawie odpowiednich zaleceń.

1. Grubość otulenia

min

c

należy przyjąć zgodnie z punktem 8.1.1.2,

2002

:

03264

B

PN

−

−

.

2. Średnica prętów nie powinna być mniejsza niż 4.5 mm, w siatkach dopuszcza się średnicę 3 mm.
3. Do podpory należy doprowadzić bez odgięć co najmniej 1/3 prętów zbrojenia głównego potrzebnych w

przęśle i nie mniej niż 3 pręty na jeden metr płyty.

4. Odgięcia prętów przechodzących ze strefy rozciąganej do ściskanej należy wykonywać pod kątem 45

°.

5. Jeżeli na podporze nie występują warunki zapewniające swobodę obrotu przekroju, należy zastosować

odpowiednie zbrojenie górne.

6. Jeżeli konstrukcja skrajnej podpory nie zabezpiecza płyty przed wystąpieniem momentu ujemnego,

należy stosować odpowiednie zbrojenie górne.

7. Pręty rozdzielcze powinny mieć rozstaw nie większy niż 300 mm, oraz łączną nośność nie mniejszą niż:

a) 1/10 nośności zbrojenia głównego przy obciążeniu równomiernie rozłożonym,
b) 1/4 nośności zbrojenia głównego przy obciążeniu równomiernie rozłożonym i obciążeniu siłami

skupianymi w przypadku, gdy momenty zginające wywołane obciążeniami skupionymi nie są
większe niż 50% momentów całkowitych. W przeciwnym przypadku zbrojenie prostopadłe do
zbrojenia głównego należy odpowiednio obliczyć.

8. Pręty zbrojenia rozdzielczego należy również umieszczać w miejscu zagięcia zbrojenia głównego płyty.
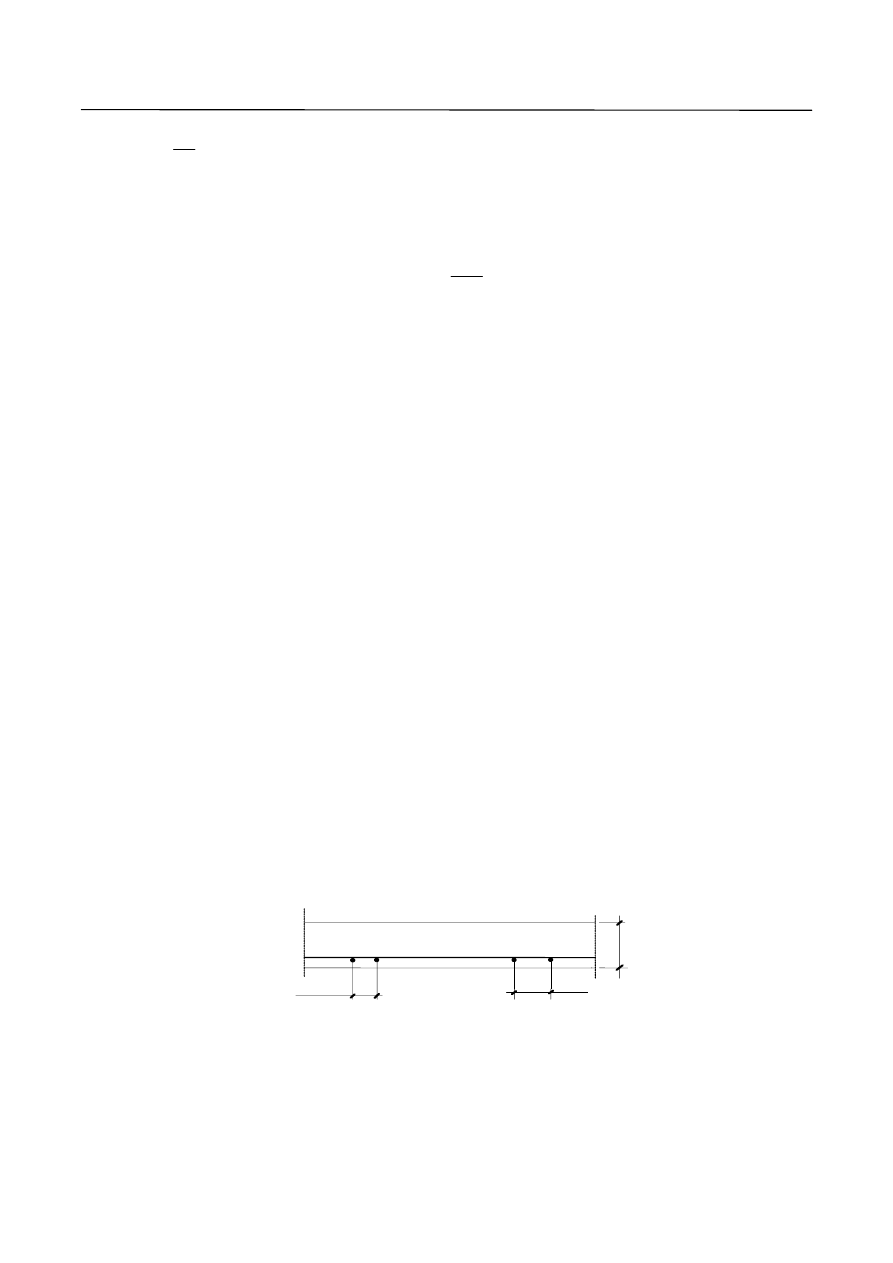
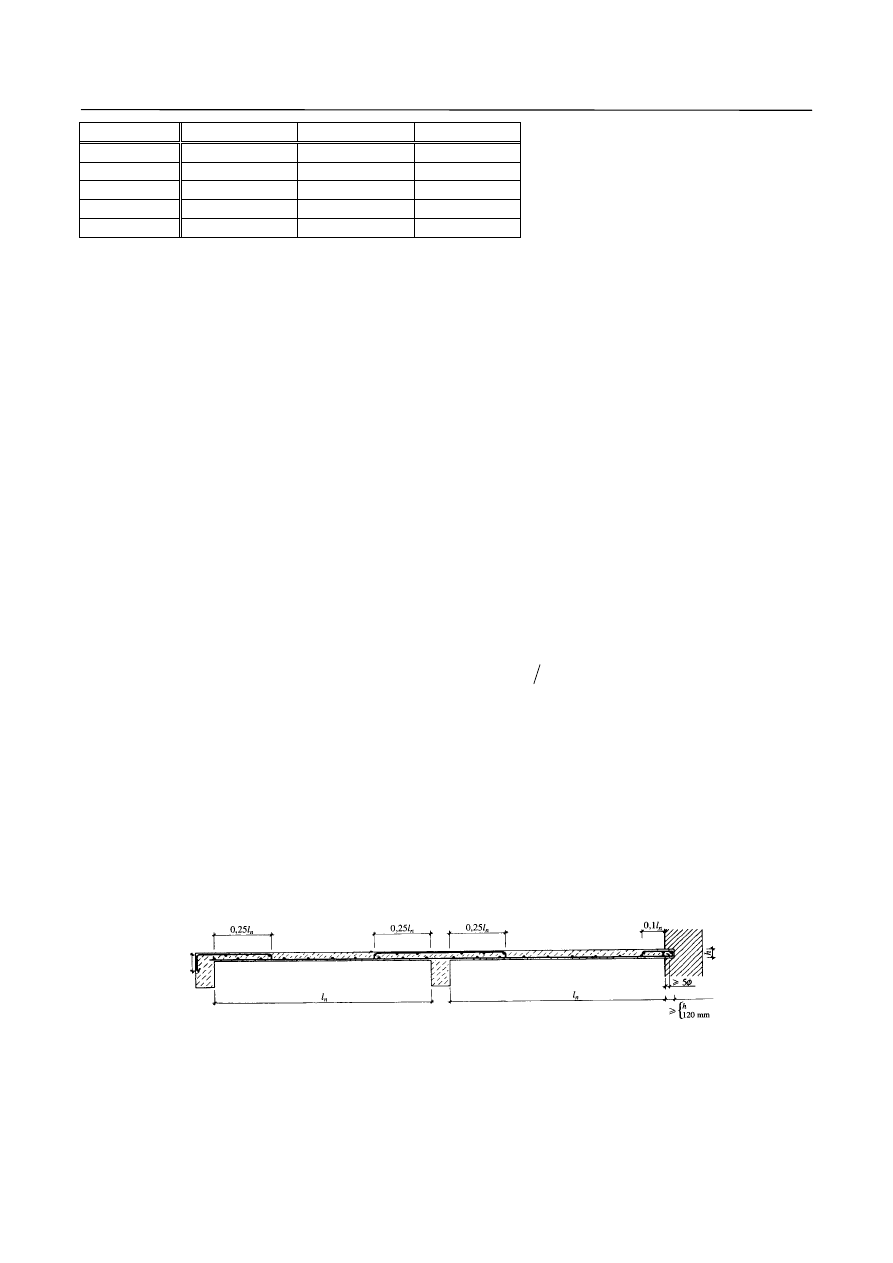
9. Maksymalny i minimalny rozstaw prętów zbrojenia głównego.

Rys. 8. Rozstaw prętów zbrojenia głównego dla płyt jednokierunkowo zbrojonych.

10. Maksymalny i minimalny rozstaw prętów zbrojenia rozdzielczego.

h

f

s

max

s

min

≥

φ

s

min

≥ 20 mm

(najczęściej w praktyce
stosuje się s

min

= 50 mm)

s

max

(ze względu na skurcz)

s

max

≤ 120 mm dla h

f

≤ 100 mm

s

max

≤









mm

250

2

.

1

f

h

dla h

f

> 100 mm

Budynek o konstrukcji mieszanej – wersja 2007

Dr inż. Maria WŁODARCZYK

Projekt techniczny STUDENT

Dr inż. Barbara GOSZCZYŃSKA

Do użytku wewnętrznego. Na prawach rękopisu.

41

Rys. 9.

Rozstaw prętów zbrojenia rodzielczego dla płyt jednokierunkowo zbrojonych.

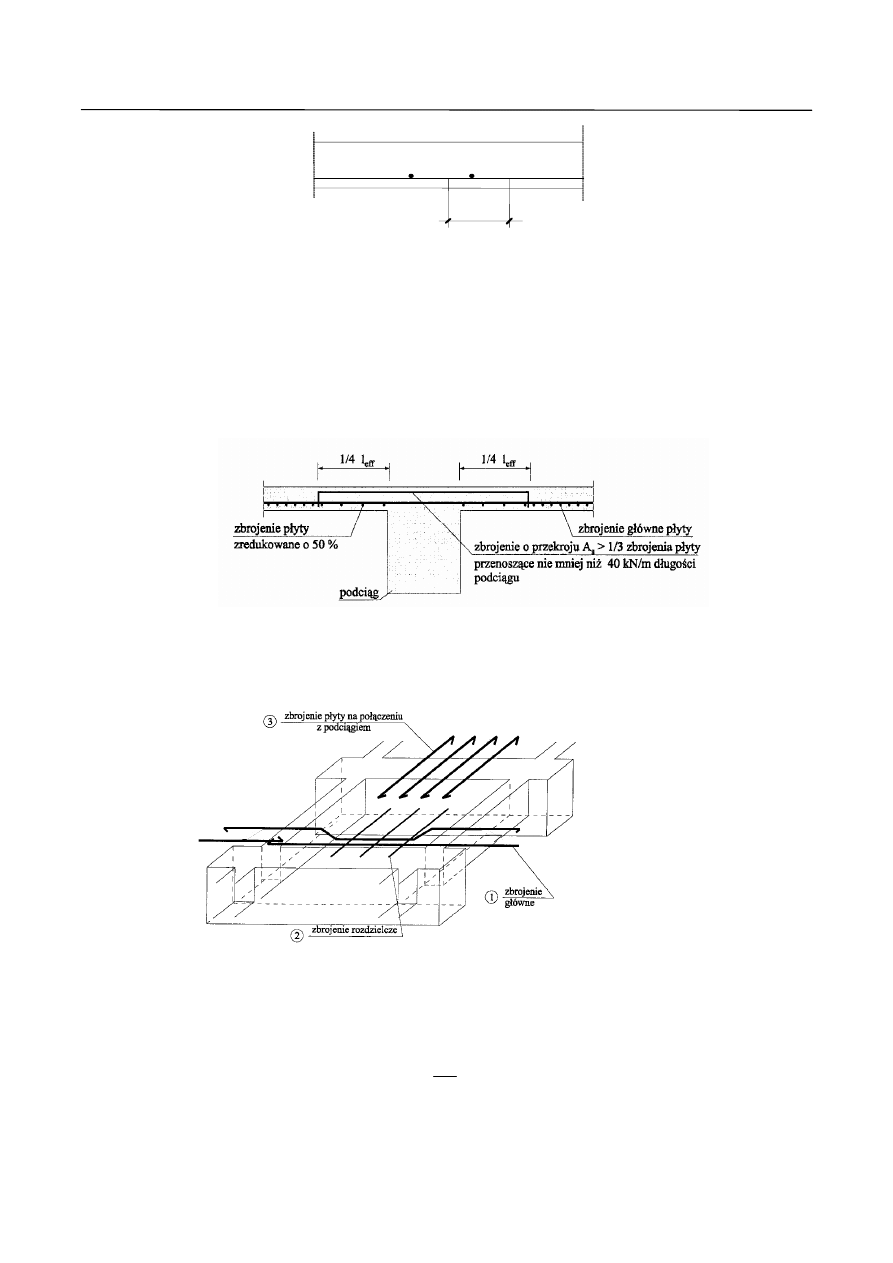
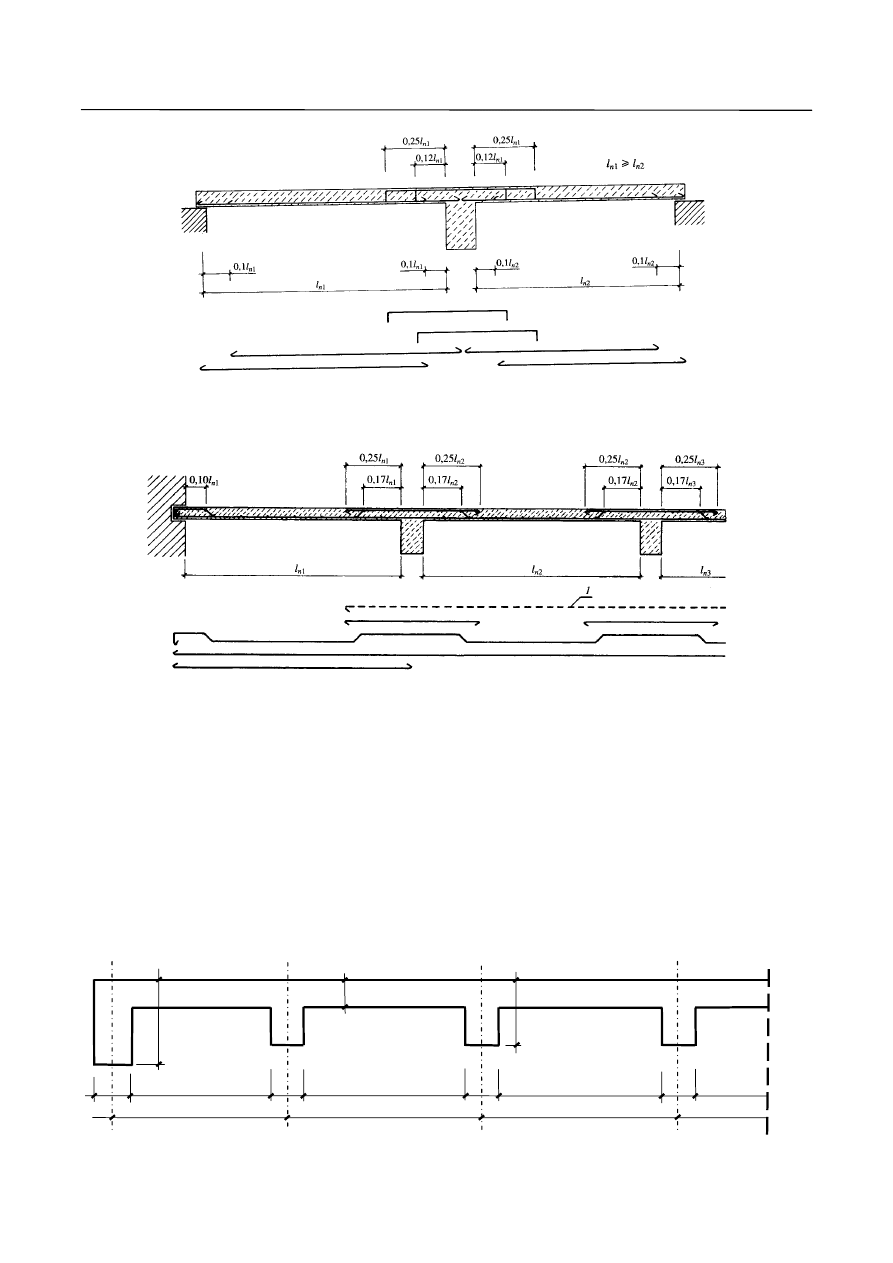
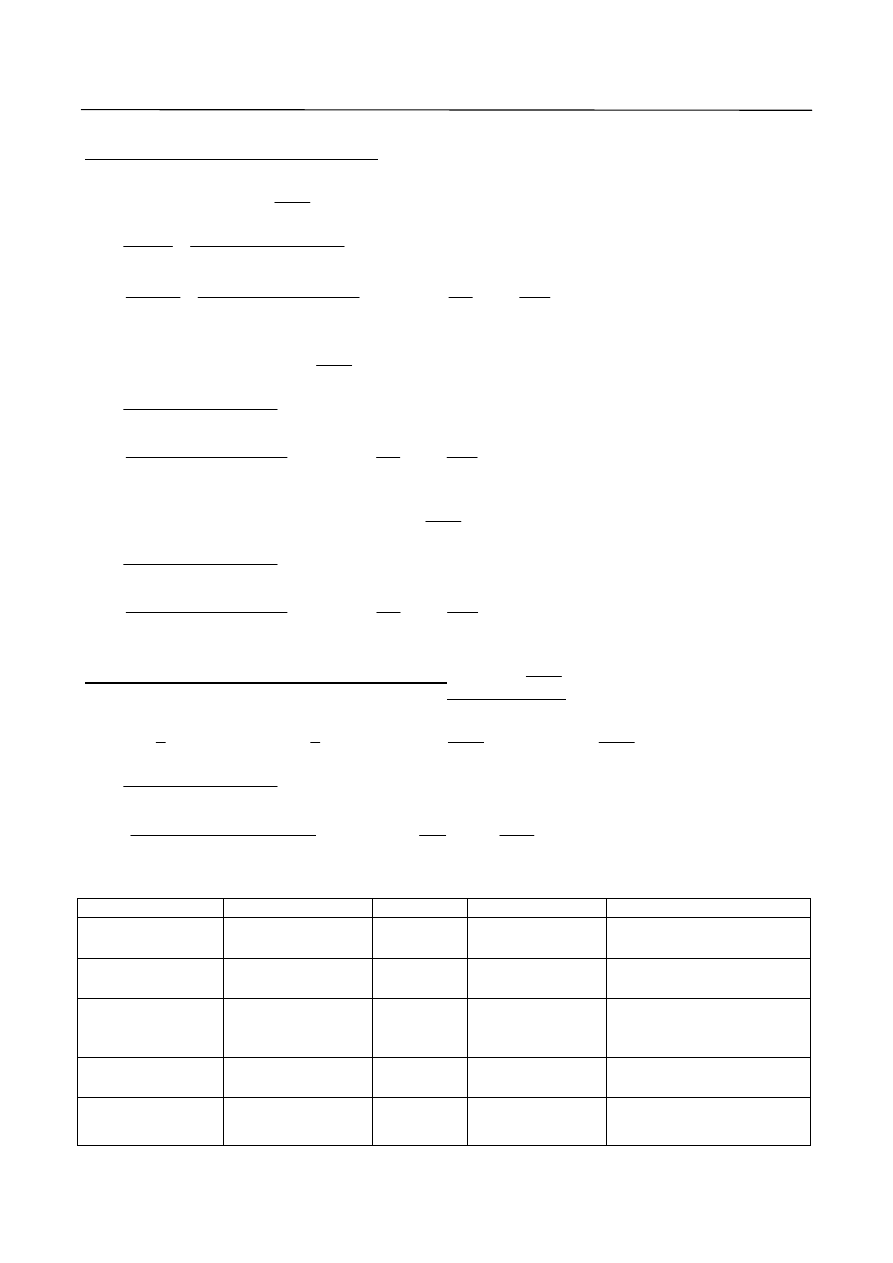
11. Maksymalny rozstaw prętów zbrojeniowych poza przekrojami krytycznymi powinien być nie większy niż 30 cm.

12. Jeżeli pracujące zbrojenie płyty jest ułożone równolegle do podciągu, w płycie należy stosować

zbrojenie górne prostopadłe do podciągu. (Rys. 10)

Dodatkowe zbrojenie górą prostopadłe do podciągu powinno zapewniać nośność nie mniejszą niż 1/3
nośności zbrojenia głównego płyty i mieć przekrój zdolny przenieść siłę rozciągającą nie mniejszą niż
40kN/m długości podciągu. Zbrojenie to powinno sięgać na odległość 0.25l

eff

płyty od lica podpory.

Na tym odcinku zbrojenie główne płyty można zredukować do 50%.

Rys. 10. Połączenie płyty z podciągiem.

Na rysunku 11 przedstawiono rodzaje zbrojenia występujące w płytach jednokierunkowo zbrojonych.

Rys. 11. Zbrojenie płyty jednokierunkowo zbrojonej.

Przykład doboru zbrojenia dla płyty jednokierunkowo zbrojonej

Przy doborze zbrojenia płyty określa jego się intensywność na 1 m długości płyty:

s

100

1

1

s

s

a

A

=

[cm

2

/m]

gdzie: a

s1

– pole powierzchni jednego pręta zbrojeniowego ,

s

– rozstaw prętów zbrojenia płyty w [cm].

s

m ax

s

m ax

≤ 3 0 0 m m

s

m in

≥ 2 0 m m

(n a jcz ę ście j w p rak tyce
sto su je się s

m in

= 5 0 m m )

Budynek o konstrukcji mieszanej – wersja 2007

Dr inż. Maria WŁODARCZYK

Projekt techniczny STUDENT

Dr inż. Barbara GOSZCZYŃSKA

Do użytku wewnętrznego. Na prawach rękopisu.

42

A B C C’

3.96

4.40

4.01

4.01

2.76 3.36

3.36

zbrojenie A

s1

w cm

2

/m

Intensywność zbrojenia płyty:
np.

φ

6 co 10 cm, intensywność zbrojenia płyty, średnica i rozstaw.

/m

cm

83

.

2

10

100

283

.

0

2

1

=

⋅

=

s

A

Przyjęcie zbrojenia najlepiej rozpocząć od uwzględnienia najmniejszej i największej wartości zbrojenia.

Zbrojenie płyty dobieramy w granicach od – 2.5% (niedozbrojenie) do + 10% (przezbrojenie) w odniesieniu
do zbrojenia obliczonego A

s1

.

Rozstaw prętów zbrojeniowych w przęśle i na podporach zakładamy taki sam, np. 10 cm.
W płytach skok średnicy zbrojenia przyjmujemy co „oczko”, np. średnica 6

φ

i 8

φ

co 10 cm.

Sposób opisania prętów zbrojenia płyty:
Sposób opisania zbrojenia płyty przy pojedynczym rozstawie prętów:

1

°

• • • • •

φ

6 co 10 cm

/m

cm

83

.

2

10

100

283

.

0

2

1

=

⋅

=

s

A

2

°

8 co 10 cm

/m

cm

03

.

5

10

100

503

.

0

2

1

=

⋅

=

s

A

Sposób opisania zbrojenia płyty przy podwójnym rozstawie prętów:

3

°

• • • • •

φ

6 co 20 cm

φ

6 co 20 cm

/m

cm

83

.

2

20

100

283

.

0

20

100

283

.

0

2

1

=

⋅

+

⋅

=

s

A

4

°

φ

6 co 20 cm

φ

8 co 20 cm

/m

cm

93

.

3

20

100

503

.

0

20

100

283

.

0

2

1

=

⋅

+

⋅

=

s

A

5

°

φ

8 co 20 cm

φ

8 co 20 cm

/m

cm

03

.

5

20

100

503

.

0

2

2

1

=

⋅

⋅

=

s

A

Sposób opisania zbrojenia płyty przy potrójnym rozstawie prętów:

6

°

2

φ

6 co 30 cm

φ

8 co 30 cm

/m

cm

56

.

3

30

100

503

.

0

30

100

283

.

0

2

2

1

=

⋅

+

⋅

⋅

=

s

A

7

°

1

φ

6 co 30 cm

2

φ

8 co 30 cm

/m

cm

30

.

4

30

100

503

.

0

2

30

100

283

.

0

2

1

=

⋅

⋅

+

⋅

=

s

A

8

°

3

φ

8 co 30 cm

/m

cm

03

.

5

30

100

503

.

0

3

2

1

=

⋅

⋅

=

s

A

Dobór zbrojenia płyty dla przykładu podanego wyżej

Niedozbrojenie

Zbrojenie

płyty Przezbrojenie

Budynek o konstrukcji mieszanej – wersja 2007

Dr inż. Maria WŁODARCZYK

Projekt techniczny STUDENT

Dr inż. Barbara GOSZCZYŃSKA

Do użytku wewnętrznego. Na prawach rękopisu.

43

2.5 %

(obliczone)

10 %

Przęsło A-B

3.76 cm

2

3.96

cm

2

4.36

cm

2

Przęsło B-C

2.69 cm

2

2.76

cm

2

3.04

cm

2

Przęsło C-C’

3.28 cm

2

3.36

cm

2

3.70

cm

2

Podpora B

4.29 cm

2

4.40

cm

2

4.84

cm

2

Podpora C

3.91 cm

2

4.01

cm

2

4.41

cm

2

Przęsło A-B: 1

φ

6 + 2

φ

8 co 30 cm 0.96 + 2

× 1.68 = 4.30 cm

2

/m

Przęsło B-C: 3

φ

6 co 30 cm 2.83 cm

2

/m

Przęsło C-C’: 2

φ

6 + 1

φ

8 co 30 cm 2

× 0.96 + 1.68 = 3.56 cm

2

/m

Podpora B: 1

φ

6 + 2

φ

8 co 30 cm 0.96 + 2

× 1.68 = 4.30 cm

2

/m

Podpora C: 1

φ

6 + 2

φ

8 co 30 cm 0.96 + 2

× 1.68 = 4.30 cm

2

/m

F. Konstruowanie zbrojenia płyty

Przy oparciu płyt na podporach, które stanowią belki lub ściany, szerokość oparcia eliminuje praktycznie
wpływ sił poprzecznych w strefie przypodporowej. Warunkiem determinującym głębokość oparcia płyty na
podporze jest prawidłowe zakotwienie prętów zbrojeniowych.

Zgodnie z zaleceniami

2002

:

03264

B

PN

−

−

głębokość oparcia powinna spełniać warunki zakotwienia

prętów zbrojeniowych według punktu 8.1.3 i powinna być nie mniejsza niż:
8 cm – przy oparciu na murze lub ścianie z betonu lekkiego lub zwykłego klasy C12/15,
6 cm – przy oparciu na ścianie z betonu zwykłego klas wyższych niż C12/15,
4 cm – przy oparciu na belkach stalowych.

Zbrojenie przęsłowe doprowadzone do podpory, należy przedłużyć poza jej krawędź o odcinek nie krótszy
niż:
- 2/3 l

bd

przy podparciu bezpośrednim

- l

bd

przy podparciu pośrednim

Długość tego odcinka dla płyt równomiernie obciążonych przy (

12

≥

h

l

eff

) można przyjmować 5

φ

.

Długość zakotwienia prętów zbrojenia rozciąganego elementów zamocowanych w murze powinna być nie
mniejsza niż

bd

l

h

+

3

.

0

(Rys. 47

2002

:

03264

B

PN

−

−

).

W przypadku zakotwienia zbrojenia dolnego na podporze pośredniej długość zakotwienia powinna być nie
mniejsza niż 10

φ

.

Zazwyczaj wystarczające są minimalne wartości ale czasami potrzebna jest dokładniejsza analiza długości
zakotwienia prętów zbrojeniowych.

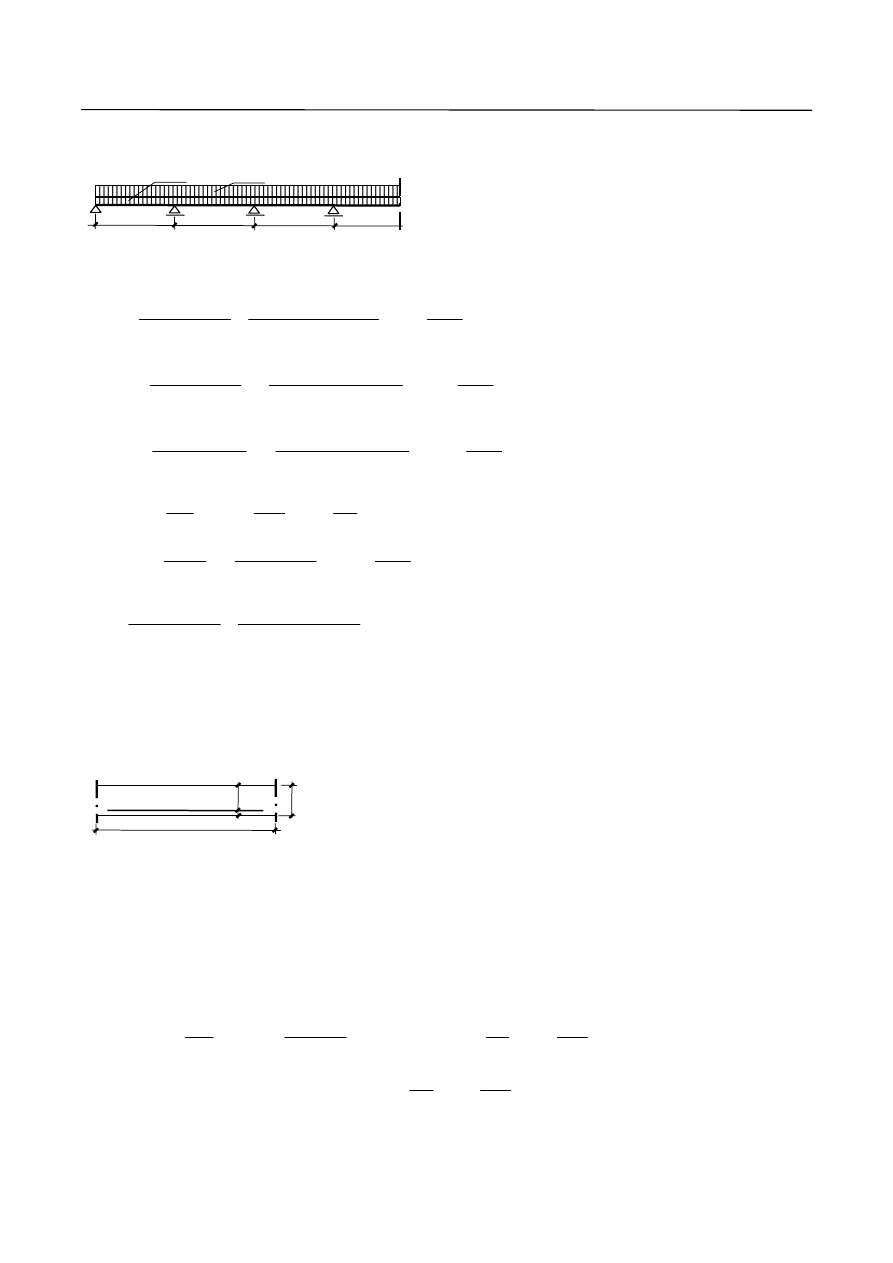
G. Przykłady zbrojenia płyty ciągłej

≥

l

bd

Rys. 12. Zbrojenie płyty ciągłej wkładkami nieodginanymi o stałej intensywności.

Budynek o konstrukcji mieszanej – wersja 2007

Dr inż. Maria WŁODARCZYK

Projekt techniczny STUDENT

Dr inż. Barbara GOSZCZYŃSKA

Do użytku wewnętrznego. Na prawach rękopisu.

44

Rys. 13. Zbrojenie płyty ciągłej wkładkami nieodginanymi o zmiennej intensywności.

Rys. 14. Zbrojenie płyty ciągłej odginane na deskowaniu: 1– wkładka dodatkowa przenosząca ujemne

momenty przęsłowe.

PRZYKAD

Poz. 2.1. Pyta stropu

A. Obciążenia działające na płytę

g

kpł

= 2.87 kN/m

2

g

Sdpł

= 3.33 kN/m

2

p

kpł

= 3.60 kN/m

2

p

Sdpł

= 4.68 kN/m

2

B. Statyka

- Rozpiętości obliczeniowe

38

20

20

20

60

8

40

l

1

=210

l

2

=230

l

2

=230

l

2

=230

l

n2

=210

l

n2

=210

l

n2

=210

l

n2

=181

Budynek o konstrukcji mieszanej – wersja 2007

Dr inż. Maria WŁODARCZYK

Projekt techniczny STUDENT

Dr inż. Barbara GOSZCZYŃSKA

Do użytku wewnętrznego. Na prawach rękopisu.

45

Wartości momentów wyznaczono przy wykorzystaniu metody plastycznego wyrównania momentów.

m

1.81

1

1

=

=

n

eff

l

l

m

2.10

2

2

=

=

n

eff

l

l

l

n1

l

n2

l

n2

l

n2

A

B

C

D

1

2

3

4

g

Sd

p

Sd

Wartości maksymalne momentów:
- moment w przęśle skrajnym

(

)

(

)

m

kNm

38

.

2

11

81

.

1

68

.

4

33

.

3

11

2

2

1

1

=

×

+

=

+

=

n

Sd

Sd

Sd

l

p

g

M

- moment krawędziowy na podporze przedskrajnej

(

)

(

)

m

kNm

21

.

3

11

10

.

2

68

.

4

33

.

3

11

2

2

2

−

=

×

+

−

=

+

−

=

n

Sd

Sd

SdB

l

p

g

M

- momenty w przęsłach pośrednich oraz momenty krawędziowe na podporach środkowych

(

)

(

)

m

kNm

21

.

2

16

10

.

2

68

.

4

33

.

3

16

2

2

2

2

±

=

×

+

±

=

+

±

=

n

Sd

Sd

Sd

l

p

g

M

Wartości momentów minimalnych w przęsłach pośrednich

2

m

kN

50

.

4

4

68

.

4

33

.

3

4

=

+

=

+

=

Sd

Sd

Sd

p

g

q

m

kNm

24

.

1

16

10

.

2

50

.

4

16

2

2

2

min

−

=

×

−

=

−

=

n

Sd

Sd

l

q

M

Zasięg momentu w przęśle skrajnym

(

)

(

)

m

40

.

0

50

.

4

8

81

.

1

68

.

4

33

.

3

8

1

=

×

×

+

=

+

=

Sd

n

Sd

Sd

BA

q

l

p

g

a

C. Dane materiałowe

Beton C20/25:

MPa

20

=

ck

f

,

MPa

3

.

13

=

cd

f

,

MPa

2

.

2

=

ctm

f

,

MPa

0

.

1

=

ctd

f

,

GPa

30

=

cm

E

Stal AII (18G2):

MPa

355

=

yk

f

, MPa

310

=

yd

f

, GPa

200

=

s

E

, 0.55

lim

,

=

eff

ξ

D. Przekrój

b = 1.0 m

A

S1

a

1

d

h

f

cm

8

=

f

h

c = 1.5 cm

– otulina zbrojenia przyjęta zgodnie z tab. 21,

2002

:

03264

B

PN

−

−

φ

= 6 mm

– wstępnie przyjęta średnica zbrojenia płyty

cm

1.8

6

.

0

5

.

0

5

.

1

5

.

0

1

=

×

+

=

+

=

φ

c

a

cm

6.2

8

.

1

8

1

=

−

=

−

=

a

h

d

f

E. Minimalny procent zbrojenia













=

×

=

×

=

=

×

=

×

×

×

×

=

≥

−

−

m

cm

81

.

0

m

m

10

06

.

8

062

.

0

0013

.

0

0013

.

0

m

cm

99

.

0

10

99

.

9

062

.

0

10

355

10

2

.

2

26

.

0

26

.

0

2

2

5

2

2

5

3

3

min

,

1

d

m

m

d

f

f

A

yk

ctm

s

Uwaga:

Dla płyt minimalny procent zbrojenia wyznaczamy na 1 m szerokości płyty.\\

Budynek o konstrukcji mieszanej – wersja 2007

Dr inż. Maria WŁODARCZYK

Projekt techniczny STUDENT

Dr inż. Barbara GOSZCZYŃSKA

Do użytku wewnętrznego. Na prawach rękopisu.

46

F. Wymiarowanie na zginanie

Wymiarowanie na momenty maksymalne

Przęsło skrajne:

m

kNm

38

.

2

=

Sd

M

047

.

0

10

3

.

13

062

.

0

0

.

1

38

.

2

3

2

2

=

×

×

×

=

=

cd

Sd

cc

f

bd

M

s

→

lim

,

048

.

0

eff

eff

ξ

ξ

<

=

,

976

.

0

=

eff

ζ

min

,

1

2

2

4

3

1

m

cm

27

.

1

m

m

10

27

.

1

10

310

062

.

0

976

.

0

38

.

2

s

yd

eff

Sd

s

A

df

M

A

>

=

×

=

×

×

×

=

=

−

ζ

Podpora przedskrajna:

m

kNm

21

.

3

=

Sd

M

063

.

0

10

3

.

13

062

.

0

0

.

1

21

.

3

3

2

=

×

×

×

=

cc

s

→

lim

,

065

.

0

eff

eff

ξ

ξ

<

=

,

968

.

0

=

eff

ζ

min

,

1

2

2

4

3

1

m

cm

72

.

1

m

m

10

72

.

1

10

310

062

.

0

968

.

0

21

.

3

s

s

A

A

>

=

×

=

×

×

×

=

−

Przęsła środkowe i podpory środkowe:

m

kNm

21

.

2

=

Sd

M

043

.

0

10

3

.

13

062

.

0

0

.

1

21

.

2

3

2

=

×

×

×

=

cc

s

→

lim

,

044

.

0

eff

eff

ξ

ξ

<

=

,

978

.

0

=

eff

ζ

min

,

1

2

2

4

3

1

m

cm

17

.

1

m

m

10

17

.

1

10

310

062

.

0

978

.

0

21

.

2

s

s

A

A

>

=

×

=

×

×

×

=

−

Wymiarowanie na minimalne momenty przęsłowe:

m

kNm

24

.

1

=

Sd

M

Moment zastępczy

(

)

(

)

m

kNm

24

.

1

m

kNm

48

.

1

24

.

1

21

.

3

3

1

3

1

min

,

min

,

max

,

,

=

>

=

+

=

+

=

przesl

Sd

przesl

Sd

pod

Sd

zast

Sd

M

M

M

M

029

.

0

10

3

.

13

062

.

0

0

.

1

48

.

1

3

2

=

×

×

×

=

cc

s

→

lim

,

029

.

0

eff

eff

ξ

ξ

<

=

,

985

.

0

=

eff

ζ

min

,

1

2

2

4

3

1

m

cm

78

.

0

m

m

10

78

.

0

10

310

062

.

0

985

.

0

48

.

1

s

s

A

A

>

=

×

=

×

×

×

=

−

G. Dobór zbrojenia

Niedozbrojenie

: 2.5% A

s1

[cm

2

/m]

Przezbrojenie:

10%

Zbrojenie dobrane

Przęsło skrajne

1.24

1.27

1.40

φ 4.5 co 10 cm
o A

s1,prov

=1.59 cm

2

/m

Przęsła środkowe 1.14

1.17 1.29

φ 4.5 co 10 cm
o A

s1,prov

=1.59 cm

2

/m

Podpora
przedskrajna

1.68 1.72

1.89

2

φ 4.5 co 30 cm

+ 6 co 30 cm
o A

s1,prov

= 2.0 cm

2

/m

Podpory środkowe 1.1

1.17

1.29

φ 4.5 co 10 cm o
A

s1,prov

=1.59 cm

2

/m

Przęsła środkowe

(zbrojenie wyznaczone dla
momentów minimalnych)

0.76 0.78

0.86

φ 4.5 co 10 cm o
A

s1,prov

=1.59 cm

2

/m

Budynek o konstrukcji mieszanej – wersja 2007

Dr inż. Maria WŁODARCZYK

Projekt techniczny STUDENT

Dr inż. Barbara GOSZCZYŃSKA

Do użytku wewnętrznego. Na prawach rękopisu.

47

H. Stan graniczny użytkowalności

Sprawdzenie stanu granicznego użytkowalności można pominąć.

I. Połączenie płyty z podciągiem

m

cm

53

.

0

3

59

.

1

3

1

2

,

=

=

≥

pł

s

s

A

A

m

kN

40

=

=

yd

s

s

f

A

F

→

m

cm

29

.

1

10

310

40

40

2

3

=

×

=

=

yd

s

f

A

Przyjęto zbrojenie:

φ 4.5 co 10 cm o A

s1,prov

=1.59 cm

2

/m

φ4.5 co 10 cm

φ4.5 co 20 cm

φ4.5 co 10 cm

φ4.5 co 30 cm

Poz. 2.2. Żebro stropu

A. Obciążenia działające na żebro

Obciążenia stałe i zmienne, charakterystyczne i obliczeniowe według poz. 2.2. projektu wstępnego.

B. Statyka
- Rozpiętości obliczeniowe należy wyznaczyć zgodnie z przepisami

2002

:

03264

B

PN

−

−

i opisanymi

w punkcie 3.2.

- Obwiednie momentów i sił tnących
Obwiednie momentów i sił tnących można wyznaczyć przy wykorzystaniu tablic Winklera. Żebro
wieloprzęsłowe o liczbie przęseł większej niż 5 korzystając z tablic Winklera zamieniamy w obliczeniach
statycznych na 5

–

przęsłowe.

C. Wymiarowanie na zginanie

Wymiarowanie na maksymalne momenty przęsłowe

Przy wymiarowaniu zginanych przekrojów przęsłowych należy uwzględnić współpracę płyty z żebrem.

Uwaga

: Zbrojenie wyznaczamy dla każdego przęsła żebra, gdyż zmieniają się wartości maksymalnych

momentów zginających.

Wymiarowanie na minimalne momenty przęsłowe

Patrz punkt 2.1. (C) projektu technicznego.

Wymiarowanie na maksymalne momenty podporowe

Zbrojenie wyznaczamy dla każdej podpory, gdzie zmieniają się wartości maksymalnych momentów
podporowych.

Przy wymiarowaniu na maksymalne momenty podporowe należy zwrócić uwagę na szerokość podpory (t),
na której opiera się płyta, i tak jeżeli:
- t = b

≤ h – wymiarujemy przekrój z uwzględnieniem tzw. skosu ukrytego (rys. 15)

Budynek o konstrukcji mieszanej – wersja 2007

Dr inż. Maria WŁODARCZYK

Projekt techniczny STUDENT

Dr inż. Barbara GOSZCZYŃSKA

Do użytku wewnętrznego. Na prawach rękopisu.

48

Rys. 15. Strefa przypodporowa belki ciągłej dla t = b

≤ h.

W tym przypadku wyczerpanie nośności występuje zazwyczaj w licu podpory (rys. 15b). Dlatego zbrojenie
powinno być obliczone w licu podpory dla działających w tym przekroju momentów krawędziowych M

k

L

k

M

=

±

M

m

0.5 V

L

b

P

k

M

=

±

M

m

0.5 V

P

b

gdzie V

L

i V

P

są to siły poprzeczne „lewe” i „prawe” w stosunku do rozważanej podpory.

Należy również sprawdzić, czy obliczone w ten sposób zbrojenie nie jest mniejsze niż w osi podpory dla
maksymalnego momentu podporowego M oraz wysokości h’ w osi podpory. Wysokość h’ określa się z

uwzględnieniem skosu ukrytego, pochylonego pod kątem

3

1

, czyli

6

'

b

h

h

+

=

,

- t = b > h – wymiarujemy na maksymalne momenty podporowe odczytane z obwiedni momentów.

D. Wymiarowanie na ścinanie

Wymiarowanie na maksymalne siły poprzeczne

Wymiarowanie na ścinanie należy wykonać zgodnie z obowiązującymi przepisami normowymi

2002

:

03264

B

PN

−

−

.

Uwaga

: Nośność na ścinanie sprawdzamy z każdej strony podpory i dla wszystkich podpór gdzie zmienia się

wartość siły tnącej V

Sd

.

Sprawdzenie ścinania pomiędzy środnikiem a półkami

Monolityczne połączenie żebra z płytą powoduje, że na styku tych elementów występują naprężenia styczne

τ

, których wypadkową jest siła rozwarstwiająca T.

Polska norma

2002

:

03264

B

PN

−

−

nośność półki przekroju teowego na podłużne ścinanie zaleca obliczać

traktując półkę jako zespół betonowych krzyżulców ściskanych połączonych cięgnami w postaci zbrojenia
poprzecznego, przy czym zakład się, że stan graniczny może być osiągnięty ze względu na ściskanie
krzyżulców betonowych lub rozciąganie zbrojenia w postaci cięgien.

Ponieważ ścinanie wynika ze zmiany naprężeń (momentów), podłużną siłę ścinającą na jednostkę długości
oblicza się ze wzoru

x

F

V

d

Sd

∆

∆

=

gdzie:

∆F

d

– zmiana siły podłużnej (ściskającej lub rozciągającej) w półce po jednej stronie środnika na

długości odcinka

∆x, wyznaczona z zależności:

a) gdy półka jest ściskana i

f

eff

h

x

<

to:

(

)

w

eff

eff

cd

d

b

b

x

f

F

−

=

∆

5

.

0

Budynek o konstrukcji mieszanej – wersja 2007

Dr inż. Maria WŁODARCZYK

Projekt techniczny STUDENT

Dr inż. Barbara GOSZCZYŃSKA

Do użytku wewnętrznego. Na prawach rękopisu.

49

b) gdy półka jest ściskana i

f

eff

h

x

≥

to:

(

)

w

eff

f

cd

d

b

b

h

f

F

−

=

∆

5

.

0

c) gdy półka jest rozciągana to:

s

yd

d

A

f

F

=

∆

w którym: A

s

– zbrojenie podłużne półki w przekroju podporowym (po jednej stronie półki).

∆x – odległość pomiędzy miejscami występowania maksymalnego i zerowego

momentu.

Długość odcinka

∆x przyjmuje się nie większą niż:

– połowa odległości między przekrojami

0

=

M

oraz

max

M

M

=

– odległość między siłami skupionymi.

W belkach swobodnie podpartych oraz ciągłych wartość podłużnej siły ścinającej można również obliczać ze
wzoru:

z

V

V

Sd

t

Sd

β

=

gdzie: V

Sd

– uśredniona wartość obliczeniowej siły poprzecznej w belce na rozpatrywanym odcinku ścinania,

z – ramię sił wewnętrznych,

β

t

– stosunek siły normalnej (ściskającej przenoszonej przez beton lub rozciągającej przenoszonej

przez zbrojenie) w półce po jednej stronie środnika do siły całkowitej w rozpatrywanym
przekroju zginanym.

Siła ta jest przenoszona w przyjętym modelu przez ściskane krzyżulce betonowe i rozciągane cięgna stalowe.
W belkach teowych role tych cięgien spełniają zwykle strzemiona znajdujące się w półce, a w stropach
płytowo-belkowych – zbrojenie płyty nad belką.

Nośność krzyżulców betonowych sprawdza się z warunku

θ

θ

h

νf

V

V

f

cd

Rd

Sd

2

2

cot

1

cot

+

=

≤

,

drugi warunek dotyczy rozciągania i ma postać

cotθ

f

s

A

V

V

yd

f

sf

Rd

Sd

=

≤

3

w których: A

sf

– pole przekroju prętów zbrojenia poprzecznego w półce na grubości h

f

,

s

f

– rozstaw prętów zbrojenia A

sf

,

h

f

– grubość półki,

ν

– współczynnik:











 −

=

250

1

6

.

0

ck

f

ν

Wartości kąta

θ

przyjmuje się:

0

.

2

cot

0

.

1

≤

≤

θ

dla

półki ściskanej,

0

.

1

cot

=

θ

dla

półki rozciąganej.

Budynek o konstrukcji mieszanej – wersja 2007

Dr inż. Maria WŁODARCZYK

Projekt techniczny STUDENT

Dr inż. Barbara GOSZCZYŃSKA

Do użytku wewnętrznego. Na prawach rękopisu.

50

+∆F

d

+∆F

d

∆x

Rys. 16. Oznaczenia dotyczące połączenia półki ze środnikiem

E. Sprawdzenie stanów granicznych użytkowalności

Sprawdzenie stanu granicznego zarysowania

Szerokość rys prostopadłych w elementach zginanych o przekroju prostokątnym, zbrojonych stalą
żebrowaną, przy wartości stosunku

95

.

0

85

.

0

/

÷

=

h

d

uważać można za ograniczoną do wartości

mm

3

.

0

lim

=

w

, jeśli maksymalna średnica prętów zbrojenia jest nie większa niż podano w tablicy D.1 –

2002

:

03264

B

PN

−

−

, str. 141.

Sprawdzenie stanu granicznego ugięć

Stanu granicznego użytkowania można nie sprawdzać jeżeli

max













≤

d

l

d

l

eff

eff

,

przy czym (

d

l

eff

)

max

jest wielkością odczytaną z tab. 13, str. 68,

2002

:

03264

B

PN

−

−

w zależności od

procentu zbrojenia –

ρ

, naprężeń w stali

σ

s

i klasy betonu. Dla wartości pośrednich graniczne wartości

z tablicy można interpolować liniowo.

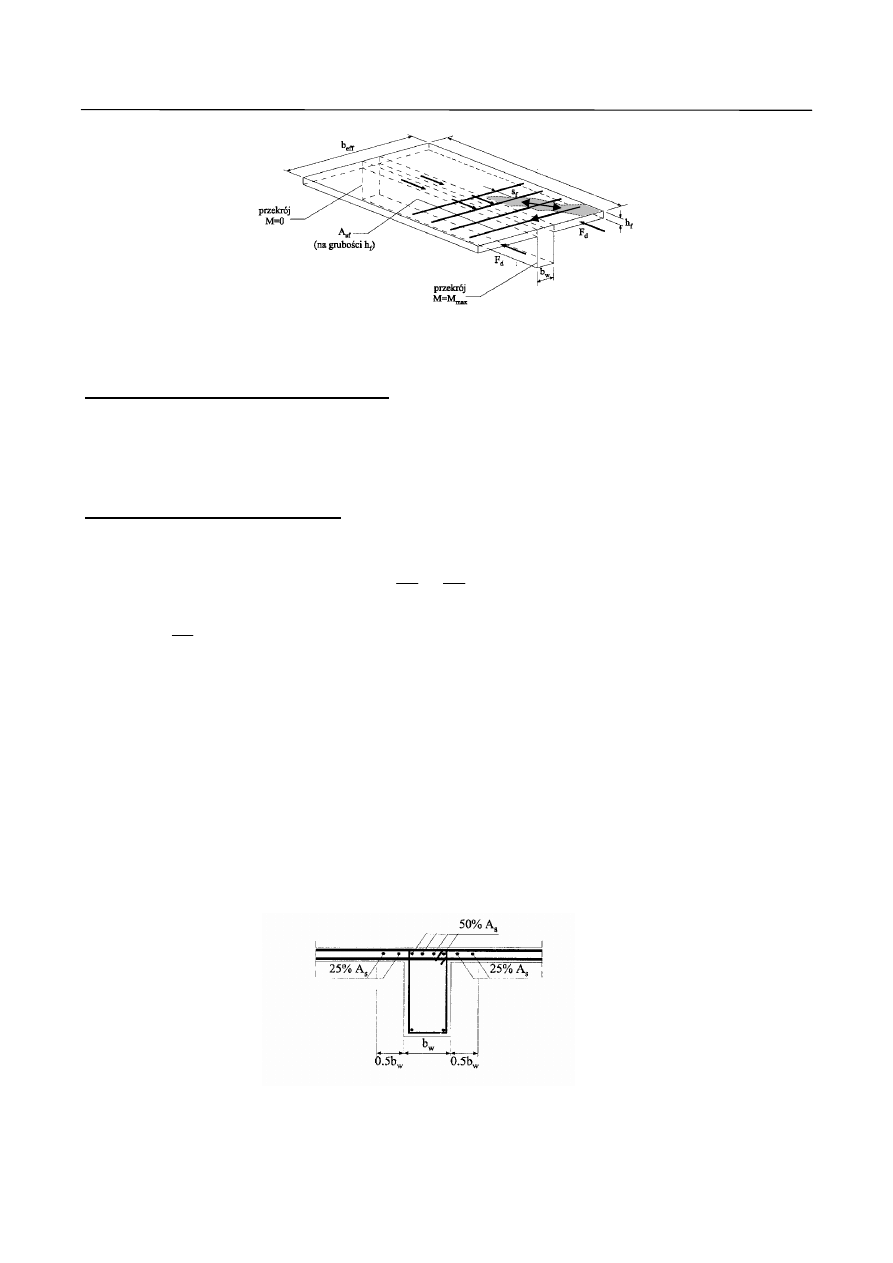
F. Dobór zbrojenia dla żebra

Zbrojenie należy dobrać i rozmieścić w przekroju belki zgodnie z obowiązującymi przepisami normowymi

2002

:

03264

B

PN

−

−

.

Przy rozmieszczeniu zbrojenia nadpodporowego belki ciągłej czasami spotykamy się z problemem
rozmieszczenia dużej ilości prętów w środniku belki. Istnieje możliwość rozdzielenia całkowitego przekroju
zbrojenia rozciąganego

A

s

pomiędzy środnik i części przyległe szerokości współpracującej płyty (rys. 17).

Rys. 17. Sposób rozmieszczenia zbrojenia górnego żebra w płycie

Budynek o konstrukcji mieszanej – wersja 2007

Dr inż. Maria WŁODARCZYK

Projekt techniczny STUDENT

Dr inż. Barbara GOSZCZYŃSKA

Do użytku wewnętrznego. Na prawach rękopisu.

51

Ma to jednak znaczenie przy sprawdzaniu ścinania pomiędzy środnikiem a półkami. Usytuowanie w tym
obszarze zbrojenia głównego żebra powoduje wystąpienie siły

F

d

, a tym samym konieczność obliczenia

dodatkowego zbrojenia poprzecznego w półce przekroju teowego.

PRZYKAD

Poz. 2.2. Żebro stropu

A. Obciążenia działające na żebro

g

żł

= 8.33 kN/m

g

Sdż

= 9.60 kN/m

p

kż

= 8.28 kN/m

p

Sdż

= 10.76 kN/m

B. Statyka

- Rozpiętości obliczeniowe

38

25

25

60

40

60

l

1

=530

l

2

=550

l

2

=550

l

n2

=525

l

n2

=525

l

n2

=498.5

m

30

.

5

m

5.23

4.985

1.05

05

.

1

1

1

1

=

<

=

×

=

=

l

l

l

n

eff

m

50

.

5

m

5.51

5.25

1.05

05

.

1

2

2

2

=

>

=

×

=

=

l

l

l

n

eff

do dalszych obliczeń przyjęto m

50

.

5

2

2

=

= l

l

eff

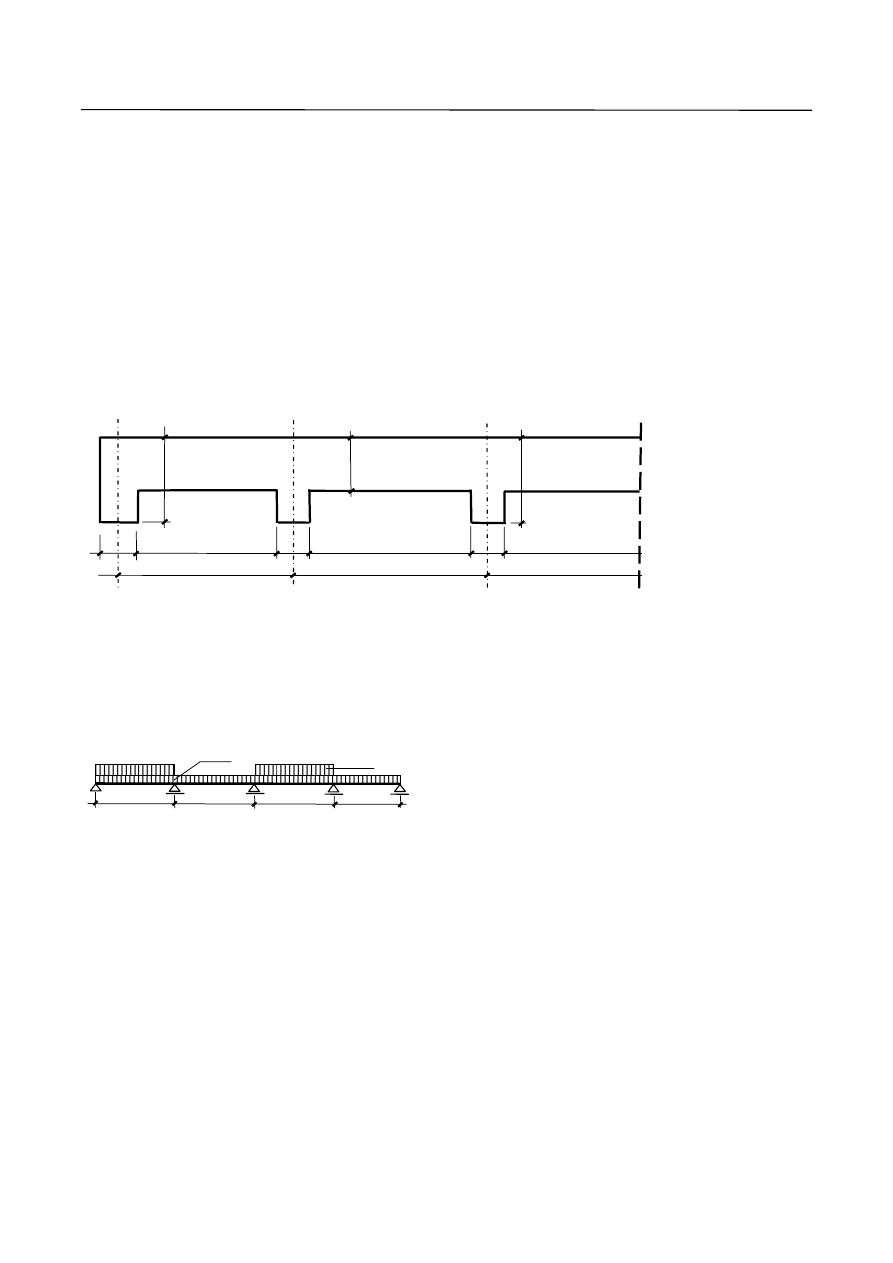
C. Wyznaczenie obwiedni sił tnących i momentów zginających od obciążeń obliczeniowych

Wartości sił tnących i momentów zaginających wyznaczono przy wykorzystaniu Tablic Winklera.

Schemat 1

l

eff1

A

B

C

B’

1

2

2’

1’

l

eff1

l

eff2

l

eff2

A

p

Sd

g

Sd

kNm

65

.

49

23

.

5

76

.

10

100

.

0

23

.

5

60

.

9

077

.

0

2

2

1

max

,

=

×

×

+

×

×

=

Sd

M

kNm

82

.

36

50

.

5

76

.

10

081

.

0

50

.

5

60

.

9

036

.

0

2

2

'

2

max

,

=

×

×

+

×

×

=

Sd

M

kNm

19

.

4

50

.

5

76

.

10

045

.

0

50

.

5

60

.

9

036

.

0

2

2

2

min

,

−

=

×

×

−

×

×

=

Sd

M

kNm

42

.

13

23

.

5

76

.

10

023

.

0

23

.

5

60

.

9

077

.

0

2

2

'

1

min

,

=

×

×

−

×

×

=

Sd

M

kN

83

.

44

23

.

5

76

.

10

446

.

0

23

.

5

60

.

9

393

.

0

=

×

×

+

×

×

=

SdA

V

kN

65

.

61

23

.

5

76

.

10

554

.

0

23

.

5

60

.

9

607

.

0

−

=

×

×

−

×

×

−

=

L

SdB

V

kN

37

.

29

50

.

5

76

.

10

018

.

0

50

.

5

60

.

9

536

.

0

=

×

×

+

×

×

=

P

SdB

V

kN

43

.

23

50

.

5

76

.

10

018

.

0

50

.

5

60

.

9

464

.

0

−

=

×

×

+

×

×

−

=

L

SdC

V

kN

02

.

53

50

.

5

76

.

10

482

.

0

50

.

5

60

.

9

464

.

0

=

×

×

+

×

×

=

P

SdC

V

kN

96

.

58

50

.

5

76

.

10

518

.

0

50

.

5

60

.

9

536

.

0

'

−

=

×

×

−

×

×

−

=

L

SdB

V

kN

52

.

33

23

.

5

76

.

10

054

.

0

23

.

5

60

.

9

607

.

0

'

=

×

×

+

×

×

=

P

SdB

V

Budynek o konstrukcji mieszanej – wersja 2007

Dr inż. Maria WŁODARCZYK

Projekt techniczny STUDENT

Dr inż. Barbara GOSZCZYŃSKA

Do użytku wewnętrznego. Na prawach rękopisu.

52

kN

69

.

16

23

.

5

76

.

10

054

.

0

23

.

5

60

.

9

393

.

0

'

=

×

×

−

×

×

=

SdA

V

Schemat 2

l

eff1

A

B

C

B’

1

2

2’

1’

l

eff1

l

eff2

l

eff2

A

p

Sd

g

Sd

kNm

04

.

67

2

5

.

5

23

.

5

76

.

10

121

.

0

2

5

.

5

23

.

5

60

.

9

107

.

0

2

2

max

,

−

=













+

×

×

−













+

×

×

−

=

B

Sd

M

kN

12

.

41

23

.

5

76

.

10

380

.

0

23

.

5

60

.

9

393

.

0

=

×

×

+

×

×

=

SdA

V

kN

37

.

65

23

.

5

76

.

10

620

.

0

23

.

5

60

.

9

607

.

0

−

=

×

×

−

×

×

−

=

L

SdB

V

kN

99

.

63

50

.

5

76

.

10

603

.

0

50

.

5

60

.

9

536

.

0

=

×

×

+

×

×

=

P

SdB

V

kN

99

.

47

50

.

5

76

.

10

397

.

0

50

.

5

60

.

9

464

.

0

−

=

×

×

−

×

×

−

=

L

SdC

V

kN

13

.

22

50

.

5

76

.

10

040

.

0

50

.

5

60

.

9

464

.

0

=

×

×

−

×

×

=

P

SdC

V

kN

67

.

30

50

.

5

76

.

10

040

.

0

50

.

5

60

.

9

536

.

0

'

−

=

×

×

−

×

×

−

=

L

SdB

V

kN

88

.

61

23

.

5

76

.

10

558

.

0

23

.

5

60

.

9

607

.

0

'

=

×

×

+

×

×

=

P

SdB

V

kN

61

.

44

23

.

5

76

.

10

442

.

0

23

.

5

60

.

9

393

.

0

'

=

×

×

+

×

×

=

SdA

V

Schemat 3

l

eff1

A

B

C

B’

1

2

2’

1’

l

eff1

l

eff2

l

eff2

A

p

Sd

g

Sd

kNm

77

.

9

2

5

.

5

23

.

5

76

.

10

013

.

0

2

5

.

5

23

.

5

60

.

9

107

.

0

2

2

min

,

−

=













+

×

×

−













+

×

×

−

=

B

Sd

M

kN

46

.

20

23

.

5

76

.

10

013

.

0

23

.

5

60

.

9

393

.

0

=

×

×

+

×

×

=

SdA

V

kN

21

.

31

23

.

5

76

.

10

013

.

0

23

.

5

60

.

9

607

.

0

−

=

×

×

−

×

×

−

=

L

SdB

V

kN

27

.

32

50

.

5

76

.

10

067

.

0

50

.

5

60

.

9

536

.

0

=

×

×

+

×

×

=

P

SdB

V

kN

53

.

20

50

.

5

76

.

10

067

.

0

50

.

5

60

.

9

464

.

0

−

=

×

×

+

×

×

−

=

L

SdC

V

kN

33

.

5

50

.

5

76

.

10

504

.

0

50

.

5

60

.

9

464

.

0

−

=

×

×

−

×

×

=

P

SdC

V

kN

05

.

1

50

.

5

76

.

10

496

.

0

50

.

5

60

.

9

536

.

0

'

=

×

×

+

×

×

−

=

L

SdB

V

kN

72

.

27

23

.

5

76

.

10

049

.

0

23

.

5

60

.

9

607

.

0

'

=

×

×

−

×

×

=

P

SdB

V

kN

97

.

16

23

.

5

76

.

10

049

.

0

23

.

5

60

.

9

393

.

0

'

=

×

×

−

×

×

=

SdA

V

Schemat 4

l

eff1

A

B

C

B’

1

2

2’

1’

l

eff1

l

eff2

l

eff2

A

p

Sd

g

Sd

kNm

45

.

55

5

.

5

76

.

10

107

.

0

50

.

5

60

.

9

071

.

0

2

2

max

,

−

=

×

×

−

×

×

−

=

C

Sd

M

kN

71

.

17

23

.

5

76

.

10

036

.

0

23

.

5

60

.

9

393

.

0

=

×

×

−

×

×

=

SdA

V

kN

50

.

32

23

.

5

76

.

10

036

.

0

23

.

5

60

.

9

607

.

0

−

=

×

×

−

×

×

−

=

L

SdB

V

kN

69

.

53

50

.

5

76

.

10

429

.

0

50

.

5

60

.

9

536

.

0

=

×

×

+

×

×

=

P

SdB

V

Budynek o konstrukcji mieszanej – wersja 2007

Dr inż. Maria WŁODARCZYK

Projekt techniczny STUDENT

Dr inż. Barbara GOSZCZYŃSKA

Do użytku wewnętrznego. Na prawach rękopisu.

53

kN

29

.

58

50

.

5

76

.

10

571

.

0

50

.

5

60

.

9

464

.

0

−

=

×

×

−

×

×

−

=

L

SdC

V

kN

29

.

58

50

.

5

76

.

10

571

.

0

50

.

5

60

.

9

464

.

0

=

×

×

+

×

×

=

P

SdC

V

kN

69

.

53

50

.

5

76

.

10

429

.

0

50

.

5

60

.

9

536

.

0

'

−

=

×

×

−

×

×

−

=

L

SdB

V

kN

50

.

32

23

.

5

76

.

10

036

.

0

23

.

5

60

.

9

607

.

0

'

=

×

×

+

×

×

=

P

SdB

V

kN

17

.

17

23

.

5

76

.

10

036

.

0

23

.

5

60

.

9

393

.

0

'

=

×

×

−

×

×

=

SdA

V

Schemat 5

l

eff1

A

B

C

B’

1

2

2’

1’

l

eff1

l

eff2

l

eff2

A

p

Sd

g

Sd

kNm

90

.

8

5

.

5

76

.

10

018

.

0

50

.

5

60

.

9

071

.

0

2

2

min

,

−

=

×

×

+

×

×

−

=

C

Sd

M

kN

87

.

43

23

.

5

67

.

10

004

.

0

23

.

5

76

.

10

433

.

0

23

.

5

60

.

9

393

.

0

=

×

×

−

×

×

+

×

×

=

SdA

V

kN

16

.

62

23

.

5

76

.

10

004

.

0

23

.

5

76

.

10

567

.

0

23

.

5

60

.

9

607

.

0

−

=

×

×

+

×

×

−

×

×

−

=

L

SdB

V

kN

03

.

32

50

.

5

76

.

10

022

.

0

50

.

5

76

.

10

085

.

0

50

.

5

60

.

9

536

.

0

=

×

×

−

×

×

+

×

×

=

P

SdB

V

kN

77

.

20

50

.

5

76

.

10

022

.

0

50

.

5

76

.

10

085

.

0

50

.

5

60

.

9

464

.

0

−

=

×

×

−

×

×

+

×

×

−

=

L

SdC

V

kN

77

.

20

50

.

5

76

.

10

022

.

0

50

.

5

76

.

10

085

.

0

50

.

5

60

.

9

464

.

0

=

×

×

+

×

×

−

×

×

=

P

SdC

V

kN

03

.

32

50

.

5

76

.

10

022

.

0

50

.

5

76

.

10

085

.

0

50

.

5

60

.

9

536

.

0

'

−

=

×

×

+

×

×

−

×

×

−

=

L

SdB

V

kN

16

.

62

23

.

5

76

.

10

567

.

0

23

.

5

76

.

10

004

.

0

23

.

5

60

.

9

607

.

0

'

=

×

×

+

×

×

−

×

×

=

P

SdB

V

kN

87

.

43

23

.

5

76

.

10

433

.

0

23

.

5

76

.

10

004

.

0

23

.

5

60

.

9

393

.

0

'

=

×

×

+

×

×

−

×

×

=

SdA

V

Obwiednia momentów zginających: kNm]

[

Sd

M

Obwiednia sił tnących: kN]

[

Sd

V

44.83

63.99

65.37

20.77

17.71

58.29

32.27

17.71

44.83

20.77

58.29

63.99

32.27

65.37

31.27

31.27

D. Dane materiałowe
Beton C20/25:

MPa

20

=

ck

f

, MPa

3

.

13

=

cd

f

, MPa

2

.

2

=

ctm

f

, MPa

0

.

1

=

ctd

f

, GPa

30

=

cm

E

Stal AII (18G2):

MPa

355

=

yk

f

, MPa

310

=

yd

f

, GPa

200

=

s

E

, 0.55

lim

,

=

eff

ξ

E. Przekrój

cm

0

.

8

=

f

h

cm

0

.

40

=

h

cm

20

=

w

b

cm

0

.

4

40

1

.

0

1

=

×

=

a

cm

36.0

0

.

4

0

.

40

=

−

=

d

Wyznaczenie szerokości płyty współpracującej z belką:

b

eff

A

s1

h

f

b

w

d

a

1

h

13.45

13.45

67.04

67.04

4.19

4.19

49.65

49.65

36.82

36.82

9.77

9.77

8.90

55.45

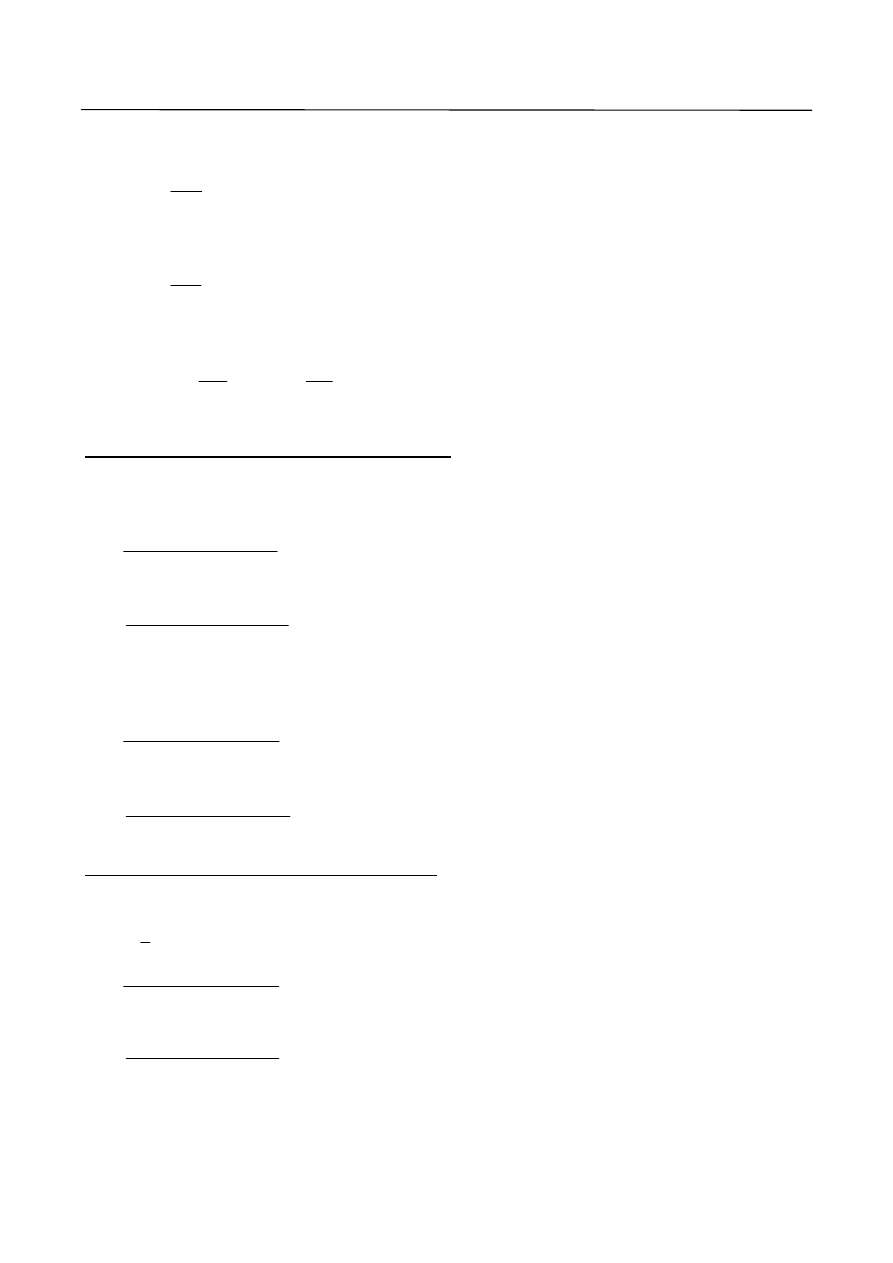
Budynek o konstrukcji mieszanej – wersja 2007

Dr inż. Maria WŁODARCZYK

Projekt techniczny STUDENT

Dr inż. Barbara GOSZCZYŃSKA

Do użytku wewnętrznego. Na prawach rękopisu.

54

- dla przęsła skrajnego

m

46

.

4

23

.

5

85

.

0

0

=

×

=

l







=

×

+

×

+

=

×

+

×

+

≤

=

+

=

m

1.16

0.08

6

0.08

6

0.2

m

2.15

2.10

0.5

1.81

0.5

0.2

m

09

.

1

5

46

.

4

20

.

0

eff

b

- dla przęsła środkowego

3.85m

50

.

5

7

.

0

0

=

×

=

l







=

+

≤

=

+

=

m

1.16

m

2.30

2.10

0.2

m

97

.

0

5

85

.

3

20

.

0

eff

b

Minimalne pole powierzchni zbrojenia rozciąganego











=

×

×

×

=

=

×

×

=

=

2

2

min

,

1

cm

16

.

1

36

20

355

2

.

2

26

.

0

26

.

0

cm

94

.

0

36

20

0013

.

0

0013

.

0

bd

f

f

bd

A

yk

ctm

s

F. Wymiarowanie ze względu na zginanie
Wymiarowanie na momenty maksymalne przęsłowe

Przęsło 1:

kNm

65

.

49

=

Sd

M

Zakładamy:

f

eff

h

x

≤

027

.

0

026

.

0

10

3

.

13

36

.

0

09

.

1

65

.

49

3

2

=

→

=

×

×

×

=

eff

cc

s

ξ

cm

8

cm

97

.

0

36

027

.

0

=

<

=

×

=

eff

eff

x

x

min

,

1

2

2

4

3

3

1

cm

54

.

4

m

10

54

.

4

10

310

10

3

.

13

09

.

1

0097

.

0

s

s

A

A

>

=

×

=

×

×

×

×

=

−

Przęsło 2:

kNm

82

.

36

=

Sd

M

Zakładamy:

f

eff

h

x

≤

022

.

0

022

.

0

10

3

.

13

36

.

0

97

.

0

82

.

36

3

2

=

→

=

×

×

×

=

eff

cc

s

ξ

cm

8

cm

79

.

0

36

022

.

0

=

<

=

×

=

eff

eff

x

x

min

,

1

2

2

4

3

3

1

cm

29

.

3

m

10

29

.

3

10

310

10

3

.

13

97

.

0

0079

.

0

s

s

A

A

>

=

×

=

×

×

×

×

=

−

Wymiarowanie na momenty minimalne przęsłowe

Przęsło 2:

kNm

19

.

4

=

Sd

M

(

)

Sd

zast

M

M

kNm

74

.

23

04

.

67

19

.

4

3

1

>

=

+

=

964

.

0

071

.

0

069

.

0

10

3

.

13

36

.

0

20

.

0

74

.

23

lim

,

3

2

=

<

=

→

=

×

×

×

=

eff

eff

eff

cc

s

ζ

ξ

ξ

min

,

1

2

2

4

3

1

cm

21

.

2

m

10

21

.

2

10

310

36

.

0

964

.

0

74

.

23

s

s

A

A

>

=

×

=

×

×

×

=

−

Budynek o konstrukcji mieszanej – wersja 2007

Dr inż. Maria WŁODARCZYK

Projekt techniczny STUDENT

Dr inż. Barbara GOSZCZYŃSKA

Do użytku wewnętrznego. Na prawach rękopisu.

55

Wymiarowanie na momenty maksymalne podporowe
Podpora B:

kNm

04

.

67

=

Sd

M

W osi podpory

cm

17

.

44

6

25

40

'

=

+

=

h

cm

42

.

4

1

=

a

cm

75

.

39

42

.

4

17

.

44

'

=

−

=

d

913

.

0

175

.

0

160

.

0

10

3

.

13

3975

.

0

2

.

0

04

.

67

eff

lim

,

3

2

=

<

=

→

=

×

×

×

=

ζ

ξ

ξ

eff

eff

cc

s

min

,

1

2

2

4

3

1

cm

96

.

5

m

10

96

.

5

10

310

3975

.

0

913

.

0

04

.

67

s

s

A

A

>

=

×

=

×

×

×

=

−

Na krawędzi podpory

kN

04

.

59

99

.

63

25

.

0

5

.

0

04

.

67

=

×

×

−

=

kr

M

905

.

0

189

.

0

171

.

0

10

3

.

13

36

.

0

2

.

0

04

.

59

eff

lim

,

3

2

=

<

=

→

=

×

×

×

=

ζ

ξ

ξ

eff

eff

cc

s

min

,

1

2

2

4

3

1

cm

84

.

5

m

10

84

.

5

10

310

36

.

0

905

.

0

04

.

59

s

s

A

A

>

=

×

=

×

×

×

=

−

Podpora C:

kNm

45

.

55

=

Sd

M

W osi podpory

929

.

0

142

.

0

132

.

0

10

3

.

13

3975

.

0

2

.

0

45

.

55

eff

lim

,

3

2

=

<

=

→

=

×

×

×

=

ζ

ξ

ξ

eff

eff

cc

s

min

,

1

2

2

4

3

1

cm

84

.

4

m

10

84

.

4

10

310

3975

.

0

929

.

0

45

.

55

s

s

A

A

>

=

×

=

×

×

×

=

−

Na krawędzi podpory

kN

16

.

48

29

.

58

25

.

0

5

.

0

45

.

55

=

×

×

−

=

kr

M

924

.

0

151

.

0

140

.

0

10

3

.

13

36

.

0

2

.

0

16

.

48

eff

lim

,

3

2

=

<

=

→

=

×

×

×

=

ζ

ξ

ξ

eff

eff

cc

s

min

,

1

2

2

4

3

1

cm

67

.

4

m

10

67

.

4

10

310

36

.

0

924

.

0

16

.

48

s

s

A

A

>

=

×

=

×

×

×

=

−

G. Sprawdzenie szerokości rys prostopadłych do osi żebra
Dopuszczalną szerokość rys sprawdzono zgodnie z załącznikiem D,

2002

:

03264

B

PN

−

−

Dopuszczalna szerokość rysy:

mm

3

.

0

lim

=

w

Przęsło 1
Moment maksymalny wywołany obciążeniami charakterystycznymi

kNm

19

.

40

23

.

5

28

.

8

100

.

0

23

.

5

33

.

8

077

.

0

2

2

1

max

,

=

×

×

+

×

×

=

Sd

M

85

.

0

%

63

.

0

%

100

36

20

54

.

4

=

→

=

×

×

=

ζ

ρ

MPa

30

.

289

kPa

87

.

289294

10

54

.

4

36

.

0

85

.

0

19

.

40

4

1

=

=

×

×

×

=

=

−

s

Sd

s

dA

M

ζ

σ

A

s1

h

h’

M

Sd

1:3

1:3

Budynek o konstrukcji mieszanej – wersja 2007

Dr inż. Maria WŁODARCZYK

Projekt techniczny STUDENT

Dr inż. Barbara GOSZCZYŃSKA

Do użytku wewnętrznego. Na prawach rękopisu.

56

Średnica zbrojenia dla

MPa

275

=

s

σ

(

)

mm

12

.

19

16

5

.

0

63

.

0

50

.

0

75

.

0

16

22

=

+

−

×

−

−

=

φ

Średnica zbrojenia dla

MPa

300

=

s

σ

(

)

mm

12

.

17

14

5

.

0

63

.

0

50

.

0

75

.

0

14

20

=

+

−

×

−

−

=

φ

Średnica zbrojenia dla

MPa

30

.

289

=

s

σ

(

)

mm

98

.

17

12

.

19

275

30

.

289

275

300

12

.

19

12

.

17

=

+

−

×

−

−

=

φ

Maksymalna średnica jaką można zastosować wynosi 16 mm

Przęsło 2
Moment maksymalny wywołany obciążeniami charakterystycznymi

kNm

34

.

29

50

.

5

28

.

8

081

.

0

50

.

5

33

.

8

036

.

0

2

2

2

max

,

=

×

×

+

×

×

=

Sd

M

9

.

0

%

46

.

0

%

100

36

20

29

.

3

=

→

=

×

×

=

ζ

ρ

MPa

24

.

275

kPa

85

.

275244

10

29

.

3

36

.

0

9

.

0

34

.

29

4

=

=

×

×

×

=

−

s

σ

Średnica zbrojenia dla

MPa

250

=

s

σ

(

)

mm

04

.

17

12

25

.

0

46

.

0

25

.

0

5

.

0

12

18

=

+

−

×

−

−

=

φ

Średnica zbrojenia dla

MPa

275

=

s

σ

(

)

mm

04

.

15

10

50

.

0

46

.

0

25

.

0

50

.

0

10

16

=

+

−

×

−

−

=

φ

Średnica zbrojenia dla

MPa

24

.

275

=

s

σ

(

)

mm

02

.

15

04

.

17

250

24

.

275

250

275

04

.

17

04

.

15

=

+

−

×

−

−

=

φ

Maksymalna średnica jaką można zastosować wynosi 14 mm

H. Dobór zbrojenia

Niedozbrojenie

: 2.5% A

s1

[cm

2

/m]

Przezbrojenie:

10%

Zbrojenie dobrane

Przęsło 1

4.43

4.54

4.99

3

φ 14 o A

s1,prov

=4.62 cm

2

Przęsła 2

3.21

3.29

3.62

3

φ 14 o A

s1,prov

=4.62 cm

2

Podpora B

5.81

5.96

6.56

4

φ 14 o A

s1,prov

=6.16 cm

2

Podpora C

4.74

4.86

5.35

4

φ 14 o A

s1,prov

=6.16 cm

2

Przęsło 2

(zbrojenie

wyznaczone dla momentu
minimalnego)

2.15 2.21 2.43

2

φ 14 o A

s1,prov

=3.08 cm

2

I. Wymiarowanie na ścinanie

Podpora A:

kN

83

.

44

=

Sd

V

0

.

1

24

.

1

36

.

0

6

.

1

6

.

1

>

=

−

=

−

=

d

k

01

.

0

006

.

0

36

20

62

.

4

<

=

×

=

=

d

b

A

w

sL

L

ρ

(

)

(

)

kN

51

.

45

36

.

0

20

.

0

006

.

0

40

2

.

1

10

0

.

1

24

.

1

35

.

0

40

2

.

1

35

.

0

kN

83

.

44

3

1

=

=

×

×

×

+

×

×

×

×

=

+

=

<

=

d

b

kf

V

V

w

L

ctd

Rd

Sd

ρ

Budynek o konstrukcji mieszanej – wersja 2007

Dr inż. Maria WŁODARCZYK

Projekt techniczny STUDENT

Dr inż. Barbara GOSZCZYŃSKA

Do użytku wewnętrznego. Na prawach rękopisu.

57

cm

4

.

32

36

9

.

0

9

.

0

=

×

=

=

d

z

55

.

0

250

20

1

6

.

0

250

1

6

.

0

=











 −

×

=











 −

=

ck

f

ν

kN

71

.

260

324

.

0

22

.

0

10

3

.

13

55

.

0

5

.

0

5

.

0

kN

83

.

44

3

2

=

×

×

×

×

×

=

=

<

=

z

b

f

V

V

w

cd

Rd

Sd

ν

Występuje odcinek I rodzaju nie ma konieczności stosowania zbrojenia na siły poprzeczne
Średnica strzemion







=

×

≥

mm

4.5

mm

8

.

2

14

2

.

0

w

φ

Maksymalny rozstaw strzemion
- w kierunku podłużnym







=

×

=

≤

cm

40

cm

27

36

75

.

0

75

.

0

max

d

s

- w kierunku poprzecznym





 =

≤

cm

60

cm

36

max

d

s

Podpora B z lewej strony:

kN

45

.

62

=

Sd

V

01

.

0

009

.

0

36

20

16

.

6

<

=

×

=

L

ρ

(

)

kN

19

.

48

36

.

0

20

.

0

009

.

0

40

2

.

1

10

0

.

1

24

.

1

35

.

0

kN

45

.

62

3

1

=

×

×

×

+

×

×

×

×

=

>

=

Rd

Sd

V

V

kN

71

.

260

324

.

0

22

.

0

10

3

.

13

55

.

0

5

.

0

kN

45

.

62

3

2

=

×

×

×

×

×

=

<

=

Rd

Sd

V

V

Jako zbrojenie na ścinanie zastosowano strzemiona dwuramienne o średnicy 6 mm ze stali AII (18G2) o

2

1

cm

56

.

0

=

sw

A

, MPa

310

1

=

ywd

f

, MPa

355

=

yk

f

;

Przyjęto: 0

.

1

cot

=

θ

cm

9

m

090

.

0

0

.

1

324

.

0

45

.

62

10

310

10

56

.

0

cot

3

4

1

1

1

=

=

×

×

×

×

×

=

=

−

θ

z

V

f

A

s

Sd

ywd

sw

Rozstaw strzemion przyjęto: cm

9

1

=

s

001

.

0

355

20

08

.

0

08

.

0

003

.

0

20

9

56

.

0

min

,

1

1

1

=

=

=

>

=

×

=

=

yk

ck

w

w

sw

w

f

f

b

s

A

ρ

ρ

Długość odcinka ścinania na którym należy zastosować zagęszczony rozstaw strzemion

m

324

.

0

0

.

1

324

.

0

cot

m

70

.

0

36

.

20

19

.

48

45

.

62

1

2

=

×

=

>

=

−

=

−

=

θ

z

q

V

V

a

Sd

Rd

Sd

w

Sprawdzenie ze względu na zmiażdżenie krzyżulców betonowych

kN

71

.

260

1

1

1

324

.

0

20

.

0

10

3

.

13

55

.

0

cot

1

cot

kN

45

.

62

2

3

2

2

=

+

×

×

×

×

×

=

+

=

<

=

θ

θ

ν

z

b

f

V

V

w

cd

Rd

Sd

Sprawdzenie nośności rozciąganego zbrojenia podłużnego w strefie przypodporowej

kN

14

.

238

0

.

1

45

.

62

5

.

0

324

.

0

04

.

67

cot

5

.

0

=

×

×

+

=

+

=

θ

Sd

Sd

td

V

z

M

F

>

kN

190.96

10

310

10

16

.

6

3

4

1

=

×

×

×

=

=

−

yd

s

s

f

A

F

Należy dozbroić strefę przypodporową ze względu na nośność pasa rozciąganego kratownicy

kN

18

.

47

96

.

190

14

.

238

=

−

=

−

=

s

td

s

F

F

F

∆

2

2

4

3

cm

52

.

1

m

10

52

.

1

10

310

18

.

47

=

×

=

×

=

=

−

yd

s

s

f

F

A

∆

∆

Jako dodatkowe zbrojnie zastosowano 14

1

φ

o

2

cm

54

.

1

=

s

A

Budynek o konstrukcji mieszanej – wersja 2007

Dr inż. Maria WŁODARCZYK

Projekt techniczny STUDENT

Dr inż. Barbara GOSZCZYŃSKA

Do użytku wewnętrznego. Na prawach rękopisu.

58

kN

14

.

238

=

td

F

<

(

)

kN

238.7

10

310

10

54

.

1

16

.

6

)

(

3

4

1

=

×

×

×

+

=

+

=

−

yd

s

s

s

f

A

A

F

∆

Sprawdzenie ze względu na rysy ukośne

kPa

36

.

867

36

.

0

20

.

0

45

.

62

=

×

=

=

d

b

V

w

Sd

τ

67

.

466

6

7

.

0

003

.

0

3

1

3

1

1

1

1

=









×

=













=

φ

η

ρ

λ

w

mm

3

.

0

mm

117

.

0

10

20

10

200

003

.

0

67

.

466

36

.

867

4

4

lim

3

6

2

2

=

<

=

×

×

×

×

×

×

=

=

w

f

E

w

ck

s

w

k

ρ

λ

τ

Podpora B z prawej strony:

kN

99

.

63

=

Sd

V

kN

19

.

48

1

=

Rd

V

<

kN

71

.

260

kN

99

.

63

2

=

<

=

Rd

Sd

V

V

Jako zbrojenie na ścinanie zastosowano strzemiona dwuramienne o średnicy 6 mm ze stali AII (18G2)
Przyjęto: 0

.

1

cot

=

θ

cm

8.7

m

087

.

0

0

.

1

324

.

0

99

.

63

10

310

10

56

.

0

3

4

1

=

=

×

×

×

×

×

=

−

s

Rozstaw strzemion przyjęto: cm

8

1

=

s

001

.

0

355

20

08

.

0

004

.

0

20

8

56

.

0

min

,

1

=

=

>

=

×

=

w

w

ρ

ρ

Długość odcinka ścinania na którym należy zastosować zagęszczony rozstaw strzemion

m

324

.

0

m

78

.

0

36

.

20

19

.

48

99

.

63

2

>

=

−

=

w

a

Sprawdzenie ze względu na zmiażdżenie krzyżulców betonowych

kN

71

.

260

kN

99

.

63

2

=

<

=

Rd

Sd

V

V

Sprawdzenie nośności rozciąganego zbrojenia podłużnego w strefie przypodporowej

kN

7

.

238

0

.

1

99

.

63

5

.

0

324

.

0

04

.

67

cot

5

.

0

=

×

×

+

=

+

=

θ

Sd

Sd

td

V

z

M

F

≤

kN

238.7

=

s

F

Sprawdzenie ze względu na rysy ukośne

kPa

75

.

888

36

.

0

20

.

0

99

.

63

=

×

=

τ

350

6

7

.

0

004

.

0

3

1

3

1

1

1

1

=









×

=













=

φ

η

ρ

λ

w

mm

3

.

0

mm

069

.

0

10

20

10

200

004

.

0

350

75

.

888

4

4

lim

3

6

2

2

=

<

=

×

×

×

×

×

×

=

=

w

f

E

w

ck

s

w

k

ρ

λ

τ

Podpora C z lewej strony:

kN

29

.

58

=

Sd

V

01

.

0

009

.

0

36

20

16

.

6

<

=

×

=

L

ρ

(

)

kN

19

.

48

36

.

0

20

.

0

009

.

0

40

2

.

1

10

0

.

1

24

.

1

35

.

0

kN

29

.

58

3

1

=

×

×

×

+

×

×

×

×

=

>

=

Rd

Sd

V

V

kN

71

.

260

kN

29

.

58

2

=

<

=

Rd

Sd

V

V

Jako zbrojenie na ścinanie zastosowano strzemiona dwuramienne o średnicy 6 mm ze stali AII (18G2)
Przyjęto:

0

.

1

cot

=

θ

Budynek o konstrukcji mieszanej – wersja 2007

Dr inż. Maria WŁODARCZYK

Projekt techniczny STUDENT

Dr inż. Barbara GOSZCZYŃSKA

Do użytku wewnętrznego. Na prawach rękopisu.

59

cm

9.6

m

096

.

0

0

.

1

324

.

0

29

.

58

10

310

10

56

.

0

3

4

1

=

=

×

×

×

×

×

=

−

s

Rozstaw strzemion przyjęto:

cm

9

1

=

s

001

.

0

355

20

08

.

0

003

.

0

20

9

56

.

0

min

,

1

=

=

>

=

×

=

w

w

ρ

ρ

Długość odcinka ścinania na którym należy zastosować zagęszczony rozstaw strzemion

m

324

.

0

m

50

.

0

36

.

20

19

.

48

29

.

58

2

>

=

−

=

w

a

Sprawdzenie ze względu na zmiażdżenie krzyżulców betonowych

kN

71

.

260

kN

29

.

58

2

=

<

=

Rd

Sd

V

V

Sprawdzenie nośności rozciąganego zbrojenia podłużnego w strefie przypodporowej

kN

29

.

200

0

.

1

29

.

58

5

.

0

324

.

0

45

.

55

=

×

×

+

=

td

F

>

kN

190.96

10

310

10

16

.

6

3

4

1

=

×

×

×

=

=

−

yd

s

s

f

A

F

Należy dozbroić strefę przypodporową ze względu na nośność pasa rozciąganego kratownicy

kN

37

.

9

96

.

190

29

.

200

=

−

=

s

F

∆

2

2

4

3

cm

30

.

0

m

10

30

.

0

10

310

18

.

47

=

×

=

×

=

−

s

A

∆

Jako dodatkowe zbrojnie zastosowano 14

1

φ

o

2

cm

54

.

1

=

s

A

kN

29

.

200

=

td

F

<

(

)

kN

238.7

10

310

10

54

.

1

16

.

6

3

4

=

×

×

×

+

=

−

s

F

Sprawdzenie ze względu na rysy ukośne

kPa

58

.

809

36

.

0

20

.

0

29

.

58

=

×

=

=

d

b

V

w

Sd

τ

67

.

466

6

7

.

0

003

.

0

3

1

3

1

1

1

1

=









×

=













=

φ

η

ρ

λ

w

mm

3

.

0

mm

102

.

0

10

20

10

200

003

.

0

67

.

466

58

.

809

4

4

lim

3

6

2

2

=

<

=

×

×

×

×

×

×

=

=

w

f

E

w

ck

s

w

k

ρ

λ

τ

Maksymalny rozstaw strzemion na środkowych odcinkach żebra
- w kierunku podłużnym







=

×

=

≤

cm

40

cm

27

36

75

.

0

75

.

0

max

d

s

- w kierunku poprzecznym





 =

≤

cm

60

cm

36

max

d

s

J. Ścinanie między środnikiem a płytą

Uwaga:

W przykładzie pokazano przykładowo obliczenia dla podpory B. W projekcie należy sprawdzić w każdym

przekroju gdzie jest to konieczne.

Podpora B z lewej strony

kN

55.32

2

19

.

48

45

.

62

=

+

=

Sd

V

Półka rozciągana

kN

84

.

19

10

310

10

64

.

0

3

4

=

×

×

×

=

=

−

yd

s

d

f

A

F

∆

Budynek o konstrukcji mieszanej – wersja 2007

Dr inż. Maria WŁODARCZYK

Projekt techniczny STUDENT

Dr inż. Barbara GOSZCZYŃSKA

Do użytku wewnętrznego. Na prawach rękopisu.

60

kN

38

.

278

10

310

10

70

.

7

10

310

10

64

.

0

2

3

4

3

4

=

×

×

×

+

×

×

×

×

=

−

−

d

F

071

.

0

38

.

278

84

.

19

=

=

t

β

kN

17

.

12

324

.

0

32

.

55

071

.

0

=

×

=

=

z

V

V

Sd

t

Sd

β

≤ V

Rd2

=

kN

60

.

292

1

1

1

08

.

0

10

3

.

13

55

.

0

cot

1

cot

2

3

2

=

+

×

×

×

×

=

+

θ

θ

h

νf

f

cd

,

kN

17

.

12

=

Sd

V

kN

20

.

99

0

.

1

10

310

1

.

0

10

32

.

0

cot

3

4

3

=

×

×

×

×

=

=

≤

−

θ

f

s

A

V

yd

f

sf

Rd

K. Stan graniczny ugięcia żebra

Przęsło 1:

kNm

19

.

40

=

Sd

M

m

23

.

5

=

eff

l

%

63

.

0

%

100

36

20

54

.

4

=

×

×

=

ρ

MPa

30

.

289

=

s

σ

(

)

84

.

22

30

.

289

250

28

5

.

0

63

.

0

50

.

0

75

.

0

28

25

53

.

14

36

.

0

50

.

5

max

=

×









+

−

×

−

−

=













≤

=

=













d

l

d

l

eff

eff

Uwaga:

Stan graniczny ugięcia należy sprawdzić dla każdego przęsła

Poz. 2.3. Podciąg stropu

A. Obciążenia działające na podciąg

Obciążenia stałe i zmienne z poz. 2.3. projektu wstępnego.

B. Statyka
- Rozpiętości obliczeniowe należy wyznaczyć zgodnie z przepisami

2002

:

03264

B

PN

−

−

i opisanymi

w punkcie 3.1.

- Obwiednie momentów i sił tnących
Obwiednie momentów i sił tnących można wyznaczyć przy wykorzystaniu tablic Winklera. Żebro
wieloprzęsłowe o liczbie przęseł większej niż 5 to zamieniamy w obliczeniach statycznych na 5–przęsłowe.

C. Wymiarowanie na zginanie

Wymiarowanie na maksymalne momenty przęsłowe

Przy wymiarowaniu zginanych przekrojów przęsłowych należy uwzględnić współpracę płyty z podciągiem.

Uwaga

: Zbrojenie wyznaczamy dla każdego przęsła podciągu, gdyż zmieniają się wartości maksymalnych

momentów zginających.

Wymiarowanie na minimalne momenty przęsłowe

Patrz punkt 2.1. (C) projektu technicznego, str. 21.

Wymiarowanie na maksymalne momenty podporowe

Wymiarowanie na maksymalne momenty podporowe jak w przypadku żebra – projekt techniczny, poz. 2. 2.

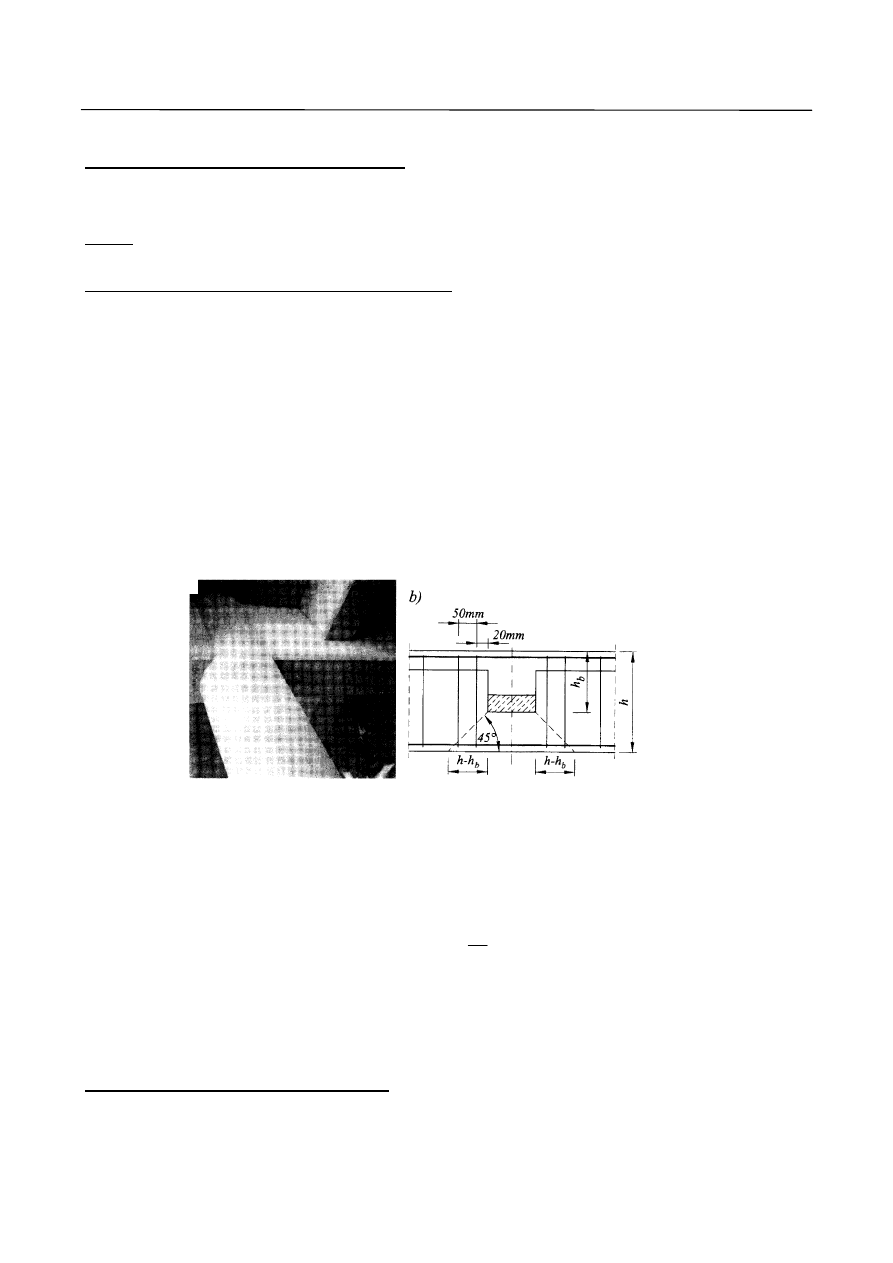
Budynek o konstrukcji mieszanej – wersja 2007

Dr inż. Maria WŁODARCZYK

Projekt techniczny STUDENT

Dr inż. Barbara GOSZCZYŃSKA

Do użytku wewnętrznego. Na prawach rękopisu.

61

D. Wymiarowanie na ścinanie

Wymiarowanie na maksymalne siły poprzeczne

Wymiarowanie na ścinanie należy wykonać zgodnie z obowiązującymi przepisami normowymi

2002

:

03264

B

PN

−

−

.

Uwaga

: Nośność na ścinanie sprawdzamy z każdej strony podpory i dla wszystkich podpór gdzie zmienia się

wartość siły tnącej V

Sd

.

Sprawdzenie ścinania pomiędzy środnikiem a półkami

Sprawdzenie ścinania pomiędzy środnikiem a pólkami jak w przypadku żebra – projekt techniczny poz. 2.2.

E. Połączenie żebra z podciągiem

W ustrojach płytowo żebrowych często zachodzi konieczność przekazywania reakcji belek drugorzędnych
(żeber) na belki główne (podciągi) w wyniku ich podwieszania lub zaczepiania na wysokości tych belek
(rys. 18). Ze względów konstrukcyjnych takie połączenie powinno być zabezpieczone dodatkowym
zbrojeniem poprzecznym, nie uwzględnionym w obliczeniach podciągu (z uwagi na siły poprzeczne). Liczba
strzemion zależy tu od wartości siły poprzecznej w podciągu w miejscu połączenia z belką drugorzędną.
Jeżeli obliczeniowa siła poprzeczna w miejscu połączenia

(

)

[

]

d

b

kf

V

V

w

cp

L

ctd

Rd

Sd

σ

ρ

14

.

0

40

2

.

1

35

.

0

1

+

+

=

≤

należy zastosować co najmniej cztery strzemiona jak na rysunku 18b.

Rys. 18. Połączenie belki głównej z drugorzędną: a) widok węzła w ustroju nośnym budynku,

b) rozmieszczenie dodatkowego zbrojenia poprzecznego w węźle.

Jeżeli warunek V

Sd

≤ V

Rd1

nie jest spełniony, to pole przekroju strzemion lub prętów odgiętych należy

obliczać z równania określającego przeniesienie przez to zbrojenie zredukowanej reakcji belki drugorzędnej
F

red

(przekazywanej na podciąg):

h

h

F

F

b

red

=

gdzie: F – reakcja żebra,

h

b

– wysokość belki drugorzędnej,

h – wysokość podciągu.

F. Sprawdzenie stanów granicznych użytkowalności

Sprawdzenie stanu granicznego zarysowania

Sprawdzenie szerokości rozwarcia rys prostopadłych do osi elementu jak w przypadku żebra – projekt
techniczny, poz. 2.2.

a)

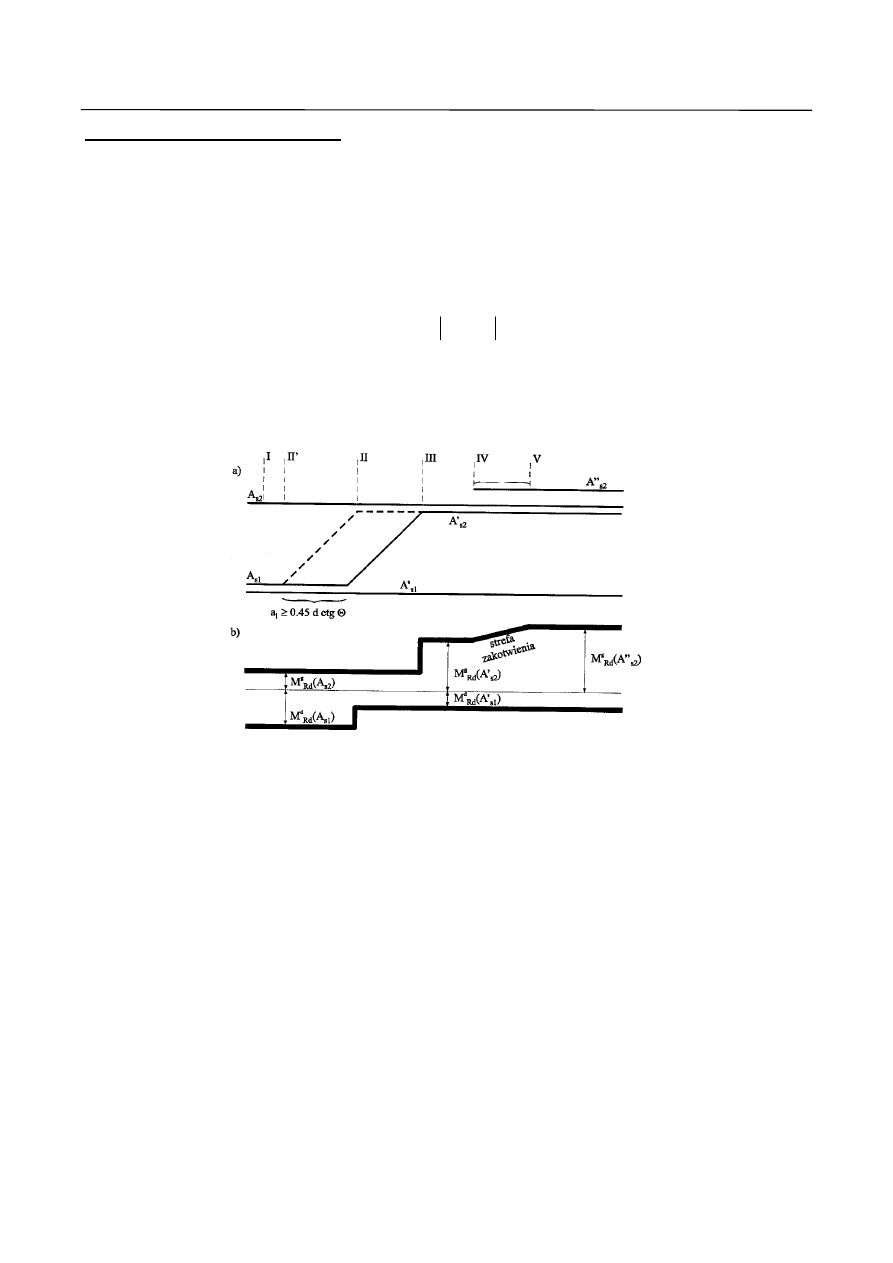
Budynek o konstrukcji mieszanej – wersja 2007

Dr inż. Maria WŁODARCZYK

Projekt techniczny STUDENT

Dr inż. Barbara GOSZCZYŃSKA

Do użytku wewnętrznego. Na prawach rękopisu.

62

Sprawdzenie stanu granicznego ugięć

Sprawdzenie stanu granicznego ugięć jak w przypadku żebra – projekt techniczny, poz. 2.2.
G. Dobór zbrojenia dla podciągu

Zbrojenie należy dobrać i rozmieścić w przekroju belki zgodnie z zgodnie z obowiązującymi przepisami
normowymi 2002

:

03264

B

PN

−

−

.

H. Sprawdzenie nośności ze względu na zginanie
Warunkiem spełnienia stanu granicznego nośności ze względu na zginanie jest spełnienie w każdym
przekroju zależności:

max

,

Sd

Rd

M

M

≥

.

Nośność obliczeniowa

Rd

M

musi być w każdym przekroju co najmniej równa momentowi obliczeniowemu

max

,

Sd

M

. Dopuszcza się niedobór nośności nie przekraczający jednak

%

5

.

2

. Ogólne zasady konstruowania

wykresu nośności przedstawiono na rysunku 19.

Rys. 19. Konstruowanie wykresu nośności: a) fragment układu zbrojenia, b) obwiednia nośności.

W przekroju I nośność jest determinowana przez zbrojenie w strefie dolnej A

s1

i górnej A

s2

. Pręt odgięty

w przekroju II zmniejsza skokowo nośność przekroju

d

Rd

M

. Pojawia się on w górnych włóknach przekroju

III (

'

2

s

A

) i powoduje skok w górnej obwiedni nośności

g

Rd

M

.Przesunięcie obwiedni o długość a

l

ma miejsce

wówczas, gdy pręt, który pierwotnie miał zostać odgięty w miejscu oznaczonym linią przerywaną (II’),
został w tym miejscu uwzględniony jako zbrojenie „na ścinanie”. Obwiednia zostaje przesunięta do
przekroju II o odcinek a

l

(rys. 19). W przekroju IV pojawia się kolejny pręt górny, który powoduje

stopniowy wzrost

g

Rd

M

na długości zakotwienia l

bd

. W przekroju V cały przekrój

''

2

s

A

stanowi o nośności

g

Rd

M

. Podane zasady pozwalają konstruować zbrojenie na całej długości belki.

PRZYKAD

Poz. 2.3. Podciąg stropu

A. Obciążenia działające na żebro

G

pd

= 53.82 kN

G

Sdpd

= 61.73 kN

P

pd

= 45.54 kN

P

Sdpd

= 59.18 kN

l

bd

Budynek o konstrukcji mieszanej – wersja 2007

Dr inż. Maria WŁODARCZYK

Projekt techniczny STUDENT

Dr inż. Barbara GOSZCZYŃSKA

Do użytku wewnętrznego. Na prawach rękopisu.

63

B. Statyka

- Rozpiętości obliczeniowe

38

35

35

Poz. 4.2

60

l

1

=670

l

2

=690

l

2

=690

l

n2

=655

l

n2

=655

l

n2

=633.5

Poz. 4.3

(

)

(

)

30

;

19

min

60

5

.

0

;

38

5

.

0

min

1

=

×

×

=

n

a

(

)

(

)

30

;

5

.

17

min

60

5

.

0

;

35

5

.

0

min

2

=

×

×

=

n

a

m

70

.

6

175

.

0

335

.

6

19

.

0

1

=

+

+

=

eff

l

m

90

.

6

175

.

0

55

.

6

5

.

17

.

0

2

=

+

+

=

eff

l

C. Wyznaczenie obwiedni sił tnących i momentów zginających od obciążeń obliczeniowych

Wartości sił tnących i momentów zaginających wyznaczono przy wykorzystaniu Tablic Winklera.

Schemat 1

l

eff1

A

B

C

B’

1

2

2’

1’

l

eff1

l

eff2

l

eff2

A’

3

l

eff2

C’

G

Sd

P

Sd

kNm

29

.

174

2

90

.

6

70

.

6

18

.

59

140

.

0

2

90

.

6

70

.

6

73

.

61

281

.

0

−

=













+

×

×

−













+

×

×

−

=

SdB

M

kNm

75

.

132

90

.

6

18

.

59

105

.

0

70

.

6

73

.

61

211

.

0

,

−

=

×

×

−

×

×

−

=

C

Sd

M

Przęsło A-B

2.10

A

B

2.30

2.30

V

SdB

L

61.73 kN

59.18 kN

V

SdA

174.29 kNm

1

2

kN

31

.

143

0

70

.

6

29

.

174

40

.

4

91

.

120

10

.

2

91

.

120

:

0

=

→

=

×

−

+

×

+

×

=

∑

L

SdB

L

SdB

A

V

V

M

kN

51

.

98

0

2

91

.

120

:

0

=

→

=

×

+

+

=

∑

SdA

L

SdB

SdA

V

V

V

sił

kNm

87

.

206

1

.

2

51

.

98

1

=

×

=

M

kNm

35

.

155

3

.

2

91

.

120

4

.

4

51

.

98

2

=

×

−

×

=

M

A

B

22.40 kN

143.31 kN

1

2

98.51 kN

Przęsło B-C

A

B

206.87 kNm

174.29 kNm

1

2

155.35 kNm

Budynek o konstrukcji mieszanej – wersja 2007

Dr inż. Maria WŁODARCZYK

Projekt techniczny STUDENT

Dr inż. Barbara GOSZCZYŃSKA

Do użytku wewnętrznego. Na prawach rękopisu.

64

2.30

B

C

2.30

2.30

V

SdC

L

61.73 kN

V

SdB

P

132.75 kNm

3

4

174.29 kNm

kN

71

.

55

0

90

.

6

75

.

132

60

.

4

73

.

61

30

.

2

61.73

174.29

-

:

0

=

→

=

×

−

+

×

+

×

+

=

∑

L

SdC

L

SdC

B

V

V

M

kN

75

.

67

0

2

73

.

61

:

0

P

=

→

=

×

+

+

=

∑

P

SdB

L

SdC

SdB

V

V

V

sił

kNm

47

.

18

3

.

2

75

.

67

29

.

174

3

−

=

×

+

−

=

M

kNm

62

.

4

3

.

2

73

.

61

6

.

4

74

.

67

29

.

174

4

−

=

×

−

×

+

−

=

M

B

C

6.02 kN

55.71 kN

3

4

67.75 kN

Przęsło C-C’

2.30

C

C’

2.30

2.30

V

SdC’

L

61.73 kN

V

SdC

P

132.75 kNm

5

6

132.75 kNm

59.18 kN

kN

91

.

120

0

90

.

6

75

.

132

60

.

4

91

.

120

30

.

2

120.91

132.75

:

0

'

'

=

→

=

×

−

+

×

+

×

+

−

=

∑

L

SdC

L

SdC

C

V

V

M

kN

91

.

120

0

2

91

.

120

:

0

'

'

P

=

→

=

×

+

+

=

∑

P

SdC

L

SdC

SdC

V

V

V

sił

kNm

34

.

145

3

.

2

91

.

120

75

.

132

5

=

×

+

−

=

M

kNm

34

.

145

3

.

2

91

.

120

6

.

4

91

.

120

75

.

132

4

=

×

−

×

+

−

=

M

C

C’

5

6

120.91 kN

120.91 kN

W podobny sposób należy rozwiązać pozostałe kombinacje obciążeń zmiennych.
Po rozwiązaniu wszystkich kombinacji obciążeń sporządzono obwiednię momentów i sił tnących.

Obwiednia momentów zginających: kNm]

[

Sd

M

A

B

C

B’

206.87

A’

C’

206.87

155.35

155.35

102.92

102.92

78.88

78.88

23.29

23.29

246.33

246.33

117.65

117.65

131.50

131.50

18.47

18.47

4.62

4.62

211.15

211.15

113.15

113.15

145.34

9.23

Obwiednia sił tnących: kN]

[

Sd

V

B

C

18.47 kNm

174.29 kNm

3

4

4.62 kNm

132.75 kNm

C

C’

145.34 kNm

5

6

132.75 kNm

132.75 kNm

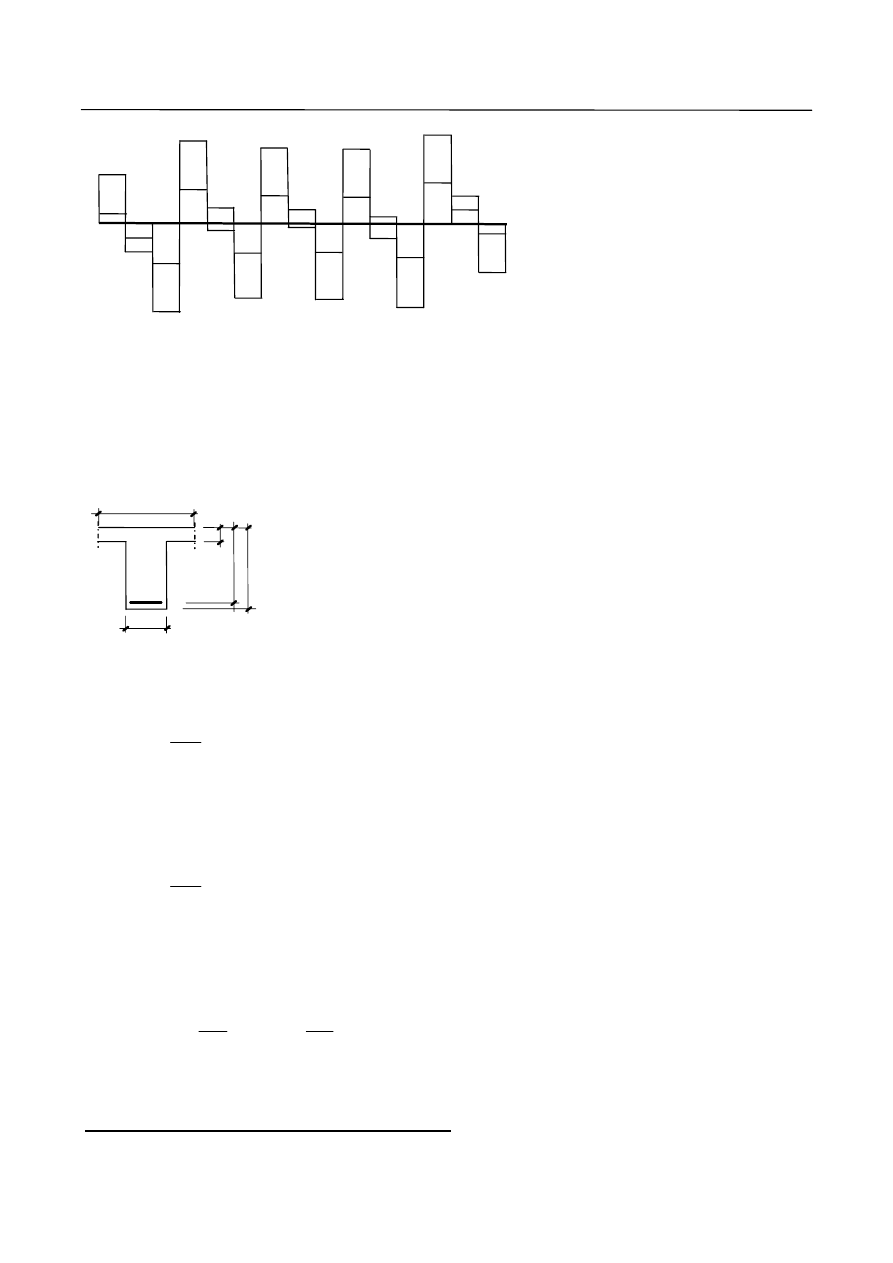
Budynek o konstrukcji mieszanej – wersja 2007

Dr inż. Maria WŁODARCZYK

Projekt techniczny STUDENT

Dr inż. Barbara GOSZCZYŃSKA

Do użytku wewnętrznego. Na prawach rękopisu.

65

A

B

C

B’

98.51

A’

C’

10.48

98.51

10.48

13.52

13.52

33.16

33.16

154.07

154.07

82.98

82.98

140.21

140.21

67.75

67.75

19.33

19.33

7.80

7.80

128.99

128.99

55.71

55.71

135.29

135.29

58.12

58.12

13.50

3.61

D. Dane materiałowe
Beton C20/25:

MPa

20

=

ck

f

, MPa

3

.

13

=

cd

f

, MPa

2

.

2

=

ctm

f

, MPa

0

.

1

=

ctd

f

, GPa

30

=

cm

E

Stal AIII (34GS):

MPa

410

=

yk

f

, MPa

350

=

yd

f

,

GPa

200

=

s

E

, 0.53

lim

,

=

eff

ξ

E. Przekrój

cm

0

.

8

=

f

h

cm

0

.

60

=

h

cm

0

.

25

=

w

b

cm

0

.

6

60

1

.

0

1

=

×

=

a

54.0cm

0

.

6

0

.

60

=

−

=

d

Wyznaczenie szerokości płyty współpracującej z belką:
- dla przęsła skrajnego

m

70

.

5

70

.

6

85

.

0

0

=

×

=

l







=

×

+

×

+

=

×

+

×

+

≤

=

+

=

m

1.21

0.08

6

0.08

6

0.25

m

5.52

5.30

0.5

5.30

0.5

0.25

m

39

.

1

5

70

.

5

25

.

0

eff

b

Ze względu na obciążenie siła skupioną zmniejszamy szerokość półki o 20%

m

97

.

0

21

.

1

2

.

0

21

.

1

'

=

×

−

=

eff

b

- dla przęsła środkowego

m

83

.

4

90

.

6

7

.

0

0

=

×

=

l







=

×

+

×

+

=

×

+

×

+

≤

=

+

=

m

1.21

0.08

6

0.08

6

0.25

m

5.52

5.30

0.5

5.30

0.5

0.25

m

22

.

1

5

83

.

4

25

.

0

eff

b

Ze względu na obciążenie siła skupioną zmniejszamy szerokość półki o 20%

m

97

.

0

21

.

1

2

.

0

21

.

1

'

=

×

−

=

eff

b

Minimalne pole powierzchni zbrojenia rozciąganego











=

×

×

×

=

=

×

×

=

=

2

2

min

,

1

cm

88

.

1

54

25

410

2

.

2

26

.

0

26

.

0

cm

76

.

1

54

25

0013

.

0

0013

.

0

bd

f

f

bd

A

yk

ctm

s

Dopuszczana szerokość rys:

mm

3

.

0

lim

=

w

F. Wymiarowanie ze względu na zginanie
Wymiarowanie na momenty maksymalne przęsłowe
Przęsło 1:

kNm

87

.

206

=

Sd

M

b

eff

A

s1

h

f

b

w

d

a

1

h

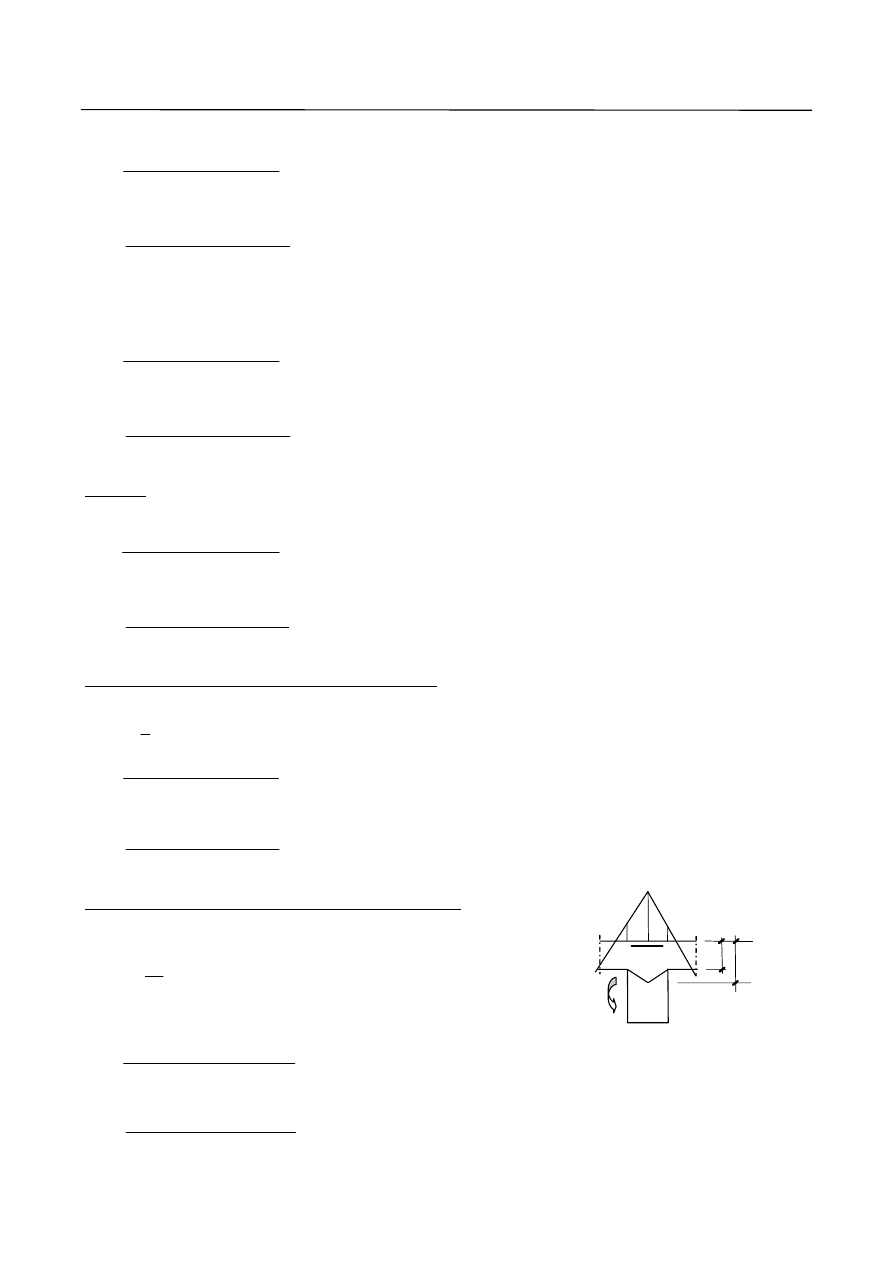
Budynek o konstrukcji mieszanej – wersja 2007

Dr inż. Maria WŁODARCZYK

Projekt techniczny STUDENT

Dr inż. Barbara GOSZCZYŃSKA

Do użytku wewnętrznego. Na prawach rękopisu.

66

Zakładamy:

f

eff

h

x

≤

057

.

0

055

.

0

10

3

.

13

54

.

0

97

.

0

87

.

206

3

2

=

→

=

×

×

×

=

eff

cc

s

ξ

cm

8

cm

08

.

3

54

057

.

0

=

<

=

×

=

eff

eff

x

x

min

,

1

2

2

4

3

3

1

cm

35

.

11

m

10

35

.

11

10

350

10

3

.

13

97

.

0

0308

.

0

s

s

A

A

>

=

×

=

×

×

×

×

=

−

Przęsło 2:

kNm

50

.

131

=

Sd

M

Zakładamy:

f

eff

h

x

≤

036

.

0

035

.

0

10

3

.

13

54

.

0

97

.

0

50

.

131

3

2

=

→

=

×

×

×

=

eff

cc

s

ξ

cm

8

cm

94

.

1

54

036

.

0

=

<

=

×

=

eff

eff

x

x

min

,

1

2

2

4

3

3

1

cm

16

.

7

m

10

16

.

7

10

350

10

3

.

13

97

.

0

0194

.

0

s

s

A

A

>

=

×

=

×

×

×

×

=

−

Przęsło 3:

kNm

34

.

145

=

Sd

M

Zakładamy:

f

eff

h

x

≤

039

.

0

039

.

0

10

3

.

13

54

.

0

97

.

0

34

.

145

3

2

=

→

=

×

×

×

=

eff

cc

s

ξ

cm

8

cm

11

.

2

54

039

.

0

=

<

=

×

=

eff

eff

x

x

min

,

1

2

2

4

3

3

1

cm

78

.

7

m

10

78

.

7

10

350

10

3

.

13

97

.

0

0211

.

0

s

s

A

A

>

=

×

=

×

×

×

×

=

−

Wymiarowanie na momenty minimalne przęsłowe
Przęsło 2:

kNm

47

.

18

=

Sd

M

(

)

Sd

zast

M

M

kNm

27

.

88

33

.

246

47

.

18

3

1

>

=

+

=

952

.

0

096

.

0

091

.

0

10

3

.

13

54

.

0

25

.

0

27

.

88

lim

,

3

2

=

<

=

→

=

×

×

×

=

eff

eff

eff

cc

s

ζ

ξ

ξ

min

,

1

2

2

4

3

1

cm

90

.

4

m

10

90

.

4

10

350

54

.

0

952

.

0

27

.

88

s

s

A

A

>

=

×

=

×

×

×

=

−

Wymiarowanie na momenty maksymalne podporowe
Podpora B:

kNm

33

.

246

=

Sd

M

W osi podpory

cm

83

.

65

6

35

60

'

=

+

=

h

cm

58

.

6

1

=

a

cm

25

.

59

58

.

6

38

.

65

'

=

−

=

d

880

.

0

240

.

0

211

.

0

10

3

.

13

5925

.

0

25

.

0

33

.

246

eff

lim

,

3

2

=

<

=

→

=

×

×

×

=

ζ

ξ

ξ

eff

eff

cc

s

min

,

1

2

2

4

3

1

cm

50

.

13

m

10

50

.

13

10

350

5925

.

0

880

.

0

33

.

246

s

s

A

A

>

=

×

=

×

×

×

=

−

A

s1

h

h’

M

Sd

1:3

1:3

Budynek o konstrukcji mieszanej – wersja 2007

Dr inż. Maria WŁODARCZYK

Projekt techniczny STUDENT

Dr inż. Barbara GOSZCZYŃSKA

Do użytku wewnętrznego. Na prawach rękopisu.

67

Na krawędzi podpory

kN

79

.

221

21

.

140

35

.

0

5

.

0

33

.

246

=

×

×

−

=

kr

M

868

.

0

263

.

0

229

.

0

10

3

.

13

54

.

0

25

.

0

79

.

221

eff

lim

,

3

2

=

<

=

→

=

×

×

×

=

ζ

ξ

ξ

eff

eff

cc

s

min

,

1

2

2

4

3

1

cm

52

.

13

m

10

52

.

13

10

350

54

.

0

868

.

0

79

.

221

s

s

A

A

>

=

×

=

×

×

×

=

−

Podpora C:

kNm

15

.

211

=

Sd

M

W osi podpory

899

.

0

201

.

0

181

.

0

10

3

.

13

5925

.

0

25

.

0

15

.

211

eff

lim

,

3

2

=

<

=

→

=

×

×

×

=

ζ

ξ

ξ

eff

eff

cc

s

min

,

1

2

2

4

3

1

cm

32

.

11

m

10

32

.

11

10

350

5925

.

0

899

.

0

15

.

211

s

s

A

A

>

=

×

=

×

×

×

=

−

Na krawędzi podpory

kN

58

.

188

99

.

128

35

.

0

5

.

0

15

.

211

=

×

×

−

=

kr

M

891

.

0

218

.

0

194

.

0

10

3

.

13

54

.

0

25

.

0

58

.

188

eff

lim

,

3

2

=

<

=

→

=

×

×

×

=

ζ

ξ

ξ

eff

eff

cc

s

min

,

1

2

2

4

3

1

cm

20

.

11

m

10

20

.

11

10

350

54

.

0

891

.

0

58

.

188

s

s

A

A

>

=

×

=

×

×

×

=

−

G. Dobór zbrojenia

Niedozbrojenie

: 2.5% A

s1

[cm

2

/m]

Przezbrojenie:

10%

Zbrojenie dobrane

Przęsło 1

11.07

11.35

12.49

4

φ 20 o A

s1,prov

=12.57 cm

2

Przęsła 2

6.98

7.16

7.88

3

φ 20o A

s1,prov

=9.43 cm

2

Przęsło 3

7.59

7.78

8.56

3

φ 20o A

s1,prov

=9.43 cm

2

Podpora B

13.18

13.52

14.87

5

φ 20 o A

s1,prov

=15.71 cm

2

Podpora C

11.04

11.32

12.45

4

φ 20 o A

s1,prov

=12.57 cm

2

Przęsło 2

(zbrojenie

wyznaczone dla momentu
minimalnego)

4.78 4.90 5.39

2

φ 20 o A

s1,prov

= 6.28 cm

2

H. Wymiarowanie na ścinanie
Podpora A:

kN

51

.

98

=

Sd

V

0

.

1

06

.

1

54

.

0

6

.

1

>

=

−

=

k

01

.

0

009

.

0

54

25

57

.

12

<

=

×

=

L

ρ

(

)

kN

13

.

78

54

.

0

25

.

0

009

.

0

40

2

.

1

10

0

.

1

06

.

1

35

.

0

kN

51

.

98

3

1

=

×

×

×

+

×

×

×

×

=

>

=

Rd

Sd

V

V

cm

6

.

48

54

9

.

0

=

×

=

z

55

.

0

250

20

1

6

.

0

=











 −

×

=

ν

kN

39

.

444

486

.

0

25

.

0

10

3

.

13

55

.

0

5

.

0

kN

51

.

98

3

2

=

×

×

×

×

×

=

<

=

Rd

Sd

V

V

Występuje odcinek II rodzaju należy zastosować zbrojenie na ścinanie

Budynek o konstrukcji mieszanej – wersja 2007

Dr inż. Maria WŁODARCZYK

Projekt techniczny STUDENT

Dr inż. Barbara GOSZCZYŃSKA

Do użytku wewnętrznego. Na prawach rękopisu.

68







=

×

≥

mm

4.5

mm

0

.

4

20

2

.

0

w

φ

Jako zbrojenie na ścinanie zastosowano strzemiona dwuramienne o średnicy 6 mm ze stali AII (18G2)
o

2

1

cm

56

.

0

=

sw

A

, MPa

310

1

=

ywd

f

, MPa

355

=

yk

f

;

Przyjęto:

0

.

1

cot

=

θ

cm

8.6

m

086

.

0

0

.

1

486

.

0

51

.

98

10

310

10

56

.

0

3

4

1

=

=

×

×

×

×

×

=

−

s

Rozstaw strzemion przyjęto: cm

8

1

=

s

001

.

0

355

20

08

.

0

003

.

0

25

8

56

.

0

min

,

1

=

=

>

=

×

=

w

w

ρ

ρ

Długość odcinka ścinania na którym należy zastosować zagęszczony rozstaw strzemion

m

10

.

2

2

=

w

a

Sprawdzenie ze względu na zmiażdżenie krzyżulców betonowych

kN

39

.

444

1

1

1

486

.

0

25

.

0

10

3

.

13

55

.

0

kN

51

.

98

2

3

2

=

+

×

×

×

×

×

=

<

=

Rd

Sd

V

V

Sprawdzenie nośności rozciąganego zbrojenia podłużnego w strefie przypodporowej

kN

26

.

49

0

.

1

51

.

98

5

.

0

=

×

×

=

td

F

∆

<

439.95kN

10

350

10

57

.

12

3

4

=

×

×

×

=

−

s

F

Sprawdzenie ze względu na rysy ukośne

kPa

70

.

729

54

.

0

25

.

0

51

.

98

=

×

=

τ

67

.

466

6

7

.

0

003

.

0

3

1

=









×

=

λ

mm

3

.

0

mm

08

.

0

10

20

10

200

003

.

0

67

.

466

70

.

729

4

lim

3

6

2

=

<

=

×

×

×

×

×

×

=

w

w

k

Podpora B z lewej strony:

kN

07

.

154

=

Sd

V

01

.

0

012

.

0

54

25

71

.

15

>

=

×

=

L

ρ

(

)

kN

14

.

80

54

.

0

25

.

0

01

.

0

40

2

.

1

10

0

.

1

06

.

1

35

.

0

kN

07

.

154

3

1

=

×

×

×

+

×

×

×

×

=

>

=

Rd

Sd

V

V

kN

39

.

444

kN

07

.

154

2

=

<

=

Rd

Sd

V

V

Jako zbrojenie na ścinanie zastosowano strzemiona czteroramienne o średnicy 6 mm ze stali AII (18G2) o

2

1

cm

13

.

1

=

sw

A

cm

11.05

m

1105

.

0

0

.

1

486

.

0

07

.

154

10

310

10

13

.

1

3

4

1

=

=

×

×

×

×

×

=

−

s

Rozstaw strzemion przyjęto: cm

11

1

=

s

001

.

0

004

.

0

25

11

13

.

1

min

,

1

=

>

=

×

=

w

w

ρ

ρ

Długość odcinka ścinania na którym należy zastosować zagęszczony rozstaw strzemion

m

30

.

2

2

=

w

a

Sprawdzenie ze względu na zmiażdżenie krzyżulców betonowych

kN

39

.

444

kN

07

.

154

2

=

<

=

Rd

Sd

V

V

Sprawdzenie nośności rozciąganego zbrojenia podłużnego w strefie przypodporowej

kN

87

.

583

0

.

1

07

.

154

5

.

0

486

.

0

33

.

246

=

×

×

+

=

td

F

>

kN

549.85

10

350

10

79

.

15

3

4

=

×

×

×

=

−

s

F

Budynek o konstrukcji mieszanej – wersja 2007

Dr inż. Maria WŁODARCZYK

Projekt techniczny STUDENT

Dr inż. Barbara GOSZCZYŃSKA

Do użytku wewnętrznego. Na prawach rękopisu.

69

Należy dozbroić strefę przypodporową ze względu na nośność pasa rozciąganego kratownicy

kN

02

.

34

85

.

549

87

.

583

=

−

=

s

F

∆

2

2

5

3

cm

97

.

0

m

10

72

.

9

10

350

02

.

34

=

×

=

×

=

−

s

A

∆

Jako dodatkowe zbrojnie zastosowano 20

1

φ

o

2

cm

14

.

3

=

s

A

kN

87

.

583

=

td

F

<

(

)

kN

659.75

10

350

10

14

.

3

79

.

15

3

4

=

×

×

×

+

=

−

s

F

Sprawdzenie ze względu na rysy ukośne

kPa

48

.

1163

54

.

0

25

.

0

07

.

154

=

×

=

τ

350

6

7

.

0

004

.

0

3

1

=









×

=

λ

lim

3

6

2

mm

118

.

0

10

20

10

200

004

.

0

350

48

.

1163

4

w

w

k

<

=

×

×

×

×

×

×

=

Podpora B z prawej strony:

kN

21

.

140

=

Sd

V

kN

14

.

80

1

=

Rd

V

<

kN

39

.

444

kN

07

.

154

2

=

<

=

Rd

Sd

V

V

Jako zbrojenie na ścinanie zastosowano strzemiona czteroramienne o średnicy 6 mm ze stali AII (18G2)

cm

12.14

m

1214

.

0

0

.

1

486

.

0

21

.

140

10

310

10

13

.

1

3

4

1

=

=

×

×

×

×

×

=

−

s

Rozstaw strzemion przyjęto: cm

12

1

=

s

001

.

0

002

.

0

25

12

13

.

1

min

,

1

=

>

=

×

=

w

w

ρ

ρ

Długość odcinka ścinania na którym należy zastosować zagęszczony rozstaw strzemion

m

30

.

2

2

=

w

a

Sprawdzenie ze względu na zmiażdżenie krzyżulców betonowych

kN

39

.

444

kN

21

.

140

2

=

<

=

Rd

Sd

V

V

Sprawdzenie nośności rozciąganego zbrojenia podłużnego w strefie przypodporowej

kN

96

.

576

0

.

1

21

.

140

5

.

0

486

.

0

33

.

246

=

×

×

+

=

td

F

<

(

)

kN

659.75

10

350

10

14

.

3

79

.

15

3

4

=

×

×

×

+

=

−

s

F

Sprawdzenie ze względu na rysy ukośne

kPa

59

.

1038

54

.

0

25

.

0

21

.

140

=

×

=

τ

700

6

7

.

0

002

.

0

3

1

=









×

=

λ

lim

3

6

2

mm

377

.

0

10

20

10

200

002

.

0

700

59

.

1038

4

w

w

k

>

=

×

×

×

×

×

×

=

Zagęszczono rozstaw strzemion do 10 cm

001

.

0

005

.

0

25

10

13

.

1

min

,

1

=

>

=

×

=

w

w

ρ

ρ

Budynek o konstrukcji mieszanej – wersja 2007

Dr inż. Maria WŁODARCZYK

Projekt techniczny STUDENT

Dr inż. Barbara GOSZCZYŃSKA

Do użytku wewnętrznego. Na prawach rękopisu.

70

73

.

309

6

7

.

0

005

.

0

3

1

=









×

=

λ

lim

3

6

2

mm

062

.

0

10

20

10

200

005

.

0

73

.

309

59

.

1038

4

w

w

k

<

=

×

×

×

×

×

×

=

Podpora C z lewej strony:

kN

99

.

128

=

Sd

V

01

.

0

009

.

0

54

25

57

.

12

<

=

×

=

L

ρ

kN

13

.

78

1

=

Rd

V

<

kN

39

.

444

kN

99

.

128

2

=

<

=

Rd

Sd

V

V

Jako zbrojenie na ścinanie zastosowano strzemiona czteroramienne o średnicy 6 mm ze stali AII (18G2)

cm

13.19

m

1319

.

0

0

.

1

486

.

0

99

.

128

10

310

10

13

.

1

3

4

1

=

=

×

×

×

×

×

=

−

s

Rozstaw strzemion przyjęto:

cm

13

1

=

s

001

.

0

003

.

0

25

13

13

.

1

min

,

1

=

>

=

×

=

w

w

ρ

ρ

Długość odcinka ścinania na którym należy zastosować zagęszczony rozstaw strzemion

m

30

.

2

2

=

w

a

Sprawdzenie ze względu na zmiażdżenie krzyżulców betonowych

kN

39

.

444

kN

79

.

128

2

=

<

=

Rd

Sd

V

V

Sprawdzenie nośności rozciąganego zbrojenia podłużnego w strefie przypodporowej

kN

96

.

498

0

.

1

99

.

128

5

.

0

486

.

0

15

.

211

=

×

×

+

=

td

F

>

kN

439.95

10

350

10

57

.

12

3

4

=

×

×

×

=

−

s

F

Należy dozbroić strefę przypodporową ze względu na nośność pasa rozciąganego kratownicy

kN

01

.

59

95

.

439

96

.

498

=

−

=

s

F

∆

2

2

4

3

cm

69

.

1

m

10

69

.

1

10

350

01

.

59

=

×

=

×

=

−

s

A

∆

Jako dodatkowe zbrojnie zastosowano 20

1

φ

o

2

cm

14

.

3

=

s

A

kN

95

.

439

=

td

F

<

(

)

kN

549.85

10

350

10

14

.

3

57

.

12

3

4

=

×

×

×

+

=

−

s

F

Sprawdzenie ze względu na rysy ukośne

kPa

48

.

955

54

.

0

25

.

0

99

.

128

=

×

=

τ

67

.

466

6

7

.

0

003

.

0

3

1

=









×

=

λ

lim

3

6

2

mm

14

.

0

10

20

10

200

003

.

0

67

.

466

48

.

955

4

w

w

k

<

=

×

×

×

×

×

×

=

Podpora C z prawej strony:

kN

29

.

135

=

Sd

V

kN

13

.

78

1

=

Rd

V

<

kN

39

.

444

kN

29

.

135

2

=

<

=

Rd

Sd

V

V

Jako zbrojenie na ścinanie zastosowano strzemiona czteroramienne o średnicy 6 mm ze stali AII (18G2)

cm

12.58

m

1258

.

0

0

.

1

486

.

0

29

.

135

10

310

10

13

.

1

3

4

1

=

=

×

×

×

×

×

=

−

s

Rozstaw strzemion przyjęto: cm

12

1

=

s

001

.

0

004

.

0

25

12

13

.

1

min

,

1

=

>

=

×

=

w

w

ρ

ρ

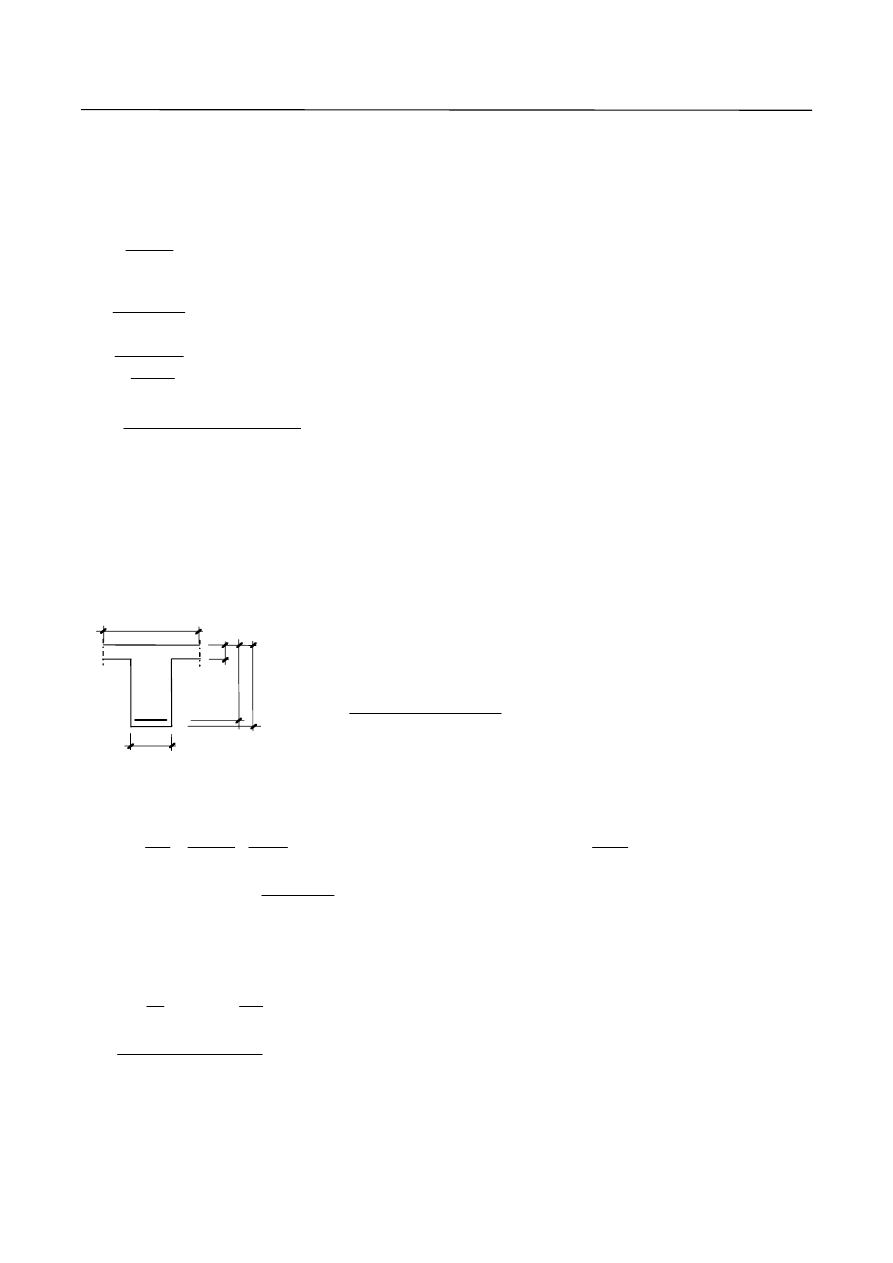
Budynek o konstrukcji mieszanej – wersja 2007

Dr inż. Maria WŁODARCZYK

Projekt techniczny STUDENT

Dr inż. Barbara GOSZCZYŃSKA

Do użytku wewnętrznego. Na prawach rękopisu.

71

Długość odcinka ścinania na którym należy zastosować zagęszczony rozstaw strzemion

m

30

.

2

2

=

w

a

Sprawdzenie ze względu na zmiażdżenie krzyżulców betonowych

kN

39

.

444

kN

29

.

135

2

=

<

=

Rd

Sd

V

V

Sprawdzenie nośności rozciąganego zbrojenia podłużnego w strefie przypodporowej

kN

11

.

502

0

.

1

29

.

135

5

.

0

486

.

0

15

.

211

=

×

×

+

=

td

F

<

(

)

kN

549.85

10

350

10

14

.

3

57

.

12

3

4

=

×

×

×

+

=

−

s

F

Sprawdzenie ze względu na rysy ukośne

kPa

15

.

1002

54

.

0

25

.

0

29

.

135

=

×

=

τ

350

6

7

.

0

004

.

0

3

1

=









×

=

λ

lim

3

6

2

mm

09

.

0

10

20

10

200

004

.

0

67

.

466

15

.

1002

4

w

w

k

<

=

×

×

×

×

×

×

=

I. Ścinanie między środnikiem a półką

UWAGA:

W przykładzie pokazano przykładowo obliczenia dla podpory A. W projekcie należy sprawdzić w każdym

przekroju gdzie jest to konieczne

Podpora A

kN

51

.

98

=

Sd

V

Półka ściskana

2

1

57

.

12

cm

A

s

=

Zakładamy

f

eff

h

x

≤

m

08

.

0

m

034

.

0

10

3

.

13

97

.

0

10

350

10

57

.

12

3

3

4

=

<

=

×

×

×

×

×

=

−

f

eff

h

x

∆F

d

= f

cd

x

eff

0.5(b

eff

– b

w

) =

(

)

kN

79

.

162

25

.

0

97

.

0

5

.

0

034

.

0

10

3

.

13

3

=

−

×

×

×

×

F

d

= f

cd

x

eff

b

ef

=

kN

63

.

438

97

.

0

034

.

0

10

3

.

13

3

=

×

×

×

kN

23

.

75

486

.

0

51

.

98

63

.

438

79

.

162

=

×

=

=

z

V

V

Sd

t

Sd

β

≤

kN

60

.

292

1

1

1

08

.

0

10

3

.

13

55

.

0

2

3

2

=

+

×

×

×

×

=

Rd

V

,

kN

23

.

75

=

Sd

V

kN

20

.

99

0

.

1

10

310

1

.

0

10

32

.

0

3

4

3

=

×

×

×

×

=

≤

−

V

Rd

J. Połączenie żebra z podciągiem
Dla przęsła skrajnego (żebro od prawej strony podpory A)

kN

60

.

80

6

.

0

4

.

0

91

.

120

=

×

=

=

h

h

F

F

b

red

cm

10.46

m

1046

.

0

0

.

1

486

.

0

60

.

80

10

310

10

56

.

0

3

4

1

=

=

×

×

×

×

×

=

−

s

W podciągu w przy żebrze należy zastosować w odległości pierwsze 2 cm od żebra, a drugie w odległości 5
cm od pierwszego. Nośność na pozostałym odcinku będzie zapewniona, ponieważ rozstaw strzemion
obliczony ze względu na przeniesienie max siły podporowej wynosi 8 cm.

b

eff

A

s1

h

f

b

w

d

a

1

h

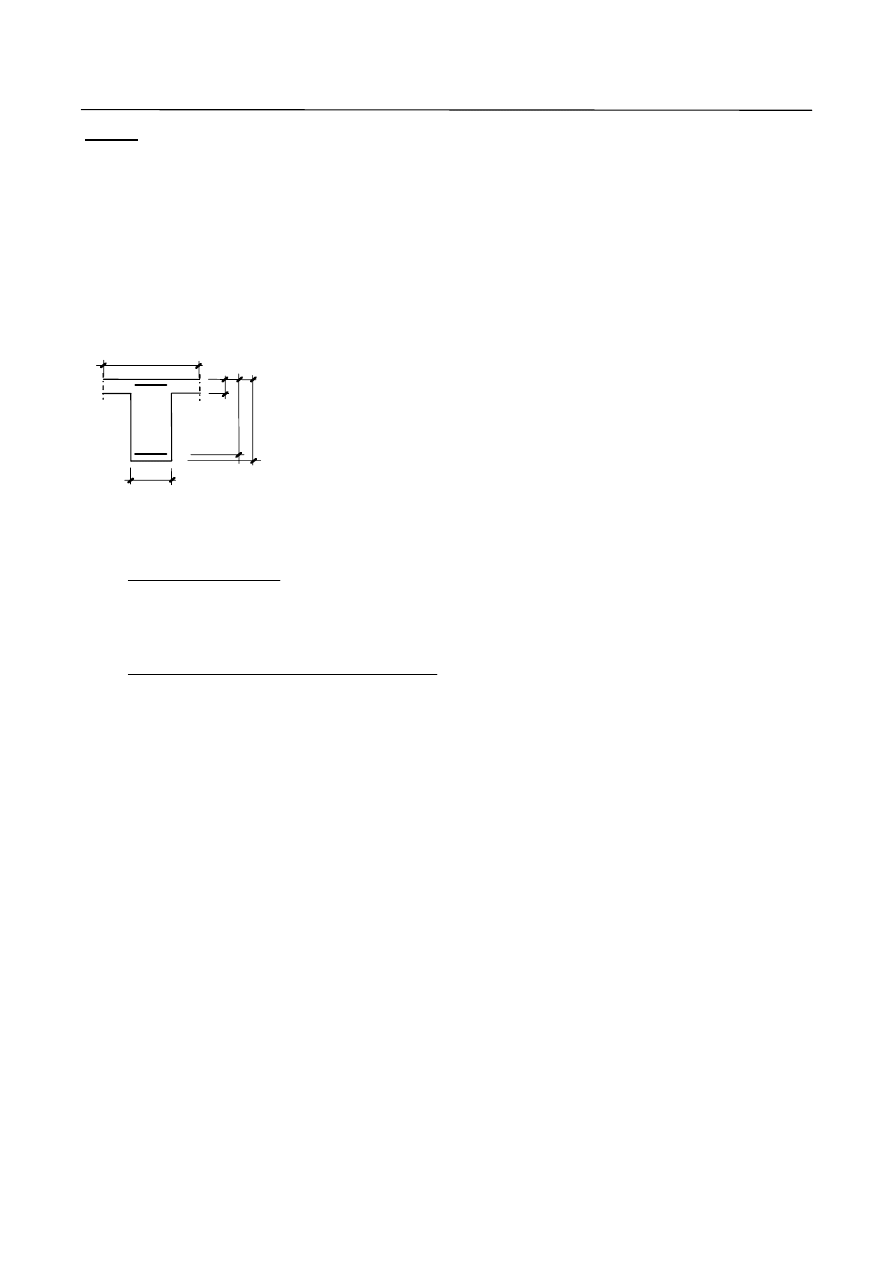
Budynek o konstrukcji mieszanej – wersja 2007

Dr inż. Maria WŁODARCZYK

Projekt techniczny STUDENT

Dr inż. Barbara GOSZCZYŃSKA

Do użytku wewnętrznego. Na prawach rękopisu.

72

Uwaga:

Ten warunek należy sprawdzić dla każdego żebra.

K. Sprawdzenie stanu granicznego użytkowalności
- stan graniczny zarysowania
Należy sprawdzać tak jak dla żebra
- stan graniczny ugięcia
Należy sprawdzać tak jak dla żebra

L. Sprawdzenie nośności
Przekrój 1

(

)

20

4

cm

57

.

12

2

1

φ

=

s

A

(

)

10

4

cm

14

.

3

2

2

φ

=

s

A

cm

6

.

3

0

.

2

5

.

0

6

.

0

0

.

2

1

=

×

+

+

=

a

cm

1

.

3

0

.

1

5

.

0

6

.

0

0

.

2

2

=

×

+

+

=

a

Rozciągane włókna dolne
Zakładamy

f

eff

h

x

≤

m

08

.

0

m

034

.

0

10

3

.

13

97

.

0

10

350

10

57

.

12

3

3

4

=

<

=

×

×

×

×

×

=

−

f

eff

h

x

(

)

kN

93

.

239

034

.

0

5

.

0

564

.

0

10

3

.

13

97

.

0

034

.

0

3

=

×

−

×

×

×

=

Rd

M

Rozciągane włókna górne

0

10

3

.

13

25

.

0

10

350

10

57

.

12

10

350

10

14

.

3

3

3

4

3

4

<

×

×

×

×

×

−

×

×

×

=

−

−

eff

x

, pomijamy pracę betonu ściskanego

(

)

kN

58

.

58

0036

569

.

0

10

350

10

14

.

3

3

4

=

−

×

×

×

=

−

Rd

M

Nośność należy określić w każdym przekroju, gdzie zmienia się pole powierzchni zbrojenia.

Poz. 4. Słupy

Poz. 4.3. Słup najniższej kondygnacji

A. Obciążenia działające na słup

Obciążenia stałe i zmienne z poz. 4.3. projektu wstępnego.

B. Długość obliczeniowa słupa
Długości obliczeniowe słupów przyjmuje się jak dla budynków, w których siły poziome przenoszone są
przez ustroje usztywniające np. w postaci ścian. Długości obliczeniowe słupów l

o

przyjmować zgodnie

załącznikiem C,

2002

:

03264

B

PN

−

−

C. Wymiarowanie na ściskanie
Słupy wspierające strop płytowo żebrowy oblicza się przy założeniu, że mimośród statyczny e

e

= 0.

D. Dobór zbrojenia dla słupa
Zbrojenie należy dobrać i rozmieścić w przekroju słupa zgodnie z zgodnie z obowiązującymi przepisami
normowymi 2002

:

03264

B

PN

−

−

.

PRZYKAD

b

eff

A

s1

h

f

b

w

d

a

1

h

A

s2

Budynek o konstrukcji mieszanej – wersja 2007

Dr inż. Maria WŁODARCZYK

Projekt techniczny STUDENT

Dr inż. Barbara GOSZCZYŃSKA

Do użytku wewnętrznego. Na prawach rękopisu.

73

Poz. 4.3. Słup najniższej kondygnacji
Dla słupa zastosowano zbrojenie symetryczne.

A. Obciążenia działające na żebro

N

kg

= 500.61kN

N

Sdg

= 563.36 kN

N

kp

= 302.84 kN

N

Sdp

= 396.11 kn

N

k43

= N

kg

+ N

kp

= 803.07 kN

N

Sd43

= N

Sdg

+ N

Sdp

= 959.47 kN

B. Wysokość słupa

m

40

.

3

=

col

l

m

38

.

2

40

.

3

7

.

0

0

=

×

=

l

C. Dane materiałowe
Beton BC20/25:

MPa

20

=

ck

f

,

MPa

3

.

13

=

cd

f

,

MPa

2

.

2

=

ctm

f

,

MPa

0

.

1

=

ctd

f

,

GPa

30

=

cm

E

Stal AIII (34GS):

MPa

410

=

yk

f

, MPa

350

=

yd

f

, GPa

200

=

s

E

, 0.53

lim

,

=

eff

ξ

cm

0

.

25

=

h

cm

0

.

25

=

b

cm

0

.

3

1

=

a

cm

0

.

22

=

d

cm

0

.

0

=

e

e



















=

=

=

=

=

cm

h

l

e

col

a

1

cm

83

.

0

30

25

30

cm

56

.

0

600

340

300

cm

83

.

0

0

=

+

=

a

e

e

e

e

0

.

7

52

.

9

25

.

0

38

.

2

>

=

=

h

l

o

, uwzględniamy wpływ smukłości i obciążeń długotrwałych

Założono: %

0

.

1

=

ρ

4

6

2

m

10

96

.

4

03

.

0

2

25

.

0

22

.

0

25

.

0

01

.

0

−

×

=













−

×

×

=

s

I

4

4

3

m

10

255

.

3

12

25

.

0

25

.

0

−

×

=

×

=

c

I









=

×

−

×

−

=

−

−

≥

=

=

05

.

0

27

.

0

3

.

13

01

.

0

52

.

9

01

.

0

5

.

0

01

.

0

01

.

0

5

.

0

033

.

0

25

.

0

0083

.

0

0

0

cd

f

h

l

h

e

Wyznaczenie współczynnika pełzania:

2002

:

03264

B

PN

−

−

, Zał. A

mm

125

250

4

250

250

2

2

0

=

×

×

×

=

=

u

A

h

c

Beton C20/25, wiek betonu 28 dni, słup wewnątrz budynku (RH = 50 %)

(

)

(

)

18

.

3

7

.

3

50

125

50

150

7

.

3

3

0

,

=

+

−

−

−

=

∞ t

φ

Budynek o konstrukcji mieszanej – wersja 2007

Dr inż. Maria WŁODARCZYK

Projekt techniczny STUDENT

Dr inż. Barbara GOSZCZYŃSKA

Do użytku wewnętrznego. Na prawach rękopisu.

74

kN

10

.

3173

10

96

.

4

10

200

1

.

0

27

.

0

1

.

0

11

.

0

93

.

1

2

10

255

.

3

10

30

38

.

2

9

1

.

0

1

.

0

11

.

0

2

9

6

6

4

6

2

0

2

0

=

=













×

×

×

+













+

+

×

×

×

×

=

























+

























+

+

=

−

−

s

s

lt

c

cm

crit

I

E

h

e

k

I

E

l

N

43

.

1

10

.

3173

47

.

959

1

1

1

1

=

−

=

−

=

crit

Sd

N

N

η

cm

19

.

1

83

.

0

43

.

1

0

=

×

=

= e

e

tot

η

cm

69

.

10

19

.

1

0

.

3

25

5

.

0

2

1

=

+

−

×

=

=

s

s

e

e

m

1166

.

0

22

.

0

53

.

0

m

2886

.

0

10

3

.

13

25

.

0

72

.

961

lim

,

3

=

×

=

>

=

×

×

=

=

eff

cd

Sd

eff

x

bf

N

x

Do dalszych obliczeń przyjęto m

1166

.

0

lim

,

=

=

eff

eff

x

x

(

)

(

)

=

−

−

−

=

=

2

lim

,

lim

,

1

2

1

5

.

0

a

d

f

x

d

bf

x

e

N

A

A

yd

eff

cd

eff

s

Sd

s

s

(

)

(

)

=

−

×

×

−

×

×

×

−

×

=

03

.

0

22

.

0

10

350

1166

.

0

5

.

0

22

.

0

10

3

.

13

25

.

0

1166

.

0

1069

.

0

72

.

961

3

3

(

)













=

×

=

×

×

=

×

=

×

×

=

>

=

×

=

−

−

−

12

2

cm

2.26

cm

06

.

2

m

10

06

.

2

10

350

961.72

0.075

cm

83

.

0

m

10

83

.

0

22

.

0

25

.

0

0015

.

0

cm

00

.

6

m

10

00

.

6

2

2

2

4

3

2

2

4

min

,

2

2

4

φ

s

A

Przyjęto:

2

,

cm

03

.

6

o

16

3

=

prov

s

A

φ

%

9

.

1

019

.

0

25

.

0

25

.

0

03

.

6

03

.

6

2

1

=

=

×

+

=

+

=

bh

A

A

s

s

ρ

, należy przeprowadzić korektę przyjętego procentu zbrojenia

Założono:

%

2

=

ρ

4

6

2

m

10

93

.

9

03

.

0

2

25

.

0

22

.

0

25

.

0

02

.

0

−

×

=













−

×

×

=

s

I

kN

44

.

4752

10

93

.

9

10

200

1

.

0

27

.

0

1

.

0

11

.

0

93

.

1

2

10

255

.

3

10

30

38

.

2

9

6

6

4

6

2

=













×

×

×

+













+

+

×

×

×

×

=

−

−

crit

N

25

.

1

44

.

4752

47

.

959

1

1

=

−

=

η

cm

04

.

1

83

.

0

25

.

1

=

×

=

tot

e

cm

54

.

10

04

.

1

0

.

3

25

5

.

0

2

1

=

+

−

×

=

=

s

s

e

e

(

)

(

)

min

,

2

2

4

3

3

2

1

cm

78

.

5

m

10

78

.

5

03

.

0

22

.

0

10

350

1166

.

0

5

.

0

22

.

0

10

3

.

13

25

.

0

1166

.

0

1054

.

0

47

.

959

s

s

s

A

A

A

>

=

×

=

−

×

×

−

×

×

×

−

×

=

=

−

Przyjęto:

2

,

cm

03

.

6

o

16

3

=

prov

s

A

φ

%

0

.

4

%

9

.

1

<

=

ρ

Rozstaw strzemion

( )











=

=

×

=

=

mm

400

mm

250

,

min

mm

240

16

15

15

1

h

b

s

φ

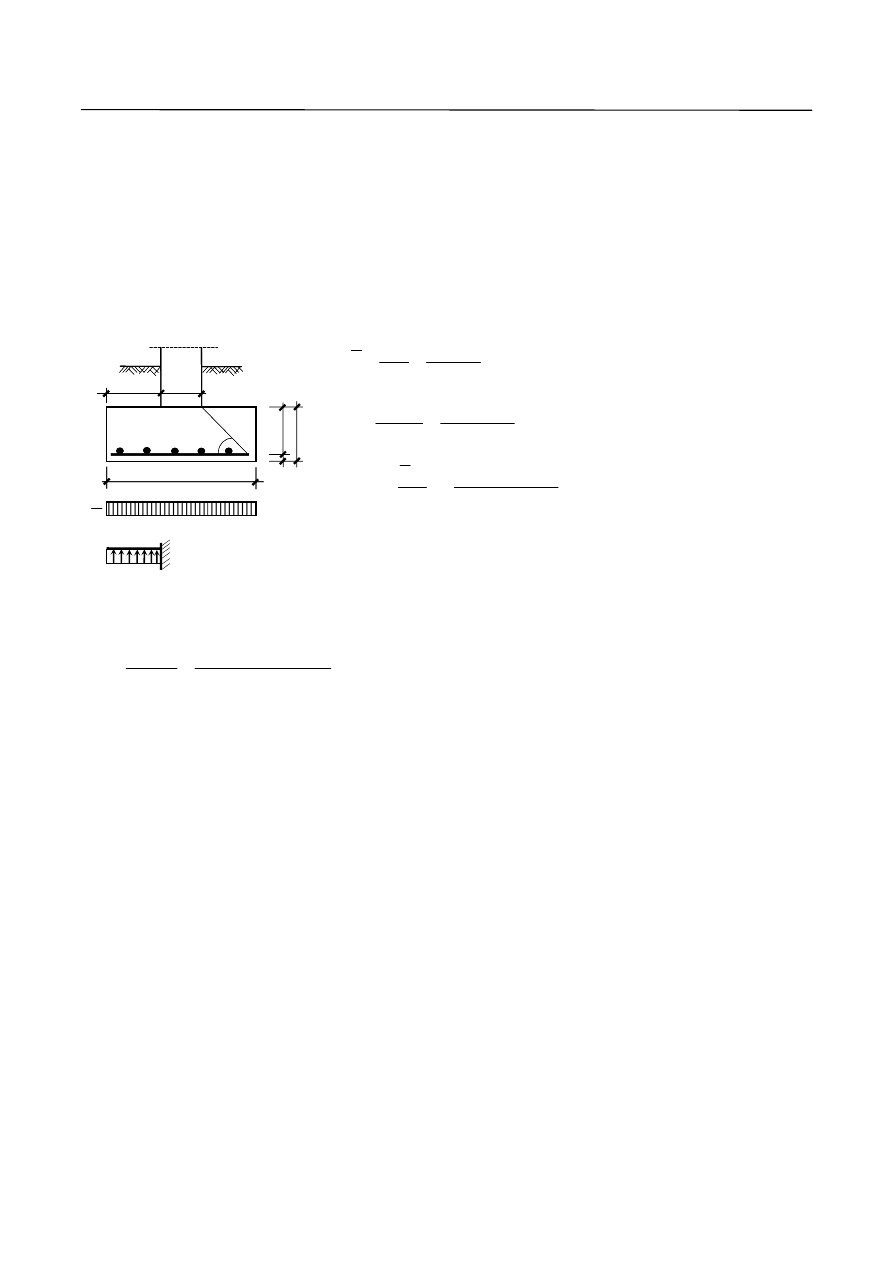
Budynek o konstrukcji mieszanej – wersja 2007

Dr inż. Maria WŁODARCZYK

Projekt techniczny STUDENT

Dr inż. Barbara GOSZCZYŃSKA

Do użytku wewnętrznego. Na prawach rękopisu.

75

Poz. 5. Stopa fundamentowa

A. Obciążenia działające na stopę

Obciążenia stałe i zmienne z poz. 4.3. projektu wstępnego.

kN

36

.

1151

47

.

959

2

.

1

=

×

=

Sd

N

Wymiary stopy:

m

30

.

2

=

= L

B

,

m

20

.

0

=

h

Pole powierzchni stopy:

2

29

.

5

m

A

=

Wymiary słupa:

m

a

a

s

s

25

.

0

2

1

=

=

Stal AIII (34GS):

MPa

410

=

yk

f

, MPa

350

=

yd

f

, GPa

200

=

s

E

a

s1

c

a

1

d

h

B

45

o

σ

MPa

q

MPa

kPa

A

N

fN

Sd

22

.

0

21764

.

0

64

.

217

29

.

5

36

.

1151

=

<

=

=

=

=

σ

m

a

B

c

s

025

.

1

2

25

.

0

30

.

2

2

1

=

−

=

−

=

kNm

b

c

M

Sd

95

.

262

30

.

2

2

025

.

1

64

.

217

2

2

2

=

×

×

=

=

σ

m

a

07

.

0

1

=

m

a

h

d

63

.

0

007

.

70

.

0

1

=

−

=

−

=

2

2

3

3

1

50

.

13

10

1350

.

0

10

350

63

.

0

9

.

0

95

.

262

9

.

0

cm

m

df

M

A

yd

Sd

s

=

×

=

×

×

×

=

=

−

Przyjęto

φ 14 co 11 cm o A

s1,prov

=13.99 cm

2

Materiały pomocnicze:
1. PN – B – 03264:2002. Konstrukcje betonowe, żelbetowe i sprężone. Obliczenia statyczne

i projektowanie.

2. Starosolski W.: Konstrukcje żelbetowe według PN – B – 03264:2002 i Eurocodu 2. PWN, Warszawa 2006,

Tom I.

3. Łapko A.: Projektowanie konstrukcji żelbetowych. Arkady, Warszawa 2001.
4. Dąbrowski K., Stachurski W., Zieliński J.L.: Konstrukcje betonowe. Arkady, Warszawa 1982.
5. Private communication: Szwed A.
6. Łapko A., Jansen B.J.: Podstawy projektowania i algorytmy obliczeń konstrukcji żelbetowych. Arkady, Warszawa

2005.

7. Private communication

: Jemioło S.

8. Kobiak J., Stachurski W.: Konstrukcje żelbetowe. Arkady, Warszawa 1984, tom I.
9. Private communication

: Goszczyński S.