Czy

m

są

f

r

a

k

t

a

le

?

Newton

i

Le

ibn

itz

(

n

iez

al

eż

n

ie

od

siebie)

stworzy

l

i

rac

hune

k

różn

ic

z

kow

y

–

d

oskona

łe

narzędzie (m

iędz

y

i

n

n

y

m

i) d

o

ba

dani

a prze

bie

gu funkc

j

i. W epoce

, kied

y

ma

sz

y

n

y

l

i

cząc

e

ni

e

p

osiadał

y

możl

iwości

w

y

ko

n

y

wa

n

ia

w

ie

lu

o

blicz

eń

w

c

ią

gu

ułam

k

a

se

kund

y,

można

b

y

ł

o

stosunkowo

łatwo

(

dzię

ki

Newtonowi

i

Le

ibn

itzowi)

przewidzieć

kszta

łt

nawet

bardz

o

sko

m-

pli

kowane

j

fun

kc

j

i,

jeś

l

i

t

y

l

ko

w

d

ostateczn

ie

du

ż

y

c

h

obszarach

b

y

ł

a

różni

cz

kowal

na.

Ró

ż-

n

icz

kowal

ność

w

i

nterpretacji

geometr

y

cz

ne

j

ozn

acza

posiada

n

ie

st

y

c

z

ne

j

okreś

lon

ej

jedn

o-

zna

cz

n

ie.

Po

d

koniec

XIX

i

na

początku

XX

wieku

prz

y

pr

ó

bach

d

ogłębne

go

zroz

umien

ia

p

ojęć

p

o

dstawow

yc

h

(ta

k

ic

h

ja

k

np.

„cią

głość”

c

z

y

„krz

y

w

a”)

zauważono

ist

n

ie

n

ie

struktur

,

które

o

becnie

n

az

y

wam

y

frakt

al

ami.

W

śró

d

matemat

y

ków

zw

i

ąza

n

y

c

h

z

fra

kta

lam

i

możem

y

w

y

m

ie

n

ić

na

prz

y

k

ład

Georga

Cantora

(

1

8

7

2)

,

Giuseppe

Peana

(1

8

9

0)

,

Dawida

Hi

lberta

(1

8

9

1

),

Hel

ge’a

von

Koch

a

(1

9

0

4)

,

Wacława

Sier

pińs

k

i

go

(1

9

1

6)

,

Gastona

J

ulię

(19

1

8)

,

cz

y

Fel

i

xa

H

ausd

orffa (1

9

1

9)

. He

l

ge

von

Koch b

y

ł

sz

wedzki

m

matemat

y

k

i

em, któr

y

w

roku 1

9

0

4

wpr

owa

dził

krz

y

w

ą

naz

y

w

a

ną obecn

ie

k

rz

y

wą Koch

a

. Li

ni

a ta

w

ka

żd

ym

punkc

ie

j

est

n

i

eró

ż-

n

icz

kowal

n

a.

Pojęc

ie

na

c

h

y

l

e

n

ia

krz

y

we

j

jest

z

g

o

dne

z

i

ntuic

ją

i

ma

zw

iąze

k

z

pojęciem

st

y

c

z

ne

j.

Jeśl

i

j

edna

k

krz

y

wa

ma

za

łama

n

ia

to

p

oj

awia

s

ię

pro

blem.

Nie

możem

y

do

pasować

jednozna

cz

n

ie

st

y

cz

ne

j.

Otóż

krz

y

wa

Kocha

jest

prz

y

k

ł

adem

krz

y

w

e

j,

która

w

każd

ym

p

un

k-

cie

ma

za

łama

n

ie,

co

pr

owa

dzi

d

o

tego,

że

ni

emo

żl

iwe

jest

okreś

le

n

ie

st

y

c

z

ne

j

w

spos

ó

b

je

d

-

nozna

cz

n

y.

Konstrukcja

krz

y

we

j

Koc

ha

prz

edstawia

s

ię

nastę

p

ująco.

Zacz

y

n

am

y

od

o

dcin

k

a

(obiekt

ten

n

azw

iem

y

i

n

ic

jatorem),

dziel

im

y

n

a trz

y

równ

e czę

śc

i, a w m

ie

j

sce

środkowej wstaw

iam

y

trójkąt

równo

b

oczn

y

i

usuwam

y

je

go

p

o

dstawę.

Kończ

y

m

y

w

te

n

spos

ó

b

p

o

dstawow

y

krok

konstrukc

j

i.

Otrz

y

ma

na

f

i

gur

a

nos

i

naz

wę

ge

n

eratora

.

Powta

rzam

y

kon

strukcję

w

t

e

n

sposó

b

,

że

w

m

ie

jsce

każdego

o

dcin

k

a

wstaw

iam

y

od

p

o

wiedn

io

zmn

ie

j

szon

y

ge

nerator.

Kil

ka

p

o

-

czątkow

y

c

h kroków

prze

dstawia

ją r

y

su

n

k

i na

na

stępnej stron

ie.

Sp

r

ó

b

ujm

y

oblic

z

y

ć

długość

kole

j

n

y

c

h

w

y

razów

cią

g

u

zbież

ne

go

d

o

krz

y

w

e

j

Kocha.

Długość

i

n

ic

jatora oznaczm

y

l

iterą

b

(zerow

y w

y

r

az c

ią

gu). Pierwsz

y

w

y

raz

s

k

łada s

ię z

czt

e-

rech

odcin

ków

o długości

3

1

b,

dr

ugi

z

4



4 o

dcin

ków

o długości

3

1



3

1

b

,

t

rzeci

-

4



4



4 o

dci

n-

ków o

długości

3

1



3

1



3

1

b,

.

..

Otrz

ymujem

y

w

ięc c

ią

g l

icz

b:

4

1



3

-

1

b

4

2



3

-

2

b

4

3



3

-

3

b

..

..

..

..

4

i



3

-

i

b

Cią

g te

n prz

y duż

yc

h

i

dąż

y do

nie

s

kończonośc

i.

Pr

o

blem

pomiar

u

długo

ści

krz

y

w

y

c

h

opisa

n

y

c

h

w

y

ż

e

j

jest

po

d

o

bn

y

do

mierzen

ia

dług

o-

śc

i l

i

n

i

i brzegowej np. Ang

l

i

i. P

omiar na mapie zal

eż

y

od

ska

l

i w ja

k

ie

j n

ar

y

sowa

no tę ma

pę.

Wokół

na

s

można

z

na

leźć

w

ie

le

obiektów

o b

u

d

o

wie

fra

kta

l

ne

j.

G

łówka

ka

la

f

iora

sk

łada

si

ę

z

róż

y

cz

e

k,

k

tóre

p

o

o

d

dzie

le

n

iu

o

d

reszt

y

prz

y

pomi

na

ją

c

a

łą

g

łówkę,

t

y

l

e

że

w

pomnie

j-

sze

n

iu.

Części

te

mogą

b

y

ć

z

nowu

p

o

dzielone

n

a

je

szcze

m

n

ie

j

sze

cz

ąst

k

i,

które

znowu

są

p

o

d

o

bne

d

o

całego

ka

la

f

iora,

jak

równie

ż

d

o

części

z

której

został

y

od

dzie

lone.

Ta

włas

ność

prz

enosi na trzec

i

ą i może czwarta

ge

nerac

ję. Potem r

óż

y

cz

k

i sta

ją

s

ię za ma

łe ż

eb

y

j

e dzie

li

ć.

W

matemat

y

cz

n

y

m

modelu

fraktal

i

w

łas

ność

sa

mo

p

o

d

o

bieństw

a

przenosi

s

ię

na

n

astępn

ą

ge

nerac

ję

ni

es

kończ

e

n

ie

w

ie

le

raz

y

.

Prowa

dzi

to

d

o

now

yc

h

pojęć

ta

k

ic

h

ja

k

w

y

m

ia

r

frakt

a

l-

n

y,

kt

ó

r

y można stosować r

ównie

ż d

o

o

biektów, nie mając

y

c

h dow

oln

ie mał

y

c

h czę

śc

i.

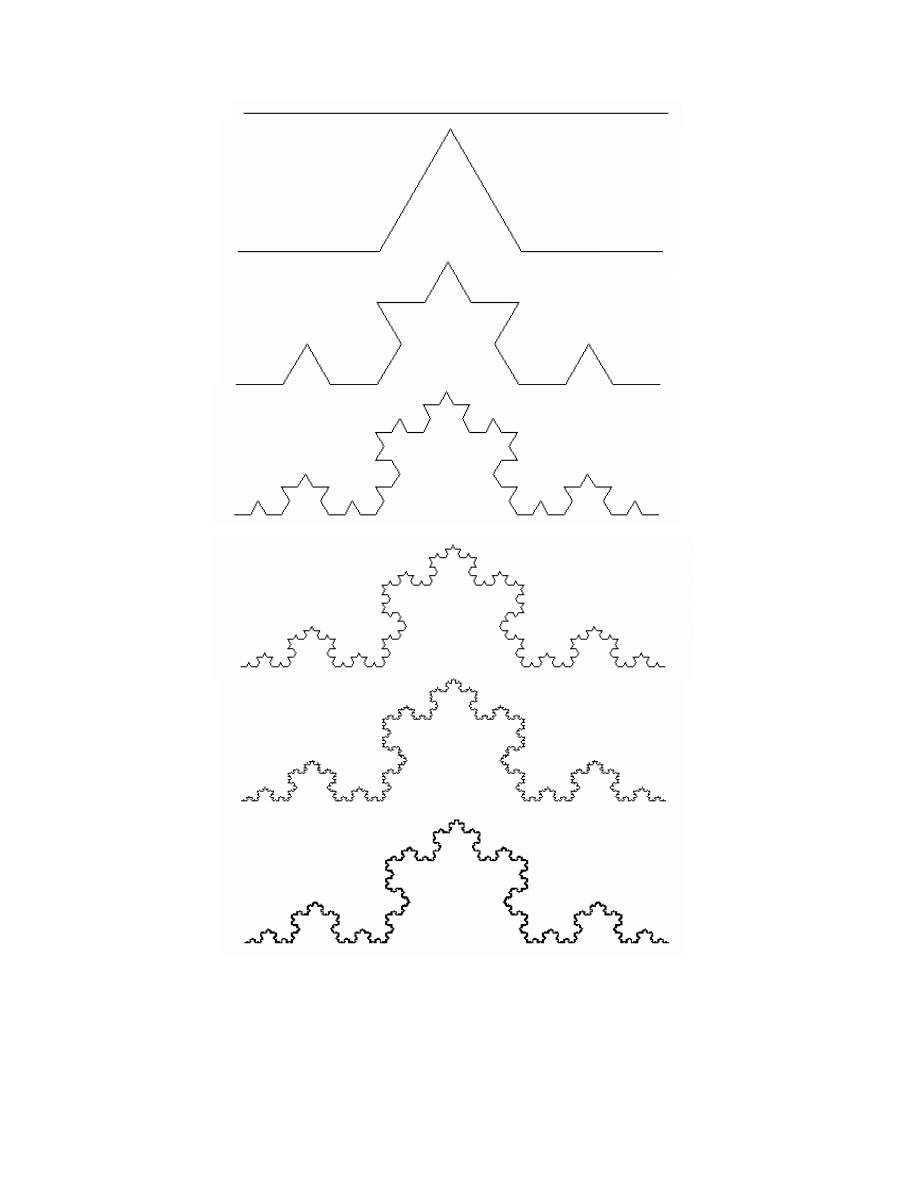
krok

0

krok

1

krok

2

krok

3

krok

4

krok

5

krok

6

R

y

s. 1. K

olej

ne w

yra

z

y c

ią

gu zbieżn

e

go

d

o krz

yw

ej Kocha.

W

ymi

ar

s

a

mopo

do

bieńst

wa

Jeżel

i bierzem

y

po

d

uwagę i

ntuic

je stojące po

d

p

ojęciem w

y

m

iaru,

t

o li

n

ie są prz

y

k

ład

a-

mi o

biektów jednow

y

m

iarow

y

c

h, a płaszcz

y

z

na

- dwuw

ym

iarowego. W natu

rze str

uktur

y

„jednow

ym

iarowe” często w

ype

ł

ni

aj

ą przestrzeń tak dokładn

ie, że p

rzebieg

a

ją przez wsz

y

s

t-

k

ie punkt

y

np.

układ krwionoś

n

y musi b

y

ć ta

k zb

u

d

owan

y

, b

y dostarcz

yć ż

y

c

iodajn

e su

bsta

n-

cje do

każdego miej

sca organ

izmu. Nerka zawiera

trz

y przeplecion

e ze so

bą r

ozgałęz

ione

s

y

s

tem

y

n

acz

y

ń

: uk

ładu tętnicze

go,

układu ż

y

l

ne

g

o

i układu

m

oczow

ego

. Każ

d

y z

n

ic

h ma

d

ostęp

d

o każdej częśc

i ner

k

i. Geometria frakta

l

na

d

ostarcza meto

d

p

ozwala

jąc

y

c

h

na u

p

o-

rządkow

a

nie ta

k

ic

h s

kompli

kowan

y

c

h struktur w

sp

os

ó

b efekt

y

w

n

y.

Waż

na

cec

hą

samop

o

d

o

bien

stwa

je

st

to,

że

małe

fragme

nt

y

moż

na

otrz

ymać

z

ca

łe

go

o

bie

ktu

p

rzez

p

rzekszta

łc

e

ni

e

p

o

d

o

bień

stwa.

Naj

l

epsz

y

m

spos

o

bem

w

yobrażenia

sobie

dzi

a-

ła

n

ia

te

go

t

ypu

przekszta

łce

ń

jest

a

na

log

ia

do

f

ot

o

kopiark

i,

która

ma

m

ożliwość

p

omnie

j

sz

e-

n

ia.

Jeże

li

weźm

iem

y

na

prz

y

k

ł

ad

krz

y

wą

Kocha,

w

łoż

y

m

y

ją

do

ko

piark

i,

na

staw

ia

ją

c

w

spółcz

y

n

n

i

k

pomnie

js

za

n

ia

n

a

1/3

i

od

bijem

y

4

kopie,

to

będziem

y

mog

l

i

ta

k

s

k

le

ić

te

k

o-

pie,

b

y z

nów

otrz

ymać

krz

y

wą Kocha. Następn

ie, j

eżel

i s

kopiujem

y

każdą z czterech

kopii, ze

współcz

y

n

n

i

k

i

em

red

ukcj

i

1/3

czter

y

raz

y

,

to

te

1

6

ko

pii

znowu

m

ożem

y

z

łoż

y

ć

ta

k

b

y

o

d-

tworz

yć

or

y

g

i

na

ł.

Jeżel

i

d

y

sponowalib

y

śm

y

ideal

ną

kopiarką,

to

pr

oces

ten

mógłb

y

b

y

ć

p

o-

wtarzan

y

w n

ie

s

kończoność.

Nie

każd

y

obiekt

samop

o

d

o

bn

y

jest

fra

kta

lem.

Weźm

y

na

prz

y

k

ł

ad

o

dcine

k,

kw

adrat,

cz

y

sześc

i

a

n.

Każd

y

z

n

i

c

h

może

b

yć

rozbit

y

na

m

n

ie

j

s

ze

fra

gme

nt

y

otrz

y

ma

ne

w

w

y

n

i

ku

prz

e-

ks

zta

łce

ń

po

d

o

bień

stwa.

Obie

kt

y

te

n

ie

są

jedn

a

k

fra

kta

lam

i.

Współcz

y

n

n

i

k

redukcj

i

t

y

c

h

o

biektów

można

w

ybrać

d

ow

oln

ie

W

ła

ś

ni

e

na

t

y

m

p

ole

ga

różnica

m

iędz

y

t

ym

i

fi

gurami

a

strukturami

frakta

l

n

y

mi.

Współcz

y

n

n

i

k

i

redukcj

i

dla

frakta

l

i

są

śc

iś

le

okreś

lone

i

za

leżą

od

danej

fi

gur

y

.

Na

prz

y

k

ład

dla

krz

y

we

j

Kocha

ws

p

ółcz

y

n

n

i

k

am

i

pomnie

jsza

n

i

a

mogą

b

yć

j

e-

d

y

n

ie

1/3

,

1/

9

,

1/

2

7

itd.

Cechą

wspólną

w

sz

y

st

k

ic

h

śc

i

ś

le

samop

o

d

o

bn

y

c

h

obiektów

jest

i

s

t-

n

ie

n

ie

re

lac

j

i

p

omiędz

y

w

spółcz

y

n

n

i

k

i

em

red

ukcj

i

a

l

iczbą

p

omnie

j

szon

y

c

h

fra

gme

ntów,

na

które r

oz

pa

da się o

biekt. Z

o

bacz tabela:

Obiekt

Li

czba częśc

i

( a

)

Współcz

y

n

n

i

k

redukcj

i

( s

)

o

dcine

k

o

dcine

k

o

dcine

k

3

6

1

7

3

1/

3

1/

6

1/

1

7

3

kwadrat

kwadrat

kwadrat

3

2

6

2

1

7

3

2

1/

3

1/

6

1/

1

7

3

sześc

i

a

n

sześ

c

i

a

n

sześc

i

a

n

3

3

6

3

1

7

3

3

1/

3

1/

6

1/

1

7

3

krz

y

wa Kocha

krz

y

wa Kocha

krz

y

wa Kocha

4

1

6

4

k

1/

3

1/

9

1/

3

k

Dla

odcin

ka,

k

wadrat

u

i

sześc

ia

nu

i

stn

i

ej

e

pr

oste

praw

o

wiążące

l

ic

zbę

częśc

i

a

i

wsp

ółcz

y

n-

n

i

k

iem red

ukcj

i

s

. Jest ono

dane wzorem:

a=

D

s

1

(*)

gdzie

D=1 dla

odcin

ka,

D=2 dla

kwadratu

,

i

D=3

dla

sze

śc

ia

nu.

Ozna

cza

to,

że

w

y

k

ł

adn

i

k

w

prawie

p

otęgow

ym

o

d

p

owiada

d

okładn

ie

l

ic

zbo

m

,

które

znam

y

ja

ko

w

ym

iar

y

odcin

ka,

kw

a-

drat

u

i

sześ

ci

a

nu. Jednak

j

eż

e

l

i

prz

y

jrz

y

m

y

s

ię

krz

y

w

e

j

Kocha,

to

związe

k

a=4

z

s

=

1/

3

i

a=

1

6

z s=

1/

9 nie bę

dzie tak

i ocz

y

w

i

st

y

.

Przekszt

ał

cam

y równa

n

ie (*) za

k

ładając, że je

st dla krz

y

we

j Kocha praw

dziwe:

4

=

3

D

log 4=D

log 3

D=

3

log

4

log



1,

2

6

1

9.

Czy otrzymamy jed

n

ak tę s

a

m

ą wartość, jeżeli weź

miemy mniejsze fragme

nty

,

n

a

przykła

d

dl

a

współczyn

nik

a

red

ukcji

1/

9

?

1

6

=

9

D

więc

log16

=D log

9

log 4

2

=D log

3

2

2

log 4

=

2D log

3

ostateczn

ie

D=



3

log

4

log

1,

2

6

1

9

.

W ogóln

ym prz

ypadku

D=

k

k

3

log

4

log

=



3

log

4

log

1,

2

6

1

9

.

Otrz

y

mujem

y

stąd,

że

praw

o

p

otęgowe,

o

pisujące

zal

eż

ność

l

ic

zb

y

fra

gme

ntów

o

d

wsp

ó

ł-

cz

y

n

n

i

k

a

redukcj

i,

daje

nam

tę

samą

l

iczbę

D,

n

ie

zale

ż

n

ie

od

sto

pnia

pomnie

j

sza

n

ia.

W

ła

ś

n

ie

tę l

ic

zbę D, zna

jdującą

si

ę pomiędz

y 1 a 2, na

z

y

w

am

y

w

ym

iarem

samop

o

d

o

bień

stwa

krz

y

we

j

Kocha.

Ogól

n

ie

j,

dla

d

ow

olne

go

o

biektu

samop

o

d

o

bneg

o

istn

ie

je

zw

ią

ze

k

pomiędz

y

współcz

y

n

n

i

-

k

iem red

ukcj

i

s

a l

ic

zbą części

a

, na które

o

biekt może

b

yć po

dzielon

y

; je

st n

im

D=

s

a

/

1

log

log

.

D naz

y

wam

y

w

y

m

ia

rem samo

p

o

d

o

bie

ństwa.

I

n

ne w

y

m

iar

y

samop

o

d

o

bień

stwa

:

Obiekt

Ska

la

s

Częśc

i

a

W

y

m

iar

D

zbiór

Cantora

1/

3

k

2

k

log2/log3



0,

6

3

0

9

trójkąt Sierpiń

s

k

ie

go

1/

2

k

3

k

log3/log2



1,

5

8

5

0

d

ywa

n Si

erpiń

s

k

ie

go

1/

3

k

8

k

log8/log3



1,

8

9

2

8

Zbi

ór Cantora m

ożem

y otrz

y

mać z

a pom

ocą nastę

p

ującej proce

d

ur

y. Zacz

y

n

am

y

od

prze

dzi

a-

łu

[0

,

1],

na

stępn

ie

usuwam

y

otwart

y

przedzia

ł

(1/2

,

2/

3)

.P

oz

ostają

dwa

przedział

y

:

[0,1/

3]

i

[2/

3

,

1],

o długości 1/

3 każd

y

. Kończ

y

m

y

w te

n

spos

ó

b p

o

dstaw

ow

y

krok

konstrukc

j

i. Nastę

p-

n

ie

powtarzam

y

krok

ko

nstrukc

j

i

w

te

n

sposó

b

,

że

z

powstał

y

c

h

po

prze

dnio

prze

działów

us

uwam

y

ic

h

częś

ć

środkową, otrz

ymując

w

te

n

s

p

os

ó

b

czter

y

przedział

y

o

długości

1/9

ka

ż-

d

y.

Da

le

j

postę

p

ujem

y

ta

k

s

amo.

W

gran

ic

y

otrz

y

mam

y

zbiór

Cantora.

Ma on

n

ieprzel

icza

l

ną

l

iczbę

p

unktów,

ale

długość

równą

zero,

jest

to

zbiór

d

o

mkn

i

ęt

y

n

i

gdzi

e

gęst

y

(

n

ie

z

aw

iera

żadne

go

n

iepustego

p

o

dz

bior

u

otwartego)

.

Na

r

y

sunku

n

iże

j

przedstawiono

k

i

l

ka

w

yr

azów

cią

gu

zbieżne

go

d

o

z

bior

u

Cantora.

Twi

erdz

enie

Bana

ch

a o punkci

e

s

tał

y

m

Definicja

1.

Przestr

zenią

metryczn

ą

(

M

;



)

n

az

y

wamy

zbi

ór

M

wraz

z

pewną

o

per

a-

cją



,

zwa

n

ą

d

alej

metryką,

kt

óra

k

aż

dej

p

arze

(x

,y)

element

ów

x

i

y

przest

rzeni

M

przyp

o-

rządk

owuje

liczbę

rzec

zy

wi

stą,

nieu

jemn

ą



(x,y),

z

wan

ą

d

alej

o

dle

gł

ości

ą

p

u

nkt

u

x

o

d

p

u

n

k-

tu

y,

przy czym o

per

acj

a



s

peł

ni

a

n

astę

p

uj

ące wa

ru

nki:



(x,y)





(x,y) +



(x,y)

z

wany

waru

nkiem tr

ójka

t

a,



(x,y) = 

(y,x)

symetria,



(x,y) =

0



x=y.

Definicja

2.

Ci

ą

g

{

a

n

}

p

u

nkt

ów

przestrz

eni

met

rycznej

(

M

;



)

n

azywamy

cią

g

iem

Ca

u-

ch

y

’e

go

,

jeżeli

dl

a

każ

de

g

o



>

0

ist

nieje

t

akie

n

0

,

że

dl

a

k

aż

de

g

o

p

i

q

większego

o

d

n

0

m

a

miejsce nierówn

ość:



(a

p

,

a

q

)

<



.

Definicja

3.

M

ówimy,

że

przestr

zeń

metryczna

(

M

;



)

jest

zu

peł

n

a,

jeżeli

każ

dy

ci

ą

g

Ca

uc

hy

’eg

o

jest z

bieżny

d

o

pewneg

o

p

u

nkt

u

przestrzeni (

M

;



).

Definicja

4

.

W

przestrzeni

metryc

znej

fu

nkcj

a

F

jest

ciąg

ł

a

w

pu

nkcie

x

0

wtedy

i

tylko

wtedy, g

dy

dl

a k

aż

de

g

o ci

ą

g

u {x

n

} z

ach

o

dzi

im

plik

acj

a

(x

n



x

o)



(F(x

n

)



F(x

0

)

Definicja

5.

Niech

(

M

;



)

bę

dzie

przestrzenią

metryczną

oraz

A:

M



M

niech

bę

dzie

cią

głym

o

dwzorowan

iem

t

akim,

że:





;0

<



<

1;



x,y



M

;



(

A

x,

Ay

)









(x,y).

Odwz

o

rowanie

A

n

azywamy wtedy

o

dwzoro

wan

iem zw

ężającym.

Twierdzenie

Ban

ach

a

;

K

ażde

ci

ą

głe

o

dwzorowan

ie

zw

ężające

A

:

M



M

zu

peł

nej

prz

e-

strzeni

metryc

znej

(

M

;



)

m

a

d

okł

a

d

nie

je

de

n

p

u

nkt

st

ały

x

*



M

.

Jest

o

n

gr

a

nic

ą

ci

ą

g

u

{x

0

,

x

1

,

x

2

,

..

.},

g

dzie x

0

jest

d

owolnym

elementem

z

bi

or

u

M

,

a x

n+1

= Ax

n

;

A

x*=x

*

.

Zac

h

o

dzi

oszac

owa

nie



(x

n

,x*)









1

n



(

x

0

,x

1

)

p

o

nieważ



(x

m

,x

n

)







(

x

m

-

1

,x

n

-

1

)





2



(x

m

-

2

,x

n

-

2

)



...





n



(

x

m

-

n

,x

0

)





n

{



(x

0

,x

1

)

+



(x

1

,x

2

)

+

+



(x

2

,x

3

)

+

..

.

+



(x

m

-

n

-

1

,x

m

-

n

)}





n



(x

0

,x

1

){1

+



1

+



2

+



3

+

..

.

+



m

-

n

-

1

}

=

=



n



(x

0

,x

1

)













1

1

1

n

m

w gra

nicy m





otrzymujemy



(x*

,x

n

)





n



(x

0

,x

1

)





1

1

(cnd)

Punkt

st

ały

Ax

*

=

x

*



M

jest

tylk

o

je

de

n

.

Jeżeli

zał

oż

ymy,

że

istniej

ą

dwa

róż

ne,

t

o

d

o

pr

o-

wadzamy

d

o

sprzeczn

ości:



(x*,y

*)

=



(

A

x*,

Ay

*)







(x,y) ;

0<



<1

.

Twie

rdzenie

B

a

n

ac

h

a

może

mieć

z

astos

owa

nie

d

o

frakt

ali

.

Z

p

o

przedn

ich

rozważa

ń

w

y-

nik

a,

że

zb

ór

Can

t

ora

czy

kr

zy

wa

Koch

a

są

gra

n

icą

cią

g

u

otrzyma

ne

g

o

w

w

yniku

pewnych

przekształceń

o

dci

nk

a.

Jeżeli

c

hcemy

d

o

o

pis

u

frakt

ali

z

astos

ować

twierdzenie

B

a

n

ac

h

a,

to

trzeb

a

zdefi

ni

ować

przestrzeń

metr

yczną

zu

peł

n

ą

.

Eleme

nt

ami

tej

przestr

zeni

bę

d

ą

zbi

ory

p

u

nkt

ów (

w n

aszym przyp

a

dk

u

p

o

dz

bi

ory

przestr

ze

ni

R

2

).

Niech (X,



)

będzie

d

owol

n

ą

przestr

zenia metryczn

a z

u

pełn

ą

. Ozn

aczmy przez

H

(X) prz

e-

strzeń,

której

eleme

nt

ami

s

ą

zwarte

i

nie

p

uste

p

o

dz

bi

ory

przestrzeni

X.

W

przestr

zeni

H

(X)

defi

ni

uje

się tzw. metrykę Haus

d

orffa

.

Niech

A

i

B

będ

ą

zwartymi

i

nie

p

ustymi

p

o

dzbi

o

rami

przestr

zeni

X,

a

x

i

y

eleme

nt

ami

przestrz

eni

X

,

przy

czym

a



A

i b



B.Jeżeli



(x,y)

ozn

acza o

dle

gł

ość

mię

dzy

ele

mentami

x

i

y

,

to

wyrażenia

d(x,B)

=

y

min

{



(

x,y): y



B},

d(y,A)

=

x

min

{



(

x,y): x



A}

oz

n

aczaj

ą o

d

p

owied

ni

o o

dle

gł

ość

p

u

nkt

u

x o

d

zbi

or

u

B

i o

dle

gł

ość

y

o

d

zb

i

oru A.

Z

k

olei

w

yraże

nia

d(A,

B)=

x

max

{d(x,

B):x



A},

d(B,

A)=

y

max

{d(y,

A):y



B}

oz

n

aczaj

ą

o

d

p

owied

ni

o

o

dle

gł

ość

zbi

or

u

A

o

d

z

bi

or

u

B

i

o

d

legł

ość

zb

i

oru

B

o

d

zb

i

oru

A.

S

ą

to

n

a

o

g

ół

róż

ne

o

dle

gł

ości.

Jeśli A



B,

t

o

d(A

,B

)=

0

Definicja

6.

Wyrażenie

h(A,

B)=m

ax{

d(A,

B)

,

d(B,

A)}

jest n

azywane

metryką

H

a

usd

orff

a

(spełn

i

a wszy

st

kie trzy aksjom

aty

metryki).

Zbi

ór

H

(X)

,

w

którym

wprowadz

o

n

o

metrykę

Ha

us

d

orffa

,

bę

dziemy

n

azywali

przestrz

e-

ni

ą fr

akt

ali i

będziem

y oz

n

aczal

i ją

przez (

H

(X),

h)

. Możn

a

u

d

owo

d

nić, że jest zupeł

n

a

, t

o zn

a-

czy ze każdy ci

ą

g

Ca

uc

hy’e

g

o

{A

n

}

m

a

gr

a

nicę

A

*

w przest

rzeni frakt

ali

.

Na

rysu

nk

u

niżej

p

ok

az

a

n

o

pierws

ze

wyrazy

ciąg

u

„

dziur

awych

trójk

ąt

ów”

(równo

b

oc

z-

nyc

h

o

b

ok

ac

h

równyc

h

je

de

n)

.

Po

nieważ

każ

dy

n

astęp

ny

trójk

ąt

z

awiera

się

w

po

przed

nim,

wię

c

odle

gł

ość

między

dwom

a

wy

razami

A

n

iA

m

(gdzie

m>

n)

te

g

o

cią

g

u

wynosi

h(A

n

,A

m

)=

d(A

n

,

A

m

)<2

-

n

.

Jest

t

o

cią

g

Ca

uc

hy’e

g

o

,

a

je

g

o

gra

nic

a

n

azywa

się

trójk

ątem

Sie

r-

pi

ńskieg

o

.

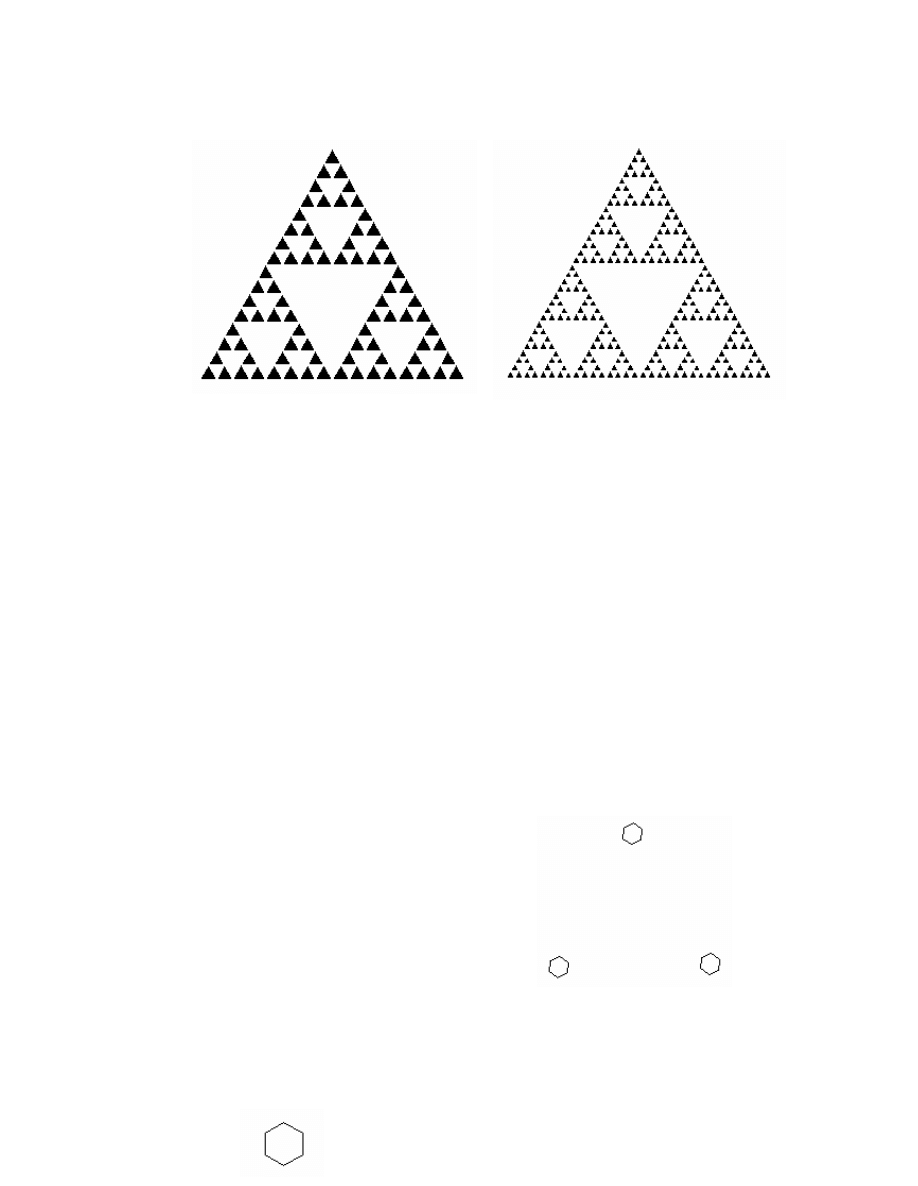
Cią

g

kończ

y

s

ię

na

szóst

y

m w

y

raz

ie ponieważ odl

eg

łość dalsz

y

c

h w

yr

azów

o

d sz

óstego

(w

sens

ie metr

y

k

i

Hausdo

rffa) jest bardz

o

mała.

Okazuj

e si

ę, że frakta

le można otrz

ymać przez o

pe

rację zdef

i

niowa

ną w

na

stępując

y

sp

osó

b: w

yobraźm

y sobie kopiarkę która

otrz

ymuj

e na we

jśc

iu o

b

raz

d

o

p

rzetwo

rzen

ia. W

y

-

p

osażona jest ona w k

il

k

a n

iez

a

leż

n

y

c

h s

y

st

emów

soczewek, z któr

y

c

h ka

żd

y pomnie

js

za

o

braz

p

oczątkow

y i umies

zcza

go gdzieś na w

y

j

ś

c

i

u

. Istotne są następujące parametr

y kopia

r-

k

i

:



l

iczba s

y

s

temów soczewek,



współcz

y

n

n

i

k pomnie

js

ze

n

ia,

os

o

bn

y

dla k

ażdego

s

y

s

temu soczewek,



ustawie

n

ie s

y

stemu soczewek prz

y tworzen

iu

o

bra

zu na w

y

j

śc

iu.

Po

dstaw

ową zasadą jest sprzężen

ie zwrotne; o

b

raz

p

o

przetw

orzeniu

przez ko

piarkę j

est

przetwarzan

y

ponownie ja

ko o

braz

wejśc

iow

y

. Pro

ces ten

jest powtarzan

y

w

ie

lokrotnie. Jeśl

i

mam

y do cz

y

n

ie

n

ia z

kopiarką o jedn

ym s

y

s

tem

ie soczewek, to wielokrotne kopiowanie pr

o-

wadzi d

o

otrz

yma

n

ia punktu (

rezultat niezb

y

t c

ie

k

aw

y

). W p

rz

ypadku zastos

owani

a wie

lu

s

y

s

temów soczewek w

y

n

i

k

i

e

ksper

y

me

ntu m

ogą b

y

ć

bardz

o

eksc

y

tują

ce (możem

y rozważać

również przekszta

łc

e

ni

a bar

dziej ogóln

e o

d

p

o

d

o

bi

eń

stw).

Zajmi

jm

y

s

ię

kopiarką z trzema s

y

stemam

i soczew

ek, z któr

y

c

h każd

y

jest ustawion

y

tak, b

y po

mni

ej

szać w s

ka

l

i ½. Po

p

omnie

jsze

n

iu trz

y

kopie ustawione są na pla

n

ie trójkąta

równo

b

ocznego. Na r

ysun

ka

c

h n

iże

j przedstawiono

w

y

n

i

k s

ześc

iokrotne

go kopi

owan

ia d

o-

wolne

go o

b

razu

p

oczątkowego. Okazuje się, że k

s

ztałt ob

razu

p

oczątkowego nie ma wpł

y

wu

na w

y

n

i

k

końcow

y

.

o

braz wejściow

y

pierwsza kopia

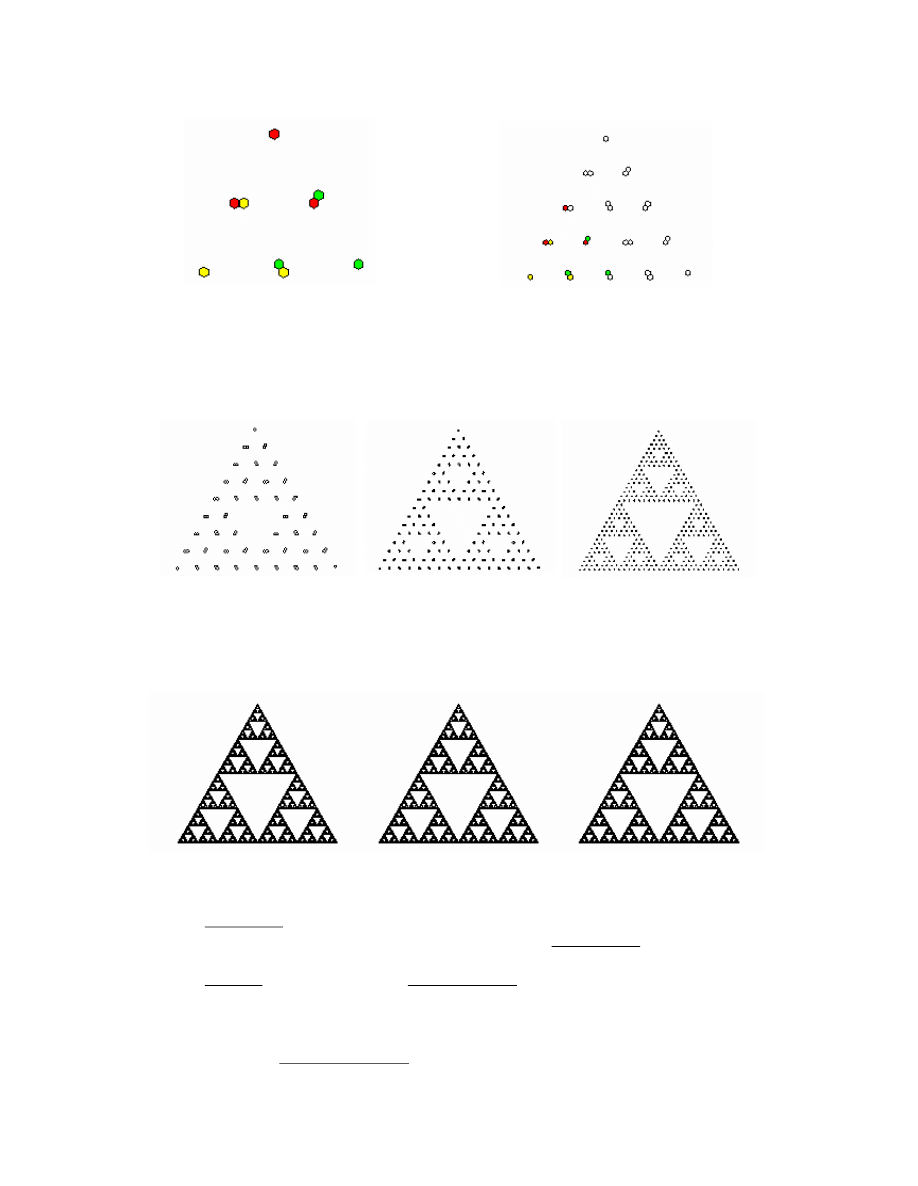
dr

uga ko

pia (kolorami oznacz

ono

trzecia kopia

trz

y zm

n

ie

jszon

e kopie)

Kolej

ne

o

peracje

przyp

omi

n

aj

ą c

or

az

b

ardziej tr

ój

kąt

S

ierpi

ńskieg

o

:

Ósmy

krok da

je n

am o

br

az, który (przy tej

rozdzielczości) nie zmieni

a się po

dcz

as d

a

l

szej

o

br

ó

bki.

Powyżs

ze roz

waża

ni

a

pr

owa

dzą

d

o wni

osków:



Niezależnie

o

d

o

br

azu

p

ocz

ątk

owego

,

p

o

wielokr

ot

nym

przet

warzan

i

u

g

o

przez

k

o-

pi

arkę

o

trzymamy

cią

g

o

br

azów,

które

d

ążą

d

o

teg

o

s

ameg

o

o

braz

u

k

o

ńcoweg

o

(char

akterystycznego

dl

a

d

a

nej k

o

pi

arki).

Nazywamy g

o

atrakt

ore

m

pr

ocesu.



Atrakt

or

p

o

d

d

a

ny k

o

pi

owa

ni

u

nie zmien

i

a się.

Okazuje

się,

że

używając

wynik

ów

Felixa

Ha

us

d

o

rffa

i

Stef

a

n

a

B

a

n

ac

h

a,

możemy

p

ok

a-

zać,

iż

d

owoln

a

KWR

(kopi

ark

a

wielokrot

nie

red

uk

uj

ąc

a)

d

o

pr

owadz

a

d

o

je

d

n

oz

n

aczne

g

o

o

br

azu

k

o

ńc

owego

,

swojeg

o

atrakt

or

a.

Je

dy

n

ą

wł

as

n

ością

,

j

aką

KWR

m

usi

speł

ni

ać

jest

to

,

a

by k

aż

dy system soczew

ek p

om

niejszał

o

br

az

p

oc

zątkowy.

Ukł

ad i

te

row

anych odwzoro

wa

ń

S

y

stem

y

soczewe

k

dla

nasz

ej

KWR

można

opisa

ć

za

pom

ocą

p

rzekszta

ł

ce

ń

a

f

i

n

icz

n

y

c

h

płaszcz

y

z

n

y

.

Przek

szta

łce

n

ie

a

fi

n

i

cz

ne

w

i

(x,

y

)

p

unktu

(x,

y)

można

przedstawić

ja

ko

ukł

ad

równań :

u

=ax+b

y+e,

v=cx+d

y+f,

gdzie (u,v)

= w

i

(x,

y).

W

an

al

iz

i

e

iterac

y

j

n

e

go

s

y

stemu

o

dwzo

r

owań

bar

dz

o

ważne

jest

badani

e

o

bie

któw,

które

są

lewostronn

ie

n

ie

zmi

e

n

ni

cze

po

d

je

go

działa

n

i

em.

D

y

spo

nując

przeks

ztał

ce

n

iem

a

f

i

n

ic

z-

n

y

m

w

i

m

ożem

y

poszukiwać

punktów,

któ

re

są

le

wostr

onn

ie

n

iezm

ie

n

n

icze

ze

wz

g

lędu

na

w

i

w

i

(x,

y) = (x,

y). Otrz

y

mujem

y uk

ład r

ówna

ń

:

x=ax+b

y+e,

y

=bx+c

y+f.

Rozwiąza

n

ie

te

go

układu

istn

ie

je

i

je

st

j

ednoznac

zne,

gd

y

w

y

z

n

acz

n

i

k

(a

- 1)(

d

-

1)

-

bc



0.

Punkt

P=(x*,

y

*

)

naz

y

wam

y

pun

ktem

sta

ł

y

m

dla

w

i

.

Jego

wsp

ółrzędne

w

yr

aża

ją

s

ię

na

stęp

u

-

jąco:

x

*=

bc

d

a

bf

d

e













)

1

)(

1

(

)

1

(

,

y

*=

bc

d

a

ce

a

f













)

1

)(

1

(

)

1

(

.

S

y

stem

y

soczewe

k

KWR

są

opisane

za

pom

ocą

zbi

or

u

przekszta

łce

ń

a

f

i

n

icz

n

y

c

h

w

1

,

w

2

,

..

.,

w

N

.

Dla

danego

o

braz

u

p

oczątkowego

A

na

jpierw

otrz

ymujem

y

pomnie

j

szone

af

i-

n

icz

n

ie

e

gzemplarze

w

1

(A),

w

2

(A),

..

.,w

k

(A)

.

Następnie

kopiarka

s

k

łada

te

kopie

razem,

b

y

w

y

tworz

y

ć ob

raz końcow

y W(A):

W(A)

= w

1

(A)



w

2

(A)



.

..



w

N

(A).

Przekszt

ał

ce

n

ie

w

i

jest

o

dwzo

r

owani

em

zwęża

jąc

y

m

przestrze

n

i

(X,



)

(w

nasz

y

m

prz

y-

k

ł

a

dzie płas

zcz

y

z

n

y

) w siebie. Dl

a wsz

y

st

k

ic

h punktów x

1

, x

2



X spełn

ion

y

je

st wię

c warunek



(w

i

(x

1

),

w

i

(x

2

))





i





(x

1

, x

2

) ;

0

<



i

<

1

Zbi

ór

N o

dwzo

r

o

wań

zwęża

j

ąc

y

c

h

naz

y

w

am

y

ukła

dem

iterowa

nyc

h

o

dwzorowa

ń

i

ozn

a-

czam

y

{X; w

1

,

w

2

,

w

3

,

..

.,

w

N

}.

Współcz

y

n

n

i

k

i

em zwęża

n

ia te

go

układu jest na

jw

i

ęk

sza ze sta

ł

y

c

h



i

t

yc

h odwz

or

owań:



=max{



1

,



2

,



3

, .

..

,



N

}.

M

ożna

pokazać,

że

operacja

W

speł

n

ia

w

p

rzestrzen

i

fra

kta

li

(

H

(X),

h)

z

metr

y

k

ą

Hau

s-

d

orffa warunek

h(W(A), W(B))

≤



h(A,

B)

Operacja

W

jest

w

ięc

operacją

zwężaj

ącą

w

prze

strzen

i

metr

y

c

z

ne

j

zupełne

j

(

H

(X),

h).

W

y

n

i

k

a

ją

stąd

wsz

y

s

t

k

ie

kon

se

kwe

nc

je

s

form

uło

wane

w

tw

ierdzen

iu

Ba

na

c

ha

o

odwz

or

ow

a

-

n

iac

h

zwęża

ją

c

y

c

h.

W

sz

cze

gól

ności,

dla

dow

oln

ego

A

0



H

(X)

cią

g

okreś

lon

y

z

a

leż

ności

ą

rekurenc

y

j

n

ą

A

n

+1

=W(A

n

)

j

est

zbież

n

y

do

gra

ni

c

y

A*,

która

je

st

jed

y

n

y

m

rozwią

za

n

iem

ró

w-

na

n

ia A=W(A)

Generowan

ie

obraz

ów

A*

(atraktor

ów

o

peracji

W

)

o

pisa

ną

w

y

że

j

meto

dą

m

oże

się

ok

a-

zać

n

awet

dla

współczes

n

y

c

h

(2

0

0

7

r

ok)

kom

p

ut

erów

cz

y

n

nośc

ią

długotrwałą.

Takie

same

w

y

n

i

k

i

z

nacz

n

ie

sz

yb

c

ie

j

można

otrz

ymać

za

p

o

mocą

l

os

owej

ko

pi

arki

wielokrot

nie

re

d

uk

u

-

jącej

(LKWR). Przekszta

łce

n

ia

n

ie będą st

os

owan

e d

o

fi

gur, a jed

y

n

ie d

o

p

ojed

y

ncz

y

c

h pun

k-

tów

.

Nie

stosujem

y

w

sz

y

st

k

ic

h

s

y

stemów

soczewek

jednocześ

n

ie.

W

każd

y

m

kroku

w

yb

i

e-

ram

y

losowo

(z

pewn

y

m

praw

d

o

p

o

d

o

bień

stwem)

jeden

z

n

ic

h

i

przeks

zta

łcam

y

z

a

je

go

p

o

-

mocą p

o

prze

dni

w

y

n

i

k.

Kopiarka

n

ie

po

p

rzestaje

na

stw

orzen

iu

o

braz

u p

ojed

y

ncz

e

go p

unktu,

ale

z

apamiętuje

wsz

y

s

t

k

ie

w

y

g

e

nerowane

wc

ześ

n

i

ej

punkt

y.

W

sz

y

st

k

i

e

te

p

unkt

y

s

k

ładają

s

i

ę

na ostatecz

n

y obraz tw

o

rz

on

y

przez nas

zą masz

y

n

ę.

KWR w

y

z

nac

zona

je

st przez N af

i

n

icz

n

y

c

h

odwz

o

rowań zwęża

jąc

y

c

h

w

1

, w

2

, w

3

, .

..

,

w

N

.

Od

p

owiednia

L

KWR

okreś

lona

j

est

przez

te

same

p

rzekszta

łc

e

ni

a

i

przez

(

d

o

datnie)

praw

d

o-

p

o

d

o

bień

stwa

ta

k

ie,

że





N

i

i

p

1

=1

.

Ko

rz

y

st

n

ie

je

st

w

ybra

ć

dla

LK

WR

punkt

początkow

y

na

l

e-

żąc

y

do

at

raktora

A*.

Każd

y

n

astępn

y

punkt

uzy

s

k

a

n

y

w

w

y

n

i

ku

p

rzekszta

ł

ce

ń

w

i

bę

dzie

również

na

leża

ł

do

tego

atrakto

ra

(w

y

n

i

ka

to

z

n

i

ezmie

n

n

ic

zości

atra

ktora

A*).

Jeżeli

punkt

p

oczątkow

y

n

i

e n

a

leż

y

do A*, t

o w

y

starcz

y

od

rz

u

cić

s

kończoną

i

lość p

oczątkow

y

c

h w

y

razów

cią

gu x

0

, x

1

, x

2

,

..

..

, gdzie x

j+1

=w

i

(x

j

)

(w

i

jest d

la ka

żdego j nie

za

leż

n

ie losowane).

Oto

prz

y

k

ład

y

dzi

ał

a

ni

a

LK

WR

(w

tabel

i

po

dane

są

współcz

y

n

n

i

k

i

zastosowan

y

c

h

prz

e-

ks

zta

łce

ń

a

f

i

n

icz

n

y

c

h

oraz

o

d

p

owiednie

prawd

o

p

o

d

o

bień

stwa,

z

któr

ym

i

te

przekszta

łc

e

ni

a

b

y

ł

y

losowane)

:

R

y

s.1.

R

y

s.2.

R

y

s.3.

R

y

s.4.

R

y

s.5.

R

y

s.6.

R

y

s.7.

R

y

s.8.

w

i

a

b

c

d

e

f

p

1

-

0

,

6

7

- 0

,

0

2

- 0

,

1

8

0

,

8

1

0

,

0

0

0

,

0

0

0

,

3

3

2

0

,

4

0

0

,

4

0

- 0

,

1

0

0

,

4

0

0

,

0

0

5

,

0

0

0

,

3

3

3

-

0

,

4

0

- 0

,

4

0

- 0

,

1

0

0

,

4

0

0

,

0

0

5

,

0

0

0

,

3

3

Ry

s.1.

4

0

,

0

0

0

,

0

0

0

,

0

0

0

,

0

0

0

,

0

0

0

,

0

0

0

,

0

0

1

-

0

,

6

7

- 0

,

0

2

- 0

,

1

8

0

,

8

1

0

,

0

0

2

,

3

0

0

,

3

0

2

0

,

4

0

0

,

4

0

- 0

,

1

0

0

,

4

0

0

,

0

0

3

,

0

0

0

,

3

0

3

-

0

,

4

0

- 0

,

4

0

- 0

,

1

0

0

,

4

0

0

,

0

0

3

,

0

0

0

,

3

0

Ry

s.2.

4

-

0

,

1

0

0

,

0

0

0

,

4

4

0

,

4

4

0

,

0

0

0

,

0

0

0

,

1

0

1

0

,

0

0

0

,

0

0

0

,

0

0

0

,

1

6

0

,

0

0

0

,

0

0

0

,

2

0

2

0

,

8

5

0

,

0

4

- 0

,

0

4

0

,

8

5

0

,

0

0

1

,

6

0

0

,

8

0

3

0

,

2

0

- 0

,

2

6

0

,

2

3

0

,

2

2

0

,

0

0

1

,

6

0

0

,

2

0

Ry

s.3.

4

-

0

,

1

5

0

,

2

8

0

,

2

6

0

,

2

4

0

,

0

0

0

,

4

4

0

,

2

0

1

-

0

,

6

7

- 0

,

0

2

- 0

,

1

8

0

,

8

1

0

,

0

0

2

,

3

0

0

,

3

3

2

0

,

4

0

0

,

4

0

- 0

,

1

0

0

,

4

0

0

,

0

0

0

,

0

0

0

,

3

3

3

-

0

,

4

0

- 0

,

4

0

- 0

,

1

0

0

,

4

0

0

,

0

0

0

,

0

0

0

,

3

3

Ry

s.4.

4

0

,

0

0

0

,

0

0

0

,

0

0

0

,

0

0

0

,

0

0

0

,

0

0

0

,

0

0

1

0

,

8

0

- 0

,

2

5

0

,

6

8

0

,

8

0

0

,

0

5

1

,

1

0

0

,

5

0

2

0

,

8

0

0

,

2

5

- 0

,

6

8

0

,

8

0

- 0

,

0

5

1

,

1

0

0

,

5

0

3

0

,

0

0

0

,

0

0

0

,

0

0

0

,

0

0

0

,

0

0

0

,

0

0

0

,

0

0

Ry

s.5.

4

0

,

0

0

0

,

0

0

0

,

0

0

0

,

0

0

0

,

0

0

0

,

0

0

0

,

0

0

1

0

,

8

0

0

,

3

0

- 0

,

2

0

1

,

0

0

- 2

,

2

0

0

,

2

0

0

,

7

0

2

0

,

2

0

0

,

3

0

- 0

,

5

0

0

,

0

0

0

,

5

0

3

,

0

0

0

,

3

0

3

0

,

0

0

0

,

0

0

0

,

0

0

0

,

0

0

0

,

0

0

0

,

0

0

0

,

0

0

Ry

s.6.

4

0

,

0

0

0

,

0

0

0

,

0

0

0

,

0

0

0

,

0

0

0

,

0

0

0

,

0

0

1

0

,

8

0

0

,

3

0

- 0

,

2

0

0

,

8

0

- 2

,

0

0

- 0

,

2

0

0

,

7

0

2

0

,

1

0

0

,

5

0

- 0

,

5

0

- 0

,

3

0

0

,

0

0

8

,

0

0

0

,

3

0

3

0

,

0

0

0

,

0

0

0

,

0

0

0

,

0

0

0

,

0

0

0

,

0

0

0

,

0

0

Ry

s.7.

4

0

,

0

0

0

,

0

0

0

,

0

0

0

,

0

0

0

,

0

0

0

,

0

0

0

,

0

0

1

0

,

5

0

0

,

0

0

0

,

0

0

0

,

5

0

3

,

0

0

0

,

0

0

0

,

3

3

2

0

,

5

0

0

,

0

0

0

,

0

0

0

,

5

0

- 3

,

0

0

0

,

0

0

0

,

3

3

3

0

,

5

0

0

,

0

0

0

,

0

0

0

,

5

0

0

,

0

0

5

,

0

0

0

,

3

3

Ry

s.8.

4

0

,

0

0

0

,

0

0

0

,

0

0

0

,

0

0

0

,

0

0

0

,

0

0

0

,

0

0

W

tabel

i

przedstawiono

wsp

ółcz

y

n

n

i

k

i

,

które

je

dnoznacz

n

ie

okreś

la

j

ą

przekszt

ał

ce

n

ia

af

i

n

icz

ne

w

i

.

U

k

ład

ki

l

ku

(w

n

asz

y

c

h

prz

y

k

ł

adac

h

dw

óch,

trzech,

lub

czterech)

przekszta

łce

ń

jednozna

cz

n

ie okre

śl

a pewie

n

obraz

. Wła

s

ność ta

może b

yć w

y

korz

y

s

ta

na do komp

resj

i obr

a-

zu.

Wpr

owa

dzeni

e

e

leme

ntu

losow

ości

d

o

kla

s

y

cz

ne

g

o

determini

st

y

cz

ne

go

fra

kta

la

jest

na

j-

p

r

ostsz

y

m spos

o

bem,

któr

y um

ożli

wi w

y

g

e

n

erowan

ie rea

l

ist

y

cz

n

y

c

h

k

szta

łtów.

Jako

prz

y

k

ład

w

y

korz

y

stam

y

drzewo

bin

arne.

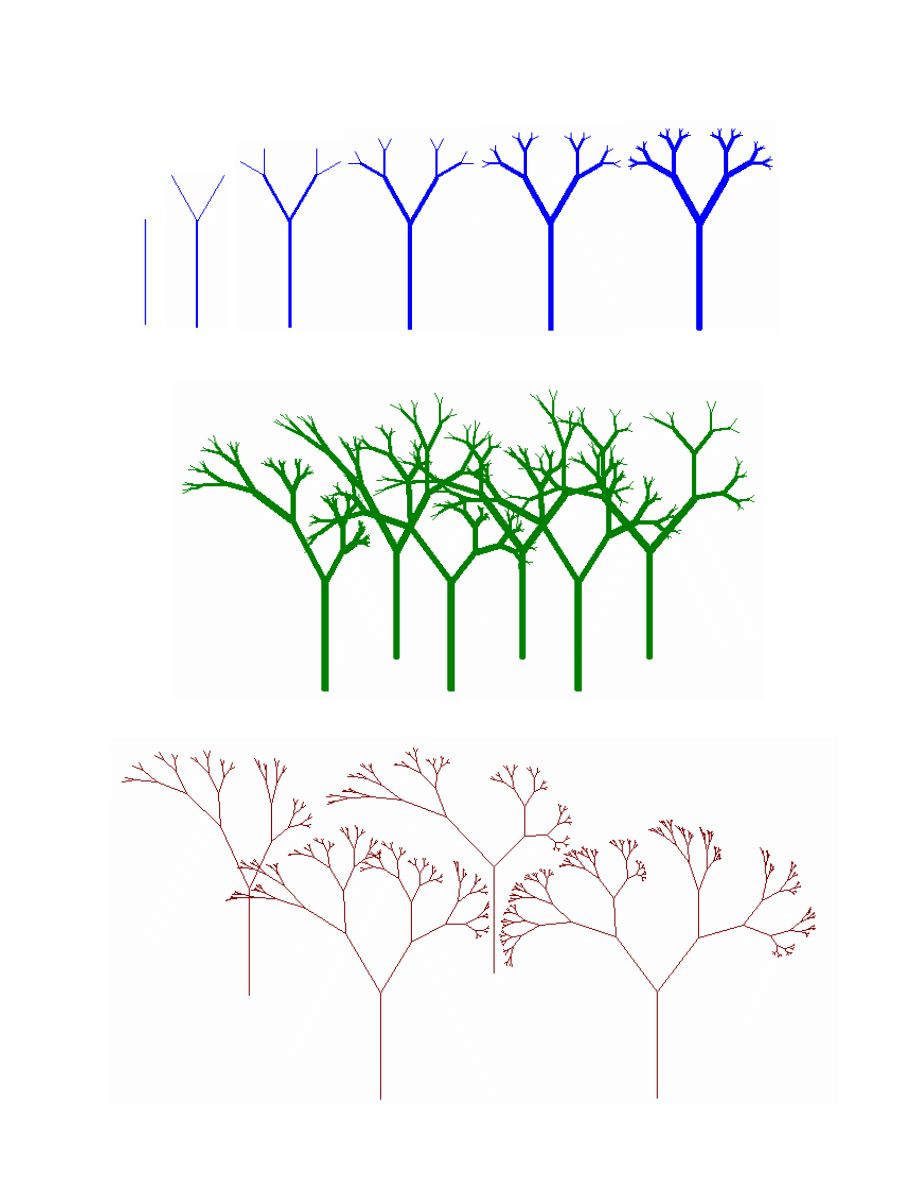
Oto

, jak real

i

zujem

y determi

n

ist

y

cz

n

y

a

l

gor

ytm w

zrost

u:

A teraz tw

orz

ym

y „l

as” bardziej real

i

st

y

c

z

n

y

:

lub