1) Przyczyny i skutki autokorelacji składnika losowego.

Skutkiem autokorelacji składnika losowego jest pogorszenie efektywności estymatora KMNK, co w konsekwencji
prowadzić może do błędu poznawczego, czyli zmniejszenia jego precyzji albo dokładności.
Jeśli w modelu wystąpi autokorelacja składnika losowego to należy ustalić jej przyczynę i tę przyczynę usunąć.
Przyczyny autokorelacji składnika losowego:
1)wadliwa postać analityczna modelu, czego konsekwencją jest dodatnia autokorelacji składnika losowego.
Najważniejszym zadaniem jest znaleźć adekwatną postać analityczną modelu w skutek czego autokorelacja znika.
2)w modelu może zabraknąć ważnej, czyli istotnej statystycznie zmiennej objaśniającej, konsekwencją tego będzie
dodatnia autokorelacji składnika losowego. W takim przypadku należy ustalić ową brakującą istotną zmienną objaśniającą i
uwzględnić ją w modelu empirycznym, w skutek tego autokorelacja znika. Musimy skonstruować taki model, w którym
będą wszystkie zmienne objaśniające, bo brak takiej powoduje autokorelację. Jednak może się zdarzyć, że w modelu
świadomie pominęliśmy ważną zmienną objaśniającą z powodu braku informacji statystycznych, albo zbyt dużego
uszczerbku w szeregu statystycznym tej zmiennej. W takiej sytuacji zaleca się dla uniknięcia autokorelacji składnika
losowego wprowadzenie tzw. zmiennej symptomatycznej, czyli zmiennej objaśniającej zastępczej. Model z taką zmienną
nosi nazwę modelu symptomatycznego.

Istotą zmiennej symptomatycznej jest:
(1) że znane są prawdziwe obserwacje statystyczne na tej zmiennej
(2) że jest ona bardzo silnie skorelowana ze zmienna przyczynową, którą w modelu zastępuje. W zasadzie ta korelacja powinna być ,,+” , a współczynnik
korelacji powinien przekraczać 0,9 , a nawet nie kiedy 0,95. Możliwość uwzględnienia danej zmiennej jako symptomatycznej istnieje tylko wtedy, gdy
posiadamy informacje dodatkowe o skorelowaniu zmiennej symptomatycznej ze zmienną przyczynową. Uwzględnienie zmiennej symptomatycznej
eliminuje z zasady dodatnią autokorelację składnika losowego.
(3) ujemna autokorelacja składnika losowego może się pojawić wówczas gdy model empiryczny zawiera nadmiar zmiennych objaśniających oznacza to
ze w modelu empirycznym występuje wiele zmiennych objaśniających nie istotnych statystycznie. W takim modelu jest duża częstotliwość zmiany
znaków przez reszty. Jeśli często zdarzają się sytuacje, że po reszcie dodatniej jest ujemna, a po ujemnej dodatnia to zdominuje ujemną autokorelację
reszt. Ujemna autokorelacja znika po wyeliminowaniu nie istotnych statystycznie zmiennych objaśniających.

2) Równania oderwane w ekonometrycznym modelu małego przedsiębiorstwa.

Równania które pozostają poza układem powiązanym sprzężeniami zwrotnymi oraz zamkniętymi cyklami powiązań
zmiennych łącznie współzależnych nazywamy równaniami oderwanymi. Charakteryzują się one tym że w roli zmiennych
objaśniających występują wyłącznie zmienne z góry ustalone. Tym samym równania te mają identyczną postać jak w
modelu prostym. Estymacja równań oderwanych może być przeprowadzona KMNK, również eksploatacja tych równań
odbywa się analogicznie jak w przypadku modelu prostego.

3) Walory zredukowanej formy modelu małego przedsiębiorstwa.
Ważną rolę w układzie równań współzależnych odgrywa tzw. zredukowana forma modelu. Powstaje ona jako zestaw
równań stochastycznych, w których zmiennymi objaśniającymi są zmienne z góry ustalone całego modelu. Każde z tych
równań jest tak skonstruowane, że zmienna łącznie współzależna jest wyjaśniana jednocześnie przez wszystkie zmienne z
góry ustalone modelu. Przydatność równań formy zredukowanej ma charakter głównie technologiczny. Po pierwsze jest
ona niezbędna w procesie estymacji parametrów równań formy strukturalnej, w zastosowanej wcześniej metodzie 2MNK.
Równania formy zredukowanej mogą okazać się niezbędne w procesie szacowania prognoz, w sytuacjach zamkniętych
cykli powiązań lub bezpośrednich sprzężeń zwrotnych w jakich pozostają zmienne łącznie współzależne.

4) Identyfikacja modelu ekonometrycznego.
Identyfikacja modelu jest drugim etapem budowy modelu ekonometrycznego. Występuje tylko w przypadku modelu
wielorównaniowego. W modelach jednorównaniowych nie ma etapu II.

BC= -A równanie identyfikacyjne modelu.
Etap identyfikacji modelu jest to badanie poprawności konstrukcji modelu wielorównaniowego. Mówimy, że model jest
identyfikowany, czyli poprawnie skonstruowany, wówczas gdy równanie identyfikacyjne posiada rozwiązanie ze względu
na składowe macierzy B oraz macierzy A przy znanych składowych macierzy C. Równanie identyfikacyjne tworzy układ
równań liniowych.
Jeżeli układ równań linowych nie posiada rozwiązania, przy znanych składowych macierzy C, ze względu na składowe
macierzy B oraz A to model jest nieidentyfikowalny oznacza to wadliwą jego konstrukcję. Taki model musi być
przebudowany, czyli konieczna jest jego respecyfikacja.
Gdy układ równań posiada rozwiązanie mogą wystąpić dwa przypadki:

1. układ posiada rozwiązanie jednoznaczne, wówczas mówimy, że model jest identyfikowalny jednoznacznie (są to

rzadkie przypadki)

2. układ posiada rozwiązanie niejednoznaczne, wówczas mówimy, że model jest identyfikowalny niejednoznacznie.

Jest to model przeidentyfikowany, który posiada prawidłową konstrukcję.

Identyfikację przeprowadza się poprzez badanie każdego równania oddzielnie. Badamy 2 warunki:
1.Badamy liczbę zmiennych, których nie ma w danym równaniu Lg
Jeżeli Lg>= G-1 to może być identyfikowalny
Jeżeli Lg<G-1 to równanie to jest nieidentyfikowalne, a zatem i model jest nieidentyfikowalny, i zachodzi potrzeba
przebudowy modelu.
Jeżeli choć jedno równanie jest nieidenytfikowalne to model jest nieidentyfikowalny to trzeba go przebudować.
2. Trzeba zbudować macierz Wg z parametrem przy zmiennych, które nie występują w Gtym równaniu. Badamy rząd tej
macierzy. Jeżeli rz(Wg)=G-1 to równanie jest identyfikowalne

a) jeżeli równanie jest identyfikowalne to jest ono identyfikowalne jednoznacznie, gdy Lg=G-1
b) jeżeli równanie jest identyfikowalne i Lg> G-1 to równanie jest identyfikowalne niejednoznacznie
c)jeżeli rz(Wg)<G-1 to równanie jest nieidentyfikowalne

Jeżeli choć jedno równanie modelu jest nieidentyfikowalne to model jest nieidentyfikowalny to wtedy trzeba go
respecyfikować.
Jeżeli wszystkie równania modelu są identyfikowalne i choć jedno z nich jest identyfikowalne niejednoznacznie to model
jest identyfikowalny niejednoznacznie.

5) Ekonometryczna analiza popytu.
Przyrost realnych dochodów konsumentów pociąga za sobą zazwyczaj zwiększanie się popytu na rozmaite dobra. Reakcje,
wyrażające się wydatkami na różne dobra mogą być odmienne w zależności od zaspokajanych potrzeb.
Wyróżniamy trzy rodzaje dóbr: podstawowe – wiele rodzajów żywności, podstawowa odzież itd. zapotrzebowanie na te
dobra występuje przy każdym poziomie dochodów, popyt na te dobra nie przekracza pewnego pułapu maksymalnego
zwanego poziomem nasycenia.
Wyższego rzędu – charakteryzują się tym że popyt na nie powstaje dopiero przy pewnych odpowiednio wysokich
dochodach, ze wzrostem dochodów rosną wydatki na te dobra aż do osiągnięcia poziomu nasycenia.
Luksusowe – popyt rozpoczyna się od pewnego, zwykle wyraźnie wyższego, niż w przypadku dóbr wyższego rzędu. Wraz
z przyrostem dochodów, nieograniczenie wzrasta popyt na dobra luksusowe.

6) Sprzężenia zwrotne w ekonometrycznym modelu małej firmy.

Sprzężenia zwrotne pomiędzy grupami zmiennych łącznie współzależnych
powodują, że konstruowany model ekonometryczny jest układem równań
współzależnych. W związku z tym powstaje konieczność zbadania czy
poszczególne równania układu są identyfikowalne. Analiza wskazuje, że
każde z nich jest przeidentyfikowane. W związku z tym należy rozstrzygnąć
jaką metodę szacowania parametrów należy zastosować. By uzyskać zgodne
estymatory powinniśmy zastosować podwójną metodę najmniejszych
kwadratów. 2MNK oznacza dwukrotne zastosowanie KMNK; w pierwszym
etapie do oszacowania parametrów równań formy zredukowanej. W drugiej
fazie wykorzystuje się rezultaty szacowania teoretycznych wartości
objaśniających zmiennych łącznie współzależnych do oszacowania
parametrów formy strukturalnej.

7) Przyczyny i skutki współliniowości zmiennych w modelu ekonometrycznym.
Model musi być tak skonstruowany, aby nie występowała w nim współliniowość stochastyczna, jednak zdarzają się takie
modele, w których współliniowość stochastyczna jest nie unikniona czego przykładem jest klasyczna funkcja produkcji
P=f(k,l,n), gdzie k-kapitał, l-praca, n-składnik losowy. Występuje tu pomiędzy „k” i „l” współliniowość stochastyczna,
która jest wypadkową dwóch rodzajów powiązań kapitału z pracą:
1

o

związków substytucyjnych

2

o

powiązań komplementarnych

Znak wpółczynnika korelacji pomiędzy k a l wskazuje na przewagę określonych zależności. Znak + oznacza przewagę
komplementarności, znak – wskazuje dominację substytucji.
Często zdarza się w modelu silne skorelowanie pary zmiennych objaśniających, czyli współliniowość stochastyczna, przy
czym obie zmienne objaśniające zawierają w sobie podobny rodzaj informacji i oddziaływań na zmienną objaśnianą.
Pozostawienie w modelu obu zmiennych alternatywnych może prowadzić do pojawienia się stanu tzw. pozornej
nieistotności obu tych zmiennych, a w konsekwencji do błędu poznawczego.

8) Charakterystyka powiązań w ekonometrycznym modelu małego przedsiębiorstwa.

Wpływy pieniężne jako rezultat wcześniejszych dostaw towarów (przychody ze sprzedaży), przychody ze sprzedaży
wynikają z produkcji gotowej oraz marketingowego potencjału przedsiębiorstwa. Na produkcję gotową wpływ mają
zasoby pracy, majątek trwały, specjalizacja produkcji, właściwości wyrobów oraz wydajność pracy. Firma
charakteryzująca się wyższą wydajnością pracy ma szanse na niższe koszty wytwarzania. Wydajność pracy jest w
sprzężeniu zwrotnym z płacą oraz podlega wpływowi postępu technicznego i specjalizacji produkcji. Płace podlegają
oddziaływaniu wydajności pracy oraz autonomicznemu procesowi wzrostu płac i wpływom pieniężnym. Wielkość i jakość
zasobów pracy determinowane są przez płace, majątek trwały oraz sytuację demograficzną. Majątek trwały jest rezultatem
inwestycji kapitałowych i efektem zużywania się składników majątkowych. Możliwości inwestowania uwarunkowane są
przez rozmiary wpływów pieniężnych.

WPŁYWY PIENIĘŻNE  rezultat PRZYCHODÓW ZE SPRZEDAŻY
PRZYCHODY ZE SPRZEDAŻY  rezultat PRODUKCJI I DZIAŁAŃ MARKETINGOWYCH
PRODUKCJA  MAJĄTEK TRWAŁY + SPECJALIZACJA PRODUKCJI + WŁAŚCIWOŚCI WYROBU + ZASOBY/WYDAJNOŚĆ PRACY

WYŻSZA WYDAJNOŚĆ PRACY = NIŻSZE KOSZTY WYTWARZANIA

WYDAJNOŚĆ PRACY sprzężenie zwrotne PŁACA
WYDAJNOŚĆ PRACY  POSTĘP TECHNICZNY + SPECJALIZACJA PRODUKCJI

PŁACA  WYDAJNOŚĆ PRACY + AUTONOMICZNY PROCES WZROSTU PŁAC + WPŁYWY PIENIĘŻNE
WIELKOŚĆ/JAKOŚĆ ZASOBÓW PRACY  PŁACA + MAJĄTEK TRWAŁY + SYTUACJA DEMOGRAFICZNA

MAJĄTEK TRWAŁY  INWESTYCJE KAPITAŁOWE + ZUŻYWANIE SIĘ SKŁADNIKÓW MAJĄTKOWYCH
INWESTOWANIE  ROZMIARY WPŁYWÓW PIENIĘŻNYCH

9) Model ekonometryczny w wyborze efektywnego robotnika.
Gospodarka rynkowa charakteryzuje się występowaniem bezrobocia. Fakt występowania na rynku pracy przewagi podaży
nad popytem nie oznacza wcale, że przedsiębiorca z łatwością może zaangażować pracownika o odpowiednich cechach
osobistych, gwarantujących sprawne wykonywanie wyznaczonych mu zadań.
Zaangażowanie odpowiedniego człowieka na określone stanowisko pracy wymaga z jednej strony umiejętności
przygotowania i wykonania działań, w wyniku których przedsiębiorca posiadał będzie odpowiednio liczny zbiór
kandydatów. Ważne miejsce w tym przedsięwzięciu zajmuje informacja o warunkach pracy (płaca, dodatkowe
uprawnienia, czas i miejsce wykonywania obowiązków, perspektywy awansu zawodowego itd.). Z drugiej zaś strony
niezbędne jest precyzyjne zdefiniowanie wymagań, które musi spełnić człowiek ubiegający się o zaoferowane miejsce.
Kryterium oceny przydatności robotnika winna być skuteczność jego pracy mierzona np. jego indywidualną wydajnością.
Dysponowanie jednorodnymi informacjami o indywidualnej wydajności każdego z pracowników oraz o ich cechach
osobistych pozwala na skonstruowanie modelu ekonometrycznego. Model taki będzie instrumentem doboru robotników na
dany rodzaj stanowiska.
Wśród cech indywidualnych wymienić można: płeć, wiek, zawód wyuczony, wykształcenie, stan cywilny, stan rodzinny,
miejsce zamieszkania, posiadany majątek itd.

10) Model logitowy + jego zastosowanie
Model logitowy stosuje się do transformacji ograniczonej zmiennej endogenicznej (zależnej) w zmienną nieograniczoną.
Ta transformacja jest po to aby wyeliminować ryzyko związane z ekstrapolacją zmiennej poza obszar obserwacji
statystycznych. Transformacja logitowa jest przekształceniem zmiennej dwustronnie ograniczonej.

11) Modele ekonometryczne rozkładu dochodów

Rozkład dochodu jest asymetryczny i jest to prawo ekonomiczne. Jest prawostronnie skośny. Wszystkie ekonomiczne zmienne
losowe charakteryzuje rozkład prawostronnie skośny, dotyczy to tzw. stymulant. Specyfiką stymulanty jest to, iż przyrost
wartości zmiennej jest zjawiskiem pozytywnym, np.:
# przyrost legalnych dochodów jest zjawiskiem pozytywnym,
# przyrost płac jest zjawiskiem pozytywnym,
# wzrost sprzedaży jest zjawiskiem pozytywnym,
# wzrost zysku jest zjawiskiem pozytywnym,
# wzrost wielkości przedsiębiorstwa jest zjawiskiem pozytywnym.

Destymulanty to takie zmienne, których przyrost wartości jest zjawiskiem negatywnym, np.:
# przyrost wielkości spożycia alkoholu jest zjawiskiem negatywnym,
# wzrost absencji.
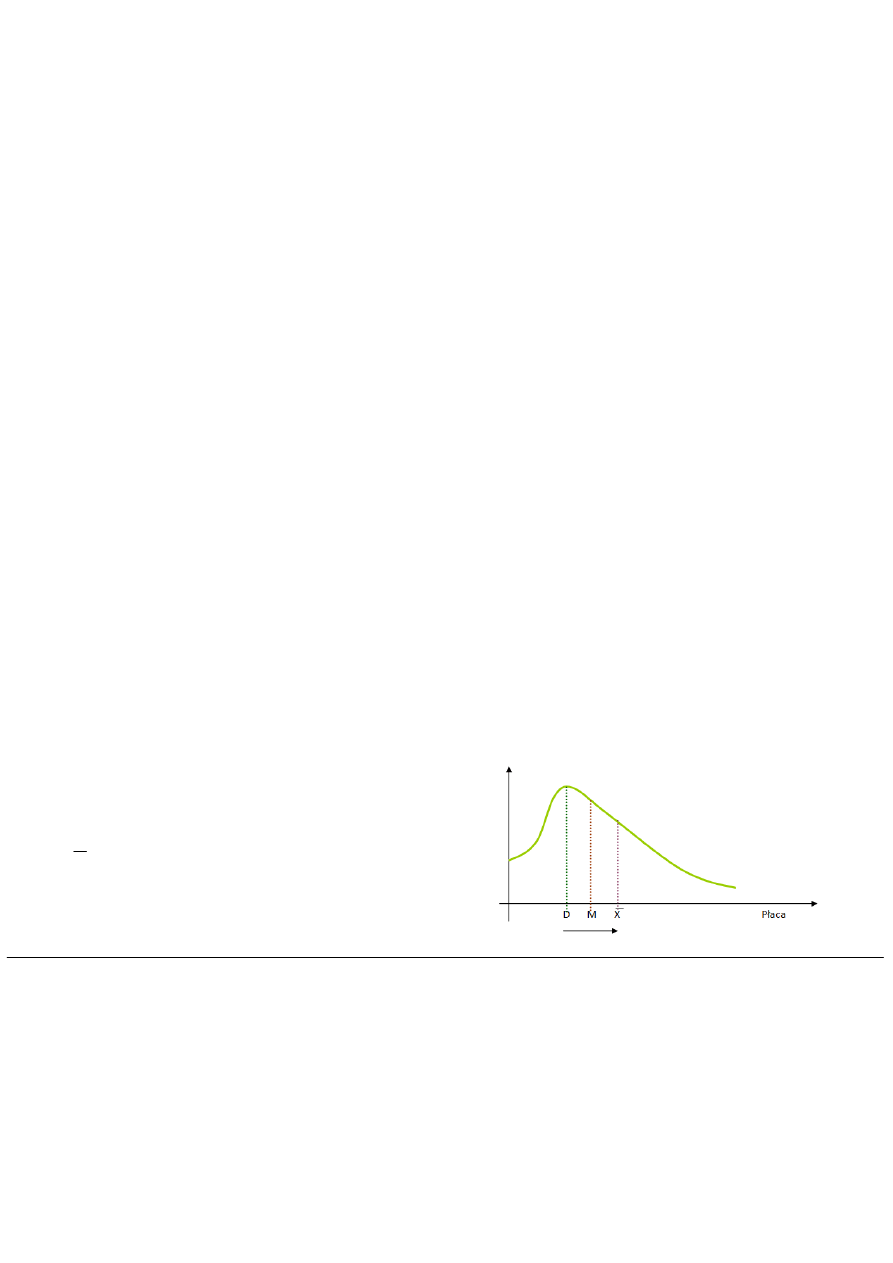
Główną składową dochodu jest płaca – jej rozkład jest prawostronnie skośny.

Usytuowanie dominanty, mediany i średniej arytmetycznej w
rozkładzie logarytmiczno-normalnym

X– średnia arytmetyczna,
D - dominanta,

M – mediana.

D < M < X





12) Etapy budowy modelu ekonometrycznego.
ETAP I – Specyfikacja modelu

ETAP II – Identyfikacja modelu

ETAP III – Estymacja parametrów modelu

ETAP IV – Weryfikacja modelu

ETAP V – Eksploatacja modelu (wyzysk modelu)

ETAP I – Specyfikacja modelu
Jak w każdym badaniu należy po pierwsze zdefiniować jego cel, określić zakres badania zarówno czasowy jak też przestrzenny
oraz wybrać metody badań.
W specyfikacji wyróżniamy dwie fazy:
Faza 1 – specyfikacja zmiennych modelu – w tej fazie rozwiązuje się problem celu, zakresu i metody,
Faza 2 – specyfikacja równań modelu.

]

)

(

1

[

1

2

2

T

T

T

T

u

T

X

X

X

X

S

V

1x1

]

,...,

,...,

1

[

1

Tk

Tj

T

T

x

x

x

x

T

T

T

u

T

X

D

X

S

V

)

(

2

2

2



ETAP II – Identyfikacja modelu – Identyfikacja występuje tylko w przypadku modelu wielorównaniowego. W modelach
jednorównaniowych nie ma etapu II.

ETAP III – Estymacja parametrów modelu
Faza 1 – wybór estymatora, funkcji narzędzia do szacowania parametrów modelu
Faza 2 – obliczenia numeryczne - zapisane w macierzach X oraz Y dane statystyczne

ETAP IV – Weryfikacja modelu
Faza 1 – Weryfikacja statystyczna

– polega na wykorzystaniu statystycznych miar ogólnej dobroci modelu lub ogólnych

dokładności modelu oraz szczegółowych miar dobroci modelu. Model będzie tym lepszy im mniejszą rolę będzie odgrywał
składnik losowy.
Faza 2 – Weryfikacja ekonomiczna

pozytywnie zweryfikowana pod względem statystycznym polega na ocenie ekonomicznej

jego logiki zwłaszcza zgodności z teorią.

ETAP V – Eksploatacja modelu - model ekonometryczny wykorzystywany jest do szacowania prognoz
Prognozy ekonometryczne stanowią grupę najdoskonalszych, najlepszych, najbardziej precyzyjnych, najmniej uzależnionych od
woluntaryzmu prognoz.

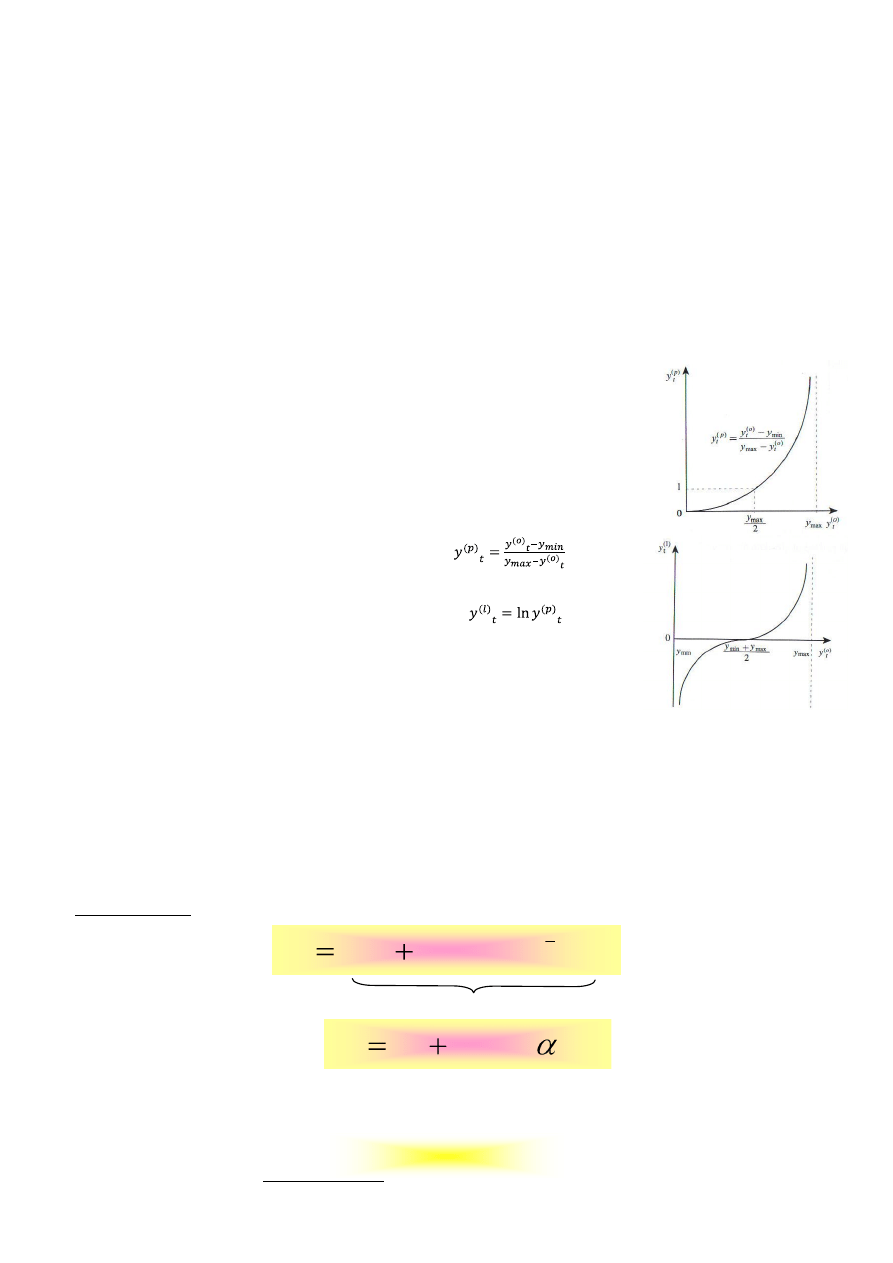
13) Modele ekonometryczne ograniczonych zmiennych zależnych.
Niekiedy pojawiają się zmienne objaśniające, które mają nawet dwustronne ograniczenia.
Konsekwencją ewentualnej ekstrapolacji poza obszar obserwacji statystycznych może być to,
że wartości ekstrapolant również będą mieściły się poza obszarem zmienności zmiennej
ograniczonej, co jest sprzeczne z logiką.

Problem rozwiązuje zastosowanie jednej z wielu możliwych transformacji ograniczonej
zmiennej zależnej.

Pierwszą z nich jest transformacja podstawowa, dana wzorem:

. Druga z

nich to transformacja logitowa, będąca logarytmem transformacji podstawowej.
Przekształca ona zmienną dwustronnie ograniczoną, w zmienną, która nie jest ograniczona
ani z dołu, ani z góry. Transformacja logitowa dana jest wzorem:

.

14) Forma zredukowana modelu ekonometrycznego małego przedsiębiorstwa.
Ważną role w układzie równań współzależnych odgrywa tzw. zredukowana forma modelu. Powstaje ona jako zestaw
równań stochastycznych, w których zmiennymi objaśniającymi są zmienne z góry ustalone całego modelu. Każde z tych
równań jest tak skonstruowane, że zmienna łącznie współzależna jest wyjaśniana jednocześnie przez wszystkie zmienne z
góry ustalone modelu.

15) Miary dokładności predykcji.

Wariancja predykcji V

2

Tp

obliczana jest następująco:

lub


S

u

2

– wariancja resztowa modelu,

(X

T

X)

-1

– odwrotność macierzy HESSA, która występuje w estymatorze KMNK. Jest to macierz, która ma wymiary (k+1) x

(k+1),
X

T

– znany wektor wartości zmiennych objaśniających w okresie T

Mając V

T

2

można obliczyć V

T

– błąd średni predykcji.

1x1 1 x (k+1) (k+1) (k+1)

(k+1) x 1

2

T

T

V

V

[%]

G

V

%

100

Tp

T

T

y

V

V

G

T

V

V

G

T

V

V

Średni błąd predykcji



V

T

- jest jednostką mianowaną i jest wyrażony w jednostce takiej jak S

u

, czyli jednostce zmiennej objaśnianej.

Prognoza będzie tym bardziej precyzyjna, dokładna im mniejsza będzie wartość V

T

.

Błąd graniczny predykcji ustala użytkownik prognozy.
Użytkownik zleca i narzuca granicę, pokazuje jaka dokładność jest wystarczająca i ustala V

G

.

V

G

– liczba niewielka, wyrażona w jednostkach zmiennej prognozowanej

Jeśli użytkownik narzuci granicę to odpowiadamy:
1.

V

T

≤ V

G

Oznacza to, że prognoza jest wystarczająco dokładna z punktu widzenia jej użytkownika i nazywamy ją

prognozą dopuszczalną.
2.

V

T

> V

G

Prognoza jest zbyt mało dokładna, gdyż nie spełnia wymogów użytkownika.

Na ogół użytkownik nie potrafi ustalić błędu w jednostkach zmiennej prognozowanej. Częściej pojawia się pojęcie względnego
błędu granicznego V

G

*

, przy czym V

G

*

jest wyrażone procentowo jako udział średniego błędu predykcji w wartości prognozy:

w skutek tego musimy posługiwać się względnym błędem predykcji V

T

*

, który obliczamy jako:

Prognoza będzie tym bardziej dokładna im V

T

*

będzie mniejsze.

Mogą pojawić się warianty:
Prognoza jest wystarczająco dokładna, czyli jest dopuszczalna.
Prognoza jest zbyt mało dokładna z punktu widzenia użytkownika przez co jest niedopuszczalna.


16) Przyczyny i skutki współliniowości zmiennych w modelu ekonometrycznym.
Model musi być tak skonstruowany aby nie występowała w nim współliniowość stochastyczna, jednak zdarzają się takie
modele w których współliniowość stochastyczna jest nie unikniona czego przykładem jest klasyczna funkcja produkcji
P=f(k,l,n), gdzie k-kapitał, l-praca, n-składnik losowy. Występuje tu pomiędzy „k” i „l” współliniowość stochastyczna,
która jest wypadkową dwóch rodzajów powiązań kapitału z pracą.
Często zdarza się w modelu silne skorelowanie pary zmiennych objaśniających, czyli współliniowość stochastyczna, przy
czym obie zmienne objaśniające zawierają w sobie podobny rodzaj informacji i oddziaływań na zmienną objaśnianą.
Pozostawienie w modelu obu zmiennych alternatywnych może prowadzić do pojawienia się stanu tzw. pozornej
nieistotności obu tych zmiennych, a w konsekwencji do błędu poznawczego.

+ ROZSZERZYĆ TO WIADOMOŚCIAMI Z JEGO KSIĄŻEK !!