MECHANIKA PŁYNÓW - LABORATORIUM

Zakład In

ż

ynierii Procesowej

1

5. PRZEPŁYW LEPKI PRZEZ CIENK

Ą

RURK

Ę

1.

Wstęp teoretyczny.

1.1.

Pomiar przepływu oraz ciśnienia.

Pomiarów przepływu dokonuje się w celu określenia ilości cieczy i gazów płynących w

rurociągach, co jest najczęściej realizowane poprzez pomiar:

a.

prędkości liniowej przepływu v [m/s],

b.

objętościowego natężenia przepływu

•

V

[m

3

/s],

c.

masowego natężenia przepływu

•

M

[kg/s].

Wielkości te są powiązane ze sobą następująco:

A

v

V

⋅

=

•

ρ

⋅

=

•

•

V

M

(1, 2)

gdzie v – prędkość liniowa przepływu [m/s], A – powierzchnia przekroju rurociągu [m

2

],

ρ

– gęstość medium [kg/m

3

].

Przeprowadzając pomiary przepływu cieczy można opierać się na właściwościach cieczy

doskonałych (nie wykazują zjawiska ściśliwości i lepkości), lub też cieczy rzeczywistych

(mała ściśliwość, lepkość w niektórych przypadkach dość znaczna, zależna od temperatury).

Niektóre ciecze rzeczywiste, między innymi wodę, można w warunkach powolnego

przepływu traktować z pewnym przybliżeniem jako ciecze doskonałe. Gazy są w swoich

właściwościach bardzo zbliżone do cieczy doskonałych (bo odznaczają się bardzo małą

lepkością), jeśli przepływ ich jest uwarunkowany niewielkimi nadwyżkami ciśnienia. Okazuje

się, że niewielkie różnice ciśnień, wywołujące bardzo nieznaczne zmiany gęstości, mogą

spowodować bardzo szybkie przepływy gazu. Teoria i obserwacje wykazują, że do prędkości

rzędu 100 [m/s] gaz można traktować jako płyn nieściśliwy.

Podstawę analizy przepływów laminarnych (warstwowych) płynów doskonałych stanowi

równanie Bernoulliego. W najprostszym przypadku przepływu cieczy przez przewód

poziomy ma ono postać:

(

)

const

p

ρ v

p

p

p

s

d

s

0

2

2

=

+

=

+

(3)

Pierwszy składnik lewej strony oznacza ciśnienie statyczne, drugi – dynamiczne.

Równanie to ma sens prawa: suma ciśnienia statycznego i dynamicznego w każdym

MECHANIKA PŁYNÓW - LABORATORIUM

Zakład In

ż

ynierii Procesowej

2

miejscu przewodu jest stała i równa ciśnieniu całkowitemu, jakie panuje w strumieniu

płynącej cieczy.

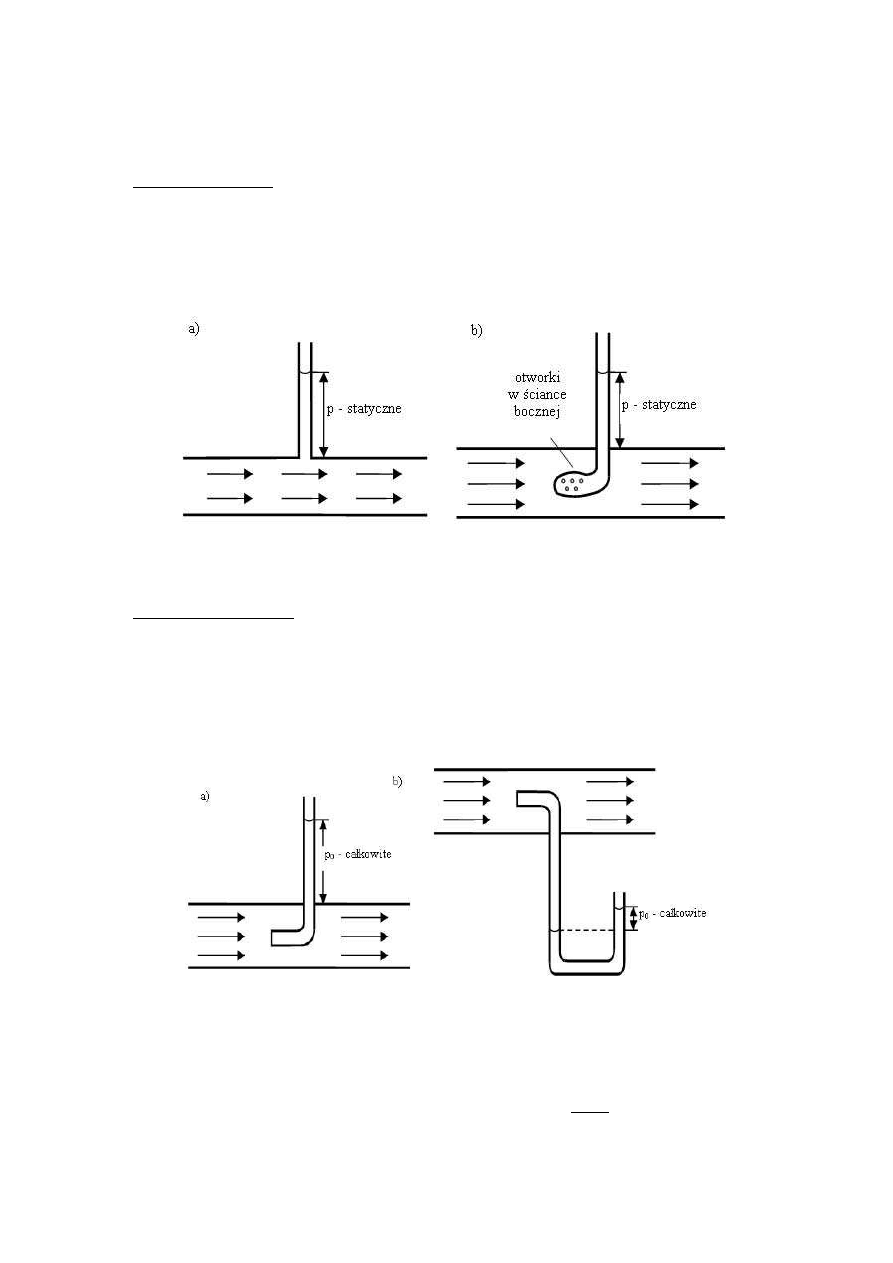
Ciśnienie statyczne jest to ciśnienie wywierane na boczne ścianki naczynia przez płynąca

ciecz. Można je zmierzyć załączając jakikolwiek manometr do otworu zrobionego w bocznej

ś

ciance naczynia (rys.1a) lub wstawiając do strumienia rurkę połączoną z manometrem i

zaopatrzoną w otworki, wzdłuż których ślizga się strumień cieczy (rys.1. b).

Rys.1. Pomiar ciśnienia statycznego.

Ciśnienie dynamiczne związane jest z ruchem cieczy i nie manifestuje się naciskiem na

boczne ścianki. Ujawni się ono dopiero wtedy, gdy ciecz poruszającą się zatrzymać, np.

płytką ustawioną prostopadle do kierunku strumienia lub rurką otwartą wstawioną do

strumienia tak, by strumień cieczy był zmuszony do zatrzymania się na powierzchni otworu

(rys.2.).

Rys.2. Pomiar ciśnienia całkowitego.

Jakikolwiek manometr, np. cieczowy połączony z tak ustawioną rurką wskaże ciśnienie

całkowite p

0

panujące w strumieniu cieczy, ciśnienie to jest sumą ciśnienia statycznego i

dynamicznego.

MECHANIKA PŁYNÓW - LABORATORIUM

Zakład In

ż

ynierii Procesowej

3

1.2.

Opory przepływu w przepływie przez rurę.

1.2.1.

Przepływ laminarny.

Ogólny wzór na objętościowe natężenie przepływu laminarnego, przez rurę o przekroju

kołowym (Re<2100), opisany jest równaniem Hagena-Poiseuille`a i ma postać:

4

8

R

l

p

V

⋅

∆

⋅

=

•

η

π

.

(4)

gdzie: p

∆

- spadek ciśnienia [Pa], η- dynamiczny współczynnik lepkości

]

[

s

Pa

⋅

, l- długość

rury [m], R- promień rury [m].

Wzór ten wykorzystuje się między innymi do obliczania strat energetycznych, występujących

podczas przepływu laminarnego, a będących konsekwencją istnienia lepkości płynu. Na

pokonanie oporów z nią związanych zużywa się bowiem energia ciśnienia, wskutek czego

następuje spadek jego wartości.

Podstawiając do równania Hagena-Poiseuiell`a (4), równanie na średnią prędkość

liniową:

A

V

v

śr

•

=

.

,

(5)

po przekształceniu otrzymamy wzór na straty ciśnienia:

2

.

4

8

8

R

v

l

R

V

l

p

śr

s

⋅

⋅

=

⋅

⋅

=

∆

•

η

π

η

.

(6)

Wysokość strat wynosi:

2

.

8

gR

v

l

g

p

h

śr

s

s

ρ

η

ρ

⋅

⋅

=

∆

=

,

(7)

gdzie g- przyśpieszenie grawitacyjne ziemi [m/s

2

].

Jak widać średnica rury ma bardzo duży wpływ na wartość oporu przepływu. Gdybyśmy np.

przy danym natężeniu przepływu

•

V , ciecz przetłoczyli raz przez rurę o średnicy D

1

, a drugi

raz przez rurę o średnicy

D

2

=2

D

1

(długości rur są identyczne l

1

=

l

2

), to uwzględniając, że

4

~

−

∆

D

p

s

otrzymamy:

16

2

4

4

1

2

2

1

=

=













=

∆

∆

D

D

p

p

s

s

.

(8)

MECHANIKA PŁYNÓW - LABORATORIUM

Zakład In

ż

ynierii Procesowej

4

A zatem, aby w obydwu przypadkach otrzymać takie samo objętościowe natężenie

przepływu, należy dla rury o średnicy D

1

wywołać 16-krotnie większą różnice ciśnień niż dla

rury o średnicy D

2

(większej).

W praktyce obliczeniowej korzysta się ze wzoru (7) przekształconego do nieco innej

postaci (wprowadza się średnicę D=2R, oraz mnoży licznik i mianownik przez (2v

śr

)). W

wyniku tych przekształceń otrzymujemy:

g

v

D

l

D

v

h

śr

śr

s

2

64

2

.

.

⋅

⋅













⋅

⋅

=

ρ

η

,

(9)

gdzie D- średnica rury [m].

Korzystając ze wzoru na liczbę Reynoldsa, definiującej charakter przepływu:

η

ρ

⋅

⋅

=

D

v

śr.

Re

,

(10)

otrzymujemy równanie Darcy-Weisbacha postaci:

g

v

D

l

h

śr

s

2

2

.

⋅

⋅

=

λ

,

(11)

gdzie λ

to bezwymiarowy współczynnik oporu opisany wzorem (dla przepływu

laminarnego):

λ

≡

Re

64

.

(12)

Wartości współczynnika oporu otrzymanego ze wzoru (12) są na ogół zgodne z

doświadczeniem dla małych liczb Reynoldsa. Jednakże w obliczeniach praktycznie stosuje się

zależność:

Re

75

≡

λ

,

(13)

ze względu na postępujące z czasem zmniejszenie prześwitu przewodu, spowodowane

osadami oraz pogarszaniem się gładkości ścian przewodu na skutek korozji.

Dla przewodów o niekołowym przekroju, zamiast średnicy

D we wzorze (11) stosuje się

ś

rednicę hydrauliczną przewodu

D

h

.

U

A

D

h

4

=

,

(14)

gdzie U – długość zwilżonego obwodu przekroju [m].

MECHANIKA PŁYNÓW - LABORATORIUM

Zakład In

ż

ynierii Procesowej

5

1.2.2.

Przepływ turbulentny.

W przypadku przepływów turbulentnych (Re>2300) do obliczenia spadku ciśnienia

s

p

∆

,

czy równoważnej wysokości strat (

g

p

h

s

s

ρ

/

∆

=

), stosuje się w zasadzie tego samego wzoru,

co w przypadku przepływu laminarnego (11). Różnica polega jedynie na tym, że

współczynnik oporu (λ) jest określany w inny sposób. W przypadku przepływów

turbulentnych ujawnia się bowiem jego zależność od prędkości tarcia.

Istnieje wiele wzorów empirycznych i półempirycznych, których ważność ograniczona

jest to określonych przedziałów liczby Re. Najpowszechniej stosowany jest jednak wzór

Blasiusa słuszny dla (

4

10

5

Re

2300

⋅

<

<

):

25

,

0

Re

3164

,

0

−

⋅

=

λ

.

(15)

Wszystkie wzory dotychczas przytoczone dotyczą współczynnik oporu w rurach gładkich.

Rury techniczne mają ściany wewnętrzne mniej lub bardziej chropowate. Nie oznacza to

jednak, że wzory te nie posiadają praktycznego zastosowania. Doświadczenie pokazuje

bowiem, że pojęcie „chropowatości” jest pojęciem względnym i wiąże się z istnieniem

podwarstwy laminarnej tuż przy ściankach przewodu.

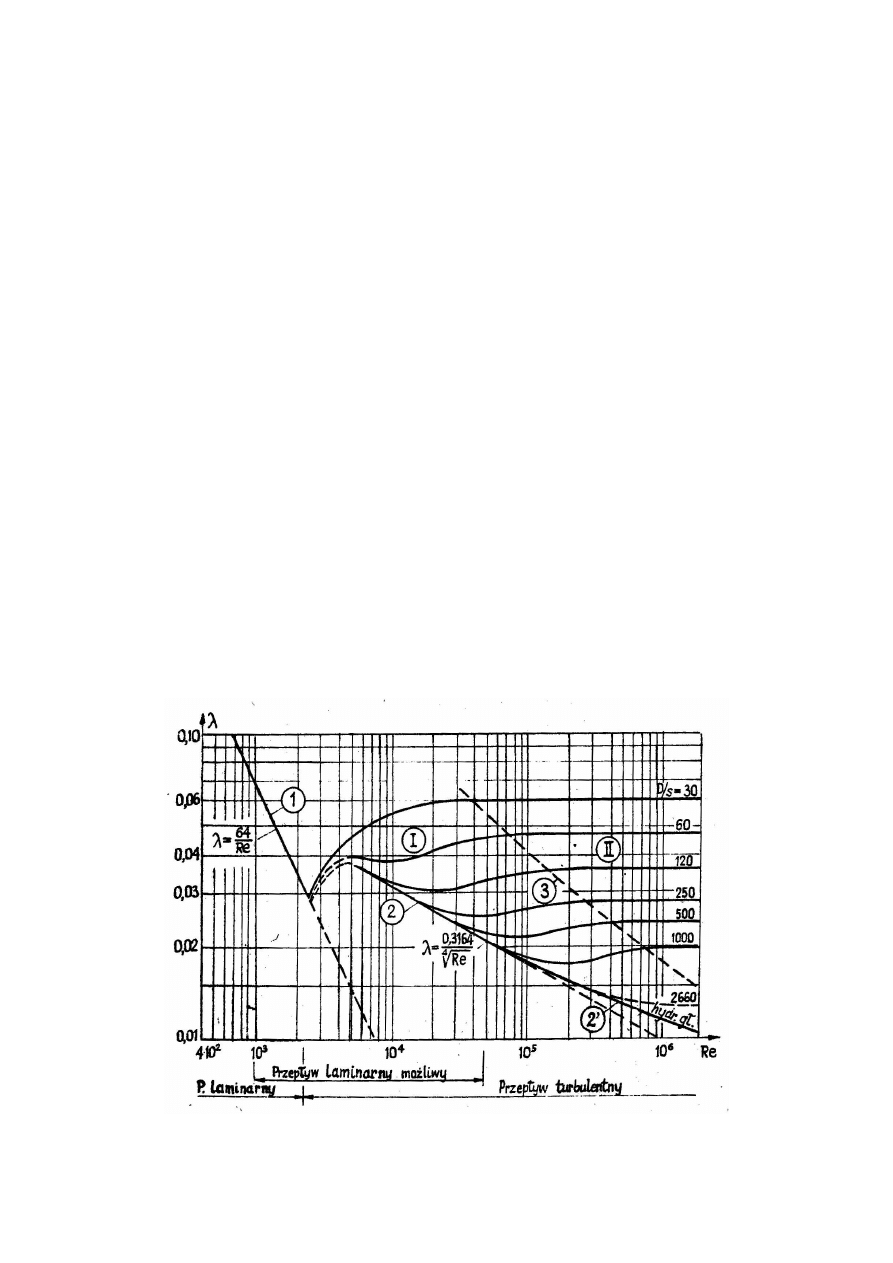
Poniżej przedstawiono wykres zależności

(Re)

f

=

λ

dla przepływu laminarnego i

turbulentnego. Widać na nim jednoznacznie że wraz ze wzrostem prędkości, a tym samym

liczby Reynoldsa opory przepływu maleją.

Rys. 3. Wykres zależności

:

(Re)

f

=

λ

1- przepływ laminarny, 2- przepływ turbulentny.

MECHANIKA PŁYNÓW - LABORATORIUM

Zakład In

ż

ynierii Procesowej

6

1.3.

Wypływ cieczy ze zbiornika przez rurę poziomą.

Procesem badanym w ćwiczeniu, jest przepływ laminarny przez rurę okrągłą,

przytwierdzą poziomo do dużego zbiornika, tak że, oś rury znajduje się na głębokości h

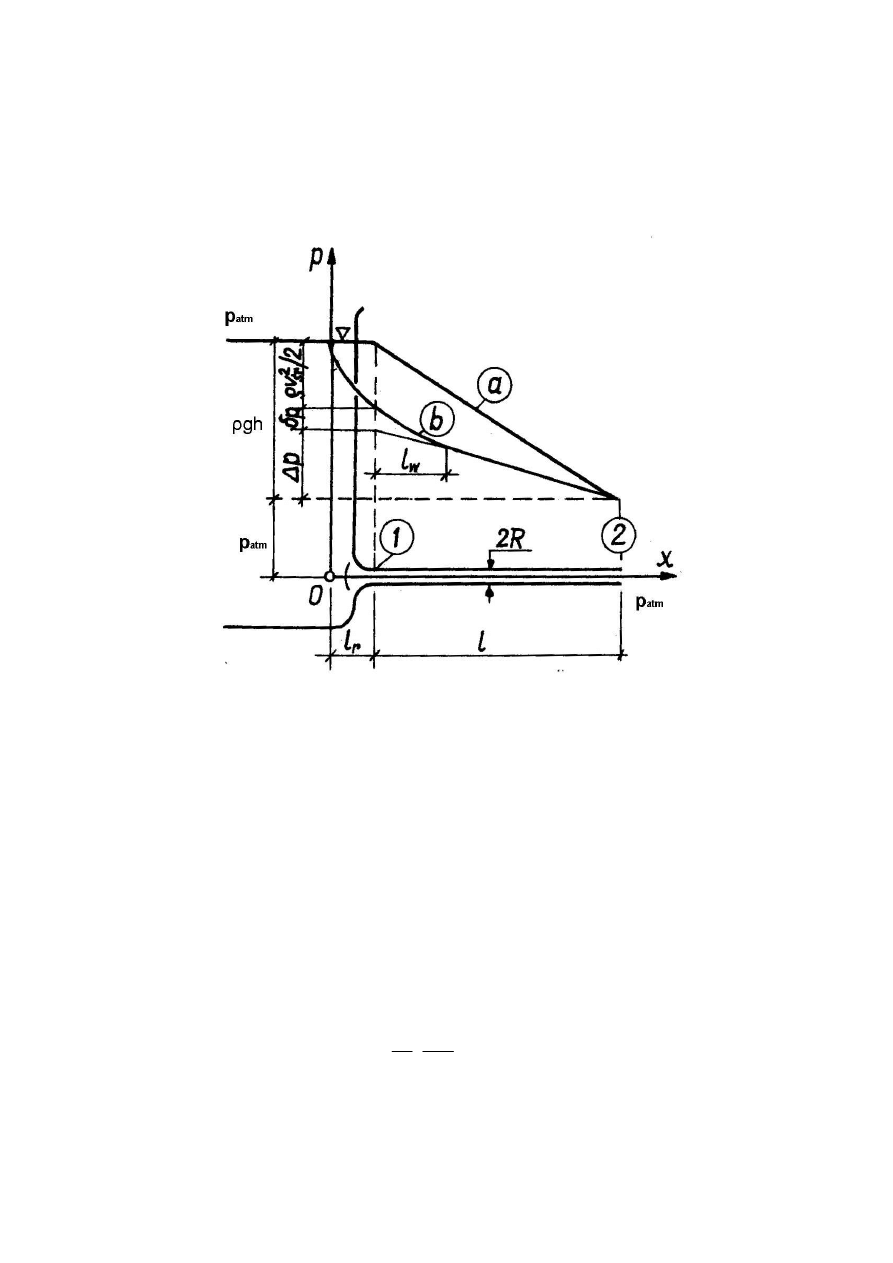
zbiornika. Uproszczony schemat rozpatrywanego procesu przedstawiono na rysunku 4.

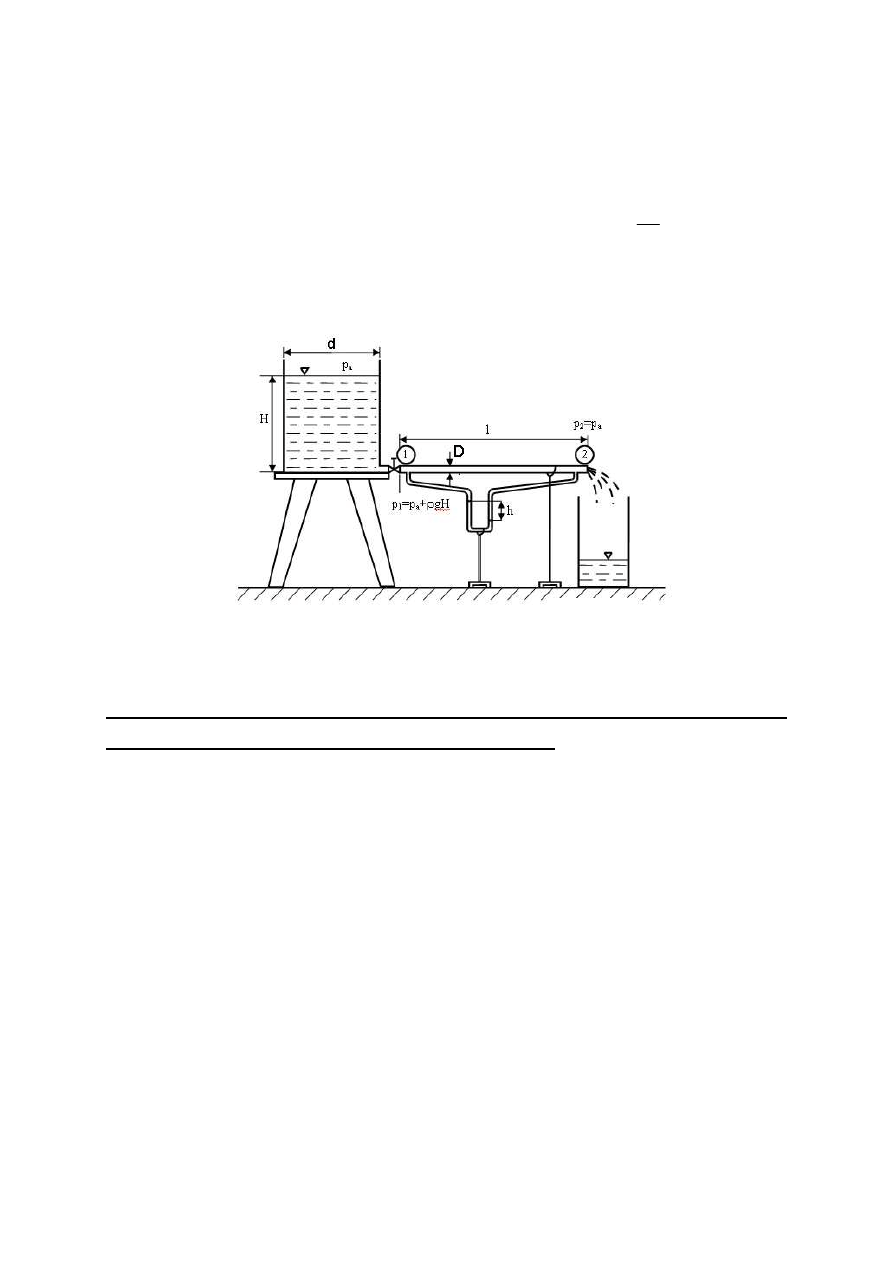
Rys. 4. Schematyczny rysunek procesu.

W zbiorniku na poziomie osi rury panuje ciśnienie p

1

:

gh

p

p

atm

ρ

+

=

.

1

,

(16)

zaś na wylocie z rury panuje ciśnienie p

2

:

.

2

atm

p

p

=

.

(17)

Zatem spadek ciśnienia na długości rury (l) wynosi:

gh

p

ρ

=

∆

.

(18)

Jeśli spadek ten podstawić do wzoru ogólnego Hagena-Poiseuiell`a (4) na objętościowe

natężenie przepływu laminarnego w rurze o przekroju kołowym otrzymamy równanie:

4

8

R

l

gh

V

⋅

⋅

=

•

ρ

η

π

.

(19)

Okazuje się jednak, że doświadczalnie wyznaczone - rzeczywiste natężenia przepływu są

nieco inne niż obliczone z powyższego wzoru. Główną przyczyną rozbieżności jest założenie,

MECHANIKA PŁYNÓW - LABORATORIUM

Zakład In

ż

ynierii Procesowej

7

ż

e spadek ciśnienia statycznego jest jednakowy na długości całej rury













=

∆

.

const

l

p

. Przy

takim założeniu, rozkład ciśnienia statycznego wzdłuż rury reprezentuje prosta

(a) (Rys. 4).

Rzeczywisty rozkład ciśnienia statycznego wzdłuż rury obrazuje natomiast krzywa

(b)

(rys. 4). Aby zrozumieć przyczynę tej różnicy należy jeszcze raz przyjrzeć się zdefiniowanym

wcześniej ciśnieniom.

Tak jak już wspomniano wcześniej ciśnienie panujące w zbiorniku na wysokości osi rury

(

h) jest równe:

gh

p

p

atm

δ

+

=

.

1

.

(20)

Zależność ta jest jednak prawdziwa tylko w obszarach oddalonych od otworu wlotowego do

rury, w których płyn posiada jeszcze znikomą prędkość linową (

0

≈

v

). Punkt O (rys. 4) jest

punktem leżącym najbliżej wlotu do rury dla którego można jeszcze przyjąć że:

gh

p

p

atm

δ

+

≈

.

1

.

(21)

Na odcinku o długości l

r

(rys. 4), nazwanym odcinkiem rozpędowym, elementy cieczy

nabierają prędkości, kosztem energii ciśnienia. Na końcu tego odcinka wszystkie elementy

płynu mają jednakową prędkość, równą co do wartości prędkości średniej (5).

A zatem w początkowym przekroju rury występuje prostokątny profil prędkości, a

ciśnienie jest mniejsze od ciśnienia panującego w punkcie (O), o wartość













2

2

v

ρ

.

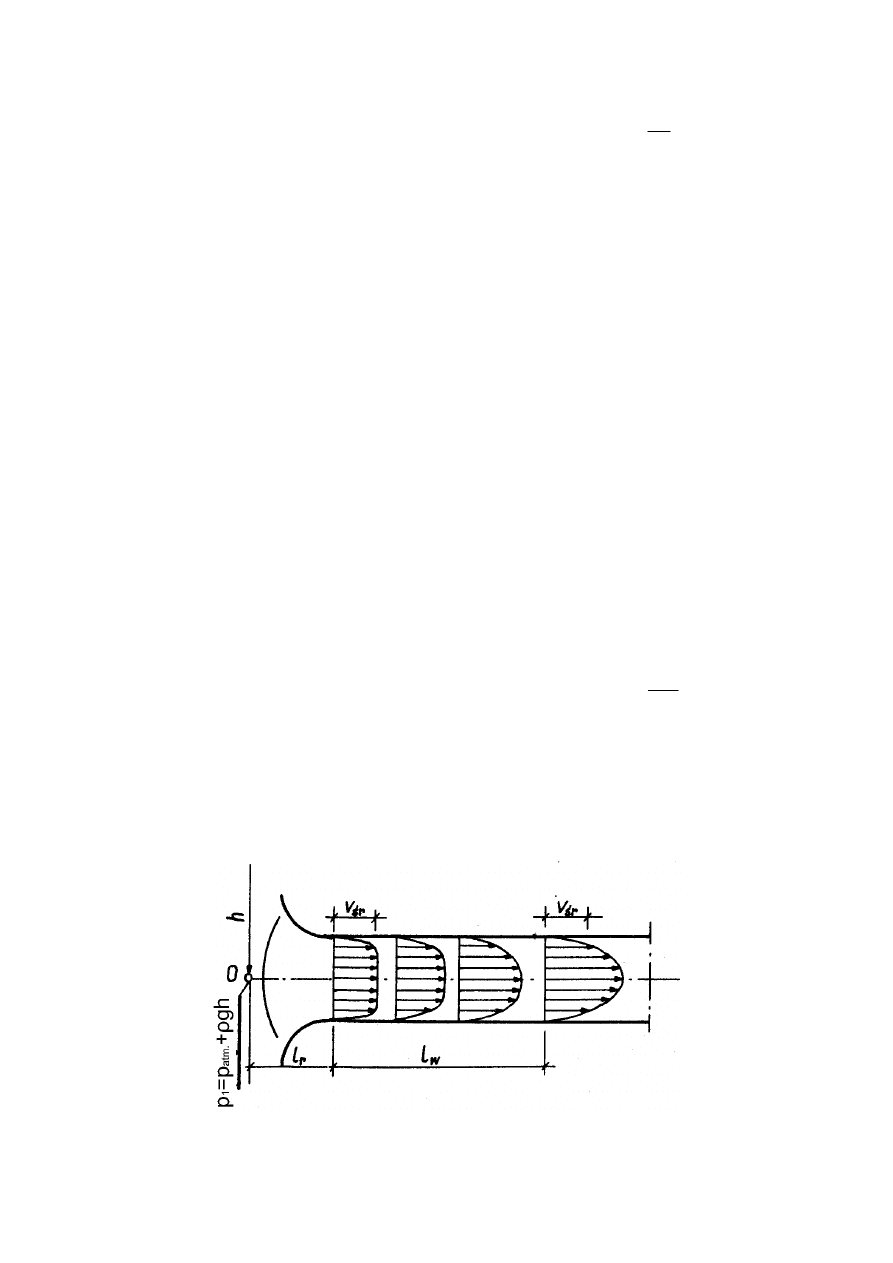
W dalszym odcinku rury (l

w

) (rys. 4, 5) następuje formowanie się profilu parabolicznego

prędkości. Jest to tzw. odcinek wstępny przepływu i dopiero po jego przekroczeniu obserwuje

się równomierny liniowy spadek ciśnienia, który założono we wzorze Hagena-Poiseuiell`a.

Poniżej przedstawiono schematyczny rysunek opisanego procesu.

Rys. 5. Kształtowanie się profilu prędkości w rurze.

MECHANIKA PŁYNÓW - LABORATORIUM

Zakład In

ż

ynierii Procesowej

8

Aby otrzymać poprawne wartości, objętościowego natężenia przepływu, należy do wzoru

Hagena-Poiseuiell`a wprowadzić rzeczywisty spadek ciśnienia na długości rury opisany:













+

⋅

−

=

∆

p

śr

rzecz

v

gh

p

δ

ρ

ρ

2

2

.

.

,

(22)

gdzie δ

p

to spadek ciśnienia na odcinku l

w

.

Pominięcie początkowych spadków ciśnienia przy obliczaniu objętościowego natężenia

przepływu jest dopuszczalne TYLKO wówczas gdy:

gh

v

śr

ρ

ρ

<<

2

2

.

.

(23)

Ma to miejsce gdy spełnione są nierówności:

R

l

v

R

śr

16

.

<<

⋅

η

ρ

,

(24)

lub

D

l

64

Re

<<

.

(25)

Zatem przybliżony wzór (19) jest wystarczająco dokładny, dla dostatecznie małych wartości

liczby Reynoldsa.

W przypadku, kiedy:

D

l

64

Re

>>

,

(26)

to spadek ciśnienia w rurze jest tak mały (wobec spadku na odcinku rozpędowym), że można

pominąć wpływ rury i objętościowe natężenie przepływu obliczać jak przy wypływie cieczy

przez mały otwór w ścianie zbiornika, korzystając z wzoru:

gh

F

V

⋅

⋅

=

•

2

0

µ

,

(27)

gdzie µ – współczynnik wypływu, F

0

– pole powierzchni otworu [m].

Długość odcinka wstępnego (l

w

) można oszacować wzorem empirycznym:

Re

03

,

0

⋅

=

D

l

w

.

(28)

W ogólnym przypadku kiedy prawdziwa jest nierówność (25) można przyjąć, iż długość

odcinka wstępnego jest znacznie mniejsza niż długość rury (l

w

<l). A więc profil prędkości

„zdąży” się uformować w obrębie rury. Natomiast kiedy prawdziwa jest nierówność (26),

długość odcinka wstępnego jest większa od długości rury (l

w

>l), a co za tym idzie profil

MECHANIKA PŁYNÓW - LABORATORIUM

Zakład In

ż

ynierii Procesowej

9

paraboliczny nie uformuje się w obrębie rury, mimo iż przepływ może być do końca

laminarny.

Ponieważ w wykonywanym ćwiczeniu wykorzystuje się długą rurkę o bardzo małej

ś

rednicy, można założyć, że straty ciśnienia na długości rury są liniowe













=

∆

.

const

l

p

.

2.

Przebieg ćwiczenia.

Rys. 6. Schemat stanowiska pomiarowego.

W trakcie trwania całego ćwiczenia poziom cieczy w zbiorniku naporowym (górnym)

należy utrzymywać na stałej wysokości oznaczonej kreską.

A.

Włączyć pompę układu wyrównawczego.

B.

Sprawdzić wskazania manometru. Wartość różną od 0 należy zanotować jako

h

0

[m] i

odejmować od każdego pomiaru.

C.

Odkręcić delikatnie zawór pomiarowy A, a następnie zwiększać „stopień otwarcia”

zaworu do czasu wystąpienia na manometrze widocznej różnicy ciśnienia.

D.

Zaczekać na ustabilizowanie się strumienia wypływającej cieczy, następnie do króćca

pomiarowego podstawić cylinder miarowy włączając jednocześnie pomiar czasu (stoper).

E.

W trakcie zbierania cieczy, z manometru odczytać wysokość

h

pom

[m].

F.

Po napełnieniu cylindra wyłączyć pomiar czasu (stoper). Wodę z cylindra wlać do

zbiornika zasilającego (dolnego).

G.

Zanotować otrzymane wyniki.

H.

Powtórzyć dwukrotnie czynności od punktu D do G dla danego „stopnia otwarcia”

zaworu.

MECHANIKA PŁYNÓW - LABORATORIUM

Zakład In

ż

ynierii Procesowej

10

I.

Zwiększyć „stopień otwarcia” zaworu A tak by nastąpiła zmiana wskazania manometru.

J.

Wykonać cykl pomiarowy D-H

K.

Pomiary kontynuować do czasu osiągnięcia granicy pomiarowej manometru.

L.

Po zakończonych badaniach zamknąć zawór pomiarowy A i wyłączyć pompę.

M.

Dla celów obliczeniowych należy zmierzyć dodatkowo temperaturę wody (T).

3.

Opracowanie wyników.

3.1.

Na podstawie otrzymanych wyników wyznaczamy objętościowe natężenie przepływu

•

V

[m

3

/s], a następnie liniową prędkość przepływu v

śr.

[m/s] z wzoru (5). Średnica rurki

D

w

= 6 [mm], długość l = 1 [m].

3.2.

Na podstawie wyliczonej prędkości v

śr.

[m/s], wyznaczyć liczbę Reynoldsa

z równania (10). Lepkość (η)

[

]

s

Pa

⋅

i gęstość (ρ) [kg/m

3

] dla wody wyznaczyć z zależności:

•

dla T = 0 ÷ 40 [

o

C]

]

[kg/m

)

2

,

67

(

57

,

503

)

283

(

)

4

(

1000

3

2

+

⋅

+

⋅

−

−

=

T

T

T

ρ

,

(29)

•

dla T = 25 ÷ 100 [

o

C]

]

[kg/m

)

67

(

7

,

466

)

273

(

)

4

(

1000

3

2

+

⋅

+

⋅

−

−

=

T

T

T

ρ

,

(30)

2

)

0

(

)

(

000221

,

0

0337

,

0

1

T

T

T

⋅

+

⋅

+

=

η

η

,

(31)

gdzie: T – temperatura [ºC], η

(0)

– lepkość wody w T=0 [ºC] (η

(0)

=0,00179

]

s

Pa

[

⋅

).

3.3.

W oparciu o wyliczoną liczbę Reynoldsa określić charakter przepływu i wyznaczyć

teoretyczny współczynnik oporu λ

teor.

z odpowiedniego równania (12) lub (15).

3.4.

Na podstawie odczytanych z manometru wartości

h [m], wyznaczyć z równania (32)

spadek ciśnienia p

∆

[Pa] w rurce o długości l:

g

h

h

p

m

⋅

−

⋅

−

=

∆

)

(

)

(

0

ρ

ρ

(32)

gdzie gęstość cieczy manometrycznej ρ

m

= 1860 [kg/m

3

].

3.5.

W oparciu o wyznaczoną wartość strat ciśnienia

p

∆

, obliczyć doświadczalny

współczynnik oporu λ

dosw.

z przekształconego równania Darcy-Weisbacha:

2

2

.

.

ρ

λ

⋅

⋅

⋅

=

∆

śr

dosw

v

D

l

p

(33)

3.6.

Porównać wartości teoretyczne i doświadczalne współczynnika oporu przepływu.

MECHANIKA PŁYNÓW - LABORATORIUM

Zakład In

ż

ynierii Procesowej

11

4.

Wykaz stosowanych oznaczeń.

Symbol: Opis:

Wymiar:

•

V

objętościowe natężenie
przepływu

[m

3

/s]

•

M

masowe natężenie przepływu

[kg/s]

A

powierzchnia

[m

2

]

D

ś

rednica

[m]

g

przyśpieszenie grawitacyjne

[m/s

2

]

H

wysokość

[m]

h

s

wysokość strat

[-]

h

wysokość

[m]

l

długość

[m]

l

r

odcinek rozpędowy

[m]

l

w

odcinek wstępny

[m]

p

ciśnienie

[Pa]

R

promień

[m]

U

długość zwilżonego obwodu

[m]

v

prędkość liniowa

[m/s]

η

c

lepkość dynamiczna

s]

[Pa

⋅

λ

współczynnik oporu przepływu

[-]

ρ

gęstość wody

[kg/m

3

]

ρ

m

gęstość cieczy manometrycznej

[kg/m

3

]

5.

Literatura uzupełniająca.

•

„Mechanika płynów z hydrauliką”, Gryboś R., Wyd. VIII, Politechnika Śląska, Skrypty

uczelniane Nr 1610, Gliwice 1990 r.

•

„Mechanika płynów w inżynierii środowiska”, Orzechowski Z., Prywer J., Zarzycki R.

WNT, Warszawa 2001 r.

•

„Laboratorium z mechaniki płynów”, praca zbiorowa pod red. Weinerowskiej K.,

Wydawnictwo Politechniki Gdańskiej, Gdańsk 2004 r.

•

„Inżyniera chemiczna i procesowa. Laboratorium”, Broniarz - Press L., Agaciński P.,

Kałek- Skrabulska A., Ochowiak M., Wydanie I, Wydawnictwo Politechniki Poznańskiej,

Poznań 2000 r.