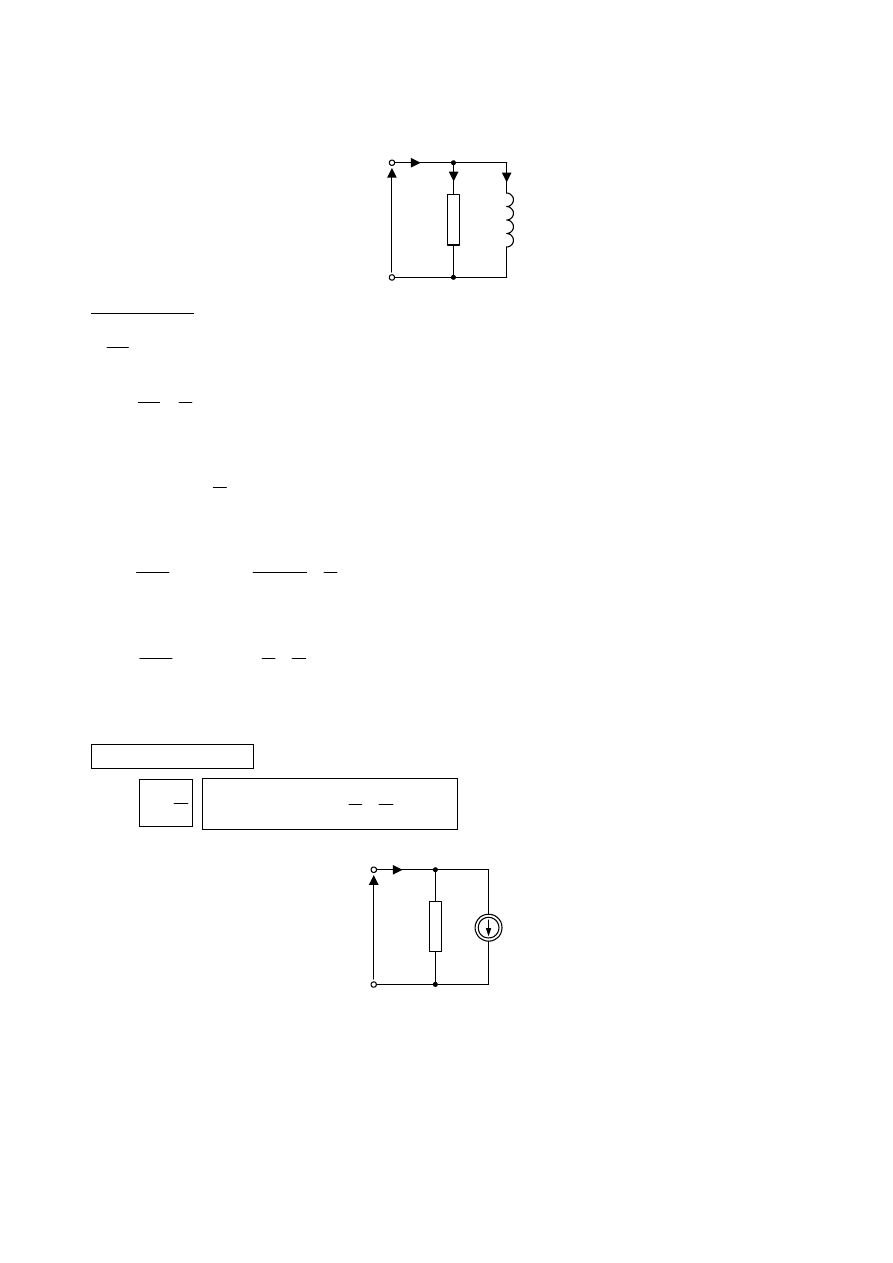
MODELE CYFROWE GAŁĘZI ZŁOŻONYCH

1. Określić model cyfrowy dla równoległego połączenia elementów: R, L, przy zastosowaniu

jawnej metody Eulera (m. prostokątów „wprzód”) do całkowania numerycznego.

L

R

u

i

i

2

i

1

Rozwiązanie:

)

(

1

t

u

dt

di

L

=

(1)

czyli:

)

(

1

1

t

u

L

dt

di =

(2)

Stosując jawną metodę Eulera (prostokątów „wprzód”) do całkowania numerycznego uzyskujemy:

)

1

(

)

1

(

)

(

1

1

−

+

−

=

k

u

L

T

k

i

k

i

(3)

Eliminując prąd

i

1

uzyskujemy:

)

1

(

)

1

(

)

1

(

)

(

)

(

−

+

−

−

−

=

−

k

u

L

T

R

k

u

k

i

R

k

u

k

i

(4)

Po uporządkowaniu mamy:

)

1

(

1

)

1

(

)

(

)

(

−











 −

+

−

+

=

k

u

R

L

T

k

i

R

k

u

k

i

(5)

Zależność (5) może być zapisana w postaci ogólnej, określającej model cyfrowy jak na poniższym
rysunku:

)

1

(

)

(

)

(

−

+

=

k

j

k

Gu

k

i

(6)

gdzie:

R

G

1

=

,

)

1

(

1

)

1

(

)

1

(

−











 −

+

−

=

−

k

u

R

L

T

k

i

k

j

j(k–1)

G

u(k)

i(k)

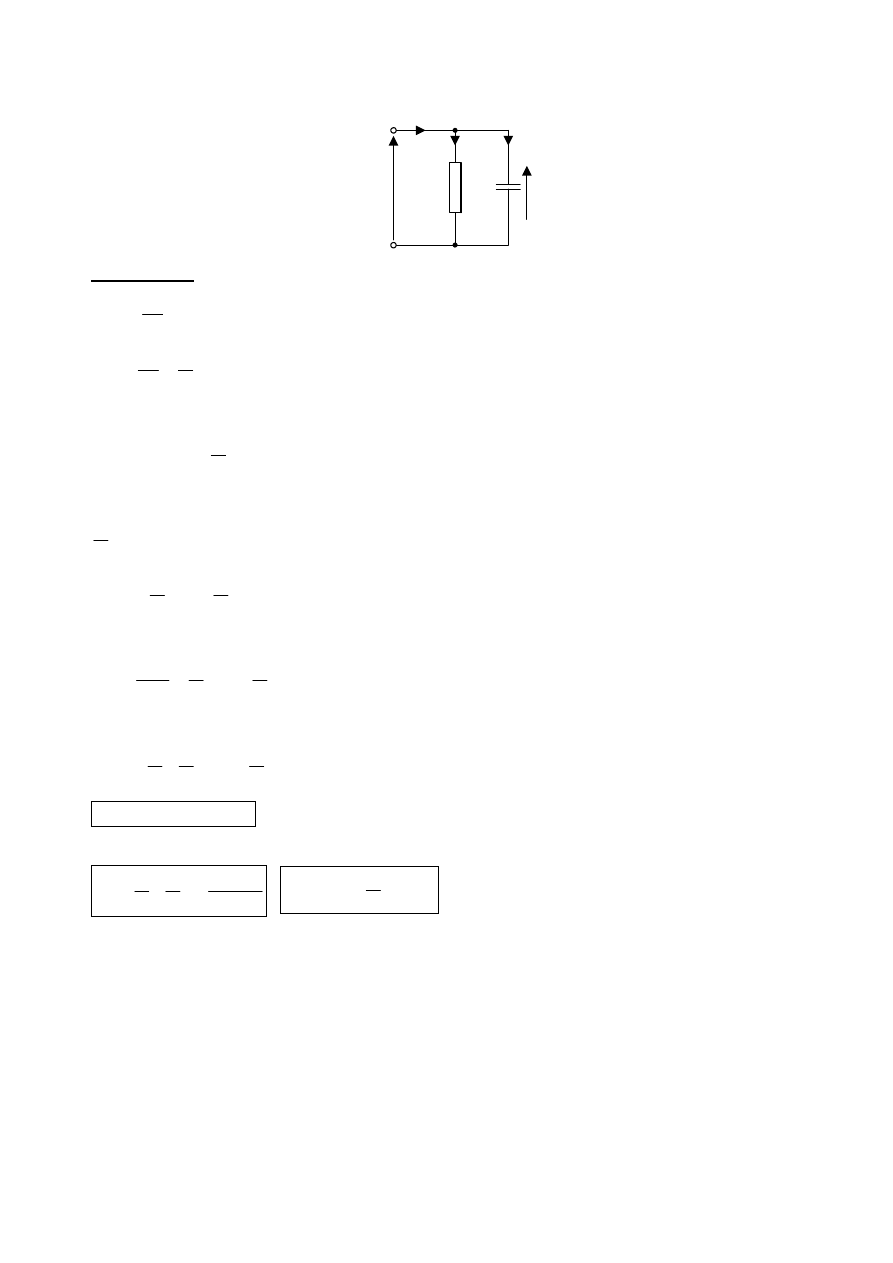
2. Określić model cyfrowy dla równoległego połączenia elementów: R, C, przy zastosowaniu

niejawnej metody Eulera (prostokątów „wstecz”) do całkowania numerycznego.

C

R

u

i

i

C

i

R

u

C

=u

Rozwiązanie:

dt

du

C

i

=

C

(1)

czyli:

C

1

i

C

dt

du =

(2)

Stosując niejawną metodę Eulera (prostokątów „wstecz”) dla całkowania numerycznego uzyskujemy:

)

(

)

1

(

)

(

C

k

i

C

T

k

u

k

u

+

−

=

(3)

Przenosząc składnik z prądem na lewą stronę uzyskuje się:

)

1

(

)

(

)

(

C

−

−

=

k

u

k

u

k

i

C

T

(4)

)

1

(

)

(

)

(

C

−

−

=

k

u

T

C

k

u

T

C

k

i

(4a)

Eliminując prąd i

C

:

)

1

(

)

(

)

(

)

(

−

−

=

−

k

u

T

C

k

u

T

C

R

k

u

k

i

(5)

Po uporządkowaniu otrzymujemy:

)

1

(

)

(

1

)

(

−

−











 +

=

k

u

T

C

k

u

T

C

R

k

i

(6)

)

1

(

)

(

)

(

−

+

=

k

j

k

Gu

k

i

(6a)

gdzie:

RT

RC

T

T

C

R

G

+

=











 +

=

1

,

)

1

(

)

1

(

−

−

=

−

k

u

T

C

k

j

W rezultacie uzyskujemy model o strukturze jak w zadaniu 1.

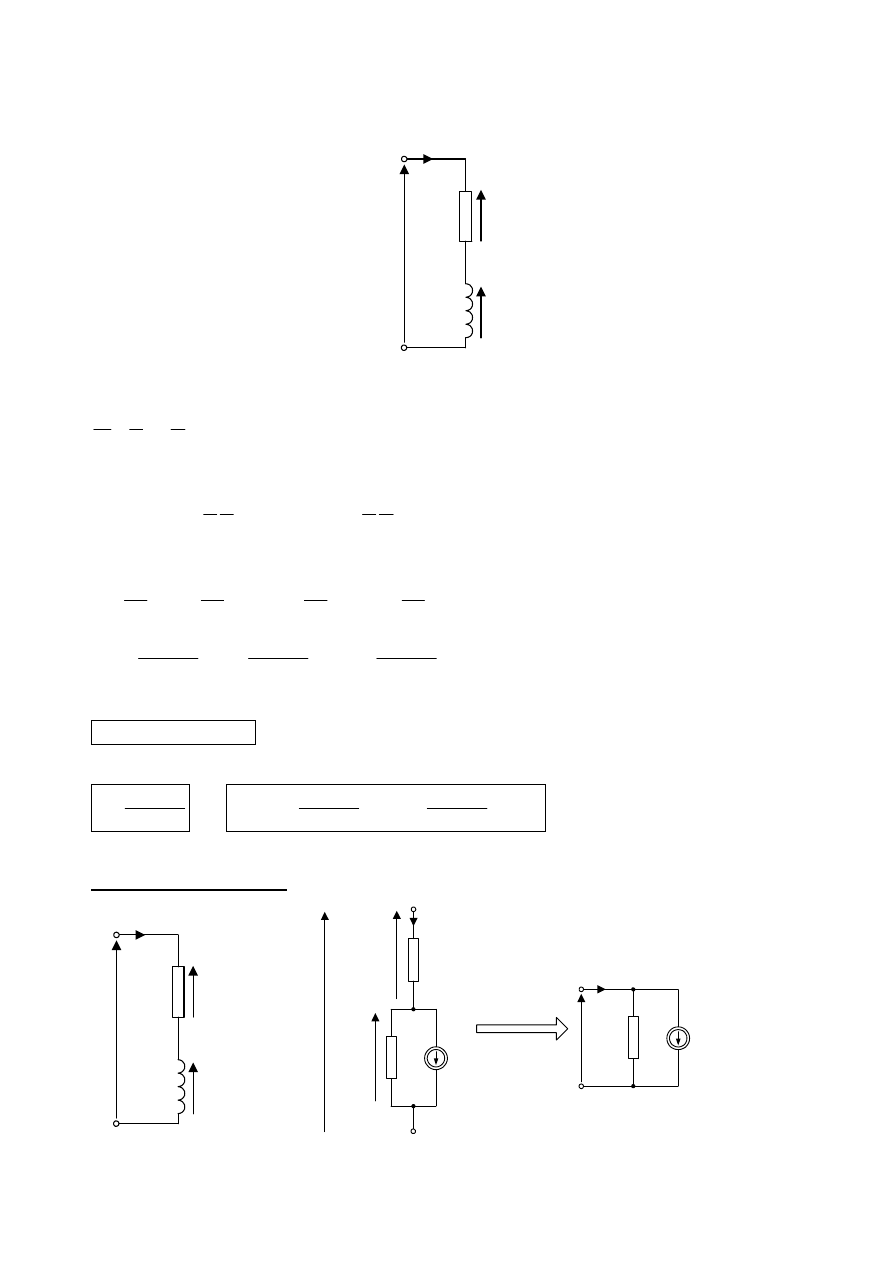
3. Określić model cyfrowy dla szeregowego połączenia elementów: R, L, przy zastosowaniu do

całkowania numerycznego metody trapezów.

L

R

u

i

u

L

u

R

Pochodna prądu i wynosi:

i

L

R

u

L

dt

di

−

=

1

(1)

Stosując metodę trapezów całkowania numerycznego do powyższego równania uzyskujemy:

)]

1

(

)

(

[

2

)]

1

(

)

(

[

1

2

)

1

(

)

(

−

+

−

−

+

+

−

=

k

i

k

i

L

R

T

k

u

k

u

L

T

k

i

k

i

(2)

Następnie uzyskujemy:

)

1

(

2

)

1

(

2

1

)

(

2

)

(

2

1

−

+

−











 −

+

=











 +

k

u

L

T

k

i

L

TR

k

u

L

T

k

i

L

TR

(3)

)

1

(

2

)

1

(

2

2

)

(

2

)

(

−

+

+

−

+

−

+

+

=

k

u

TR

L

T

k

i

TR

L

TR

L

k

u

TR

L

T

k

i

(3a)

Uzyskujemy więc następujący zapis modelu cyfrowego (więc jak w poprzednich zadaniach):

)

1

(

)

(

)

(

−

+

=

k

j

k

Gu

k

i

(4)

gdzie:

TR

L

T

G

+

=

2

,

)

1

(

2

)

1

(

2

2

)

1

(

−

+

+

−

+

−

=

−

k

u

TR

L

T

k

i

TR

L

TR

L

k

j

Inny sposób rozwiązania:

L

R

u

i

u

L

u

R

j

L

(k–1)

G

L

u

L

(k)

G

R

u

R

(k)

i(k)

j(k–1)

G

u(k)

i(k)

u(k)

Rys. Szeregowe połączenie elementów R, L oraz szeregowe zestawienie modeli elementów R, L i
końcowy model gałęzi.

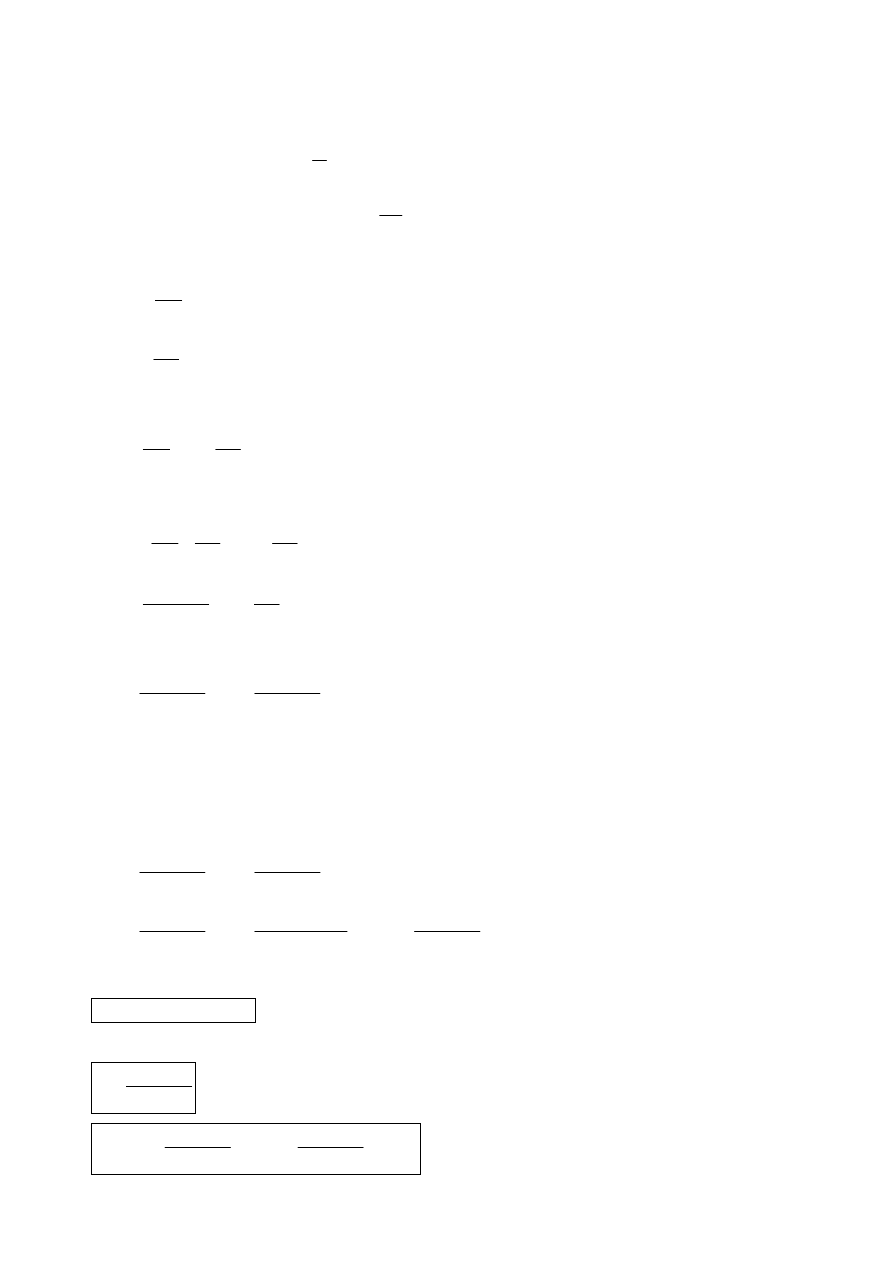
Dla szeregowego połączenia elementów R, L zachodzi:

L

R

u

u

u

+

=

(1)

Modele poszczególnych elementów R, L są następujące:

)

(

)

(

R

R

k

u

G

k

i

=

, gdzie:

R

G

1

R

=

(2)

)

1

(

)

(

)

(

L

L

L

−

+

=

k

j

k

u

G

k

i

, gdzie:

L

T

G

2

L

=

,

)

1

(

)

1

(

)

1

(

L

L

L

−

+

−

=

−

k

u

G

k

i

k

j

(3)

Przechodząc na równania prądowe dla elementów R, L mamy:

)

(

1

)

(

R

R

k

i

G

k

u

=

(4)

)]

1

(

)

(

[

1

)

(

L

L

L

−

−

=

k

j

k

i

G

k

u

(5)

Rozpisując (1) uzyskujemy:

)]

1

(

)

(

[

1

)

(

1

)

(

L

L

R

−

−

+

=

k

j

k

i

G

k

i

G

k

u

(6)

Po dalszym przekształceniu:

)

1

(

1

)

(

1

1

)

(

L

L

L

R

−

−













+

=

k

j

G

k

i

G

G

k

u

(6a)

)

1

(

1

)

(

)

(

L

L

L

R

L

R

−

−

+

=

k

j

G

k

i

G

G

G

G

k

u

(6b)

Przekształcając (6b) do postaci prądowej uzyskujemy:

)

1

(

)

(

)

(

L

L

R

R

L

R

L

R

−

+

+

+

=

k

j

G

G

G

k

u

G

G

G

G

k

i

(7)

W następnym kroku należy rozważyć źródło prądowe

)

1

(

L

−

k

j

i wyeliminować w nim niepożądane

zmienne, tj. wszystkie oprócz: i, u:

(

) (

)

)

1

(

)

1

(

1

)

1

(

)

1

(

)

1

(

)

1

(

)

1

(

)

1

(

L

L

L

L

L

L

−

+

−

−

=

−

−

−

+

−

=

−

+

−

=

−

k

u

G

k

i

R

G

k

Ri

k

u

G

k

i

k

u

G

k

i

k

j

(8)

Wstawiając (8) do (7) uzyskamy:

(

)

[

]

)

1

(

)

1

(

1

)

(

)

(

L

L

L

R

R

L

R

L

R

−

+

−

−

+

+

+

=

k

u

G

k

i

R

G

G

G

G

k

u

G

G

G

G

k

i

`

(9)

(

)

)

1

(

)

1

(

1

)

(

)

(

L

R

L

R

L

R

L

R

L

R

L

R

−

+

+

−

+

−

+

+

=

k

u

G

G

G

G

k

i

G

G

R

G

G

k

u

G

G

G

G

k

i

,

(9a)

Ostatecznie uzyskujemy następujący zapis modelu cyfrowego (jak w poprzednich zadaniach):

)

1

(

)

(

)

(

−

+

=

k

j

k

Gu

k

i

(10)

gdzie:

L

R

L

R

G

G

G

G

G

+

=

,

)

1

(

)

1

(

)

1

(

L

R

L

R

L

R

L

R

−

+

+

−

+

−

=

−

k

u

G

G

G

G

k

i

G

G

G

G

k

j

{uwzględniono, że:

1

R

=

R

G

}

Uzyskany zapis (10) można jeszcze (ale niekoniecznie) przekształcić, uwzględniając, że:

R

G

1

R

=

,

L

T

G

2

L

=

Otrzymujemy:

RT

L

T

L

T

R

L

T

R

G

G

G

G

G

+

=

+

⋅

=

+

=

2

2

1

2

1

L

R

L

R

Uwzględniając, że:

RT

L

RT

L

L

T

R

L

T

R

G

G

G

G

+

−

=

+

−

=

+

−

2

2

2

1

2

1

L

R

L

R

źródło prądowe można zapisać w postaci:

)

1

(

2

)

1

(

2

2

)

1

(

)

1

(

)

1

(

L

R

L

R

L

R

L

R

−

+

+

−

+

−

=

−

+

+

−

+

−

=

−

k

u

RT

L

T

k

i

RT

L

RT

L

k

u

G

G

G

G

k

i

G

G

G

G

k

j

Wniosek: uzyskano identyczny wynik, jak w prostszym sposobem rozwiązania.