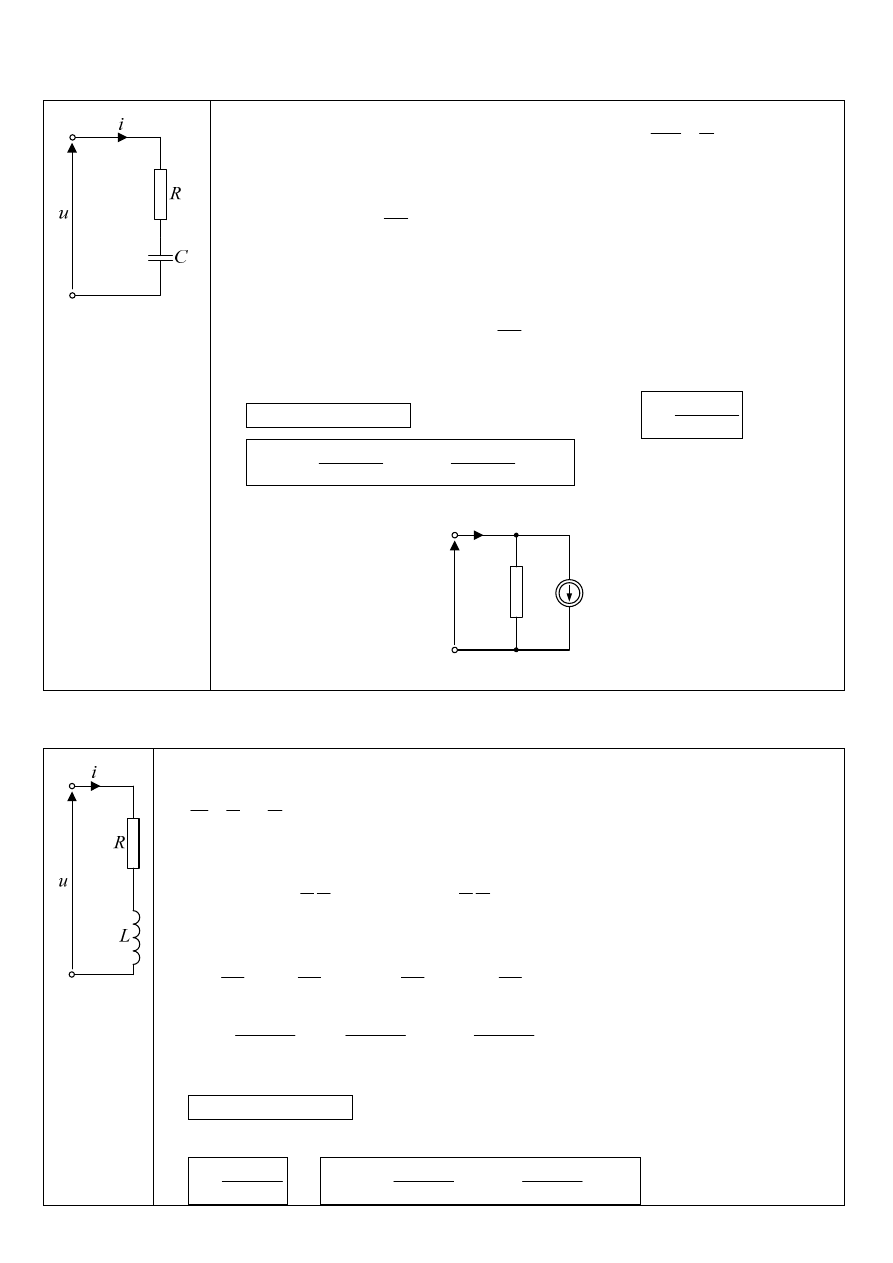
1. Określić model cyfrowy dla szeregowego połączenia elementów: R, C, przy zastosowaniu

metody trapezów do całkowania numerycznego.

Formułujemy równanie różniczkowe dla kondensatora:

i

C

dt

du

1

C

=

Stosując metodę trapezów całkowania numerycznego uzyskujemy:

)]

1

(

)

(

[

2

)

1

(

)

(

C

C

−

+

+

−

=

k

i

k

i

C

T

k

u

k

u

Uwzględniając, że:

)

(

)

(

)

(

C

k

Ri

k

u

k

u

−

=

oraz

)

1

(

)

1

(

)

1

(

C

−

−

−

=

−

k

Ri

k

u

k

u

uzyskujemy:

)]

1

(

)

(

[

2

)

1

(

)

1

(

)

(

)

(

−

+

+

−

−

−

=

−

k

i

k

i

C

T

k

Ri

k

u

k

Ri

k

u

A po przekształceniach:

)

1

(

)

(

)

(

−

+

=

k

j

k

Gu

k

i

gdzie:

T

RC

C

G

+

=

2

2

,

)

1

(

2

2

)

1

(

2

2

)

1

(

−

+

−

−

+

−

=

−

k

u

T

RC

C

k

i

T

RC

T

RC

k

j

j(k–1)

G

u(k)

i(k)

2. Określić model cyfrowy dla szeregowego połączenia elementów: R, L, stosując metodę

trapezów do całkowania numerycznego.

Pochodna prądu i wynosi:

i

L

R

u

L

dt

di

−

= 1

Stosując metodę trapezów całkowania numerycznego do powyższego równania uzyskujemy:

)]

1

(

)

(

[

2

)]

1

(

)

(

[

1

2

)

1

(

)

(

−

+

−

−

+

+

−

=

k

i

k

i

L

R

T

k

u

k

u

L

T

k

i

k

i

Następnie uzyskujemy:

)

1

(

2

)

1

(

2

1

)

(

2

)

(

2

1

−

+

−













−

+

=













+

k

u

L

T

k

i

L

TR

k

u

L

T

k

i

L

TR

)

1

(

2

)

1

(

2

2

)

(

2

)

(

−

+

+

−

+

−

+

+

=

k

u

TR

L

T

k

i

TR

L

TR

L

k

u

TR

L

T

k

i

Uzyskujemy więc następujący zapis modelu cyfrowego, analogiczny jak w poprzednim zadaniu:

)

1

(

)

(

)

(

−

+

=

k

j

k

Gu

k

i

gdzie:

TR

L

T

G

+

=

2

,

)

1

(

2

)

1

(

2

2

)

1

(

−

+

+

−

+

−

=

−

k

u

TR

L

T

k

i

TR

L

TR

L

k

j