DANE DO PROJEKTU

1. MATERIAŁY
element ceramiczny pustak Porotherm 44Si

f

b

=10 MPa

grubość muru

44 cm

kategoria produkcji

I

klasa wykonania robót

kat. B

beton użyty do wykonania stropu

C16/20 E

cm

=30 GPa

zaprawa cementowo-wapienna o wytrzymałości

10 MPa

2. WYMIARY ELEMENTÓW

szerokość filarka

wysokość filarka

grubość filarka

grubość stropu

szerokość pasma stropu

wysokość wieńca

bf

1m

:=

hf

2.78m

:=

t

0.44m

:=

hs

0.17m

:=

bs

2.5m

:=

hw

0.17m

:=

3. OBCIĄŻENIA STAŁE:

Stropodach

Strop

Ściana zewnętrzna

Wieniec

ZMIENNE:

Stropodach

Strop

Wiatr parcie

Wiatr ssanie

Gst

7.51

kN

m

2

:=

Gs

7.43

kN

m

2

:=

Gsz

4.93

kN

m

2

:=

Gw

2.15

kN

m

2

:=

zst

1.42

kN

m

2

:=

zs

5.25

kN

m

2

:=

wp

0.75

kN

m

2

:=

ws

0.48

kN

m

2

:=

4. OBLICZENIOWE SIŁY PODŁUŻNE W
POSZCZEGÓLNYCH PRZEROJACH FILARKA

obliczeniowa siła pionowa w przekroju pod stropem (1-1)

·

obliczeniowa siła pionowa w połowie wysokości ściany

·

(m-m)

obliczeniowa siła pionowa w przekroju nad stropem (2-2)

·

N1_1

51.82kN

:=

Nm_m

61.93kN

:=

N2_2

75.44kN

:=

5. WYTRZYMAŁOŚĆ CHARAKTERYSTY CZNA MURU NA ŚCISKANIE

K

0.40

:=

fb

15MPa

:=

fm

10MPa

:=

fk

K fb

0.7



fm

0.3



:=

fk 5.313 10

6



Pa

=

WYTRZYMAŁOŚĆ OBLICZENIOWA MURU

ɣm

2.0

:=

częściowy współczynnik bezpieczeństwa

Amuru

bf t

:=

Amuru 0.44 m

2

=

ɣRd

1.0

:=

fd

fk

ɣm ɣRd



:=

fd 2.656 10

6



Pa

=

CHARAKTERYSTYKI POSZCZEGÓLNYCH PRĘTÓW

Moduł sprężystości muru

E

1000 fk



:=

E

5.313

10

9



Pa

=

Eb

30GPa

:=

Moduł sprężystości betonu

Momenty bezwładności prętów poziomych (filarków)

If

bf

t

3

12



:=

If

7.099

10

3

-



m

4

=

Momenty bezwładności prętów pionowych (stropów)

Is

bs

hs

3

12



:=

Is 1.024 10

3

-



m

4

=

MOMENTY ZGINAJĄCE W POSZCZEGÓLNYCH PRZEKROJACH

Moment u góry ściany:

obciążenie pasm a stropu

·

q

Gst zst

+

:=

q

8.93

10

3



Pa

=

lsś

6.75m

:=

rozpiętość stropu w świetle

w4a

q lsś



:=

w4a 6.028 10

4



kg

s

2

=

współczynnik braku sztywności pręta

·

n4a

4

:=

n1a

4

:=

E1a

E

:=

E1a 5.313 10

9



Pa

=

E4a

Eb

:=

E4a 3 10

10



Pa

=

h1a

hf

:=

h1a 2.78 m

=

l4a

lsś

:=

l4a 6.75 m

=

I1a

If 7.099 10

3

-



m

4

=

:=

I4a

Is 1.024 10

3

-



m

4

=

:=

km

n4a

E4a I4a



l4a













n1a

E1a I1a



h1a













:=

km 0.335

=

η

1

km

4

-

:=

η

0.916

=

M1d

η w4a

l4a

2

4 n4a 1

-

(

)





















n1a E1a



I1a

h1a















n1a E1a



I1a

h1a













n4a E4a



I4a

l4a













+

:=

M1d 1.57 10

5



J

=

Moment u dołu ściany:

obciążenie pasm a stropu

·

w4b

w4a 6.028 10

4



kg

s

2

=

:=

n1b

4

:=

n2b

4

:=

n4b

4

:=

E1b

Eb 3 10

10



Pa

=

:=

E2b

E

5.313

10

9



Pa

=

:=

E4b

Eb 3 10

10



Pa

=

:=

h1b

h1a

:=

h2b

hf

:=

l4b

l4a

:=

I1b

I1a

:=

I2b

I1b

:=

I4b

I4a

:=

km

n4b

E4b I4b



l4b



n1b

E1b I1b



h1b













n2b

E2b I2b



h2b













+

:=

km 0.05

=

η

1

km

4

-

:=

η

0.987

=

M2d

η w4b

l4b

2

4 n4b 1

-

(

)





















n2b E2b



I2b

h2b















n1b E1b



I1b

h1b













n2b E2b



I2b

h2b













+

n4b E4b



I4b
l4b













+

:=

M2d 3.237 10

4



J

=

Moment w węźle środkowym:

Mmd

0.5 M1d



0.5 M2d



-

:=

Mmd 6.233 10

4



J

=

OBLICZENIOWY MOMENT ZGINAJĄCY WYWOŁANY OBCIĄŻENIEM POZIOMYM
(WIATR) DZIAŁAJĄCYM NA ŚCIA NĘ

parcie wiatru:

ssanie wiatru:

Mwp

wp bs



hf

2

16



:=

Mws

ws bs



hf

2

16



:=

Mwp 905.672 J

=

Mws 579.63 J

=

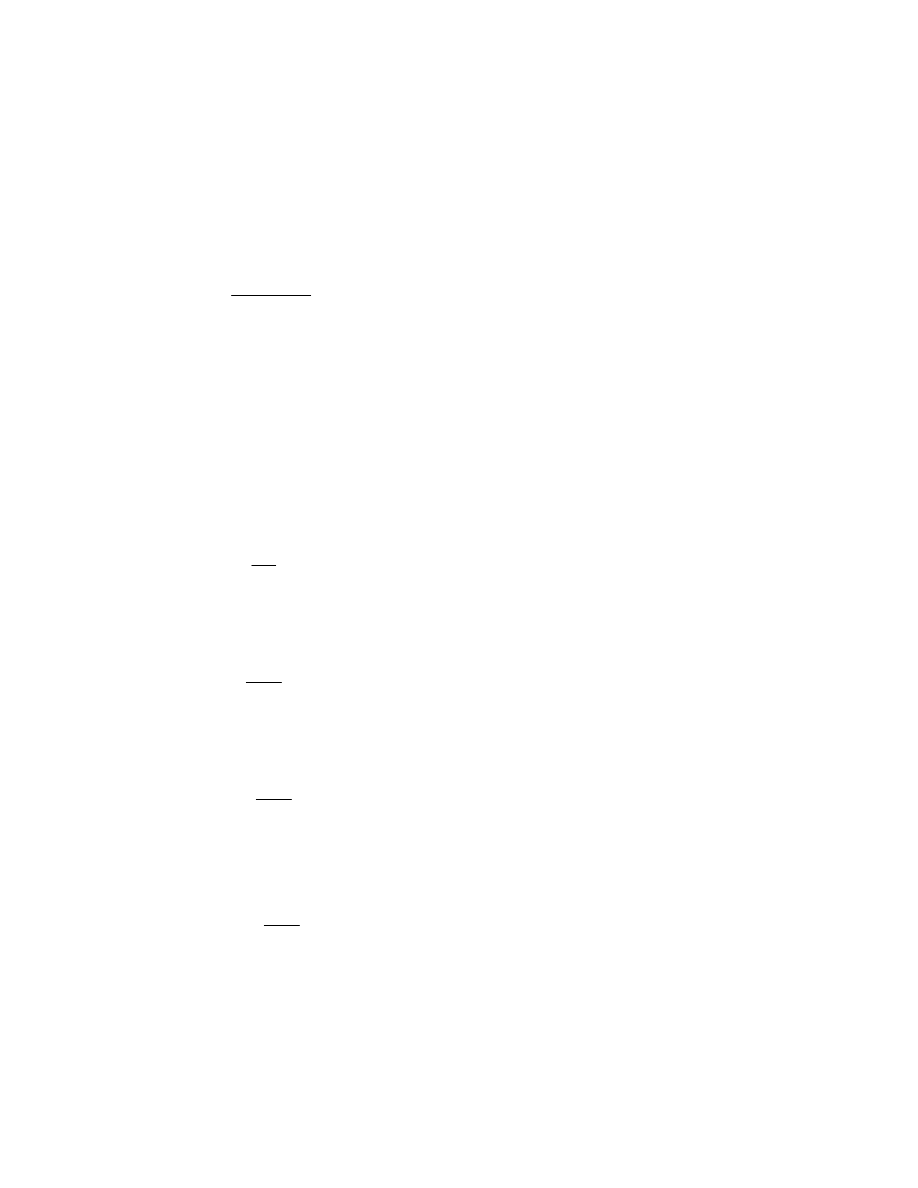
WYSOKOŚĆ EFEKTYWNA Ś CIAN Y

m im ośród na górnej krawędzi

e1

M1d Mwp

+

N1_1

:=

e1 3.048 m

=

t

0.44 m

=

0.25 t



0.11 m

=

e1 0.25t

>

ρn

1.0

:=

hf 2.78 m

=

hef

ρn hf



:=

hef

2.78 m

=

SPRAWDZE NIE NOŚNOŚCI FILARKA

m im ośród początkowy

einit

hef

450

:=

einit 6.178 10

3

-



m

=

m im ośród od obciążenia poziomego (wiatr-parcie)

ehe

Mwp

N1_1

:=

ehe 0.017 m

=

m im ośród od obciążenia poziomego (wiatr-ssanie)

ehd

Mws

N2_2

:=

ehd 7.683 10

3

-



m

=

m im ośród u góry ściany

e1a

M1d

N1_1

einit

+

ehe

+

:=

e1a 3.054 m

=

t

0.44 m

=

0.05 t



0.022 m

=

e1a 0.05t

>

m im ośród u dołu ściany

e2a

M2d

N2_2

einit

+

ehd

+

:=

e2a 0.443 m

=

e2a 0.05t

>

PRZEKRÓJ 1-1

ehe 0.017 m

=

e1a 3.054 m

=

0.05 t



0.022 m

=

0.45 t



0.198 m

=

e1a 0.45t

>

m odel niesłuszny

zgodnie z zał. C:

x

min

N1_1

fb bs



0.1 t



,











:=

x

1.382

10

3

-



m

=

z

0.1t

0.044 m

=

:=

M1d

N1_1 0.5t 0.5x

-

(

)



:=

M1d 1.136 10

4



J

=

e1a

t

2

z

-

0.1 t



-

:=

e1a 0.132 m

=

współczynnik redukcyjny

φ1

1

2

e1a

t



-

:=

φ1 0.4

=

Nośność obliczeniowa ściany w przekroju 1-1

NRdl1

φ1 t fd



bf



:=

NRdl1 4.675 10

5



N

=

N1_1 5.182 10

4



N

=

nośność wystarczająca

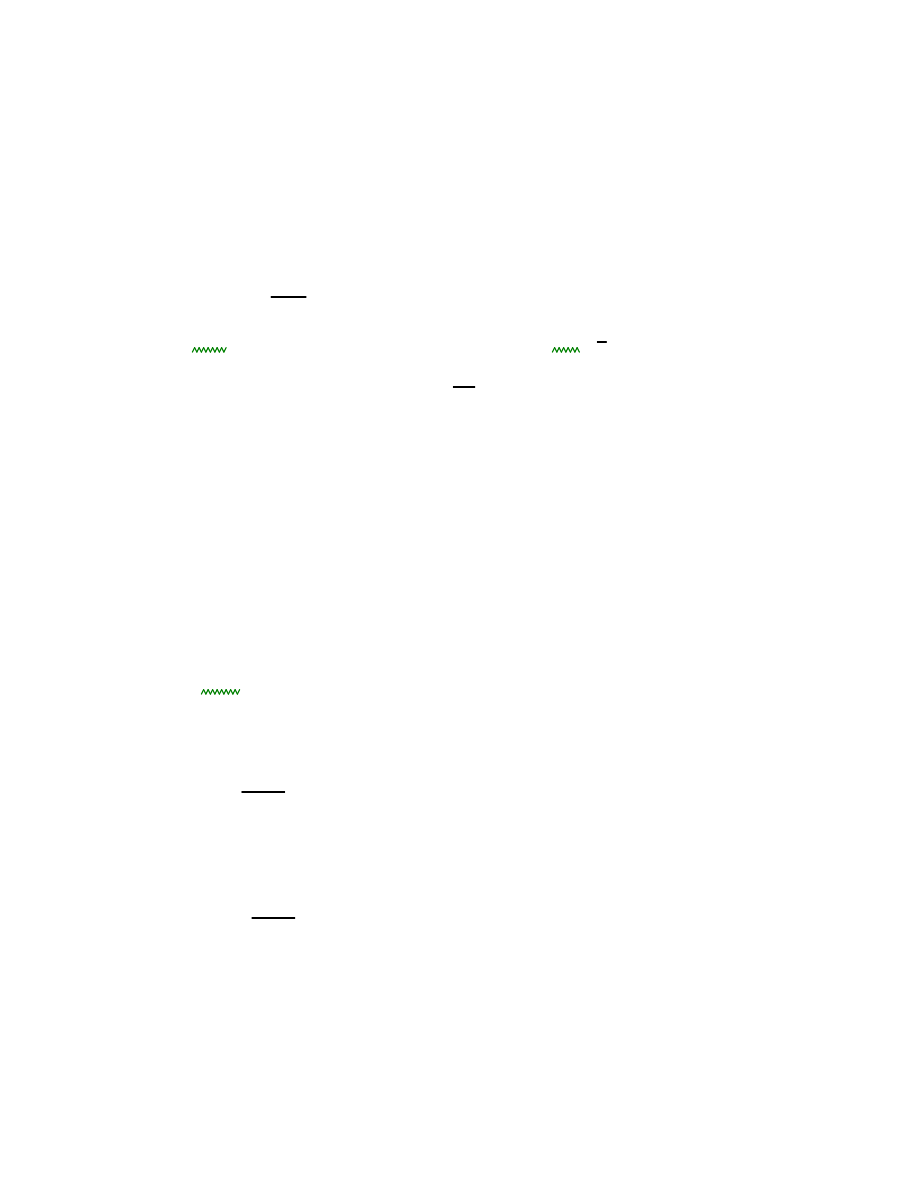
PRZEKRÓJ 2-2

e2a 0.443 m

=

0.05t

0.022 m

=

ehd 7.683 10

3

-



m

=

0.45t

0.198 m

=

e2a 0.45t

<

m odel niesłuszny

x2

min

N2_2

fb bs



0.1 t



,











:=

x2 2.012 10

3

-



m

=

z2

0.1t

0.044 m

=

:=

M2d

N2_2 0.5t 0.5x2

-

(

)



:=

M2d 1.652 10

4



J

=

e2a

t

2

z2

-

0.1t

-

:=

e2a 0.132 m

=

φ2

1

2

e2a

t



-

:=

φ2 0.4

=

Nośność obliczeniowa ściany w przekroju 2-2

NRdl2

φ2 t fd



bf



:=

NRdl2 4.675 10

5



N

=

N2_2 7.544 10

4



N

=

nośność wystarczająca

PRZEKRÓJ m-m

Mmd

0.5M2d 0.5M1d

-

2.578

10

3



J

=

:=

Mwp 905.672 J

=

ehm

Mwp

Nm_m

:=

ehm 0.015 m

=

Mim ośród działania obciążenia

em1

Mmd

Nm_m

ehm

+

einit

+

:=

em1

0.062 m

=

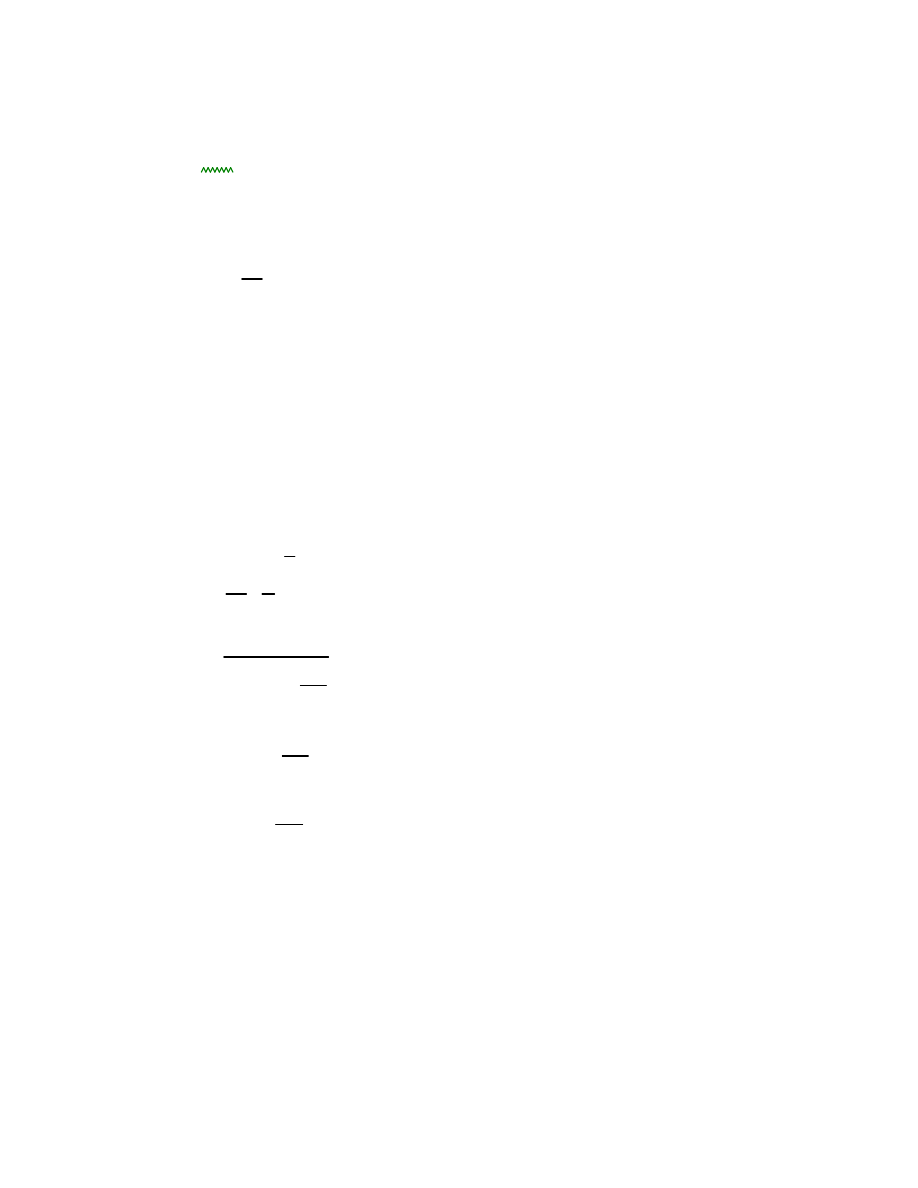
em1

max em1 0.05 t

,

(

)

:=

em1

0.062 m

=

Mim ośród wywołany przez pełzanie

λc

hef

t

:=

λc 6.318

=

λc 15

<

ek

0

:=

m im ośród m -m

emk

em1 ek

+

:=

emk 0.062 m

=

współczynnik redukcyjny

E

5.313

10

9



Pa

=

tef

t

0.44 m

=

:=

λ

hef

tef

fk

E













1

2



:=

λ

0.2

=

u

λ

0.063

-

(

)

0.73

1.17

emk

t



-

:=

u

0.243

=

A1

1

2

emk

t



-

:=

A1 0.716

=

φm

A1 e

u

2

-

2



:=

φm 0.695

=

Nośność obliczeniowa w środku ściany

NRdm

φm t fd



bf



:=

NRdm 8.129 10

5



N

=

Nm_m 6.193 10

4



N

=

nośność wystarczająca

FILAREK SPEŁNIA W YMAGANIA NOŚNOŚCI