Materiał pomocniczy do ćw. 2 z Elektrodynamiki (P. Kowalczyk)

1

Funkcja liniowa

Funkcją nazywamy przyporządkowanie każdemu elementowi danego zbioru, zwanego dziedziną,

jednej (i tylko jednej) konkretnej wartości z innego zadanego zbioru (zwanego przeciwdziedziną).

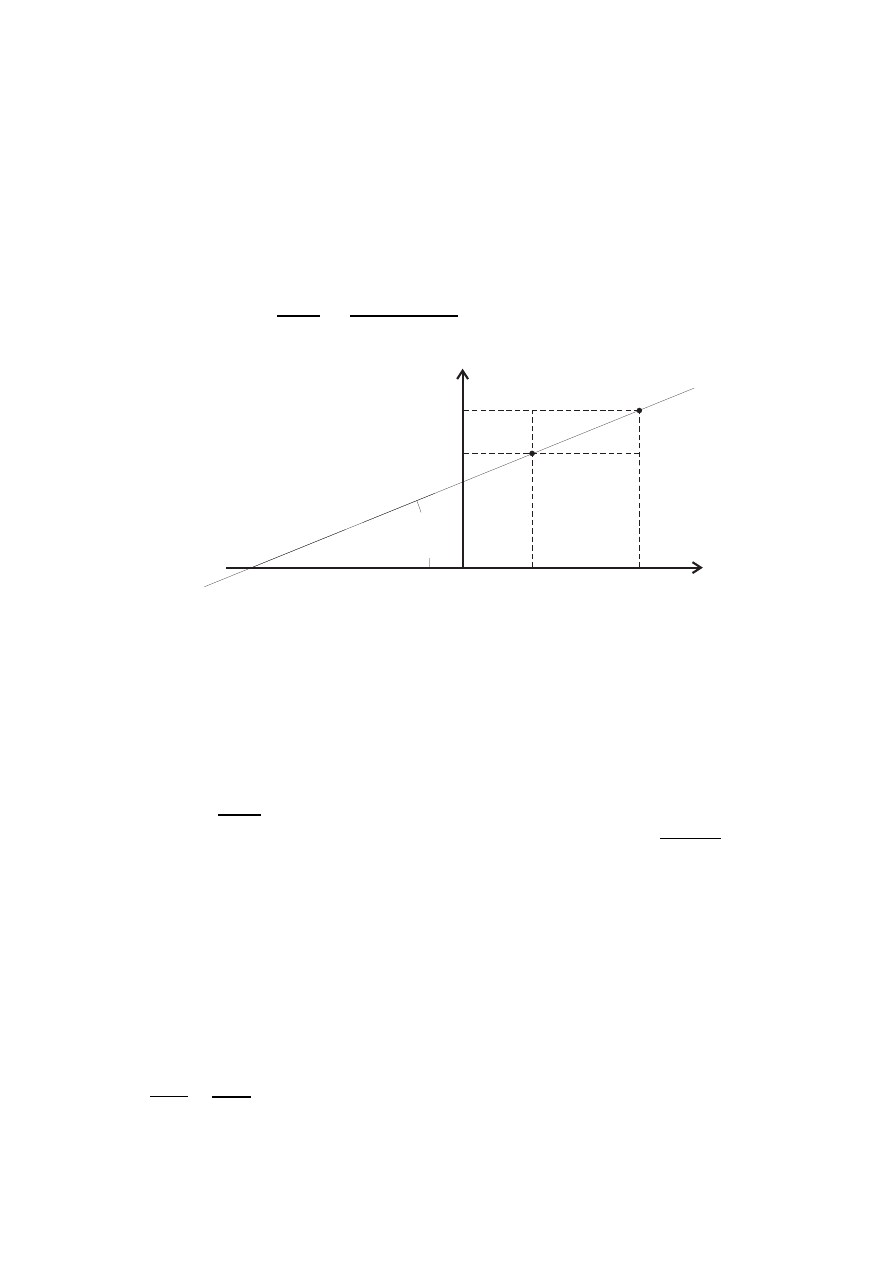
Funkcja liniowa (której wykresem jest prosta) najczęściej zapisywana jest w postaci kierunkowej

y = ax + b. Rozważmy dwa punkty należące do tej prostej A(x

A

, y

A

) i B(x

B

, y

B

) (patrz rys. 1).

Zachodzi dla nich relacja y

A

= ax

A

+ b oraz y

B

= ax

B

+ b. Tangens kąta jaki prosta tworzy z osią

odciętych x jest równy współczynnikowi kierunkowemu a. Wynika to bezpośrednio z następujących
przekształceń tan α =

y

B

−y

A

x

B

−x

A

=

(ax

B

+b)−(ax

A

+b)

x

B

−x

A

= a. Parametr b jest równy wartości funkcji w

punkcji x = 0 i nazywa się parametrem przesunięcia.

a

y

1

y

2

x

1

x

2

D

x

D

y

x

y

Rysunek 1: Funkcja liniowa

Przykłady

1. Znajdź równanie prostej przechodzącej przez punkt P (1, 3) tworzącej z prostą y = 1/2x + 1

kąt π/4.
Rozwiązanie:
Rozważmy dwie proste o kątach nachylenia do osi rzędnych wynoszących odpowiednio α

1

oraz

α

2

. Ich współczynniki kierunkowe sa wówczas równe a

1

= tan α

1

oraz a

2

= tan α

2

. Oznaczmy

przez ϕ kąt pomiędzy prostymi ϕ = α

2

− α

1

. Korzystając ze wzoru na tangens różnicy kątów

tan ϕ =

a

2

−a1

1+a

1

a

2

. Stąd znając współczynnik kierunkowy (a

1

) jednej z prostych wyznaczyć

można współczynnik prostej nachylonej pod kątem większym o ϕ a

2

=

a

1

+tan ϕ

1−a

1

tan ϕ

. W zadaniu

musimy rozważyć dwa przypadki ϕ

+

= π/4 oraz ϕ

−

= −π/4. Odpowiednio w każdym z

przypadków dla a

1

= 1/2 otrzymujemy a

2+

= 3 oraz a

2−

= −1/3. Współczynniki przesunięcia

w obu wariantach wyznaczyć można podstawiając współrzędne punktu A do równań prostych
y

+

= 3x + b

+

oraz y

−

= −1/3x + b

−

. Ostatecznie y

+

= 3x oraz y

−

= −1/3x + 4

2. Znajdź równanie stycznej do paraboli y = x

2

w punkcie x

0

= 1.

Rozwiązanie:
Podstawiając do równania paraboli zadane x

0

wyznaczyć można drugą współrzędną punktu

styczności y

0

= 1. Jednak, znajomość tych współrzędnych nie wystarczy do jednoznacznego

wyznaczenia równania stycznej. Obierzmy zatem drugi punkt leżący na paraboli o współrzęd-
nej odciętej zwiększonej o pewną wartość h x

1

= x

0

+ h = 1 + h, wówczas y

1

= 1 + 2h + h

2

.

Współczynnik kierunkowy prostej przechodzącej przez te punkty wyraża zatem relacja a(h) =

y

1

−y

0

x

1

−x

0

=

2h+h

2

h

= 2+h, a jego wartość uzależniona jest od wyboru h. Otrzymany w ten sposób

współczynnik kierunkowy nie jest jednoznaczny i w zależności od zadanej wartości h będzie
przyjmował różne wartości. Dla przypadku gdy h → 0, współczynnik kierunkowy stanie się

1

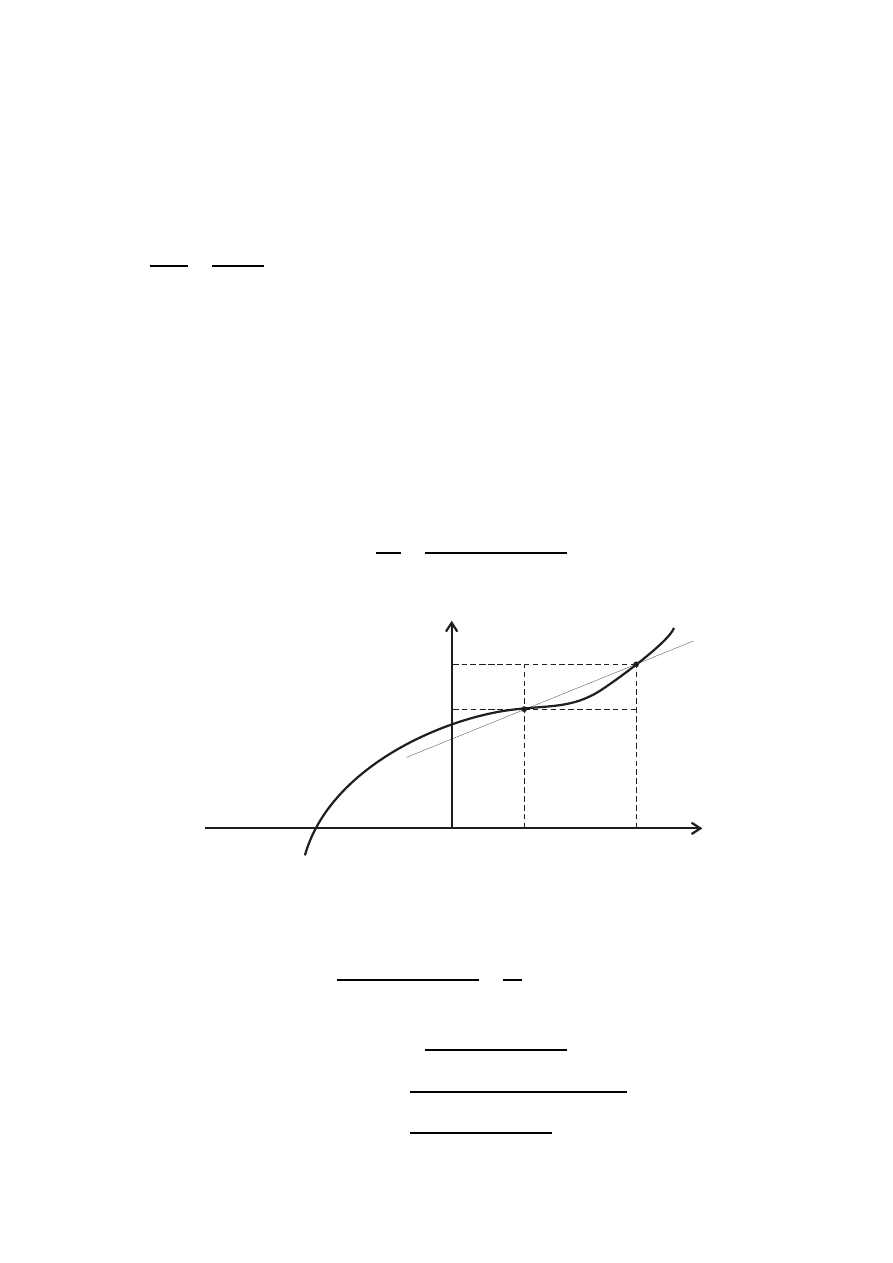
współczynnikiem kierunkowym prostej stycznej a = 2. Pozostaje jeszcze wyznaczyć wartość
współczynnika b. Otrzymujemy ją podstawiając do równania y = 2x + b współrzędne x

0

i y

0

.

Ostatecznie styczna ma postać y = 2x − 1.

3. Wyznacz współczynnik kierunkowy stycznej do paraboli y = x

2

w dowolnym punkcie x

0

.

Rozwiązanie:
Podobnie jak w poprzednim przykładzie obieramy dwa punkty leżące na paraboli o odciętych
x

0

i x

1

= x

0

+ h oraz rzędnych równych odpowiednio y

0

= x

2

0

i y

1

= x

2

0

+ 2x

0

h + h

2

.

Współczynnik kierunkowy prostej przechodzącej przez te punkty wyraża relacja a(h, x

0

) =

y

1

−y

0

x

1

−x

0

=

2x

0

h

+h

2

h

= 2x

0

+h. Podobnie jak w poprzednim przykładzie, gdy h → 0, współczynnik

kierunkowy stanie się współczynnikiem kierunkowym prostej stycznej a(x

0

) = 2x

0

. Warto tu

zwrócić uwagę, że współczynnik kierunkowy stycznej wyraża charakter zmienności funkcji,
tzn. wartość współczynnika jest duża w punktach w których funkcja jest szybkozmienna,
natomiast bliska zeru w punktach gdzie funkcja zmienia się wolno.

2

Pochodna funkcji jednej zmiennej - interpretacja i zastosowanie

Geometrycznie pochodna funkcji interpretowana jest jako współczynnik kierunkowy prostej stycznej
do funkcji. Dla zadanej funkcji f (x) wybieramy punkt do niej należący (x

0

, f (x

0

)). W celu określenia

współczynnika nachylenia stycznej obieramy dodatkowo drugi punkt (również należący do krzywej
f (x)) o współrzędnych (x

0

+ ∆x, f (x

0

+ ∆x)) (patrz rys. 2). Współczynnik kierunkowy prostej

przechodzącej przez te punkty wyraża się następującym wzorem (ilorazem różnicowym):

a =

∆f
∆x

=

f (x

0

+ ∆x) − f(x

0

)

∆x

,

(2.1)

i jest on oczywiście zależny od doboru przyrostu ∆x. Gdy ∆x → 0 rozważana prosta staje się stycz-

f(x )

0

x

0

x + x

0

D

Dx

Df

f(x + x)

0

D

x

f(x)

Rysunek 2: Interpretacja graficzna pochodnej funkcji

ną do funkcji f (x) w punkcie x

0

, a otrzymany współczynnik kierunkowy nazywany jest pochodną

funkcji

a = lim

∆x→0

f (x

0

+ ∆x) − f(x

0

)

∆x

=

df

dx

(x

0

) = f

′

(x

0

).

(2.2)

Warto zaznaczyć, że istnieją też inne równoważne definicje pochodnej

f

′

(x

0

) = lim

∆x→0

f (x

0

+ ∆x) − f(x

0

)

∆x

= lim

∆x→0

f (x

0

+ ∆x/2) − f(x

0

− ∆x/2)

∆x

= lim

∆x→0

f (x

0

) − f(x

0

− ∆x)

∆x

.

(2.3)

2

2.1

Gradient jednowymiarowy

Wartość pochodnej w danym punkcie informuje o charakterze zmienności funkcji w tym punkcie.
Dodatnia wartość pochodnej oznacza, że funkcja rośnie, zaś ujemna, że funkcja maleje. Nie tylko
znak pochodnej jest istotny, dodatkowo jej wartość mówi o tempie wzrostu lub spadku funkcji.
Własność ta wykorzystana jest w operatorze różniczkowym nazywanym gradientem. Gradient w
przestrzeni jednowymiarowej definiowany jest w następujący sposób:

gradf (x) =

df

dx

(x)i

x

.

(2.4)

Wynikiem działania tego operatora na funkcję jest pole wektorowe, przyporządkowujące każdemu
punktowi dziedziny wektor wskazujący kierunek najszybszego wzrostu funkcji (patrz przykłady).

2.2

Różniczka funkcji jednej zmiennej

Różniczką nazywamy nieskończenie małą zmianę wartości funkcji df , która wynika z nieskończenie
małej zmiany argumentu dx:

df = f

′

(x)dx.

(2.5)

Powyższa relacja jest wykorzystywana do wyznaczania przybliżonej wartości funkcji, w przypadku
gdy znana jest wartość funkcji w jej niedalekim sąsiedztwie. Zakładając, że znamy wartość funkcji
w punkcji x

0

, przybliżona wartość funkcji w punkcie odległym o ∆x wyraża się wzorem:

f (x

0

+ ∆x) ≈ f(x

0

) + f

′

(x)∆x.

(2.6)

Przykłady

1. Korzystając z definicji, wyznacz pochodną funkcji f (x) = x

n

.

Rozwiązanie:
Wartości funkcji w punktach x

0

i x

0

+ ∆x wynoszą odpowiednio f (x

0

) = x

n

0

i f (x

0

+ ∆x) =

(x

0

+ ∆x)

n

=

P

n

k

=0

n
k

!

x

n−k

0

∆x

k

Podstawiając te wartości do definicji pochodnej otrzy-

mujemy f

′

(x

0

) = lim

∆x→0

P

n
k=1

n
k

!

x

n−k
0

∆x

k

∆x

= lim

∆x→0

P

n

k

=1

n
k

!

x

n−k

0

∆x

k−1

= nx

n

0

.

2. W arkuszu tektury o wymiarach 210×297mm (A4) wycięto kwadraty w czterech narożnikach

i sklejono ją w taki sposób, że powstało pudełko bez wieczka. Określ jaka powinna być długość
boku kwadratu, aby pojemność pudełka była największa.
Rozwiązanie:
Objętość pudełka opisuje relacja V (x) = (210 − 2x)(297 − 2x)x, gdzie x jest długością boku
kwadratu. Ponieważ argument x należy do przedziału (0, 105) i na obu krańcach przedziału
wartość pola jest zerowa, to wewnątrz przedziału istnieje punkt, w którym jest ona najwięk-
sza. Punkt ten wyznaczyć można poprzez znalezienie x

max

dla którego pochodna z objętości

w funkcji x będzie równa zero V

′

(x) = 12x

2

− 2028x + 62370 oraz V

′

(x

max

) = 0. Ostatecz-

nie znajdujemy dwa punkty x =

169±

√

7771

2

spełniające warunek zerowania się pochodnej.

Jednakże tylko jeden należy do zadanego przedziału x

max

=

169−

√

7771

2

≈ 40.4mm.

3. Wyznacz wymiary beczki o pojemności V

0

= 200l tak aby była ona najtańsza i najlżejsza

(miała najmniejsze pole powierzchni całkowitej). Zakładamy, że beczka jest w przybliżeniu
walcem.
Rozwiązanie:

3

Pole powierzchni całkowitej walca wyraża się wzorem P (r, h) = 2πrh + 2πr

2

, gdzie r jest

promieniem podstawy, zaś h wysokością walca. Ustalona objętość determinuje relację po-
między promieniem i wysokością V

0

= πr

2

h, stąd P (r) = 2πr

2

+

2V

0

r

. Ponieważ argument

r należy do przedziału (0, ∞) i na obu krańcach przedziału wartość pola jest nieskończo-
na, to wewnątrz przedziału istnieje punkt, w którym jest ona najmniejsza. Podobnie jak w
poprzednim przykładzie punkt ten wyznaczyć można poprzez znalezienie r

min

dla którego po-

chodna pola całkowitego będzie równa zero P

′

(r) = 4πr −

2V

0

r

2

oraz P

′

(r

min

) = 0. Ostatecznie

r

min

=

3

q

V

0

2π

≈ 3.17dm.

4. Wyznacz wyrażenie na gradient funkcji f (x) = x

3

/15 − 3x

2

/5 + x + 2 oraz oblicz i zaznacz

na wykresie gradient w punktach x = 0, 1, 2, . . . , 6.
Rozwiązanie:
Gradient funkcji f (x) ma postać gradf (x) = (x

2

/5 − 6x/5 + 1)i

x

(patrz rys. 3).

-1

0

1

2

3

4

5

6

7

-1

0

1

2

3

x

f(x)

Rysunek 3: Funkcja i jej gradient.

5. Określ przybliżoną wartość wyrażenia

√

3.98.

Rozwiązanie:
Wprowadzamy funkcję pomocniczą f (x) =

√

x, której pochodna ma postać f

′

(x) =

1

2

√

x

.

Korzystając z relacji (2.6), przy założeniu x

0

= 4 oraz ∆x = −0.02 , otrzymujemy f(3.98) ≈

f (4) − 0.02f

′

(4) = 1.995.

3

Funkcja wielu zmiennych

Dziedzinę dla funkcji wielu zmiennych stanowią punkty należące do przestrzeni wielowymiarowej:
dla funkcji dwóch zmiennych dziedziną jest pewien obszar powierzchni (dwuwymiarowej), zaś dla
funkcji trzech zmiennych dziedzina jest pewna objętość. Na rys. 4 przedstawiono wykres funkcji
dwóch zmiennych z = f (x, y) - każdemu punktowi na płaszczyźnie xy przyporządkowana jest pewna
wartość liczbowa z.

3.1

Pochodne cząstkowe - interpretacja i zastosowanie

Pochodna cząstkowa po zadanej zmiennej, liczona jest identycznie jak pochodna zwyczajna przy
założeniu, że wszystkie pozostałe zmienne przyjmują ustaloną wartość (traktowane są jak parame-
try). Pochodne cząstkowa funkcji f (x, y) definiuje się następująco: pochodna cząstkowa po zmiennej
x

∂f
∂x

(x

0

, y

0

) = lim

∆x→0

f (x

0

+ ∆x, y

0

) − f(x

0

, y

0

)

∆x

.

(3.7)

4

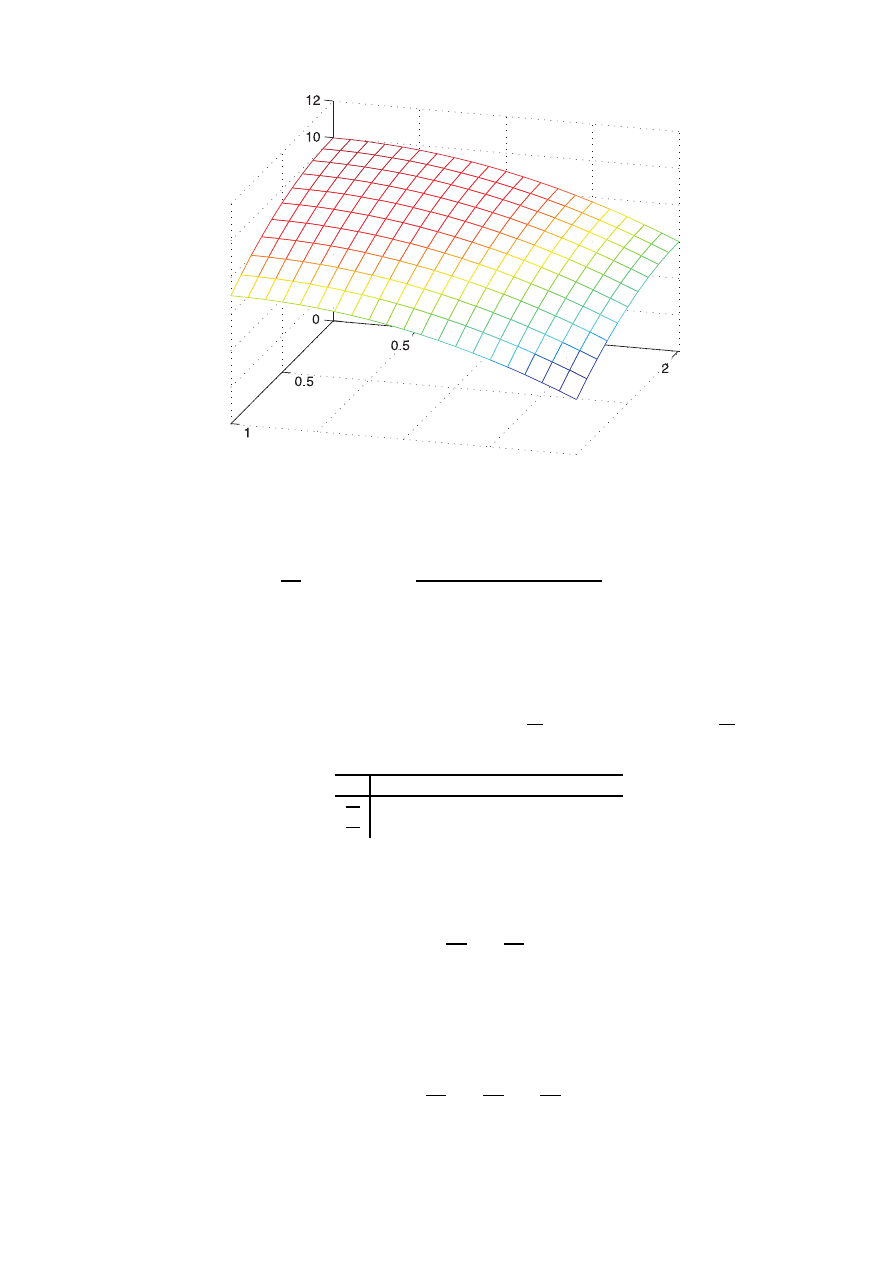
x

y

z

Rysunek 4: Funkcja dwóch zmiennych f (x, y) = 10 − 3x

2

− y

2

oraz pochodna cząstkowa po zmiennej y

∂f

∂y

(x

0

, y

0

) = lim

∆y→0

f (x

0

, y

0

+ ∆y) − f(x

0

, y

0

)

∆y

.

(3.8)

Przykłady

1. Wyznacz pochodne cząstkowe funkcji f (x, y) = 1 − x

2

/6 − y

2

/6 w punktach: A(−2, −2),

B(0, −2), C(2, −2), D(−2, 0), E(0, 0), F (−2, 2) .
Rozwiązanie:
Pochodne cząstkowe funkcji wynoszą odpowiednio

∂f
∂x

(x

0

, y

0

) = −x

0

/3 oraz

∂f
∂y

(x

0

, y

0

) =

−y

0

/3. Zatem (patrz rys. 5):

A

B

C

D

E

F

∂f
∂x

2/3

0

-2/3

2/3

0

2/3

∂f
∂y

2/3

2/3

2/3

0

0

-2/3

3.2

Gradient wielowymiarowy

W przypadku dwuwymiarowym gradient definiuje się jako:

gradf (x, y) =

∂f
∂x

i

x

+

∂f

∂y

i

y

.

(3.9)

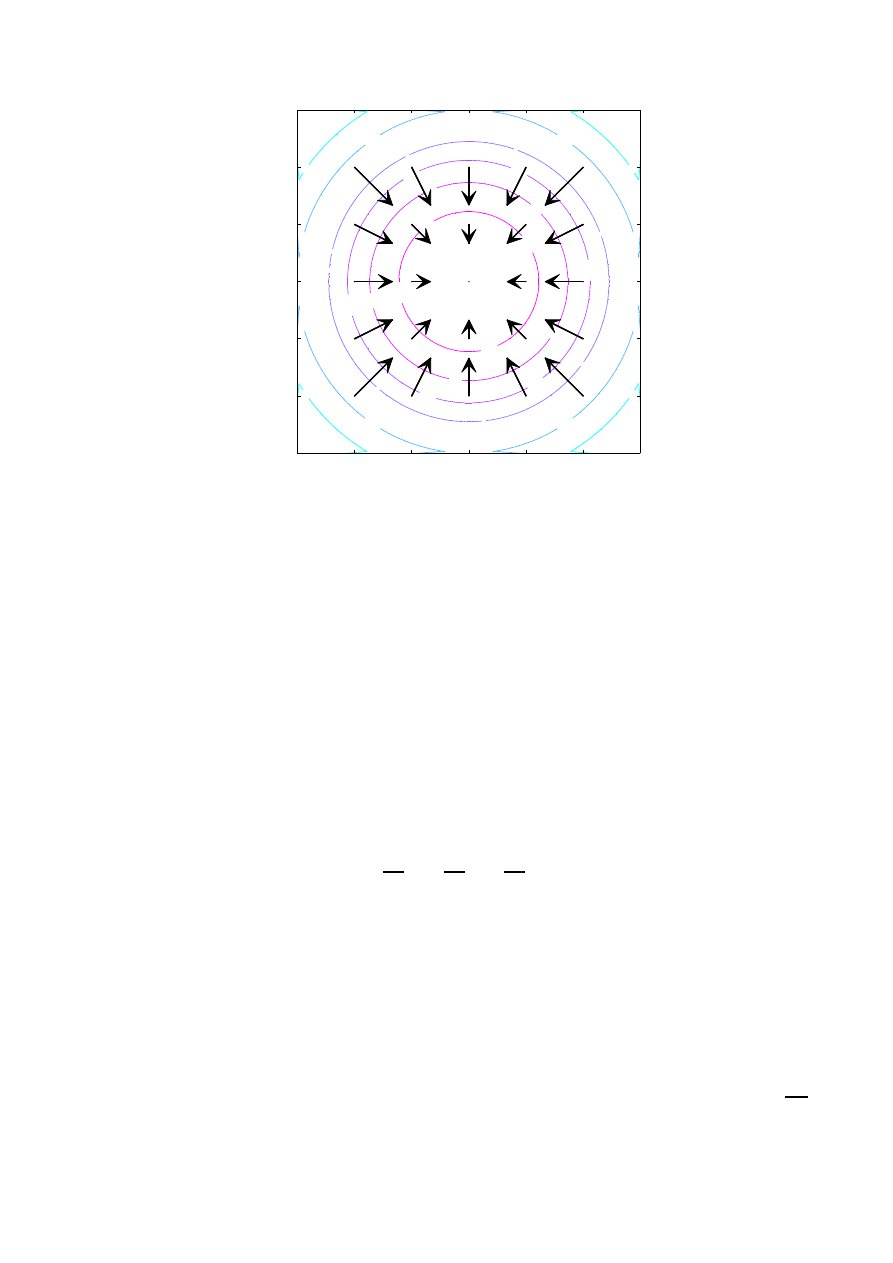
Na rysunku 5 przedstawiono gradient funkcji f (x, y) = 1−x

2

/6−y

2

/6 w kilku wybranych punktach

- gradf (x, y) = −x/3i

x

−y/3i

y

. Jak widać (podobnie jak w przypadku jednowymiarowym) gradient

wskazuje kierunek najszybszego wzrostu funkcji.

Definicję (3.9) łatwo uogólnić na przypadek trójwymiarowy:

gradf (x, y, z) =

∂f
∂x

i

x

+

∂f

∂y

i

y

+

∂f

∂z

i

z

.

(3.10)

5

−1

−1

−1

−1

−0.5

−0.5

−0.5

−0.5

−0.5

−0.5

−0.5

−0.5

0

0

0

0

0

0

0

0

0.25

0.25

0.25

0.25

0.25

0.25

0.5

0.5

0.5

0.5

0.5

0.75

0.75

0.75

0.75

x

y

−3

−2

−1

0

1

2

3

−3

−2

−1

0

1

2

3

Rysunek 5: Funkcja i jej gradient.

Przykłady

1. Oblicz gradient funkcji f (x, y, z) = x + xy + xyz.

Rozwiązanie:
Gradient funkcji f (x, y, z) ma postać gradf (x, y, z) = (1 + y + yz)i

x

+ (x + xz)i

y

+ xyi

z

2. Oblicz gradient funkcji f (x, y, z) = xy

2

z

3

w punkcie (1, 2, −1).

Rozwiązanie:
Gradient funkcji f (x, y, z) ma postać gradf (x, y, z) = y

2

z

3

i

x

+ 2xyz

3

i

y

+ 3xy

2

z

2

i

z

. Wartość

gradientu w zadanym punkcie wynosi gradf (1, 2, −1) = −4i

x

− 4i

y

+ 12i

z

.

3.3

Różniczka zupełna

Różniczką zupełną nazywamy nieskończenie małą zmianę wartości funkcji df , która wynika z nie-
skończenie małych zmian jej argumentów. Dla funkcji trzech zmiennych:

df =

∂f
∂x

dx +

∂f

∂y

dy +

∂f

∂z

dz

(3.11)

Podobnie jak w przypadku jednowymiarowym relacja ta może być wykorzystywana do wyznacza-
nia przybliżonej wartości funkcji, w przypadku gdy znana jest wartość funkcji w jej niedalekim
sąsiedztwie.

4

Całka Riemanna - interpretacje i zastosowania

Całka oznaczona

b

R

a

f (x)dx interpretowana jest jako pole zawarte pomiędzy krzywą f (x) a osią Ox

na przedziale (a, b).

Przybliżoną wartość całki otrzymuje się sumując pola N prostokątów o podstawie ∆x =

b−a

N

i wysokościach f (a), f (a + ∆x), f (a + 2∆x),..., f (b − ∆x), f(b − ∆x) (lub w zwartej formie
h

i

= f (a + ∆x(i − 1)), i = 1, 2, 3, ..., N)

6

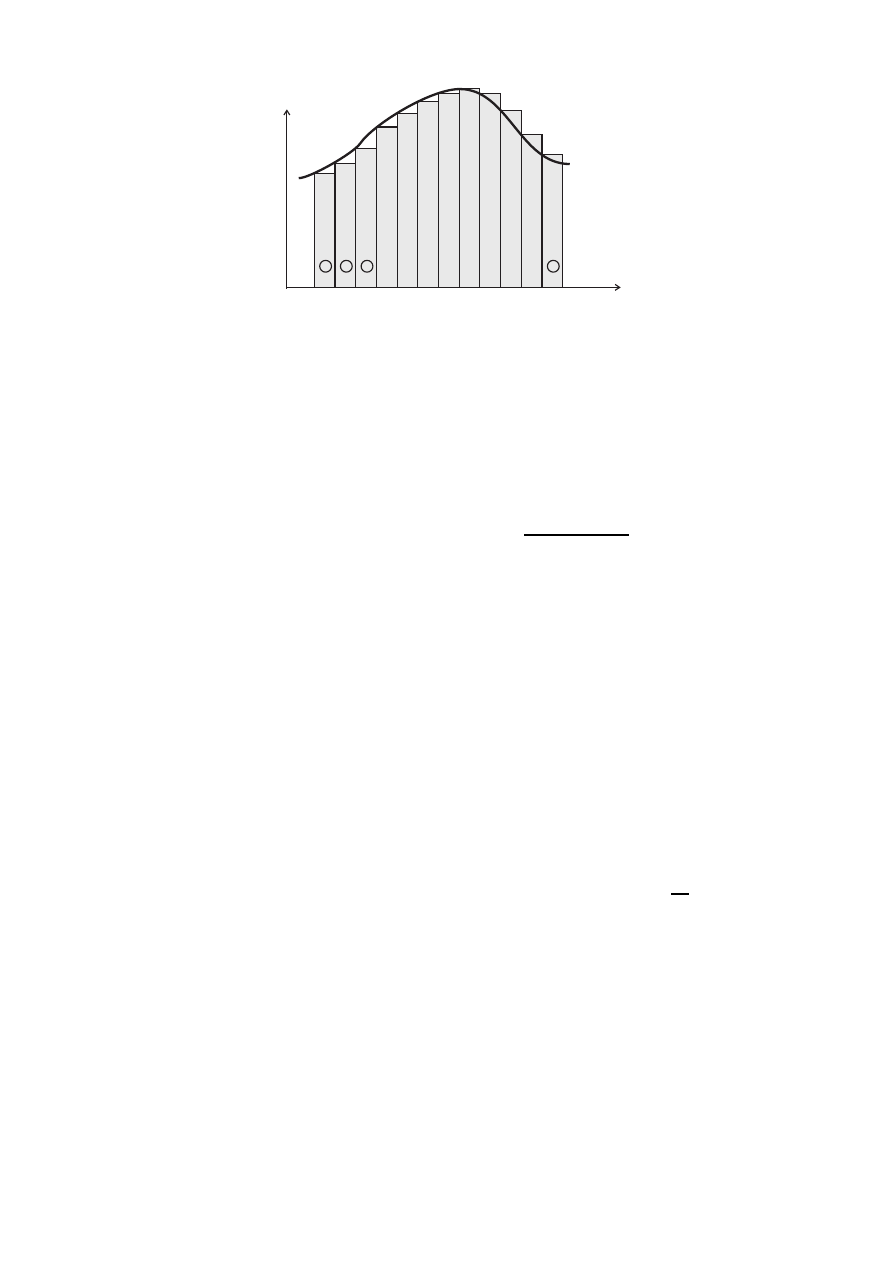
a

b

Dx

x

y

1

2

3

N

f(x)

Rysunek 6: Całkowanie

b

Z

a

f (x)dx ≈ f(a)∆x + f(a + ∆x)∆x + f(a + 2∆x)∆x + ... + f(b − 2∆x)∆x + f(b − ∆x)∆x

= ∆x [f (a) + f (a + ∆x) + f (a + 2∆x) + ... + f (b − 2∆x) + f(b − ∆x)]

(4.12)

Dowód:
Gdy ∆x → 0 (N → ∞) możemy napisać f(x

0

) = lim

∆x→0

F

(x

0

+∆x)−F (x

0

)

∆x

, gdzie F (x) jest funkcją

pierwotną funkcji f (x). Wówczas f (x

0

)∆x = F (x

0

+ ∆x) − F (x

0

), zaś

b

Z

a

f (x)dx = f (a)∆x + f (a + ∆x)∆x + f (a + 2∆x)∆x + ... + f (b − 2∆x)∆x + f(b − ∆x)∆x =

= [F (a + ∆x) − F (a)] + [F (a + 2∆x) − F (a + ∆x)] + [F (a + 3∆x) − F (a + 2∆x)] +

+... + [F (b − ∆x) − F (b − 2∆x)] + [F (b) − F (b − ∆x)] = F (b) − F (a)

(4.13)

4.1

Całka podwójna - interpretacja

Całka podwójna często interpretowana jest objętość bryły o podstawie S określonej granicami cał-
kowania. Zakłada się przy tym, że funkcja podcałkowa jest w tym obszarze dodatnia. Na rysunku 7

pokazano wykres funkcji f (x, y) = 10 − 3x

2

− y

2

określonej na powierzchni S :

(

x ∈ (0, 1)
y ∈ (0, 2)

.

Objętość bryły otrzymanej w ten sposób wyniesie:

V =

Z Z

S

f (x, y)ds =

Z Z

S

f (x, y)dxdy =

2

Z

0





1

Z

0

f (x, y)dx





dy =

46

3

(4.14)

4.2

Całka potrójna - interpretacja

Całkę potrójną interpretować można na kilka sposobów np. wynikiem całki jest masa bryły zaj-
mującej objętość V , gdy założymy że funkcja podcałkowa reprezentuje gęstość objętościową masy.
Równie często wynik całki potrójnej reprezentować może całkowity ładunek zawarty w obszarze V ,
wówczas funkcja podcałkowa określa gęstość objętościową ładunku. Do przestawienia wykresu funk-
cji trzech zmiennych należałoby użyć przestrzeni czterowymiarowej. Na rysunku 8 przedstawiono

jedynie obszar całkowania V :











x ∈ (0, 1)
y ∈ (0, 2)

z ∈ (0, 3)

, na którym zdefiniowana jest funkcja f (x, y, z) = xy+z.

7

x

y

z

Rysunek 7: Objętość ograniczona funkcją dwóch zmiennych f (x, y) = 10 − 3x

2

− y

2

V

1

2

3

x

y

z

Rysunek 8: Objętość ograniczona funkcją dwóch zmiennych f (x, y) = 10 − 3x

2

− y

2

Przyjmując że funkcja podcałkowa jest gęstością objętościową masy, całkowita masa bryły wy-

niesie:

m =

Z Z Z

V

f (x, y, z)dv =

3

Z

0







2

Z

0





1

Z

0

f (x, y, z)dx





dy







dz = 12

(4.15)

8