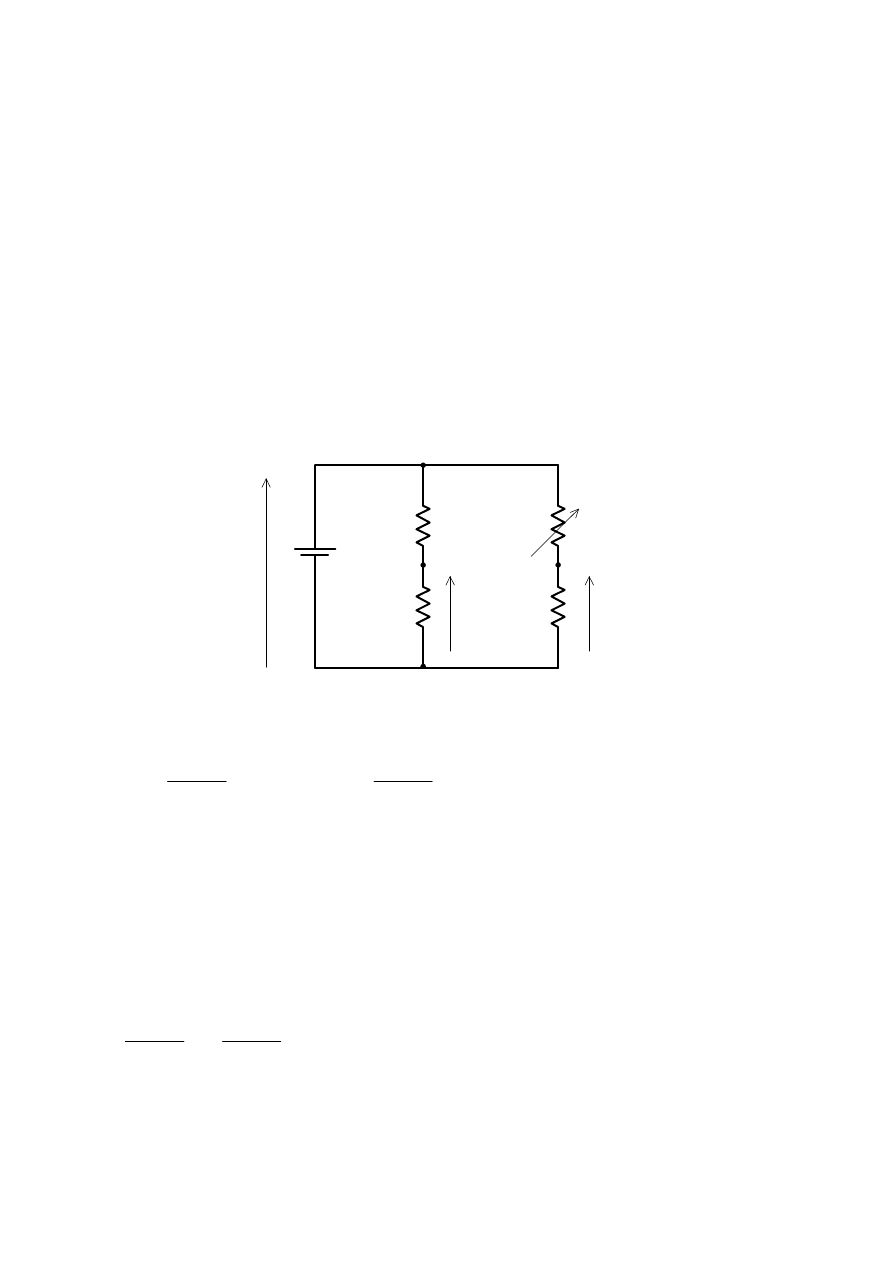
ĆWICZENIE 7.
MOSTKI PRĄDU STAŁEGO
Kursywą oraz * zaznaczono rozszerzony program ćwiczenia
Pomiary rezystancji różnych rezystorów mostkiem laboratoryjnym Wheatstona.
Wyznaczanie błędu nieczułości mostka i całkowitej niepewności pomiaru.
Pomiary małych rezystancji mostkiem technicznym Thompsoma. Błąd wywołany
nieprawidłowym, dwuprzewodowym połączeniem mostka.
Opracowanie sprawozdania.
Każdy mostek pomiarowy działa na zasadzie równoważenia napięć U
A
i U
B
występujących
na dwóch dzielnikach napięcia tworzących gałęzie mostka, co ilustruje rysunek 7.1:
U
x
R
2
R
3
R
4
R
A
U
B
U
A
B
Wartości napięć (długość strzałki)
U
A
i
U
B
zależą od wartości napięcia zasilania mostka
U
oraz stosunku odpowiednich rezystorów.
4
3
4
2
2
R
R
R
U
U
;
R
R
R
U
U
B
x
A
+
=
+
=
Wartość napięcia
U
A
, w tym przykładzie, jest stała ponieważ zarówno rezystor
R
2
jak i
R
x
mają stałe wartości. Natomiast wartość napięcia
U
B
może się zmieniać ponieważ rezystor
R
3
jest regulowany. Jeżeli wartość
R
3
rośnie wówczas
U
B
maleje i odwrotnie.
Proces równoważenia mostka polega na takim wyregulowaniu wartości napięcia
U
B
aby
zrównało się co do wartości z napięciem
U
A
, czyli żeby ich różnica była równa zero.
Stwierdzenie tego faktu umożliwia tzw. wskaźnik zera, czyli czuły przyrząd, włączony w
strukturę mostka pomiędzy punkty
A
i
B
.
Jeżeli
U
A
jest równe
U
B
wówczas
zachodzi zależność:
4
3
4
2
2
R
R
R
U
R
R
R
U
x
+
=
+
którą można przekształcić do postaci:
Rys. 7.1
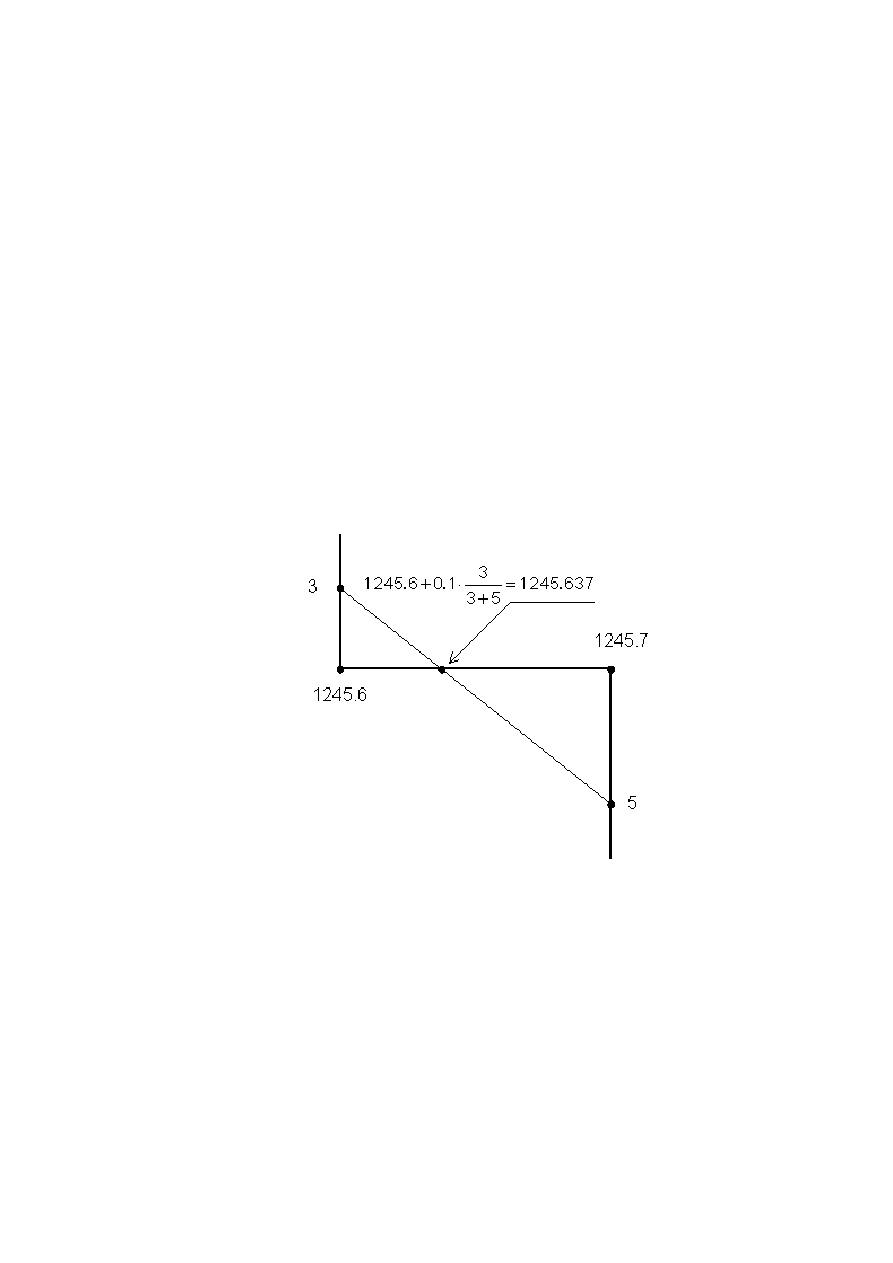
3
2
4
R
R
R
R
x
⋅
=
⋅
Ta zależność umożliwia wyznaczenie nieznanej wartości rezystora
R
x
, jeżeli pozostałe
wartości rezystorów są znane, a tak jest w praktyce, gdyż używa się do tego celu rezystorów
wzorcowych. Najczęściej rezystory
R
2
i
R
4
są wzorcowymi rezystorami o stałej wartości, a
rezystor
R
3
jest rezystorem dekadowym.
Przy dochodzeniu do stanu równowagi napięć
U
A
i
U
B
możliwe są dwie sytuacje wynikające
z faktów, że rezystor dekadowy można regulować tylko w sposób skokowy, a nie ciągły, oraz
że wskaźnik zera ma skończoną czułość.
To, że rezystor dekadowy można regulować tylko skokowo, może spowodować, że nie uda
się doprowadzić do całkowitego zrównoważenia mostka ( napięć
U
A
i
U
B
). Wskaźnik zera
przyjmie np. pozycję 3 działki w lewo, a po zmianie wartości rezystora dekadowego o jedną
pozycję na dekadzie o najniższej wartości np. 5 działek w prawo. W takiej sytuacji można
posłużyć się metodą interpolacji liniowej i oszacować wartość rezystancji, która doprowadziła
by mostek do stanu pełnej równowagi.
Przykład:
Nastawa rezystora dekadowego 1245.6 Ω powoduje wychylenie wskaźnika zera 3 działki w
lewo, a nastawa 1245.7 Ω, 5 działek w prawo.
Można więc obliczyć, na podstawie konstrukcji przedstawionej na rysunku 7.2, że wartość
1245.637Ω (niemożliwa do ustawienia na rezystorze dekadowym) spowodowała by
wyzerowanie wskaźnika, czyli zrównoważenie mostka.
Całkiem odwrotna sytuacja istnieje, jeżeli wskaźnik zera nie jest wystarczająco czuły.
Okazuje się wówczas, że nie można zauważyć wychylenia wskaźnika zera pomimo, że
zmienia się wartość rezystora dekadowego w zakresie kilku pozycji jednej z dekad.
Istnieje wówczas niepewność, którą wartość należy przyjąć do obliczeń.
Przyjmuje się wówczas dowolną wartość jednej z tych pozycji i dodatkowo powiększa się
niepewność wyniku pomiaru o tzw. błąd nieczułości.
Wartość względnego błędu nieczułości wyznacza się praktycznie na podstawie odczytu liczby
pozycji dekady, których zmiana nie powoduje zauważalnego rozrównoważenia wskaźnika
zera.
Ta liczba pozycji dekady określa wartość ∆
R
3
, a sam błąd nieczułości δ
n
oblicza się jako:
Rys. 7.2
3
3
R
R
n
∆
=
δ
Całkowita niepewność pomiaru rezystancji mostkiem wyraża się zatem sumą błędów
względnych (klas) rezystorów wzorcowych i błędu nieczułości.
W praktyce pomiarowej często zachodzi potrzeba pomiaru bardzo małych wartości
rezystancji, porównywalnej z rezystancją przewodów używanych do jej podłączenia do
układu mostka.
Istnieje odmiana mostka Wheatstona zwana mostkiem Thomsona (lub Kelvina), który za
pomocą pomysłowej konstrukcji umożliwia pomiar małych rezystancji, eliminując
rezystancje przewodów, pod warunkiem prawidłowego połączenia rezystancji mierzonej za
pomocą czterech a nie dwóch przewodów.
1. Pomiary rezystancji mostkiem Wheatstona
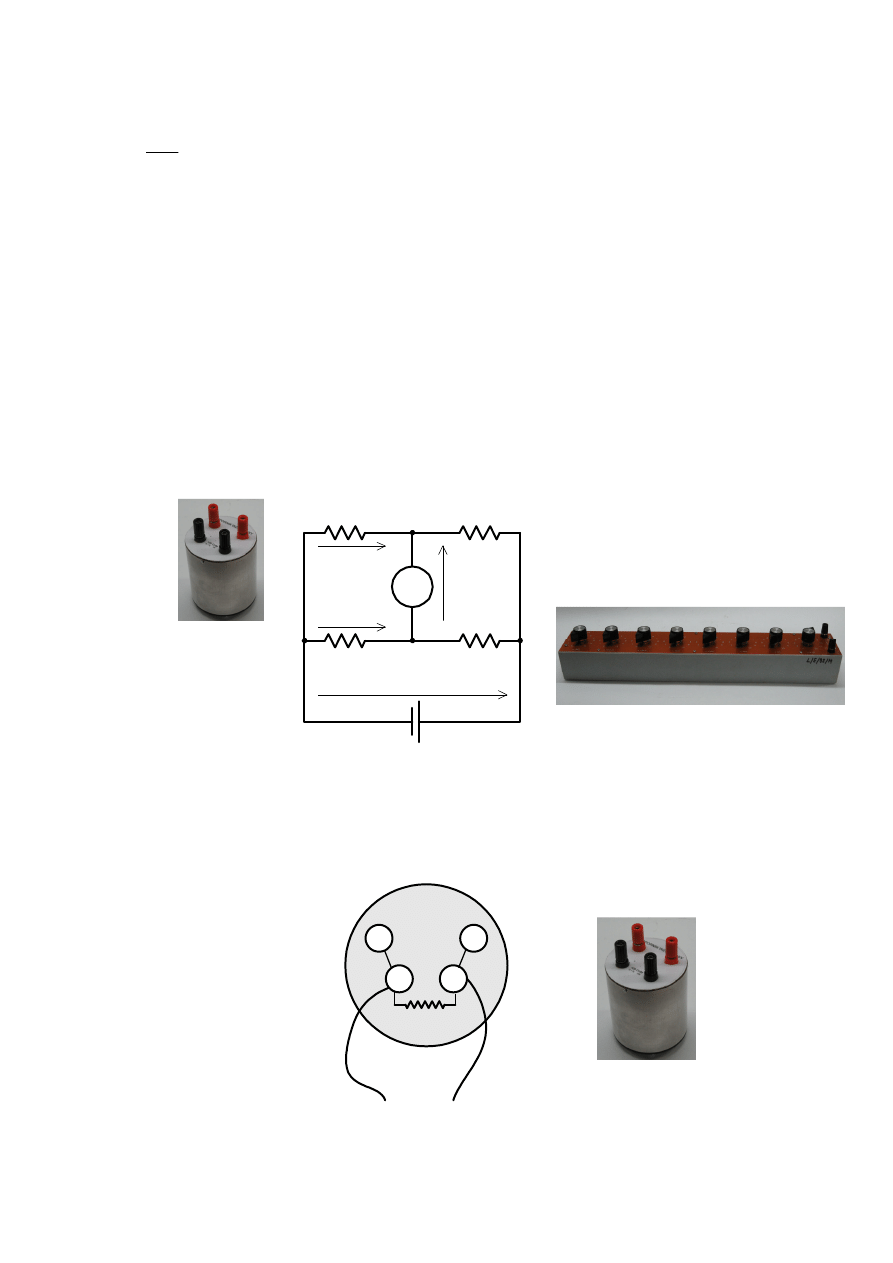
Połączyć mostek Wheatstona według schematu na rysunku 7.3:
1
R
2
R
3
R
4
R
U
1
U
3
U
o
U
W.Z.
Jako rezystory
R
2
i
R
4
należy użyć stałych rezystorów wzorcowych o wartości 100Ω, a jako
rezystor
R
3
opornik dekadowy.
Rezystory wzorcowe posiadają 4 zaciski. Należy użyć pary zacisków wewnętrznych, zgodnie
z rysunkiem 7.4, ponieważ pomiędzy nimi jest bezpośrednio włączona rezystancja
wzorcowa.
R
W
100
Ω
Rys. 7.3
Rys.7.4
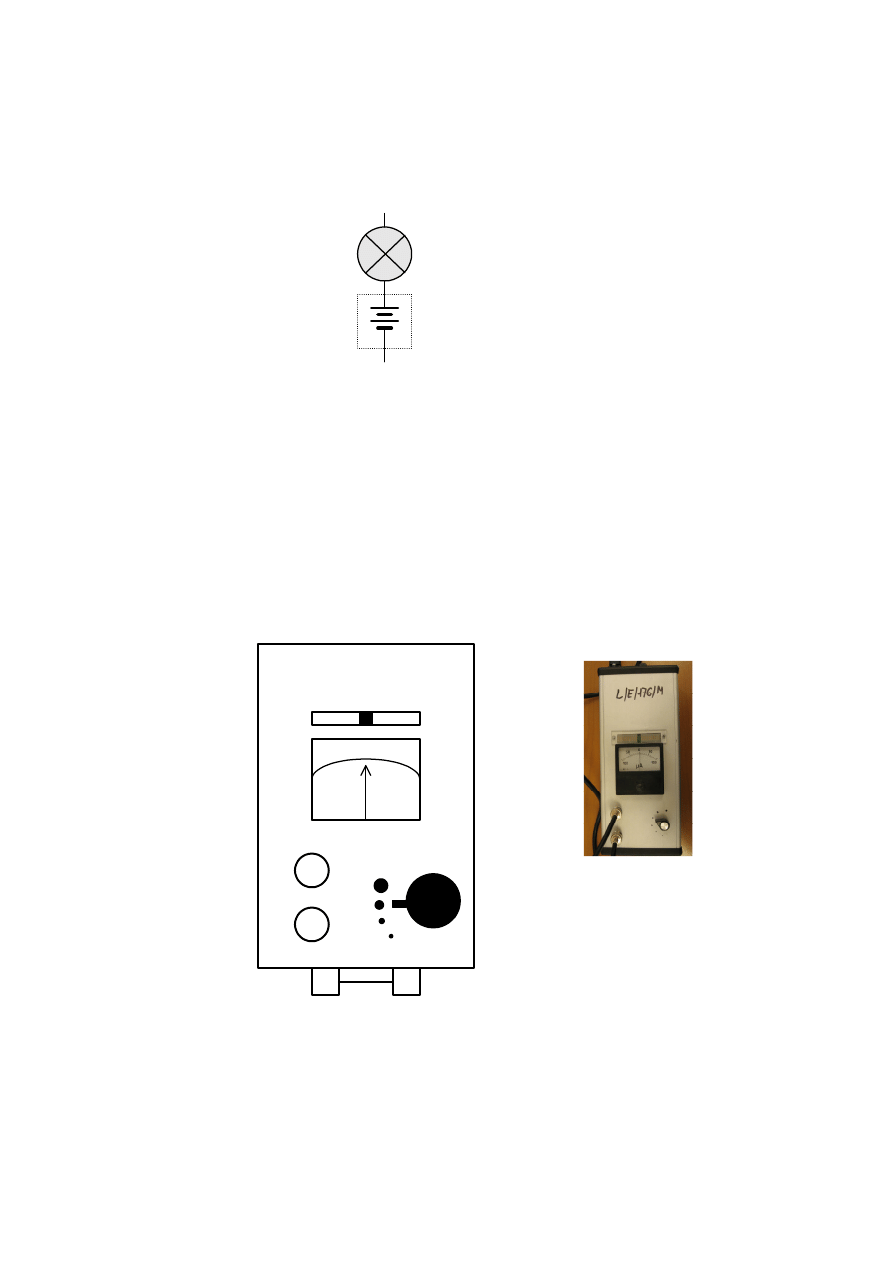
Jako źródło zasilania
U
zastosować akumulator 12 V wyposażony w rezystor
ograniczający prąd połączony z zaciskiem +. Jeżeli akumulator nie jest wyposażony w
taki rezystor należy w szereg z zaciskiem + połączyć żarówkę 5W wg schematu na
rysunku 7.5.
.
Akumulator
Żarówka 5W
Wskaźnik zera
W.Z.
jest układem elektronicznym zasilanym z sieci, pokazanym na
rysunku 7.6.
Wskaźnik jest wyposażony w przyrząd wskazówkowy oraz linijkę świetlną, która ułatwia
równoważenie mostka.
Gniazda A i B należy połączyć przewodami ekranowanymi do odpowiednich punktów
mostka, a zaciski M dowolnym przewodem do minusa akumulatora.
W prawym dolnym rogu wskaźnika znajduje się przełącznik czułości C, który
początkowo należy ustawić na najmniejszej kropce, czyli najmniejszej czułości. W trakcie
równoważenia mostka czułość wskaźnika należy zwiększać.
W
0
A
B
M
C
W miejsce rezystora
R
1
włączać kolejno rezystory mierzone.
Rys. 7.5
Rys. 7.6
Dla każdego rezystora zrównoważyć mostek tj. doprowadzić do zerowego wskazania
wskaźnika regulując nastawy rezystora dekadowego poczynając od dekad o najwyższej
wartości. Nastawy rezystora dekadowego w stanie równowagi mostka zapisać w tabeli.
* Każdorazowo po osiągnięciu stanu równowagi wyznaczyć minimalną zmianę wartości
rezystora dekadowego, która wywołuje zauważalne rozrównoważenie wskaźnika zera.
Wyniki pomiarów zapisać w poniższej tabeli.
Rezystor mierzony Nastawa rezystora
R
3
dekadowego w stanie
równowagi [Ω]
* Zmiana wartości
rezystora dekadowego
∆
R
3
[
Ω
]
* Względna zmiana
rezystora dekadowego
∆
R
3
.
100/ R
3
[%]
1
2
3
Z warunków równowagi mostka wynika, że nastawa rezystancji dekadowej
R
3
w stanie
równowagi jest równa rezystancji mierzonej
R
x
= R
3
gdyż:
4
2
3
1
R
R
R
R
R
x
=
=
a rezystory
R
2
i
R
4
są równe sobie
R
2
=
R
4
=100 Ω , czyli:
R
x
= R
3
2. Wyznaczanie niepewności wyników pomiaru
Określić niepewność wyznaczenia wartości nieznanych rezystancji na podstawie klas
dokładności użytych rezystorów wzorcowych.
* Zmiana wartości
∆
R
3
, powodująca zauważalne rozrównoważenie wskaźnika zera określa
błąd nieczułości mostka, czyli niepewność wyniku pomiaru wynikającą ze skończonej czułości
wskaźnika zera. Ta niepewność względna
∆
R
3
.
100/ R
3
[%] dodana do niepewności pomiaru
wynikającej z klasy użytych rezystorów wzorcowych określa całkowitą niepewność pomiaru
mostkiem.
Rezystor mierzony
1
2
3
Klasa rezystora
R
2
[%]
Klasa rezystora
R
4
[%]
Klasa rezystora
dekadowego
R
3
[%]
* Błąd nieczułości
∆
R
3
.
100/ R
3
[%]
------------------
Suma [%]
3. Pomiar małej rezystancji (odcinka drutu) mostkiem Thomsona. Próba pomiaru w
układzie 2-przewodowym.
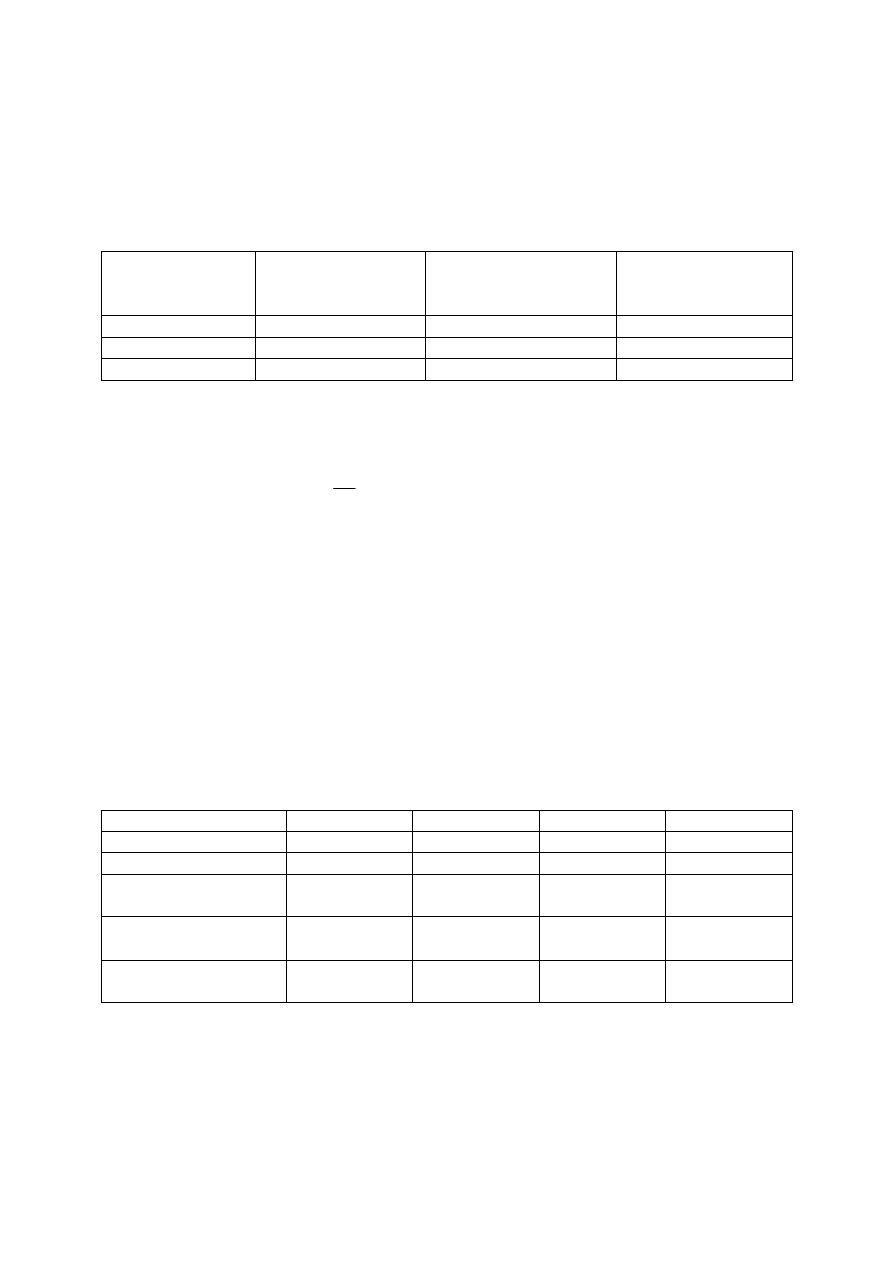
Dokonać pomiaru rezystancji 10 cm odcinka drutu mostkiem Thomsona. Połączyć mostek
tak jak na rysunku 7.7. Przewody do drutu przyłączyć za pomocą krokodylków.
10 cm
Mostek
Thomsona
Wynik pomiaru: R=
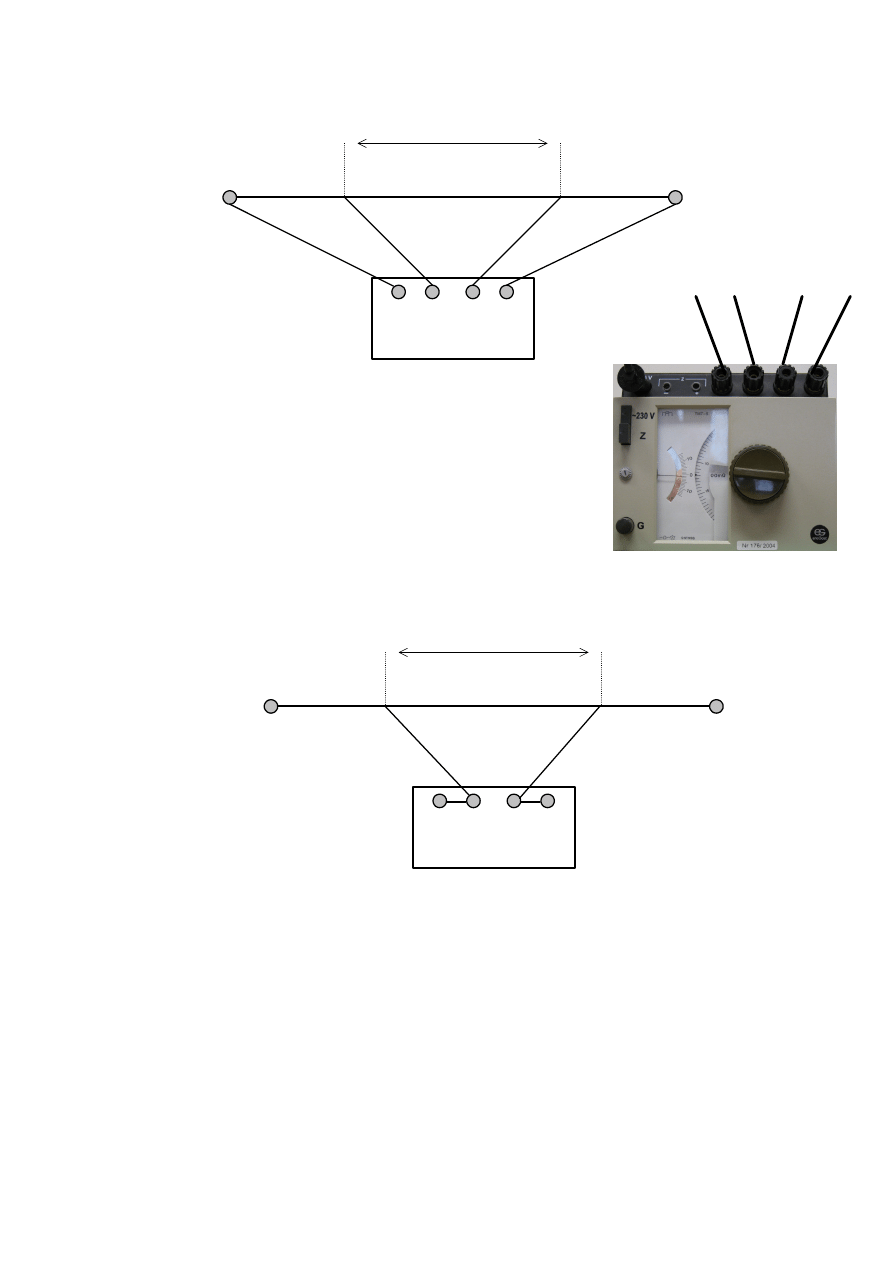
Połączyć mostek nieprawidłowo wg rysunku 7.8:
10 cm
Mostek
Thomsona
Wynik pomiaru: R=
Wyjaśnić różnicę wskazań:
Aparatura:
1. 2 rezystory wzorcowe – stałe
2. Opornica dekadowa
3. Zestaw rezystorów do pomiarów
Rys. 7.7
Rys. 7.8

4. Elektroniczny wskaźnik równowagi mostka
5. Akumulator
6. Techniczny mostek Thomsona
7. Drut do pomiaru
Wyszukiwarka
Podobne podstrony:
25) TSiP 2010 11 ćw07
cw07, Akademia Morska, 1 rok, Fizyka, FIZYKA1, fiza
Cw07
Cw07 MK1 Dzialanie DSM51
Cw07 S
Cw07 Matlab1
cw07
cw07 pomiar natezenia swiatla
cw07
izs cw07 id 221279 Nieznany
cw07
GW CW07 BUD C Przyklad
cw07 pas1
cw07
Cw07 S
Urz Zew Cw07
ćw07 Ocena jakości używek - herbata
więcej podobnych podstron