9. Optyka
9.6. Promieniowanie rentgenowskie. Dyfrakcja promieniowania
rentgenowskiego (prawo Bragga).
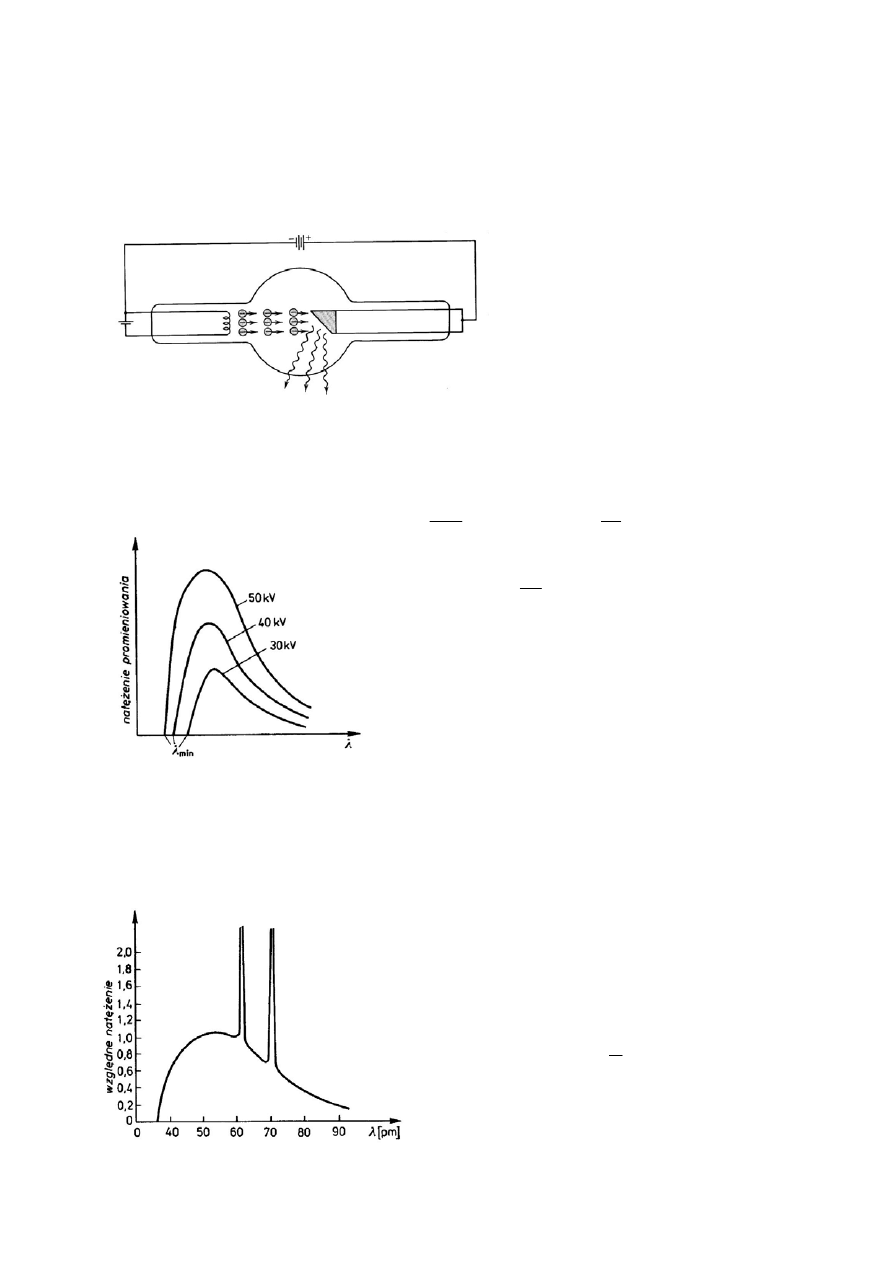
Schemat budowy lampy
rentgenowskiej.
Przyspieszone do dużej prędkości
elektrony uderzają w antykatodę
zmniejszając swoją energię.
Energia elektronów zamienia się w energię promieniowania rentgenowskiego wskutek
hamowania elektronów w polu atomów antykatody (daje to tzw. promieniowanie
hamowania), lub zużywana jest na jonizację atomów antykatody.
2
2
mv
Ue
=
oraz
λ
ν
hc
h
Ue
=
=
stąd
Ue
hc
gr
=
=
λ
λ
min
Widmo ciągłe promieniowania rentgenowskiego
(promieniowanie hamowania). Przy większych
napięciach przyspieszających natężenie jest większe,
ale zawsze istnieje minimalna długość promieniowania
λ
B
gr
B
(tzw. krótkofalowa granica promieniowania
rentgenowskiego) ograniczająca widmo.
Podczas jonizacji atomów antykatody, atomy wzbudzone przez wiązkę elektronów
przechodzą do stanów o mniejszej energii wysyłając fale elektromagnetyczne o określonych
(zależnych o materiału antykatody) długościach fali. Jest to tzw. promieniowanie
charakterystyczne, które nakłada się na widmo
ciągłe.
Przykładowe widmo rentgenowskiego
promieniowania charakterystycznego. Od lewej –
serie linii K oraz L.
Prawo Moseley’a:
(
)
2
1
−
=
=
Z
A
c
λ
ν
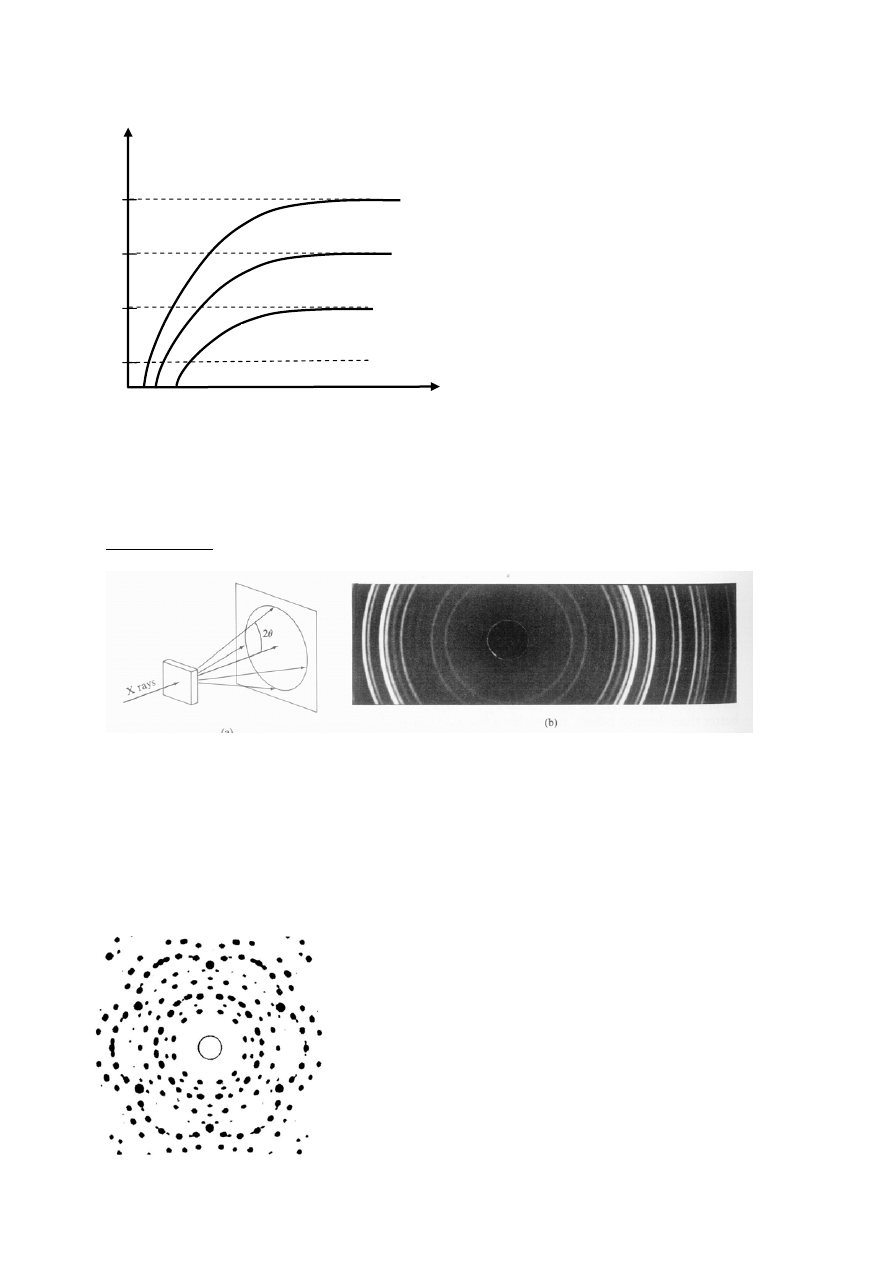
Z
ν = c/λ
K
L
M
8
32
62
92
Gdzie: A – stała; Z – liczba porządkowa w układzie okresowym
Pierwiastki ciężkie Z > 62
emitują linie K, L, M
Pierwiastki lekkie 8 < Z < 32
emitują tylko linię K
widmo ciągłe – zastosowanie w medycynie,
widmo charakterystyczne – badania struktury atomowej.
U
Prawo Bragga.
Promienie ugięte przechodzą przez polikrystaliczną próbkę wzdłuż tworzących stożków
koncentrycznych, dając na kliszy układ współśrodkowych pierścieni. Tworzące nachylone są
pod kątem 2
θ
do kierunku wiązki pierwotnej.
Atomy tworzą 3-wymiarową siatkę dyfrakcyjną.
Dyfraktogram Lauego (1912)
Obraz dyfrakcji promieniowania rentgenowskiego na
monokrysztale berylu. Tzw. obraz Lauego powstaje wskutek
ugięcia promieni tak, że odległość płaszczyzn atomowych i
kąt padania
θ
spełniają prawo Bragga.
Badając rozmieszczenie i natężenie punktów możemy
odtworzyć strukturę kryształu.
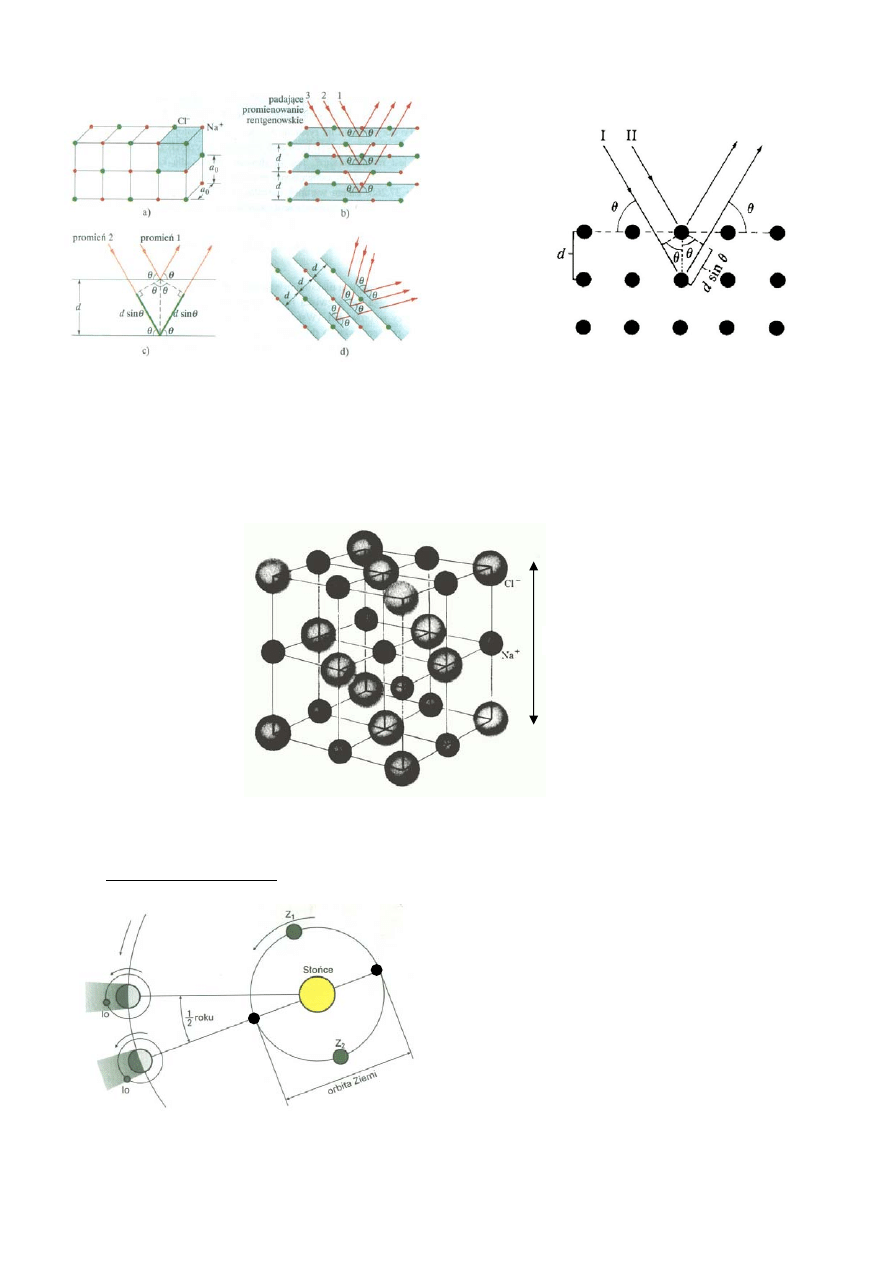
Prawo dyfrakcji Bragga:
2d
⋅
sin
θ
= m
λ
gdzie m = 1, 2, …
Aby otrzymać wzmocnienie w kierunku określonym przez kąt
θ
, promienie odbite od rodziny
płaszczyzn muszą się wzmacniać. Oznacza to, że różnica dróg wiązek odbitych musi być
równa całkowitej wielokrotności
λ
⇒
Δ
= m
λ
9.7. Prędkość światła (metody pomiaru, teoria eteru).
U
Pomiary astronomiczne
1676 Römer – z obserwacji zaćmień księżyca Io
Jowisza co pół roku – występuje różnica
czasu wyjścia Io z cienia Jowisza.
Wynika ona z ruchu obrotowego Ziemi
wokół Słońca. Obserwacje wykazały, że
światło potrzebuje ok. 16,5 minuty na przebycie
a
B
0
B
= 5,627 Å
24.XII
24.VI
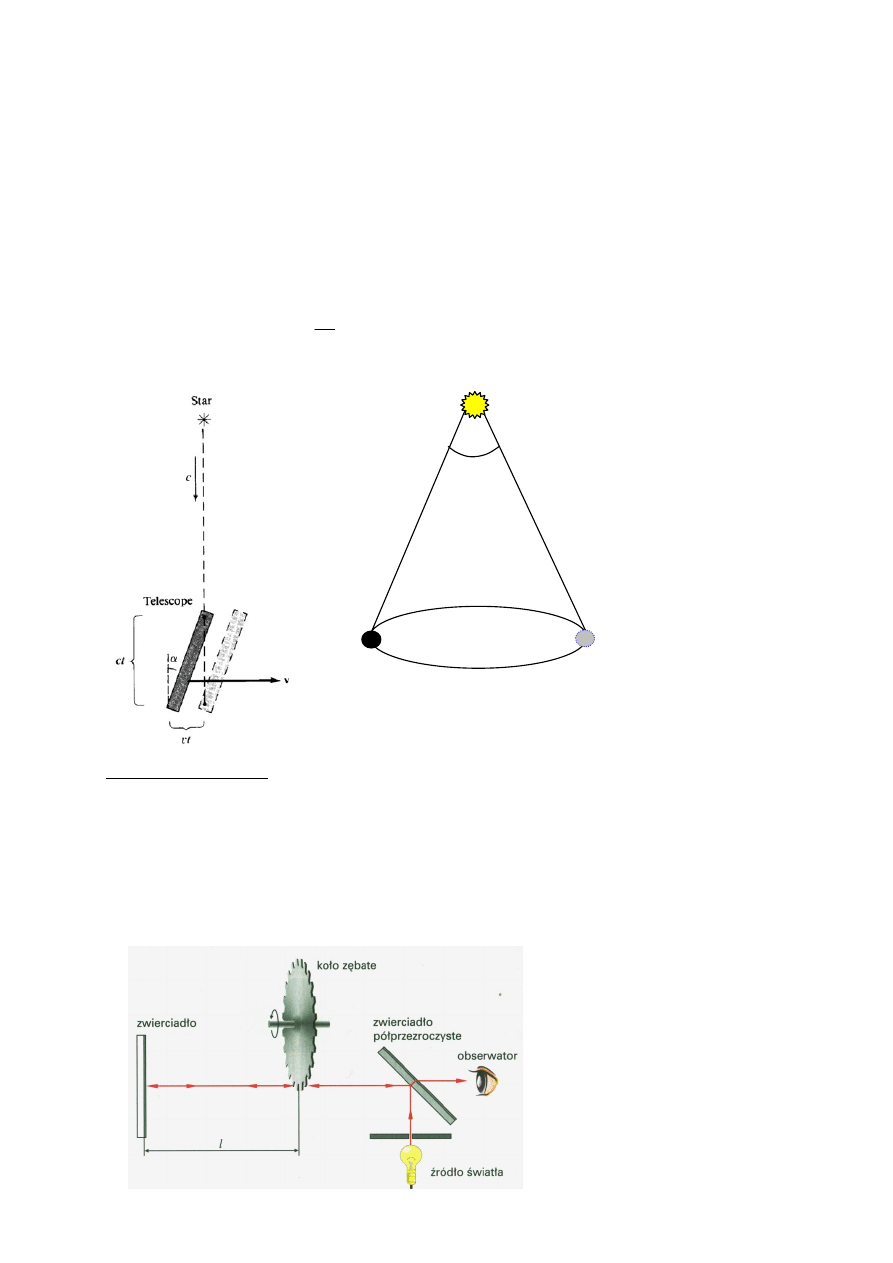
średnicy ziemskiej orbity okołosłonecznej. Obliczona stąd prędkość światła wyniosła
215 000km/s.
1725 - Bradley z pomiarów aberacji światła gwiazd stałych. (analogia do parasola, który
biegnąc w deszczu musimy trzymać pod kątem zależnym od szybkości z jaka biegniemy).
Ziemia obraca się w przybliżeniu po kole
2
α
= 40’9’’
⇒
=
c
v
tg
Z
α
c = 303 000 km/s
U
Pomiary laboratoryjne
1849 Fizeau – koło zębate. Jeżeli częstotliwość obrotów jest niewielka, to światło zdąży
wrócić przez to samo wycięcie przez które wyszło. Istnieje taka minimalna częstotliwość
obrotów, przy której światło nie jest już widoczne, bo trafia w ząbek tarczy. Czas przelotu
światła od tarczy do zwierciadła i z powrotem jest równy czasowi w jakim tarcza się obróci
od przerwy miedzy zębami do najbliższego ząbka.
Znając: odległość l (8,6 km)
N - ilość zębów
α
V
B
Z
B
= 30 km/s
V
B
Z
B
B
eter V
eter V
A
ω
B
m
B
- prędkość kątową m-tego zaciemnienia, można zapisać:
N
m
c
l
m
π
ω
2
2
1
2
⎟
⎠
⎞
⎜
⎝
⎛ −
=
Stąd c = 313 000 km/s
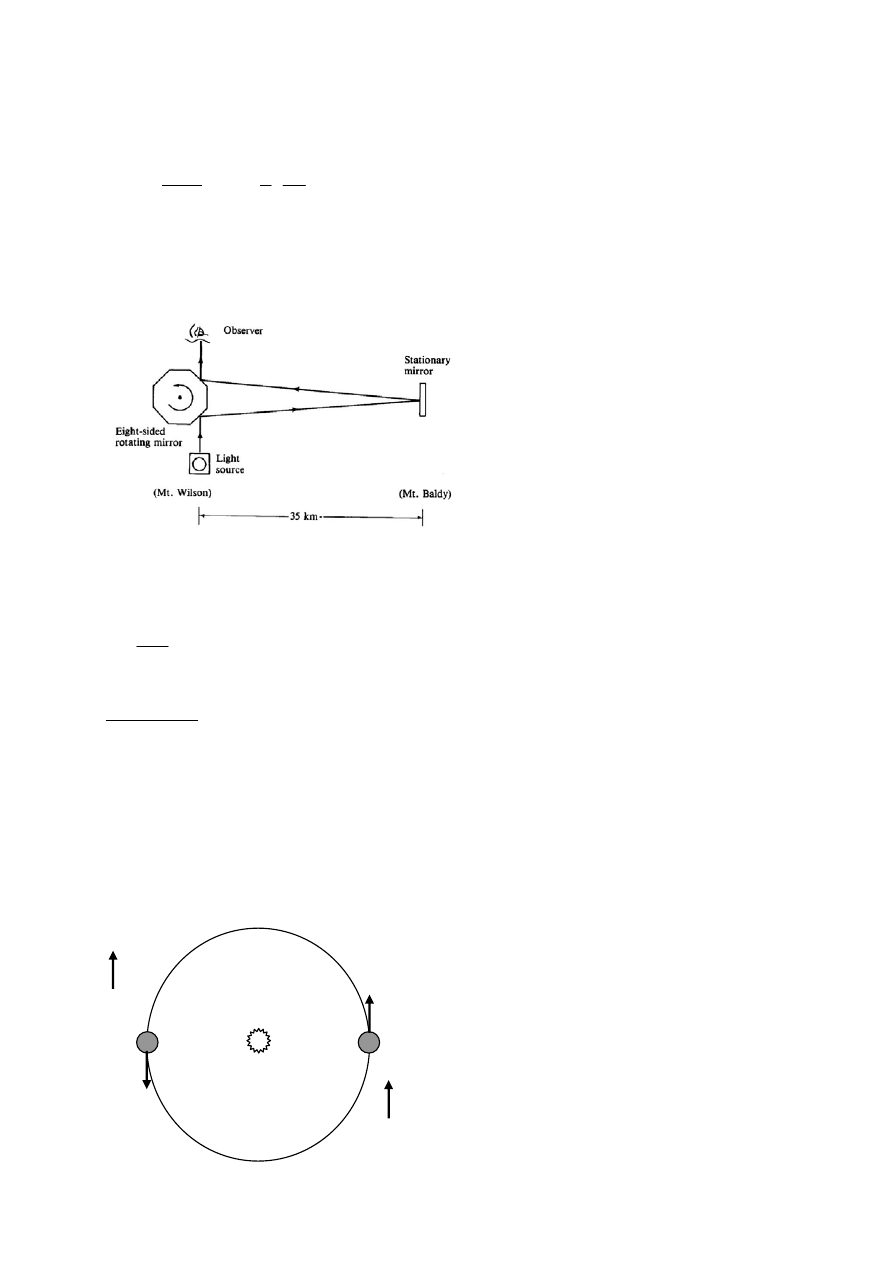
1862 Foucault i 1878 Michelson – wirujące zwierciadła
Michelson - podobna idea, ale bardzo duża
odległość między wirującym i nieruchomym
zwierciadłem umieszczonymi na sąsiednich
wzgórzach w odległości 35 km.
Foucault: c = 298 600 km/s (
± 500)
Michelson c = 299 910 km/s (
± 50)
1972 Evenson – wykorzystanie mikrofal. Znając długość fali i częstość rezonansową
π
λ
ω
2
r
c
=
wyznaczył prędkość - c = 299 792,4562 km/s (
± 1,1 m/s !!)
U
Teoria eteru.
U
„Eter” – sprężysty ośrodek rozchodzenia się fal świetlnych. Bezwzględny układ odniesienia.
Teoria Maxwella – „eter” = fale i pola elektromagnetyczne. „Ośrodek” wypełniający
Wszechświat.
Czy „eter” jest unoszony przez ciała w ruchu ? Jaki jest wpływ ruchu Ziemi względem
„eteru” na prędkość światła?
(A) dla obserwatora na Ziemi c + v
B
Z
B
(B)
c - v
B
Z
B
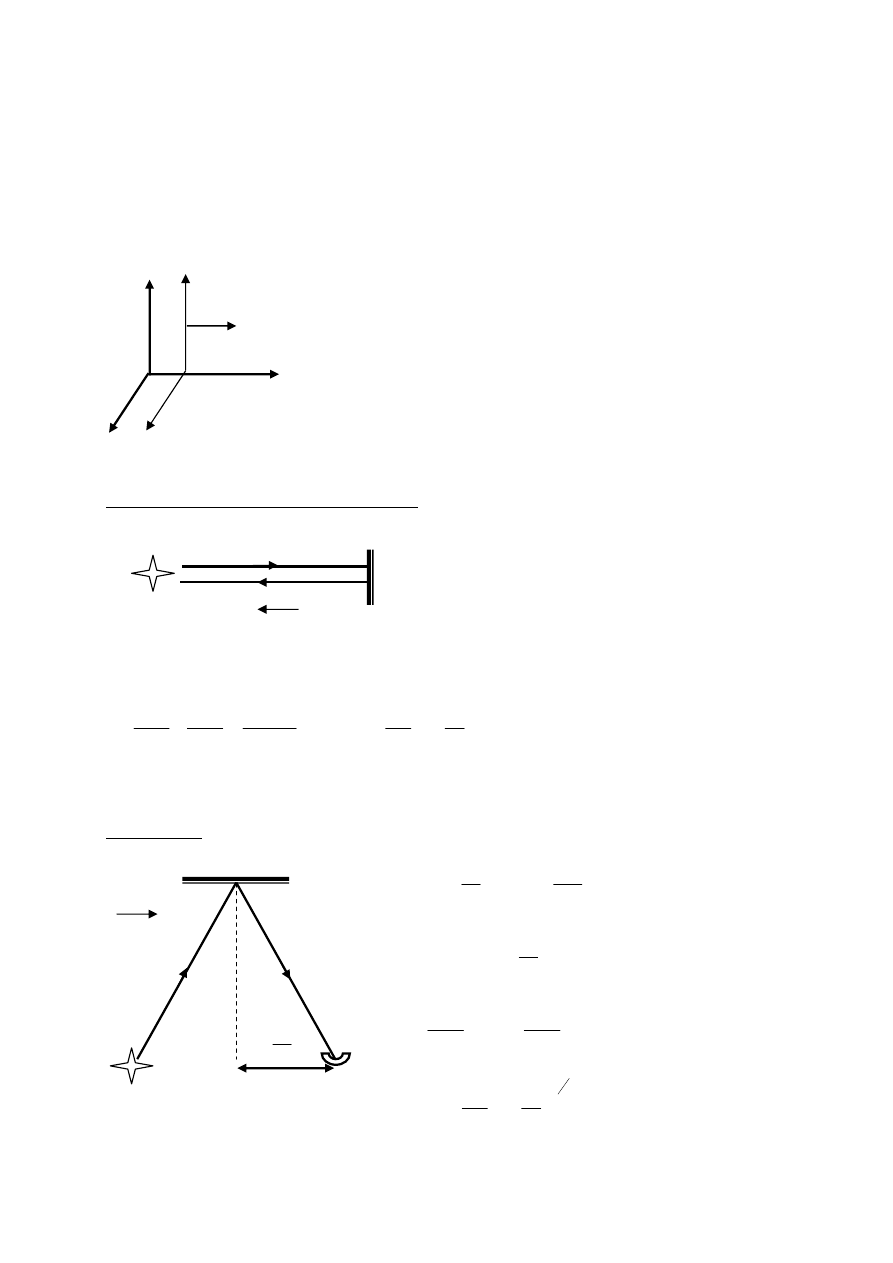
Stąd prędkość światła c
B
R
B
względem poruszającego się odbiornika: c
B
R
B
= c
±
v
Gdzie v – prędkość odbiornika.
Jest to wynik zgodny z transformacją Galileusza.
'
;'
;'
;'
'
t
t
z
z
y
y
vt
x
x
=
=
=
=
=
U
Doświadczenie Michelsona-Morley’a 1887
2
2
2
v
c
Dc
v
c
D
v
c
D
t
−
=
+
+
−
=
1
2
2
1
2
−
⎟⎟
⎠
⎞
⎜⎜
⎝
⎛
−
=
⇒
c
v
c
D
t
U
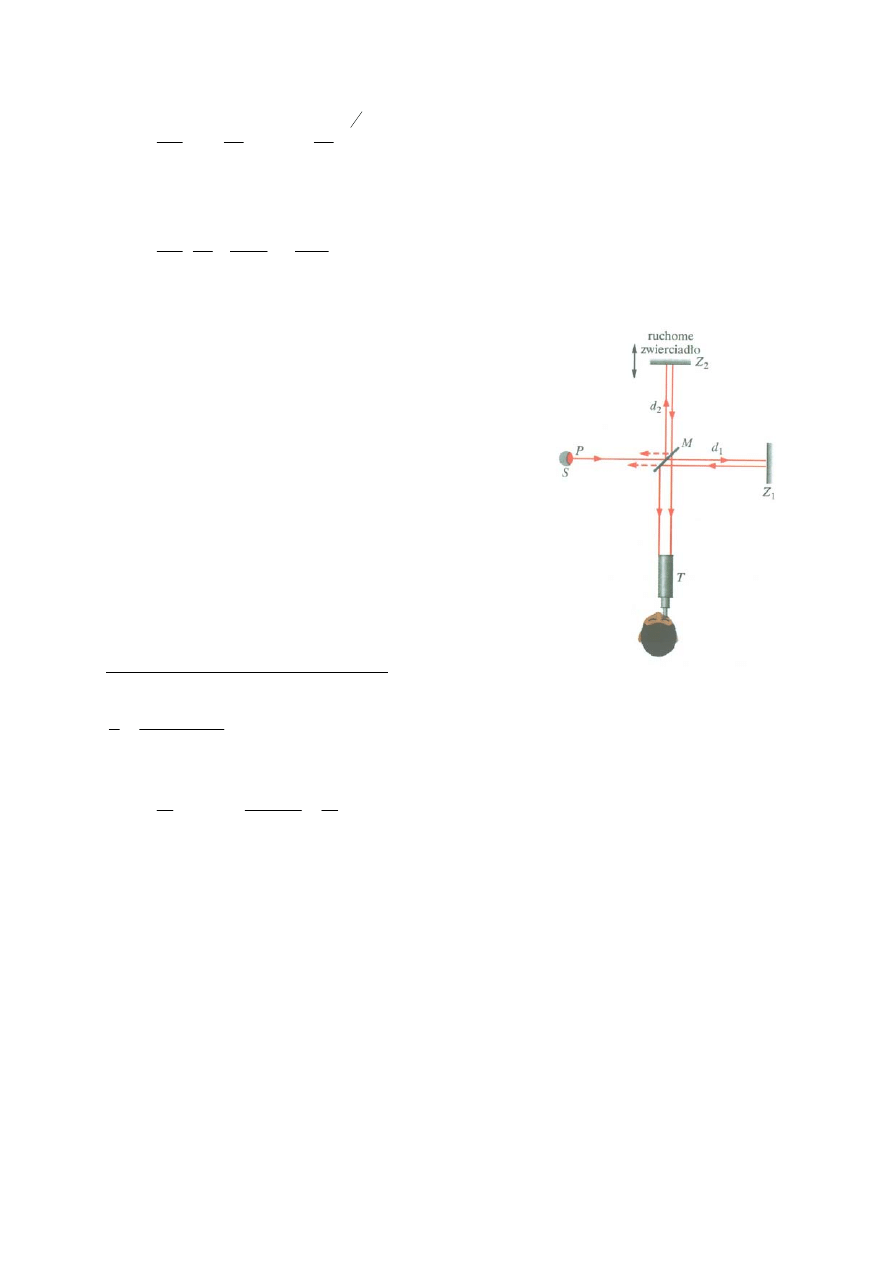
Interferometr
c
D
t
ct
D
'
2
'
2
'
'
=
⇒
=
2
2
2
2
'
'
⎟
⎠
⎞
⎜
⎝
⎛
+
=
vt
D
D
4
'
4
'
2
2
2
2
2
t
v
D
t
c
+
=
⇒
⎟⎟
⎠
⎞
⎜⎜
⎝
⎛
−
=
−
2
1
2
2
2
1
2
'
c
v
c
D
t
Z
Z’
X
X’
Y
Y’
V
v
B
eter
Zwierciadło
D
D
v
B
eter
Zwierciadło
D’
D’
2
'
vt
(
)
4
4
4
4
3
4
4
4
4
2
1
nE
E
n
c
v
c
v
c
D
t
t
−
≈
−
−
−
⎥
⎥
⎦
⎤
⎢
⎢
⎣
⎡
⎟⎟
⎠
⎞
⎜⎜
⎝
⎛
−
−
⎟⎟
⎠
⎞
⎜⎜
⎝
⎛
−
=
−
1
1
2
1
2
2
1
2
2
1
1
2
'
3
2
2
2
2
2
2
'
c
Dv
c
v
c
v
c
D
t
t
=
⎥
⎦
⎤
⎢
⎣
⎡
−
=
−
Światło wychodząc ze źródła S trafia na
półprzepuszczalne zwierciadło M, dzieli się na dwie
wiązki podążające do zwierciadeł Z
B
1
B
i Z
B
2
B
. Po odbiciu od
nich i odbiciu lub przejściu przez M trafiają do teleskopu
obserwacyjnego T. Różnica dróg nakładających się w
teleskopie fal wynosi 2d
B
2
B
– 2d
B
1
B
i wobec tego możliwe
do zaobserwowania są prążki interferencyjne.
Jeżeli na skutek ruchu Ziemi względem „eteru” (z
prędkością 30 km/s) powstanie różnica czasu t – t’ to
powinno to zmienić amplitudy obrazu interferencyjnego.
U
Oszacowanie przewidywanego wyniku
4
5
10
/
10
3
/
30
−
=
⋅
=
s
km
s
km
c
v
a
więc
( )
s
D
D
c
D
t
t
16
8
8
2
4
10
3
10
3
10
10
'
−
−
−
⋅
=
⋅
⋅
=
=
−
Dla D = 3m (długość ramienia interferometru) otrzymujemy:
[ ]
(
)
[ ]
m
t
t
c
s
t
t
8
16
8
16
10
3
10
10
3
'
10
'
−
−
−
⋅
=
⋅
⋅
=
−
=
Δ
⇒
=
−
λ
jest to efekt dobrze mierzalny !
Ale otrzymano negatywny wynik doświadczenia – światło emitowane przez źródło
interferometru, niezależnie od jego orientacji względem ruchu Ziemi, zawsze biegnie z
prędkością c względem źródła i zwierciadeł.
Wniosek końcowy – pojecie „eteru” okazało się niepotrzebne !