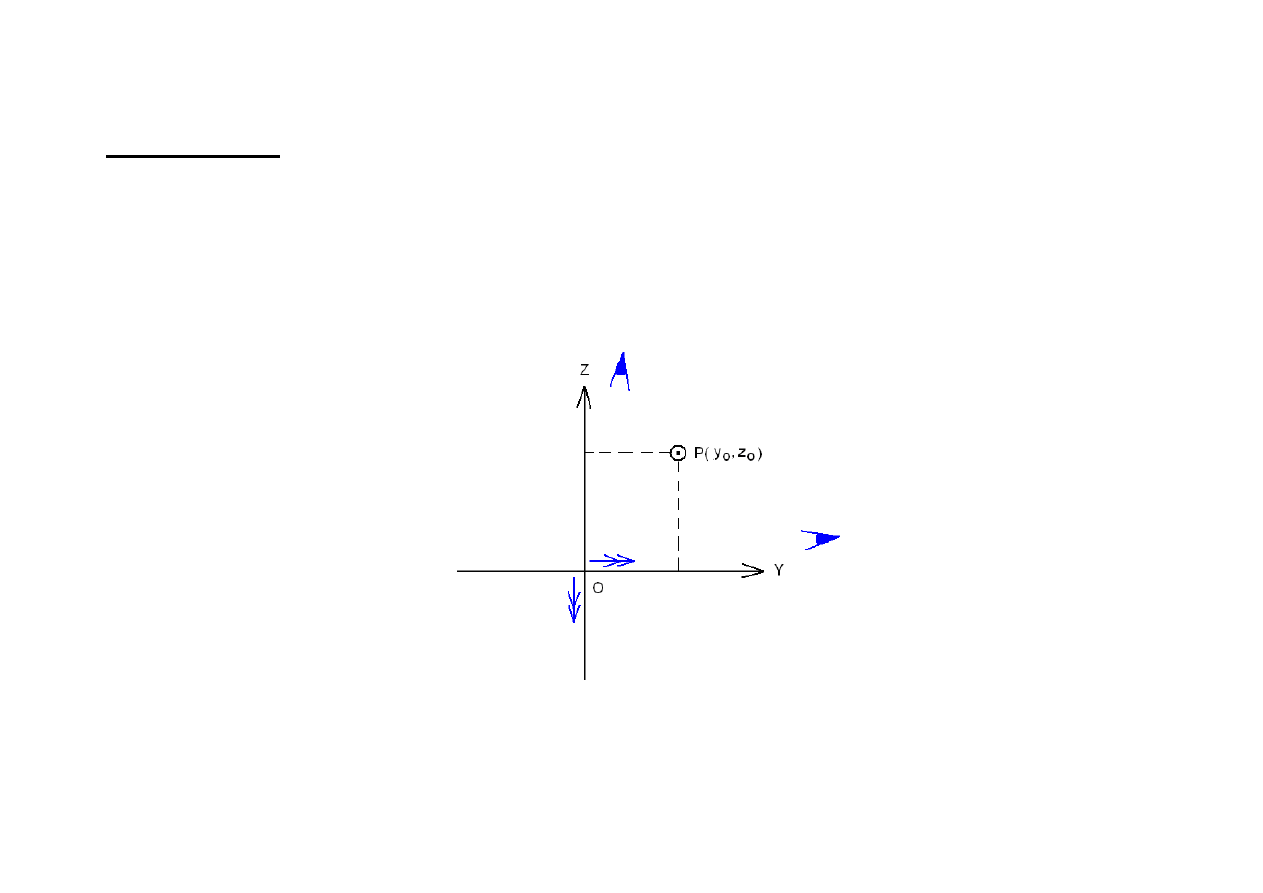
Ć
WICZENIE 6
(12.11.2008 )
Mimo
ś
rodowe rozci
ą
ganie
Redukcja do
ś
rodka ci
ęż
ko
ś
ci
N
P
= +
0
y
M
Pz
= +
0
z
M
Py
= −
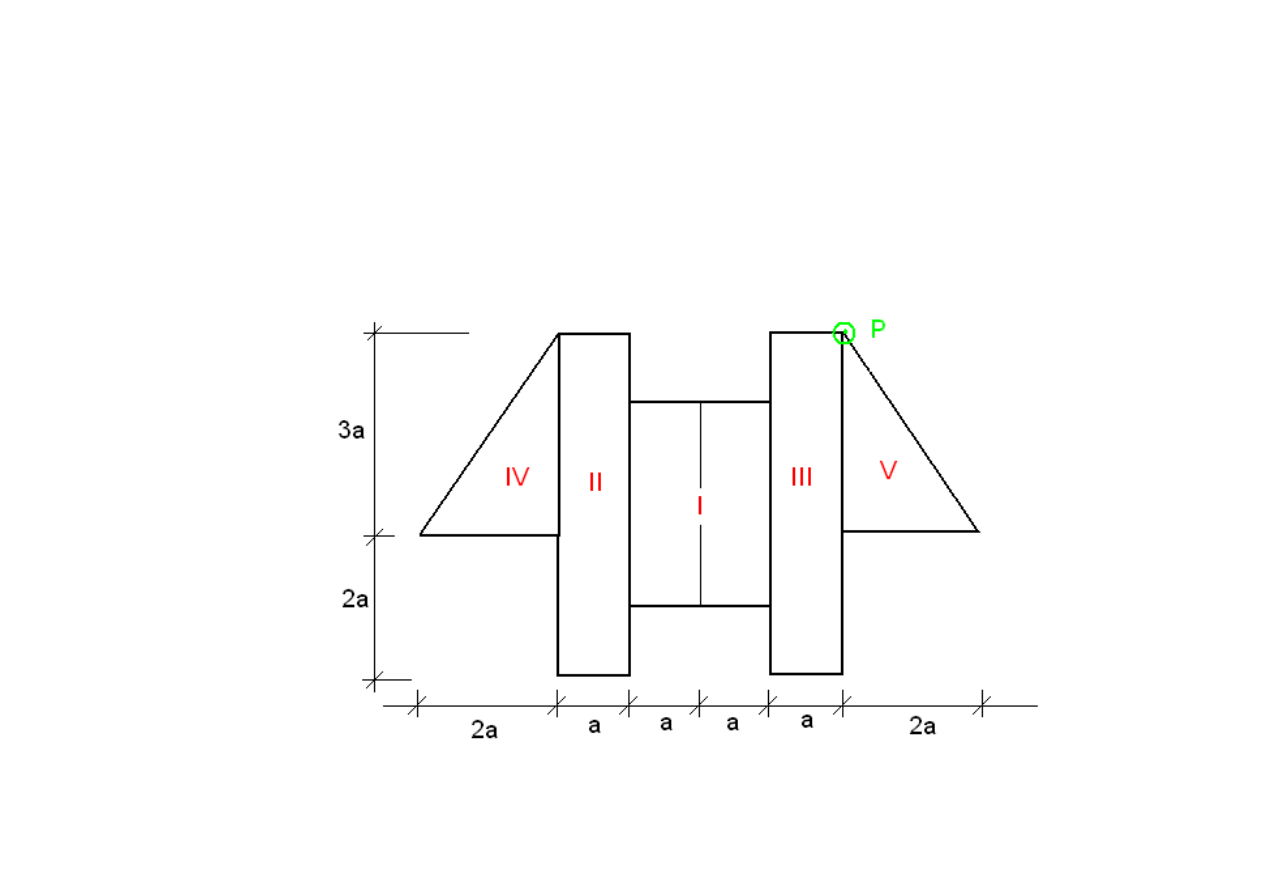
PROJEKT
Zaprojektowa
ć
parametr a przekroju, wyznaczy
ć
o
ś
oboj
ę
tn
ą
oraz brył
ę
napr
ęż
e
ń
.
Wyznaczy
ć
rdze
ń
przekroju. Przekrój obci
ąż
ono sił
ą
N=200 kN przyło
ż
on
ą
w punkcie P.
Dane:
obl
R
=180MPa.

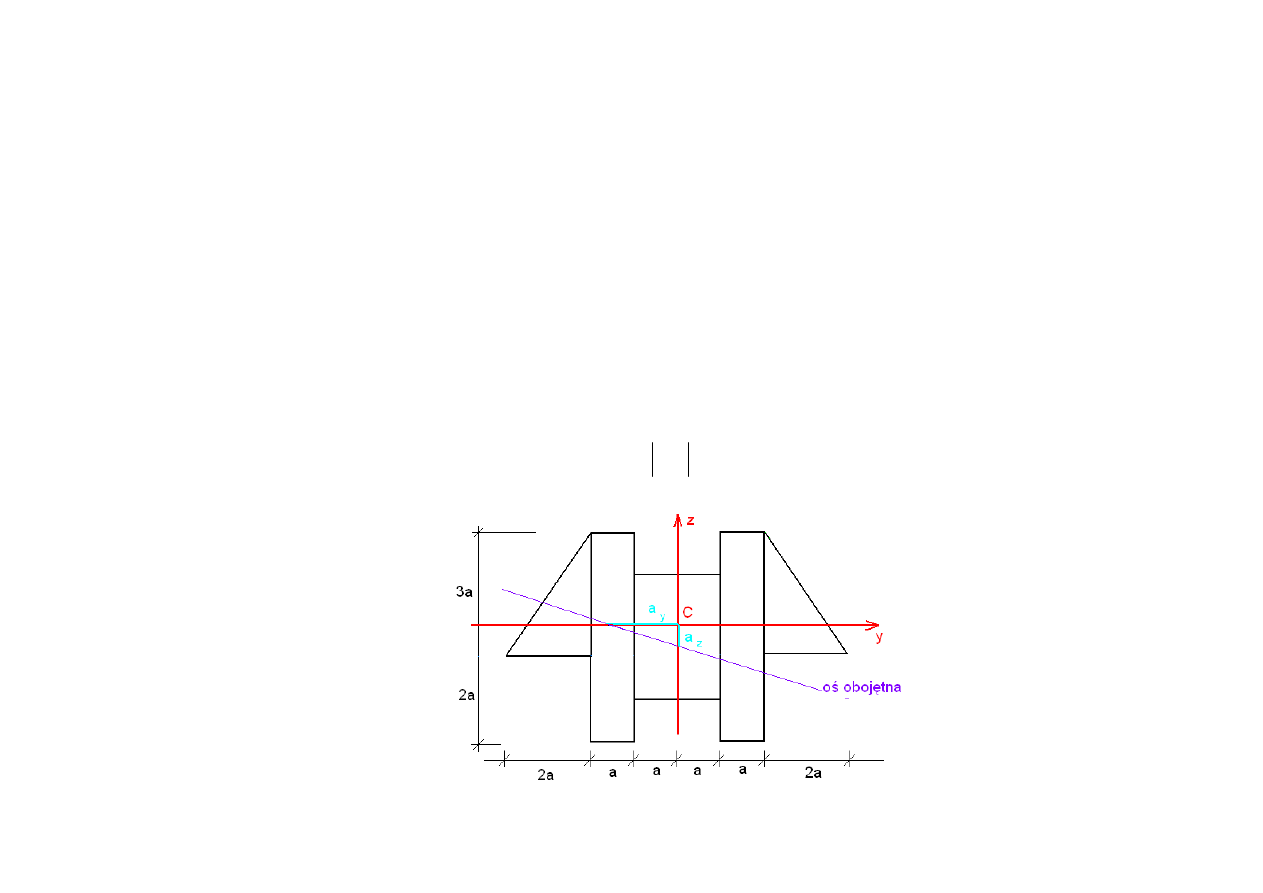
a) Wyznaczenie głównych centralnych osi bezwładno
ś
ci przekroju i głównych
momentów bezwładno
ś
ci
C -
ś
rodek ci
ęż
ko
ś
ci figury
i
C
-
ś
rodki ci
ęż
ko
ś
ci figur składowych , współrz
ę
dne:
(
)
i
ci
ci
C y ,z
I
C
0 ,
2
a
2
I
A
2
3
6
a
a
a
=
⋅
=
II
3
C
,
2
2
a
a
−
2
II
A
5
5
a a
a
=
⋅ =
III
3
C
,
2
2
a
a
2
III
A
5
5
a a
a
=
⋅ =
(
)
IV
C
4 ,
a a
−
2
IV
1
A
2
3
3
2
a
a
a
=
⋅
=
(
)
V
C
4 ,
a a
2
V
1
A
2
3
3
2
a
a
a
=
⋅
=
V
i
i=I
A
A
=
∑
2
A
22 a
=
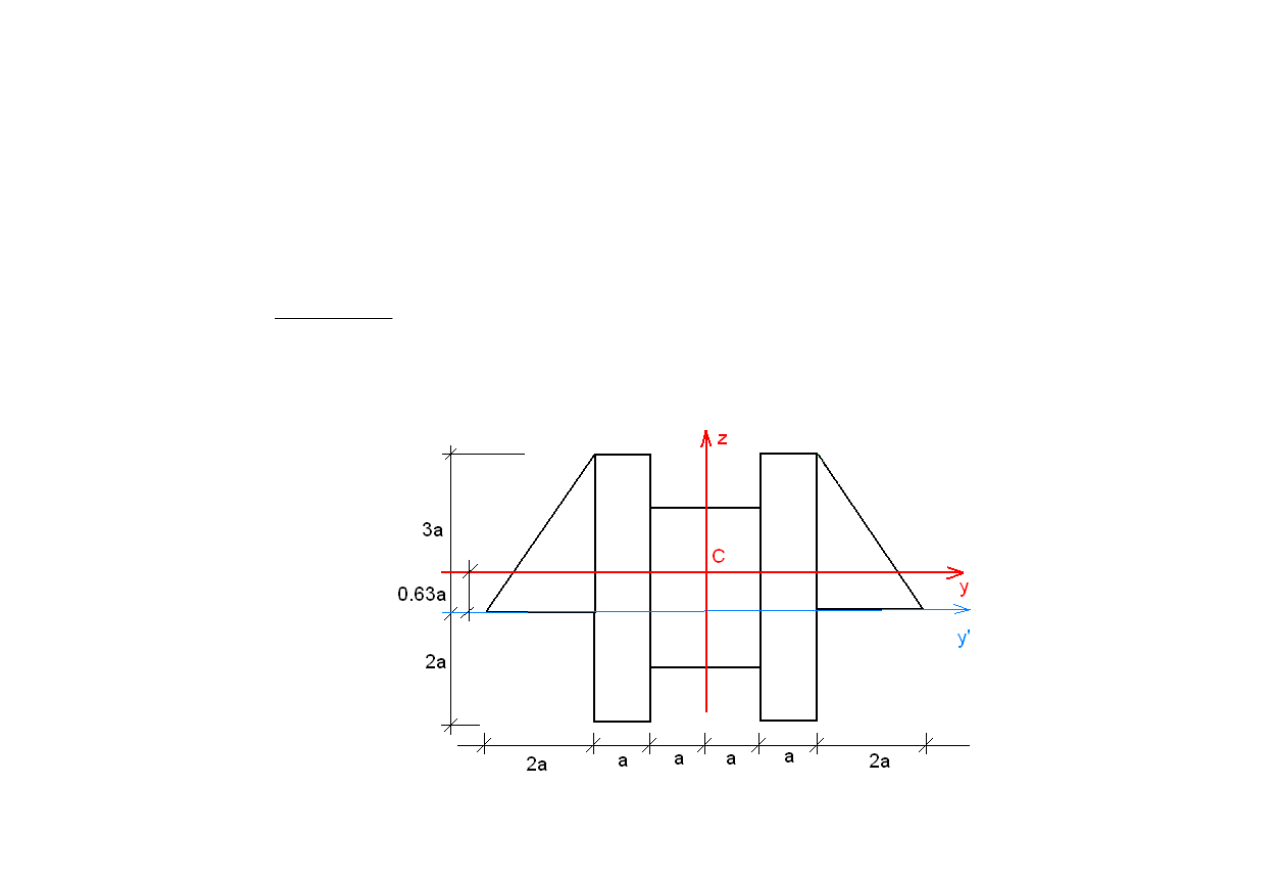
Współrz
ę
dne
ś
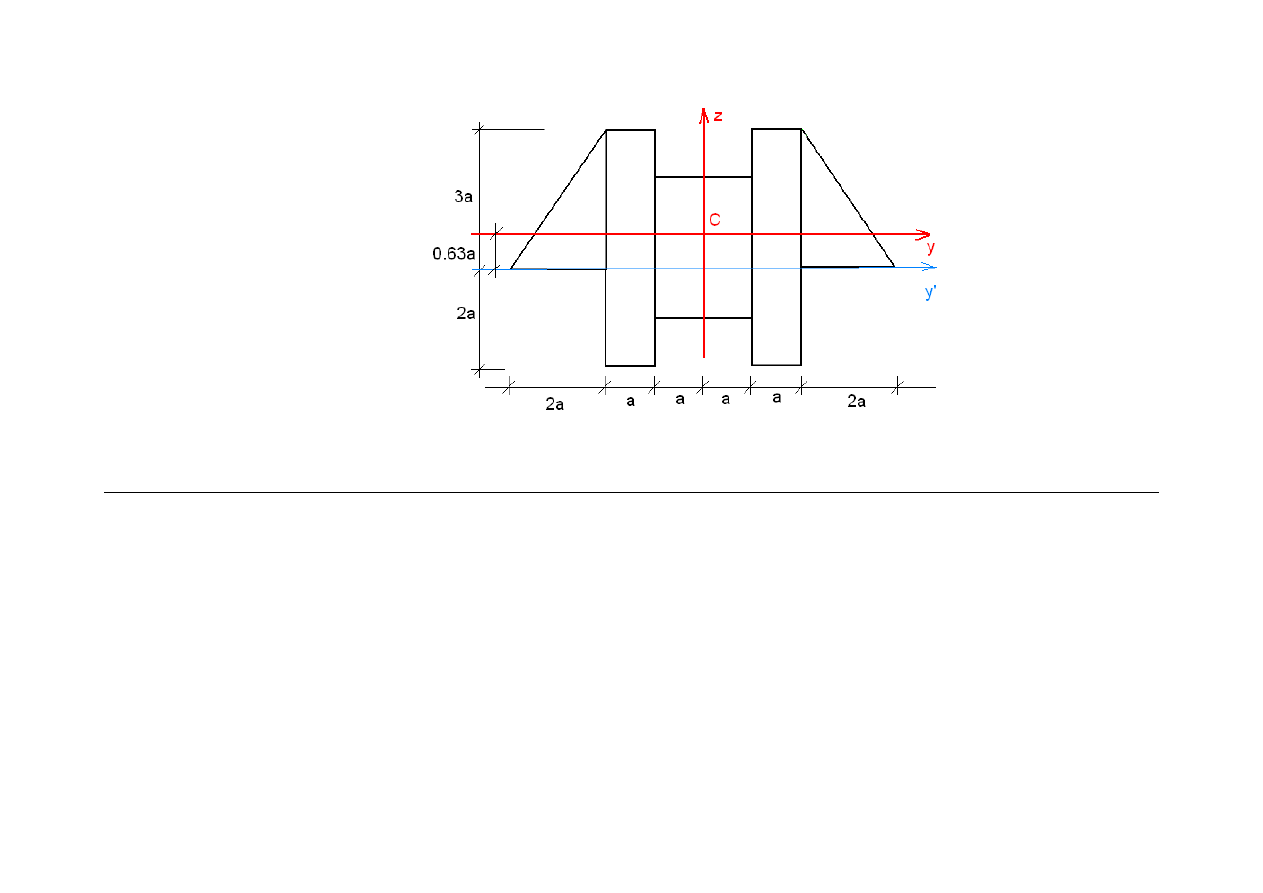
rodka całej figury:
C
y
0
=
ze wzgl
ę
du na symetri
ę
figury
V
Ci
i
i=I
C
V
i
i=I
z
A
z
A
⋅
=
∑
∑
C
z
0.63
a
=

Obliczenia:
4
yC
J
29.42
a
=
4
zC
J
69.33
a
=
Promienie bezwładno
ś
ci:
yC
2
yC
J
i =
A
2
zC
zC
J
i =
A
Obliczenia:
2
2
yC
i =1.34
a
2
2
zC
i =3.15
a
Współrz
ę
dne punktu przyło
ż
enia siły w układzie osi głównych centralnych:
(
)
0
0
P
,
y z
(
)
(
)
P 2 , 3
0.63
a
a
a
−
2. Poło
ż
enie osi oboj
ę
tnej:
1
y
z
y
z
a
a
+
=
gdzie:
2
0
z
y
i
a
y
= −
2
0
y
z
i
a
z
= −
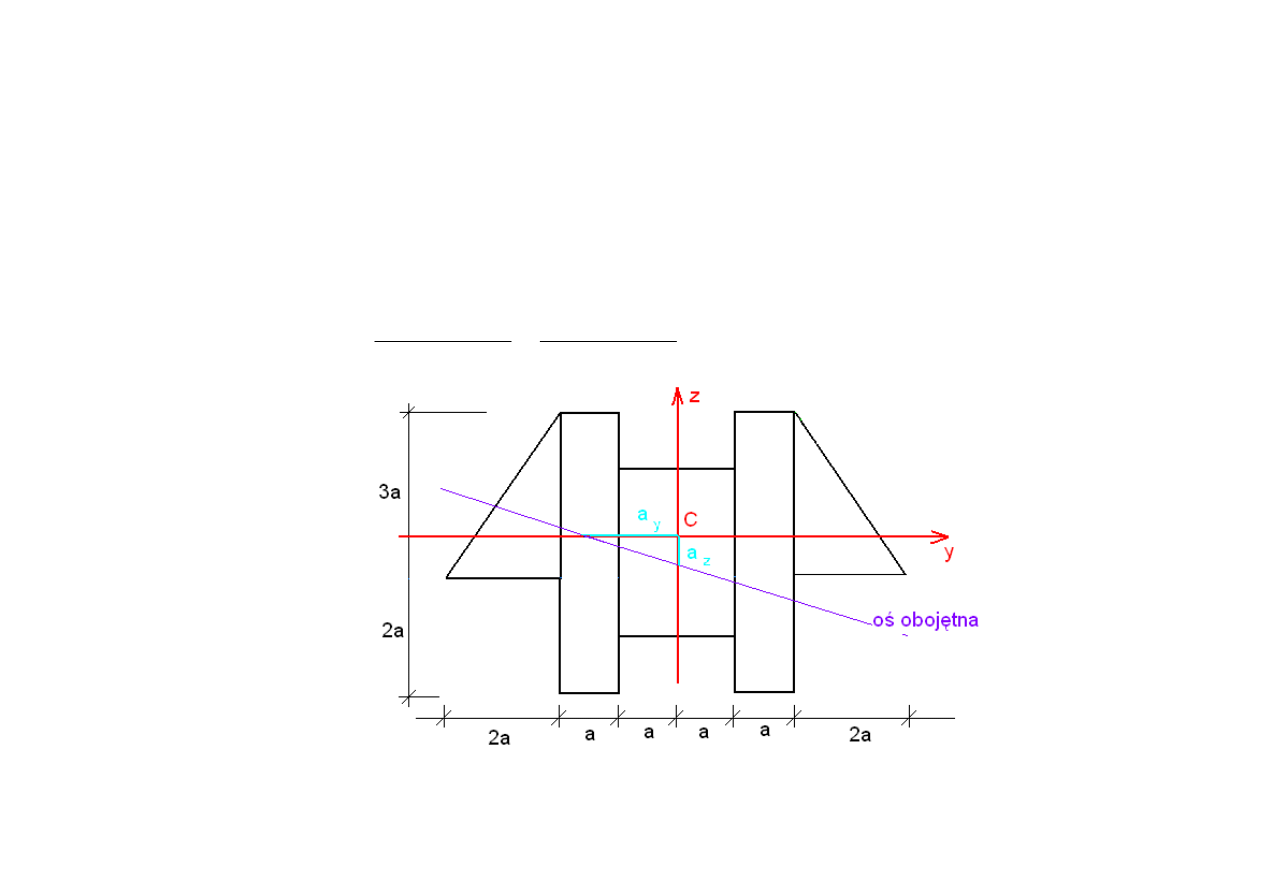
Obliczenia:
1.576
y
a
a
= −
0.566
z
a
a
= −
Równanie osi oboj
ę
tnej:
(
) (
)
1
1.576
0.566
y
z
a
a
+
=
−
−
3. Projektowanie – wyznaczanie parametru a
Redukcja obci
ąż
enia do
ś
rodka ci
ęż
ko
ś
ci przekroju:
200
N
N
kN
= + =
0
200 2.36 [
]
y
M
Nz
a kNm
= +
=
⋅
0
200 2 [
]
z
M
Ny
a kNm
= −
= −
⋅
Warunek wytrzymało
ś
ciowy
max
x
obl
R
σ
≤
y
z
x
y
z
M
M
N
z
y
A
J
J
σ
=
+
−
Punkt najbardziej oddalony od osi oboj
ę
tnej to punkt P, wstawiamy jego współrz
ę
dne i
otrzymujemy:
(
)
(
)
3
2
4
4
200 2.36
200 2
200
max
2.36
2
180 10 [
]
22
29.42
69.33
x
a
a
a
a
kPa
a
a
a
σ
⋅
−
⋅
=
+
−
≤
∗
0.02
a
m
⇒
≥
Podstawiamy teraz warto
ść
obliczonego parametru do kolejnych oblicze
ń
. Liczymy
napr
ęż
enia w wierzchołkach konturu przekroju, czyli punktach
P
i
.
( )
P
y
z
x
i
i
i
y
z
M
M
N
z
y
A
J
J
σ
=
+
−
Dokonanie oblicze
ń
jest mo
ż
liwe po zestawieniu współrz
ę
dnych tych punktów w osiach
głównych, dla przyj
ę
tej warto
ś
ci parametru a.
(
)
P
,
i
i
i
y z
( )
P
x
i
σ
(
) (
)
A 4 , 0.63
0.08, 0.01266
a
a
−
=
−
( )
54.98
x
A
MPa
σ
= +
(
) (
)
B 2 , 0.63
0.04, 0.01266
a
a
−
=
−
( )
26.09
x
B
MPa
σ
= +
(
) (
)
C 2 , 2.63
0.04, 0.05266
a
a
−
=
−
( )
54.34
x
C
MPa
σ
= −
(
) (
)
D
, 2.63
0.02, 0.05266
a
a
−
=
−
( )
68.77
x
D
MPa
σ
= −
(
) (
)
E
, 1.63
0.02, 0.03266
a
a
−
=
−
( )
28.54
x
E
MPa
σ
= −

(
) (
)
F
, 1.63
0.02, 0.03266
a
a
− −
= −
−
( )
57.39
x
F
MPa
σ
= −
(
) (
)
G
, 2.63
0.02, 0.05266
a
a
− −
=
−
( )
97.61
x
G
MPa
σ
= −
(
) (
)
H
2 , 2.63
0.04, 0.05266
a
a
−
−
=
−
( )
112.04
x
H
MPa
σ
= −
(
) (
)
I
2 , 0.63
0.04, 0.01266
a
a
−
−
= −
−
( )
31.59
x
I
MPa
σ
= −
(
) (
)
J
4 , 0.63
0.08, 0.01266
a
a
−
−
=
−
( )
60.44
x
J
MPa
σ
= −
(
)
(
)
(
)
K
2 , 3 0.63
0.04, 0.04733
a
a
−
−
= −
( )
89.07
x
K
MPa
σ
= +
(
)
(
)
(
)
L
, 3 0.63
0.02, 0.04733
a
a
−
−
= −
−
( )
103.49
x
L
MPa
σ
= +
(
)
(
)
(
)
M
, 2 0.63
0.02, 0.02733
a
a
−
−
= −
−
( )
63.27
x
M
MPa
σ
= +
(
)
(
)
(
)
N
, 2 0.63
0.02, 0.02733
a
a
−
=
( )
92.12
x
N
MPa
σ
= +
(
)
(
)
(
)
, 3 0.63
0.02, 0.04733
O a
a
−
=
( )
132.34
x
O
MPa
σ
= +
(
)
(
)
(
)
P 2 , 3 0.63
0.04, 0.04733
a
a
−
=
( )
146.67
x
P
MPa
σ
= +
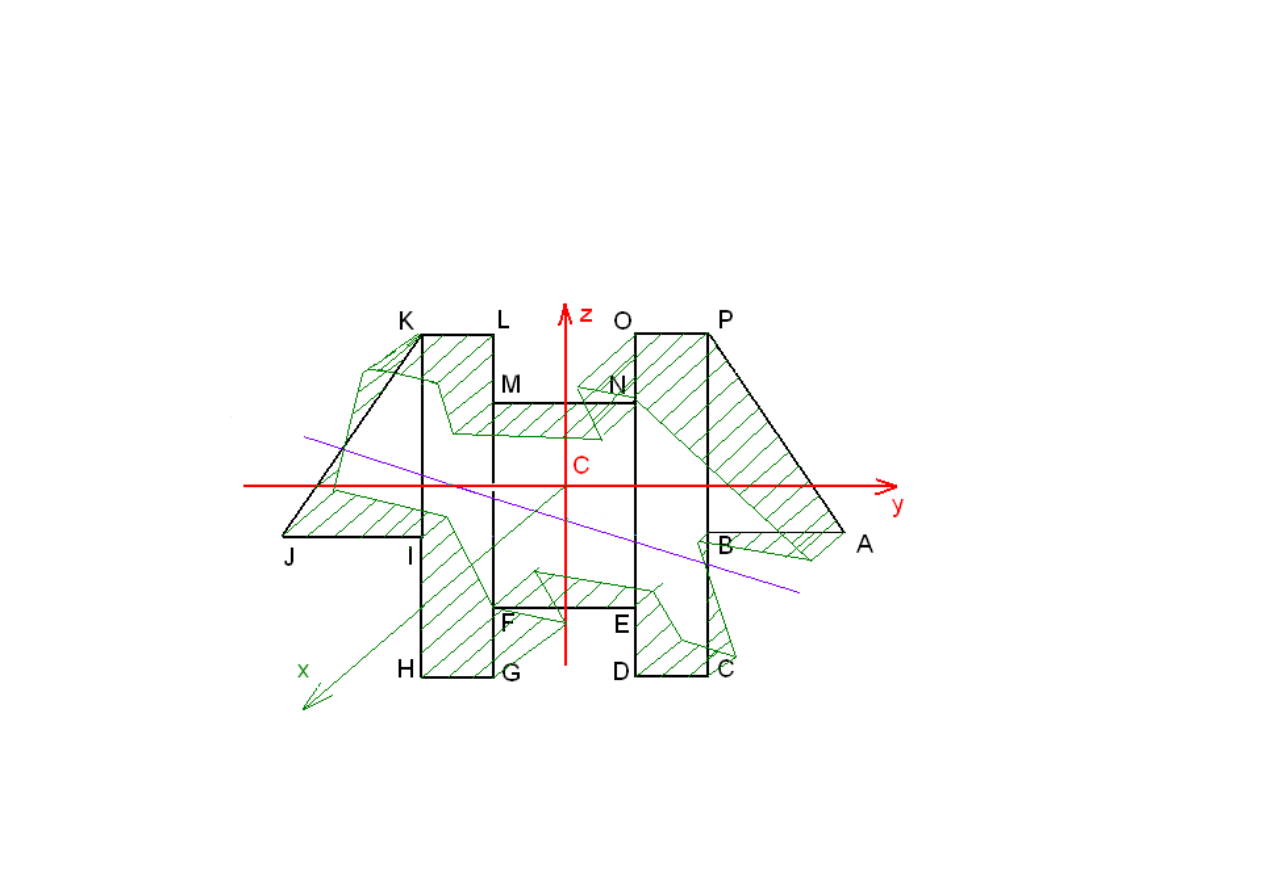
Powy
ż
ej obliczone napr
ęż
enia tworz
ą
tzw. brył
ę
napr
ęż
e
ń
, która powstaje jako rzut
aksonometryczny wyskalowanych napr
ęż
e
ń
odniesionych na o
ś
x w punktach
P
i
i
poł
ą
czonych odcinkami prostymi pomi
ę
dzy kolejnymi wierzchołkami.
napr
ęż
enia rozci
ą
gaj
ą
ce
napr
ęż
enia
ś
ciskaj
ą
ce
(18.11.2008)
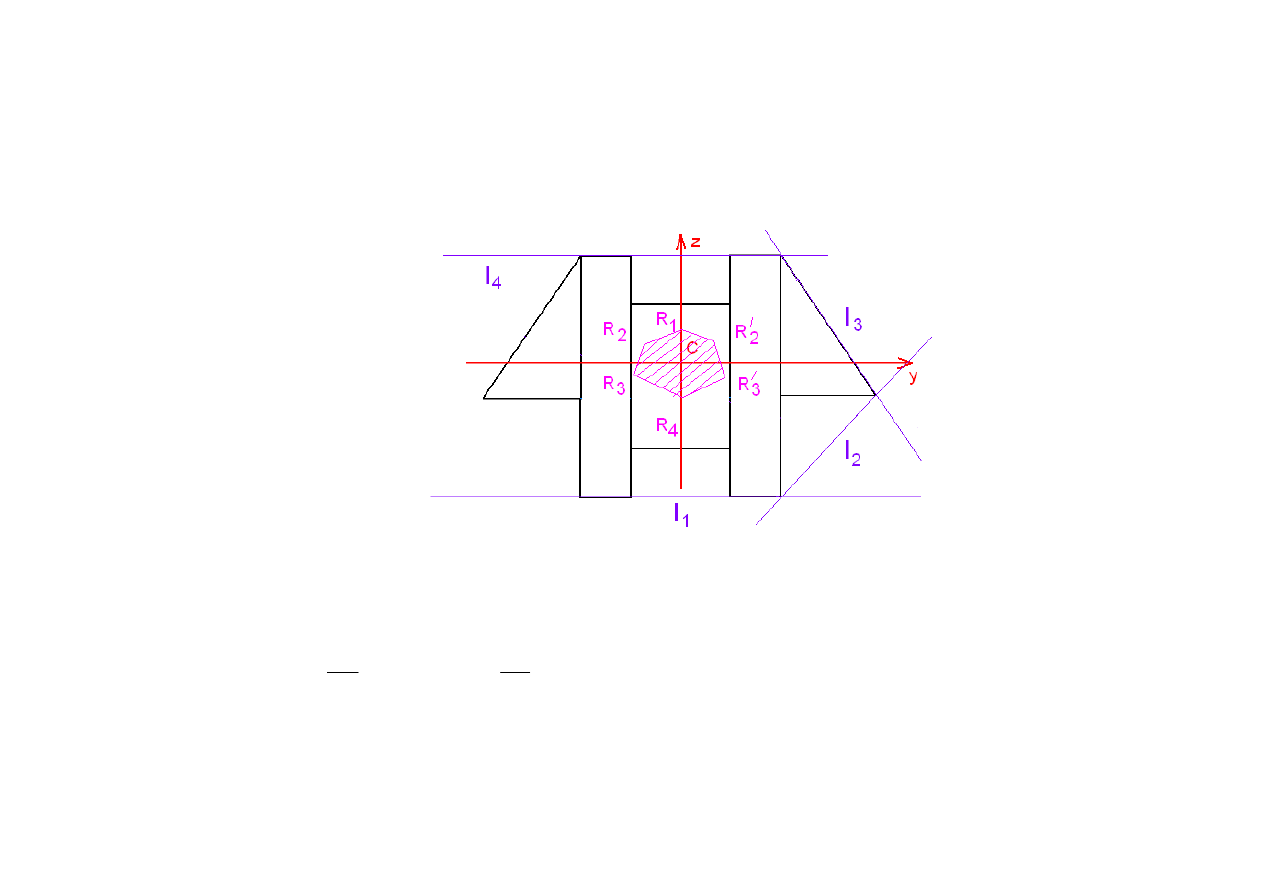
Rdze
ń
przekroju o jednej osi symetrii –przykład 1
Dla ka
ż
dej prostej
i
l
z obwiedni poszukujemy takiego punktu
(
)
,
i
oi
oi
R y
z
,
ż
e
współrz
ę
dne tego punktu wyznaczone s
ą
z zale
ż
no
ś
ci:,
2
0
z
i
yi
i
y
a
= −
2
0
y
i
zi
i
z
a
= −
gdzie :
yi
a
,
zi
a
s
ą
współczynnikami w postaci odcinkowej tej prostej.

O
ś
z jest osi
ą
symetrii. Tworzymy obwiedni
ę
przekroju prostymi stycznymi do jego
konturu. Obwiednia ta jest równie
ż
symetryczna, st
ą
d analiza połowy przekroju
Prosta
1
l
1
y
a
= ±∞
,
1
2.63
z
a
a
= −
punkt
1
R
01
0
y
=
01
0.507
z
=
Prosta
2
l
2
4.65
y
a
a
= −
,
2
4.63
z
a
a
= −
punkt
2
R
02
0.677
y
a
=
02
0.288
z
=
Prosta
3
l
3
3.55
y
a
a
= −
,
(
)
3
3 0.63
z
a
a
= −
punkt
3
R
03
0.887
y
=
03
0.249
z
= −
Prosta
4
l
4
y
a
= ±∞
,
(
)
4
3 0.63
z
a
a
= −
punkt
4
R
04
0
y
=
04
0.56
z
= −
Punkty
2
R
′
,
3
R
′
s
ą
odbiciem symetrycznym punktów
2
R
,
3
R
.

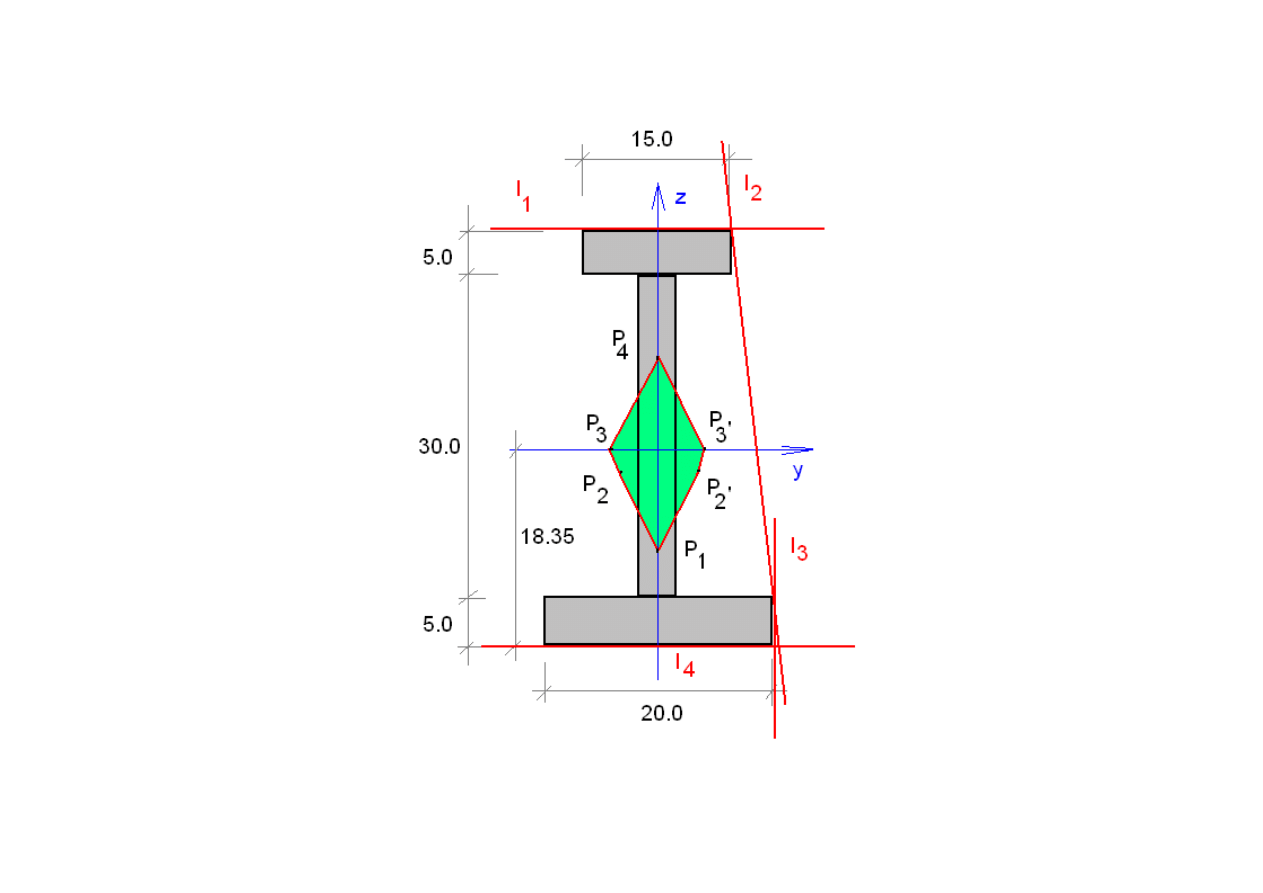
Rdze
ń
przekroju o jednej osi symetrii –przykład 2
Zadanie pomocnicze: dane dwa punkty
(
) (
)
,
,
A
A
B
B
A y z
B y z
wyznaczy
ć
równanie
odcinkowe prostej przechodz
ą
cej przez te dwa punkty.
A
B
A
B
z
z
tg
y
y
β
−
=
−
(
)
A
A
z
z
tg
y
y
β
−
=
−
to równanie kierunkowe tej prostej , które nale
ż
y przekształci
ć
do
postaci odcinkowej

(
)
(
)
(
)
3
3
3
2
2
2
y
15 5
3 30
20 5
J
15 5 19.2
3 30 1.65
20 5 15.85
12
12
12
⋅
⋅
⋅
=
+ ⋅ ⋅
+
+ ⋅ ⋅
+
+
⋅ ⋅
3
3
3
z
5 15
30 3
5 20
J
12
12
12
⋅
⋅
⋅
=
+
+
A 15 5 20 5 30 3
= ⋅ +
⋅ + ⋅
Obliczenia:
4
y
J
60129.0 cm
=
4
z
J
4807.1 cm
=
2
A
265 cm
=
2
2
226.9
y
i
cm
=
2
2
18.1
z
i
cm
=
Prosta
1
l
1
y
a
= ±∞
,
1
21.65
z
a
=
punkt
1
P
01
0
y
=
01
226.9
10.5
21.65
z
−
=
= −

Prosta
2
l
2
9.0
y
a
=
,
2
126.65
z
a
=
punkt
2
P
02
18.1
2.1
9
y
−
=
= −
02
226.9
1.8
126.65
z
−
=
= −
Prosta
3
l
3
10.0
y
a
=
,
3
z
a
= ±∞
punkt
3
P
03
18.1
1.81
10
y
−
=
= −
03
0
z
=
Prosta
4
l
4
y
a
= ±∞
,
4
18.35
z
a
= −
punkt
4
P
o współrz
ę
dnych
04
0
y
=
04
226.9
18.35
z
−
=
=
−
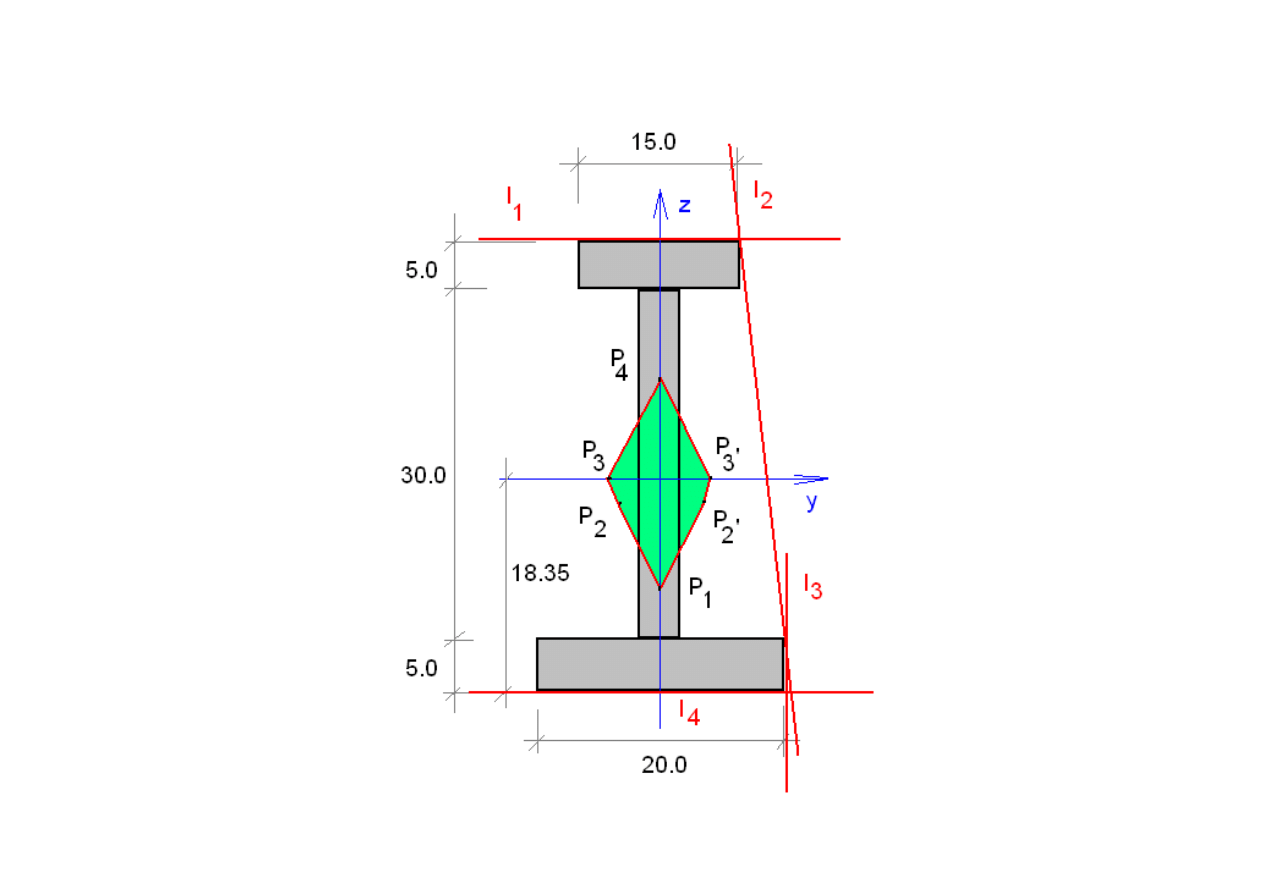
Punkty
2
'
P
3
'
P
s
ą
odbiciem symetrycznym punktów
2
P
,
3
P
.

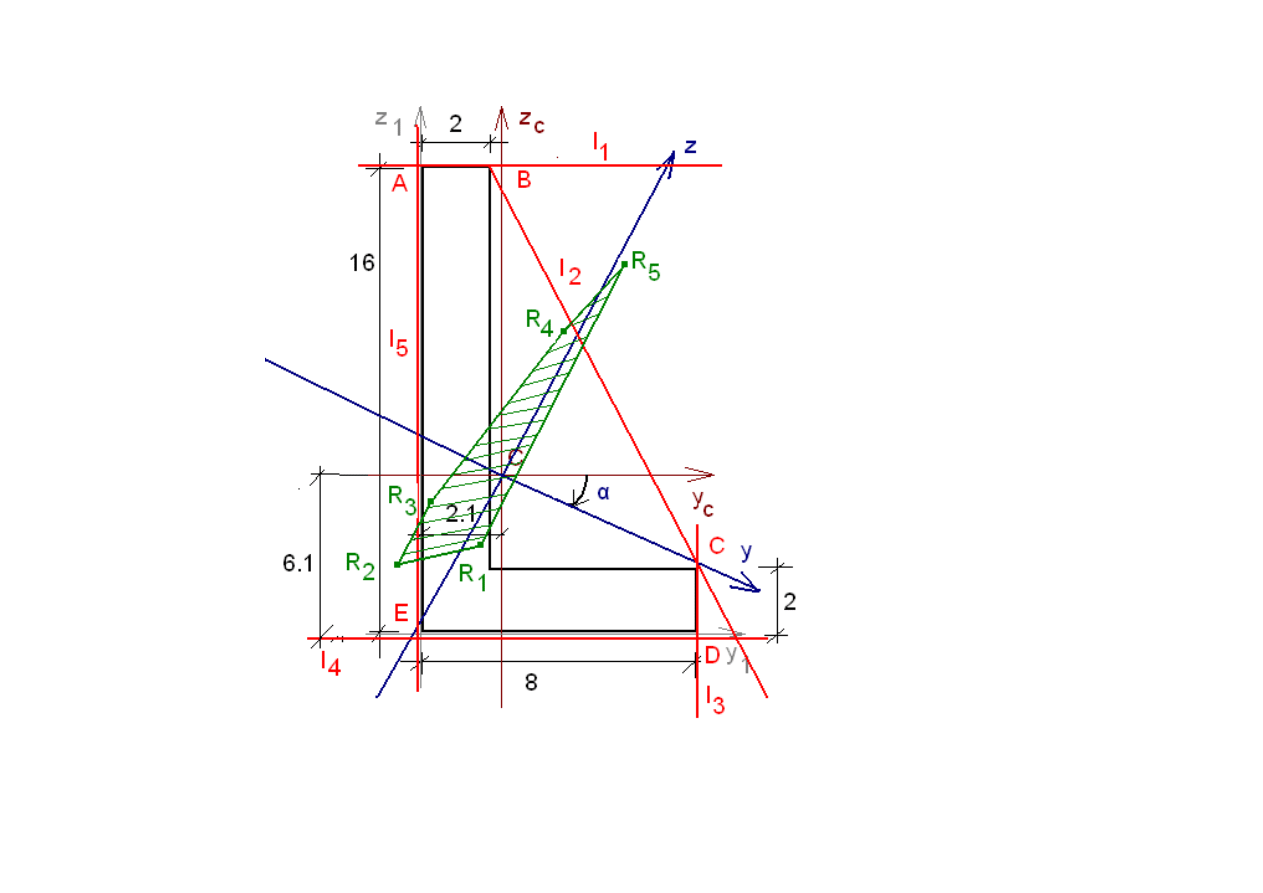
PROJEKT 6
Rdze
ń
przekroju nie posiadaj
ą
cego osi symetrii
Algorytm
1. wyznaczenie centrum figury
•
wyznaczenie głównych osi i obliczenie: A,
y
J
,
z
J
•
promienie bezwładno
ś
ci:
2
y
i
,
2
z
i
2. wykre
ś
lenie obwiedni przekroju prostymi
i
l
stycznymi do konturu
3. wyznaczenie równa
ń
kierunkowych tych prostych na podstawie znajomo
ś
ci
współrz
ę
dnych dwóch punktów, przez które ta prosta przechodzi
4. przekształcenie równa
ń
do postaci odcinkowych i wyznaczenie punktów rdzenia
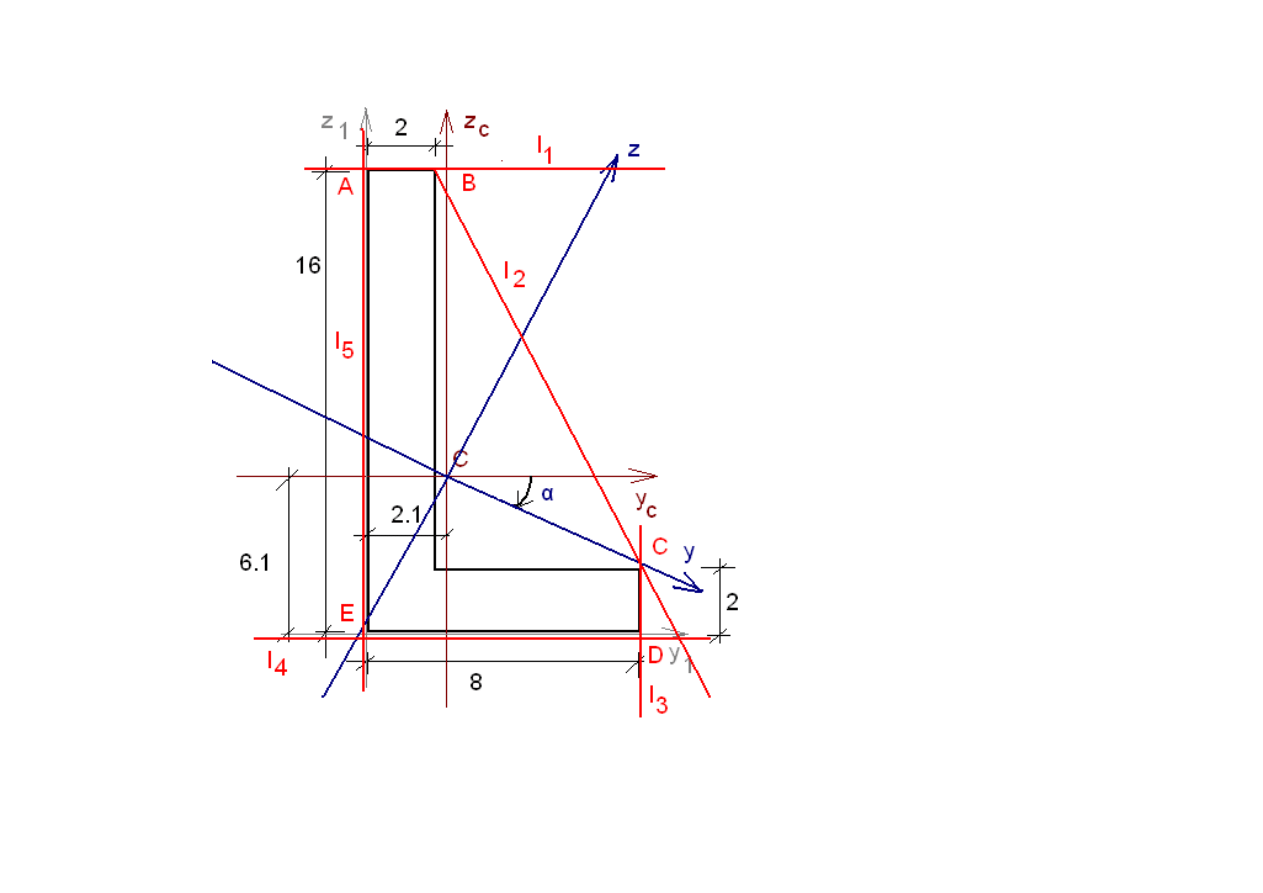
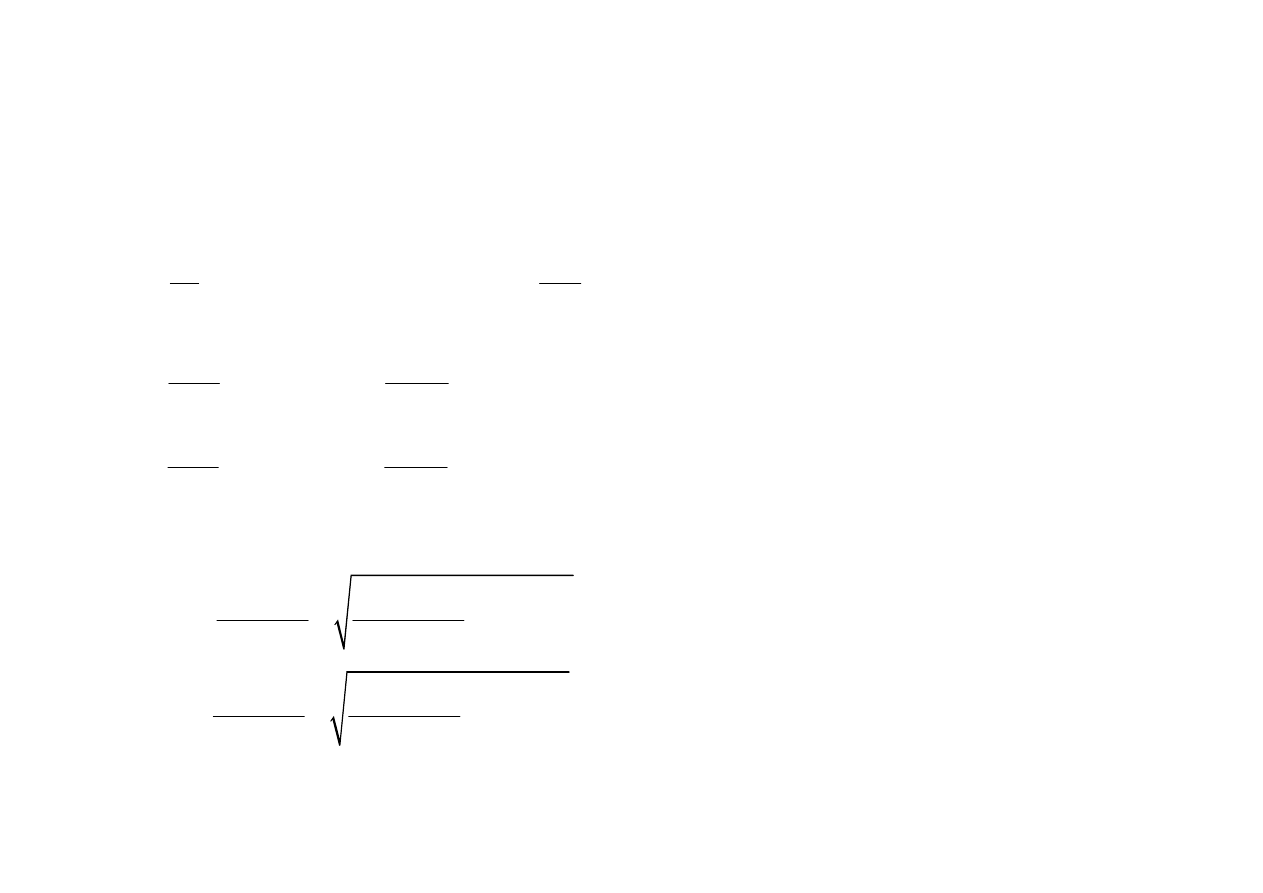
2
14 2 8 2
44 [
]
F
cm
= ⋅ + ⋅ =
4
1
8 2 1 14 2 9
268 [
]
y
S
cm
= ⋅ ⋅ + ⋅ ⋅ =
4
1
14 2 1 8 2 4
92 [
]
z
S
cm
= ⋅ ⋅ + ⋅ ⋅ =
1
92
2.1 [
]
44
C
y
cm
=
=
1
268
6.1 [
]
44
C
z
cm
=
=
( )
( )
3
3
2
2
4
yC
8 2
2 14
J
8 2 5.1
14 2 2.9
1114.3 [
]
12
12
cm
⋅
⋅
=
+ ⋅ ⋅
+
+ ⋅ ⋅
=
( )
( )
3
3
2
2
4
zC
2 8
14 2
J
8 2 1.9
14 2 1.1
186.2 [
]
12
12
cm
⋅
⋅
=
+ ⋅ ⋅
+
+ ⋅ ⋅
=
(
) ( )
( ) (
)
4
yC zC
J
0 8 2
5.1
1.9
14 2 2.9
1.1
244.4 [
]
cm
= + ⋅ ⋅ −
⋅
+ ⋅ ⋅
⋅ −
=
(
) ( )
2
yC
zC
yC
zC
4
y
max
yCzC
J
J
J
J
J =J
J
1174.6 [
]
2
2
cm
−
+
=
+
+
=
(
) ( )
2
yC
zC
yC
zC
4
z
min
yCzC
J
J
J
J
J =J
J
126.0 [
]
2
2
cm
−
+
=
−
+
=

( )
yC
yC
zC
2J
2 1114.3
2
2.4
J
J
1114.3 186.2
tg
α
−
⋅
=
= −
= −
−
−
(
)
2
2.4
arctg
α
=
−
33.7
α
⇒
= −
o
Promienie bezwładno
ś
ci:
y
2
2
yC
J
i =
25.3 [
]
A
cm
=
2
2
z
z
J
i =
4.2 [
]
A
cm
=
Transformacja współrz
ę
dnych kolejnych punktów z układu współrz
ę
dnych centralnych
do osi głównych (transformacja przez obrót).
(
)
(
)
cos
33.7
0.83
sin
33.7
0.55
−
=
−
= −
o
o
cos
sin
0.83
0.55
sin
cos
0.55
0.83
Q
α
α
α
α
−
=
=
−
cos
sin
sin
cos
i
Ci
i
Ci
y
y
z
z
α
α
α
α
=
=
−

Wyniki oblicze
ń
:
(
)
P
,
i
Ci
Ci
y
z
(
)
P
,
i
i
i
y z
(
)
A
2.1, 9.9
= −
(
)
A
7.1, 7.0
= −
(
)
B
0.1, 9.9
= −
(
)
B
5.5, 8.1
= −
(
)
C
5.9,
4.1
=
−
(
)
C
7.2,
0.2
=
−
(
)
D
5.9,
6.1
=
−
(
)
D
8.3,
1.9
=
−
(
)
E
2.1,
6.1
= −
−
(
)
E
1.7,
6.3
=
−
Do dalszych oblicze
ń
wykorzystuje si
ę
współrz
ę
dne w głównych osiach (prawa
kolumna tabeli)
Prosta
i
l
przechodz
ą
ca przez punkty
P
k
,
P
l
współczynnik kierunkowy
k
l
i
k
l
z
z
tg
y
y
β
−
=
−
równanie prostej
(
)
k
i
k
z
z
tg
y
y
β
− =
−
posta
ć
odcinkowa
1
yi
zi
y
z
a
a
+
=

punkt rdzenia
(
)
0
0
R
,
i
i
i
y
z
gdzie:
2
0
z
i
yi
i
y
a
= −
2
0
y
i
zi
i
z
a
= −
punkt rdzenia
(
)
0
0
R
,
i
i
i
y
z
współrz
ę
dne punktu rdzeniowego s
ą
głównych osiach
centralnych
Prosta
1
l
przechodz
ą
ca przez punkty A , B
współczynnik kierunkowy
1
0.69
tg
β
=
równanie prostej
(
)
(
)
8.1 0.69
5.5
z
y
−
=
− −
posta
ć
odcinkowa
1
17.2
11.88
y
z
+
=
−
punkt rdzenia
(
)
(
)
1
01
01
R
,
0.24,
2.13
y
z
=
−
Prosta
2
l
przechodz
ą
ca przez punkty B, C
współczynnik kierunkowy
2
0.65
tg
β
= −

równanie prostej
(
)
(
)
0.2
0.65
7.2
z
y
− −
= −
−
posta
ć
odcinkowa
1
6.92
4.5
y
z
+
=
punkt rdzenia
(
)
(
)
2
02
02
R
,
0.61,
5.62
y
z
= −
−
Prosta
3
l
przechodz
ą
ca przez punkty C, D
współczynnik kierunkowy
3
1.54
tg
β
= −
równanie prostej
(
)
(
)
1.9
1.54
8.3
z
y
− −
= −
−
posta
ć
odcinkowa
1
7.07
10.89
y
z
+
=
punkt rdzenia
(
)
(
)
3
03
03
R
,
0.59,
2.32
y
z
= −
−
Prosta
4
l
przechodz
ą
ca przez punkty D, E
współczynnik kierunkowy
4
0.66
tg
β
=
równanie prostej
(
)
(
)
6.3
0.66
1.7
z
y
− −
=
−

posta
ć
odcinkowa
1
11.26
7.43
y
z
+
=
−
punkt rdzenia
(
)
(
)
4
04
04
R
,
0.37, 3.41
y
z
= −
Prosta
5
l
przechodz
ą
ca przez punkty E, A
współczynnik kierunkowy
5
1.5
tg
β
= −
równanie prostej
(
)
(
)
7
0.65
7.1
z
y
− = −
− −
posta
ć
odcinkowa
1
24.8
3.7
y
z
+
=
−
−
punkt rdzenia
(
)
(
)
5
05
05
R
,
0.15, 6.84
y
z
=

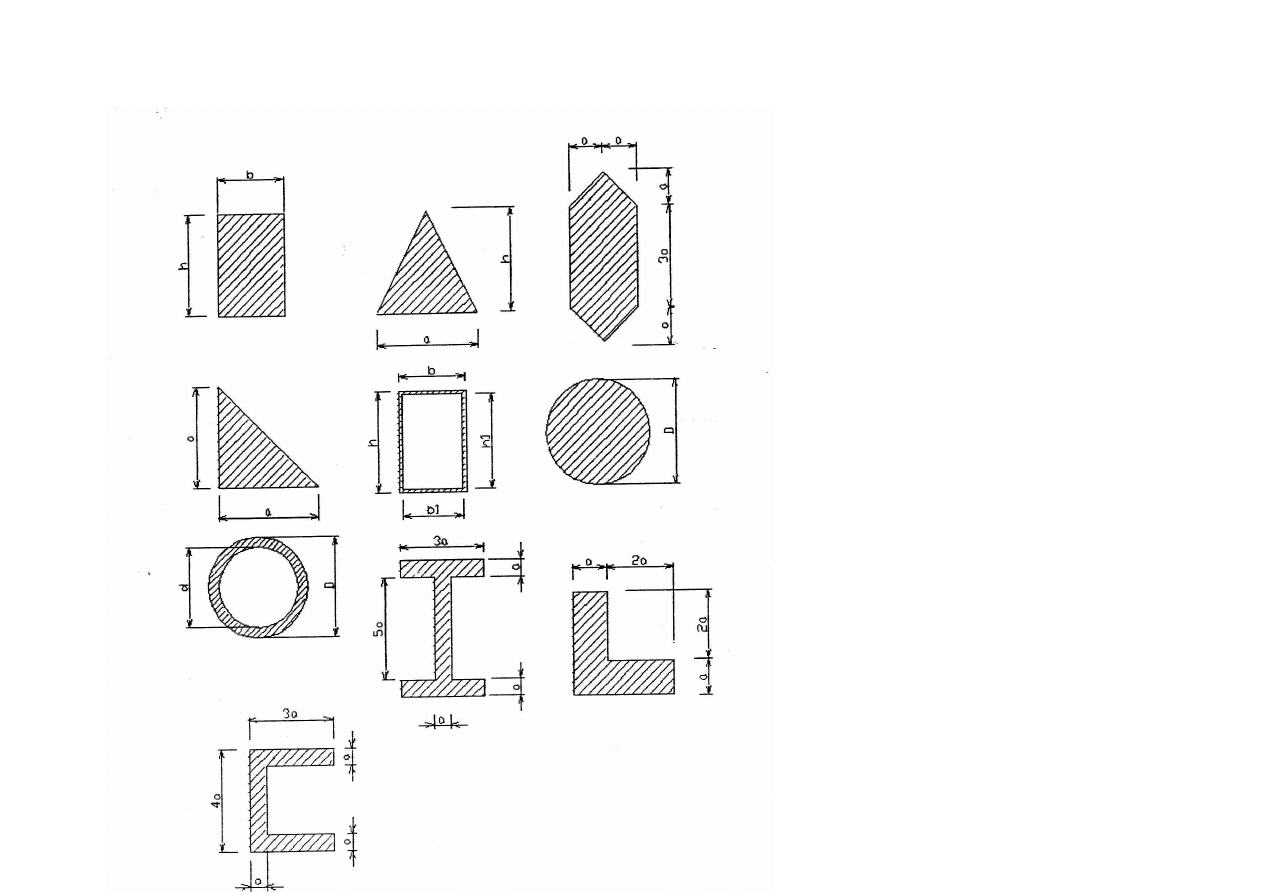
Ć
WICZENIA: Przyj
ąć
wymiary przekrojów i wyznaczy
ć
ich rdzenie
STOPA FUNDAMENTOWA
Mimo
ś
rodowe
ś
ciskanie
Norma: wymiary podstawy fundamentu nale
ż
y ustala
ć
z zachowaniem nast
ę
puj
ą
cych
warunków:
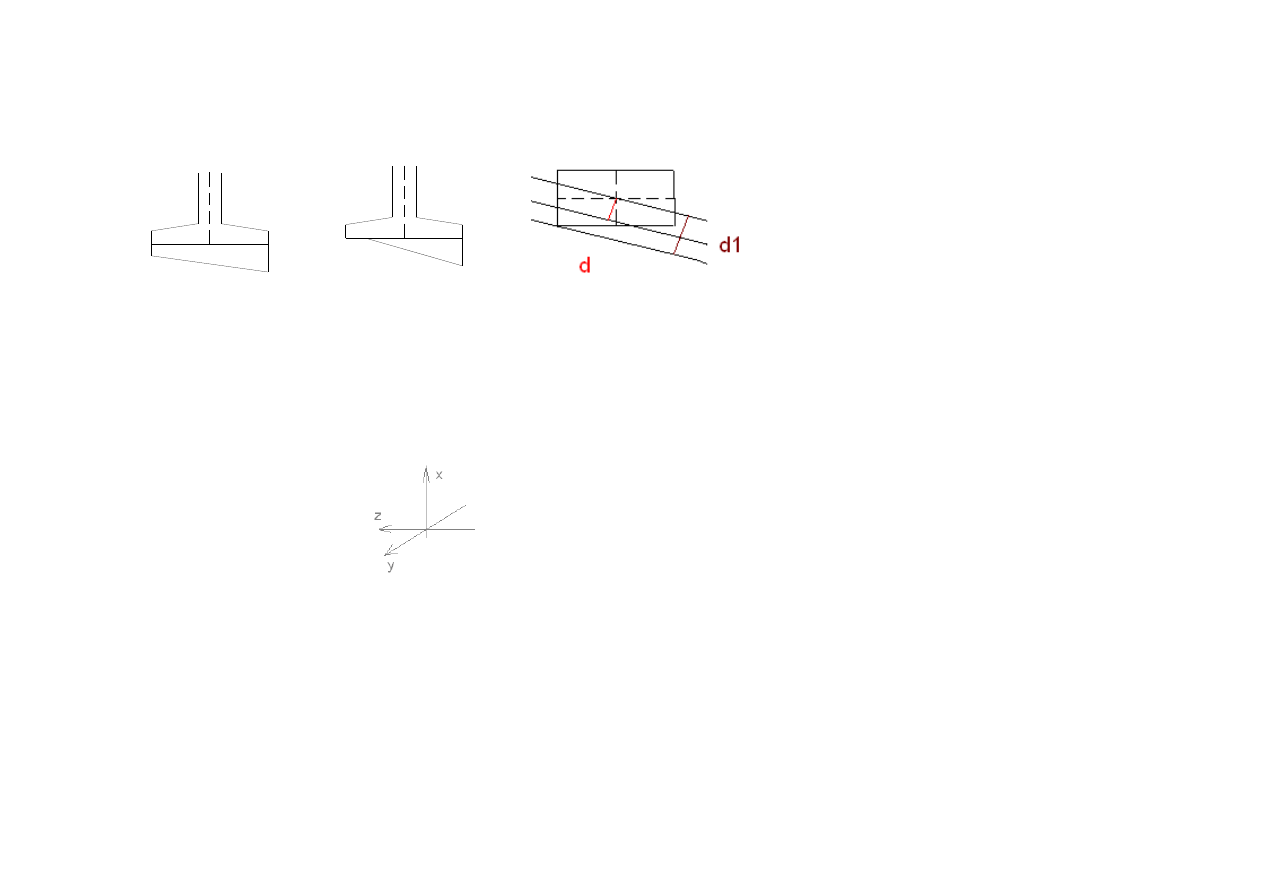
a) rozkład obliczeniowego obci
ąż
enia jednostkowego w podstawie fundamentu nale
ż
y
przyjmowa
ć
liniowy w/g rys.b. Nie wolno uwzgl
ę
dnia
ć
sił rozci
ą
gaj
ą
cych mi
ę
dzy
podło
ż
em i podstaw
ą
fundamentu
b) wypadkowa sił od obliczeniowego obci
ąż
enia nie powinna wychodzi
ć
poza rdze
ń
podstawy fundamentu
c) przy uwzgl
ę
dnieniu wszystkich obci
ąż
e
ń
obliczeniowych dopuszcza si
ę
powstanie
szczeliny mi
ę
dzy podło
ż
em i podstaw
ą
fundamentu w/g rys c, której zasi
ę
g c nie
mo
ż
e by
ć
wi
ę
kszy od połowy odległo
ś
ci c
′
mi
ę
dzy prost
ą
przechodz
ą
c
ą
równolegle
do osi oboj
ę
tnej przez
ś
rodek ci
ęż
ko
ś
ci całej podstawy a prost
ą
przechodz
ą
c
ą
przez skrajny punkt podstawy le
żą
cy po stronie osi oboj
ę
tnej.
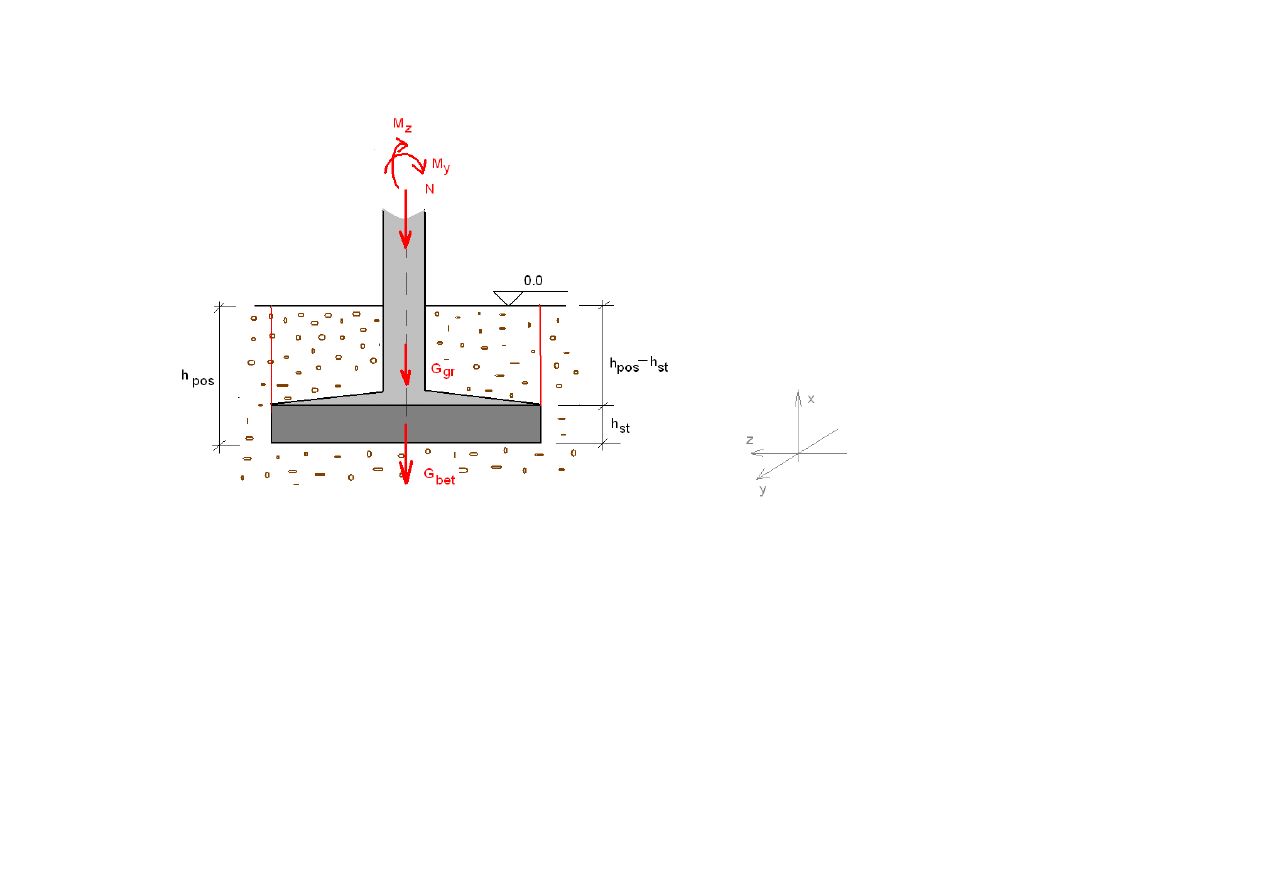
PROJEKT
(
)
300, ~: 500
N
kN
= −
−
(
)
400 ~: 800
y
M
kNm
= ±
±
(
)
400 ~: 800
z
M
kNm
= ±
±
(
)
1.2, ~:1.4
pos
h
m
=
0.6
st
h
m
=
(
)
3
18 ~: 21
/
gr
kN m
ρ
=
3
25
/
bet
kN m
ρ
=
PRZYKŁAD
Dane:
400
N
kN
= −
500
y
M
kNm
= +
600
z
M
kNm
= −
1.1
pos
h
m
=
0.6
st
h
m
=
3
18
/
gr
kN m
ρ
=
3
25
/
bet
kN m
ρ
=
Szukane: wymiary fundamentu B,H
przyj
ę
to wst
ę
pne wymiary stopy:
4
B
m
=
3
H
m
=
Obliczenie całkowitej siły działaj
ą
cej na stop
ę
(
)
x
gr
bet
gr
pos
st
bet
st
N
N
G
G
N
B H
h
h
B H h
ρ
ρ
= −
−
= −
⋅ ⋅
−
−
⋅ ⋅
(
)
400 18 1.1 0.6 3 4 25 3 4 0.6
688
x
N
kN
= −
−
−
⋅ − ⋅ ⋅ ⋅
= −
Obliczenie charakterystyk geometrycznych przekroju stopy:
F
B H
= ⋅
3
12
y
BH
J
=
3
12
z
B H
J
=
Poło
ż
enie osi oboj
ę
tnej
y
x
z
x
y
z
M
N
M
z
y
F
J
J
σ
=
+
−
3
3
668
500
600
4 3
3 4
12
12
12
x
z
y
σ
−
−
=
+
−
⋅
⋅
688
500
600
0
12
9
16
z
y
−
−
=
+
−

0.654
1.032
z
y
= −
+
Równanie prostej równoległej do osi oboj
ę
tnej przechodz
ą
cej przez wierzchołek (B/2,
H/2)
Po wrysowaniu zobaczy
ć
który to wierzchołek czy ma dodatnie współrz
ę
dne czy
ujemne
Wyraz wolny w postaci kierunkowej c rzutowany na prost
ą
prostopadła do osi oboj
ę
tnej
daje d
Oraz wyraz wolny rzutowany tak samo daje d1
d1-d< (1/2 )d1 ???? je
ś
li nie to powi
ę
kszy
ć
fundament
Wrysowa
ć
i sprawdzi
ć
warunek


*******************************
Wyszukiwarka
Podobne podstrony:
Mimośrodkowe rozciąganie pręta
Mimośrodowe Rozciąganie
mimosrodowe rozciaganie, MIMOŚRODOWE ROZCIĄGANIE
Mimośrodkowe rozciąganie pręta przykład
wytrzymka laborki, 5 Badanie rozkładu naprężeń w przekroju poprzecznym mimośrodowo rozciąganego pręt
14 Mimosrodowe rozciaganie i sciskanie
Mimośrodowe rozciąganie
druk dyik, Mimośrodowe rozciąganie lub ściskanie jest to taki przypadek obciążenia przyłożonego do ś
mimosrodowe rozciaganie
Mimośrodkowe rozciąganie pręta
Mimośrodowe rozciąganie
7 Rozciąganie , Ścinanie mimośrodowe
Rozciaganie Sciskanie mimosrodowe
więcej podobnych podstron