1. Mimośrodowe rozciąganie lub ściskanie jest to taki przypadek obciążenia przyłożonego do ścianek czołowych pręta prostego, pryzmatycznego, o dowolnym litym przekroju poprzecznym, które na obu końcach pręta redukuje się do siły równoległej do osi pręta, ale nie leżącej na tej osi
W przypadku połączeń mimośrodowych pojedynczych prętów rozciąganych można je traktować jako osiowe pod warunkiem, że do obliczeń przyjmuje się sprowadzone pole przekroju:
![]()
A1 - pole części przylgowej kątownika brutto lub netto
A2 - pole przekroju części odstającej
w przypadku sprawdzania stanu granicznego pręta rozc. mimośrodowo
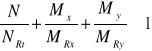
mimośrodowe rozc. elementów mocowanych za pomocą nitów lub śrub, czyli osłabionych na otwory:
![]()
σ' - naprężenia średnie dla przekroju brutto
Δσ - naprężenia rozc. max od zginania elementu przekroju netto
AtΨ - pole sprowadzone rozc. strefy przekroju
![]()
Re - granica plastyczności
An - najmniejsze pole płaskiego lub łamanego przekroju netto
Elementy ściskane
-pręt, w którym wypadkowa sił ściskających działa wzdłuż jego osi lub też w płaszczyźnie równoległej do jego osi (mimośrodowo).
Wymiarowanie elem. ścisk. wymaga sprawdzenia wytrzymałości i stateczności.
![]()
le - odległość wyboczenia
i - min. promień bezwładności przekroju poprzecznego
Nie uwzględniamy wyboczenia gdy:
![]()
WYBOCZENIE zjawisko gwaltownego przejscia od jednej postaci deformacji /osiowego sciskania preta do jakosciowo innej postaci deformacji zginania. Zjawisko to podowuje gwałtowną redystrybucję sił wewnętrzych przez co jest niebezpoieczne dla konstrukcji. Teoretycznie gdy pret jest idealnie symetryczny a siła ściskająca idealnie osiowa i centryczna, istnieje dokladnie jeden stan deformacji w którym jest zachowana równowaga. Jeśli uwzglednia się wpływ ugięcia to możliwe jest 2 rozwiazanie - kiedy siła ściskająca osiąga pewną wartość zwaną siła krytyczną Pkr. Przy wyznaczaniu siły krytycznej dla pręt posiadającego krzywiznę początkową można posłużyć się sposobem przybliżonym zakładając , że początkowa linia ugięcia ma kształt sinusoidalny, która nie zmienia się także po przyłozeniu silz osiowej P. Metoda southwella 12. metoda SOUTHWELLA.
Zależność (15) δ =f(P)) jest zależnością hiperboliczną przedstawioną na rysunku
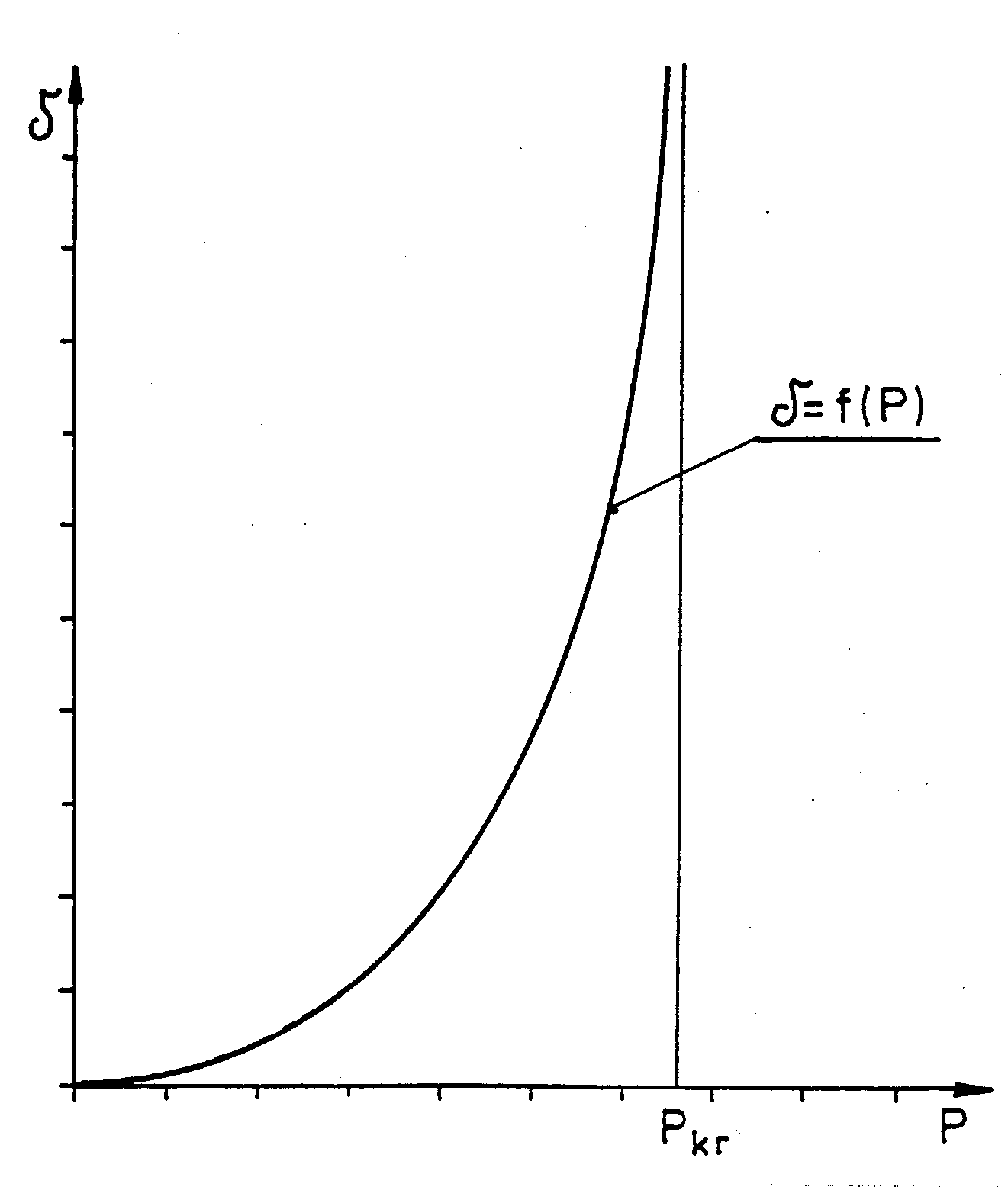
Wykres zależności δ =f(P) dla pręta zamocowanego .
Sporządzając taki wykres możemy odczytać wartość siły krytycznej wyboczenia giętego jako pionową asymptatę krzywej δ = f(P).
Zależność (15) można przedstawić po przekształceniu w postaci: ![]()
Wyznaczenie siły krytycznej z powyższego wzoru nazywane jest metodą SOUTHWELLA.
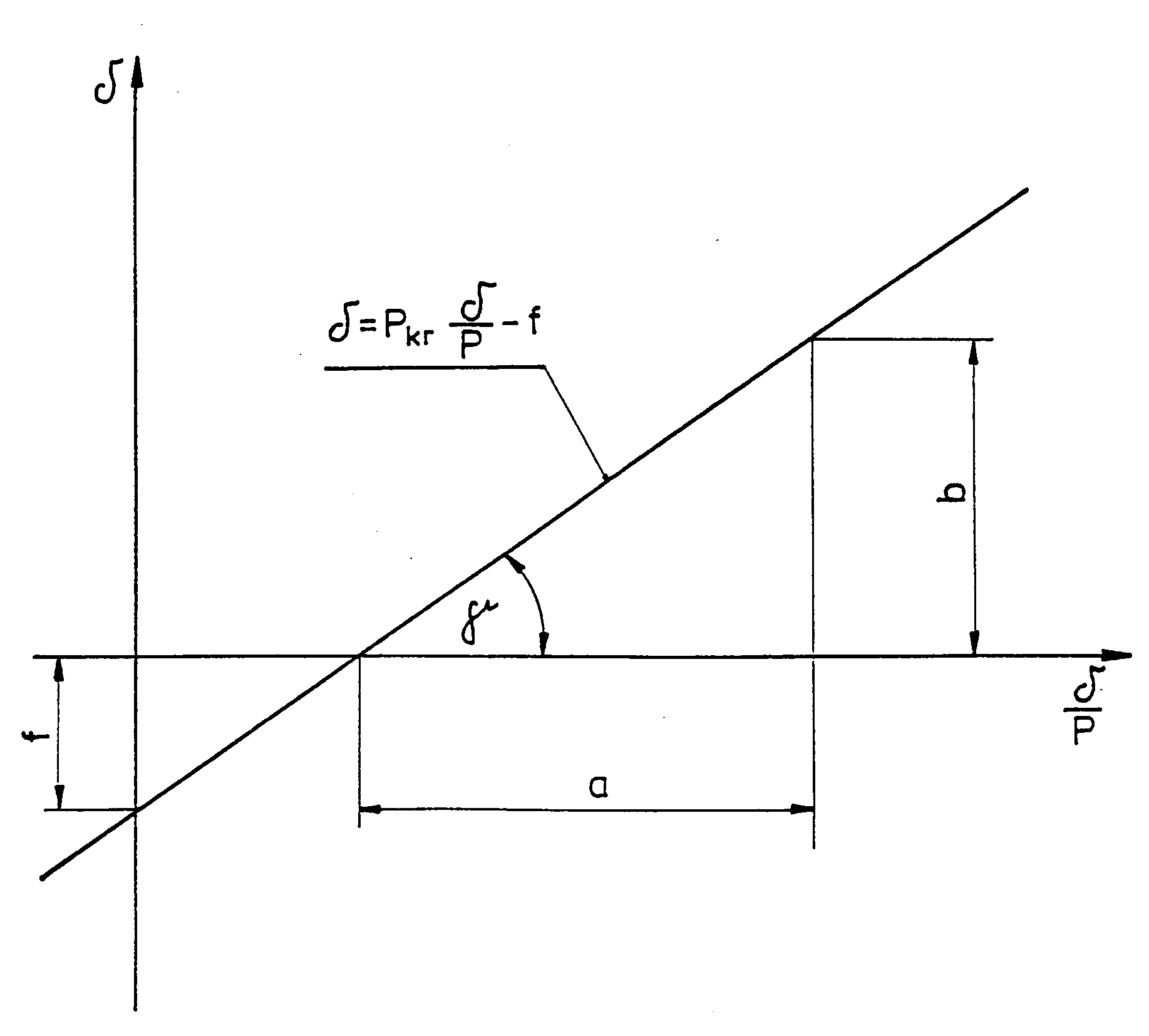
W powyższym wzorze zależność ![]()
jest zależnością liniową o pewnym współczynniku kierunkowym jak to pokazuje rysunek
2. Naprężenie krytyczne odpowiadające sile Eulera:
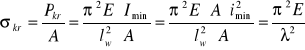
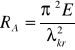
![]()
3. Zginanie jednokierunkowe belek
-konieczne sprawdzenie wytrzymałości pręta zginanego, jego stateczności ogólnej (zwichrzenia), stateczności miejscowej (miejscowe wyburzenie się ścianki) oraz dodatkowo sztywności (ugięcia belki)
![]()
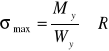
M - moment zginający
Iz - moment bezwładności
W - wskaźnik wytrzymałości przekroju przy zginaniu
Podstawowy, normowy warunek wytrzymałości belki zginanej w jednej płaszczyźnie
![]()
4. Kratownice
Prety kratownicy wskutek dzialania sil osiowych doznaja odksztalcenia a wezly przemieszczenia. Material z którego sa wykonane prety podlega prawu Hooke'a. Wplyw na przemieszcenie wezlow maja wewnetrzne sily osiowe, czyli pod wplywem obciazenia zewnetrznego kratownica doznaje odksztalcen w wyniku którego wezly ulegaja przemieszczeniom obrotowym. W pretach powstaja również momenty gnace i sily poprzeczne które wywoluja naprezenia normalne i styczne. Sily osiowe i momenty gnace wywoluja niejednorodny stan naprezenia.
Zasady obliczania kratownic
Kratownice płaskie oblicza się przyjmując założenia:
1.Pręty połączone są w węzłach przegubowych h/l<=1/12 (wpływ sztywności pomija się)
h- wysokość przekroju pręta w płaszczyźnie kraty
l - długość pręta
2.Pręty są wyłącznie proste
3.Osie prętów przechodzące przez środki ciężkości tych prętów pokrywają się z zarysem geometrycznym kratownicy (siły w węzłach muszą być w równowadze)
4.Pręty połączone są w węzłach współśrodkowo tj osie ciężkości przecinają się w jednym pktcie. Nie przestrzeganie tego warunku powoduje powstanie w węźle dodatkowego momentu.
5.Pręty kratownicy leżą w jednej płaszczyźnie.
Sztywność kratownic
Ugięcie kratownicy można obliczyć ze wzoru określającego przemieszczenie węzła kratownicy:
![]()
Ni - siła w pręcie i wywołana obciążeniem zewn.
N1i - siła w pręcie i wywołana obciążeniem P=1 przyłożonym w węźle
l -rozpiętość kratownicy
5. Graniczne przemieszczenia (ugięcia) poziome
Graniczne ugięcia (przemieszczenia poziome) elementów stalowych budowli nie powinny przekraczać:
1) ram parterowych bez suwnic - h/150,
2) ram parterowych przy obudowie wrażliwej na pękanie - h/250, gdzie:
h -wysokość słupa ramy,
3) ram wielokondygnacyjnych - hi/500, gdzie:
hi -wysokość mierzona od górnego poziomu fundamentu do poziomu rygla (stropu) sprawdzanej kondygnacji.
Zginanie dwukierunkowe
6. Mostek Wheatstone'a
znając wartości rezystancji R2, R3 i R4 można dokładnie wyznaczyć nieznaną wartość rezystancji Rx.
Czułość mostka Sm zależy od napięcia wejściowego (zasilającego) Uwe oraz zmiany wartości rezystancji R2:
Jest on zbudowany z czterech rezystorów tworzących ramiona mostka. W jedną z jego przekątnych włączone jest źródło napięcia stałego zasilające mostek. Tą przekątną mostka nazywamy przekątną zasilania
Warunkiem uzyskania równowagi mostka Wheatstone'a jest spełnienie warunku
R1*R4=R2*R3
7. TENSOMETRia: punktowa metoda pomiarów odkształceń materiału badanej konstrukcji, pozwalająca na wyznczenie odkształceń wybranych punktów powierzchni obiektu za pomocą tensometrów przyklejnoych w tych punktach.
-rezystencyjne R=f(Wnepsilon) np odksztalcenia w betonie
-indukcyjne L=f(Wnepslion) do pomiaru odksztalcen i przemieszczen
- pomiarowe C=f(WNEPsilon) pojemnosc zalezy o odksztalcenia
8. REZYSTENCJA:
Czyli opor przewodu:
R=ρ*(l/S)
Gdzie
l-dlugosc przewodu
s-pole przekroju
ρ-opor wlasciwy
9. WSPOLCZYNNIK CZULOSCI TENSOMETRU:
K
Zalezy od materialu z jakiego wykonany jest drut
ΔR/R=K*(Δl / l)
10. OS OBOJETNA
Rozkład naprężeń przy zginaniu w płaszczyźnie xz
Rozkład naprężeń w przekroju poprzecznym nie zależy od współrzędnej y, czyli dla wszystkich włókien o tej samej współrzędnej z naprężenia normalne mają tą samą wartość. Rozkład naprężeń jest funkcją liniową, maksymalne naprężenia występują w skrajnych
włóknach przekroju, natomiast we włóknach leżących na osi y naprężenia te są równe zeru. Oś y nazywa się z tego powodu osią obojętną przy zginaniu. Rozkład naprężeń przy zginaniu pręta momentem My
Ponieważ rozciąganiu przypisujemy znak "+", zatem naprężenia w punktach leżących powyżej osi obojętnej będą dodatnie a zwrot wektorów naprężenia narysujemy zgodnie z normalną zewnętrzną przekroju
11. METODY WYZNACZENIA LINII UGIECIA BELEK
1-metoda analityczna
jest na calej dlugosci belki
EJ(d²y/dx²)=Mg
EJ(dy/dx)=Mg+c=>Ø
Ejy=Mg+Cx+D=>f
Y=f(x)
2-metoda wykreslno-analityczna
stosujemy gdy ineresuja nas ugiecia i katy w poszczegolnych przekrojach belki
Wykres momentow staje się obciazeniem wtornym dla belki fikcyjnej(M=qf)
Momenty zginajace w belce fikcyjnej odp.wtedy ugieciom belki rzeczywistej pomnozonym przez sztywnosc belki(Mf=Ejy) a sily tnące = katom nachylenia stycznych przechodzacych przez sztywnosc
(Tf=EJØ) i Cf=C i Df=D
3.METODY ENERGETYCZNE
A)TW CASTIGLIANO:
dL=dV=δL/δP
b) całka MAXWELLA MOHRA
bierzemy pod uwage ta czesc energii która pochodzi od zginania
V=∫(Mg²dx/2EJ)
C) ZASADA WERESZCZAGINA
U=1/EJ * Ωys
12. metoda SOUTHWELLA.
Zależność (15) δ =f(P)) jest zależnością hiperboliczną przedstawioną na rysunku
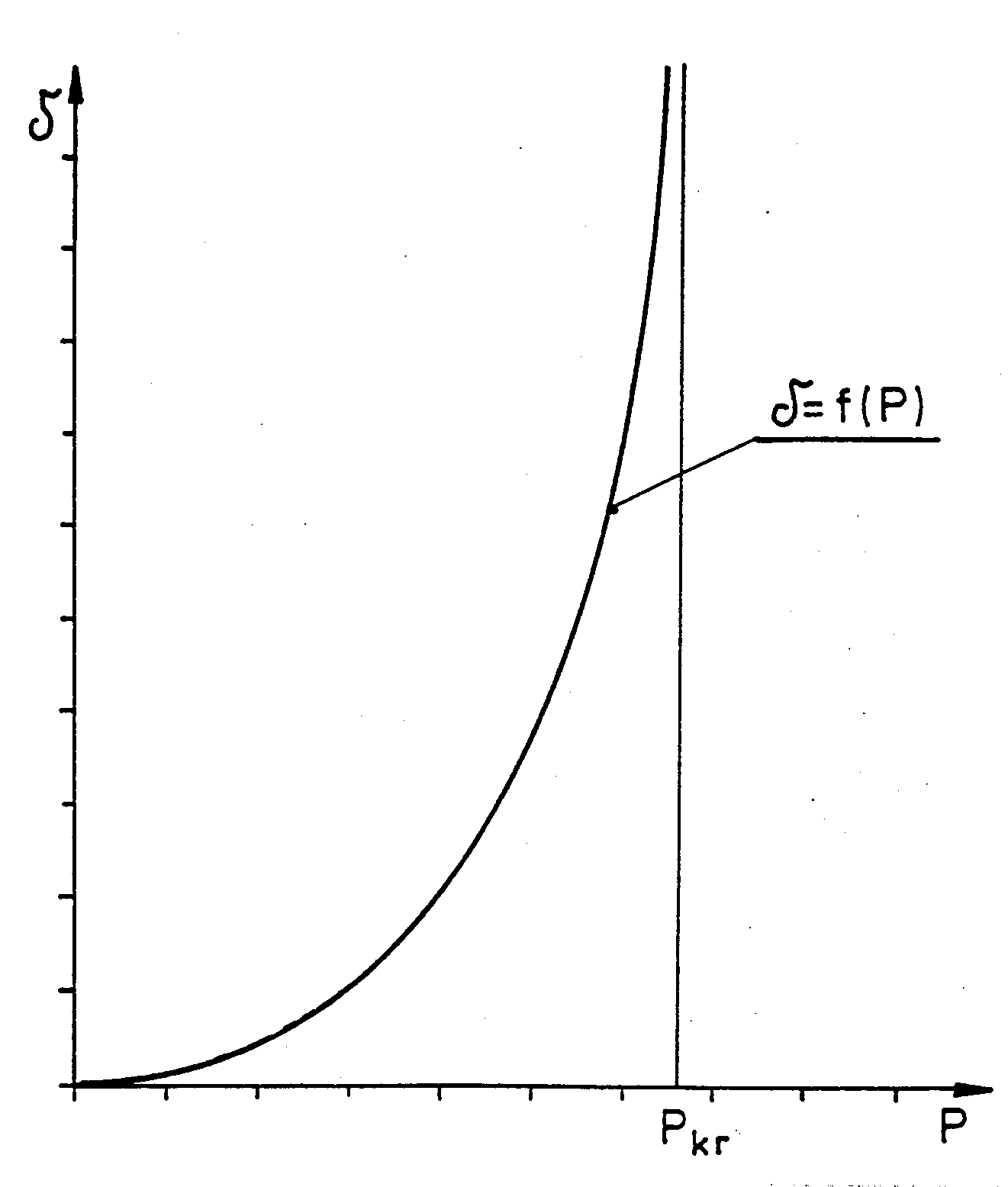
Wykres zależności δ =f(P) dla pręta zamocowanego .
Sporządzając taki wykres możemy odczytać wartość siły krytycznej wyboczenia giętego jako pionową asymptatę krzywej δ = f(P).
Zależność (15) można przedstawić po przekształceniu w postaci: ![]()
Wyznaczenie siły krytycznej z powyższego wzoru nazywane jest metodą SOUTHWELLA.
W powyższym wzorze zależność ![]()
jest zależnością liniową o pewnym współczynniku kierunkowym jak to pokazuje rysunek
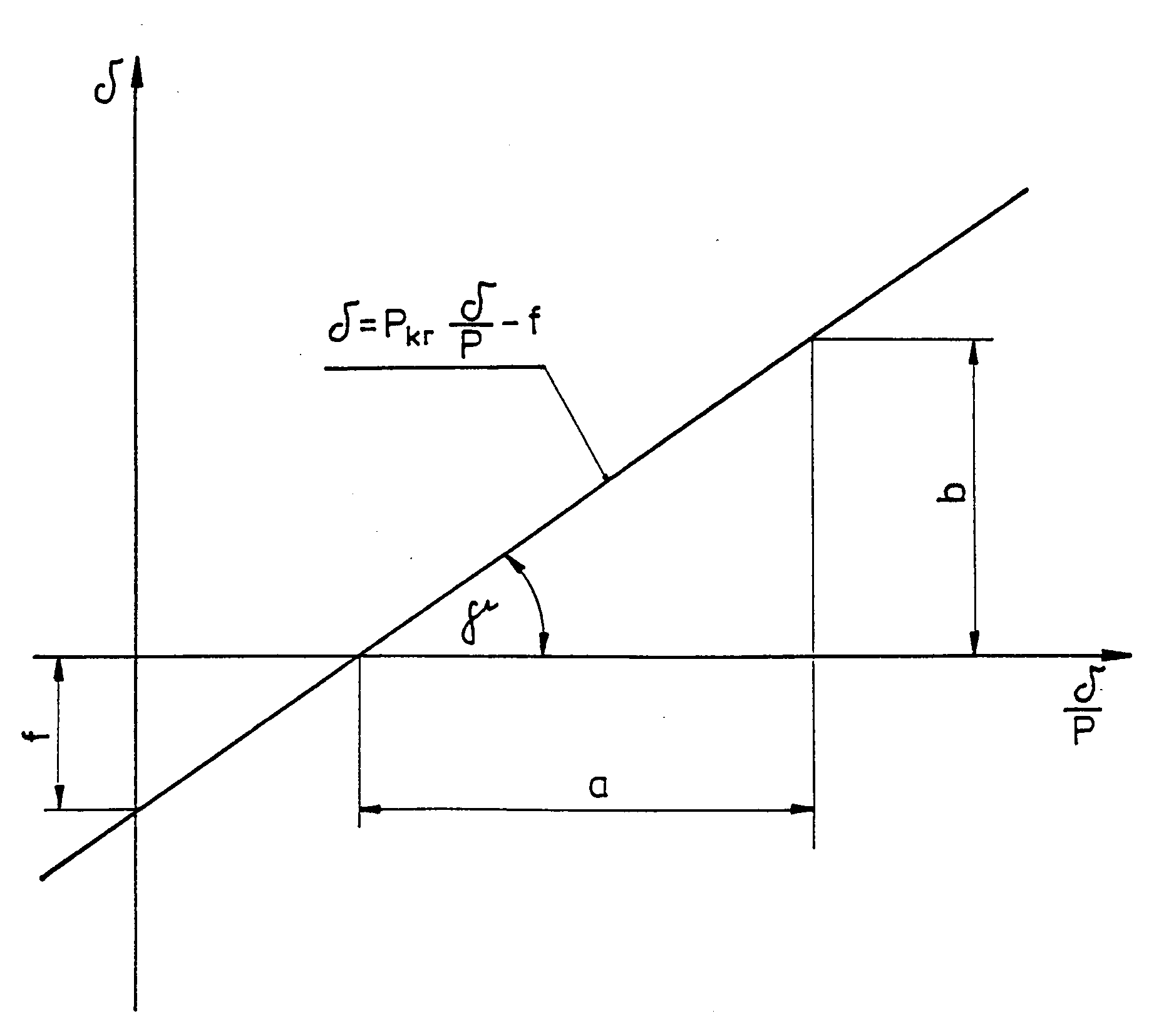
13.
Środek ścinania to punkt przez który powinna przechodzić siła poprzeczna T, aby w płaszczyźnie przekroju nie występowało ścinanie.
Teoretyczny środek ścinania wyznaczamy
przyrównując do zera sumy momentów wszystkich sił względem szukanego środka ścinania
oznaczonego przez S co daje równanie:
∑Mis=0 ⇒ T1(h-t)^2 - T2 e = 0
po uwzględnieniu że T2 = T wyznaczymy
teoretyczne położenie środka ścinania dla ceownika:
K1 Wyznaczenie rzeczywistych sił wewn. wyst. W przekrojach prętów konstrukcji kratowej Pręty kratownic wskutek działania w nich sił osiowych doznają odkształceń, a węzły przemieszczeń. Odkształcenia prętów przyjmowane są jako bardzo małe w stosunku do wymiarów geometrycznych kratownicy, stąd przyjęto jako zasadne prawo zesztywnienia określające, że obciążenia działają na kratownicę już odkształconą w ten sposób jak i przed odkształceniem. Materiał z którego wykonane są pręty kratownicy podlega prawu Hooke'a, zaś odkształcenia są liniowymi funkcjami obciążeń. Struktura prętowa spełniająca powyższe założenia stanowi idealny ustrój kratowy.
Założenia idealizujące strukturę prętową bardzo ułatwiają wprawdzie obliczenia statyczne lecz jednocześnie odbiegają od rzeczywistego charakteru pracy ustroju. Najbardziej odbiega od rzeczywistości założenie idealnych beztarciowych przegubów, które nigdy nie jest spełnione. Pręty bowiem połączone w węzłach za pomocą nitów, spoin lub śrub nie zapewniają beztarciowego systemu połączenia, lecz nadają mu charakter połączenia sztywnego lub sprężystego. Innymi słowy rzeczywisty charakter pracy kratownicy zbliżony jest do ustroju ramowego, w którym istotny wpływ na przemieszczenie węzłów mają wewnętrzne siły osiowe. W rzeczywistości pod wpływem obciążenia zewnętrznego kratownica doznaje odkształcenia w wyniku którego węzły ulegają przemieszczeniom obrotowym.
W prętach struktury kratownicy powstają zatem oprócz sił osiowych momenty gnące i siły poprzeczne, które wywołują naprężenia normalne i styczne. Naprężenia te w stosunku do naprężeń podstawowych (pierwszorzędnych) określanych dla idealnego ustroju kratowego (normalnych od wewnętrznych sił osiowych) noszą nazwę naprężeń drugorzędnych. Im większa sztywność węzła tym większy jego odpór sprężysty, a tym samym większy współczynnik sprężystego bądź w pełni sztywnego zamocowania prętu w węźle.
Przyjmując , że o wytężeniu prętów konstrukcji kratowych decyduje wartość sił osiowych i momentów gnących, które w przekrojach prętów wywołują niejednorodny osiowy stan naprężenia (mimośrodowe ściskane lub rozciągane) to dla opisu tak ukształtowanej płaszczyzny stanu naprężenia, która jest nachylona do płaszczyzny przekroju, wystarczy znać położenia trzech punktów na tej płaszczyźnie (wartości naprężeń) które jednoznacznie ją opisują.
Poniżej podano znane wzory określające dla omawianego przypadku wartości naprężeń w funkcji siły osiowej i składowych momentów gnących przedstawionych na rysunku
Siły wewnętrzne w przekroju kątowym pręta kratownicy.
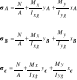
gdzie:
N, Mx, My - odpowiednie wartości siły osiowej momentu gnącego Mx ( w płaszczyźnie głównej), My ( w płaszczyźnie głównej yz),
σA,, σB, σC - wartości naprężeń w badanych punktach A, B, C,
Ixg, Iyg - główne centralne momenty bezwładności,
A - pole przekroju pręta,
E - moduł Younga,
xA,B,C, yA,B,C - współrzędne punktów naklejenia tensometrów naprężno oporowych w odniesieniu do głównych centralnych osi bezwładności, przekroju pręta.
Rozwiązując układ równań (1) względem sił wewnętrznych N, Mx, My otrzymano:
![]()
![]()
![]()
gdzie:
σA, σB, σC- naprężenia w badanych punktach,
XA, XB, XC, - YA, YB, YC- współrzędne punktów naklejenia tensometrów w odniesieniu do osi głównych przekroju w cm,JXg, JYg- główne centralne momentu bezwładności w cm4,
A- przekrój kątownika w cm2.
2.Eksperymentalne wyznaczenie sił wewnętrznych.
Celem przeprowadzenia eksperymentu wykonano kratę złożoną z kątowników równoramiennych połączonych z blachami węzłowymi przy pomocy śrub. Schemat prętowy pokazuje rysunek 2.
Schemat prętowy kratownicy z lokalizacją przekrojów pomiarowych.
Celem obliczenia składowych sił wewnętrznych wykorzystano tensometrię naprężno - oporową. Pomiary naprężeń w punktach A B C o współrzędnych jak na rysunku 3 pozwolą na określenie sił wewnętrznych (N, Mx, My) z równań (2). Pomiary należy wykonać w układzie ćwierć mostka (czujnik czynny + czujnik kompensacyjny).
Opis współrzędnych punktów naklejenia tensometrów naprężno - oporowych odniesionych do głównych centralnych osi bezwładności przekroju.
Po dokonaniu pomiarów naprężeń w trzech punktach i wyznaczeniu sił wewnętrznych można przeprowadzić analizę wyników w stosunku do kraty o idealnych węzłach, które momentów nie przenoszą - występują tylko siły osiowe. Siły w prętach kraty na której wykonywane były pomiary wynoszą odpowiednio:
![]()
; N2 = P
(momenty zginające są równe zero).
K2 Wyzn.siły krytycznej pręta o przekroju prostokątnym posiadającego krzywiznę początkową Elementy prętowe są nieodzownymi częściami konstrukcji stalowych, którymi mogą być kraty płaskie i przestrzenne, słupy, belki itp. W zależności od przekroju pręta i sposobu jego zamocowania wyboczenie może występować w obu płaszczyznach głównych a możemy mieć do czynienia także z wyboczeniem skrętnym. Rozwiązując odpowiednie równania różniczkowe prętów o dowolnych warunkach podparcia ściskanych siłą osiową P, można wyznaczyć najmniejsze wartości obciążeń Px, Py, Pϕ, które nazwane są siłami krytycznymi [ ] a można je wyznaczyć ze wzorów:
![]()
,![]()
, ![]()
gdzie: l - długość pręta,
μx, μy,μϕ - współczynniki długości wyboczeniowej zależne od warunków podparcia, Ix, Iy, Iω, It - momenty bezwładności względem osi oraz wycinkowy i czystego skręcania. E, G - moduły sprężystości podłużnej i poprzecznej.
Wartość naprężenia krytycznego określa się ze wzoru: ![]()
W powyższym wzorze ς = x,y, ϕ. λς - smukłość pręta w zależności od analizowanego wyboczenia, którą określa się:
![]()
, ![]()
![]()
gdzie: ix, iy - promienie bezwładności.
Współczynniki długości wyboczeniowej w zależności od rodzaju podparcia przyjmuje się:
- przegubowe podparcie obu końcówμ = 1- utwierdzenie obu końców μ = 0,5- jeden koniec utwierdzony, drugi wolny μ = 2,0
jeden koniec utwierdzony, drugi przegubowy μ = 0,7.
2. Doświadczalne wyznaczanie siły krytycznej metodami przybliżonymi.
Celem ćwiczenia jest określenie siły krytycznej w kierunku mniejszej sztywności zginania EJmin podpartego przegubowo na obu końcach. Siłę krytyczną będziemy wyznaczać teoretycznie i doświadczalnie. Ponieważ wyznaczenie siły krytycznej dla prętów rzeczywistych jest trudne do zrealizowania (niemożliwość wykonania idealnego pręta) dlatego posługujemy się metodami pośrednimi. Analizowany pręt posiada krzywiznę początkową co pokazuje rysunek 1.
Schemat pręta z krzywizną początkową.
Przy wyznaczaniu siły krytycznej dla pręta posiadającego krzywiznę początkową można posłużyć się sposobem przybliżonym. Zakładamy , że początkowa linia ugięcia ma kształt sinusoidalny: ![]()
,
która nie zmienia się także po przyłożeniu siły osiowej P:
![]()
Będziemy rozpatrywać ugięcia w środku pręta gdzie:![]()
Różniczkowe równanie linii ugięcia dla stanu początkowego:![]()
gdzie: M(z)- zastępczy moment, który powoduje ugięcie początkowe f.
Gdy przyłożymy siłę osiową P równanie różniczkowe linii ugięcia możemy zapisać:
![]()
![]()
a po zróżniczkowaniu:
![]()
Po podstawieniu ![]()
oraz fp= f +δ ![]()
gdzie: f - ugięcie początkowe w środku pręta, δ - ugięcie od siły osiowej P, Pkr - Eulerowska siła krytyczna dla wyboczenia sprężystego.
Zależność (15) δ =f(P)) jest zależnością hiperboliczną przedstawioną na rysunku 2.
Wykres zależności δ =f(P) dla pręta zamocowanego
Sporządzając taki wykres możemy odczytać wartość siły krytycznej wyboczenia giętego jako pionową asymptatę krzywej δ = f(P).
Zależność (15) można przedstawić po przekształceniu w postaci:
![]()
Wyznaczenie siły krytycznej z powyższego wzoru nazywane jest metodą SOUTHWELLA.
W powyższym wzorze zależność ![]()
jest zależnością liniową o pewnym współczynniku kierunkowym jak to pokazuje rysunek 3.
Wykres zależności ![]()
dla pręta zamocowanego jak na rysunku 1.
Aby wyznaczyć siłę krytyczną wyboczenia giętego Pkr należy sporządzić wykres ![]()
a współczynnik kierunkowy jest jej wartością:![]()
Schemat stanowiska pomiarowego z zamocowanym prętem o przekroju prostokątnym do wyznaczania eksperymentalnej siły krytycznej pokazuje rys. 4.
Schemat stanowiska pomiarowego: 1- maszyna wytrzymałościowa, 2 - pręt ściskany, 3 - czujnik zegarowy.
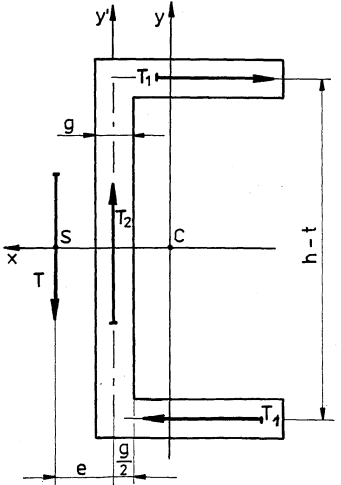
K3 Wyzn.położenia środka ścinania dla pręta cienkościennego Stan naprężenia w zginanej belce cienkościennej to naprężenia normalne od zginania a także naprężenia styczne, które występują w dwóch kierunkach jak to pokazuje rysunek 1.
Rozkład naprężeń stycznych τzy i τzx na przekroju ceownika..
Rozpatrujemy belkę wspornikową zginaną w jednej płaszczyźnie siłą P. Wartość naprężeń stycznych τzy obliczmy ze wzoru:![]()
gdzie: T - siła poprzeczna,
![]()
- moment statyczny części odciętej, b(y) - szerokość przekroju w miejscu wyznaczenia naprężeń, Ix - osiowy moment bezwładności przekroju.
Występujące naprężenia styczne τzx wyznaczamy ze wzoru:![]()
τzx= ![]()
gdzie: h - wysokość przekroju ceownika, t - grubość półki ceownika, x - zmienna po szerokości półki od 0 do S-g.
Z podanych powyżej wzorów na naprężenia styczne naprężenia styczne τzy i τzx można wyznaczyć siły wypadkowe, które je zastępują. Wypadkową siłę T1 określamy przez całkowanie:
![]()
Siła wypadkowa T2 pochodząca od naprężeń τzy dla prętów cienkościennych, jest równa sile poprzecznej T2≅ T. Wypadkowe siły styczne, które działają w przekroju cienkościennego ceownika przedstawiono na rysunku 2.
Wypadkowe siły styczne pochodzące od naprężeń stycznych.
Aby w płaszczyźnie przekroju nie występowało skręcanie, siła poprzeczna T winna pochodzić przez punkt nazwany środkiem ścinania. Teoretyczny środek ścinania wyznaczamy przyrównując do zera sumy momentów wszystkich sił względem szukanego środka ścinania oznaczonego przez S co daje równanie:
![]()
T1 (h-t)2 - T2 e = 0
Z równania (4) po podstawieniu (3) i uwzględnieniu że T2 = T wyznaczymy teoretyczne położenie środka ścinania dla ceownika: ![]()
2. Eksperymentalne wyznaczenie środka ścinania dla cienkościennego ceownika stanowiącego belkę wspornikową.
Ceowniki cienkościenne to profile w których stosunek wysokości i szerokości do grubości jest większy od dziesięciu. Do eksperymentu przyjęto ceownik zimno gięty o wysokości 50mm, szerokości 30mm i grubości ścianki 3mm. Doświadczalnie środek ścinania wyznaczamy poszukując takiego położenia siły obciążającej P przy którym nie będzie skręcania. Schemat stanowiska do eksperymentalnego wyznaczania środka ścinania pokazuje rysunek 3.
Schemat stanowiska do eksperymentalnego wyznaczenia środka ścinania: 1- belka cienkościenna, 2- listwa pomiarowa, 3- czujniki zegarowe, 4 - obciążenie belki.
Obciążając belkę siłą P przemieszczającą się po listwie pomiarowej odczytujemy wskazania czujników zegarowych wskazujących pionowe przemieszczenia listwy. Można znaleźć takie położenie siły P dla którego wskazania obu czujników będzie takie same, to położenie będzie środkiem ścinania. Można także położenie środka ścinania wyznaczyć metodą pośrednią wyznaczając kąt skręcenia belki z poniższego wzoru:
![]()
gdzie: ypi - wskazania czujnika prawego, yli - wskazania czujnika lewego,
a - odległość między czujnikami.
Kąt skręcenia jest funkcją położenia obciążenia xi.
Dla kilku położeń xi obliczamy kąt ϕi i sporządzamy wykres ϕi=ƒ(xi) jak to pokazuje rysunek 4. Otrzymane wyniki aproksymujemy prostą . Położenie środka ścinania wyznacza przecięcie prostej z osią poziomą xi
Zależność kąta skręcenia od położenia obciążenia.
K4 Pomiar ugięć belki o przekroju dwuteowym Ugięcia belek są wynikiem działania obciążeń zewnętrznych. Ugięcie definiuje się jako odległość między odkształconą a nieodkształconą osią belki mierzoną prostopadle do nieodkształconej osi belki. Wartość maksymalnego ugięcia nazywamy strzałką ugięcia, którą to wielkość wykorzystuje się do wymiarowania belek z warunku sztywności. Informacją o rzeczywistym zachowaniu się konstrukcji jest znajomość ugięć belki w różnych jej punktach, którą można uzyskać przez ich pomiar.
Do pomiaru ugięć elementów konstrukcji belkowych czy kratowych stosuje się różne techniki i przyrządy pomiarowe. W pomiarach ugięć stosuje się najczęściej czujniki przemieszczeń. Mogą to być czujniki zegarowe, indukcyjne, czujniki w których do pomiaru przemieszczeń wykorzystano tensometry rezystancyjne oraz metody bezkontaktowe do których zaliczmy metodę interferencji siatek rastorowych (metoda mory) i metodę holograficzną w której wykorzystano interferometrię plankową..
Do wyznaczania ugięć badanej belki wykorzystamy metodę analityczną, metodę obciążeń wtórnych, a do pomiaru na stanowisku pomiarowym wykorzystane będą indukcyjne czujniki przemieszczeń. Schemat belki pomiarowej pokazuje rysunek 1. Belka będzie obciążona siłą skupioną P przyłożoną w dowolnej odległości od podpory A. Do wyznaczenia ugięć w dowolnym punkcie i wyznaczenie maksymalnego ugięcia między podporami posłużymy się metodą analityczną a ugięcie swobodnego końca obliczymy metodą obciążeń wtórnych.
Schemat analizowanej belki.
W metodzie analitycznej ugięcie wyznaczamy przez dwukrotnie całkowanie przybliżonego równania linii ugięcia, które ma postać:![]()
Po rozwiązaniu równania (1) ze względu na y i wyznaczenie stałych całkowania z warunków brzegowych i ciągłości otrzymujemy wzory na ugięcie w dowolnym przekroju belki:
- w przedziale AD
![]()
- w przedziale DB
![]()
W tym przedziale wystąpi ekstremum ugięcia a zachodzi to w punkcie, w którym kąt obrotu y2' jest równy zero.
Zatem gdy ![]()
.
Obliczając ugięcie w odległości z0 otrzymamy maksymalne ugięcie które wyniesie:
![]()
Ugięcie swobodnego końca yc wyznaczamy metodą obciążeń wtórnych jak to pokazuje rysunek 2. Wartość ugięcia i kąta obrotu wyznaczamy:
![]()
![]()
gdzie: ![]()
- moment wtórny i siła poprzeczna wtórna w punkcie w którym liczymy ugięcie i kąt obrotu, E J - sztywność zginania.
Rys. 2. Schemat obliczania ugięć metodą obciążeń wtórnych: a-schemat belki rzeczywistej,
b-belka wtórna obciążona wykresem momentów gnących belki rzeczywistej,
c - schemat wyznaczania sił i momentów wtórnych.
Aby wyznaczyć ugięcie w punkcie C należy na podstawie rysunku 2 wyznaczyć wartość momentu wtórnego ![]()
korzystając z równań statyki. Obliczmy kolejno:
- wtórne siły
skupione![]()
- reakcję wtórną w punkcie ![]()
![]()
![]()
- moment wtórny w punkcie ![]()
![]()
![]()
Ostatecznie ugięcie w punkcie C wynosi:![]()
2. Doświadczalne wyznaczenie ugięcia na stanowisku pomiarowym.
Do badań doświadczalnych użyto belki wykonanej z dwuteownika 140, która została poddana zginaniu na maszynie wytrzymałościowej. Schemat stanowiska pomiarowego pokazuje rysunek 3. Do pomiaru ugięć zastosowano czujniki indukcyjne i zegarowe.
Rys. 3. Schemat belki pomiarowej: 1- maszyna wytrzymałościowa, 2 - belka dwuteowa, 3 - czujnik indukcyjny.
Wyszukiwarka
Podobne podstrony:
Wytrzymalosc Materialow Zbigniew Brzoska Rozdzial 2 Rozciaganie lub sciskanie
Teoria polityki, Władza polityczna, Władza polityczna- jest to taki rodzaj władzy, który występuje w
Dojrzałość szkolna jest to taki poziom rozwoju dziecka, cośki
Ruch postępowy bryły sztywnej jest to taki ruch, Fizyka
25 123805 Eurologistyka projekt , Eurologistyka jest to taki system połączonych ze sobą firm, w któr
20031014194918, Motywacja jest to psychologiczny stan przyczyniający się do stopnia, w jakim człowie
mikro gotowe, Drobnoustroje - nie jest to pojęcie systematyczne, jest to pewna grupa organizmów nale
BILANS, BILANS CIEPLY, Bilans cieplny silnika jest to zestawienie rozdziału ciepła dostarczonego do
mikrobiologia mala, Drobnoustroje - nie jest to pojęcie systematyczne, jest to pewna grupa organizmó
Folia Poj cia, definicje, Pojęcie jest to opisana za pomocą określonego słowa (lub zestawu słów) tre
Podatki (25 stron) , PODATEK według encyklopedii PWN jest to świadczenia pieniężne na rzecz państwa
Logika [ ściąga prof. P.Gabrielem], logika, Znak - jest to dostrzegalny układ rzeczy lub zjawisko st
Referaty, CZYTELNICTWO, Wydawnictwo zwarte-jest to dzieło stanowione zamkniętą całość, jedna lub wie
14 Mimosrodowe rozciaganie i sciskanie
PODSTAWY PRAWA, Podstawy Prawa2, Prawo - jest to zespół norm postępowania ustanowionych lub przyjęty
fiyka, Tarcie jest to siła działająca na ciało przesuwane lub toczone po pewnej powierzchni
logika 1 zm , Nazwa- jest to wyrażenie, które w dowolnym zdaniu podmiotowo- orzecznikowym nadaje się
gleba 2, FRAKCJA GRANULOMETRYCZNA -jest to zgrupowanie cz˙stek gleby wed˙ug ich rozmiar˙w lub ˙redni
NORMA ADAPTACYJNA POPULACJI jest to mniej lub bardziej trwały kompleks zmienności genetycznych dosto
więcej podobnych podstron