MIMOŚRODOWE ROZCIĄGANIE

Mimośrodowym rozciąganiem nazywamy taki przypadek obciążenia (siłami biernymi i czynnymi) przyłożonego na ściankach poprzecznych, które redukuje się na każdej z nich do wypadkowej o zwrocie zgodnym z normalną zewnętrzną danej ścianki poprzecznej, (układy sił przyłożone do obydwu ścianek poprzecznych równoważą się) .

1. CHARAKTERYSTYKI GEOMETRYCZNE

1. Przyjęcie układu współrzędnych (y₁, z₁) o początku w punkcie O₁

- przyjmujemy układ współrzędnych tak, aby rachunki były jak najprostsze (aby mieć pewność poprawnego i możliwie prostego liczenia)

- ze względu na dokładność obliczeń rachunkowych układ współrzędnych przyjmujemy w punkcie, który jest blisko spodziewanego środka masy układu złożonego.

- (0₁, y₁, z₁) - układ współrzędnych przyjęty w celu wyznaczenia środka masy (i innych pomocniczych obliczeń)

- (S, y₂, z₂) - układ centralny w celu zbudowania tensora bezwładności w punkcie S, którym posługujemy się do obliczenia układu osi głównych centralnych (S,y,z)

UWAGA :

Symbole y i z rezerwujemy na oznaczenie osi głównych centralnych przekroju poprzecznego

1. Wyznaczamy pole powierzchni przekroju figury złożonej

- Pamiętaj o jednoznaczności oznaczeń !!

- oznaczenia nie mogą się powtarzać

- jednoznaczność tzn. np. dla wysokości kolejnych figur - h₁, h₂ … itd.

- Pole całego przekroju poprzecznego jest sumą pól poszczególnych figur elementarnych (prostokąt, trójkąt, koło, kwadrat, itd. )

2. Wyznaczamy momenty statyczne dla całego przekroju.

W wytrzymałości Materiałów ρ
1

Ważne !!!

- Oznaczenie momentu statycznego Sxy₁ względem płaszczyzny xy₁ w Wytrzymałości Materiałów możemy uprościć i określać jako Sy₁

- Momenty statyczne, bezwładności i dewiacji dla zadanego przekroju obliczamy dzieląc figurę na skończoną liczbę prostokątów, trójkątów, wycinków koła, itd.

Wynika to z tw. o addytywności całki powierzchniowej względem podobszarów, po których całkujemy

UWAGA :

- Jeżeli brzeg figury opisującej przekrój poprzeczny składa się tylko z odcinków prostych, wówczas tę figurę można zawsze wyznaczyć jako sumę trójkątów i prostokątów (o podstawach równoległych do wybranej osi).

- Moment statyczny jest równy zero, gdy liczony jest względem dowolnej płaszczyzny* (prostej) przechodzącej przez środek masy figury.

* w Wytrzymałości Materiałów zastało to uproszczone; liczymy moment statyczny względem prostej

- Moment statyczny figury, liczony względem dowolnej prostej jest równy momentowi statycznemu środka masy tej figury względem tej prostej (punktowi przypisujemy masę równą polu figury).

UWAGA !!!

1. Jeżeli figura posiada oś symetrii l, to

• środek masy tej figury należy do l

• tensory bezwładności wyznaczone w dowolnym punkcie B należącym do l posiadają układ własny, którego jedna oś jest osią symetrii ( l ), a druga ( p ) jest do niej prostopadła. Jeżeli B=0 (środek masy) to układ (l, p) jest układem osi głównych centralnych (y || l i z || l )

Jeżeli figura posiada dwie osie symetrii wzajemnie prostopadłe to :

• S jest punktem przecięcia l i p

• układ (l, p) jest układem osi głównych centralnych

3. Jeżeli figura posiada co najmniej dwie osie symetrii, które nie są do siebie prostopadłe (np. trójkąt równoboczny), to :

• S jest punktem przecięcia prostych l i p

• tensor bezwładności wyznaczony w punkcie S posiada I_l = I_p = I_t , gdzie t jest dowolną prostą przechodzącą przez punkt S (w tym przypadku istnieje nieskończenie wiele osi głównych centralnych)

1. Wyznaczamy środek masy figury

Środek masy S to punkt geometryczny , któremu przypisujemy pole A równe polu całego przekroju poprzecznego, a jego położenie określamy według wzorów :

y_S=Sz₁/A z_S=Sy₁/A .

2. Obliczamy momenty bezwładności i dewiacji układzie (0₁, y₁, z₁)

UWAGA :

- ze względu na łatwość rachunków warto wyznaczyć tensor bezwładności w punkcie O₁ w układzie osi (y₁, z₁)

(choć można by od razu liczyć momenty bezwładności i dewiacji w układzie centralnym

(S, y₂, z₂) )





< 0 lub =0 lub >0

- Do obliczeń wykorzystujemy już wyprowadzone i udowodnione wzory.

UWAGA :

(S, y_S, z_S) - układ centralny poszczególnych figur

(0₁, y₁, z₁) - układ wygodny do stosowania w niektórych przekrojach o kształtach złożonych




















































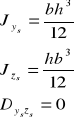
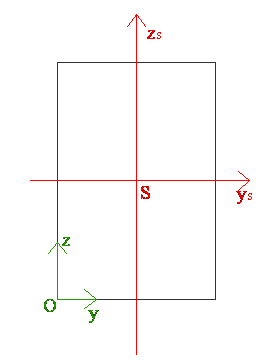
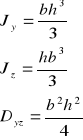
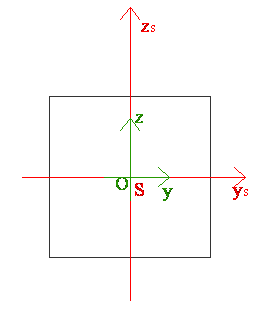
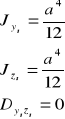
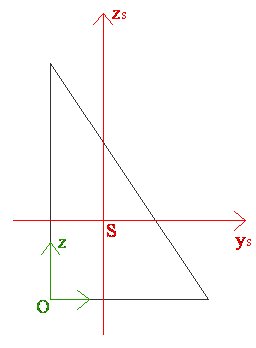
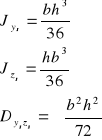
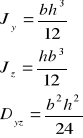
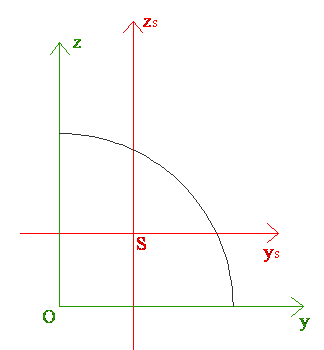
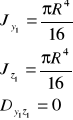
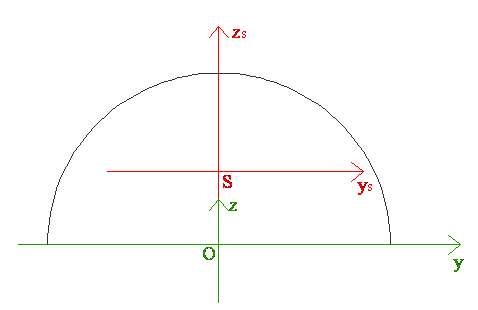
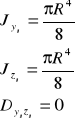
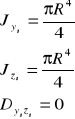
- Uwaga (warto pamiętać)

- Figury takie jak kwadrat, okrąg, trójkąt równoboczny i wszystkie figury foremne, które posiadają co najmniej dwie osie symetrii, nie będące do siebie prostopadłe mają :

* Momenty bezwładności takie same względem każdej prostej przechodzącej przez środek masy figury.

* Moment dewiacji równy zero względem każdych dwóch osi wzajemnie prostopadłych

- Moment dewiacji figury względem prostokątnego układu osi (y, z), których chociaż jedna jest osią symetrii tej figury, jest zawsze zero.

1. Przyjmujemy nowy, centralny układ współrzędnych (o początku w środku masy)

- odpowiednie osie równoległe (y₂ || y₁ , z₂ || z₁ ) (punkt O₂
O
S )

- zestawiamy tensor bezwładności w środku masy

- korzystając z tw. Steinera należy zwrócić uwagę na precyzyjne (ścisłe) spełnienie założeń, przy których przyjmuje ono postać :

I_l=I_l* - a²A

Moment bezwładności układu materialnego liczonego względem prostej l jest równy momentowi bezwładności układu względem prostej l₀ przechodzącej przez środek masy i równoległej do prostej l, pomniejszonemu o iloczyn pola figury i kwadratu odległości między tymi prostymi.

Iy₁= Iy₀ - Az₀² Iz₁= Iz₀ - Ay₀² (tutaj należy y₀ i z₀ traktować jako współrzędne

środka masy w układzie osi (y₁, z₁) )

Analogicznie dla momentu dewiacji :

Iy₁ z₁= Iy₀ z₀ - Ay₀z₀

2. Wyznaczamy główne centralne momenty bezwładności i położenie ich osi (czyli osie główne centralne )




UWAGA :

Osie : 1
y ; 2
z

Osie główne centralne będziemy oznaczać (y, z) (bez indeksów)

3. Wyznaczamy współrzędne przekroju poprzecznego w układzie osi głównych centralnych


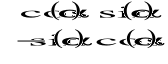
W celu wyznaczenia współrzędnych punktów w układzie osi głównych, centralnych należy dokonać transformacji współrzędnych


, gdzie *_i,k =

2. REDUKCJA SIŁ W UKŁADZIE OSI GŁÓWNYCH CENTRALNYCH

W zagadnieniu mimośrodowego rozciągania układ sił redukuje się do :

{N, M_y, M_z} F_x=N≠0 ; F_y=0; F_z=0; M_x=0; M_y, M_z

lub wypadkowej {N, y_o, z_o}

Najprostszą postacią tego układu jest wypadkowa {N, (y₀, z₀)}

3. ROZKŁAD NAPRĘŻEŃ NORMALNYCH ORAZ RÓWNANIE OSI OBOJĘTNEJ




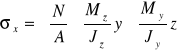
UWAGA ! ZNAKI NALEŻY USTALIĆ !

Lub przy przyjęciu zwrotów Nx , M_yy , M_zz :







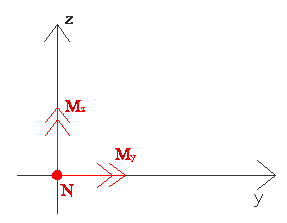
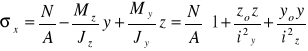
Równanie osi obojętnej : σ_x(y,z)=0


gdzie i_y²=I_y/A i_z²=I_z/A

UWAGA :

- Wszystkie charakterystyki geometryczne oraz składowe sił przekrojowych wyznaczamy w osiach głównych centralnych.

- Można obliczenia wykonać w innym układzie współrzędnych, wtedy należy jednak wyprowadzić odpowiednie, nowe wzory.

4. WYZNACZENIE BRYŁY NAPRĘŻEŃ

- rysujemy przekrój w aksonometrii

- znajdujemy wartości naprężeń w punktach charakterystycznych (wierzchołki figury)

PAMIĘTAJ :

Bryła naprężeń jest wyznaczona przez płaszczyznę (!!!) naprężeń, płaszczyzną przekroju poprzecznego i powierzchnię boczną pręta.

Def.

Płaszczyzną naprężeń jest zbiór końców wektorów naprężeń normalnych zaczepionych w punktach przekroju poprzecznego.

5. WYZNACZENIE RDZENIA PRZEKROJU

Dowolnej osi obojętnej stycznej do konturu przekroju musi odpowiadać jeden punkt przyłożenia siły, któremu ta oś odpowiada (np. "styczna 1" odpowiada punktowi P₁ ). Kreśląc kolejne styczne uzyskuje się kolejne, odpowiadające im punkty przyłożenia sił P_i. Zbiór tych punktów tworzy kontur obszaru, który nazywamy rdzeniem przekroju.

Dowolnej osi obojętnej leżącej całkowicie poza obszarem przekroju (tzn. nie przecinającej go) musi odpowiadać punkt przyłożenia siły leżący w obszarze rdzenia.

Położenie osi obojętnej stycznej do konturu przekroju lub całkowicie poza jego obszarem oznacza, że naprężenia w całym przekroju są tego samego znaku ( skoro na osi obojętnej wynoszą one zero, to po jednej ze stron osi muszą być dodatnie, a po drugiej ujemne).

Definicja :

Rdzeń przekroju to miejsce geometryczne położenia punktów, w których przyłożona działająca siła (rozciągająca lub ściskająca) powoduje powstanie w każdym przekroju poprzecznym naprężeń jednakowego znaku.

(+ dla siły rozciągającej, - dla siły ściskającej)

Własności rdzenia przekroju

Rdzeń przekroju jest zawsze figurą wypukłą

UWAGA :

Jeżeli punkty przyłożenia siły przemieszczają się po prostej, to odpowiednie osie obrotu tworzą pęk. (obracają się wokół ustalonego punktu)

PYTANIA

• Co to są główne osie bezwładności, jakie mają własności.

GŁÓWNE OSIE BEZWŁADNOŚCI I GŁÓWNE CENTRALNE OSIE BEZWŁADNOŚCI

Głównym momentom bezwładności przyporządkowane są główne osie bezwładności, wyznaczone przez wektory własne tensora bezwładności ( w dowolnym punkcie).

Jeżeli dla układu materialnego tensor bezwładności zestawimy w środku masy, to odpowiadające mu wartości własne nazywamy głównymi centralnymi momentami bezwładności, zaś osie wyznaczone przez wektory własne tego tensora - głównymi centralnymi osiami bezwładności.

WŁASNOŚCI (w D3) :

• Każdy układ materialny (w przestrzeni) w każdym punkcie posiada co najmniej trzy główne osie bezwładności,

• dokładnie trzy, gdy wartości własne ₁≠₂≠₃,

• jedną główną oś i całą płaszczyznę osi bezwładności prostopadłych do tej osi, gdy ₁≠₂=₃ lub ₂≠₁=₃ lub ₃≠₁=₂

• całą przestrzeń głównych osi bezwładności, gdy ₁=₂=₃ (każde trzy osie przechodzące przez dany punkt i wzajemnie prostopadłe, tworzą układ osi głównych)

• Momenty bezwładności liczone względem głównych osi bezwładności są ekstremalne

• Momenty dewiacji liczone względem płaszczyzn wyznaczonych przez główne osie bezwładności są równe zeru.

• Momenty dewiacji osiągają największe bezwzględne wartości względem osi
  

6







R

R

h

b

ab

h

b

---