Z

A

KŁ

D

M

S

Y

N

EL

TR

C

H

A

A

Z

Y

YN

Z

EK

C

*

*

* PO

L

IM N

i PE

WR

.

.

Politechnika Wrocławska

Instytut Maszyn, Napędów i Pomiarów Elektrycznych

Materiał ilustracyjny

do przedmiotu

ELEKTROTECHNIKA

Prowadzący:

Dr inż. Piotr Zieliński (I-29, A10 p.408, tel. [phone])

(Cz. 2)

Wrocław 2005/6

PRĄD ZMIENNY

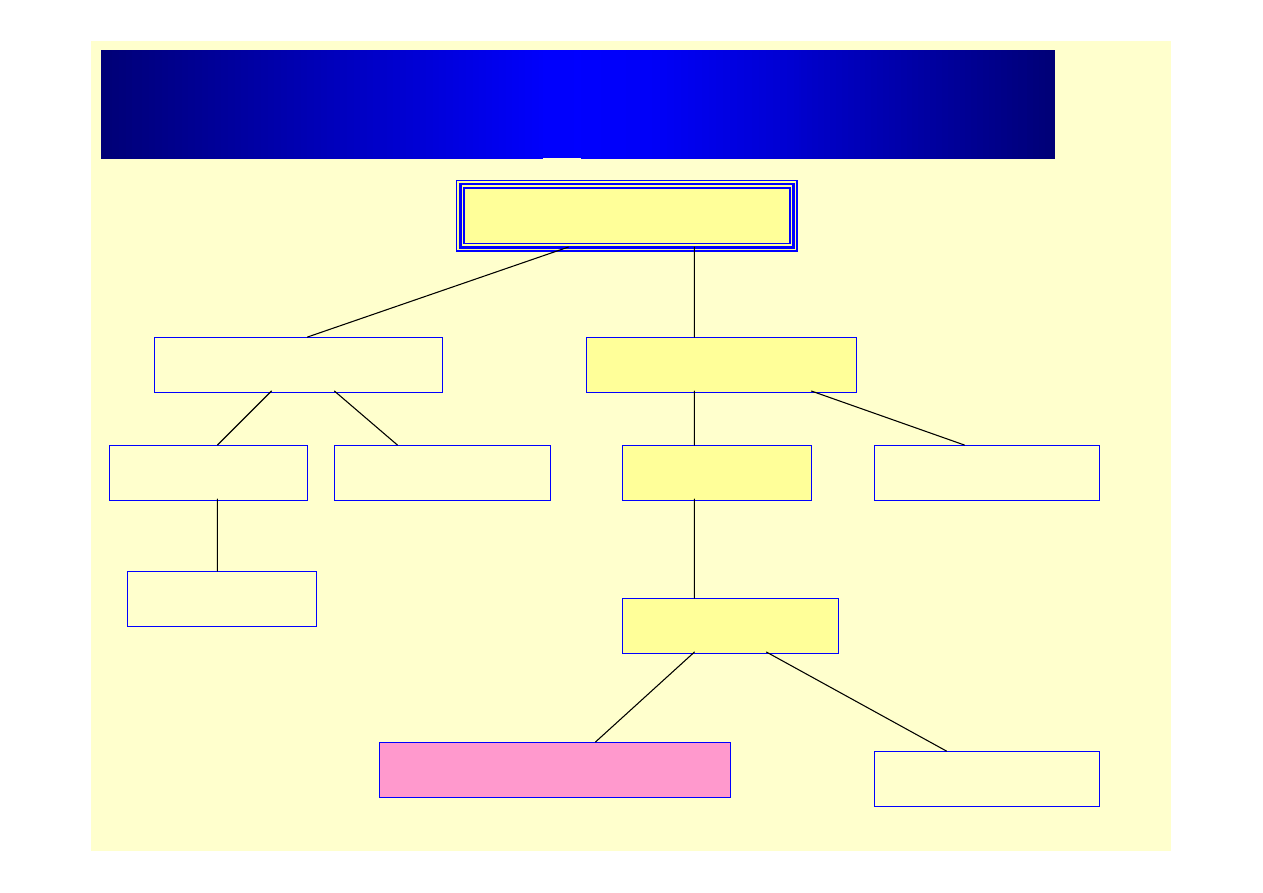
Klasyfikacja prądów zmiennych

Prąd zmienny

jednokierunkowy

dwukierunkowy

okresowy

nieokresowy

okresowy

nieokresowy

pulsujący

przemienny

sinusoidalnie zmienny

odkształcony

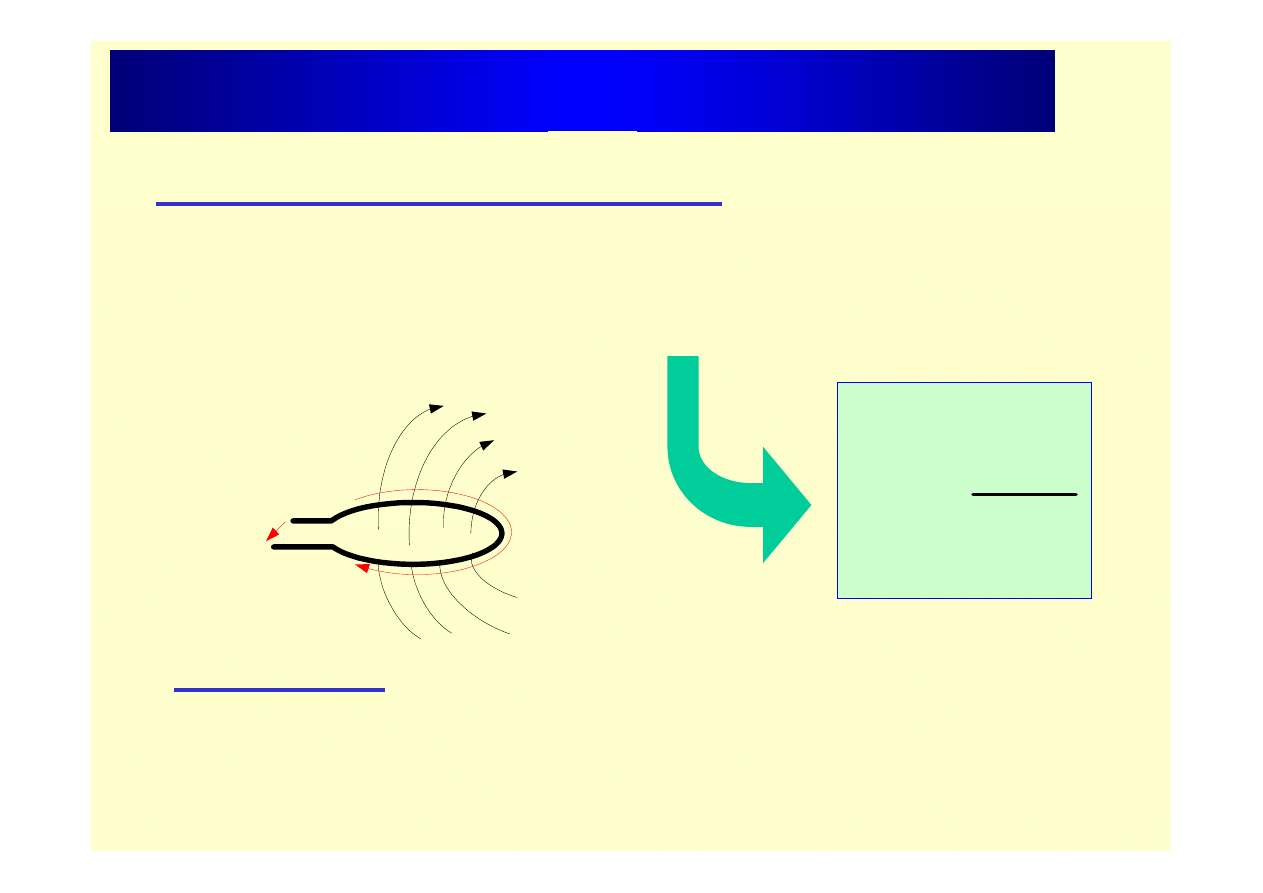
Indukcja elektromagnetyczna

Prawo indukcji elektromagnetycznej

Jeżeli wartość strumienia magnetycznego sprzężonego z obwodem
elektrycznym zmienia się w czasie, to w obwodzie tym indukuje się
siła elektromotoryczna o wartości:

dt

d

e

φ

=

d

Φ / dt>0

e

Φ

e

Reguła Lenza

Zwrot indukowanej sem jest taki, że prąd płynący pod jej
wpływem przeciwstawia się zachodzącym zmianom strumienia.

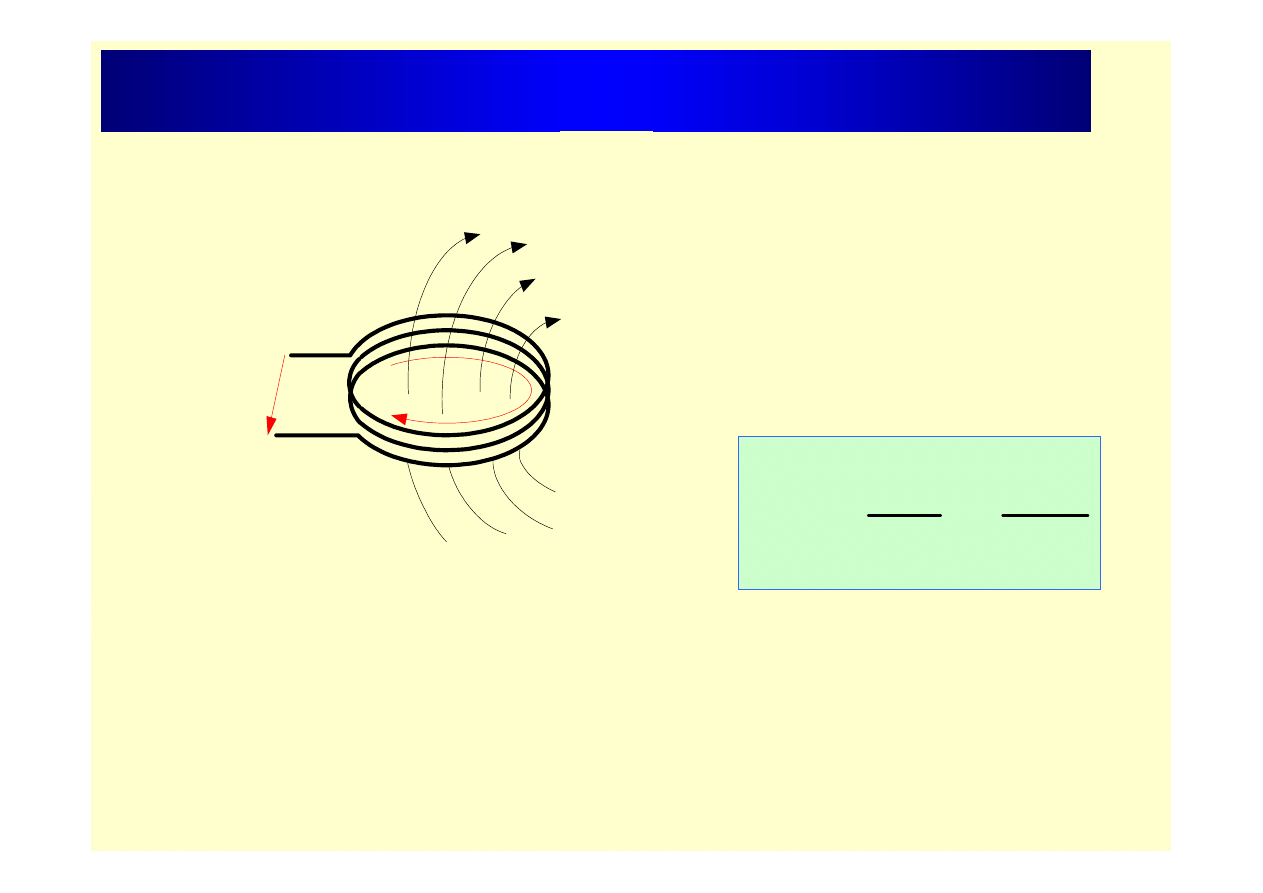
Strumień magnetyczny sprzężony

d

Φ / dt>0

e

e

Φ

z

φ

ψ

z

=

dt

d

dt

d

z

e

ψ

φ

=

=

gdzie: z - liczba zwojów

ψ - sprzężenie magnetyczne

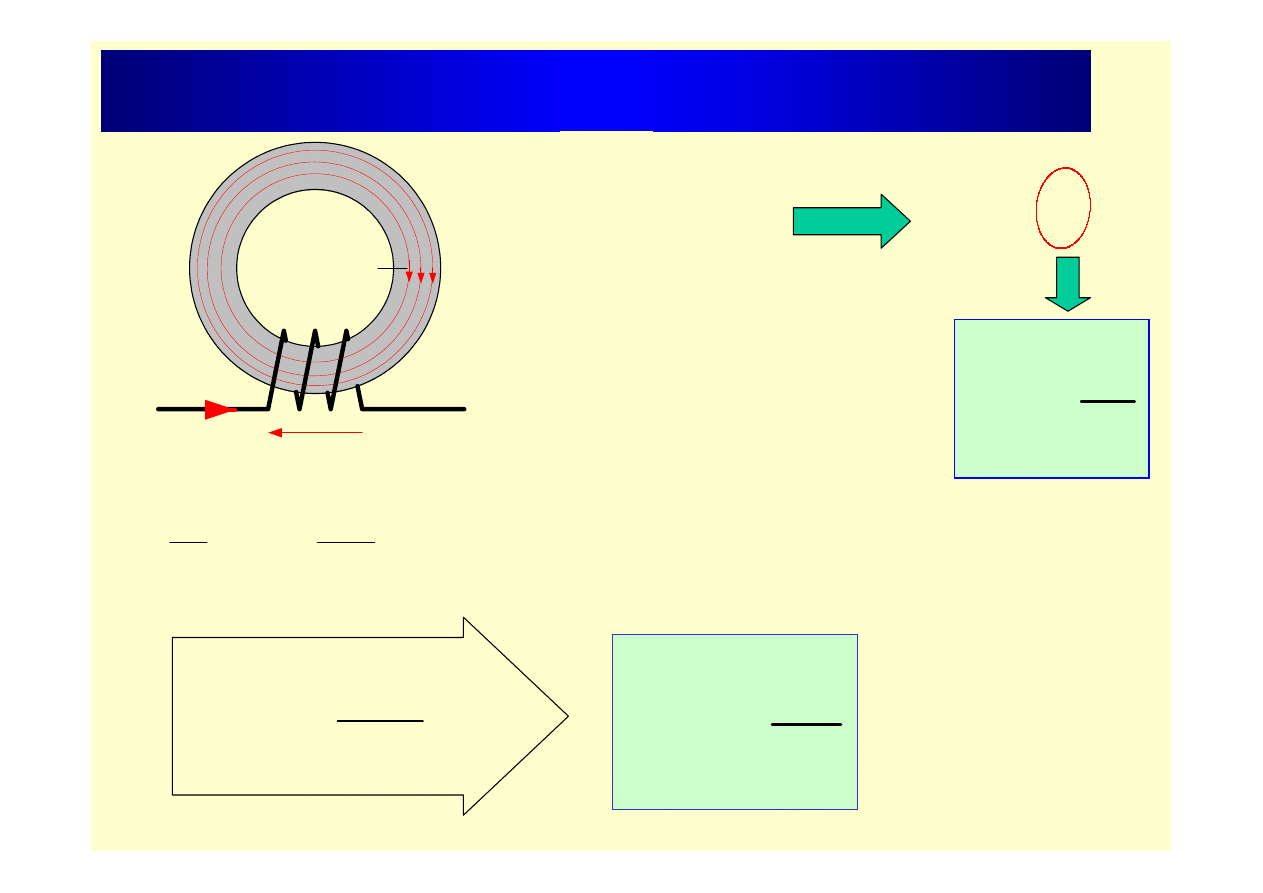
Samoindukcja

e

i

Φ

i

L

=

ψ

i

∝

ψ

Współczynnik

proporcjonalności

L

jest

nazywany

współczynnikiem

indukcyjności własnej

lub

indukcyjnością

.

dt

d

e

ψ

=

i

def

ψ

L

=

0

;

0

≠

≠

dt

d

dt

di

ψ

[L]=1H (henr)

dt

i

d

L

e

=

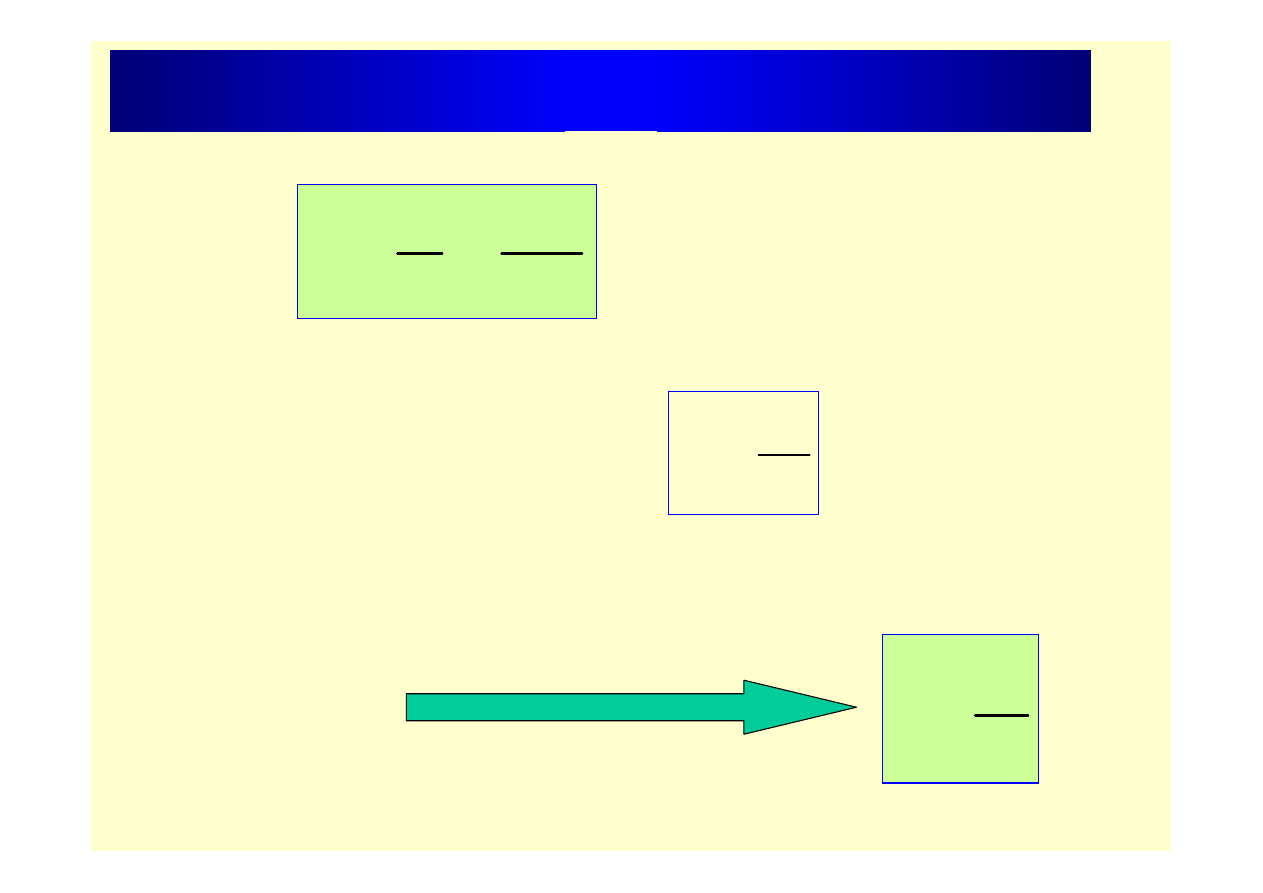
Współczynnik samoindukcji

i

Φ

z

i

L

=

=

ψ

R

z

i

Φ

=

Podstawienie w miejsce

Φ

zależności wynikającej z prawa

Ohma dla obwodu magnetycznego....

.... daje wzór ilustrujący, jak indukcyjność
danego obiektu zależy od jego parametrów
konstrukcyjnych.

R

2

z

L

=

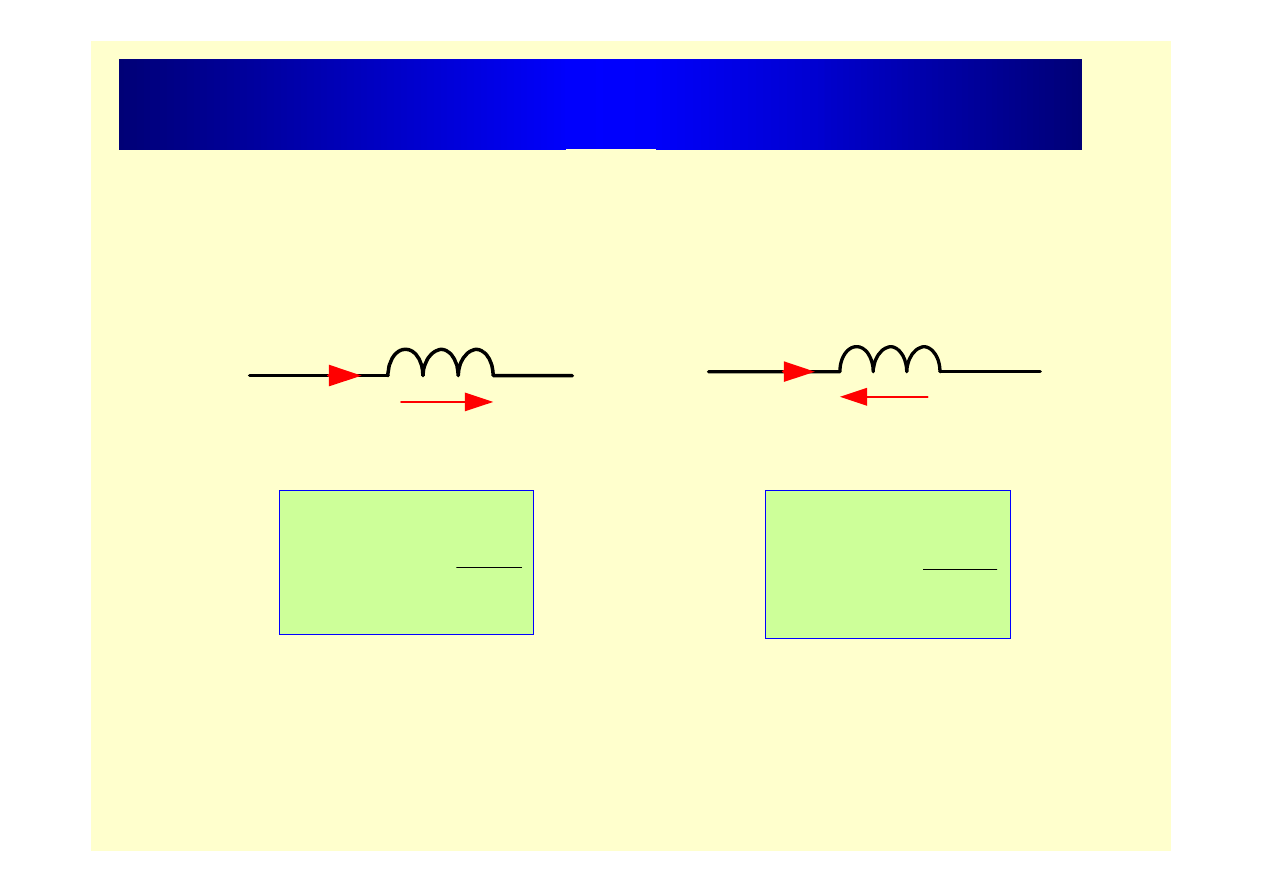
Samoindukcja – zasady strzałkowania

e

2

L

i

2

e

1

L

i

1

dt

di

L

e

1

1

−

=

dt

di

L

e

2

2

=

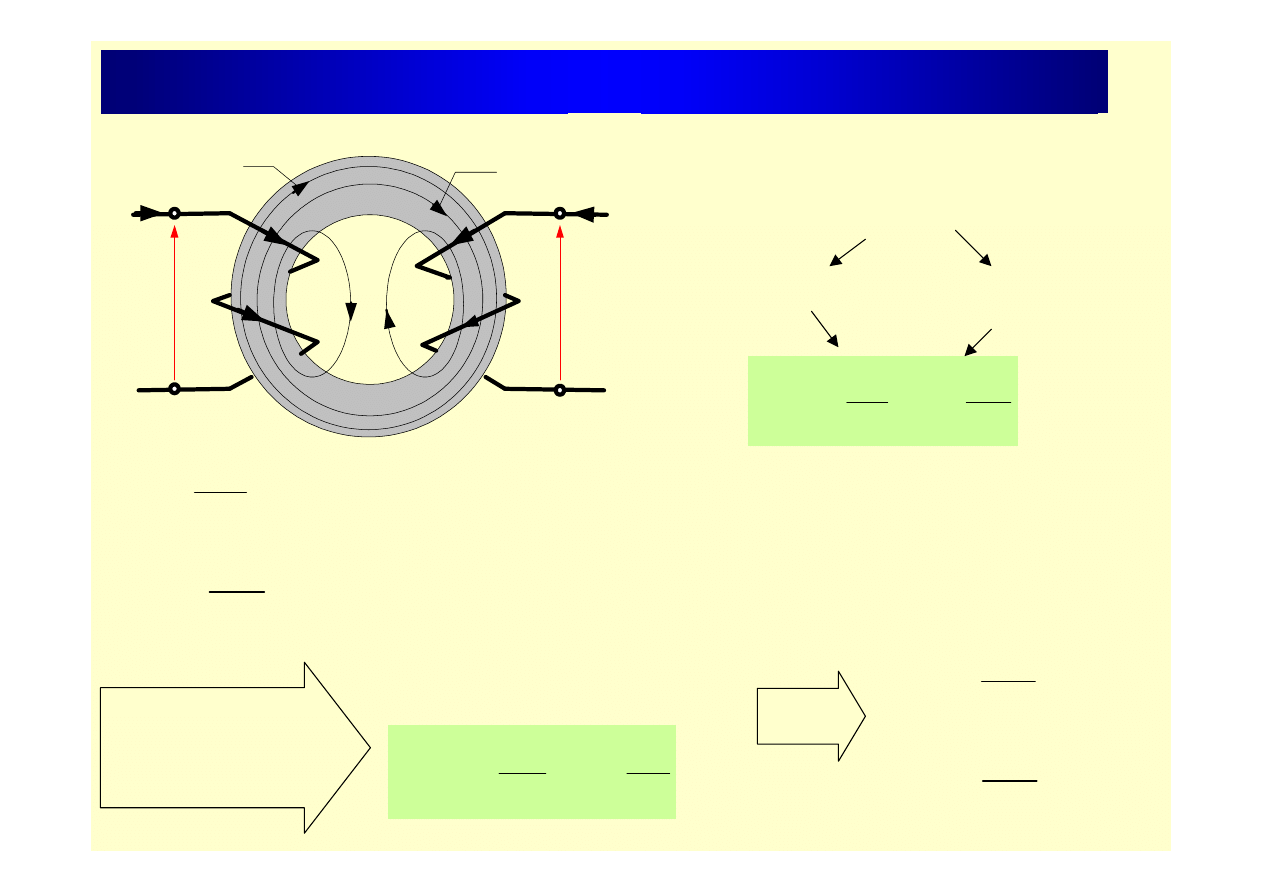
Zjawisko indukcji wzajemnej – transformacja (1)

i

1

i

2

Φ

1r

Φ

2r

Φ

12

e

1

e

2

Φ

21

dt

di

L

dt

di

L

e

2

21

1

1

1

+

=

21

11

1

e

e

e

+

=

sem samoindukcji

sem indukcji
wzajemnej

Sem indukowana w uzwojeniu 1.

1

11

1

i

L

ψ

=

2

21

21

i

L

ψ

=

- współczynnik indukcji własnej uzwojenia 1.

- współczynnik indukcji wzajemnej między uzwojeniem 2 i 1.

2

12

2

i

L

ψ

=

1

12

12

i

L

ψ

=

dt

di

L

dt

di

L

e

1

12

2

2

2

+

=

12

22

2

e

e

e

+

=

Analogicznie,
sem indukowana
w uzwojeniu2.

gdzie:

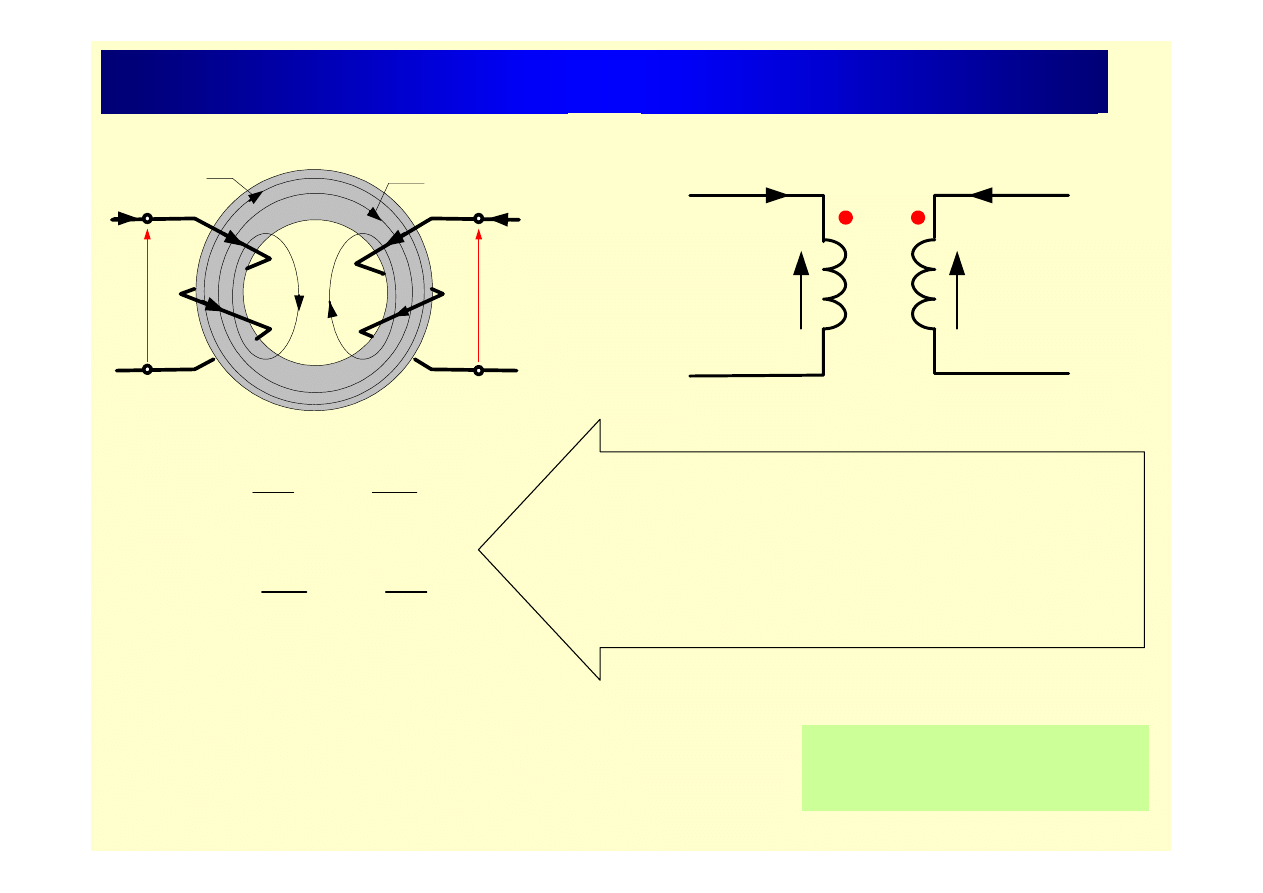
Zjawisko indukcji wzajemnej – transformacja (2)

L

1

L

12

e

2

i

1

i

2

L

2

e

1

i

1

i

2

Φ

1r

Φ

2r

Φ

12

e

1

e

2

Φ

21

Znaki

(+)

w wyrażeniach na e

1

i e

2

wystąpią

gdy obydwa prądy wpływają do zacisków
jednoimiennych. W przeciwnym przypadku
wystąpią znaki

(-)

. Zaciski jednoimienne na

schemacie powyżej oznaczono kropkami.

dt

di

L

dt

di

L

e

2

21

1

1

1

±

=

dt

di

L

dt

di

L

e

1

12

2

2

2

±

=

Można udowodnić, że współczynniki indukcji
wzajemnej

L

12

i

L

21

są sobie równe. W literaturze są

one często oznaczane literą

M

.

M

L

L

=

=

21

12

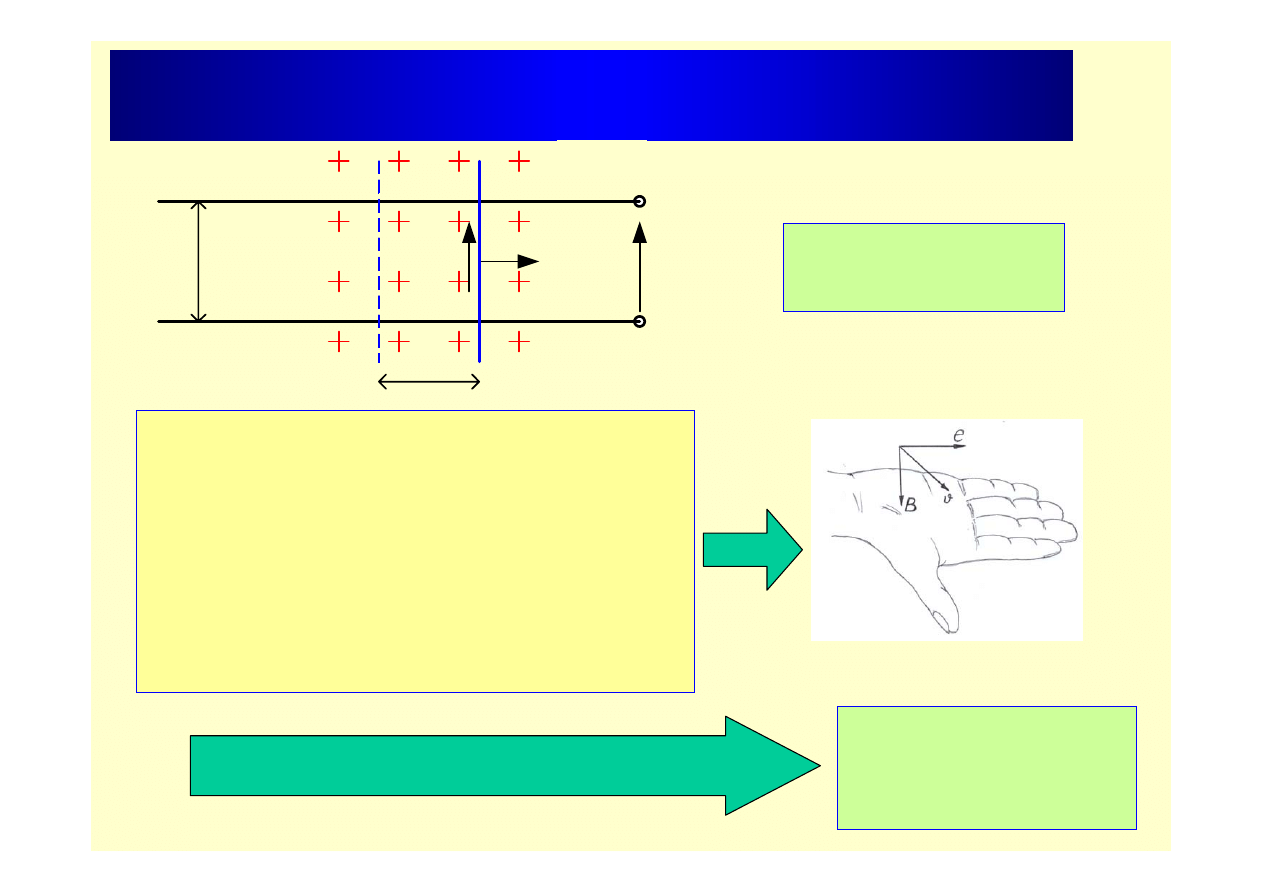
Siła elektromotoryczna ruchu

B

e

v

e

l

dx

[

]

B

v

×

= l

e

Reguła prawej dłoni

Jeżeli prawą dłoń umieścimy w polu
magnetycznym tak by linie sił pola były
skierowane ku dłoni a odgięty kciuk
wskazywał kierunek ruchu przewodnika to
wyciągnięte palce wskażą

kierunek

indukowanej sem.

v

l

B

e

=

Jeśli B,l,v są wzajemnie prostopadłe to:

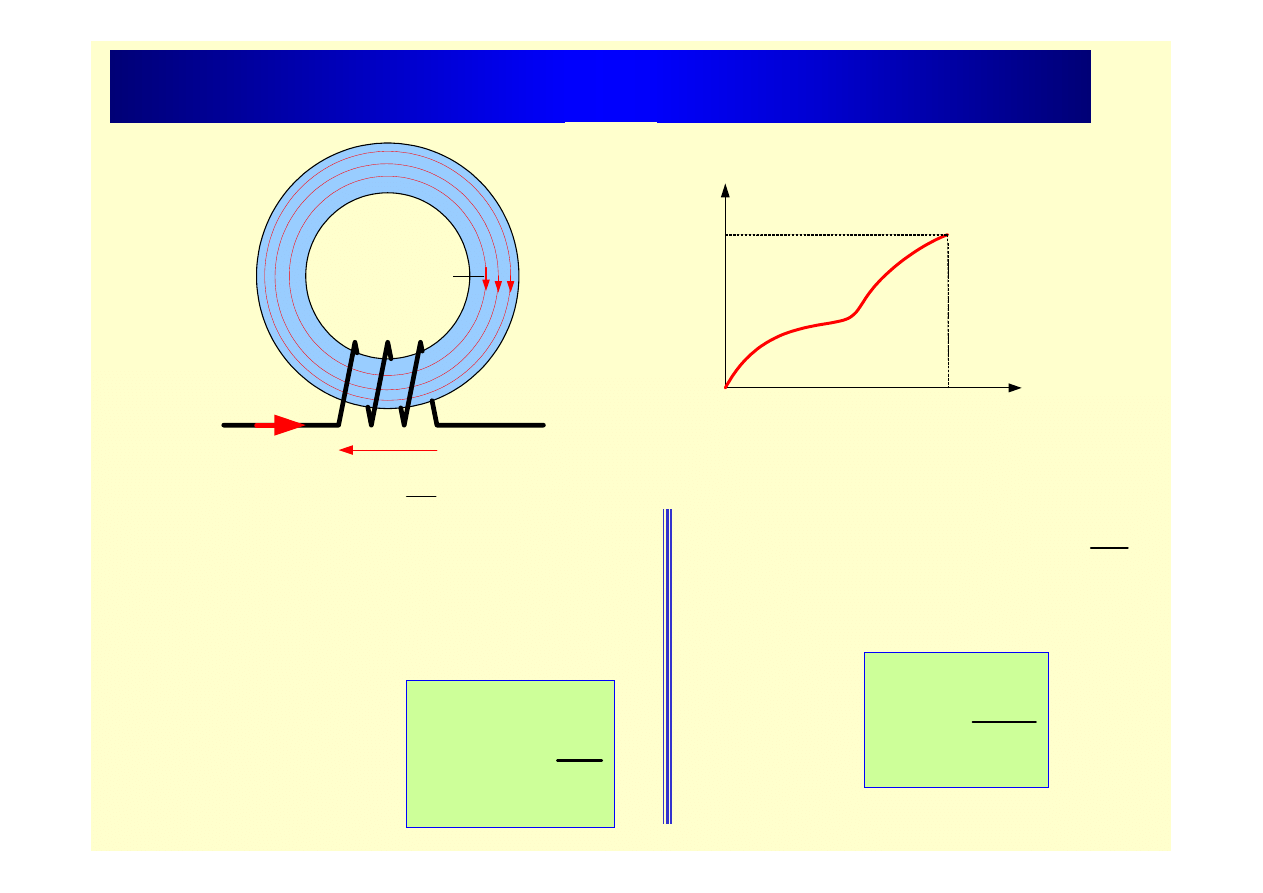
Energia pola magnetycznego

i

Φ

dt

di

L

e

=

i

,ψ

t

I

0

T

i

L

ψ

=

Po uwzględnieniu:

dt

i

e

dW

=

i

∫

=

di

i

L

W

0

2

i

W

ψ

=

2

2

i

L

W

=

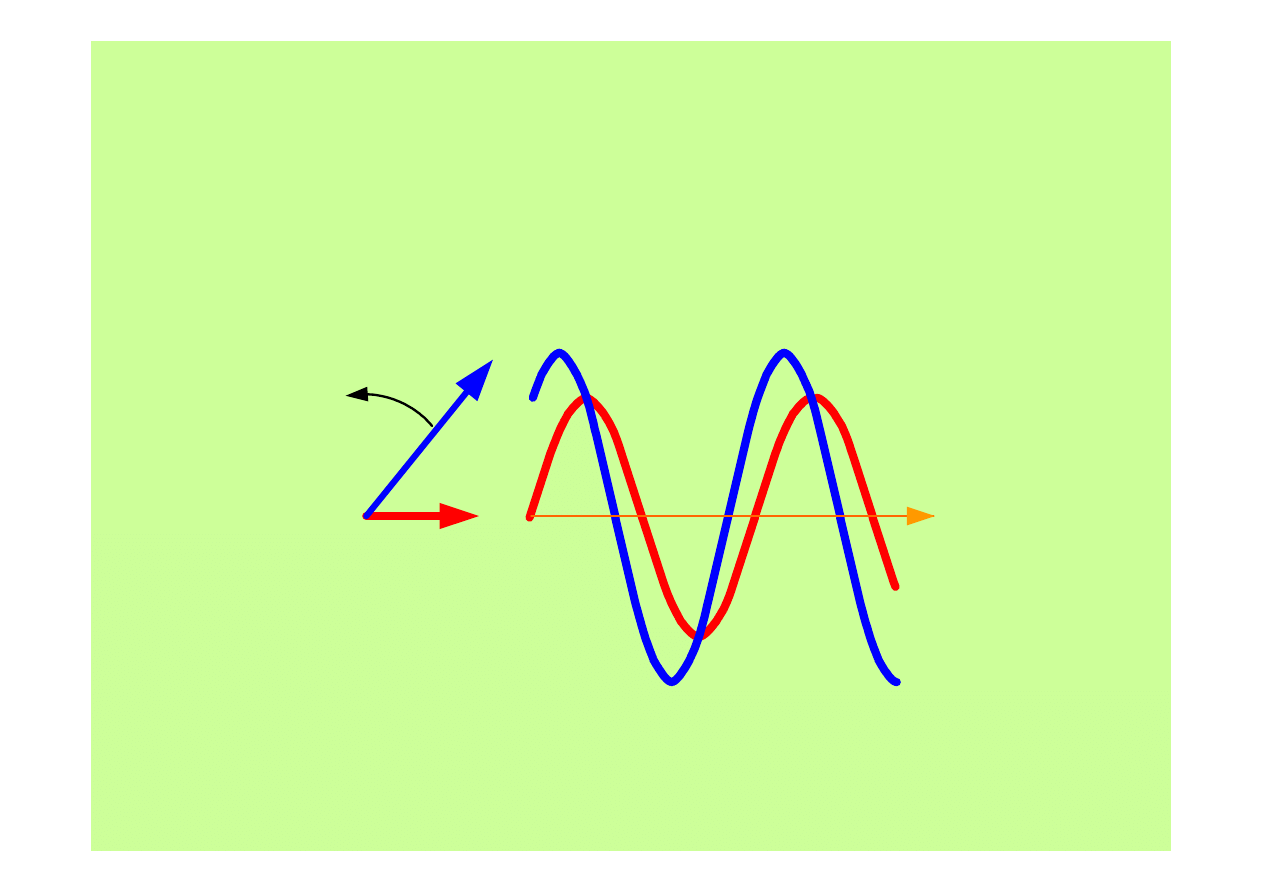
Prąd zmienny sinusoidalny

(przemienny)

ω

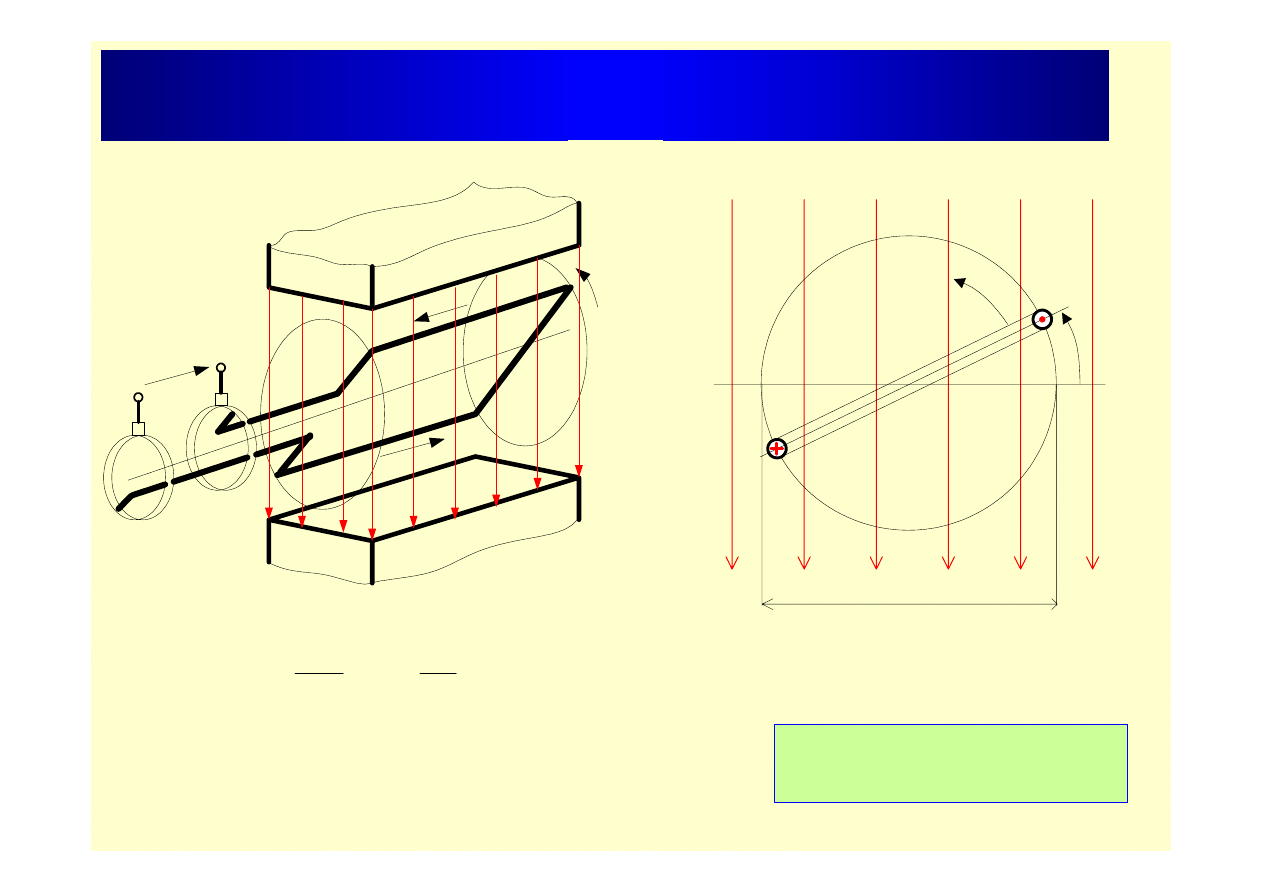
Wytwarzanie napięcia sinusoidalnego

ω

e

e

e

B

B

ω

α

d

)

cos

(

α

φ

Bld

dt

d

dt

d

e

−

=

−

=

t

E

e

m

ω

sin

=

Bld

E

t

m

ω

ω

α

=

=

;

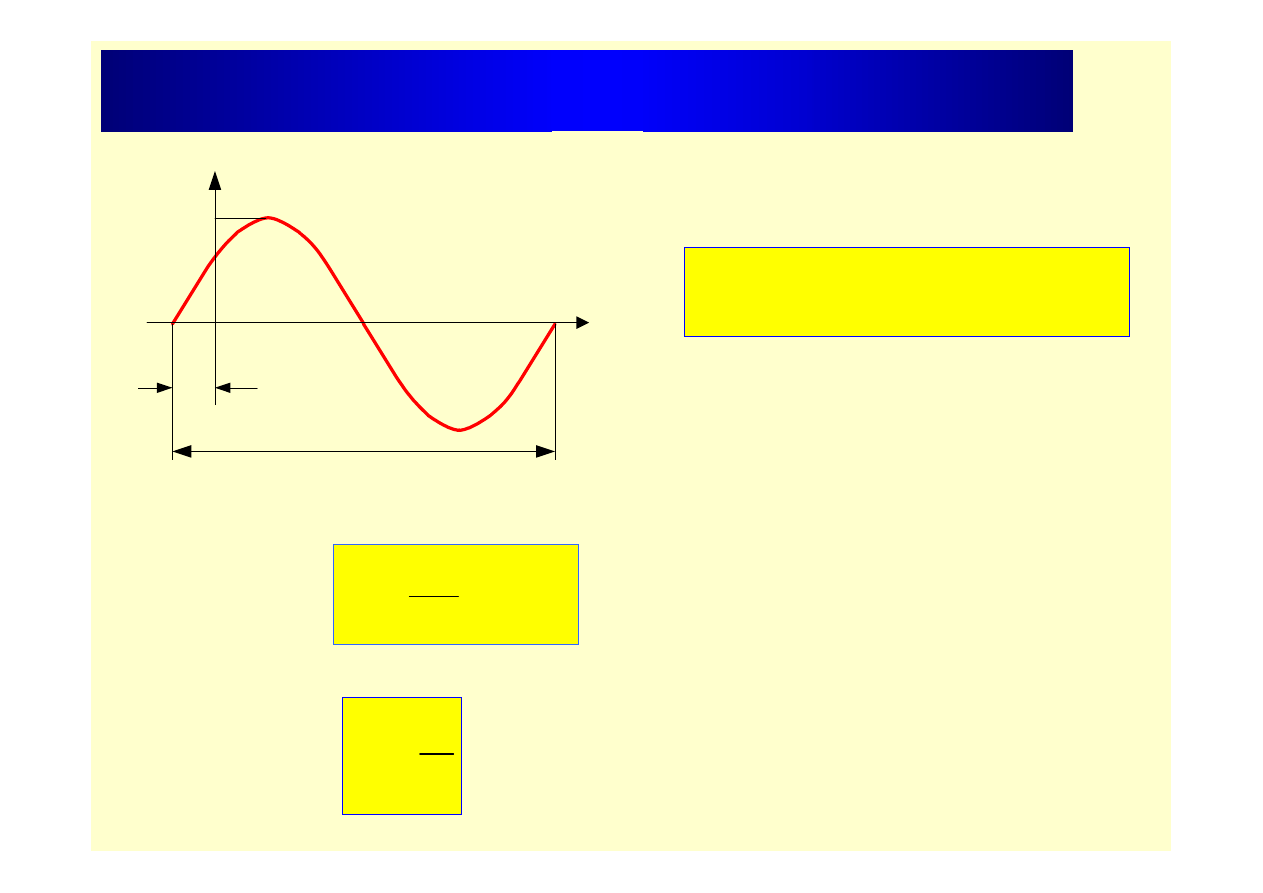
Parametry przebiegu sinusoidalnego

e

ωt

T

ψ

E

m

)

sin(

ψ

ω +

=

t

E

e

m

E

m

– wartość maksymalna

f

T

π

π

ω

2

2 =

=

Pulsacja -

f

– częstotliwość

f

T

1

=

ψ

– faza początkowa

Okres -

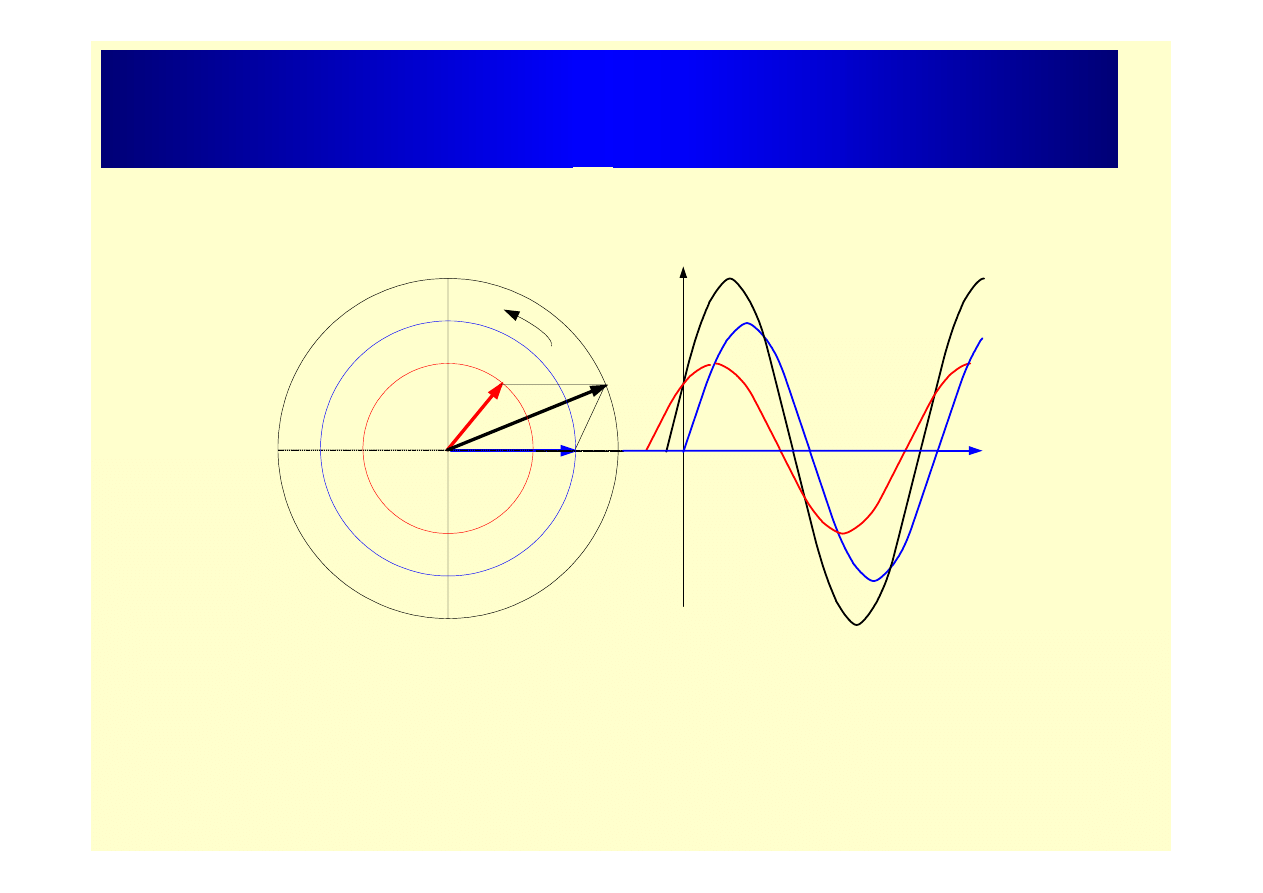
Przedstawianie przebiegów sinusoidalnych

za pomocą wirujących wektorów

ω

B

C

a

b

c

ω t

A

Sumowanie przebiegów sinusoidalnych

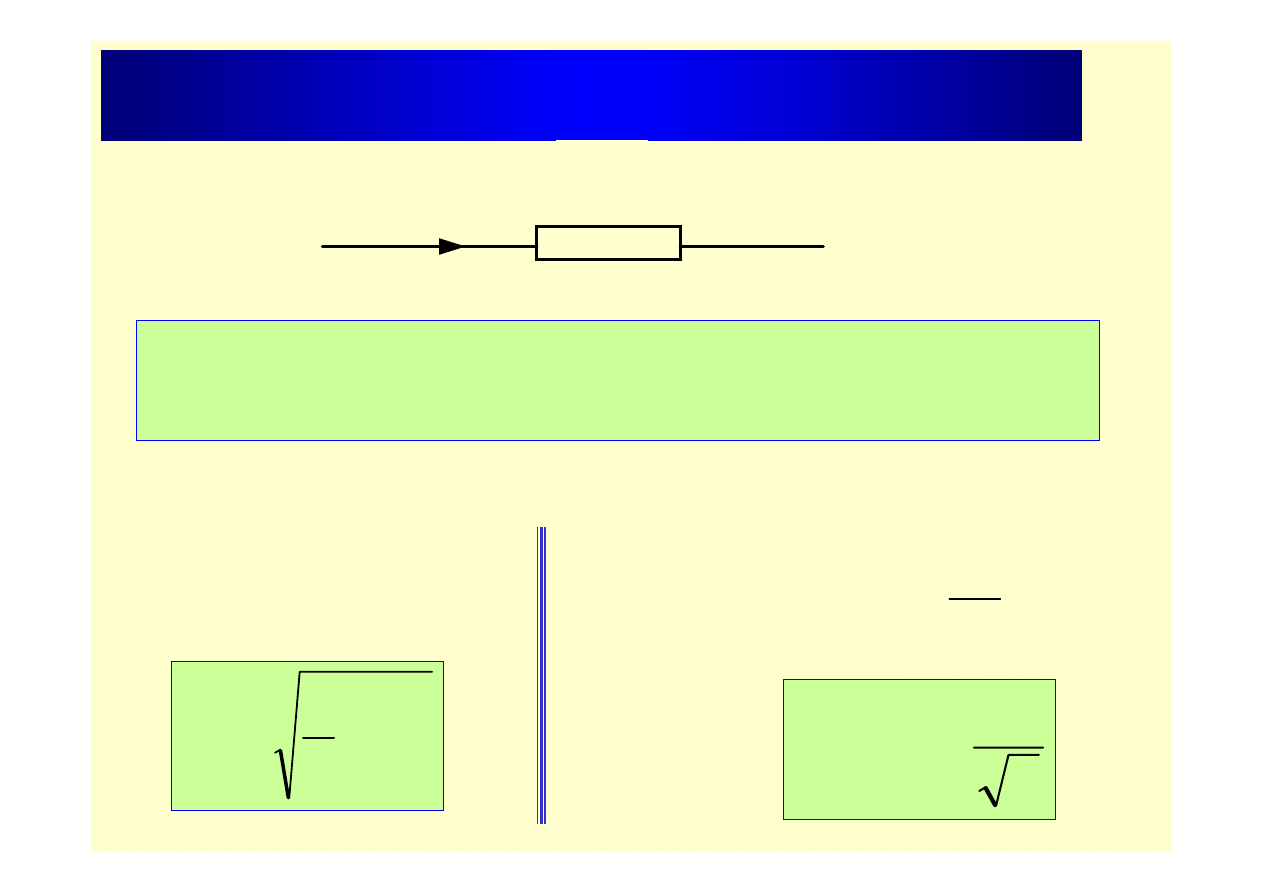
Wartość skuteczna prądu zmiennego

i ( I

sk

)

R

Wartość skuteczna prądu zmiennego okresowego jest równa wartości prądu
stałego, który płynąc w ciągu jednego okresu przez taką samą rezystancję co
prąd zmienny wywołuje taki sam skutek cieplny.

W przypadku przebiegu sinusoidalnego

T

R

I

dt

R

i

sk

T

2

0

2

=

∫

t

T

I

i

m

π

2

sin

=

∫

=

T

def

sk

dt

i

T

I

0

2

1

2

m

sk

I

I

I

=

=

Zatem

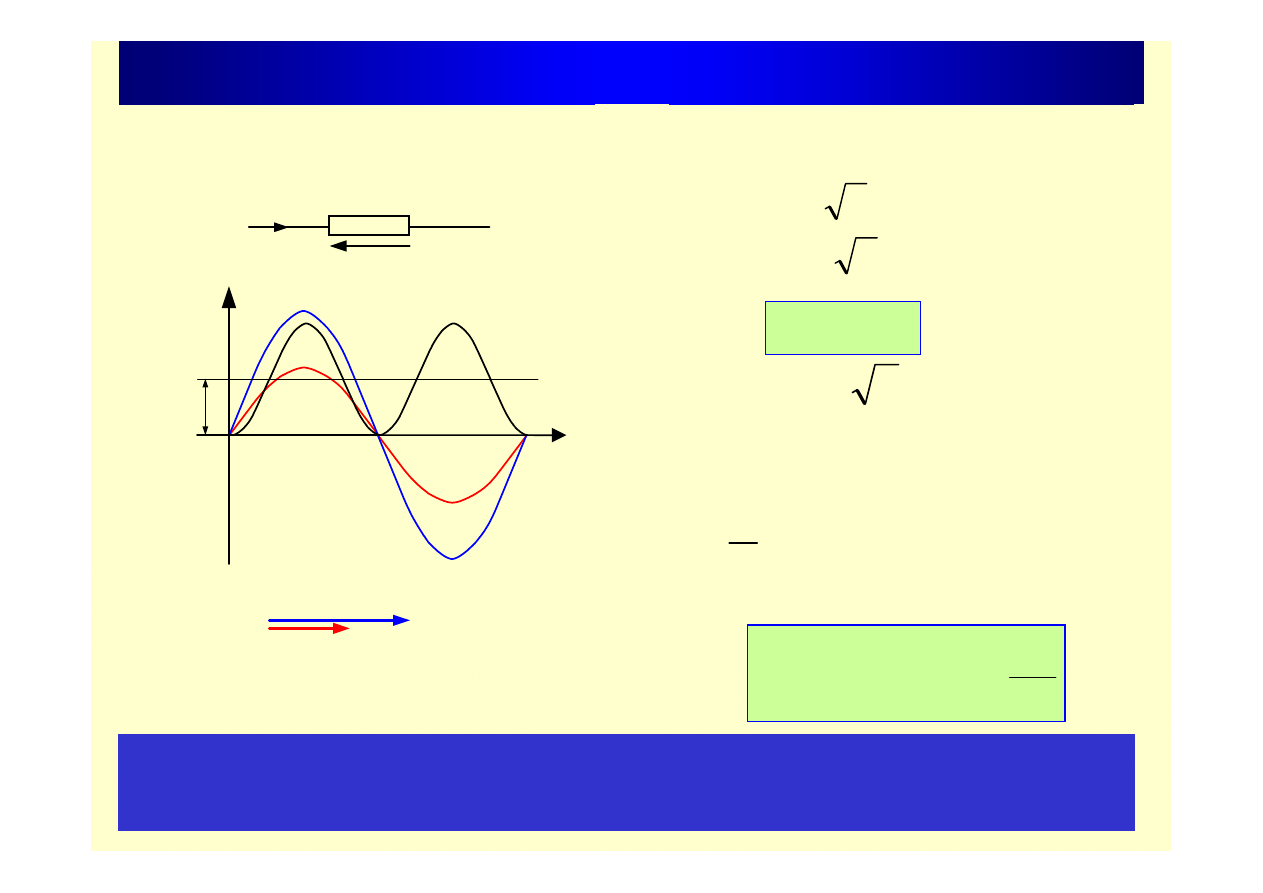
Rezystancja obwodzie prądu przemiennego

R

i

u

R

R

=

t

I

i

R

R

ω

sin

2

=

t

R

I

u

R

R

ω

sin

2

=

R

I

U

R

R

=

t

U

u

R

R

ω

sin

2

=

t

I

U

i

u

p

R

R

R

R

ω

2

sin

2

=

=

R

U

R

I

I

U

P

R

R

R

R

2

2

=

=

=

i

R

;I

R

u

R

;U

R

R

U

R

I

R

u

R

i

R

u

R

i

R

t

p

P = P

sr

R

R

T

R

R

śr

I

U

dt

t

I

U

T

P

P

=

=

=

∫

0

2

sin

2

1

ω

Prąd płynący przez rezystancję R jest w fazie względem napięcia na

tym elemencie.

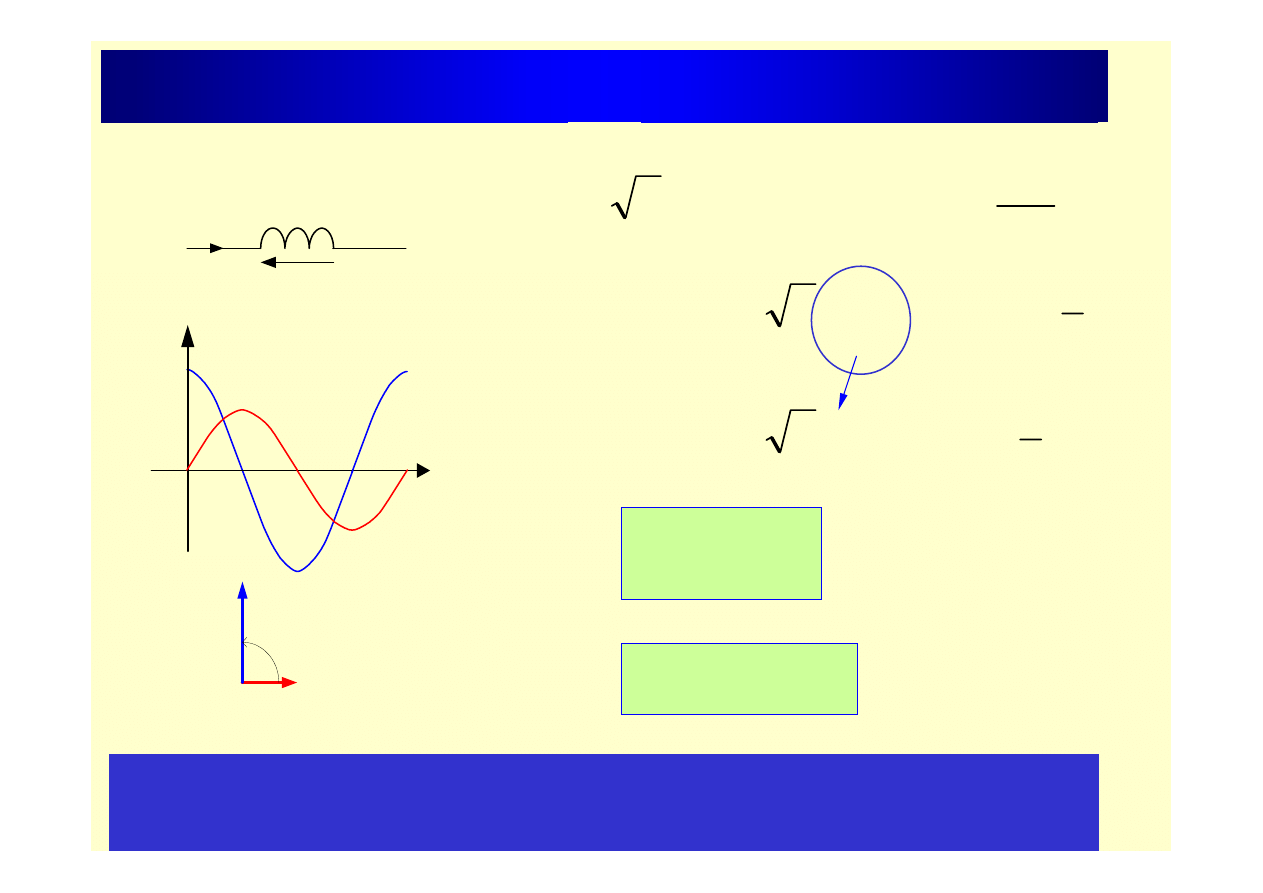
Indukcyjność w obw. prądu przemiennego

dt

di

L

u

L

L

=

t

I

i

L

L

ω

sin

2

=

i

L

;I

L

u

L

;

U

L

X

L

U

L

I

L

u

L

i

L

u

L

i

L

t

f

p

)

sin(

2

2

π

ω

ω

+

=

t

L

I

u

L

L

)

sin(

2

2

π

ω +

=

t

U

u

L

L

L

X

def

L

ω

=

- reaktancja ind. [

Ω

]

L

L

L

X

I

U

=

Prąd płynący przez indukcyjność L jest opóźniony względem

napięcia na tym elemencie o kąt f= 90

o

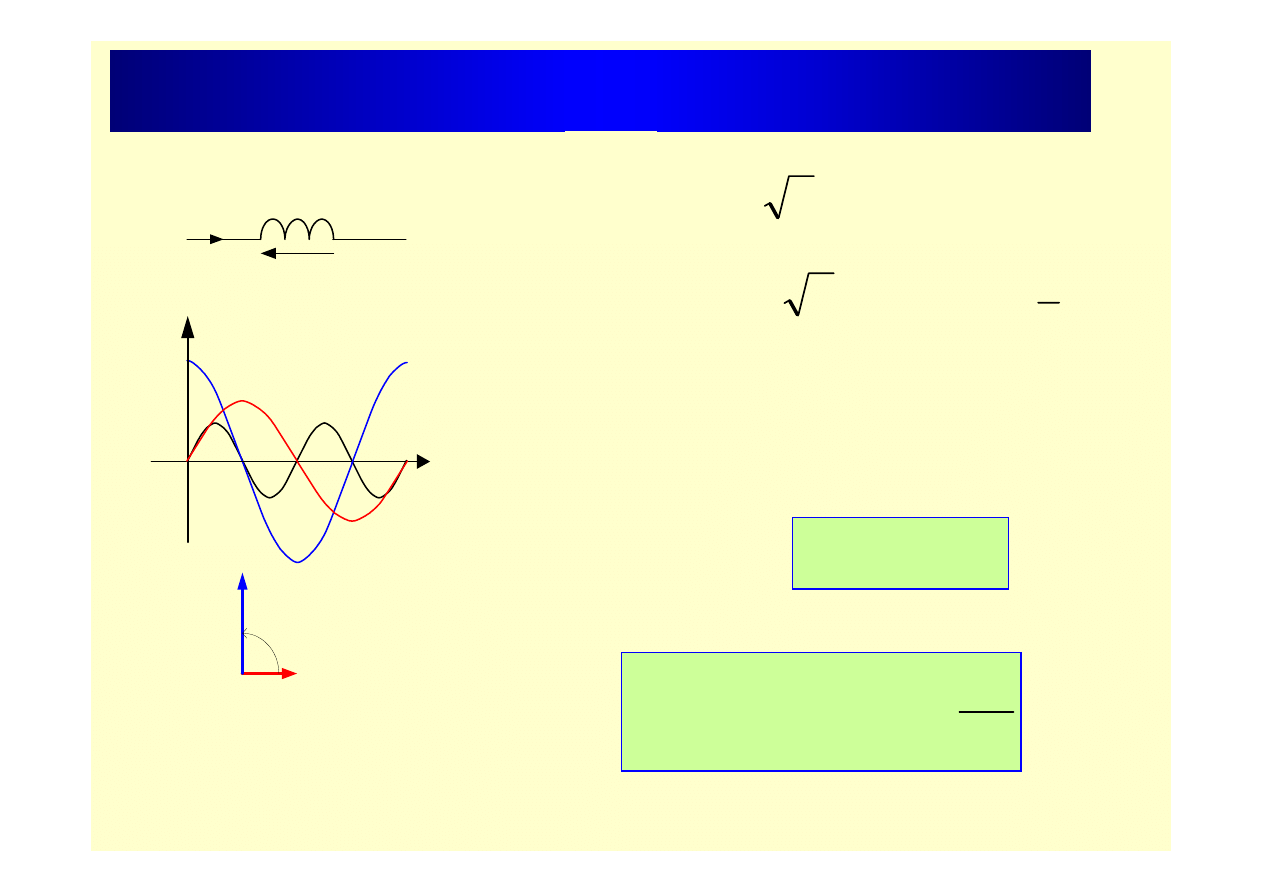
Moc odbiornika indukcyjnego

L

L

L

L

L

def

L

X

U

X

I

I

U

Q

L

2

2

=

=

=

t

I

U

i

u

p

L

L

L

L

ω

2

sin

=

=

0

=

=

śr

P

P

i

L

;I

L

u

L

;

U

L

X

L

U

L

I

L

u

L

i

L

u

L

i

L

t

f

p

p

t

I

i

L

L

ω

sin

2

=

)

sin(

2

2

π

ω +

=

t

U

u

L

L

Moc bierna -

Moc czynna -

[var]

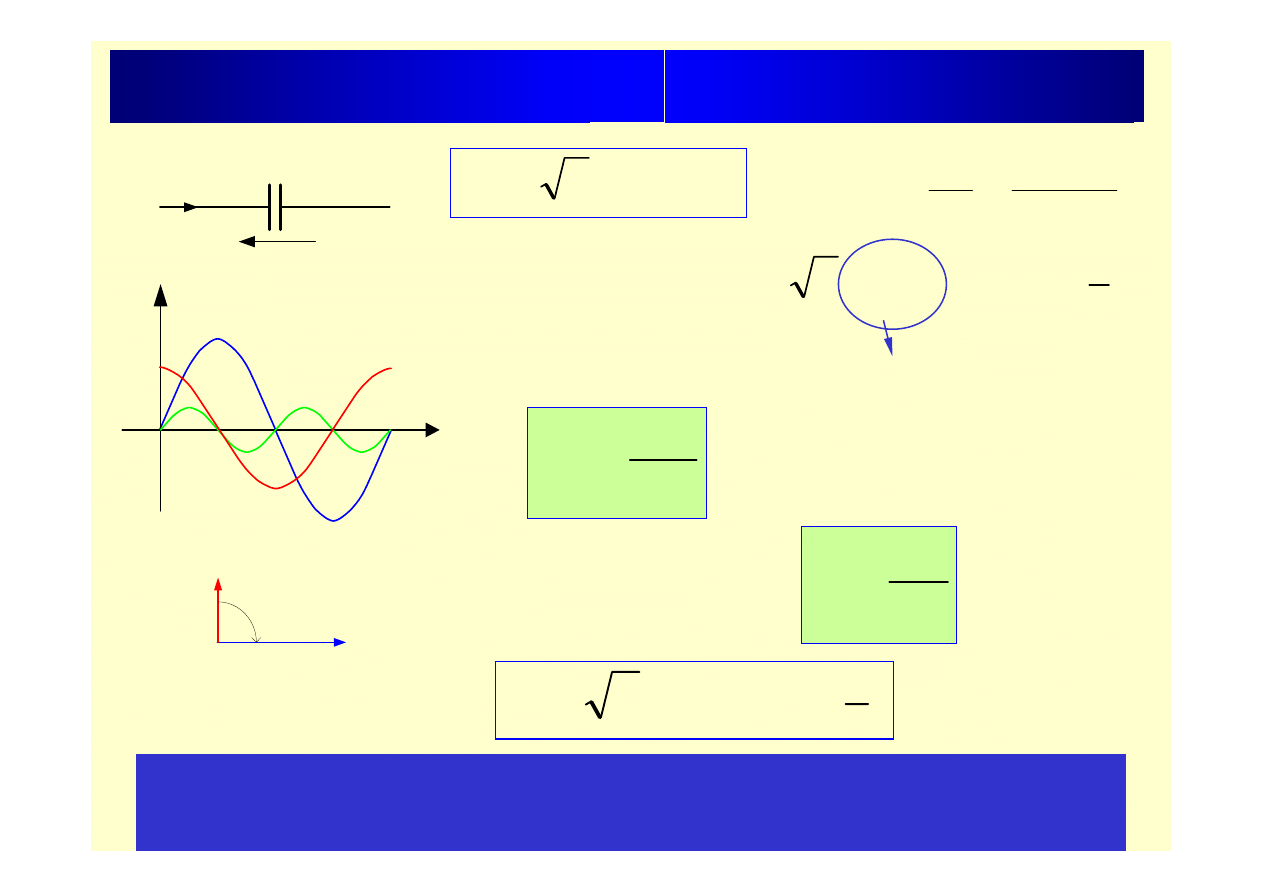
Pojemność w obw. prądu przemiennego

I

C

U

C

C

U

C

I

C

u

C

i

C

u

C

i

C

t

f

p

)

sin(

2

2

π

ω

ω

+

=

t

C

U

i

C

C

t

U

u

C

C

ω

sin

2

=

C

C

C

X

U

I

=

dt

u

C

d

dt

dq

C

)

(

=

=

C

U

I

C

C

ω

=

C

X

def

C

ω

1

=

i

- reaktancja poj. (

Ω

)

)

sin(

2

2

π

ω +

=

t

I

i

c

C

Prąd płynący przez pojemność C wyprzedza napięcie na tym

elemencie o kąt f= 90

o

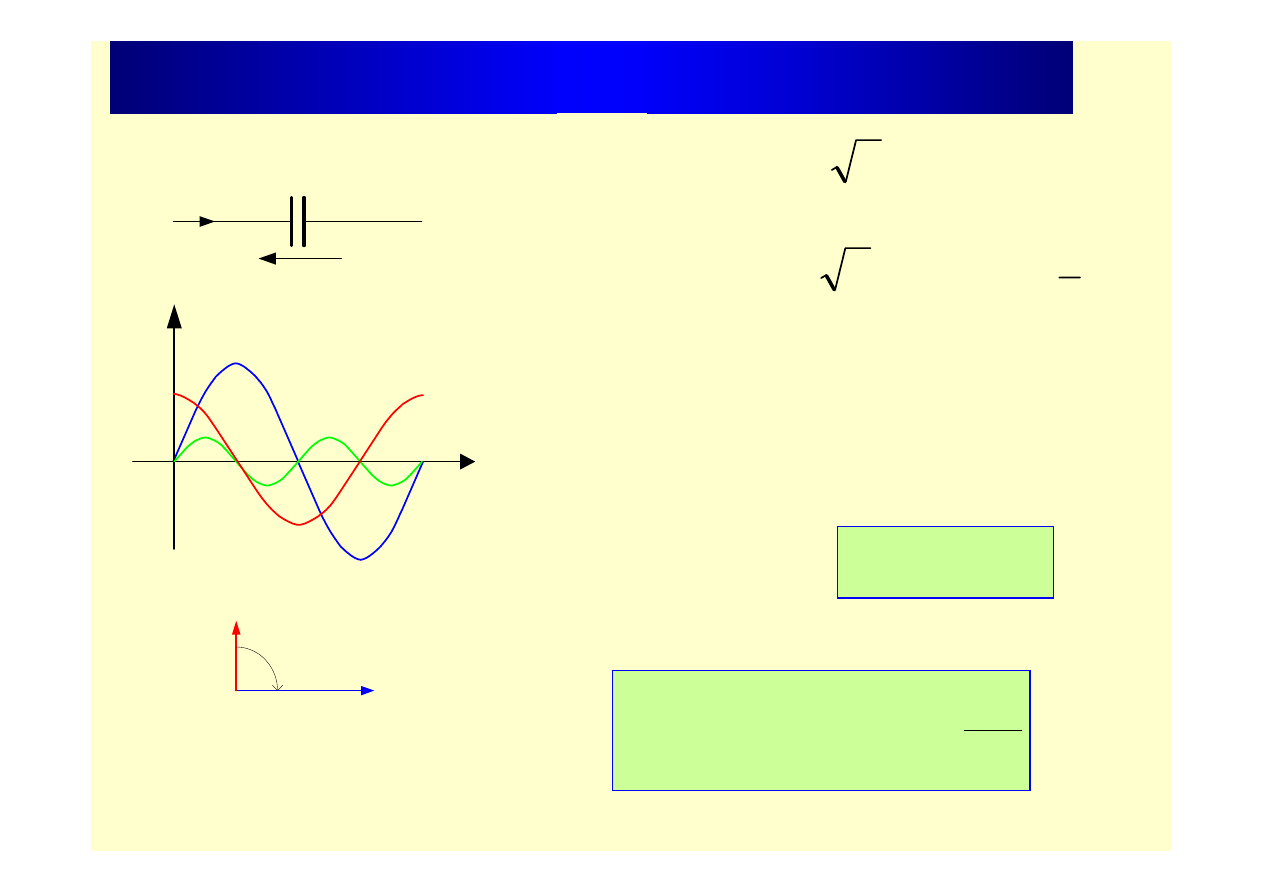
Moc odbiornika pojemnościowego

I

C

U

C

C

U

C

I

C

u

C

i

C

u

C

i

C

t

f

p

t

I

U

i

u

p

C

C

C

C

ω

2

sin

2

=

=

t

U

u

C

C

ω

sin

2

=

)

sin(

2

2

π

ω +

=

t

I

i

c

C

0

=

=

śr

P

P

C

C

C

C

C

C

def

C

X

U

X

I

I

U

Q

2

2

=

=

=

Moc bierna -

Moc czynna -

[var]

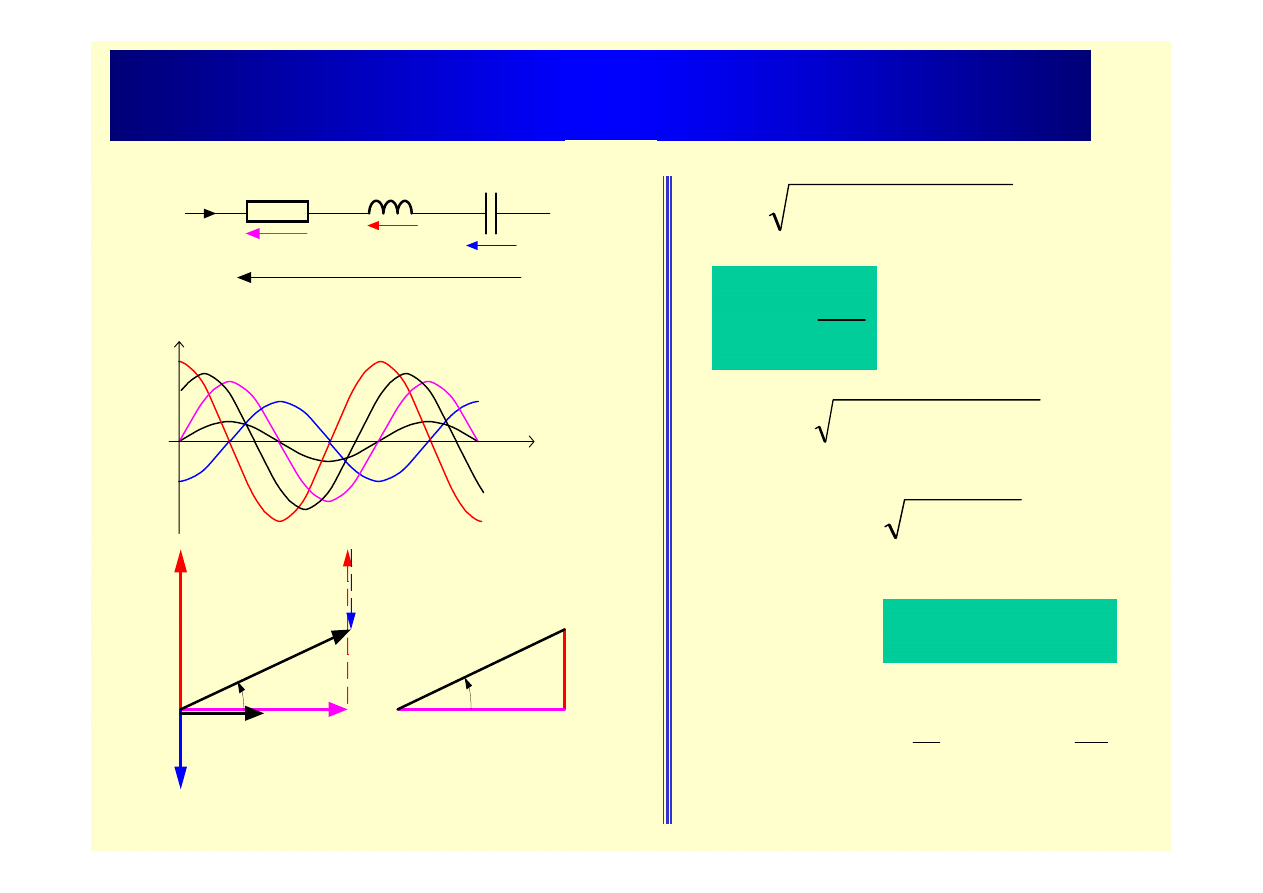
Szeregowe połączenie elementów R,L,C

U

U

R

U

L

L

U

C

R

C

I

U

R

U

U

L

I

U

C

Z

X

R

f

f

u

C

u

R

u

u

L

i

ω t

2

2

)

(

C

L

R

U

U

U

U

−

+

=

I

U

Z

def

=

- impedancja (

Ω

)

C

L

)

(

X

X

R

Z

−

+

=

2

2

2

2

X

R

Z

+

=

Reaktancja
zastępcza

C

L

X

X

X

−

=

)

(

)

(cos

R

X

tg

arc

Z

R

arc

=

=

ϕ

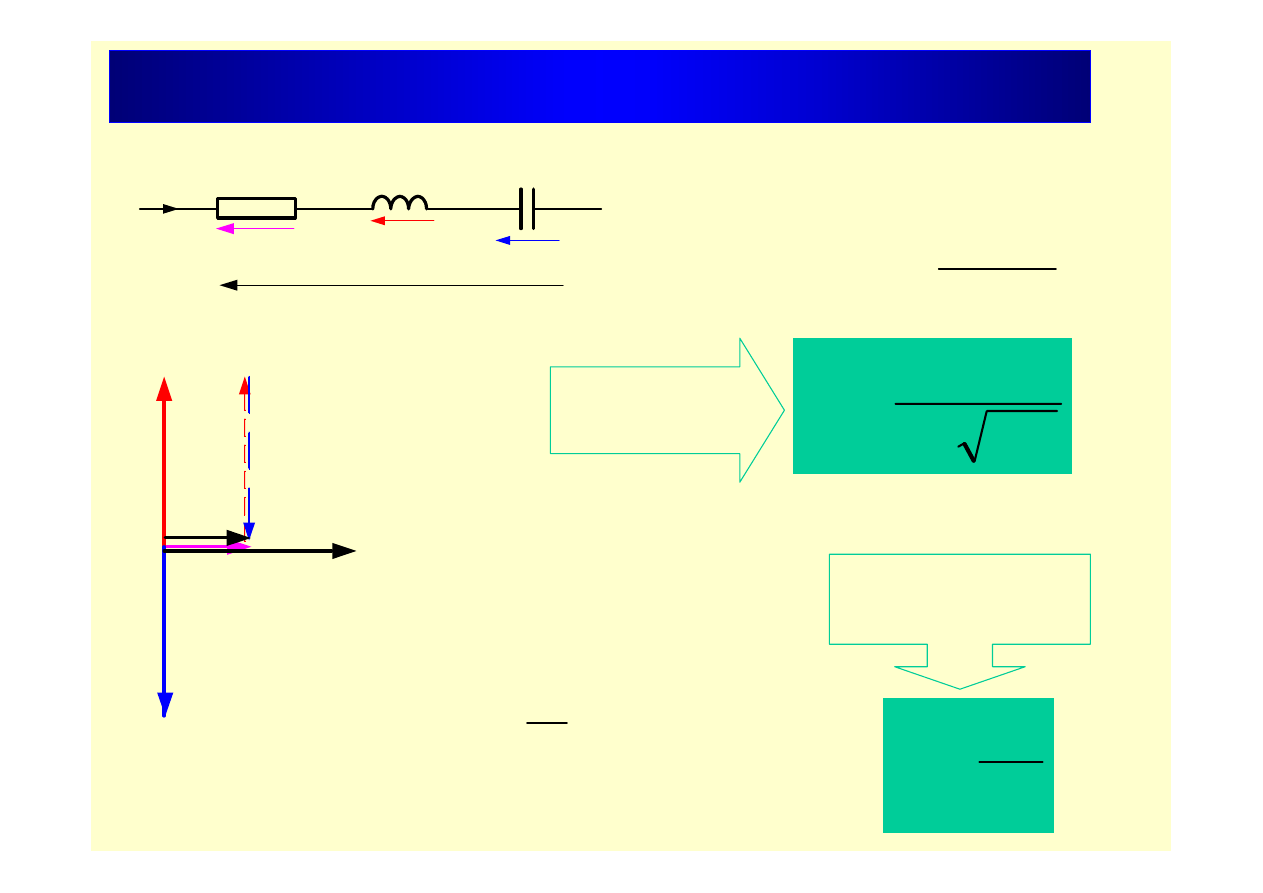
Rezonans napięć

C

L

X

X

=

U

U

R

U

L

X

L

U

C

R

X

C

I

C

f

L

f

π

π

2

1

2

=

LC

f

r

π

2

1

=

Częstotliwość
rezonansowa

U

R

U

U

L

I

U

C

R

U

U

=

Dobroć obwodu
rezonansowego

R

Z

=

R

U

I

=

R

L

def

U

U

Q

=

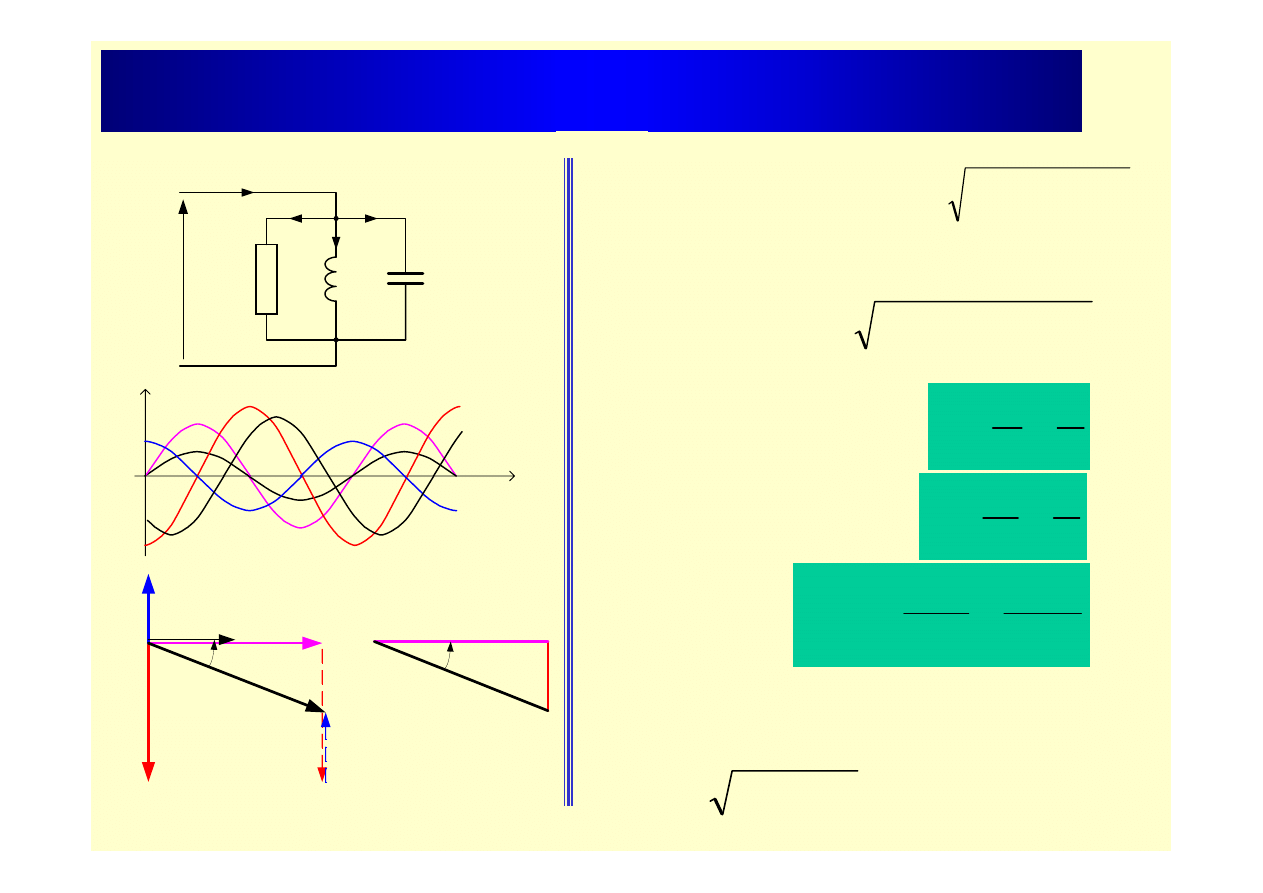
Równoległe połączenie elementów R,L,C

U

I

R

I

L

L

I

C

R

C

I

I

R

U

I

L

I

I

C

f

Y

G

f

i

L

i

R

i

i

L

u

ω t

B

2

2

)

(

C

L

R

I

I

I

I

−

+

=

Z

U

I

Y

def

1

=

=

2

2

)

(

C

L

B

B

G

Y

−

+

=

C

L

B

B

B

−

=

2

2

B

G

Y

+

=

Z wykresu wektorowego:

Po podzieleniu przez napięcie U otrzymamy:

gdzie:

R

U

I

G

R

1

=

=

susceptancja

ind.(poj) –

)

(

)

(

)

(

1

C

L

C

L

def

C

L

X

U

I

B

=

=

– susceptancja

zastępcza

[S]

[S]

[S]

admitancja –

konduktancja –

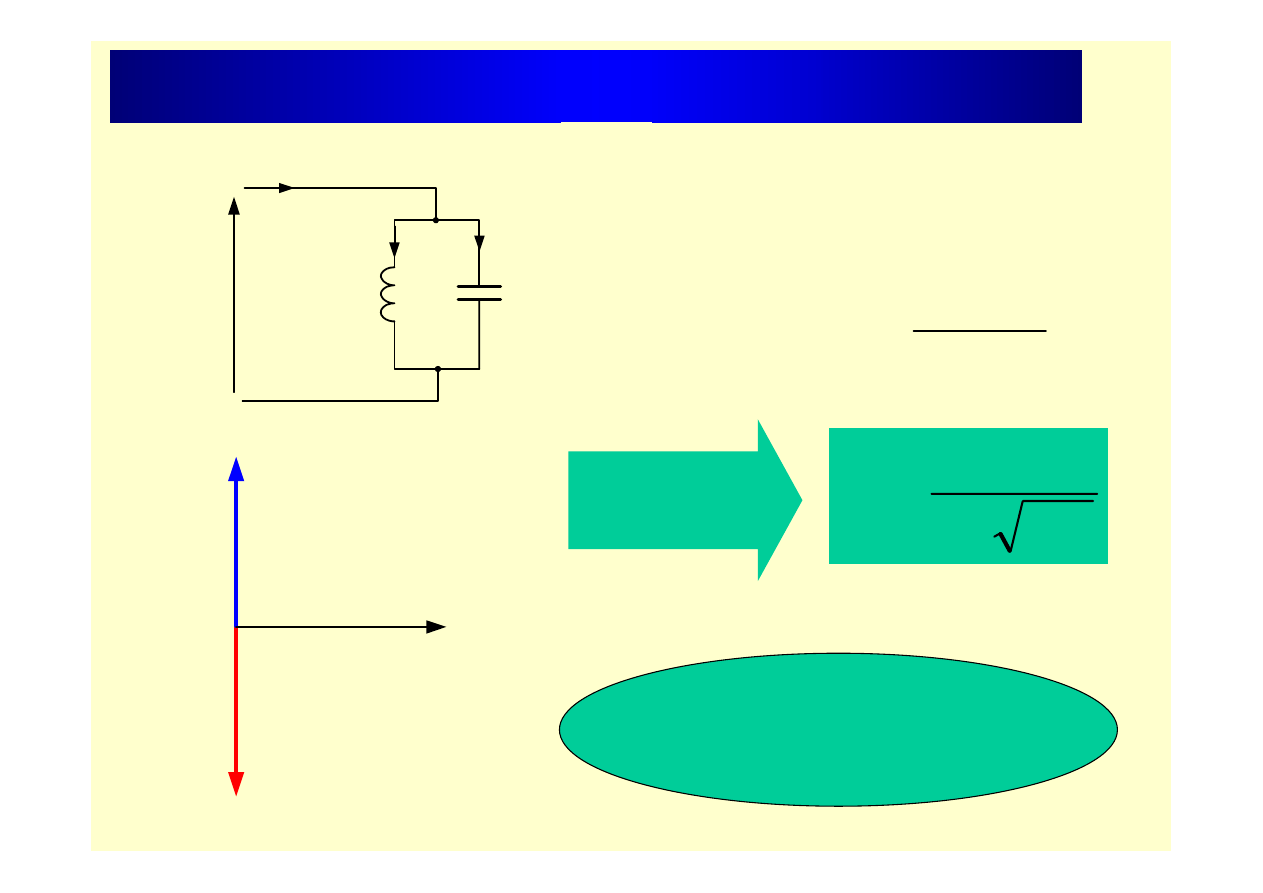
Rezonans prądów (obwód idealny)

U

I

L

X

L

I

C

X

C

I

C

L

C

L

X

X

B

B

=

⇒

=

C

f

L

f

π

π

2

1

2

=

Częstotliwość
rezonansowa

LC

f

r

π

2

1

=

U

I

L

I

C

I=0

∞

=

⇒

=

Z

I 0

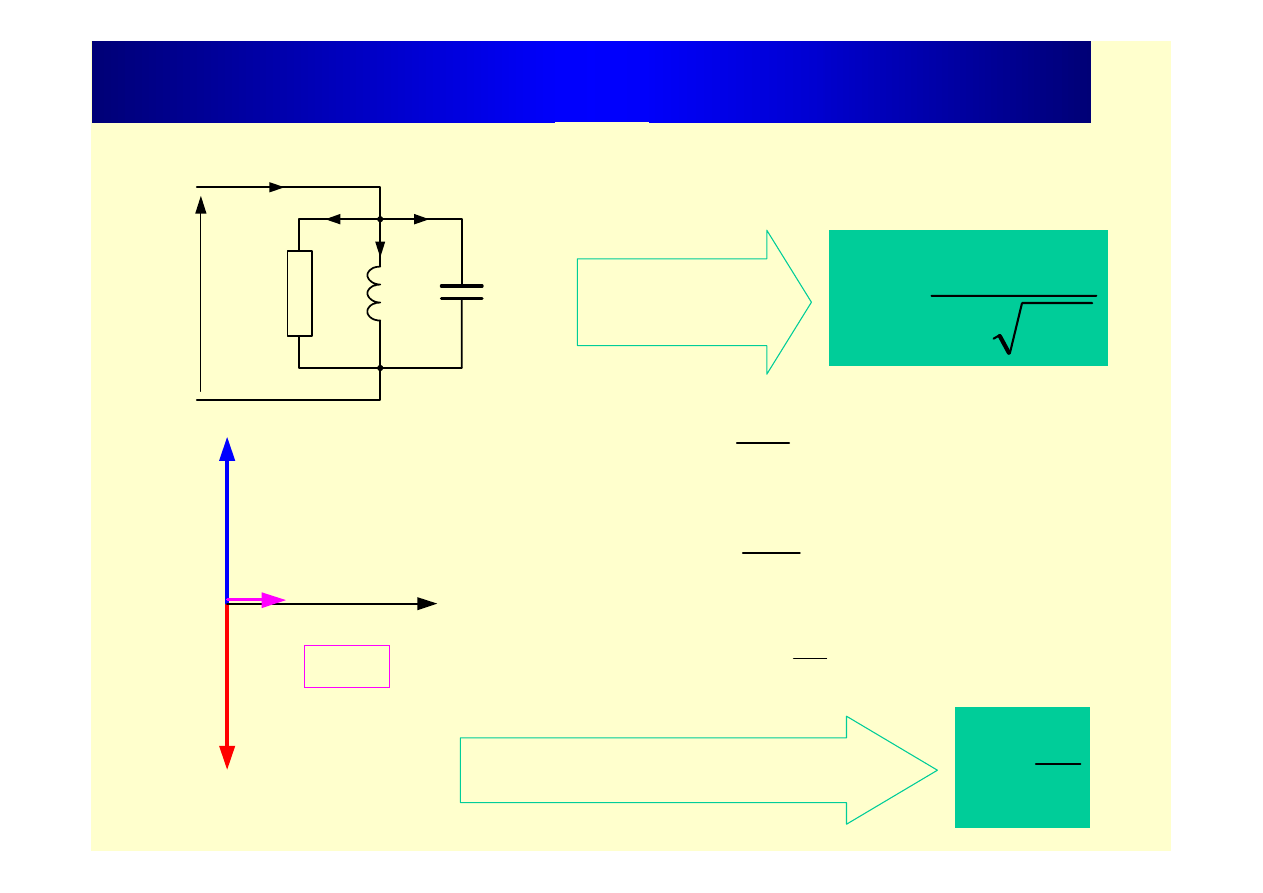
Rezonans prądów (obwód rzeczywisty)

C

L

C

L

X

X

B

B

=

⇒

=

U

I

R

I

L

X

L

I

C

R

X

C

I

Częstotliwość

rezonansowa

LC

f

r

π

2

1

=

G

U

R

U

I

I

R

=

=

=

L

L

L

B

U

X

U

I

=

=

C

C

C

B

U

X

U

I

=

=

U

I

L

I

C

I=I

R

I

R

R

L

I

I

Q

=

Dobroć obwodu rezonansowego

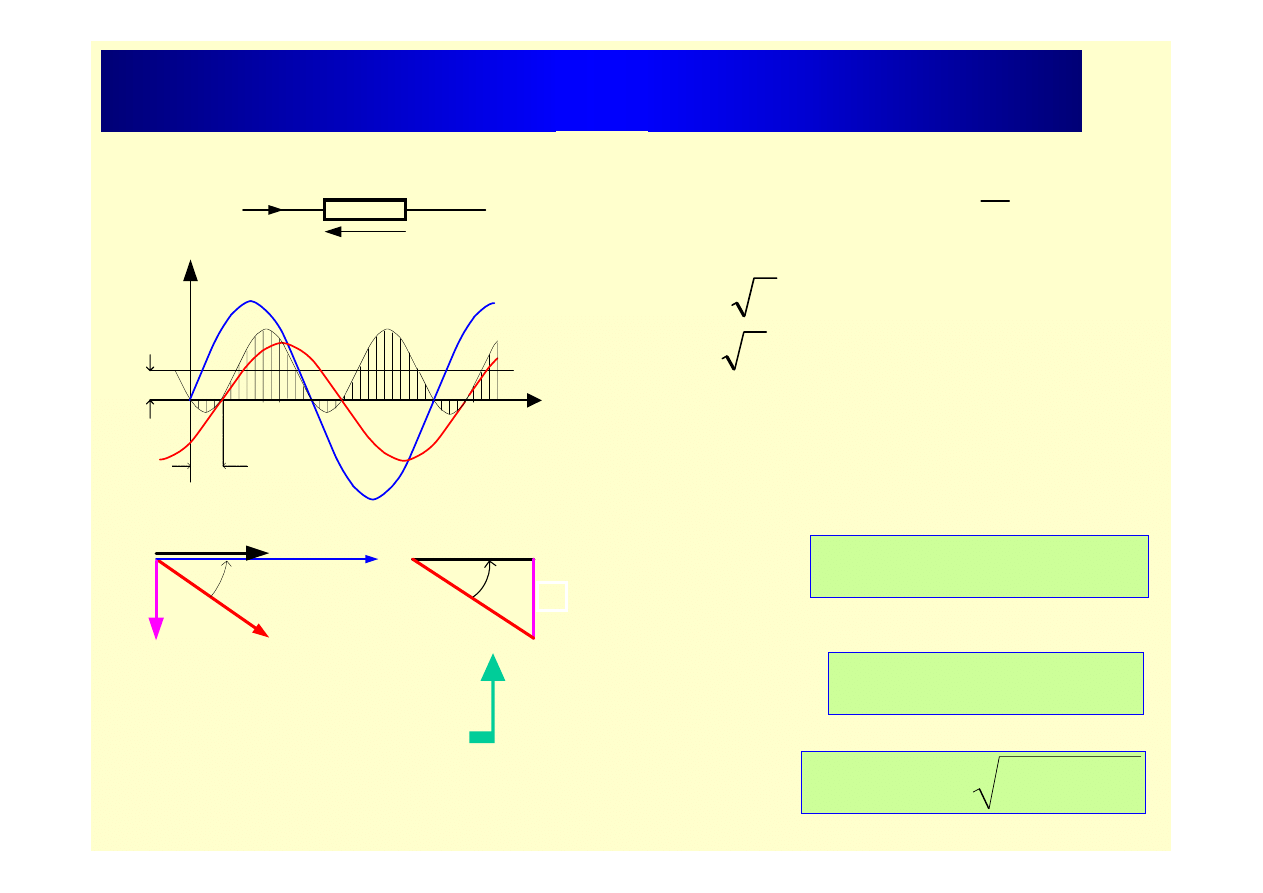
Moc odbiornika prądu przemiennego

∫

=

=

T

śr

dt

i

u

T

P

P

0

1

P

sr

0

ϕ

u

i

u

i

t

p

p

U

I

I

cz

I

b

P

Q

S

ϕ

ϕ

I

U

Z

Moc czynna -

gdzie:

t

U

u

ω

sin

2

=

)

sin(

2

ϕ

ω −

=

t

I

i

- prąd odbiornika

- napięcie odbiornika

Po podstawieniu i przekształceniach
otrzymujemy:

cz

I

U

I

U

P

=

=

ϕ

cos

Moc czynna -

b

UI

I

U

Q

=

=

ϕ

sin

Moc bierna -

Trójkąt mocy

2

2

Q

P

I

U

S

+

=

=

Moc pozorna -

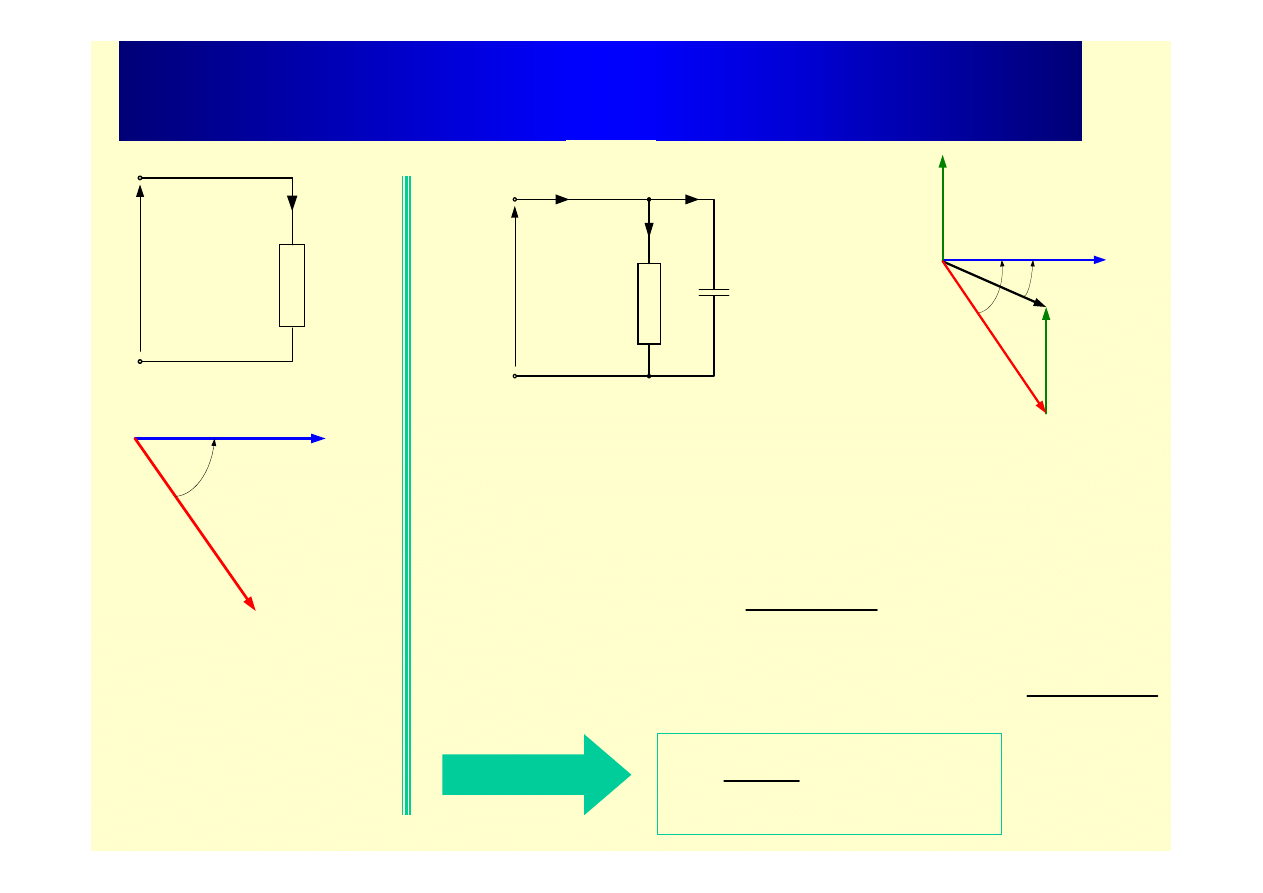
f

odb

U

I

odb

f

I

C

I

C

I

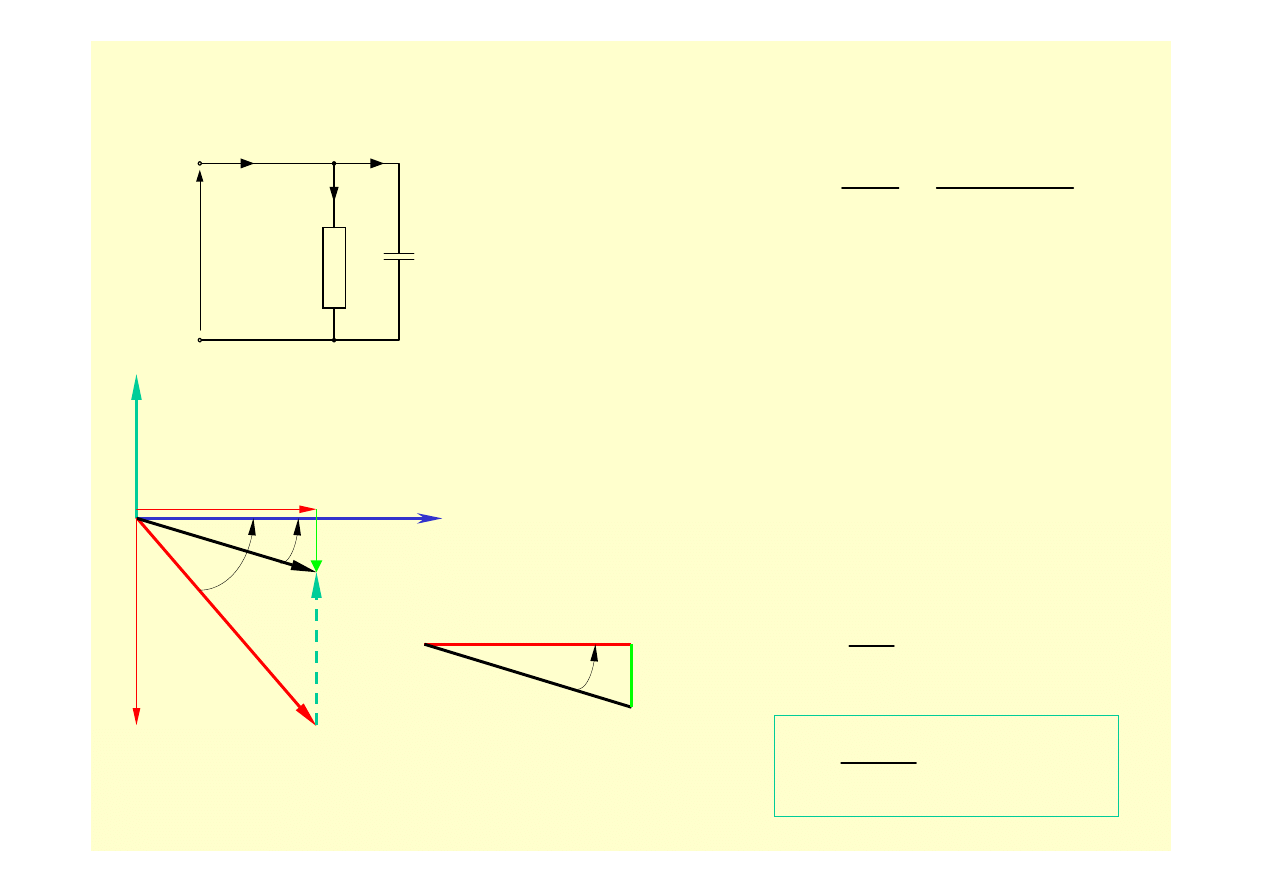
Kompensacja mocy biernej

Poprawa współczynnika mocy

I

odb

U

P

odb

cos

f

odb

I

I

C

C

I

odb

U

P

odb

cosf

odb

Obliczenie pojemności C jaką należy włączyć na
zaciski odbiornika aby zwiększyć współczynnik

mocy z cosf

odb

na cosf:

f

odb

U

I

odb

C

U

I

C

ω

=

odb

odb

odb

U

P

I

ϕ

cos

=

C

odb

odb

odb

odb

I

I

tg

I

−

=

ϕ

ϕ

ϕ

sin

cos

ϕ

ϕ

ϕ

cos

odb

C

odb

I

I

tg

tg

−

=

)

(

2

ϕ

ϕ

ω

tg

tg

U

P

C

odb

odb

−

=

otrzymujemy:

odb

odb

odb

I

U

P

ϕ

cos

=

Po podstawieniu:

oraz

Kompensacja mocy biernej (2)

I

odb

U

P

odb

cos

f

odb

I

I

C

C

odb

C

odb

odb

P

Q

Q

P

Q

tg

−

=

=

ϕ

odb

odb

tg

P

Q

ϕ

=

ϕ

ϕ

tg

P

tg

P

Q

odb

odb

odb

C

−

=

f

P

S

Q

I

C

U

I

odb

I

C

I

f

odb

f

I

odb

cosf

odb

I

odb

sinf

odb

)

(

ϕ

ϕ

tg

tg

P

Q

odb

odb

C

−

=

C

U

X

U

Q

C

C

ω

2

2

=

=

)

(

2

ϕ

ϕ

ω

tg

tg

U

P

C

odb

−

=

Obliczanie obwodów prądu

sinusoidalnego przy użyciu rachunku

zespolonego

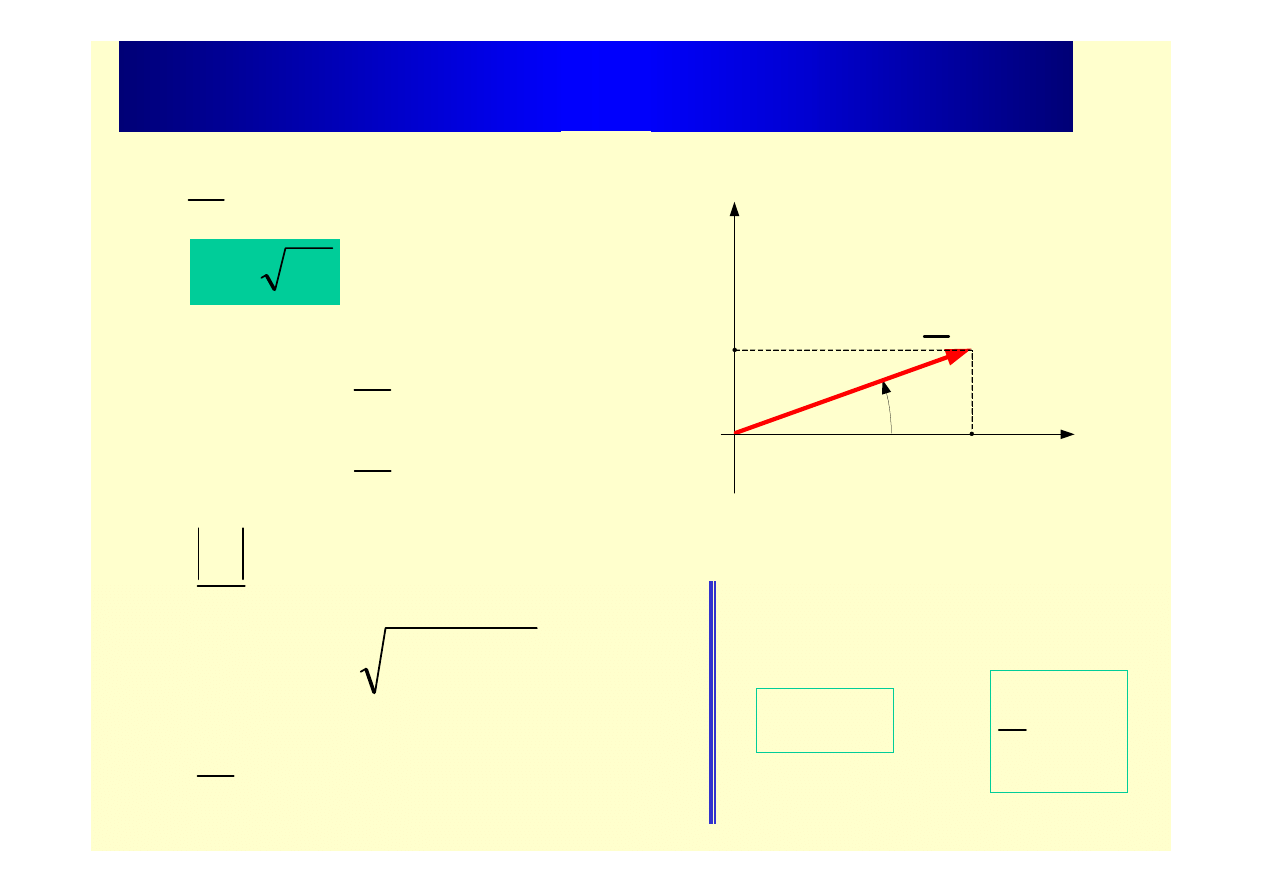
Liczby zespolone (postać algebraiczna)

y

x

jW

W

W

+

=

Im

Re

α

W

W

x

W

y

1

−

=

j

)

Re(W

W

x

=

)

Im(W

W

y

=

W

W

=

Warto zapamiętać!

2

2

y

x

W

W

W

+

=

j

j

−

=

1

1

2

−

=

j

α

α

sin

cos

W

j

W

W

+

=

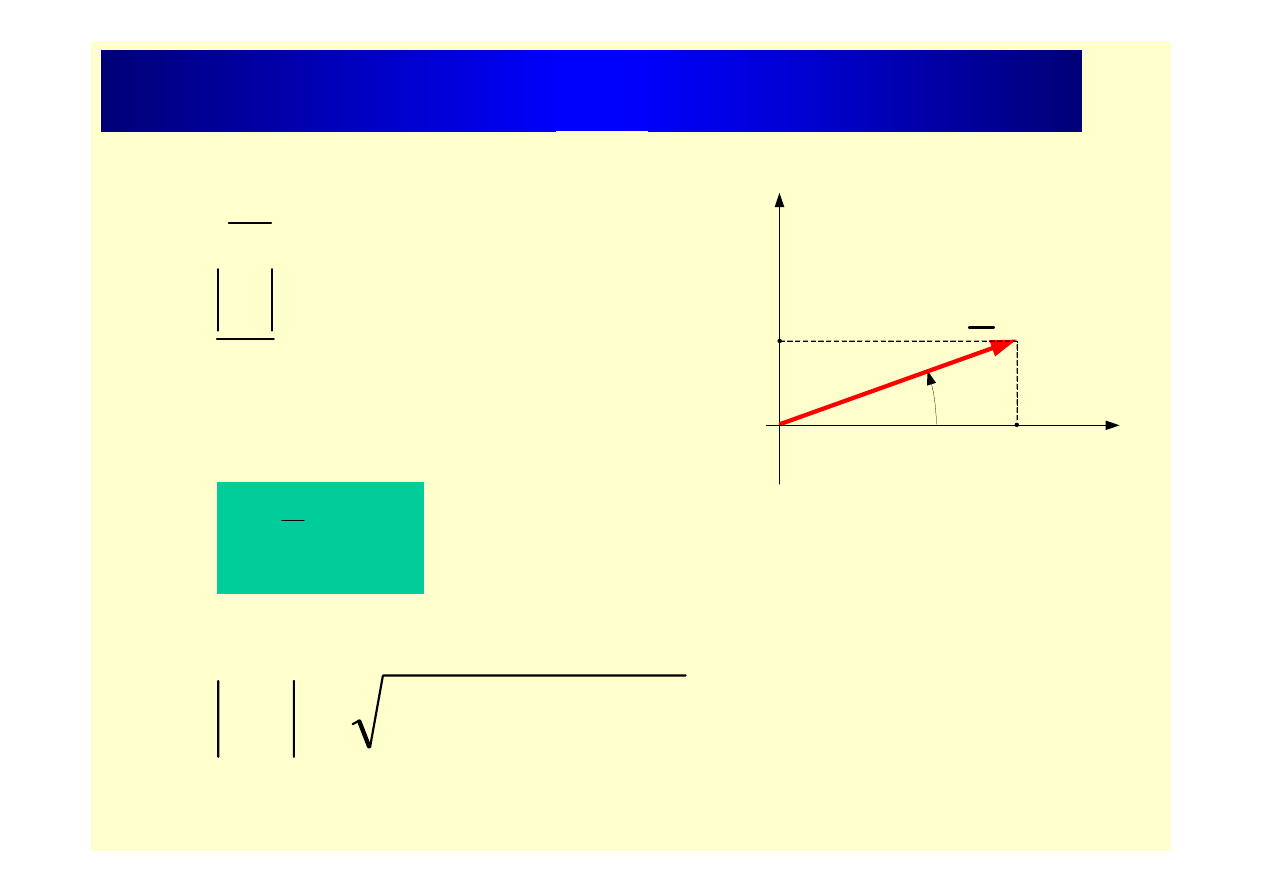
Liczby zespolone (postać wykładnicza)

α

j

We

W

=

Im

Re

α

W

W

x

W

y

W

W

=

α

α

α

sin

cos

j

e

j

+

=

j

e

j

=

2

π

1

sin

cos

2

2

=

+

=

α

α

α

j

e

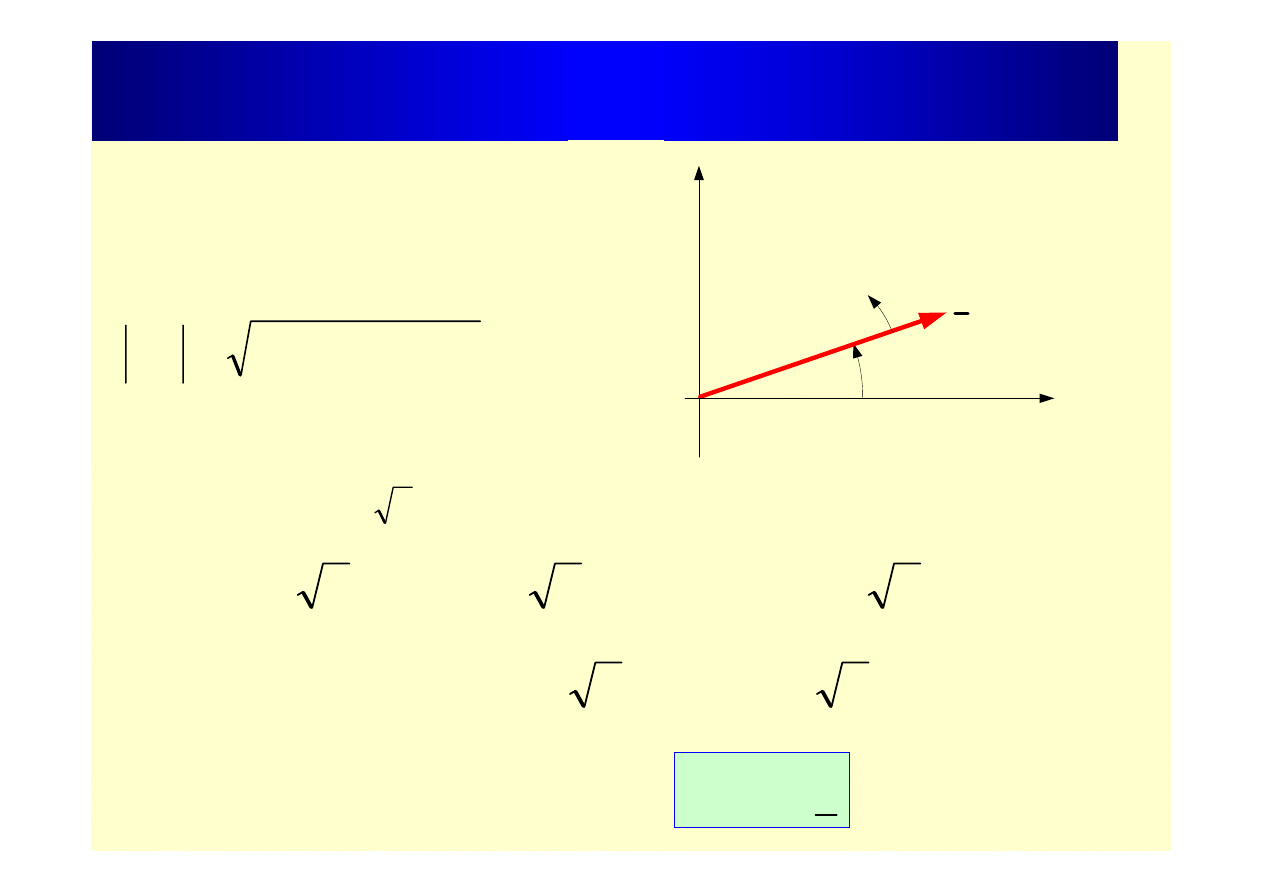
Wielkości sinusoidalne na płaszczyźnie

zespolonej

α

α

α

sin

cos

j

e

j

+

=

1

sin

cos

2

2

=

+

=

α

α

α

j

e

Im

I

Re

ω

α

Wektor o amplitudzie wirujący na płaszczyźnie zespolonej z prędkością

ω

.

I

2

)

sin(

2

)

cos(

2

2

)

(

α

ω

α

ω

α

ω

+

+

+

=

+

t

I

j

t

I

Ie

t

j

)

sin(

2

)

2

Im(

)

(

α

ω

α

ω

+

=

=

+

t

I

Ie

i

t

j

Wartość chwilowa

I

Ie

j

=

α

Skuteczna wartość zespolona

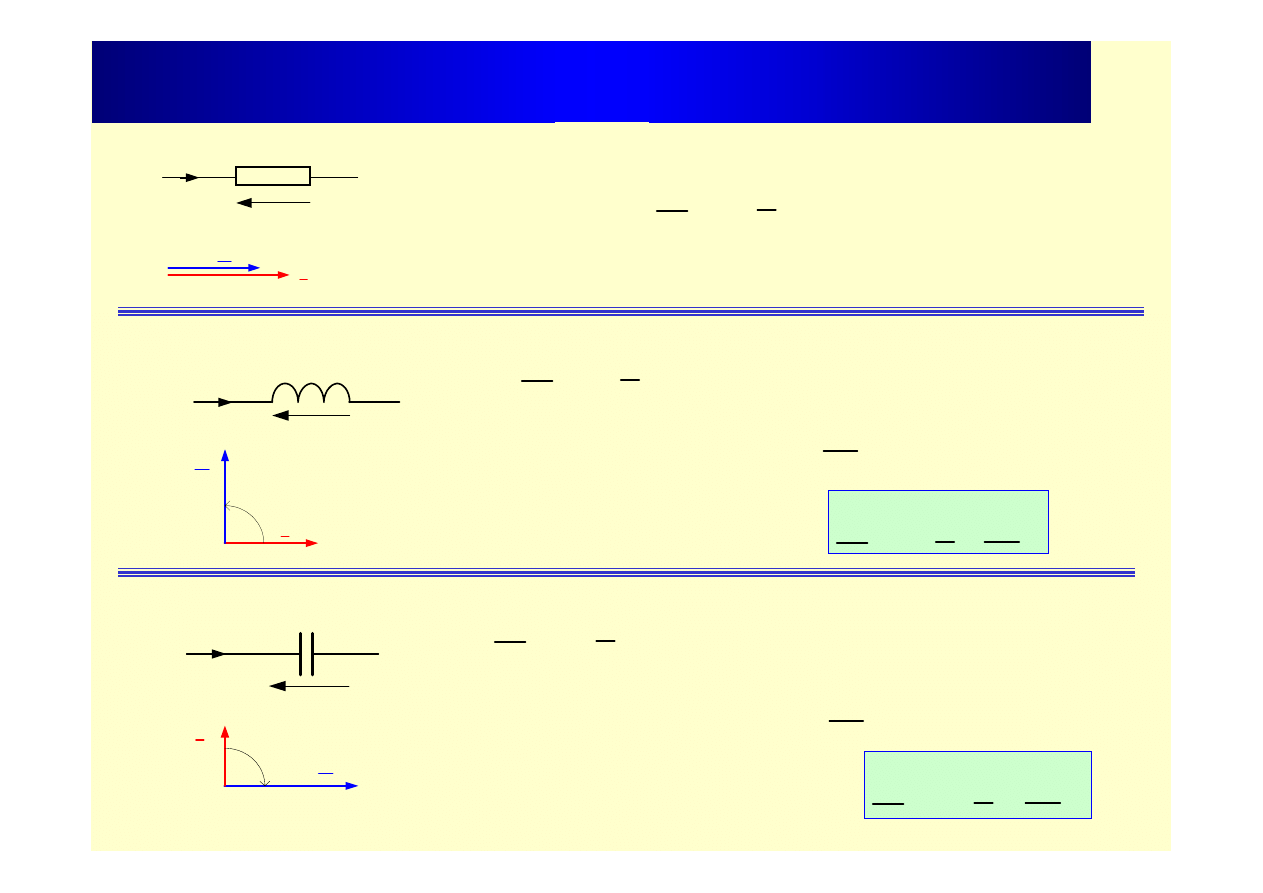
Obwody z elementami R,L,C

I

R

U

R

R

U

R

I

R

R

I

U

R

R

=

L

L

L

jX

I

U

=

I

L

U

L

X

L

U

L

I

L

f

L

L

X

jX

=

L

L

L

X

I

U

=

)

(

C

C

C

jX

I

U

−

=

I

C

U

C

X

C

U

C

I

C

f

C

C

X

jX

=

−

C

C

C

X

I

U

=

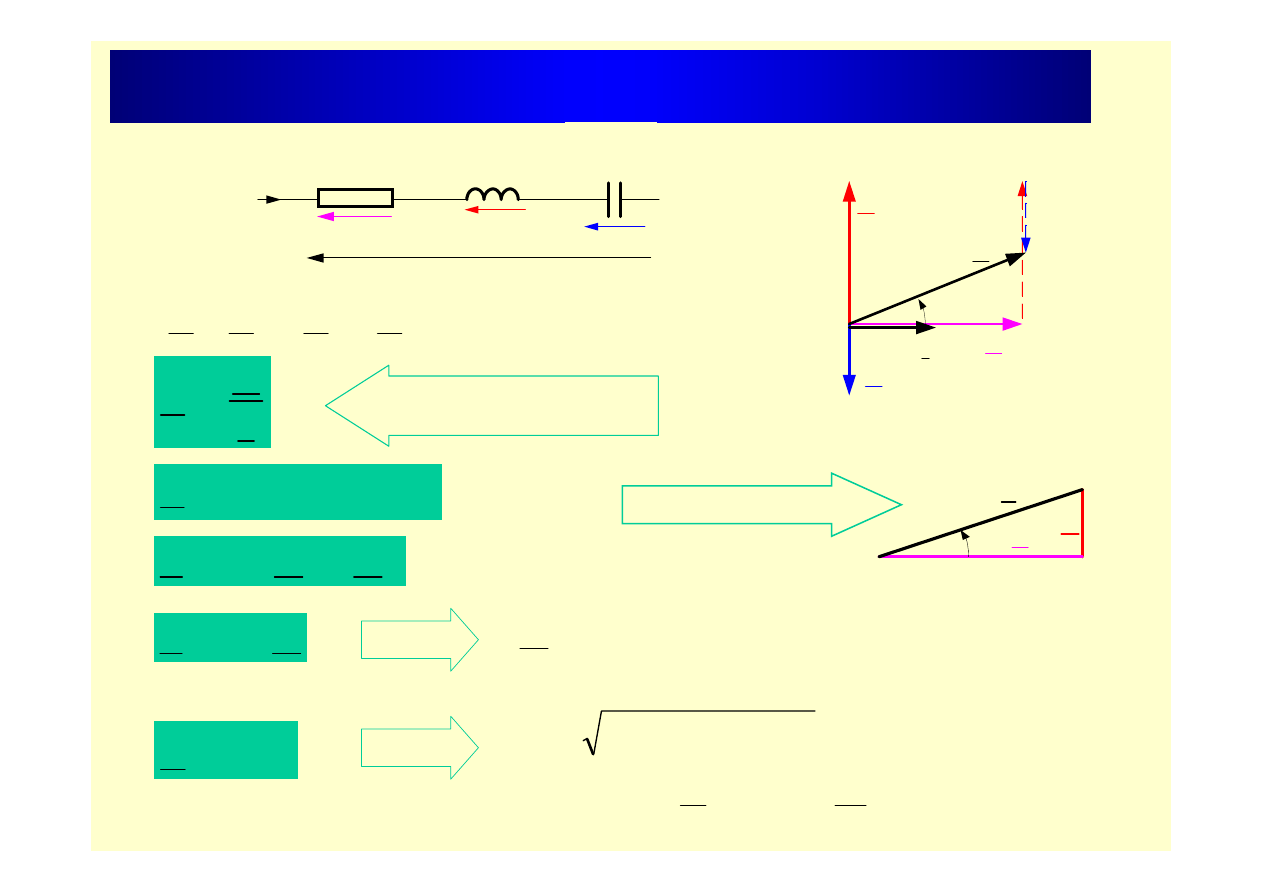
Szeregowe łączenie R,L,C

U

U

R

U

L

X

L

U

C

R

X

C

I

U

R

U

U

L

I

U

C

f

C

L

R

U

U

U

U

+

+

=

I

U

Z

def

=

zastępcza impedancja

zespolona

C

L

jX

jX

R

Z

−

+

=

Z

X

R

f

Trójkąt impedancji

C

L

X

X

R

Z

+

+

=

ϕ

j

Ze

Z

=

)

(

)

(cos

R

X

tg

arc

Z

R

arc

=

=

ϕ

2

2

)

(

C

L

X

X

R

Z

−

+

=

X

R

Z

+

=

gdzie:

)

(

C

L

X

X

j

X

−

=

gdzie:

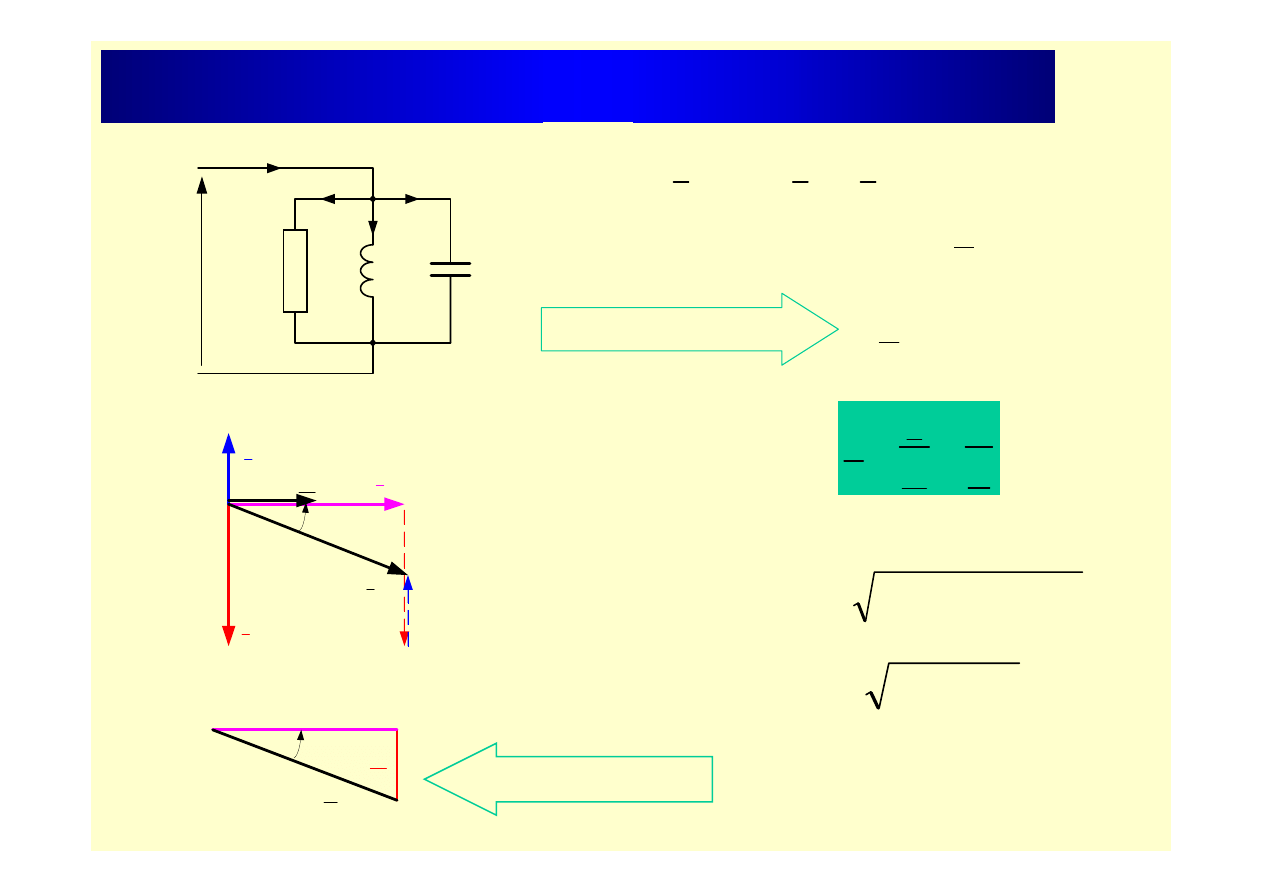
Równoległe łączenie R,L,C

U

I

R

I

L

X

L

I

C

R

X

C

I

C

L

R

I

I

I

I

+

+

=

Po podzieleniu powyższego przez U otrzymujemy:

admitancja zespolona

C

L

jB

jB

G

Y

+

−

=

Z

U

I

Y

1

=

=

I

R

U

I

L

I

I

C

f

2

2

)

(

C

L

R

I

I

I

I

−

+

=

2

2

B

G

Y

+

=

Y

B

G

f

Trójkąt admitancji

C

L

B

B

B

−

=

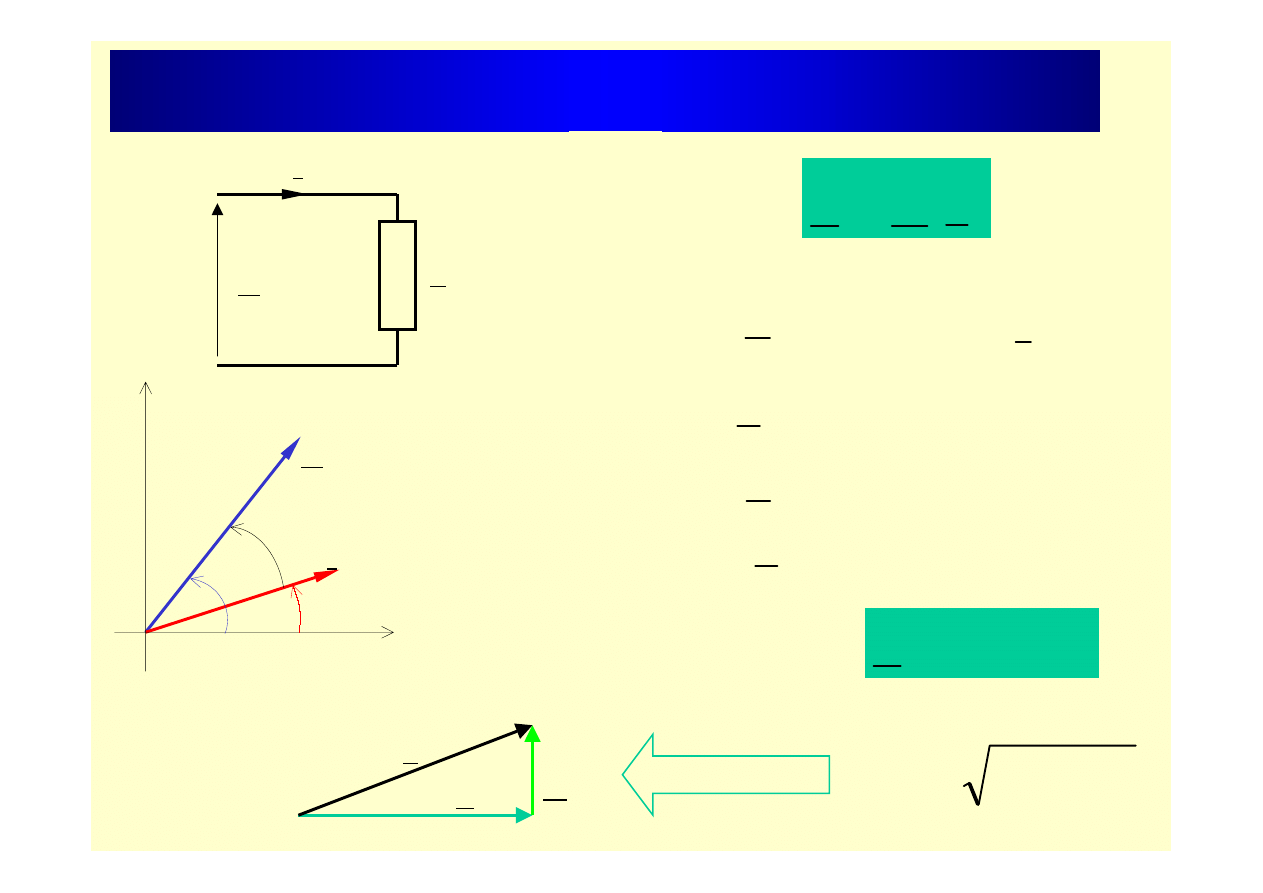
Moc zespolona

I

*

I

U

S

=

Moc zespolona -

Im

Re

y

U

y

I

f

U

I

Z

Po podstawieniu:

U

U

j

Ue

U

ψ

=

I

j

Ie

I

ψ

−

=

*

oraz

otrzymujemy:

ϕ

ψ

ψ

j

j

e

I

U

Ie

U

S

I

U

=

=

−

)

(

ϕ

j

e

S

S

=

ϕ

ϕ

sin

cos

I

jU

I

U

S

+

=

Q

j

P

S

+

=

S

P

Q

Trójkąt mocy

2

2

Q

+

= P

S

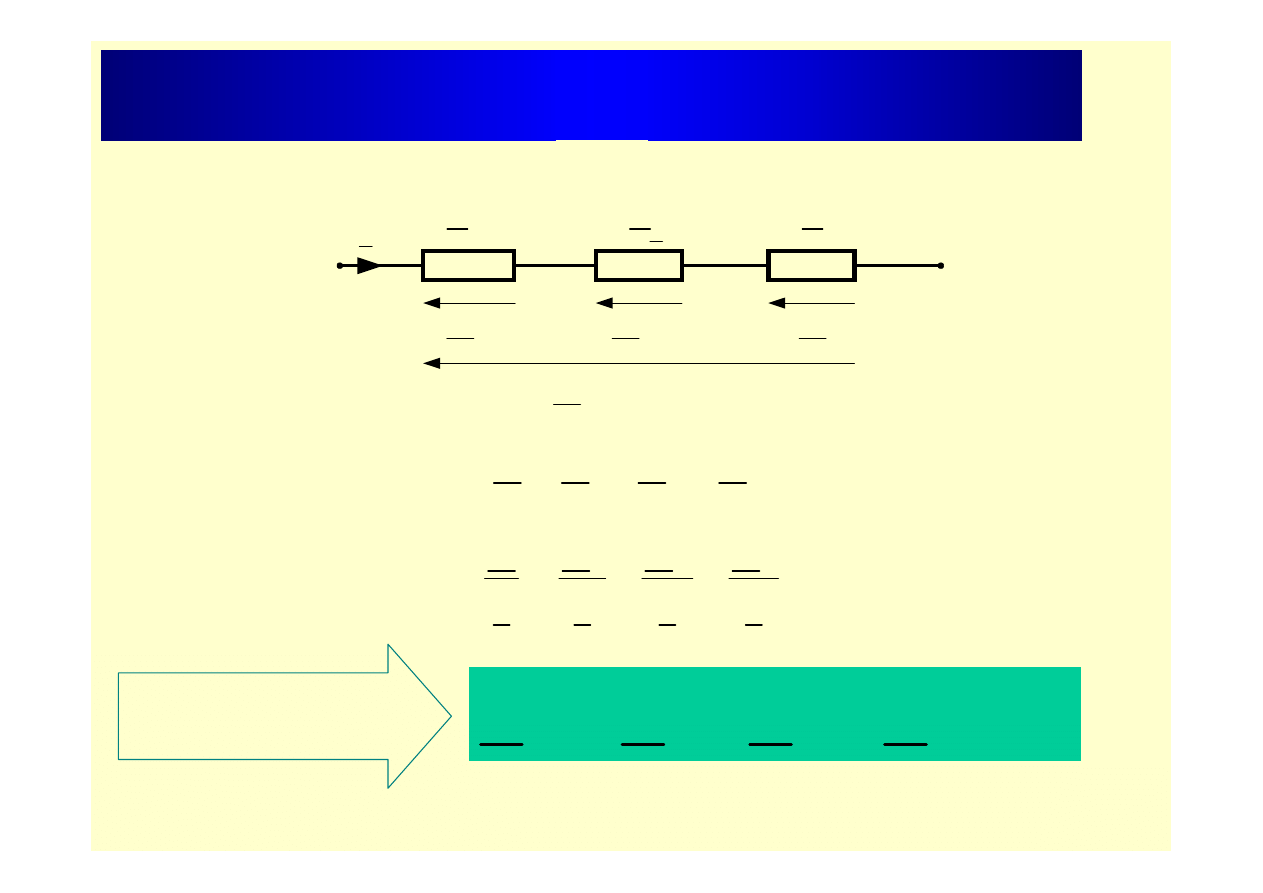
Szeregowe łączenie impedancji

Z

1

Z

2

Z

3

U

1

U

3

U

I

U

2

3

2

1

U

U

U

U

+

+

=

I

U

I

U

I

U

I

U

3

2

1

+

+

=

zastępcza impedancja

zespolona

⋅⋅

⋅

+

+

+

=

3

2

1

Z

Z

Z

Z

z

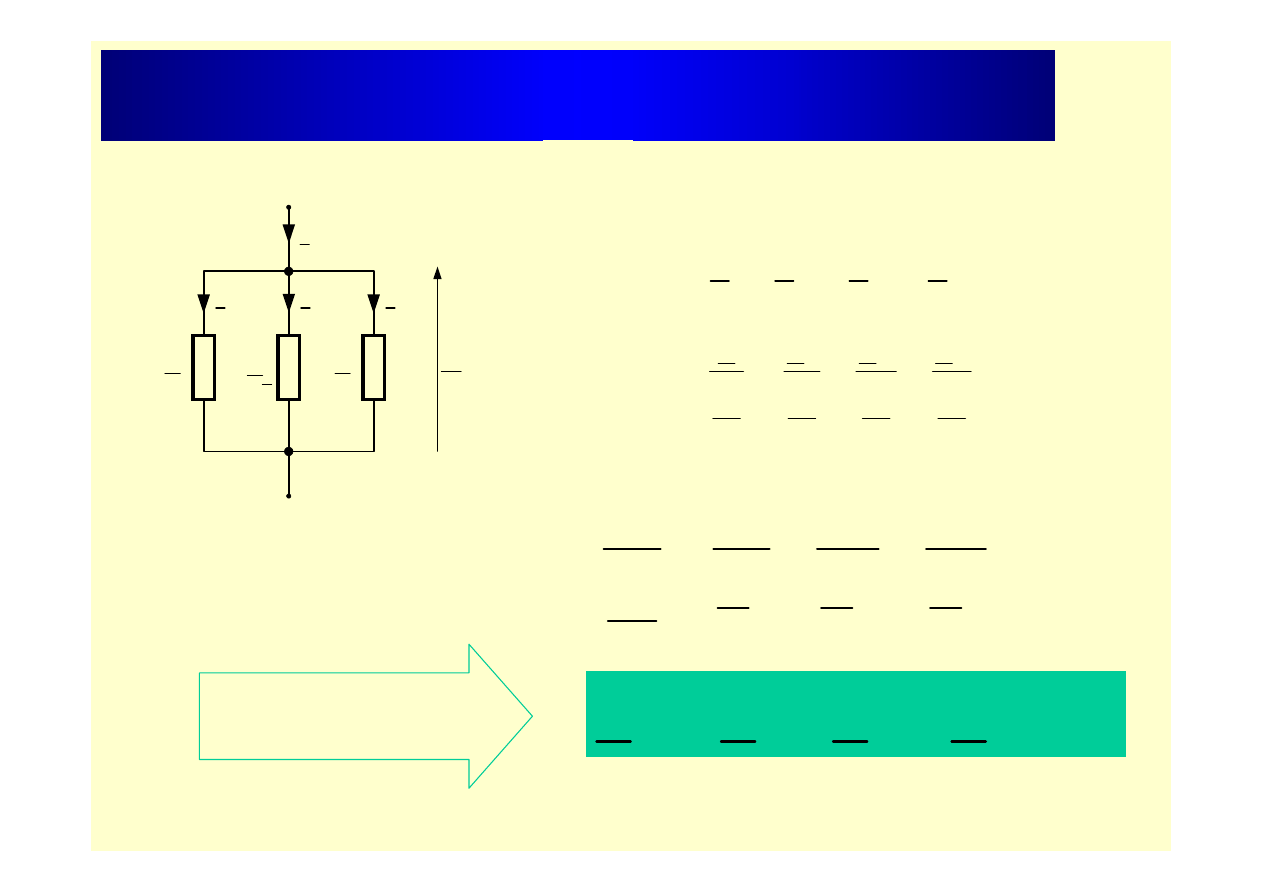
Równoległe łączenie impedancji

Z

1

Z

2

Z

3

I

1

I

2

I

3

I

U

3

2

1

I

I

I

I

+

+

=

U

I

U

I

U

I

U

I

3

2

1

+

+

=

⋅⋅

⋅

+

+

+

=

3

2

1

1

1

1

1

Z

Z

Z

Z

z

zastępcza admitancja

zespolona

⋅⋅

⋅

+

+

+

=

3

2

1

Y

Y

Y

Y

z

Układy prądu trójfazowego

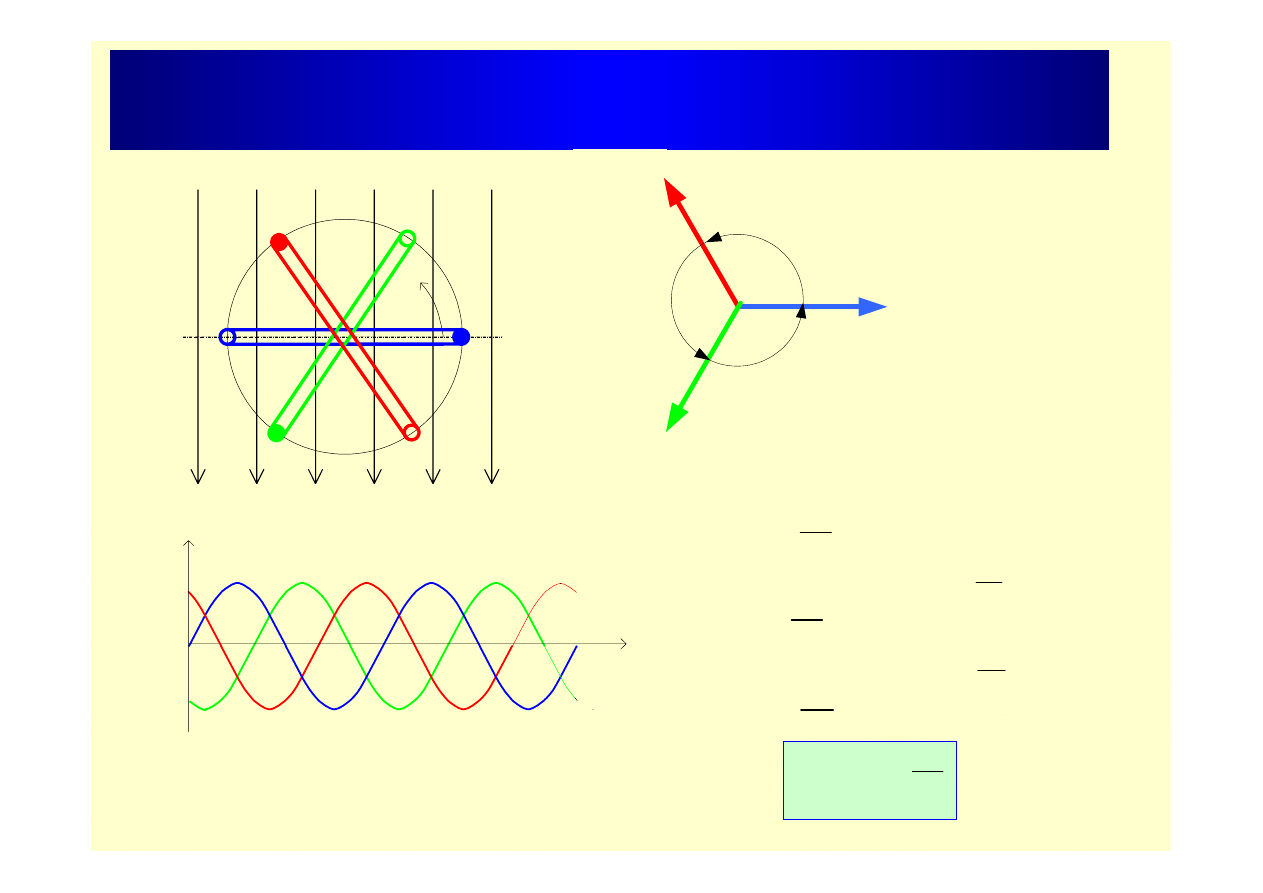
Napięcie trójfazowe (wytwarzanie)

U

a

U

c

U

b

120

o

120

o

120

o

U

U

U

U

c

b

a

=

=

=

B

ω

U

U

a

=

u

a

u

b

u

c

ω t

U

a

e

U

U

j

b

2

3

2

=

=

−

π

U

a

e

U

U

j

c

=

=

3

2

π

3

2

π

j

e

a

=

przy czym:

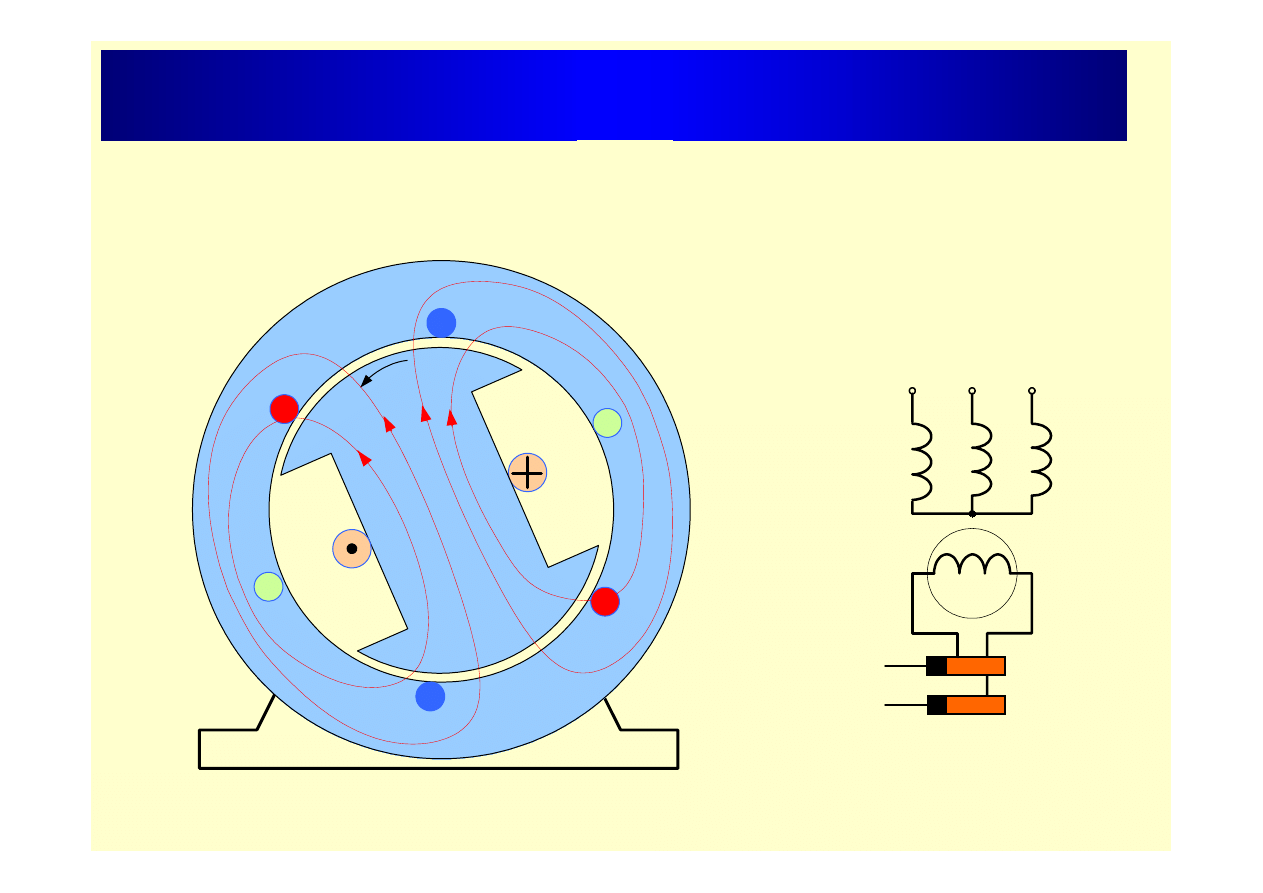
Prądnica napięcia trójfazowego

(zasada konstrukcji)

W

W ’

U

U ’

V

V ’

Φ

stojan

wirnik

U

V

W

+

-

U

A

I

A

U

B

U

C

I

B

I

C

f

f

f

U

A

I

A

f

U

B

I

B

f

U

C

I

C

f

C

B

A

I

I

I

I

+

+

=

0

I

A

U

B

U

C

U

A

I

B

I

C

U

A

U

B

U

C

Z

f

Z

f

Z

f

I

A

U

B

U

C

U

A

I

B

I

C

U

A

U

B

U

C

U

CA

U

AB

U

BC

I

0

=0

Z

f

Z

f

Z

f

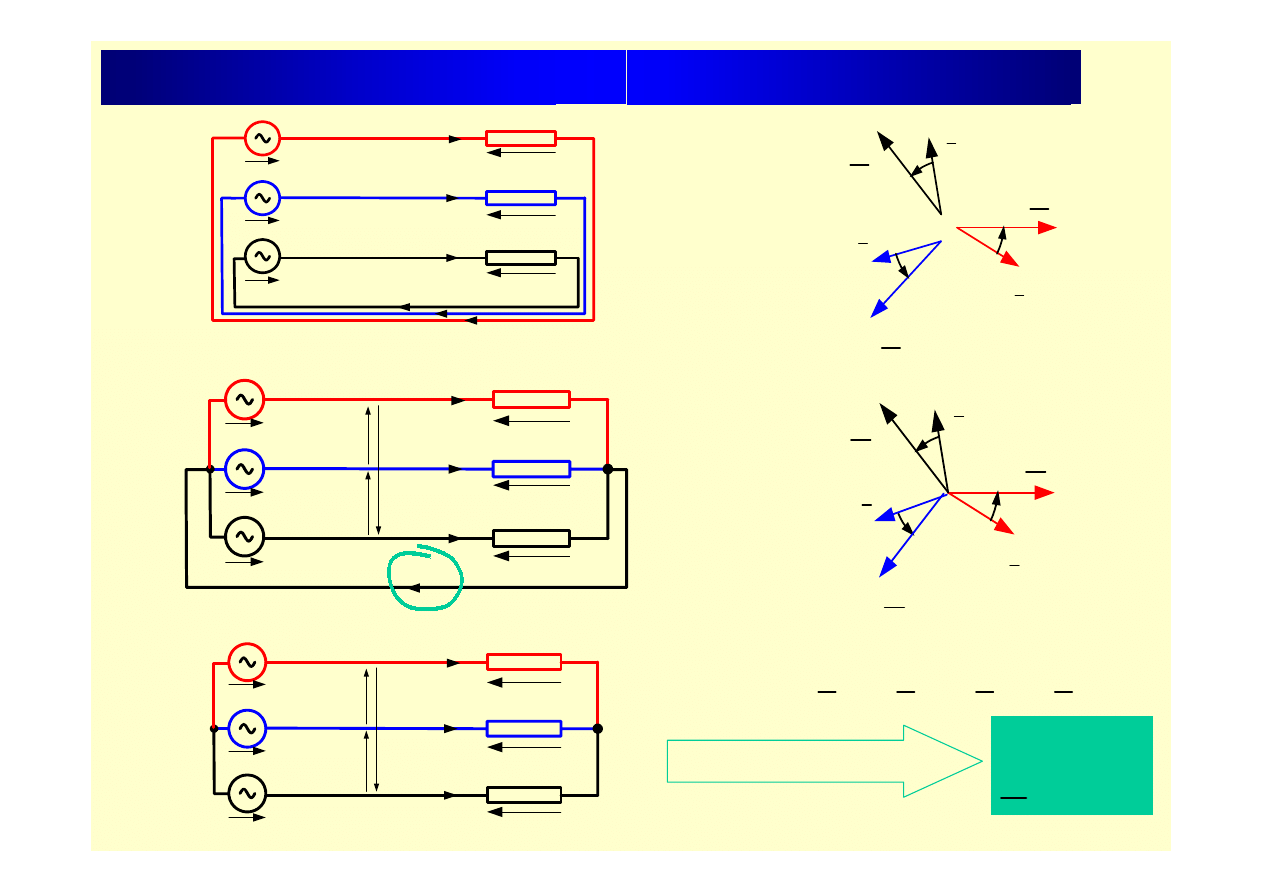
Układ trójfazowy jako zespół 3.symetrycznych obwodów jednofazowych

I

A

U

B

U

C

U

A

I

B

I

C

U

A

U

B

U

C

U

CA

U

AB

U

BC

Z

f

Z

f

Z

f

0

0

=

I

W układzie symetrycznym:

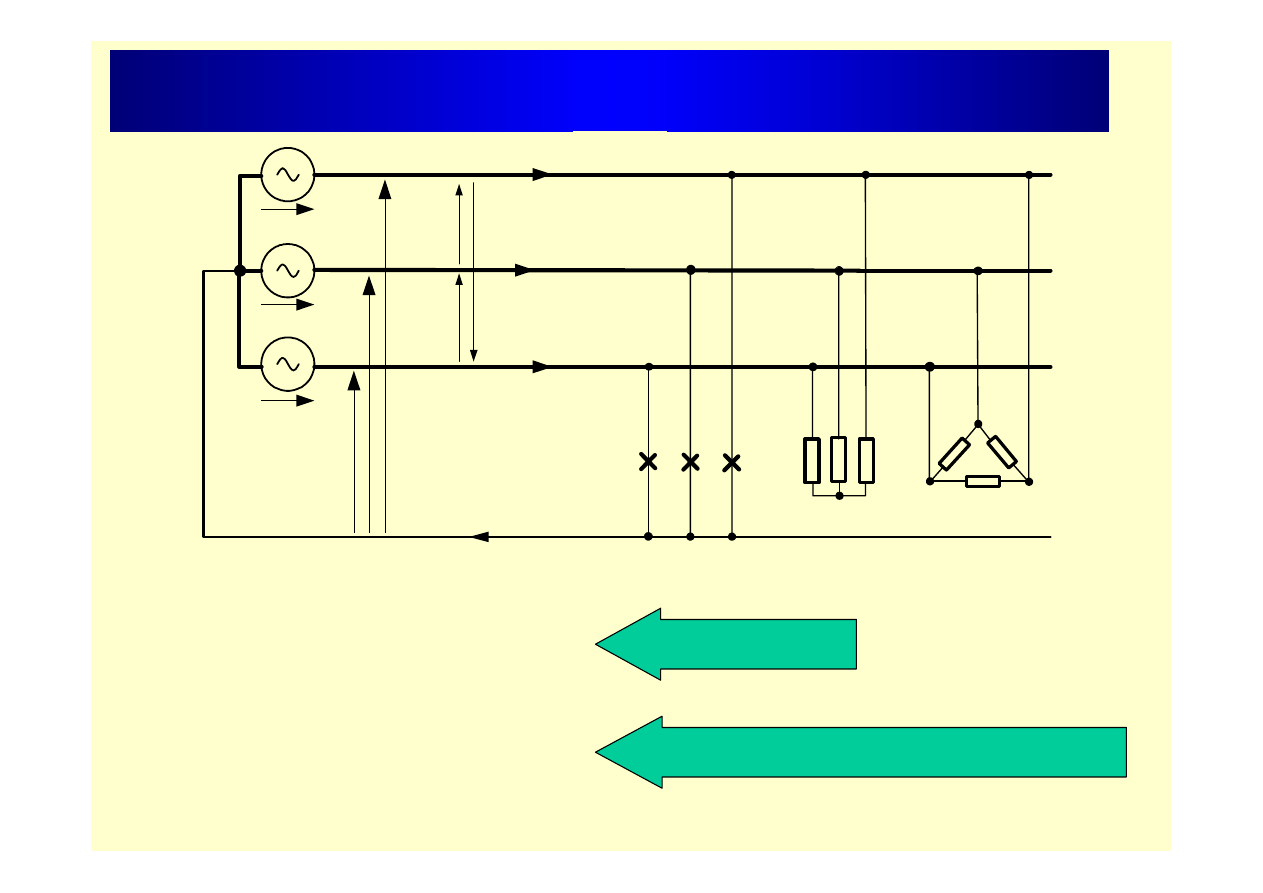
I

A

U

C

U

CA

U

AB

U

BC

I

B

I

C

I

O

U

A

U

B

Układ czteroprzewodowy

napięcia fazowe

f

C

B

A

U

U

U

U

=

=

=

napięcia przewodowe (międzyfazowe)

U

U

U

U

CA

BC

AB

=

=

=

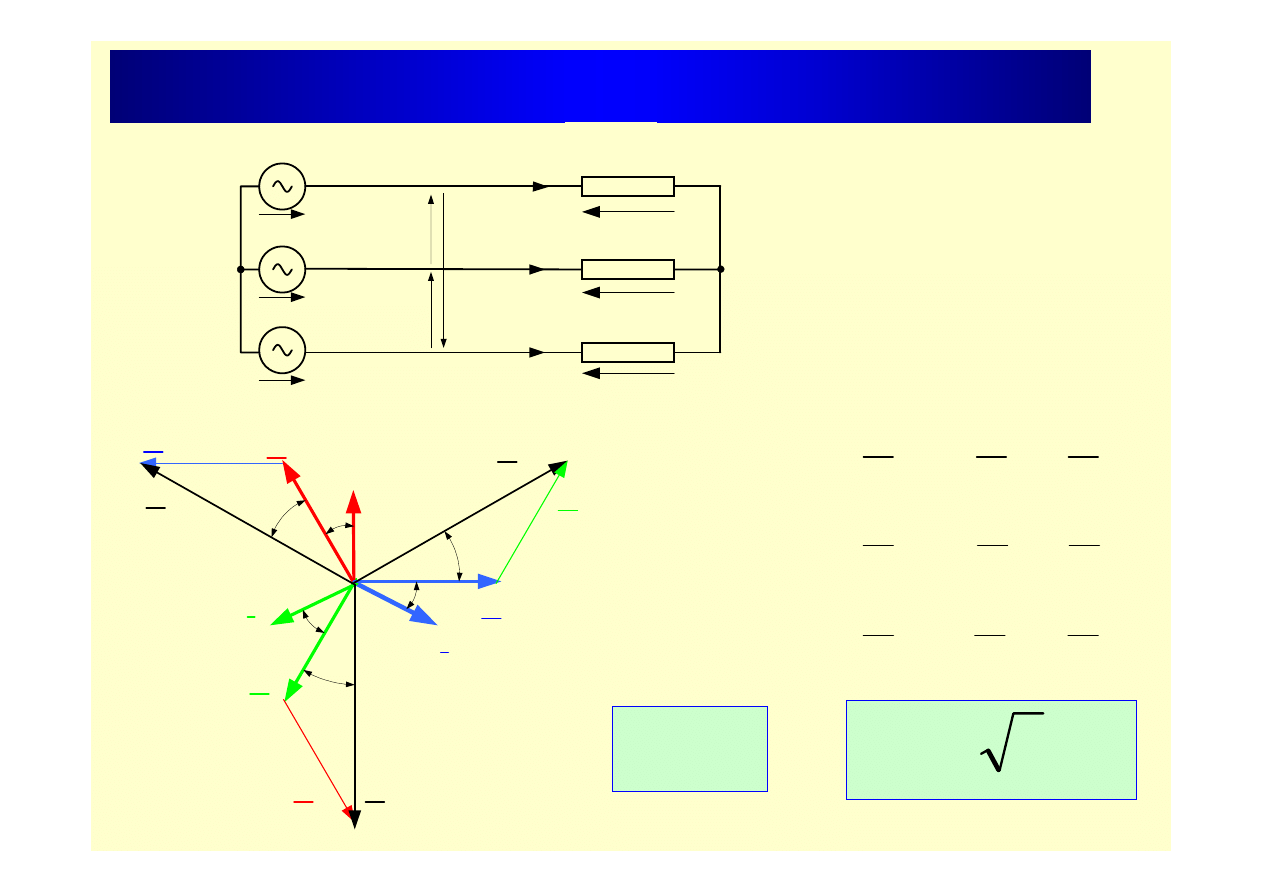
Układ połączeń w gwiazdę

f

p

I

I

=

U

C

U

B

U

A

I

C

I

A

I

B

-U

A

U

CA

U

BC

U

AB

-U

C

-U

B

30

o

30

o

30

o

f

f

f

I

A

U

B

U

C

U

A

I

B

I

C

U

A

U

B

U

C

U

CA

U

AB

U

BC

Z

Z

Z

f

p

I

I

=

B

A

AB

U

U

U

−

=

C

B

BC

U

U

U

−

=

A

C

CA

U

U

U

−

=

f

p

U

U

3

=

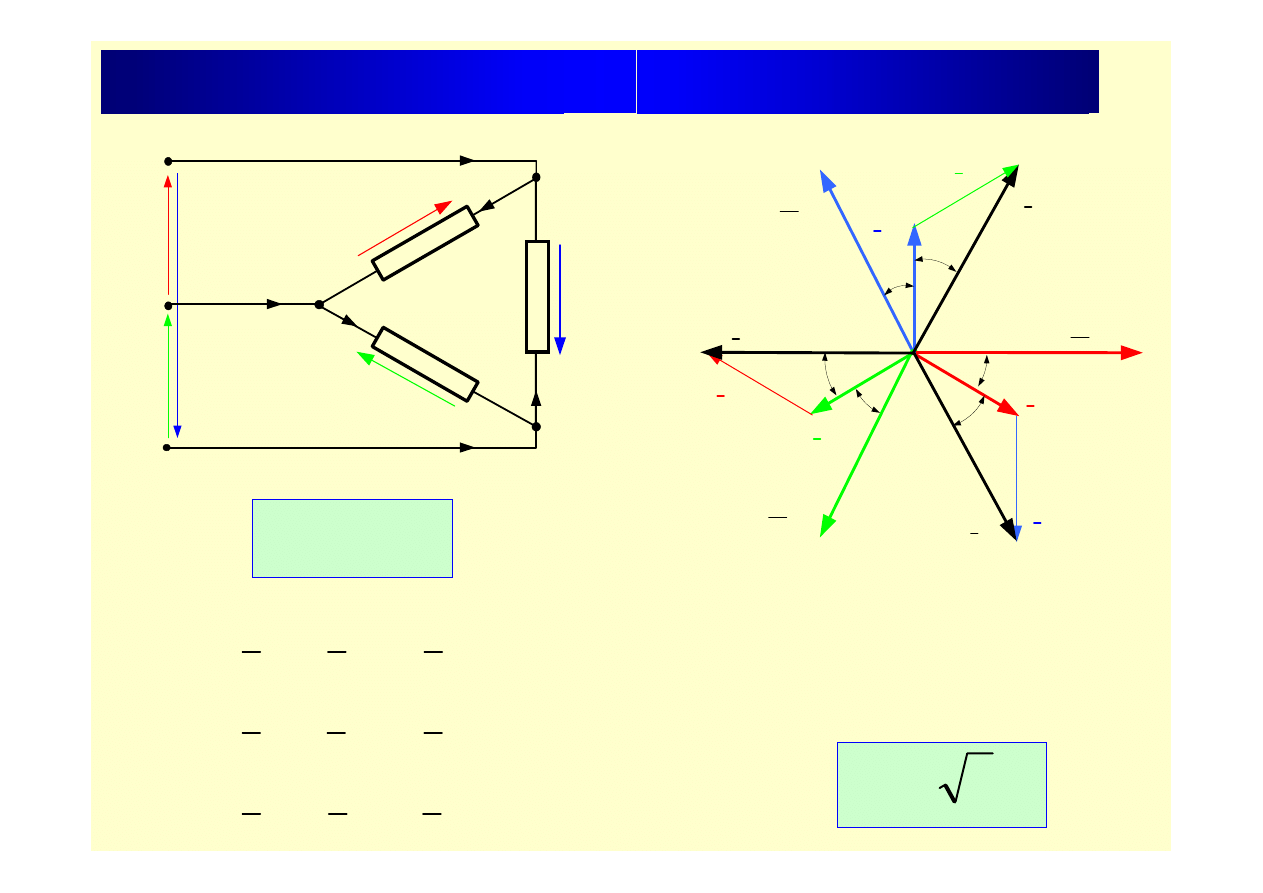
Układ połączeń w trójkąt

U

BC

U

CA

U

AB

A

B

C

I

A

I

B

I

C

U

CA

U

AB

U

BC

A

B

C

I

AB

I

BC

I

CA

Z

f

Z

f

Z

f

U

AB

30

o

I

C

I

A

I

B

U

CA

U

BC

30

o

30

o

I

AB

-I

CA

f

f

f

-I

AB

I

CA

I

BC

-I

CB

f

p

U

U

=

Z wykresu wektorowego wynika:

CA

AB

A

I

I

I

−

=

°

=

30

cos

2

f

p

I

I

AB

BC

B

I

I

I

−

=

Zatem:

f

p

I

I

3

=

BC

CA

C

I

I

I

−

=

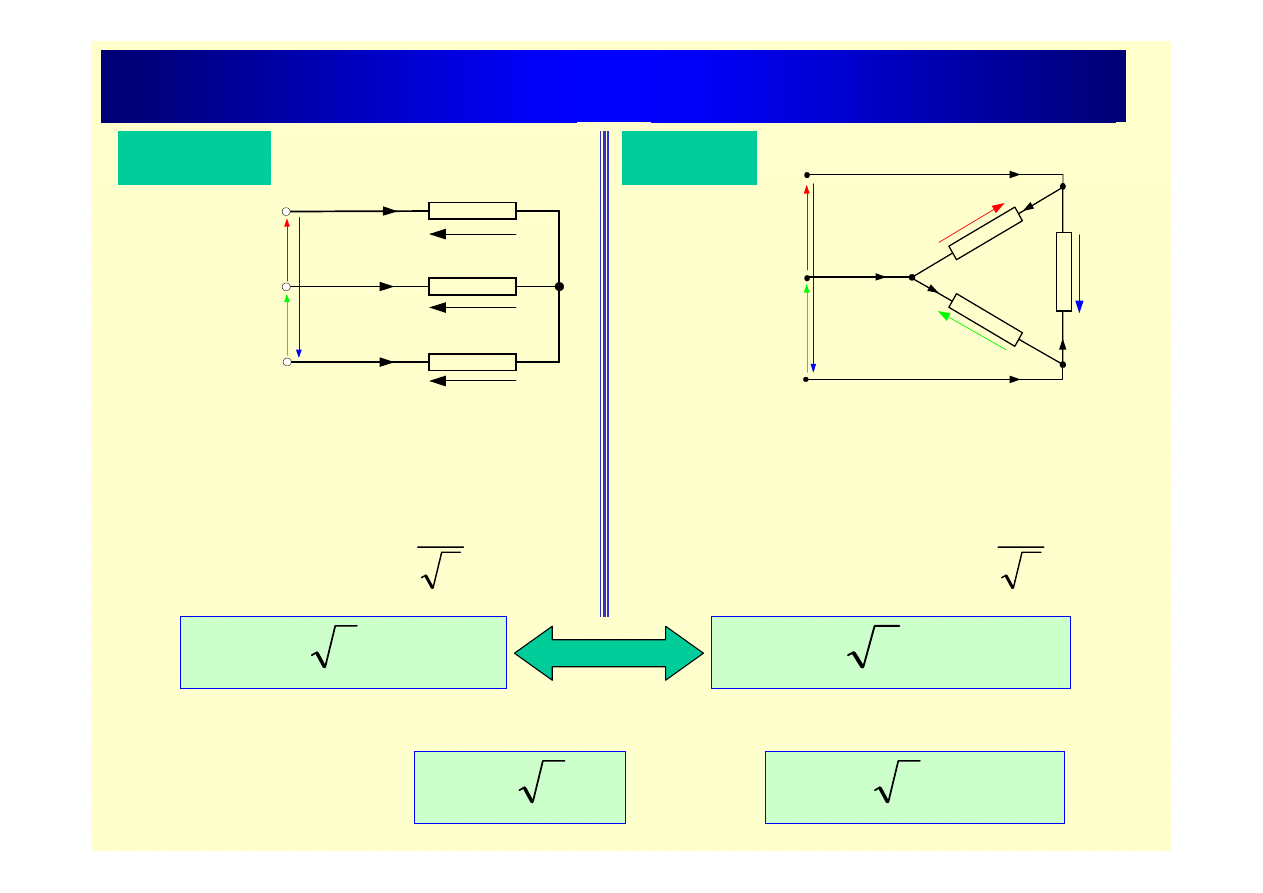
Moc w układzie 3-fazowym

Gwiazda

f

C

B

A

f

P

P

P

P

P

1

3

3

=

+

+

=

I

A

U

B

U

C

U

A

I

B

I

C

U

CA

U

AB

U

BC

Z

f

Z

f

Z

f

A

B

C

Trójkąt

U

BC

U

CA

U

AB

A

B

C

I

A

I

B

I

C

U

CA

U

AB

U

BC

A

B

C

I

AB

I

BC

I

CA

Z

f

Z

f

Z

f

f

C

B

A

f

P

P

P

P

P

1

3

3

=

+

+

=

ϕ

ϕ

cos

3

cos

1

I

U

I

U

P

f

f

f

=

=

ϕ

ϕ

cos

3

cos

1

I

U

I

U

P

f

f

f

=

=

ϕ

cos

3 I

U

P

gwiaz

=

ϕ

cos

3 I

U

P

trójk

=

I

U

S

f

3

3

=

ϕ

sin

3

3

I

U

Q

f

=

Analogicznie:

oraz