Logika. Zadania z tematu 2.

Tabelki prawdy i ich zastosowanie

Zadanie 1. Wypełnić poniższe schematy:

∧

⇒

∧

⇒

∧

⇒

∧

⇒

∧

⇒

∧

⇒

∧

⇒

⇔

∧

⇒

⇒

∧

⇒

⇔

∧

⇒

⇒

∧

∧

⇒

⇔

⇔

⇒

⇒

⇒

⇒

⇒

Zadanie 2. Obliczyć wartość logiczną następujących schematów prawdziwościowych:

a) 0

∧ ~ 1,

b) ~ 0

∧ ~ 1,

c) ~ ( 0

∧ 1 ),

d) ~ 0

∧ 1,

e) ( 0

∧ 1 ) ∨ 1,

f) 0

∧ ( 1 ∨ 1 ),

g) 0

⇒ ( 1 ∧ 1),

h) ( 0

⇒ 1 ) ∧ 1,

i) (~ 0

∧ 1 ) ⇒ ~ 1, j) ( ~ 0 ∧ ~ 1 ) ⇒ 1,

k) ~ 0

⇒ 0,

l) ~ ( 0

⇒ 0),

m) ~ ( ~ 0

⇒ 0 ),

n) ~ 0

⇒ ( 1 ∨ 0 ),

o) ~ 0

⇒ ( ~ 1 ⇒ 0 ),

p) ~ 0

⇒ ( ~ 0 ∧ ~ 1 ),

r) ( 0

∨ 1 ) ⇒ 0,

s) 0

∨ ( 1 ⇒ 0 ),

t) (1

∧ 0) ∨ ( 1 ∧ 1 ),

u) 0

⇔ ( ~ 1 ∧ ~ 1 ),

w) ( ~ 0

∧ 1 ) ⇒ ~ ( 0 ⇔ 0 ), y) ( 1 ∧ ~ 0 ) ⇒ ~ ( 1 ⇒ 0 ), z) ~ ( 0 ∧ 0 ) ⇒ ~ ( 0 ∧ 1 ).

Zadanie 3. Zdanie p jest prawdziwe, zdania q i r są fałszywe. Określić wartość logiczną zdań:
a) p

∧ ~ q,

b) ~ p

∧ ~ q,

c) ~ ( p

∧ q ),

d) ~ p

∧ q,

e) ( p

∧ q ) ∨ r,

f) p

∧ ( q ∨ r ), g)

p

⇒ ( q ∧ r),

h) ( p

⇒ q ) ∧ r,

i) (~ p

∧ q ) ⇒ ~ r,

j) ( ~ p

∧ ~ q ) ⇒ r,

k) ~ p

⇒ r,

l) ~ ( p

⇒ r),

m) ~ ( ~ p

⇒ r ),

n) ~ p

⇒ ( q ∨ r ),

o) ~ p

⇒ ( ~ q ⇒ r ),

p) ~ r

⇒ ( ~ p ∧ ~ q ),

r) ( p

∨ q ) ⇒ r,

s) p

∨ ( q ⇒ r ),

t) (q

∧ p) ∨ ( q ∧ r ),

u)

p

⇔ ( ~ q ∧ ~ r ),

w) ( ~ p

∧ q ) ⇒ ~ ( p ⇔ q ), y) ( r ∧ ~ p ) ⇒ ~ ( r ⇒ p ), z) ~ ( p ∧ q ) ⇒ ~ ( p ∧ r ).

Logika. Zadania z tematu 2

2

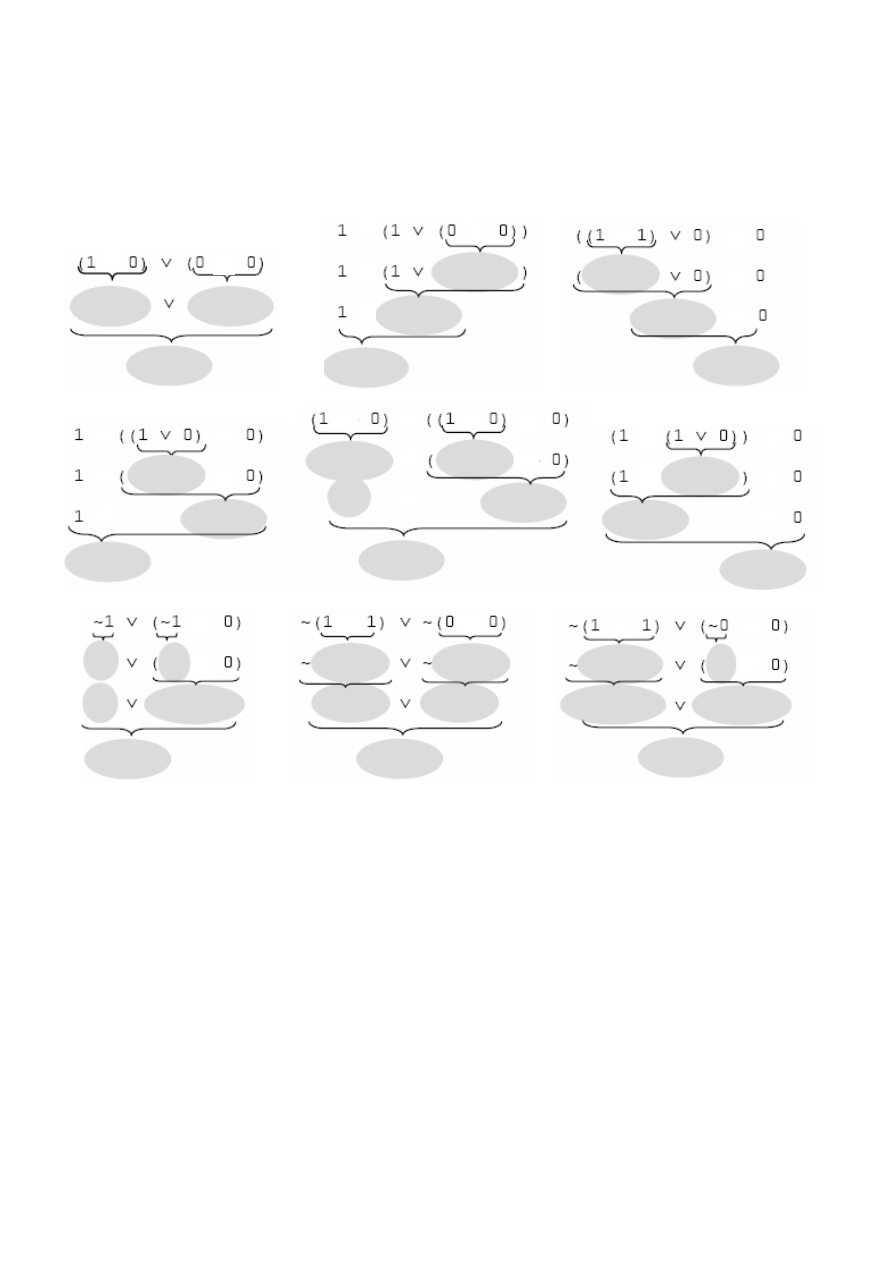
Zadanie 4. Zastosować uzasadnione skróty w określaniu wartości logicznej zdań złożonych:
a) 0

⇒ [0 ⇔ (0 ∨ (1 ∧ 0))]

b) [0

⇔ (1 ∨ (0 ∧ 1))] ⇒ 1

c) 0

∧ [(0 ⇔ 0) ∨ (1 ⇒ 1)]

d) 1

∨ [1 ⇔ ~ (1 ∧ (1 ∧ 1))]

e) ~ 1

∧ [(1 ⇒ 1) ∨ (1 ⇒ 1)]

f) ~ 1

⇒ [1 ∨ ~ (0 ⇒ (0 ⇒ 0))]

g) ~ 0

⇒ [(1 ⇒ (~ 1 ∧ ~ 1) ∨ ~ 0]

h) ~ 0

⇔ [~ 1 ∧ ~(1 ⇒ (0 ⇒ 1))]

i) ~ (1

∨ 1) ∧ [(0 ⇔ 1) ∧ (1 ⇔ 1)]

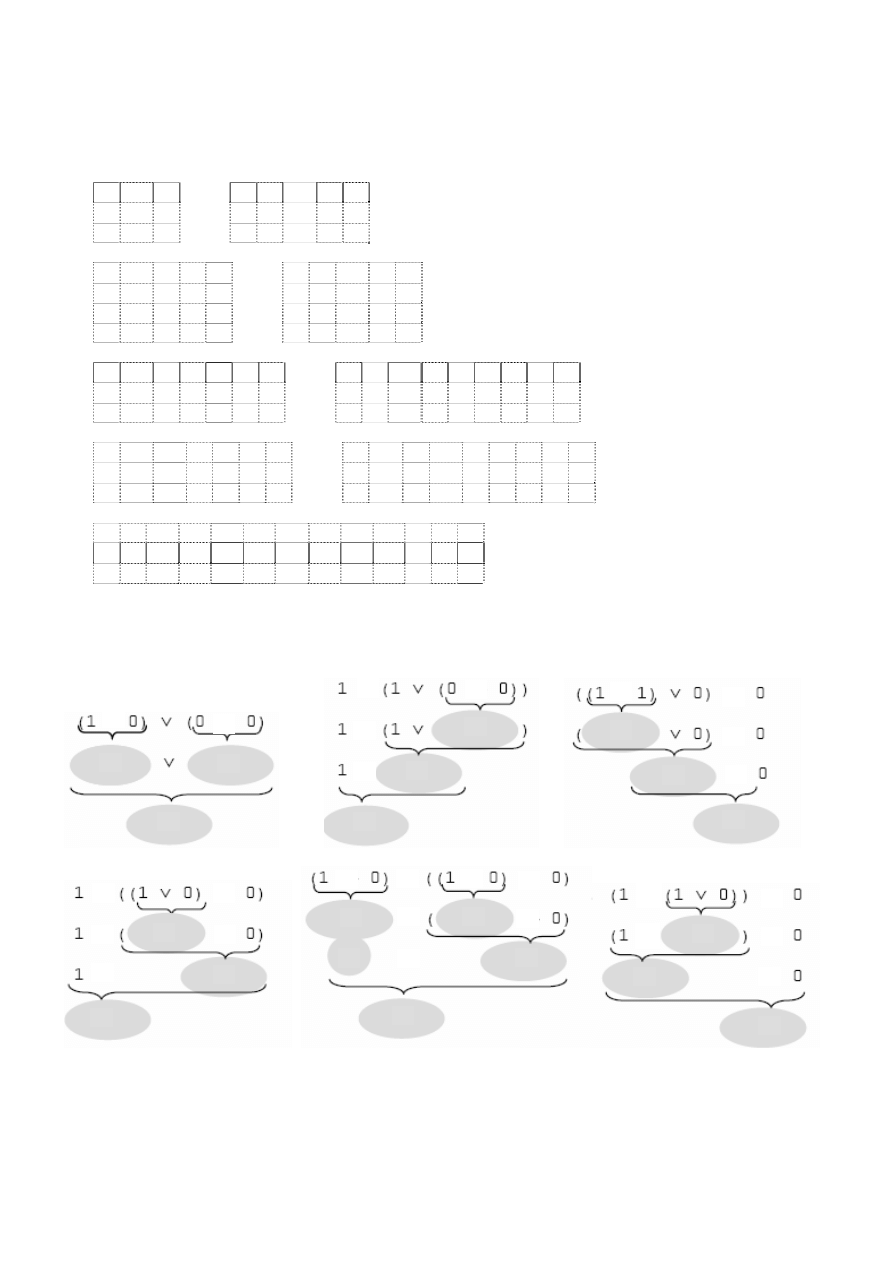
Zadanie 5.
Jakie wartości muszą przybrać zmienne aby po podstawieniu w podanych niżej schematach zdaniowych otrzymać
fałsz. Przykłady zostały tak dobrane, aby można było jednoznacznie określić te wartości:

⇒

⇒

⇔

⇒

⇒

⇒

⇒

⇔

⇒

⇔

⇒

⇔

⇒

⇔

⇒

⇒

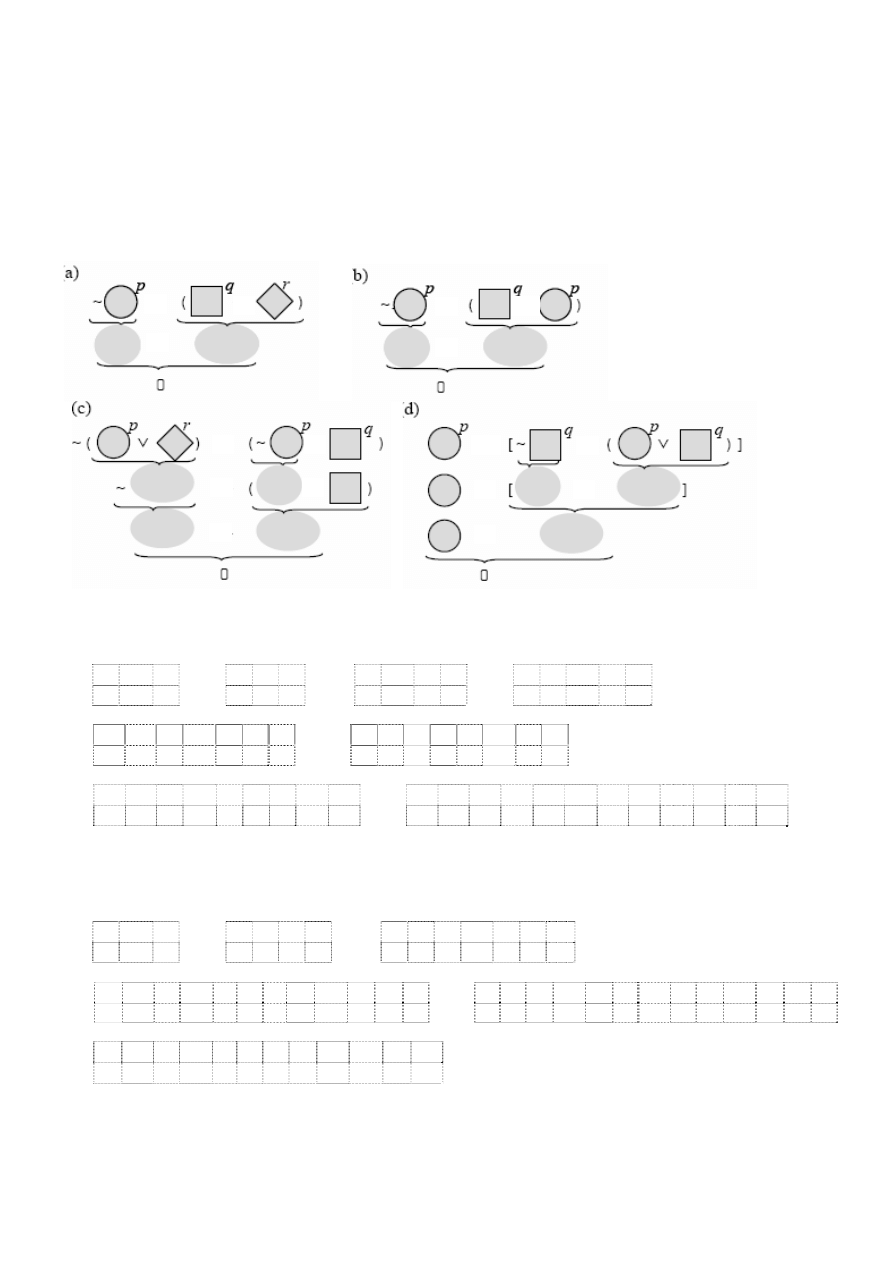
Zadanie 6.
Jakie wartości muszą przybrać zmienne aby po podstawieniu w podanych niżej schematach zdaniowych otrzymać
fałsz. Przykłady zostały tak dobrane, aby można było jednoznacznie określić te wartości:

a) p

⇒ q b) p ∨ q c) p ⇒ ~ q d) ~ p ∨ ~ q

e) ~

( p

∧ ~ q ) f) p ∨ ( ~ q ⇒ r )

g) ~ [

( p

⇒ q ) ∧ p

]

h) (

p

∧ r

)

⇒ (

q

⇔ ~ p )

Zadanie 7.
Jakie wartości muszą przybrać zmienne aby po podstawieniu w podanych niżej schematach zdaniowych otrzymać
prawdę. Przykłady zostały tak dobrane, aby można było jednoznacznie określić te wartości:

a) p

∧ q b) p ∧ ~ q c) ~ ( p ⇒ ~ q )

d) ( p

∧ r

)

∧ ( q ⇔ ~ p ) e) ~ ( p ⇒ r ) ∧ ( q ∨ ~ p )

f) ~ [

( p

⇒ r ) ∨ ( r

⇔ q ) ]

Logika. Zadania z tematu 2

3

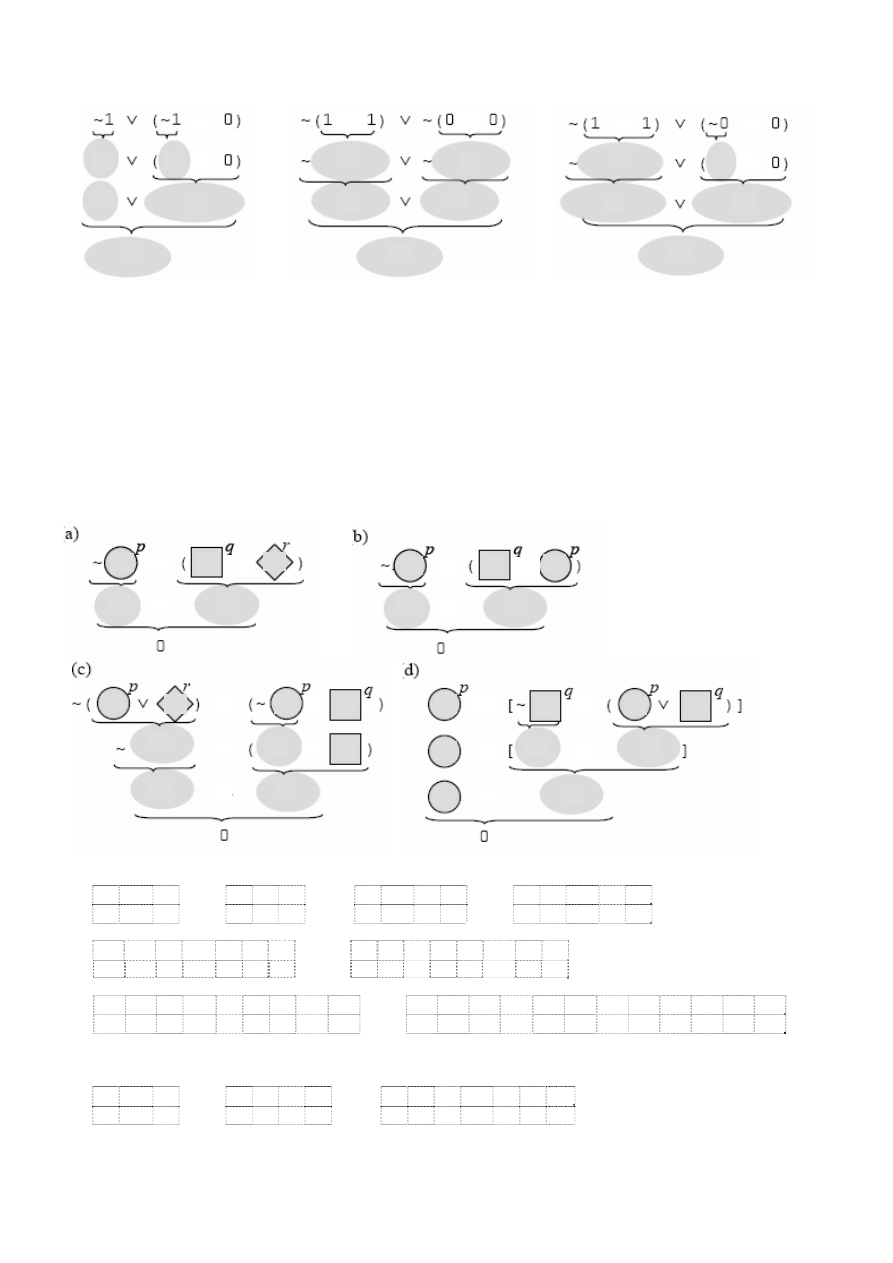
Zadanie 8.
Jakie wartości muszą przybrać zmienne aby po podstawieniu w podanych niżej schematach zdaniowych otrzymać
zadaną wartość logiczną:

a)

1

b)

0

p

⇔ q

~ p

⇔ ~ q

1

0

c) ~ p

∧ ~ q

d) ~ p

∨ ~ q

0

1

0

1

0

1

e)

0

f)

1

( p

∧ q ) ∨ q

~ q

∧ ( p ∨ ~ q )

0

1

g)

1

h) 1

( p

⇒ q ) ∧ q

~ [ {

p

⇔ r ) ∨ q )

1

1

g)

0

~

( p

∨ q )

⇔ ( ~ p ∧ q )

0

Odpowiedzi

Zadanie 1.

∧

⇒

∧

⇒

∧

⇒

1

1

∧

⇒

0

1

1

∧

1

⇒

0

1

1

∧

⇒

∧

⇒

⇔

∧

⇒

⇒

0

0

∧

⇒

1

⇔

1

∧

⇒

⇒

0

1

∧

∧

0

1

⇒

0

0

0

Logika. Zadania z tematu 2

4

⇔

⇔

⇒

⇒

⇒

1

0

0

1

1

1

⇒

⇒

0

1

0

0

0

0

0

1

0

Zadanie 2.

a) 0, b) 0, c) 1, d) 1, e) 1, f) 0, g) 1, h) 1, i) 0, j) 1, k) 0, l) 0,
m) 1, n) 1, o) 1, p) 0, r) 0, s) 0, t) 1, u) 1, w) 0, y) 1, z) 1.

Zadanie 3.
a) 1, b) 0, c) 1, d) 0, e) 0, f) 0, g) 0, h) 0, i) 1, j) 1, k) 1, l) 1,
m) 0, n) 1, o) 1, p) 0, r) 0, s) 1, t) 0, u) 1, w) 1, y) 1, z) 1.

Zadanie 4.
a) 1, b) 1, c) 0, d) 1, e) 0, f) 1, g) 1, h) 0, i) 0.

Zadanie 5.

0

0

1

0

⇒

0

1

⇒

⇔

⇒

0

1

⇒

1

0

⇒

0

0

0

1

0

1

⇒

⇔

1

1

⇒

⇔

0

1

1

0

⇒

⇔

0

1

⇒

⇔

1

0

⇒

0

1

⇒

Zadanie 6.

a) p

⇒ q b) p ∨ q c) p ⇒ ~ q d) ~ p ∨

~ q

1

0

0 0

0

0 1

0

0

1 0

1

0

0

1

e) ~

( p

∧

~ q )

f) p

∨ ( ~ q ⇒ r )

0 1 1 1 0

0 0 1 0 0 0

g) ~ [

( p

⇒ q ) ∧ p

]

h) (

p

∧

r

)

⇒ (

q

⇔ ~ p )

0 1 1 1 1 1 1 1 1

0 1 0 0 1

Zadanie 7.

a) p

∧

q

b) p

∧ ~ q c) ~ ( p ⇒ ~ q )

1

1

1 1

1

1

0 1

1

0

0

1

Logika. Zadania z tematu 2

5

d) ( p

∧ r

)

∧ ( q ⇔ ~ p ) e) ~ ( p ⇒ r ) ∧

(

q

∨

~ p )

1 1 1 1 0 1 0 1 1 1 0 0 1 1 1 0 1

f) ~ [

( p

⇒ r ) ∨ (

r

⇔ q ) ]

1 1 0 0 0 0 0 1

Zadanie 8.

a) 0 1 0

b) 0 1 0 1 0

p

⇔ q

~ p

⇔ ~ q

1 1 1

1

0 0

0

1

c) ~ p

∧ ~ q

d) ~ p

∨

~ q

0 1 0 0 1

0 1 1 1 0

0 1 0 1 0

1 0 1 0 1

1 0 0 0 1

1 0 1 1 0

e) 0 0 0

0 0

f) 1 0 1 0 1 1 0

( p

∧ q ) ∨ q

~ q

∧ ( p ∨ ~ q )

1 0 0 0 0

1 0 1 1 1 1 0

g) 0 1 1 1 1

h) 1 1 0 0 0 0

( p

⇒ q ) ∧ q

~

[ { p

⇔ r ) ∨ q )

1 1 1 1 1

1 0 0 1 0 0

g) 0 0 1 1

0

1 0 1 1

~

( p

∨

q

)

⇔ ( ~ p

∧ q )

1 0 0 0 0 1 0 0 0