Sprawozdanie z laboratorium

Metrologii i Technik Pomiarowych

„Zastosowanie oscyloskopu katodowego”

WIMIR, AiR, rok II, gr.13, 2009/2010

Nieduziak Miłosz, Niedzień Dawid, Nytko Krystian,

Olchawski Tomasz, Olsza Szymon

Część teoretyczna

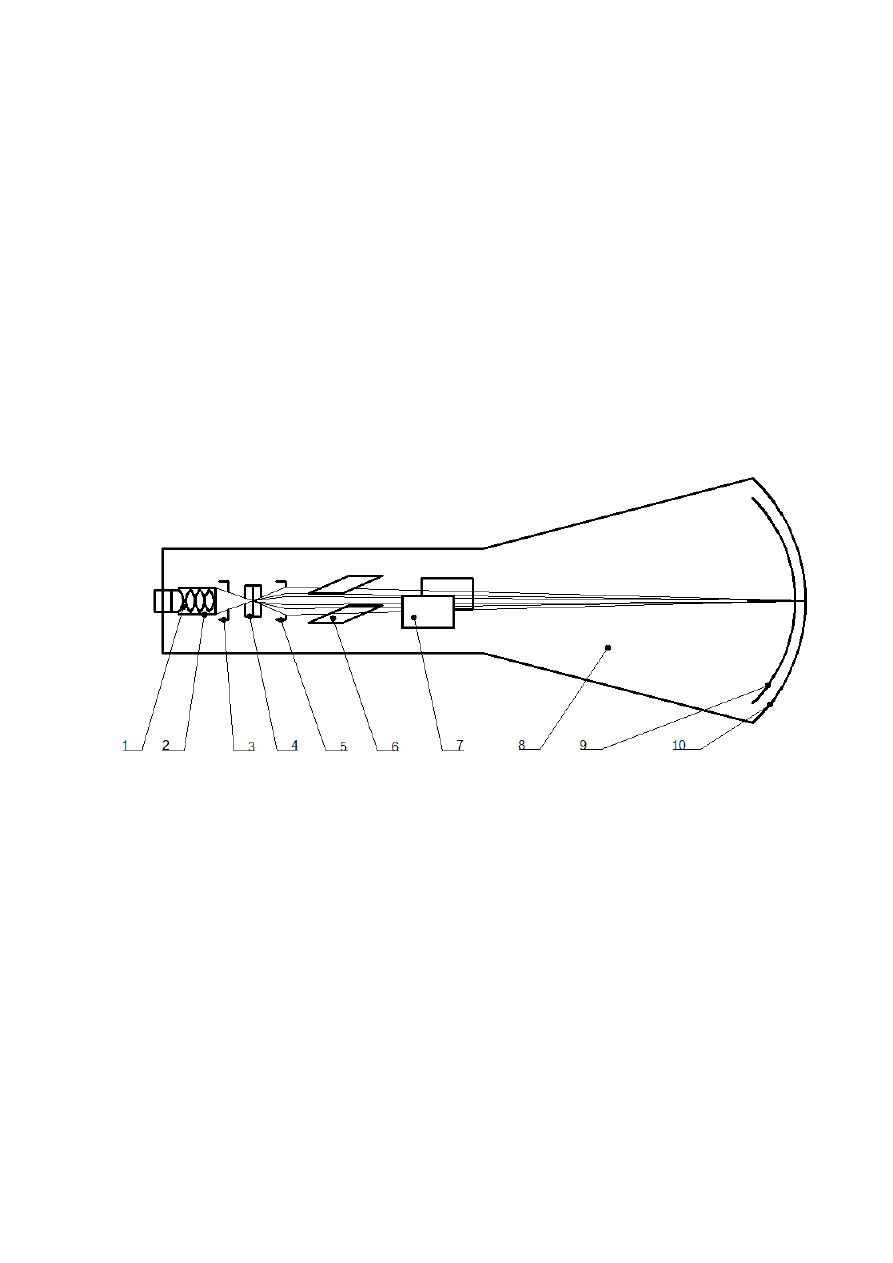
Schemat lampy oscyloskopowej

Opis działania

Grzejnik 1 podgrzewa katodę 2, która emituje elektrony, które następnie są skupianie
wstępnie przez siatkę 3. Anoda 4 przyspiesza ruch elektronów, które są w następnie
formowane w wiązkę przez elektrodę ogniskową 5. Następnie poprzez dwie pary
elektrod 6 i 7 wiązka jest odchylana w pionie i w poziomie. Elektroda 8 przyspiesza
ruch elektronów, które następnie padają na pokryte luminoforem 9 dno bańki szklanej
10.

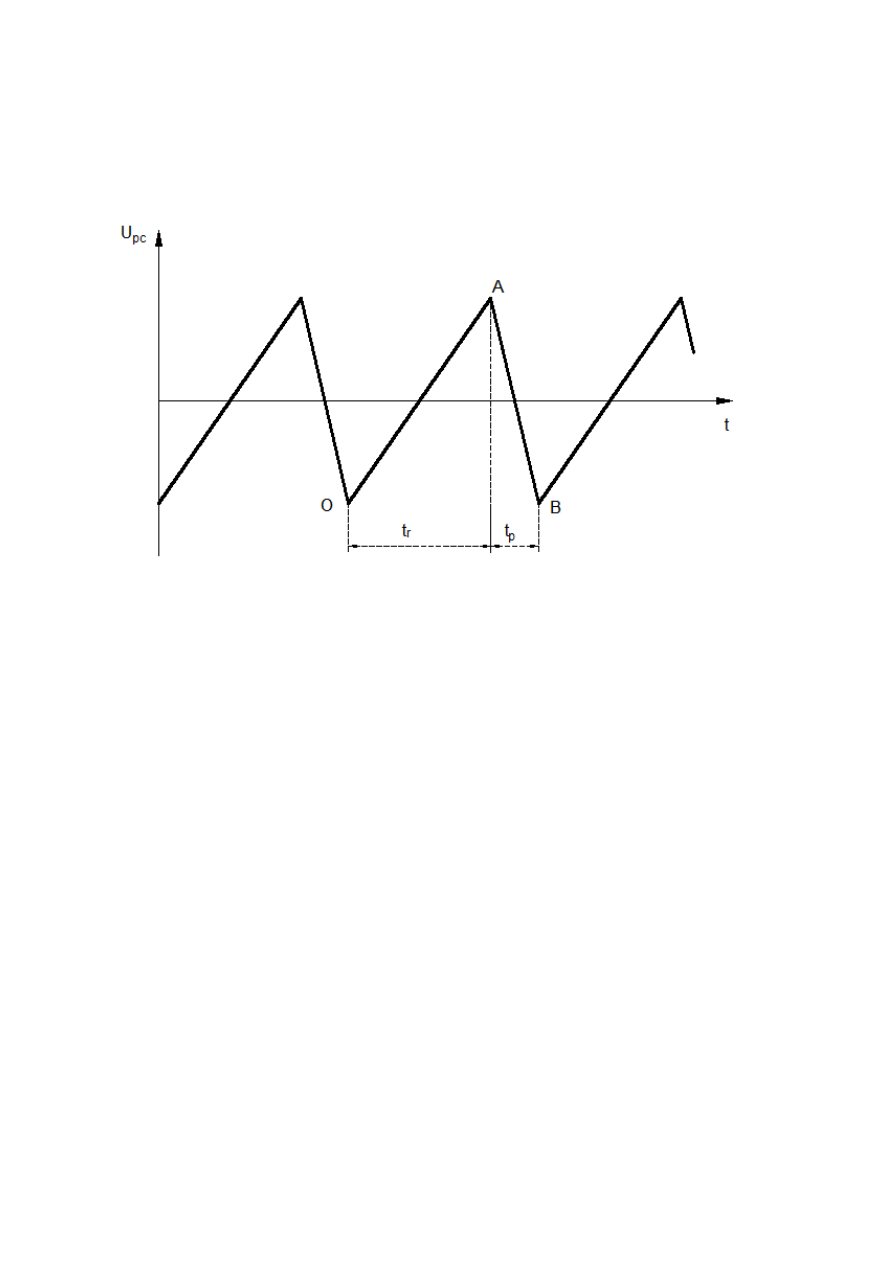
Ruch punktu po ekranie

Do płytek 6 podłączone jest badane napięcie. Do płytek 7 podłączony jest generator
podstawy czasu. Poniżej wykres piłokształtnego napięcia generowanego przez
podstawę czasu:

Odcinek t

r

narastania napięcia powoduje przesuwanie się punktu ze skrajnego

lewego do skrajnego prawego położenia na ekranie. Odcinek t

p

powoduje powrót

punktu z powrotem do lewego skrajnego położenia, przy czym t

r

>> t

p

.

Aby uzyskany obraz był nieruchomy częstotliwość podstawy czasu f

pc

i częstotliwość

badanego przebiegu f

b

muszą spełniać zależność:

pc

b

nf

f =

Część doświadczalna

Doświadczenia przeprowadzono przy pomocy następujących przyrządów:

• oscyloskopu analogowo-cyfrowego OS-3040
• uniwersalnego zestawu pomiarowego METEX MS-1960
• filtra dolnoprzepustowego RC

Doświadczenie 1.

Dla nastaw sygnałów sinusoidalnych wykonanych przez osobę prowadzącą zajęcia
należało określić amplitudę i okres tych sygnałów przy pomocy oscyloskopu.

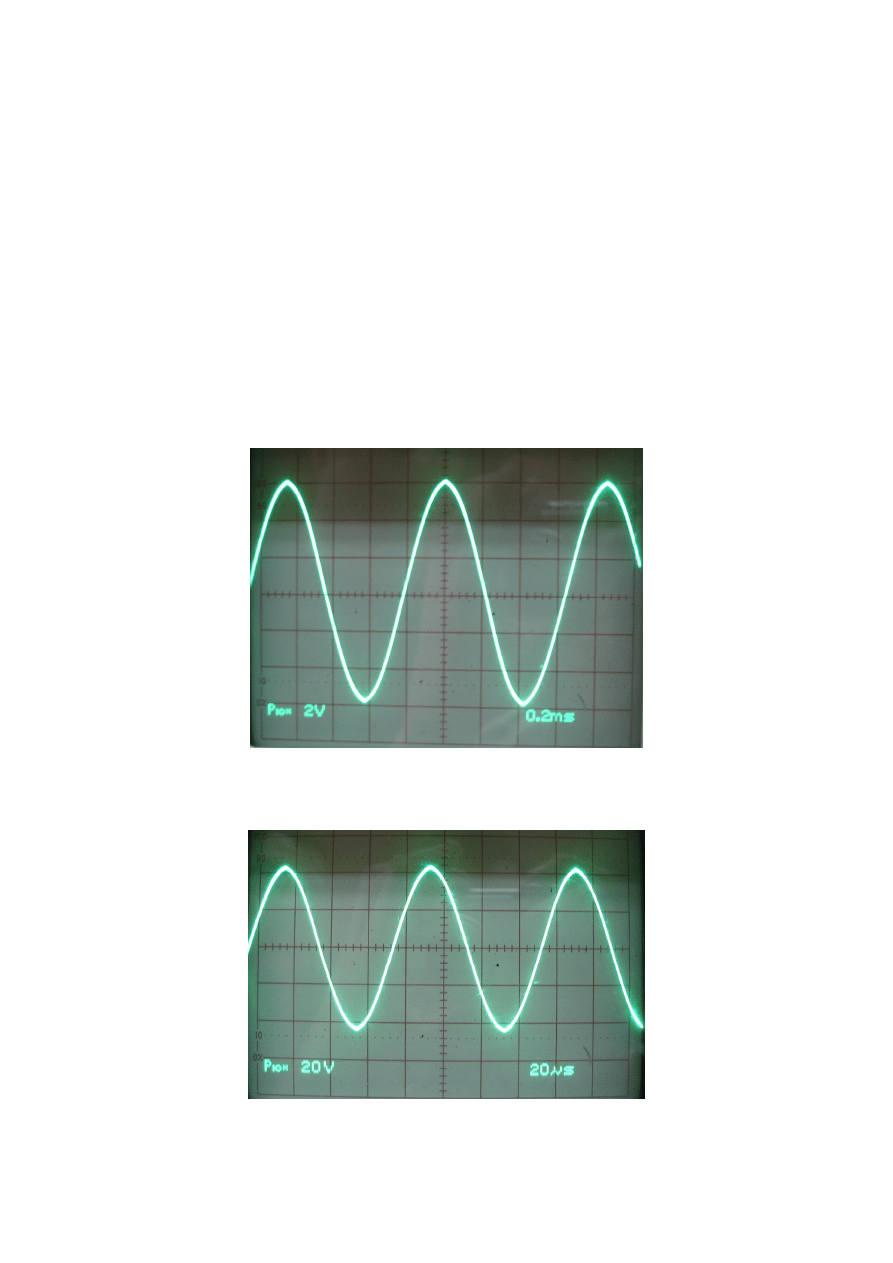
Fot. 1. Sygnał nr 1

Fot. 2 Sygnał nr 2

Odczytane wartości zostały zebrane w tabeli:

Oś napięcia

Oś czasu

Nr

sygnału

Stała

podziałki

[V/dz]

Liczba

działek

Amplituda

[V]

Stała

podziałki

[ms/dz]

Liczba

działek

Okres [ms]

1

0,2

3 ± 0,1

0,6 ± 0,02

0,2

4,2 ± 0,1 0,84 ± 0,02

2

2

2,2 ± 0,1

4,4 ± 0,2

0,02

4 ± 0,1 0,08 ± 0,002

Na podstawie pomiarów oscyloskopem obliczono częstotliwość i porównano ją z
częstotliwością oczytaną z generatora sygnału:

Nr

sygnału

Częstotliwość

obliczona [Hz]

Częstotliwość

odczytana z generatora

1

1162 ÷1220

1165

2

12195 ÷12820

12941

Doświadczenie 2.

Należało wyznaczyć amplitudę i stałą składową dla zadanego sygnału.

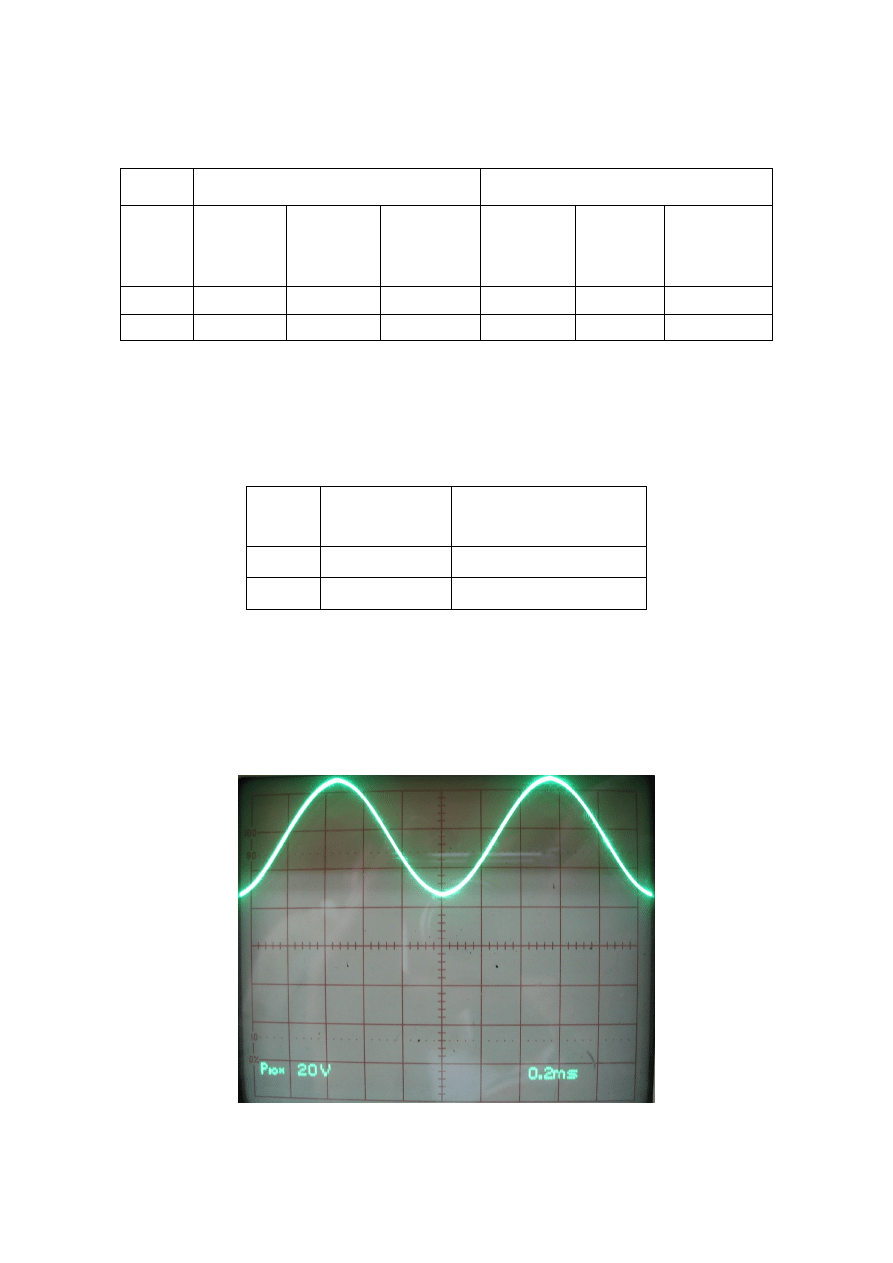
Fot. 3 Sygnał ze składową stałą

Wynik pomiarów przedstawia tabela:

Amplituda

Stała składowa

Stała podziałki

[V/dz]

Liczba działek

Wartość [V]

Liczba działek

Wartość [V]

2

1,5 ± 0,1

3 ± 0,2

2,8 ± 0,1

5,6 ± 0,2

Doświadczenie 3.

Wykorzystując filtr dolnoprzepustowy RC o stałej czasowej T = 0,63 s należało
wyznaczyć jego wzmocnienie K oraz różnicę faz między sygnałem podanym
bezpośrednio z generatora do oscyloskopu, a sygnałem zmodyfikowanym przez filtr.

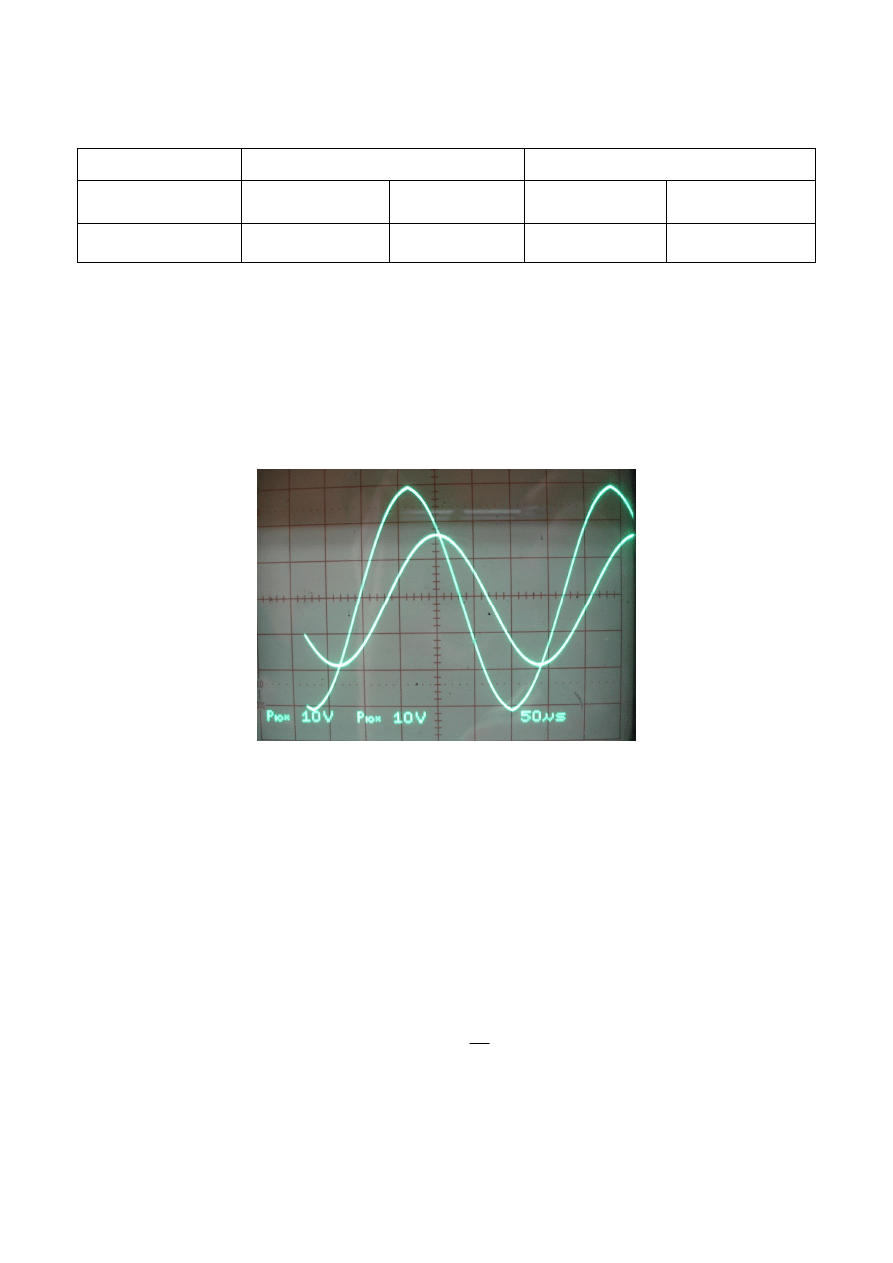
Fot. 4 Sygnały z wejścia i wyjścia filtra

W doświadczeniu wykorzystano oba kanały oscyloskopu, do jednego podając sygnał
wejściowy, a do drugiego wyjściowy. Dzięki temu można je było zobaczyć
jednocześnie.

Wzmocnienie K wyznaczono dzieląc amplitudę sygnału wyjściowego przez amplitudę
sygnału wejściowego.

Różnicę faz wyznaczono natomiast ze wzoru:

2

x

x

l

l

ϕ

π

=

gdzie:
l – długość odcinka odpowiadającego okresowi napięcia
l

x

– długość odcinka odpowiadającego różnicy faz

Amplituda

wejścia [V]

Amplituda

wyjścia [V]

Liczba działek

na okres

Liczba działek

różnicy faz

Wzmocnienie

Przesunięcie

fazowe [rad]

3 ± 0,1

1,6 ± 0,1

5,5 ± 0,1

0,8 ± 0,1

0,48 ÷ 0,59

0,79 ÷ 1,05

Znając wzmocnienie i stałą czasową można zapisać transmitancję przetwornika RC:

0, 53

( )

1

0, 63 1

K

G s

Ts

=

≈

+

+

Doświadczenie 4.

Przy pomocy tego samego przetwornika RC należało wyznaczyć przesunięcie
fazowe i wzmocnienie wykorzystując tryb X-Y oscyloskopu.

Fot. 5 Efekt doprowadzenia do płytek odchylania poziomego i pionowego napięcia o

tej samej częstotliwości

Wykorzystano wzór pozwalający obliczyć przesunięcie fazowe:

arcsin

y

x

ϕ

= −

Z kolei wzmocnienie określa iloraz amplitud widocznych na rysunku jako x i a.

x [dz]

y [dz]

a [dz]

Wzmocnienie Przesunięcie fazowe [rad]

1,8 ± 0,1 1,4 ± 0,1

3 ± 0,1

0,54 ÷ 0,66

-0,75 ÷ -1,08

Wnioski

Przeprowadzone doświadczenia ukazały wielość zastosowań oscyloskopu.

Odczytywanie wartości z jego ekranu jest czynnością prostą, ale wynik zawsze

obarczony jest błędem, co zauważono już podczas pierwszego doświadczenia.

Rozsądnym rozwiązaniem było takie modyfikowanie obrazu na oscyloskopie, by

zajmował możliwie największą część ekranu – wówczas dokładność pomiaru była

największa. Wydaje się, że na błąd pomiaru nałożyły się dwa czynniki: ograniczona

dokładność odczytu wartości napięcia przez osobę dokonującą pomiaru oraz

dodatkowo dokładność wykonania oscyloskopu, która według danych technicznych

wynosiła 3%. W przeciwnym razie, gdyby winna była tylko osoba dokonująca

odczytu, zakresy wartości częstotliwości obliczone w pierwszym ćwiczeniu dla

drugiego sygnału powinny obejmować wartości odczytane z generatora.

Doświadczenie trzecie i czwarte pokazało, jak wykorzystać oscyloskop do badania

obiektu inercyjnego I-rzędu i uwidoczniło sens istnienia drugiego kanału w

oscyloskopie. Dzięki takiemu kanałowi można wygodnie porównywać przebiegi

napięć, mając również możliwość w każdej chwili wyłączenia któregoś z nich bez

konieczności wypinania przewodów. Wyniki pomiarów w trybie dwukanałowym

okazały się inne, niż w trybie X-Y. Różnice w otrzymanych wartościach wzmocnienia

okazały się większe niż różnice wartości przesunięcia fazowego. Znak minus w

przypadku przesunięcia fazowego uzyskanego w doświadczeniu nr 4 określa

dodatkowo, że napięcie wejściowe wyprzedza na wykresie napięcie wyjściowe.

Trudno powiedzieć, który sposób pomiaru był dokładniejszy – tryb X-Y czy też

dwukanałowy, ponieważ pomiary w obu tych trybach opierały się na przeliczeniu

ilości działek na oscyloskopie. Warto natomiast zauważyć, że nawet dysponując

wyłącznie oscyloskopem jednokanałowym można było wykonać wszystkie

doświadczenia opisane w tym sprawozdaniu.