ROK WYD. LXVIII

앫 ZESZYT 11/2009

1 8

Dr in˝. Marek K´sy i prof. dr hab. in˝. Krzysztof Tubie-

lewicz sà pracownikami Instytutu Technologii Maszyn
i Automatyzacji Produkcji Politechniki Cz´stochowskiej.

Dzia∏alnoÊç rynkowa przedsi´biorstw produkcyj-

nych uwarunkowana jest silnà konkurencjà, wyso-
kimi wymaganiami odbiorców oraz ciàg∏ymi wa-
haniami popytu. Konieczne jest stosowanie w nich
takich rozwiàzaƒ techniczno-organizacyjnych, które
pozwolà na ∏atwe i szybkie dopasowanie si´ do zmie-
niajàcych si´ wymagaƒ. Zarzàdzanie produkcjà, obej-
mujàc wiele dzia∏aƒ podejmowanych przed oraz
w czasie wytwarzania, w zakresie tzw. operatywnego
sterowania produkcjà zajmuje si´ m.in. procedurà
planowania zadaƒ produkcyjnych lub operacji tech-
nologicznych oraz modyfikacjà dzia∏aƒ, w przypad-
kach pojawiajàcych si´ zak∏óceƒ pracy systemu
wytwórczego.

Planowanie i sterowanie produkcjà

Zakres i stopieƒ szczegó∏owoÊci procesu plano-

wania i sterowania produkcjà uzale˝niony jest od
aktualnej sytuacji przedsi´biorstwa, jego poziomu
technicznego i organizacyjnego. Planowanie produk-
cji sprowadza si´ do ustalenia programu dzia∏aƒ,
harmonogramu prac wytwórczych oraz zapotrze-
bowania na zasoby produkcyjne. Z kolei w zakresie
poj´ciowym sterowania produkcjà mieszczà si´ czyn-
noÊci planowania, sterowania, organizowania i kon-
trolowania rzeczywistego obiegu wyrobów i jego
informacyjnych uwarunkowaƒ. Poj´ciem podrz´d-
nym w stosunku do sterowania produkcjà jest ste-
rowanie przep∏ywem produkcji, ograniczone do pro-
cedur planowania, sterowania, kontroli i ewentual-

Algorytmy genetyczne w in˝ynierii produkcji

MAREK K¢SY
KRZYSZTOF TUBIELEWICZ

nie korygowania przep∏ywu materia∏ów i wyrobów
przez systemy produkcyjne w odpowiedniej liczbie
i czasie.

Sterowanie produkcjà nie mo˝e odbywaç si´

wed∏ug przypadkowych regu∏, musi byç oparte na
okreÊlonych metodach i algorytmach post´powania.
EfektywnoÊç procedur sterowania produkcjà uza-
le˝niona jest w du˝ej mierze od szczegó∏owoÊci pla-
nowania operatywnego, którà rozpatrywaç mo˝na
w aspekcie parametrów: czasu, przedmiotów pracy
oraz Êrodków pracy. Do prawid∏owego okreÊlenia,
jakimi zadaniami produkcyjnymi i w jakich jednost-
kach czasu obcià˝one zostanà stanowiska produk-
cyjne, s∏u˝à harmonogramy operacyjne. Ich tworze-
nie stanowi wa˝ny etap zarzàdzania produkcjà, od
którego zale˝y jakoÊç rozplanowania wykonywania
poszczególnych zadaƒ w czasie. Procedury plano-
wania i sterowania procesami wytwarzania uzale˝-
nione sà g∏ównie od charakteru produkcji. W przy-
padku produkcji na zamówienie, wielkoÊç oraz pro-
cedury planowania i sterowania procesami produk-
cji uzale˝nione sà od nap∏ywajàcych w ró˝nych ter-
minach zleceƒ, stanowiàcych podstaw´ wytworze-
nia wyrobów – w zamówionej liczbie, asortymencie
i okreÊlonym czasie wykonania. Brak „stabilizacji”
wytwórczej powoduje, ˝e plany produkcyjne i har-
monogramy operacyjne produkcji ulegajà cz´stym
korektom, wynikajàcym g∏ównie z koniecznoÊci do-
konania zmian w obcià˝eniu stanowisk produkcyj-
nych. Mo˝e to byç m.in. wynikiem nap∏ywu nowego
priorytetowego zlecenia, zak∏ócenia wynikajàcego
z awarii obrabiarki itd., co powoduje koniecznoÊç
tworzenia harmonogramów wykazujàcych cechy
dynamicznej zmiennoÊci [1].

ROK WYD. LXVIII

앫 ZESZYT 11/2009

1 9

Techniki planowania i sterowania produkcjà

W przypadku produkcji na zamówienie, w zakresie

procedur planowania nast´puje wyznaczenie kolej-
noÊci wykonywania zleceƒ produkcyjnych z okreÊ-
lonego zbioru oczekujàcych. Z pozoru wydawaç si´
mo˝e, ˝e problematyka ustalenia kolejnoÊci wy-
konania jest prosta do rozwiàzania. W rzeczywistoÊci
jednak jest to zagadnienie wieloaspektowe, okreÊlo-
ne m.in. przez: ró˝norodnà i zmiennà w czasie liczb´
realizowanych zleceƒ, ograniczenia wytwórcze sys-
temu produkcji, brak mo˝liwoÊci zmiany kolejnoÊci
wykonania operacji. Tego typu zmiennych i zak∏óceƒ
jest w rzeczywistoÊci bardzo du˝o, dlatego te˝ opra-
cowanie harmonogramu jest zagadnieniem z∏o˝o-
nym.

Decydowanie o kolejnoÊci wykonania zadaƒ pro-

dukcyjnych w systemach lub operacji na stanowis-
kach produkcyjnych jest jednym z podstawowych
zagadnieƒ sterowania przep∏ywem produkcji. Wy-
bór zlecenia lub operacji spoÊród zbioru oczekujà-
cych odbywa si´ przez nadanie najwy˝szego stopnia
pilnoÊci – priorytetu. Planowanie obcià˝eƒ stano-
wisk produkcyjnych odbywa si´ przez bardziej lub
mniej Êwiadome, sukcesywne nadawanie priory-
tetów zleceniom i/lub operacjom produkcyjnym.
W praktyce procesy opracowywania harmonogra-
mów produkcyjnych oparte byç mogà na procedu-
rach heurystycznych (np. regu∏y priorytetu), algo-
rytmach optymalizacyjnych oraz metodach sztucz-
nej inteligencji.

Regu∏a priorytetu jest funkcjà lub przyj´tà zasadà,

która ka˝demu zadaniu produkcyjnemu oczekujàce-
mu na wykonanie przyporzàdkowuje wielkoÊç zwa-
nà wskaênikiem priorytetu i wybiera jedno z mini-
malnà lub maksymalnà wartoÊcià tego wskaênika,
okreÊlajàc tym samym jego wykonanie w pierwszej
kolejnoÊci. Regu∏y priorytetu to przyj´te zasady na-
dawania priorytetów decydujàcych o kolejnoÊci
wykonania zadaƒ produkcyjnych oczekujàcych na
wykonanie w okreÊlonym momencie lub przedziale
czasu. Zadaniem regu∏ priorytetu w sterowaniu
przep∏ywem produkcji jest ustalenie odpowiedniej
kolejnoÊci wykonywania operacji produkcyjnych
na stanowiskach i wp∏ywanie w ten sposób na uzys-
kiwanie okreÊlonych efektów pracy systemu pro-
dukcyjnego. W ogólnym przypadku ró˝ne regu∏y
priorytetu dajà ró˝ne kolejnoÊci wykonywania ope-
racji, a tym samym ró˝ne efekty dzia∏alnoÊci. Za-
stosowanie wybranej regu∏y priorytetu umo˝liwia
zrealizowanie okreÊlonych celów, jak np. przyspie-
szenie wykonania okreÊlonych zleceƒ, skracanie
cykli produkcyjnych, zmniejszenie obcià˝enia Êrod-
ków pracy itp. W literaturze znanych jest ponad
100 ró˝nych regu∏ priorytetu wykorzystujàcych ró˝ne
informacje i opisujàcych przebieg procesu produkcji
w systemie produkcyjnym [2, 3].

Oprócz regu∏ priorytetu do rozwiàzania proble-

mów harmonogramowania stosuje si´ tak˝e przybli-
˝one metody analityczne, które pozwalajà na spo-
rzàdzenie harmonogramu produkcji na podstawie
mniej lub bardziej z∏o˝onego algorytmu optymali-
zacyjnego. Ze wzgl´du na z∏o˝onoÊç obliczeniowà
wymagajà one zazwyczaj przyj´cia uproszczeƒ w mo-
delu matematycznym, które z kolei decydujà o ich
efektywnoÊci i skutecznoÊci optymalizacyjnej. Do
najbardziej znanych algorytmów optymalizacyjnych

zaliczyç mo˝na m.in.: algorytm Johnsona, Palmera
i

Gupty [4].

Stosowane metody sztucznej inteligencji bazujà

na za∏o˝eniu naÊladowania dzia∏aƒ istot ˝ywych, jak
np. tzw. inteligencji roju (algorytmy mrówkowe) lub
nauki o genetyce (algorytmy genetyczne). Algorytmy
genetyczne stanowià prób´ wykorzystania mecha-
nizmów znanych z teorii ewolucji ˝ywych organiz-
mów oraz nauki o genetyce do poszukiwania opty-
malnych rozwiàzaƒ stworzonych przez cz∏owieka
problemów. Procedur´ poszukiwania rozwiàzania
i analizy uzyskanego zbioru mo˝liwoÊci mo˝na po-
równaç do mechanizmów dostosowawczych za-
chodzàcych w populacji organizmów ˝ywych. Przy-
pisujàc poszczególnym rozwiàzaniom ich indywi-
dualne oceny przystosowania do postawionych wa-
runków, mo˝na stymulowaç procesy ewolucyjne,
reprodukujàc w kolejnych „pokoleniach” lepsze spo-
Êród rozwiàzaƒ, eliminujàc natomiast te, które s∏abo
spe∏niajà zadane kryteria. W teorii algorytmów ge-
netycznych zak∏ada si´, ˝e rozwiàzanie problemu
decyzyjnego nie jest nierozdzielnà ca∏oÊcià, lecz sumà
pewnych elementów sk∏adowych. Pozwala to na
wzbogacenie ewolucyjnej regu∏y „silniejszy wygry-
wa” o analogi´ do procesu reprodukcji kodu gene-
tycznego, a konkretnie o mo˝liwoÊç zestawiania
ze sobà idei czàstkowych i otrzymywania w ten
sposób innowacyjnych rozwiàzaƒ rozpatrywanego
problemu. Od strony technicznej wymaga to przyj´-
cia sposobu przekszta∏cania konkretnego rozwiàza-
nia w jednoznacznie je identyfikujàcy ciàg kodowy.
Tak zdefiniowane ciàgi kodowe mo˝na poddawaç
przetwarzaniu, otrzymujàc tà drogà inne – repre-
zentujàce nowe rozwiàzania. Dla oceny skutecznoÊci
dzia∏ania metod optymalizacji stosuje si´ okreÊlo-
ne kryteria tej oceny, wyznaczajàc odpowiadajàce
tym kryteriom wskaêniki [5].

Badania efektywnoÊci

metod planowania przebiegu produkcji

W artykule zaprezentowano mo˝liwoÊç wykorzys-

tania metodyki algorytmu genetycznego w zakresie
planowania pracy systemu produkcji, porównujàc
efektywnoÊç przyj´tej procedury obliczeniowej z re-
zultatami otrzymanymi w wyniku zastosowania algo-
rytmów przybli˝onych (

Palmera i Gupty) oraz przy-

j´tych regu∏ priorytetu (najkrótszego i najd∏u˝sze-
go czasu operacji oraz najwi´kszej i najmniejszej ca∏-
kowitej stanowiskowoÊci).

Obliczenia planistyczne przeprowadzone zosta∏y

w zakresie sekwencyjnej pracy gniazda produkcyj-
nego dla przyj´tych, deterministycznych i statycznych
warunków produkcji i zamkni´tego zbioru oczekujà-
cych na wykonanie zadaƒ produkcyjnych.

Przedstawiona procedura opracowania harmono-

gramu produkcji za pomocà metody algorytmów
genetycznych i quasi-optymalizacyjnych oraz regu∏
priorytetu odnosi si´ do prostego problemu ustale-
nia kolejnoÊci wykonania 3 zadaƒ produkcyjnych
oczekujàcych na realizacj´ w przedmiotowym gnieê-
dzie wytwórczym (rys. 1).

Poszczególne zadania produkcyjne charaktery-

zujà si´ jednakowymi sekwencjami (odnoszàcymi
si´ do rodzaju i kolejnoÊci) wykorzystywanych Êrod-
ków pracy, zaÊ elementami ró˝nicujàcymi i jedno-
czeÊnie stanowiàcymi podstaw´ obliczeƒ sà czasy

ROK WYD. LXVIII

앫 ZESZYT 11/2009

2 0

TABELA I: Czasy obcià˝enia stanowisk wytwórczych pra-
cujàcych w gnieêdzie produkcyjnym

Stanowisko

Zadania produkcyjne

wytwórcze

ZP_1

ZP_2

ZP_3

M1

5

7

2

M2

6

9

2

M3

9

21

4

M4

11

14

2

M5

18

14

6

obcià˝enia poszczególnych stanowisk

t

ij

, których

wartoÊci przedstawiono w tab. I.

Analiza skutecznoÊci metod optymalizacji oparta

zosta∏a na sekwencyjnie wyznaczanych terminach
realizacji zadaƒ, okreÊlonych na podstawie ustalonych
momentów rozpocz´cia i zakoƒczenia poszczegól-
nych operacji produkcyjnych. Ogólne zale˝noÊci
dotyczàce wyznaczenia czasów okreÊlone sà jako [6]:

tr

ij

= max(

tz

(

i – 1)j

;

tz

i (j – 1)

)

tz

ij

=

tr

ij

+

t

ij

gdzie:

tr

ij

,

tz

ij

– terminy rozpocz´cia i zakoƒczenia

j-tej

operacji

i-tego zadania produkcyjnego,

t

ij

– czas obcià˝enia stanowiska wytwórcze-

go (

j ) zwiàzany z realizacjà i-tego zadania produkcyj-

nego.

W procedurze wyznaczenia kolejnoÊci realizacji

zadaƒ produkcyjnych za pomocà algorytmu gene-
tycznego, ciàg kodowy tworzà liczby b´dàce nume-
rami zadaƒ. Specyfika ciàgu kodowego powoduje
koniecznoÊç zastosowania operatora krzy˝owania
porzàdkowego, który gwarantuje jednoznacznoÊç
interpretacyjnà tworzonych ciàgów kodowych. Przy-
j´tà funkcjà przystosowania weryfikujàcà efektyw-
noÊç optymalizacyjnà algorytmu genetycznego jest
sumaryczna d∏ugoÊç cykli produkcyjnych oczeku-
jàcych na wykonanie zadaƒ [7].

Efektem zastosowania algorytmu genetycznego

w zakresie ustalenia kolejnoÊci wykonania zadaƒ
produkcyjnych w gnieêdzie produkcyjnym jest two-
rzona w kolejnych iteracjach obliczeniowych lista
z nadanymi numerami zadaƒ. Wyznaczone wartoÊci
funkcji przystosowania, w zakresie analizowanej ite-
racji obliczeniowej, stanowià podstaw´ wyboru ro-
dziców nast´pnego pokolenia. Wybrane ciàgi rodzi-
ców poddane sà „operacjom genetycznym”, tzn.
krzy˝owaniu i mutacji. Dla analizowanego przypad-
ku obliczeniowego, w wyniku zastosowania algoryt-
mu genetycznego, ustalona zosta∏a kolejnoÊç wy-
konania zadaƒ produkcyjnych: ZP_3, ZP_1, ZP_2.
Przyk∏adowy ekran aplikacji obliczeniowej wyko-
rzystujàcej metodyk´ algorytmów genetycznych
prezentuje rys. 2.

Sekwencja wyznaczonych terminów rozpocz´cia

tr

ij

i zakoƒczenia

tz

ij

operacji produkcyjnych, dla wyz-

naczonej kolejnoÊci realizacji zadaƒ produkcyj-
nych i deklarowanych czasów

t

ij

, przedstawiona zosta-

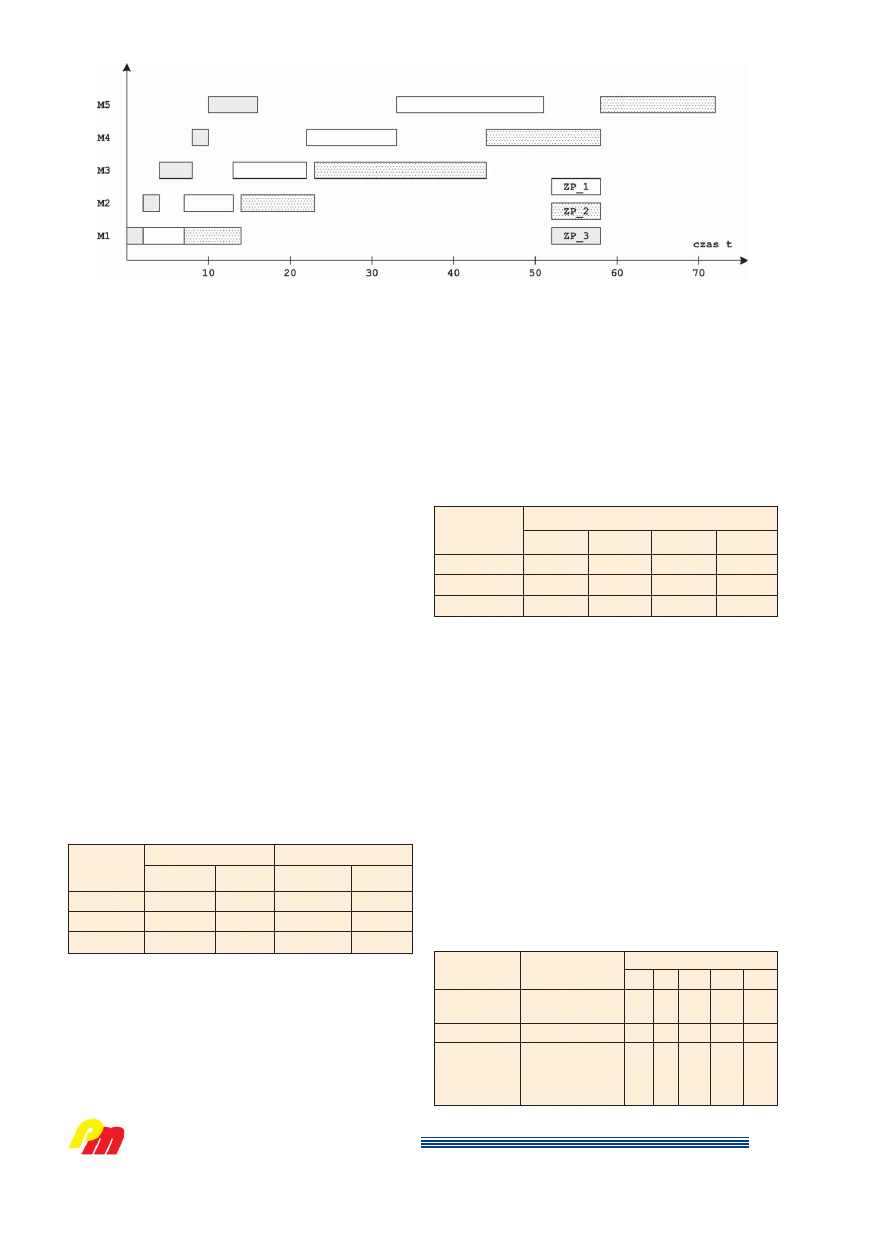
∏a na rys. 3, zaÊ odpowiadajàcy jej wykres obcià˝eƒ
Êrodków wytwórczych, w postaci wykresu

Gantta,

na rys. 4.

W procedurze wyznaczenia kolejnoÊci wykona-

nia zadaƒ produkcyjnych wykorzystano algorytmy

Palmera i Gupty [4]. W przypadku
algorytmu

Palmera podstawà

ustalenia kolejnoÊci sà obliczone
wartoÊci wskaênika

SI

i

, obliczone

jako:

Rys. 1. Schemat systemu produkcyjnego

Rys. 2. Procedura wyznaczenia kolejnoÊci wykonania zadaƒ
produkcyjnych wykorzystujàca metodyk´ algorytmów gene-
tycznych

Rys. 3. Sekwencja terminów rozpo-
cz´cia i zakoƒczenia operacji produk-
cyjnych dla wyznaczonej kolejnoÊci
realizacji zadaƒ produkcyjnych

ROK WYD. LXVIII

앫 ZESZYT 11/2009

2 1

TABELA II: KolejnoÊç wykonania zadaƒ produkcyjnych usta-
lona wed∏ug algorytmów optymalizacyjnych

Zadanie Algorytm

Palmera Algorytm Gupty

produkcyjne

ZP_i

WartoÊç

SI

i

Pozycja

WartoÊç

G

i

Pozycja

ZP_1

62

1

-0,0910

2

ZP_2

38

2

-0,0625

3

ZP_3

16

3

-0,2500

1

TABELA III: KolejnoÊç wykonania zadaƒ produkcyjnych usta-
lona wed∏ug regu∏ priorytetu

Zadanie

Regu∏a priorytetu

produkcyjne

ZP_i

NK_CO

ND_CO

NW_CS

NM_CS

ZP_1

3

2

3

2

ZP_2

1

1

1

1

ZP_3

2

3

2

3

TABELA IV: Parametry i wskaêniki przyj´te do analizy efek-
tywnoÊci metod planowania

Metoda

KolejnoÊç

Parametry i wskaêniki

wykonania

T

C

Êr

W

n

V

Êr

W

Êr

Rp: ND_CO
Rp: NM_CS

ZP_2, ZP_3, ZP_1

89

75 0,58 1,73 20,33

A_Palmera

ZP_1, ZP_2, ZP_3

76

65 0,67 1,50 21,67

A_Genetyczny
A_Gupty
Rp: NK_CO

ZP_3, ZP_1, ZP_2

72

46 0,94 1,07 3,00

Rp: NW_CS

Rys. 4. Wykres

Gantta dla wyznaczonej kolejnoÊci realizacji zadaƒ produkcyjnych

M

j =1

SI

i

=

∑

(

M – 2 · j + 1) · t

i M – j + 1

gdzie:

M – liczba stanowisk w systemie produkcyj-

nym,

t

iM

– czas jednostkowy operacji

i-tego zadania

na stanowisku

M,

t

iM–j+1

– czas jednostkowy operacji

i-tego zadania

na stanowisku

M–j+1,

j – liczba operacji realizowanych w zakresie

zadania produkcyjnego.

KolejnoÊç wykonania zadaƒ ustalona zasta∏a zgod-

nie z za∏o˝eniami algorytmu, wed∏ug kolejnoÊci okreÊ-
lonej przez ciàg malejàcych wartoÊci wskaênika

SI

i

.

Z kolei zastosowanie algorytmu

Gupty oparte jest

na obliczanych wartoÊciach wskaênika

G

i

, obliczanego

jako:

G

i

=

e

i

/ min(

t

ij

+

t

ij + 1

)

gdzie:

e

i

= dla 1 ≤ j ≤ M – 1

Utworzony ciàg w kolejnoÊci wartoÊci niemale-

jàcych wskaênika

G

i

wskazuje na kolejnoÊç wyko-

nywania zadaƒ. Efekt zastosowania algorytmów
optymalizacyjnych

Palmera i Gupty przedstawiono

w tab. II.

W zakresie analizy porównawczej dokonano rów-

nie˝ ustalenia kolejnoÊci realizacji zadaƒ produkcyj-
nych, stosujàc wybrane regu∏y priorytetu [3], tj.:

쐌 regu∏a NajKrótszego Czasu Operacji (NK_CO)

– porzàdkujàca zadania produkcyjne wed∏ug naj-
krótszego czasu pierwszych operacji sekwencyjnej
pracy systemu produkcji;

쐌 regu∏a NajD∏u˝szego Czasu Operacji (ND_CO)

– porzàdkujàca zadania produkcyjne wed∏ug naj-

d∏u˝szego czasu pierwszych operacji sekwencyjnej
pracy systemu produkcji;

쐌 regu∏a NajWi´kszej Ca∏kowitej StanowiskowoÊci

zadania produkcyjnego (NW_CS);

쐌 regu∏a NajMniejszej Ca∏kowitej StanowiskowoÊci

zadania produkcyjnego (NM_CS).

KolejnoÊç wykonania zadaƒ produkcyjnych usta-

lonà wed∏ug przyj´tych regu∏ priorytetu przedsta-
wiono w tab. III.

Weryfikacja skutecznoÊci

optymalizacyjnej metod planowania

Weryfikacja skutecznoÊci optymalizacyjnej zasto-

sowanych metod planowania przebiegu produkcji
przeprowadzona zosta∏a za pomocà [3, 7]:

쐌 parametru – d∏ugoÊci harmonogramu produkcji T,

쐌 parametru – Êredniej d∏ugoÊci cykli produkcyj-

nych

C

Êr

,

쐌 wskaênika normatywnoÊci cykli produkcyjnych

zbioru zadaƒ

W

n

,

쐌 Êredniego wskaênika wyd∏u˝enia cykli produk-

cyjnych

V

Êr

,

쐌 parametru – Êredniej czasu oczekiwania zadaƒ

produkcyjnych na obróbk´

W

Êr

.

Zestawienie przyj´tych do analizy wielkoÊci przed-

stawione zosta∏o w tab. IV.

– 1

dla t

i1

<

t

iM

+1

dla t

i1

≥ t

iM







ROK WYD. LXVIII

앫 ZESZYT 11/2009

2 2

Wykorzystane w obliczeniach metody i algoryt-

my optymalizacyjne wskazujà trzy ró˝niàce si´ sek-
wencje kolejnoÊci obróbki (z n! = 3! = 6 mo˝liwych).
Ze wzgl´du na przyj´te kryteria oceny najlepszà
kolejnoÊç wykonania zadaƒ wyznaczono, stosujàc
metodyk´ algorytmów genetycznych, algorytm

Gupty

oraz regu∏y priorytetu NK_CO i NW_CS. Wyznaczo-
na kolejnoÊç wykonania powoduje minimalizacj´
d∏ugoÊci harmonogramu obróbki zbioru zadaƒ, Êred-
niego cyklu wykonania zadaƒ, wskaênika wyd∏u˝e-
nia cykli produkcyjnych oraz Êredniego czasu ocze-
kiwania zadaƒ na obróbk´, przy jednoczesnym
wysokim poziomie normatywnoÊci cykli produkcyj-
nych. Z kolei kolejnoÊç wykonania zadaƒ wyznaczo-
na w wyniku zastosowania regu∏ priorytetu ND_CO
oraz NM_CS – spowodowa∏a efekt przeciwny do wy-
kazanego powy˝ej. Zastosowanie algorytmu

Palmera

spowodowa∏o ustalenie kolejnoÊci wykonania zadaƒ
o poÊredniej efektywnoÊci.

Wnioski

Przedstawiajàc mo˝liwoÊç wykorzystania metody

algorytmów genetycznych w zakresie prostego przy-
padku harmonogramowania pracy gniazda pro-
dukcyjnego, wykazano jej efektywnoÊç optymali-
zacyjnà. Algorytmy genetyczne, stanowiàc typowo
matematyczne podejÊcie w zakresie opisu i rozwià-
zaƒ optymalizacyjnych procesów technicznych,
organizacyjnych i ekonomicznych, rozpatrywane
byç mogà w kategoriach skutecznych narz´dzi wspo-
magajàcych procedury planowania i sterowania
procesami produkcji. Wadà algorytmów genetycz-

nych jest du˝a ró˝norodnoÊç koncepcyjna, wymu-
szajàca koniecznoÊç indywidualnego opracowania,
stanowiàcych podstaw´ obliczeƒ, ciàgów kodowych
oraz funkcji przystosowania. LosowoÊç operatorów
genetycznych (procedur krzy˝owania i mutacji) nie
gwarantuje uzyskania rozwiàzania optymalnego,
powtarzalnoÊci, a tym samym przewidywalnoÊci,
sekwencji obliczeniowych. Prowadzone analizy i obli-
czenia wykaza∏y, ˝e rozwiàzanie optymalne lub zbli-
˝one do optimum uzyskaç mo˝na, stosujàc inne
procedury optymalizacyjne lub quasi-optymaliza-
cyjne, tj. algorytmy przybli˝one oraz regu∏y priory-
tetu – prostsze w opracowaniu i zastosowaniu. Stàd
te˝ metodyka algorytmów genetycznych mo˝e byç
stosowana jako jedna z metod optymalizacji, zw∏asz-
cza w zakresie „niezdiagnozowanych” problemów
decyzyjnych, wskazujàc pewne przybli˝enie roz-
wiàzania optymalnego.

LITERATURA

1.

Pajàk E.: Zarzàdzanie produkcjà. PWN, Warszawa 2006.

2.

Wróblewski K. J.: Podstawy sterowania przep∏ywem pro-
dukcji. WNT, Warszawa 1993.

3.

Wróblewski K. J. i inni: Regu∏y priorytetu w sterowaniu
przep∏ywem produkcji. WNT, Warszawa 1984.

4.

Brzeziƒski M.: Sterowanie produkcjà. Wyd. Liber, Lublin
2001.

5. Badania operacyjne. Praca pod red. W. Sikory. PWE, War-

szawa 2008.

6. Zarzàdzanie produkcjà. Praca pod red. Z. Jasiƒskiego. Wyd.

AE im. O. Langego, Wroc∏aw 1993.

7.

Knosala R. i zespó∏: Zastosowanie sztucznej inteligencji
w in˝ynierii produkcji. WNT, Warszawa 2002.