GEODEZJA I KARTOGRAFIA

Tom XLI, z. 3–4 (1992), s. 203–212

Kazimierz M. Borkowski

Katedra

Radioastronomii

Uniwerytet M. Kopernika
(87-100 Toruń, ul. Chopina 12/18)

Zagadnienie transformacji współrzędnych pomiędzy układem geocentrycznym a geodezyjnym
występuje w codziennej praktyce w geodezji i astrometrii, a współczesne pomiary astrogeodezyjne
wymagają zgodnej pary transformat, których dokładności utrzymują się w dużym przedziale
wysokości na dowolnej szerokości geograficznej. O ile zamiana elipsoidalnych współrzędnych
geodezyjnych, szerokości

φ

, długości

λ

i wysokości nad elipsoidą odniesienia h, na geocentryczne

współrzędne kartezjańskie (x,y,z) lub biegunowe (szerokość, długość i promień wodzący) nie stanowi
ż

adnego problemu, o tyle proces odwrotny sprawia pewne trudności. Odwrotne przekształcenie

wykonuje się zwykle w sposób przybliżony w procesie iteracyjnym (np. [3], [8], [9]), [17]), albo
używając przybliżeń w postaci szeregów potęgowych (np. [10], [12], [13], [16]) lub innych zwartych
wyrażeń (np. [15], [2]). Dzieje się tak mimo, że istnieją ścisłe rozwiązania na zamianę współrzędnych
kartezjańskich na geodezyjne ([6], [7], [14], [18]), o czym zdaje się nie wiedzieć wielu autorów
poważnych publikacji (np. [1], [2], [8], [10], [16], [19]).

Rozwiązania ścisłe są w zasadzie wolne od błędów, jednak w praktyce błędy powstają wskutek
zaokrągleń wyników pośrednich w stosunkowo złożonych algorytmach. Niemniej, w pewnych
zastosowaniach te ścisłe algorytmy mogą być preferowane ze względu na ich dokładność i
kompletność (zakresy współrzędnych).

W tym raporcie przedstawię dwa nowe rozwiązania, z których jedno jest bardzo prostym algorytmem
przybliżającym rozwiązanie ścisłe tak dobrze, że w praktyce mu wcale nie ustępuje. Druga
propozycja zawiera prawdziwie ścisłe rozwiązanie niezależne od znanych mi z literatury, a
przewyższające je głównie swą prostotą. Prostota wynika z faktu, że rozwiązaniu poddaje się
równanie czwartego stopnia, w którym tylko dwa spośrod pięciu współczynników różnią się od zera
lub jedynki (nieliczni inni autorzy rozwiązują ogólną postać takiego równania). Podam także wyniki
porównań moich algorytmów z kilku innymi.

Na początek przypomnijmy mniej lub bardziej znane wzory zamiany współrzędnych geodezyjnych na

Algorytmy

zamiany współrz

ę

dnych

kartezja

ń

skich na

elipsoidalne

W pracy przedstawiono dwa nowe sposoby bardzo precyzyjnego przeliczenia współrzędnych
prostokątnych na elipsoidalne (geodezyjne). Oba polegają na rozwiązaniu równania 2 sin(

ψ

−

Ω

) = c

sin2

ψ

, gdzie

Ω

= arctg [bz/(ar)], c = (a

2

−

b

2

)/[(ar)

2

+ (bz)

2

]

1/2

, a i b są półosiami elipsoidy odniesienia, r

i z — składową rownikową i biegunową geocentrycznego wektora, a

ψ

— tzw. parametryczną

szerokością. W ścisłym podejściu podstawienie tg(

π

/4

−

ψ

/2)

≡

t prowadzi do wielomianu: t

4

+ 2Et

3

+

2Ft

−

1 = 0, gdzie E = tg

Ω

−

c/cos

Ω

, zaś F = tg

Ω

+ c/cos

Ω

, do którego można zastosować metodę

Ferrari. Szerokość oraz wysokość geodezyjną oblicza się ze wzorów

φ

= arctg[a(1

−

t

2

)/(2bt)] oraz h = (r

−

at)cos

φ

+ (z

−

b)sin

φ

. Zarówno to rozwiązanie ścisłe jak i rozwiązanie przybliżone (metodą Newtona)

dają porównywalnie wysokie dokładności — o kilka rzędów wielkości lepiej niż w typowych
algorytmach.

Page 1 of 10

Algorytmy zamiany współrzędnych

2008-05-27

http://www.astro.uni.torun.pl/~kb/Papers/geod/Geod-GK.htm

kartezjańskie:

gdzie a (b) jest wielką (małą) półosią elipsoidy odniesienia (rysunek 1), a r (składowa równikowa)
rozkłada się na x i y przez pomnożenie przez funkcje kosinus i sinus, odpowiednio, długości
geograficznej. Parametr

ψ

, nazywany niekiedy szerokością parametryczną lub zredukowaną albo

ekscentryczną, oblicza się ze wzoru:

Częściej wzory (1) przedstawiane są równoważnie następująco:

gdzie N = a/(1

−

e

2

sin

2

φ

)

1/2

, zaś e

2

= (a

2

−

b

2

)/a

2

.

r = a cos

ψ

+ h cos

φ

oraz

(1a)

z = b sin

ψ

+ h sin

φ

,

(1b)

ψ

= arctg(

b

a

tg

φ

).

(2)

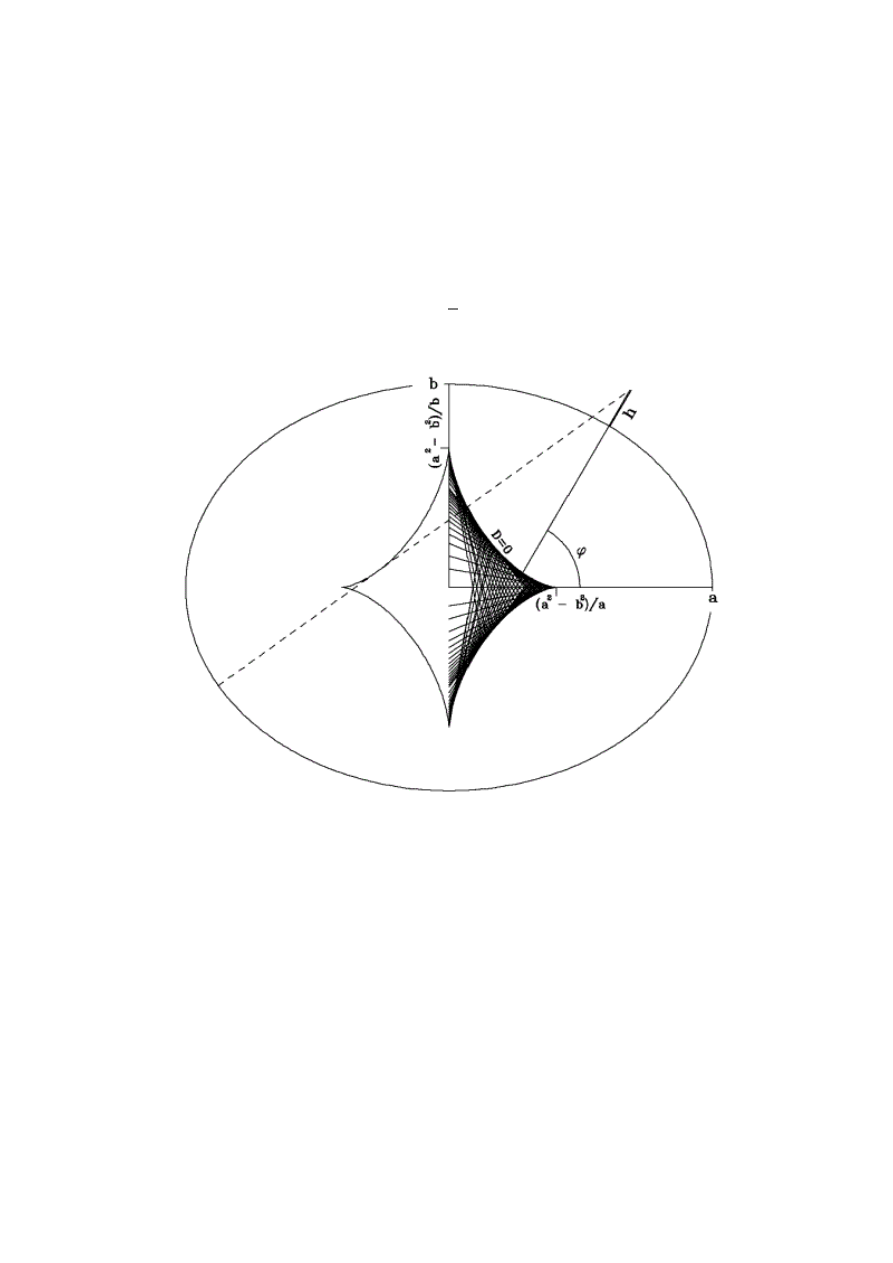
Rys. 1. Przykład okre

ś

lenia współrz

ę

dnych geodezyjnych (

φ

,h) dla elipsoidy o

du

ż

ym spłaszczeniu [(a

−

b)/a = 0,23; parametr ten dla elipsoidy ziemskiej wynosi

zaledwie ok. 0,003]. Współrz

ę

dne prostok

ą

tne r i z biegn

ą

od

ś

rodka elipsy wzdłu

ż

osi a i b, odpowiednio. D jest ujemne wewn

ą

trz asteroidy (jej połow

ę

zakreskowano

w sposób zgodny z kierunkami szeroko

ś

ci geodezyjnych — tak, by pokaza

ć

ż

e ich

obwiednia wyznacza krzyw

ą

D = 0) i wyst

ę

puj

ą

tu 4 rozwi

ą

zania rzeczywiste na

(

φ

,h) ka

ż

dego punktu (w kierunkach prostopadłych do elipsy: jeden w danej

ć

wiartce, trzy skierowane na przeciwległ

ą

półkul

ę

). W innych miejscach (D

≥

0) s

ą

dwa takie rozwi

ą

zania, z których jedno ma

|φ|

> 90° (tu: linia przerywana wzdłu

ż

ujemnej wysoko

ś

ci).

r = (N + h)cos

φ

(3a)

z = [N(1

−

e

2

) + h]sin

φ

,

(3b)

Page 2 of 10

Algorytmy zamiany współrzędnych

2008-05-27

http://www.astro.uni.torun.pl/~kb/Papers/geod/Geod-GK.htm

Problemem jest znalezienie

φ

i h, gdy dane są r i z. Geometrycznie oznacza to wyznaczenie kierunku

prostej prostopadłej do elipsoidy z danego punktu (r,z). Kąt, pod którym prosta taka przebija
płaszczyznę równika, jest szerokością geodezyjną,

φ

, konwencjonalnie liczoną dodatnio na północ od

równika, a ujemnie — na południe. Odległość punktu od elipsoidy jest wysokością, h (dodatnią na
zewnątrz elipsoidy). Chociaż nie jest to oczywiste, ale Czytelnik używając elementarnych
przekształceń może w wolnej chwili sprawdzić, że problem ten sprowadza się do rozwiązania
równania ar tg

ψ

= bz + (a

2

−

b

2

)sin

ψ

albo:

gdzie

Ω

= arctg[bz/(ar)], zaś c = (a

2

−

b

2

)/[(ar)

2

+ (bz)

2

]

1/2

.

Taka reprezentacja omawianego problemu wydaje się być całkiem oryginalna i głównie dzięki
przedstawieniu (4) nasze rozwiązanie okaże się o wiele dokładniejsze od innych. Wartość

ψ

uzyskaną

z rozwiązania równania (4), na mocy równiania (2), można użyć do obliczenia szerokości
geodezyjnej:

Ten wynik z kolei pozwala znaleźć wysokość nad elipsoidą ziemską z jednego albo obu równań (1),
np.:

(W swoich obliczeniach, które przedstawiam niżej, stosowałem inne wyrażenie na h — to, które
podałem w angielskim streszczeniu tej pracy).

Rozwiązanie równania typu (4) nie powinno w zasadzie sprawiać żadnych kłopotów (dziś nawet
podręczne kalkulatory posiadają wbudowaną operację znajdowania zera funkcji przestępnych)
niemniej, dla wygody Czytelnika, podam tutaj gotowy algorytm sprawdzony w praktyce.
Rozwiązanie zaczynamy od obliczenia wygodnej wartości

ψ′

— początkowej dla następnych

przybliżeń

ψ

. Możemy w to miejsce wziąć np. arctg[az/(br)], które — jak to widać z (1) — jest ścisłe

na powierzchni elipsoidy (dla h = 0), a więc będzie z pewnością optymalnym wyborem dla
większości zastosowań praktycznych. Innego rodzaju wymierne korzyści (uproszczenie pierwszych
wyrażeń w ciągu iteracyjnym) osiągniemy wybierając mniej optymalnie

ψ′ = Ω

. Zastosowanie

metody Newtona na znajdowanie zera lewej strony równości (4) w każdym przypadku prowadzi do
bardzo szybko zbieżnego ciągu przybliżeń. W metodzie tej korzysta się z pochodnej badanej funkcji
względem danej zmiennej (u nas

ψ

). W naszym przypadku pochodna ta ma postać:

Ocenę następnego przybliżenia dostaje się z:

gdzie

ψ′

oznacza wartość początkową albo poprzednie przybliżenie. Z testów numerycznych wynika,

ż

e dwie iteracje dają dokładności o całe rzędy wielkości przewyższające potrzeby nawet bardzo

2sin(

ψ

−

Ω

)

−

c sin2

ψ

= 0,

(4)

φ

= arctg(

a

b

tg

ψ

).

(5)

h = (r

−

a cos

ψ

)cos

φ

+ (z

−

b sin

ψ

)sin

φ

.

(6)

w = 2 [cos(

ψ′ − Ω

)

−

c cos2

ψ′

].

(7)

ψ

=

ψ′

−

2sin(

ψ′ − Ω

)

−

c sin2

ψ′

w

,

(8)

Page 3 of 10

Algorytmy zamiany współrzędnych

2008-05-27

http://www.astro.uni.torun.pl/~kb/Papers/geod/Geod-GK.htm

wymagającego użytkownika. A są one rzędu 10

−

9

rad w szerokości geodezyjnej dla wszystkich

punktów położonych dalej niż ok. 1000 km od środka Ziemi. W praktyce jest to jakieś sześć rzędów
wielkości lepiej niż w przypadku algorytmów znanych mi z literatury (oczywiście wyłączając
rozwiązania ścisłe).

W tabeli 1 zebrałem błędy pozycji obliczonych za pomocą 9 różnych algorytmów. Błędy są tam
zdefiniowane jako odległości prawdziwych położeń od tych obliczonych. Pierwsze trzy algorytmy
(oparte na pracach [8], [1] oraz [3], w takiej kolejności) są iteracyjnymi, a wyniki podane przed
pochyłą kreską (/) dotyczą dwóch iteracji, zaś trzech iteracji — po tej kresce. Dalsze algorytmy
zaczerpnąłem z prac [10], [12] (wzory 8 i 15 w tej pracy), [2] i [15], odpowiednio. Wzór Baranova i
in. ([2]) poprawiłem na niewątpliwe przekłamanie w druku (parametr a w wyrażeniu na \tgí został w
cytowanej pracy pomyłkowo podniesiony do kwadratu). Z tego zestawienia jasno wynika, że z
naszym względnie prostym algorytmem, którego błędy zawiera przedostatnia kolumna tabeli, mogą
konkurować jedynie rozwiązania ścisłe (ostatnia kolumna tabeli odpowiada mojemu rozwiązaniu
przedstawianemu wcześniej w [4] oraz niżej w tej pracy). Chociaż nasze przybliżone rozwiązanie jest
w istocie iteracyjnym to jednak, dzięki wyjątkowo szybkiej zbieżności, cały proces można ograniczyć
do zaledwie dwóch wzorów, które odpowiadają pierwszemu przybliżeniu:

ψ′ = Ω

+ 0,5 c sin2

Ω

/[1

−

c cos2

Ω

] (wzór 8 z

ψ′ = Ω

) i drugiemu (wzór 8). Taką właśnie wersję użyłem do obliczeń

odpowiednich składników tabeli 1.

Tabela 1

Bł

ę

dy pozycji [mm] i czasy wykonania [0,1 ms] dziewi

ę

ciu algorytmów. Uko

ś

na

kreska (/) oddziela wyniki dla dwóch i trzech iteracji, a gwiazdkami zaznaczono
warto

ś

ci wi

ę

ksze od 10 000 mm. Oznaczenia algorytmów s

ą

zgodne z

odpowiednimi publikacjami ze spisu literatury z wyj

ą

tkiem ostatnich dwóch kolumn,

odnosz

ą

cych si

ę

do niniejszej pracy (te

ż

[4] i [5]), z których pierwsza odpowiada

algorytmowi rozwi

ą

zania przybli

ż

onego, a druga —

ś

cisłego. W algorytmie [3]

rozwi

ą

zania dla h = 0 s

ą

nieokre

ś

lone.

φ

h

Algorytm

[

°

]

[km]

[8]

[1]

[3]

[10] [12] [2]

[15]

Ta praca

89 100000

109 /0

0 /0

1 /0

721

190

1

925 0.000024 0.000000

89

1000

228 /1

0 /0

25 /0

721

857

0

0 0.000000 0.000000

89

0

0 /0

0 /0

- /-

721 1219

0

0 0.000000 0.000000

89

−

1000

431 /3

0 /0

64 /0

721 1836

0

1 0.000000 0.000001

89

−

4000 9005 /164

0 /0 3000 /27 718 ****

3 5564 0.000001 0.000001

70 100000

89 /0

0 /0

0 /0

550

112

248 **** 0.000017 0.000000

70

1000

187 /1

6 /0

11 /0

660

370

5

6 0.000000 0.000000

70

0

0 /0

9 /0

- /-

646

506

0

0 0.000000 0.000000

70

−

1000

353 /2

12 /0

29 /0

611

734

10

34 0.000000 0.000001

70

−

4000 7352 /118

62 /0 1347 /9

330 4391

813 **** 0.000003 0.000001

45 100000

30 /0

1 /0

0 /0

167

24

452 **** 0.000000 0.000000

45

1000

63 /0

181 /1

0 /0

587

215

9

14 0.000001 0.000001

45

0

0 /0

242 /1

- /-

636

327

0

0 0.000000 0.000000

45

−

1000

120 /0

340 /1

0 /0

695

519

18

81 0.000000 0.000001

45

−

4000 2479 /23 1733 /16

0 /0

768 3648 1461 **** 0.000058 0.000000

20 100000

2 /0

2 /0

0 /0

13

22

91 **** 0.000017 0.000015

Page 4 of 10

Algorytmy zamiany współrzędnych

2008-05-27

http://www.astro.uni.torun.pl/~kb/Papers/geod/Geod-GK.htm

Przedstawię teraz rozwiązanie ścisłe. Równanie (4) na kilka sposobów można przekształcić do
wielomianu czwartego stopnia. Jeśli wyrazimy je w tg(

π

/4

−ψ

/2)

≡

t, to dostaniemy wyjątkowo prostą

postać takiego wielomianu:

gdzie

Istnieją standartowe rozwiązania równań czwartego stopnia (np. [11]), z których w naszym przypadku
najodpowiedniejszym zdaje się być tzw. rozwiązanie Ferrariego. W już zredukowanej formie jest ono
następujące:

gdzie

oraz

20

1000

3 /0

358 /2

11 /0

424

72

2

7 0.000000 0.000000

20

0

0 /0

478 /3

- /-

546

121

0

0 0.000001 0.000001

20

−

1000

6 /0

672 /5

28 /0

736

205

4

35 0.000000 0.000000

20

−

4000

126 /0

3407 /54 1303 /9 3284 1552

288 **** 0.000002 0.000001

1 100000

0 /0

0 /0

1 /0

0

1

0

922 0.000000 0.000015

1

1000

0 /0

25 /0

24 /0

25

10

0

0 0.000000 0.000000

1

0

0 /0

33 /0

- /-

33

17

0

0 0.000000 0.000000

1

−

1000

0 /0

47 /0

63 /0

47

27

0

1 0.000000 0.000000

1

−

4000

0 /0

236 /4 2887 /26 236

192

0 7000 0.000000 0.000000

Czas wyk.:

56 /78

51 /70

50 /63

44

34

46

146

74

53

t

4

+ 2Et

3

+ 2Ft

−

1 = 0,

(9)

E = tg

Ω −

c

cos

Ω

=

bz

−

(a

2

−

b

2

)

ar

(10)

F = tg

Ω

+

c

cos

Ω

=

bz + (a

2

−

b

2

)

ar

.

(11)

t =

±



√

G

2

+

F

−

vG

2G

−

E

−

G,

(12)

G =

(

±

√

E

2

+ v

+ E

)

/2,

(13)

v = (

√

D

−

Q)

1/3

−

(

√

D + Q)

1/3

,

(14a)

D = P

3

+ Q

2

,

(15)

P =

4

3

(EF + 1)

(16)

Page 5 of 10

Algorytmy zamiany współrzędnych

2008-05-27

http://www.astro.uni.torun.pl/~kb/Papers/geod/Geod-GK.htm

Dla przypadku D < 0, aby uniknąć arytmetyki liczb zespolonych, można użyć równoważnego ale
wygodniejszego od (14a) wyrażenia:

Warto jednak wiedzieć, że przypadek D < 0 (między środkiem elipsy i krzywą D = 0 na rysunku 1)
będzie w praktyce co najwyżej marginalnie użyteczny, gdyż D jest dodatnie wszędzie dalej niż około
21 – 45 km od środka elipsoidy ziemskiej. W ogólności krzywa D = 0, albo 27[abrz(a

2

−

b

2

)]

2

= [(a

2

−

b

2

)

2

−

(ar)

2

−

(bz)

2

]

3

, osiąga osie r oraz z w punktach

±

(a

2

−

b

2

)/a oraz

±

(a

2

−

b

2

)/b, a jej

minimalna odległość od początku układu kartezjańskiego przypada dla

Ω

=

π

/4 i wynosi (a/b

−

b/a)

√

{(a

2

+ b

2

)/8}. Ciekawe, że jest ona obwiednią prostych prostopadłych do elipsy w sąsiednim

kwadrancie (jest więc tzw. ewolutą elipsy).

Każde rozwiązanie rzeczywiste z czterech podanych (odpowiadających czterem kombinacjom
znaków +/

−

w równaniach 12 i 13) reprezentuje inną parę współrzędnych geodezyjnych, a

odpowiadające im kierunki są stycznymi do właściwych gałęzi ewoluty. Współrzędne te można
odzyskać z t w następujący sposób:

oraz

Oczywiście, w praktyce nie są potrzebne wszystkie cztery rozwiązania (wszystkie one są rzeczywiste
dla D < 0, a tylko dwa są takie w przeciwnym przypadku). Aby uzyskać wygodny do
zaprogramowania algorytm dający to pojedyncze pożądane rozwiązanie wystarczy opuścić podwójne
znaki (

±

) we wzorach (12) i (13) pozostawiając tam dodatnie wartości pirwiastków. Taki algorytm

będzie poprawny tylko dla a > b (co w praktyce jest zawsze spełnione) i

φ

> 0. Także to ostatnie

ograniczenie niewiele ujmuje z ogólności rozwiązania, gdyż na południowej półkuli mamy takie same
wyniki, tyle że z przeciwnym znakiem szerokości. Ponadto, w naszym algorytmie istnieje prosty
sposób automatycznego przypisania właściwego znaku wynikowi: nadanie małej półosi b znaku
współrzędnej z przed procesem rozwiązywania problemu czyni podany algorytm (ten uproszczony do
dodatnich pierwiastków) poprawnym na obu półkulach — bez konieczności wyszukiwania
właściwego rozwiązania pośród czterech.

Przetestowałem ten algorytm (wzory od 10 do 19) w szerokim zakresie płaszczyzny (r,z) nie
napotykając żadnych problemów. Również błędy zaokrągleń okazują się nieznaczące dla
praktycznych zastosowań (używałem fortranowskiej opcji DOUBLE PRECISION), chociaż są one
wyraźnie większe w pobliżu osi r i z niż gdzie indziej. Głównym źródłem tych błędów jest obliczanie
wyrażenia (14a), które zawiera różnicę pierwiastków sześciennych (zaprogramowanych jako
eksponent z trzeciej części logarytmu naturalnego). Problem ten obszedłem przez poprawienie
wyniku otrzymanego z (14a), mówmy v

′

, korzystając z resolwenty równania (9) (której jednym z

trzech pierwiastków jest właśnie v bądź v

′

):

Q = 2(E

2

−

F

2

).

(17)

v = 2

√

−

P

cos







1

3

arccos







Q

√

−

P

3













.

(14b)

φ

= arctg

a(1

−

t

2

)

2bt

(18)

h = (r

−

at)cos

φ

+ (z

−

b)sin

φ

.

(19)

v

′

3

+ 2Q

Page 6 of 10

Algorytmy zamiany współrzędnych

2008-05-27

http://www.astro.uni.torun.pl/~kb/Papers/geod/Geod-GK.htm

Nietrudno jest pokazać, że v z powyższego równania jest dokładniejsze niż v

′

o ile tylko v

2

<

|

P

|

, co

jest spełnione wszędzie poza kołem o promieniu ok. 70 km wokół środka ziemskiej elipsoidy.
Rozwiązanie Heikkinena (w [7]), które także zawiera pierwiastki sześcienne (lecz nie w różnicy) nie
ma tej słabości, ale za to nie obejmuje przypadku D < 0. Dla przypadku D > 0 i z poprawką (20) w
moim algorytmie, te dwa rozwiązania wydają się jednakowo dobre.

W celu porównania efektywności omawianych algorytmów zmierzyłem czas potrzebny na ich
wykonanie na IBM PC (z koprocesorem) z kompilatorem FORTRANu firmy Lahey Computer
Systems. Wyniki, w jednostkach 0,1 ms podane w ostatnim wierszu tabeli 1, wskazują że wszystkie
czasy są porównywalne mimo dość znacznych różnic w złożoności algorytmów. Wydaje się, że jest
tak dlatego, że główny wkład do czasu wykonania pochodzi od obliczania funkcji
trygonometrycznych, których w każdym programie jest po kilka. Na przykład, obliczenie funkcji
kosinus zajmuje około 0,6 ms albo 6 jednostek tabeli 1. Ponieważ czasy obliczeń okazały się tak mało
zróżnicowane, a obliczanie w sumie tanie, nie próbowałem optymalizować w tym względzie żadnych
z implementowanych algorytmów. Dotyczy to także objętości poszczególnych programów, które są
porównywalne (zajmują 7 – 15 linii FORTRANu) z wyjątkiem algorytmu [15], ale ten i tak zdaje się
być najgorszy w każdym względzie. Wiedzieć jednak warto, że nasz algorytm ścisły będzie znacząco
szybszy, gdy równanie (14a) zastąpimy przez równoważne:

gdzie s = (

√

D + Q)

1/3

, co pozwala wyeliminować obliczanie jednego z dwóch pierwiastków

sześciennych (s nigdzie nie znika dla D > 0). Poniższa procedura GEOD zawiera już to usprawnienie.

v =

−

3P

.

(20)

v =

P

s

−

s,

(14c)

subroutine GEOD(r,z,fi,h)
c Program to transform Cartesian to geodetic coordinates
c Input: r, z = equatorial [m] and polar [m] components
c Output: fi, h = geodetic coord's (latitude [rad], height [m])
implicit real*8(a-h,o-z)
c IAU ellipsoid: semimajor axis and inverse flattening
data a,frec /6378140.d0,298.257d0/
b=dsign(a-a/frec,z)
if(r.eq.0d0) return
E=((z+b)*b/a-a)/r
F=((z-b)*b/a+a)/r
P=(E*F+1.)*4d0/3.
Q=(E*E-F*F)*2.
D=P*P*P+Q*Q
if(D.ge.0d0) then
s=dsqrt(D)+Q
s=dsign(dexp(dlog(dabs(s))/3d0),s)
v=P/s-s
v=-(Q+Q+v*v*v)/(3*P)
else
v=2.*dsqrt(-P)*dcos(dacos(Q/P/dsqrt(-P))/3.)
endif
G=.5*(E+dsqrt(E*E+v))
t=dsqrt(G*G+(F-v*G)/(G+G-E))-G
fi=datan((1.-t*t)*a/(2*b*t))
h=(r-a*t)*dcos(fi)+(z-b)*dsin(fi)
end

Test:
r z fi h

Page 7 of 10

Algorytmy zamiany współrzędnych

2008-05-27

http://www.astro.uni.torun.pl/~kb/Papers/geod/Geod-GK.htm

Podsumowując można stwierdzić, że algorytmy iteracyjne, takie jak [8], albo publikowane w
roczniku astronomicznym [1], są najprostszymi do zaprogramowania i dają przyzwoite dokładności
po 3 – 4 iteracjach. Z jeszcze jedną lub dwiema dodatkowymi iteracjami można ich bezpiecznie
używać także, gdy jest wymagana wyższa dokładność. Jednak, z powodu błędów maszynowej
reprezentacji liczb, próby z więcej niż 6 iteracjami mogą nie poprawiać już dokładności, która może
być niekiedy nieco gorsza niż przy użyciu algorytmów opartych o rozwiązania ścisłe. W takich
przypadkach bardziej właściwe wydają sie dwa algorytmy przedstawione tutaj albo algorytm z pracy
[7]. Gwarantują one dokładności kilka rzędów wielkości poniżej 1 mm na całym praktycznie
użytecznym obszarze płaszczyzny (r,z) — od kilkudziesięciu kilometrów od centrum Ziemi do wielu
promieni ziemskich ponad jej powierzchnię. W tych zastosowaniach nasza poprawka (20) do
matematycznie ścisłego rozwiązania może być bezpiecznie pominięta. W przypadku poszukiwania
bardziej ogólnych rozwiązań na transformację współrzędnych prostokątnych na geodezyjne, jedynym
gotowym algorytmem jest nasze ścisłe rozwiązanie (oryginalnie przedstawione pełniej, lecz z
przykrym przekłamaniem, w pracy [4]).

Po złożeniu tego raportu w Redakcji ukazała się praca Laskowskiego [20], który zwrócił uwagę na
całkiem prosty algorytm iteracyjny Bowringa [21] i stwierdził, że jest on równie dokładny jak nasz
przybliżony, ale jest nieco odeń szybszy. Ponadto w rozwiązaniu ścisłym odkryłem osobliwość przy
EF = –1, która występuje w odległości 41 – 46 km od środka Ziemi, jest więc niegroźna dla
praktycznych zastosowań.

[1] Astronomical Almanac for the Year 1989, USNO and RGO, Washington and London, str. K11.

[2] Baranov V.N. i in., Kosmicheskaya geodeziya, Nedra, Moskva, 1986, str. 27.

[3] Bartelme N., Meissl P., Ein einfaches, rasches und numerisch stabiles Verfahren zur Bestimmung
des kürzesten Abstandes eines Punktes von einen sphäroidischen Rotationsellipsoid, AVN, Heft 12,
1975, 436 – 439 (Wichmann, Karlsruhe).

[4] Borkowski K.M.,

Transformation of Geocentric to Geodetic Coordinates without Approximations

,

Astrophys. Space Sci., 139, 1987, 1 – 4 (Erratum: 146, 1988, 201).

[5] Borkowski K.M.,

Accurate Algorithms to Transform Geocentric to Geodetic Coordinates

, Bull.

Géod., 63, 1989, 50 – 56.

[6] Hedgley D.R., An Exact Transformation from Geocentric to Geodetic Coordinates for Nonzero
Altitudes, NASA Techn. Rep. R-458 (1976).

[7] Heikkinen M., Geschlossene Formeln zur Berechnung raumlicher geod„tischer Koordinaten aus
rechtwinkligen Koordinaten, Zeitschrift Vermess., 107, 1982, 207 – 211.

[8] Heiskanen W.A. i Moritz H., Physical Geodesy, W.H. Freeman and Co., San Francisco, 1967, str.
181.

[9] Hlibowicki R. (red.), Geodezja wyższa i astronomia geodezyjna, PWN, Warszawa, 1981, str. 273.

[10] Izotov A.A. i in., Osnovy sputnikovoj geodezii, Nedra, Moskva, 1974, str. 34.

4000000. 6000000. 0.985526645027216 847786.688189974
4000.000 -6000.000 -1.48883906081174 -6350591.52477262

LITERATURA

Page 8 of 10

Algorytmy zamiany współrzędnych

2008-05-27

http://www.astro.uni.torun.pl/~kb/Papers/geod/Geod-GK.htm

[11] Korn G.A. i Korn T.M., Mathematical Handbook for Scientists and Engineers, McGraw-Hill,
New York, 1961, str. 24 (tłum. polskie: PWN, Warszawa, 1983, str. 36).

[12] Long S.A.T., General Altitude Transformation between Geocentric and Geodetic Coordinates,
Celestial Mech., 12, 1975, 225 – 230.

[13] Morrison J. i Pines S., The Reduction from Geocentric to Geodetic Coordinates, Astron. J., 66,
1961, 15 – 16.

[14] Paul M.K., A Note on Computation of Geodetic Coordinates from Geocentric (Cartesian)
Coordinates, Bull. Géod., Nouv. Ser., No 108, 1973, 135 – 139.

[15] Pick M., Closed Formulae for Transformation of the Cartesian Coordinate System into a System
of Geodetic Coordinates, Studia geoph. et geod., 29, 1985, 112 – 119.

[16] Taff L.G., Celestial Mechanics. A Computational Guide for the Practitioner, J. Wiley and Sons,
New York, 1985, rozdz. 3.

[17] Urmaev M.S., Orbital'nye metody kosmicheskoj geodezii, Nedra, Moskva, 1981, str. 14.

[18] Vanček P. i Krakiwski E.J., Geodesy: The Concepts, North Holland Publ. Co., Amsterdam,
1982, str. 324.

[19] Woolard E.W. i Clemence G.M., Spherical Astronomy, Academic Press, New York, 1966, rozdz.
3.

[20] Laskowski P., Is Newton's Iteration Faster than Simple Iteration for Transformation between
Geocentric and Geodetic Coordinates?, Bull. Géod., 65, 1991, 14 – 17.

[21] Bowring B.R., Transformation from Spatial to Geographical Coordinates, Survey Review,
XXIII, 181, 1976, 323 – 327.

Praca wpłynęła do Redakcji 1991.04.08

Akceptowana do druku 1992.10.20

Kazimierz M. Borkowski

Two very accurate closed solutions are proposed of which one is
approximate in nature and the other is exact. They are shown to be
superior to others, found in literature and in practice, in both or either
accuracy and/or simplicity. In the approximation algorithm one determines
the eccentric latitude:

ψ = Ψ −

[sin(

Ψ − Ω

)

−

0.5c sin2

Ψ

]/[cos(

Ψ − Ω

)

−

c cos2

Ψ

]

to find the geodetic latitude and height above a reference ellipsoid:

φ

= arctg[(a/b)tan

ψ

],

Algorithms to Transform Geocentric to Geodetic Coordinates

S u m m a r y

Page 9 of 10

Algorytmy zamiany współrzędnych

2008-05-27

http://www.astro.uni.torun.pl/~kb/Papers/geod/Geod-GK.htm

File translated from T

E

X by

T

T

H

, version 3.12 on 26 Jul 2002.

h = [za sin

ψ −

ab + rb cos

ψ

]/[(a sin

ψ

)

2

+ (b cos

ψ

)

2

]

1/2

,

where c = (a

2

−

b

2

)/[(ar)

2

+ (bz)

2

]

1/2

,

Ω

= arctg[bz/(ar)],

Ψ

=

Ω

+ 0.5c

sin2

Ω

/(1

−

c cos2

Ω

), a and b are the semi-axes of the reference ellipsoid, z

and r are respectively the polar and equatorial components of the position
vector in the Cartesian system of coordinates.

Page 10 of 10

Algorytmy zamiany współrzędnych

2008-05-27

http://www.astro.uni.torun.pl/~kb/Papers/geod/Geod-GK.htm