Wyznaczenie w miarodajnych przekrojach wartości sił wewnętrznych

ISIE – semestr IV

1

I. Dane liczbowe

l

eff

= 6,2 m,

l

wsp

= 1,7 m,

l

bel

= 2,7 m,

q

k

= 3,00 kN/m

2

,

G

k

= 13,0 kN,

Q

k

= 18,0 kN.

NORMY:

[1]

PN-82/B-02001 Obciążenia budowli. Obciążenia stałe.

[2]

PN-82/B-02003 Obciążenia budowli. Obciążenia zmienne technologiczne.

Podstawowe obciążenia technologiczne i montażowe.

II. Płyta stropowa

1. Zestawienie obciążeń na płytę stropową

1.1. Obciążenia stałe

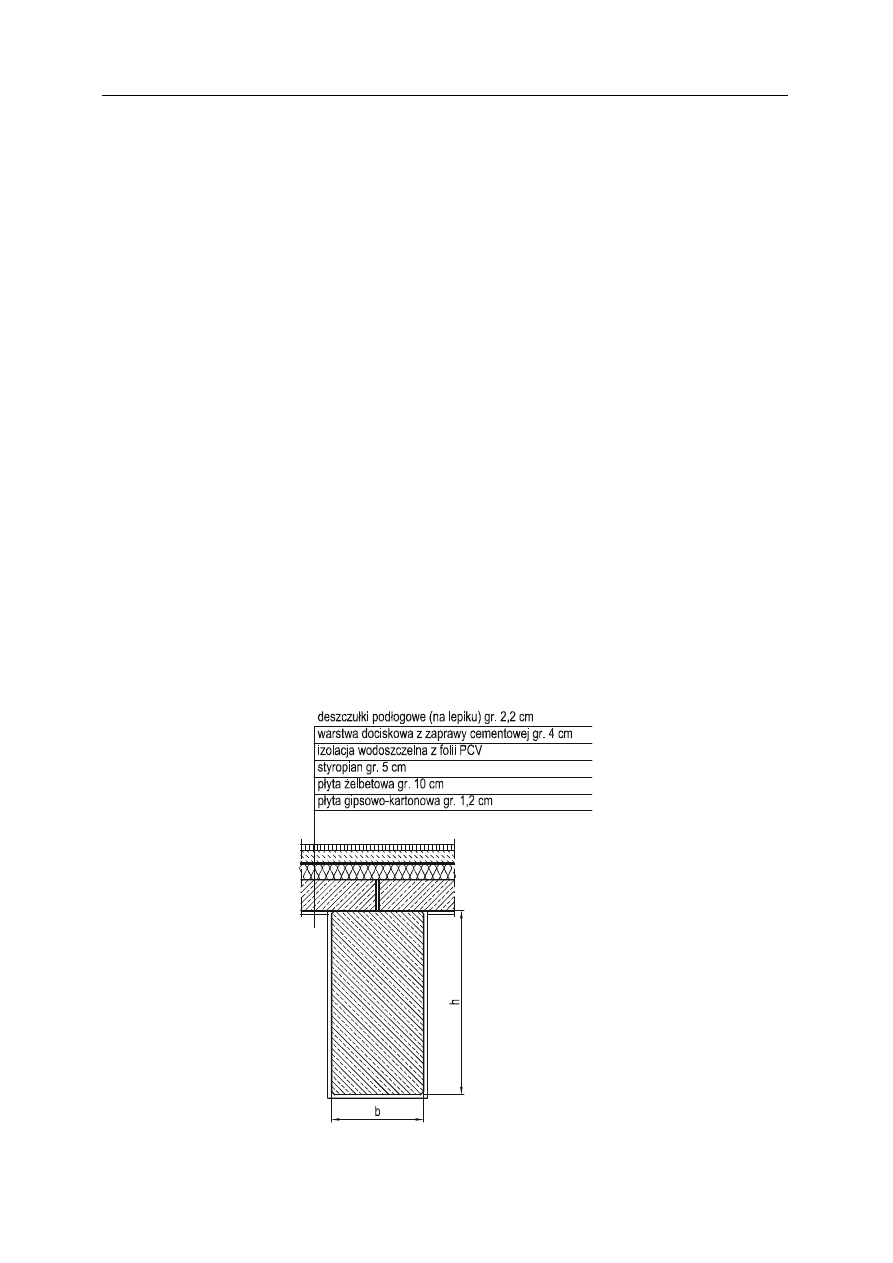
Przyjęto (wstępnie) grubość płyty żelbetowej: h

p

= 100 mm.

Rys. 1. Przyjęte warstwy podłogi.

Wyznaczenie w miarodajnych przekrojach wartości sił wewnętrznych

ISIE – semestr IV

2

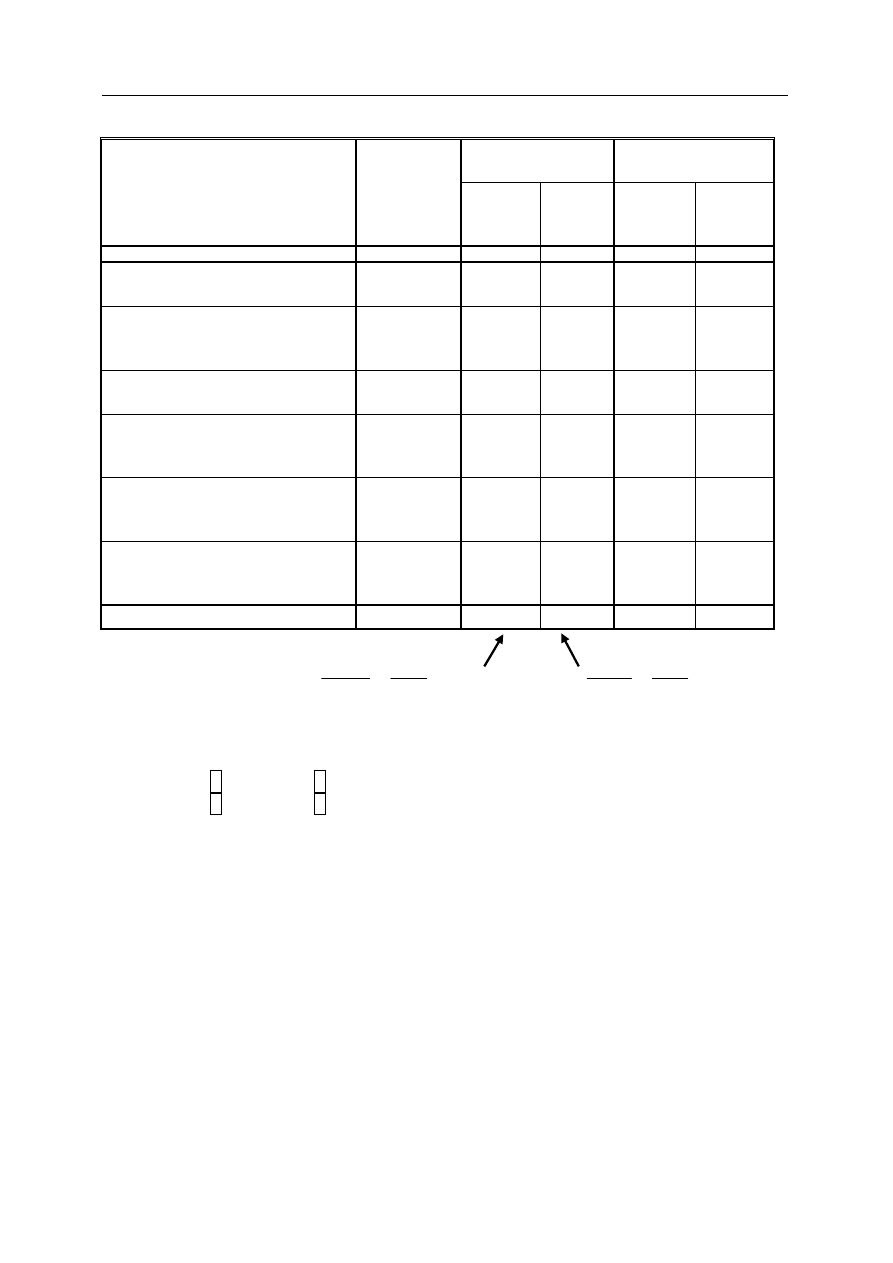
Tablica 1. Zestawienie obciążeń stałych na 1m

2

płyty.

Współczynnik

obciążenia

2)

Obciążenie

obliczeniowe

Rodzaj obciążenia

Obciążenie
charaktery-

styczne g

k

kN/m

2

max

γ

f

> 1

min

γ

f

< 1

max

3)

g

pmax

kN/m

2

min

4)

g

pmin

kN/m

2

1 2

3

4

5

6

1. Płyta żelbetowa
0,10

⋅25,0

1)

2,50 1,1

0,9

2,75

2,25

2. Płyty gipsowo-kartonowe
gr. 1,2 cm
0,012

⋅12,0

1)

0,144 1,2 0,9

0,173

0,130

3. Styropian gr. 5 cm
0,05

⋅0,45

1)

0,023 1,2 0,9

0,028

0,021

4. Izolacja wodoszczelna z
folii PCV
0,035

1)

0,035 1,2 0,9

0,042

0,032

5. Warstwa dociskowa z za-
prawy cementowej gr. 4 cm
0,04

⋅21,0

1)

0,840 1,3 0,8

1,09

0,672

6. Deszczułki podłogowe na
lepiku gr. 2,2 cm
0,230

1)

0,230 1,2 0,9

0,276

0,207

RAZEM:

3,77 1,16

0,878

4,36

3,31

16

1

77

3

36

4

,

,

,

g

g

k

max

p

=

=

878

0

77

3

31

3

,

,

,

g

g

k

min

p

=

=

1)

− ciężary materiałów (kN/m

3

lub kN/m

2

) wg PN-82/B-02001 [1],

2)

− współczynnik obciążenia

γ

f

wg PN-82/B-02001, pkt. 5 [1],

3)

− kolumna 2 × kolumna 3,

4)

− kolumna 2 × kolumna 4.

1.2. Obciążenia zmienne technologiczne

q

p

= q

k

⋅γ

f

= 3,0

⋅1,3 = 3,90 kN/m

2

,

przy q

k

≤ 2 kN/m

2

⇒

γ

f

=1,4,

2 kN/m

2

< q

k

≤ 5 kN/m

2

⇒

γ

f

=1,3,

q

k

> 5 kN/m

2

⇒

γ

f

=1,2,

γ

f

− współczynnik obciążenia wg PN-82/B-02003, tablica 7 [2].

Wyznaczenie w miarodajnych przekrojach wartości sił wewnętrznych

ISIE – semestr IV

3

2. Maksymalny obliczeniowy moment zginający w płycie

W wypadku prefabrykatów, płytę oblicza się zbierając obciążenie z ich szero-

kości b

pref

, natomiast przy szerokich płytach oblicza się pasmo szerokości b

pref

= 1 m.

Płyta oparta jest na stropowych belkach, w osiowym rozstawie l

bel

= 2,7 m, przy czym

teoretyczna rozpiętość płyty przy szerokości belki b = 0,25 m (b dokładnie wyznaczy

się dopiero po obliczeniu belki) wynosi

l

eff

= l

bel

– b/2 = 2,7 – 0,25/2 = 2,575 m.

Maksymalny

moment

zginający w środku przęsła płyty wynosi wtedy

45

6

8

575

2

0

1

90

3

36

4

8

2

2

,

,

,

)

,

,

(

l

b

)

q

g

(

M

bel

pref

p

max

p

max

p

=

⋅

⋅

+

=

⋅

⋅

+

=

kNm.

III. Belka stropowa

1. Zestawienie obciążeń na belkę

1.1. Obciążenia stałe równomiernie rozłożone

Orientacyjne wymiary poprzecznego przekroju belki:

•

wysokość belki,

56

69

12

10

620

11

9

÷

=

÷

=

÷

=

eff

l

h

cm,

•

szerokość belki,

24

30

5

2

2

60

5

2

2

÷

=

÷

=

÷

=

,

,

h

b

cm.

Przyjmuje się b = 30 cm, h = 60 cm.

Wyznaczenie w miarodajnych przekrojach wartości sił wewnętrznych

ISIE – semestr IV

4

Tablica 2. Zestawienie obciążeń stałych na 1mb belki.

Współczynnik

obciążenia

Obciążenie

obliczeniowe

Rodzaj obciążenia

Obciążenie
charaktery-

styczne

g

k

kN/m

max

γ

f

> 1

min

γ

f

< 1

max

g

max

kN/m

min
g

min

kN/m

1 2

3

4

5

6

1. Belka żelbetowa
0,60

⋅0,30⋅25,0

4,50 1,1

0,9

4,95

4,05

2. Płyta żelbetowa z warstwa-
mi podłogi i płytami gipsowymi
3,77

⋅2,7

4)

10,2 1,16

0,878

11,8

8,96

3. Płyty gipsowo kartonowe gr.
1,2 cm na bocznych po-
wierzchniach belki
(2

⋅0,6)⋅0,012⋅12,0

0,173 1,2 0,9

0,208

0,156

RAZEM

14,9 1,14

0,88

17,0 13,2

4)

− osiowy rozstaw belek (l

bel

).

1.2. Obciążenia stałe skupione

G

max

= G

k

⋅γ

f

= 13,0

⋅1,2 = 15,6 kN,

G

min

= G

k

⋅γ

f

= 13,0

⋅0,9 = 11,7 kN.

1.3. Obciążenia zmienne równomiernie rozłożone

q

= q

k

γ

f

⋅

l

bel

= 3,0

⋅1,3⋅2,7 = 10,5 kN/m.

1.4. Obciążenia zmienne skupione

Q

= Q

k

γ

f

= 18,0

⋅1,2 = 21,6 kN,

γ

f

− współczynnik obciążenia wg PN-82/B-02003, tablica 7 [2].

Wyznaczenie w miarodajnych przekrojach wartości sił wewnętrznych

ISIE – semestr IV

5

2. Ekstremalne siły wewnętrzne w belce

2.1. Momenty zginające

Obliczeniowe wartości obciążeń przyjęte w obliczeniach:

g

max

= 17,0 kN/m,

G

max

= 15,6 kN,

g

min

= 13,2 kN/m,

G

min

= 11,7 kN,

q

= 10,5 kN/m,

Q

= 21,6 kN.

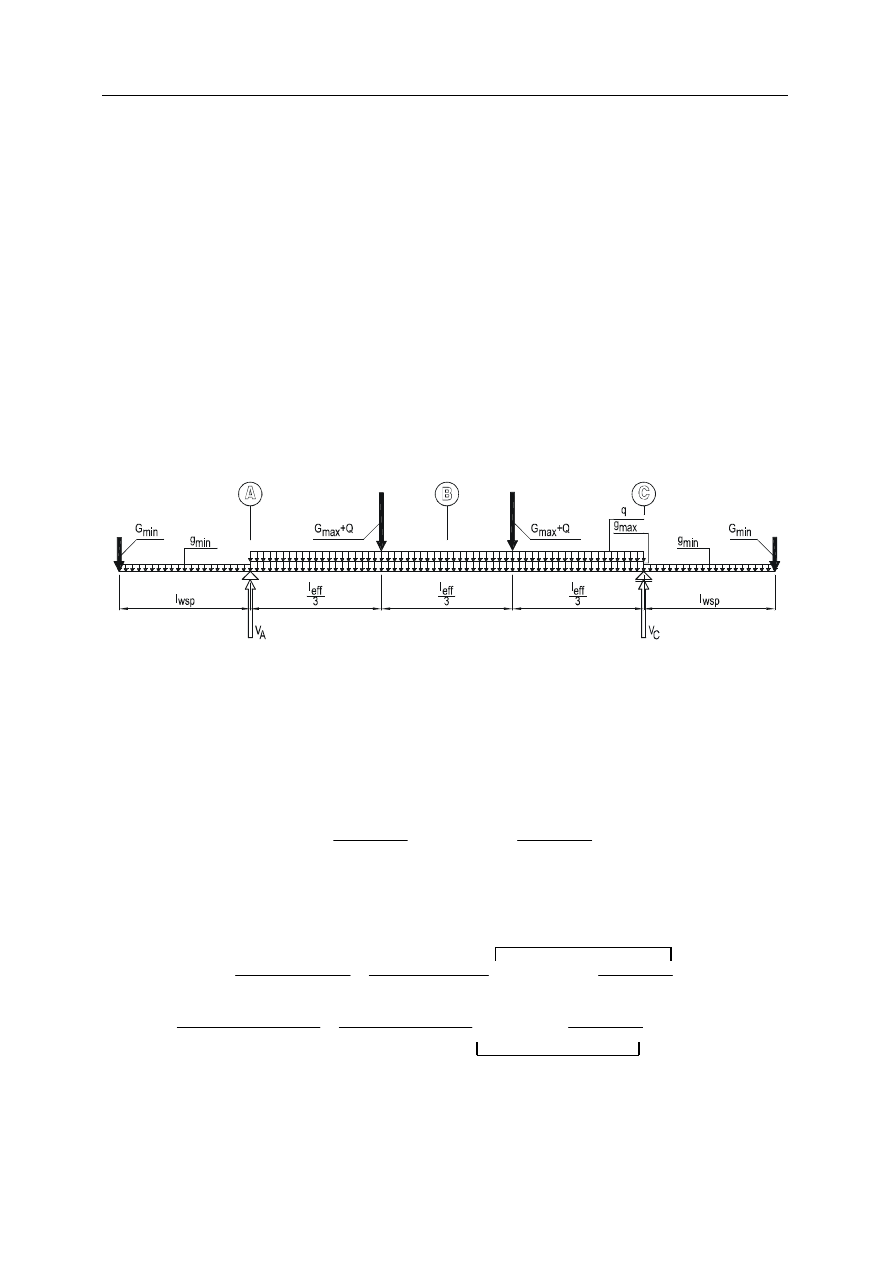
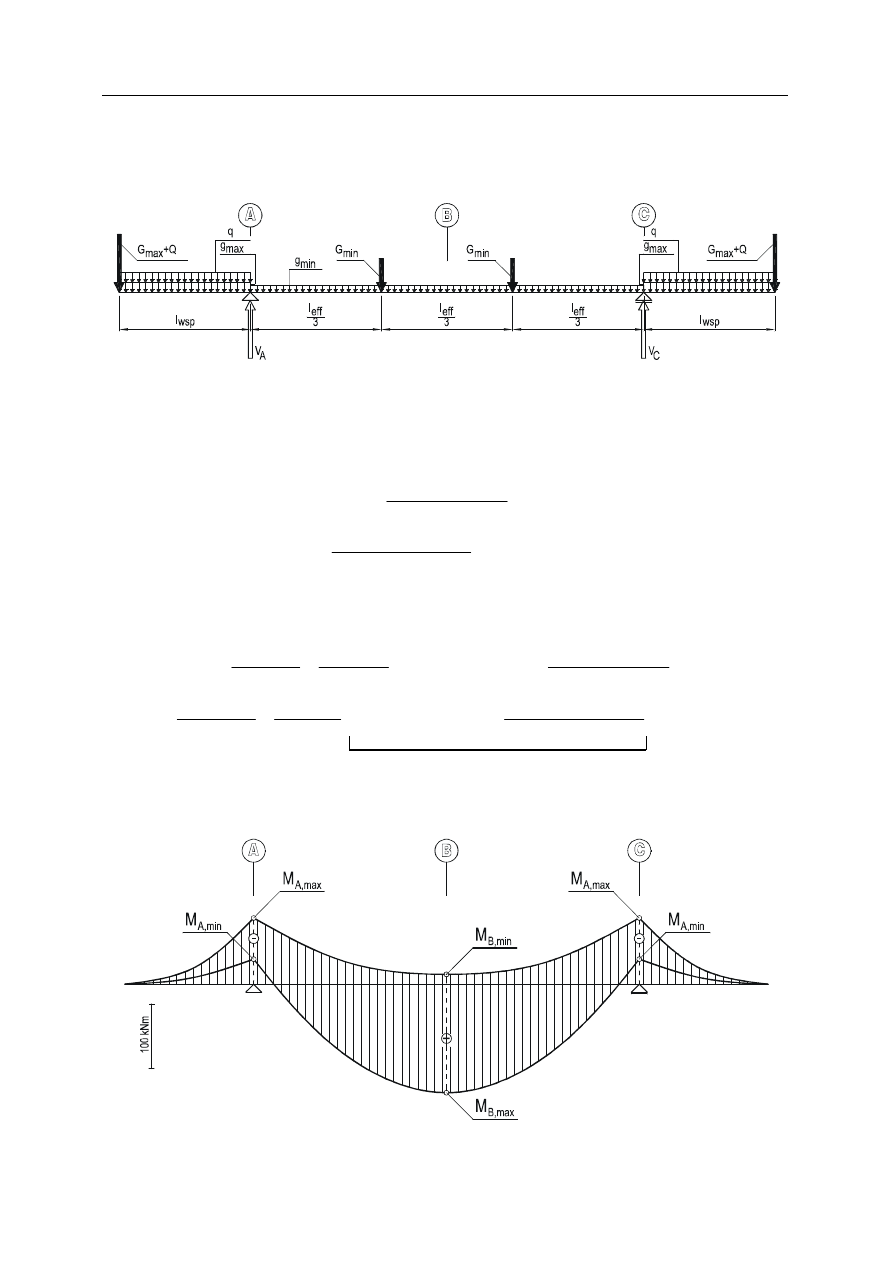
UKŁAD STATYCZNY NR 1

EKSTREMALNE MOMENTY ZGINAJĄCE

Rys. 2. Minimalny moment w przekroju A i maksymalny moment w przekroju B

Układ statyczny jest symetryczny. Ekstremalne momenty zginające w przekro-

jach A i B wyznacza się sumując ekstrema z symetrycznych układów poszczegól-
nych obciążeń (jak przedstawiono to na poprzednich ćwiczeniach).

•

Moment zginający w przekroju A,

kNm.

0

39

2

7

1

2

13

7

1

7

11

2

2

2

,

,

,

,

,

l

g

l

G

M

wsp

min

wsp

min

min

,

A

−

=

⋅

−

⋅

−

=

⋅

−

⋅

−

=

•

Moment zginający w przekroju B,

M

A,min

kNm.

170

2

7

1

2

13

7

1

7

11

3

2

6

6

21

6

15

8

2

6

5

10

0

17

2

3

8

2

2

2

2

=

⋅

−

⋅

−

⋅

+

+

⋅

+

=

=

⋅

−

⋅

−

⋅

+

+

⋅

+

=

,

,

,

,

,

)

,

,

(

,

)

,

,

(

l

g

l

G

l

)

Q

G

(

l

)

q

g

(

M

wsp

min

wsp

min

eff

max

eff

max

max

,

B

M

A,min

Wyznaczenie w miarodajnych przekrojach wartości sił wewnętrznych

ISIE – semestr IV

6

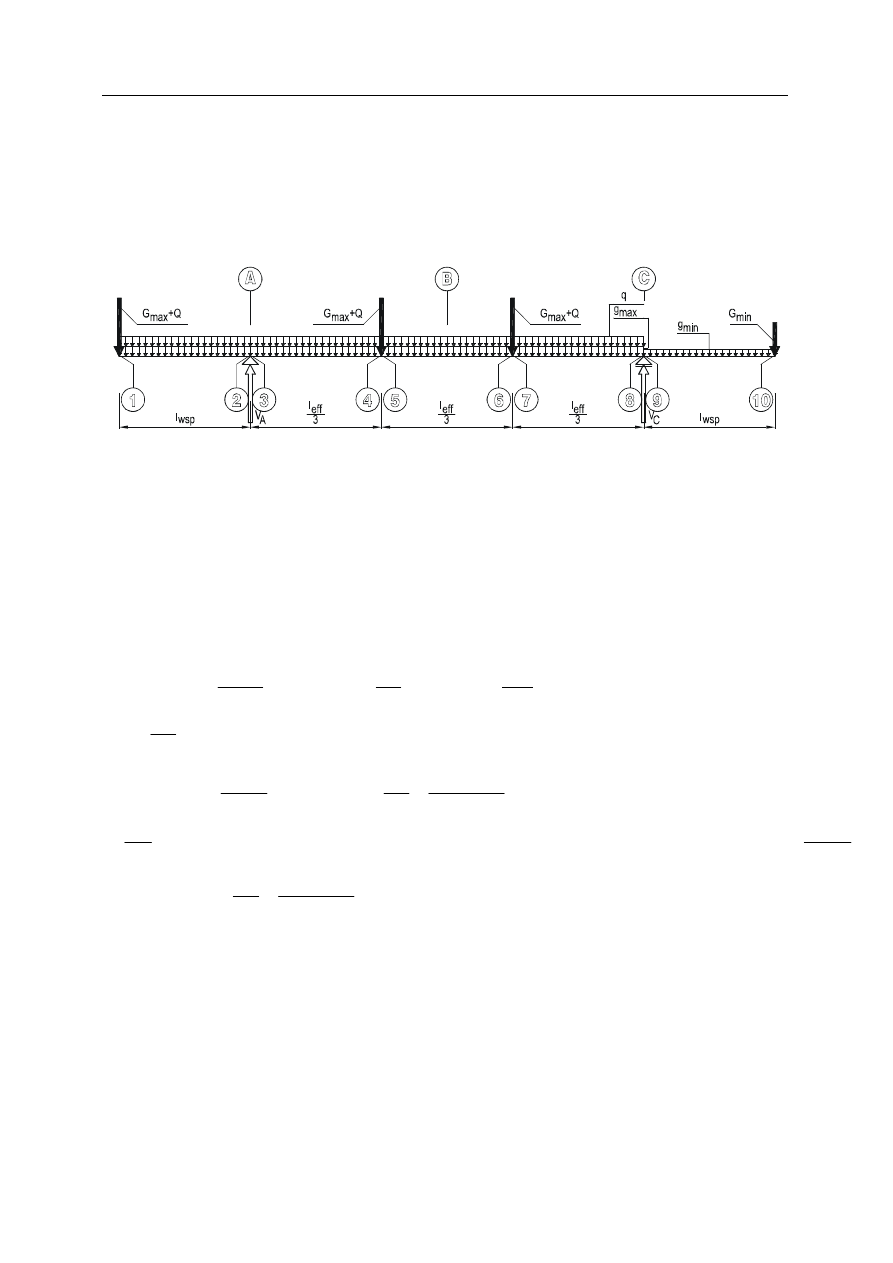
UKŁAD STATYCZNY NR 2

EKSTREMALNE MOMENTY ZGINAJĄCE

Rys. 3. Maksymalny moment w przekroju A i minimalny moment w przekroju B

•

Moment zginający w przekroju A,

kNm.

103

2

7

1

5

10

0

17

7

1

6

21

6

15

2

2

2

−

=

⋅

+

−

⋅

+

−

=

=

⋅

+

−

⋅

+

−

=

,

)

,

,

(

,

)

,

,

(

l

)

q

g

(

l

)

Q

G

(

M

wsp

max

wsp

max

max

,

A

•

Moment zginający w przekroju B,

kNm.

4

15

2

7

1

5

10

0

17

7

1

6

21

6

15

3

2

6

7

11

8

2

6

2

13

2

3

8

2

2

2

2

,

,

)

,

,

(

,

)

,

,

(

,

,

,

,

l

)

q

g

(

l

)

Q

G

(

l

G

l

g

M

wsp

max

wsp

max

eff

min

eff

min

min

,

B

−

=

⋅

+

−

⋅

+

−

⋅

+

⋅

=

=

⋅

+

−

⋅

+

−

⋅

+

⋅

=

M

A,max

Rys. 4. Szkic obwiedni momentów zginających.

Wyznaczenie w miarodajnych przekrojach wartości sił wewnętrznych

ISIE – semestr IV

7

2.2. Siły poprzeczne

UKŁAD STATYCZNY NR 3

EKSTREMALNE SIŁY POPRZECZNE

Rys. 5. Maksymalna reakcja podporowa na podporze A i ekstremalne siły

poprzeczne w przekroju 2 i 3

Układ statyczny nie jest symetryczny. Nie korzysta się z sumowania pojedyn-

czych schematów.

•

Reakcja na podporze A,

∑

= 0

C

M

,

,

0

2

3

3

2

5

0

=

⋅

+

⋅

⋅

+

⋅

+

−

⋅

⋅

+

−

−

+

⋅

⋅

+

⋅

+

−

+

⋅

+

−

⋅

wsp

min

wsp

wsp

min

eff

max

eff

max

eff

wsp

eff

wsp

max

wsp

eff

max

eff

A

l

G

l

l

g

l

)

Q

G

(

l

)

Q

G

(

)

l

l

(

,

)

l

l

(

)

q

g

(

)

l

l

(

)

Q

G

(

l

V

kN.

217

7

1

7

11

2

7

1

2

13

3

2

6

6

21

6

15

3

2

6

2

6

21

6

15

7

1

2

6

5

0

2

6

7

1

5

10

0

17

7

1

2

6

6

21

6

15

6,2

1

2

3

3

2

5

0

1

2

2

=

⋅

−

⋅

−

⋅

+

+

+

⋅

⋅

+

+

+

⋅

⋅

+

⋅

+

+

+

⋅

+

=

=

⋅

−

⋅

−

⋅

+

+

⋅

⋅

+

+

+

+

⋅

⋅

+

⋅

+

+

+

⋅

+

=

]

,

,

,

,

,

)

,

,

(

,

)

,

,

(

)

,

,

(

,

)

,

,

(

)

,

,

(

)

,

,

(

)

,

,

[(

]

l

G

l

g

l

)

Q

G

(

l

)

Q

G

(

)

l

l

(

,

)

l

l

(

)

q

g

(

)

l

l

(

)

Q

G

[(

l

V

wsp

min

wsp

min

eff

max

eff

max

eff

wsp

eff

wsp

max

wsp

eff

max

eff

A

•

Siła poprzeczna w przekroju 1, po prawej stronie

kN.

2

37

6

21

6

15

1

,

)

,

,

(

)

Q

G

(

V

max

,

Sd

−

=

+

−

=

+

−

=

•

Siła poprzeczna w przekroju 2,

kN.

0

84

7

1

5

10

0

17

2

37

1

2

,

,

)

,

,

(

,

l

)

q

g

(

V

V

wsp

max

,

Sd

,

Sd

−

=

⋅

+

−

−

=

⋅

+

−

=

Wyznaczenie w miarodajnych przekrojach wartości sił wewnętrznych

ISIE – semestr IV

8

•

Siła poprzeczna w przekroju 3,

kN.

133

217

0

84

2

3

=

+

−

=

+

=

,

V

V

V

A

,

Sd

,

Sd

•

Siła poprzeczna w przekroju 4,

kN.

9

75

3

2

6

5

10

0

17

133

3

3

4

,

,

)

,

,

(

l

)

q

g

(

V

V

eff

max

,

Sd

,

Sd

=

⋅

+

−

=

⋅

+

−

=

•

Siła poprzeczna w przekroju 5,

kN.

7

38

6

21

6

15

9

75

4

5

,

)

,

,

(

,

)

Q

G

(

V

V

max

,

Sd

,

Sd

=

+

−

=

+

−

=

•

Siła poprzeczna w przekroju 6,

kN.

1

18

3

2

6

5

10

0

17

7

38

3

5

6

,

,

)

,

,

(

,

l

)

q

g

(

V

V

eff

max

,

Sd

,

Sd

−

=

⋅

+

−

=

⋅

+

−

=

Dotąd jest potrzebne, ale można pociągnąć aż do końca.

•

Siła poprzeczna w przekroju 7,

kN.

3

55

6

21

6

15

1

18

6

7

,

)

,

,

(

,

)

Q

G

(

V

V

max

,

Sd

,

Sd

−

=

+

−

−

=

+

−

=

•

Siła poprzeczna w przekroju 8,

kN.

112

3

2

6

5

10

0

17

3

55

3

7

8

−

=

⋅

+

−

−

=

⋅

+

−

=

,

)

,

,

(

,

l

)

q

g

(

V

V

eff

max

,

Sd

,

Sd

Teraz oblicza się z prawej strony belki (nie jest potrzebna reakcja Vc, chyba że

do sprawdzenia poprawności obliczeń).

•

Siła poprzeczna w przekroju 10,

kN.

11,7

10

=

=

min

,

Sd

G

V

•

Siła poprzeczna w przekroju 9,

kN.

1

34

7

1

2

13

11,7

9

,

,

,

l

g

G

V

wsp

min

min

,

Sd

=

⋅

+

=

⋅

+

=

Wyznaczenie w miarodajnych przekrojach wartości sił wewnętrznych

ISIE – semestr IV

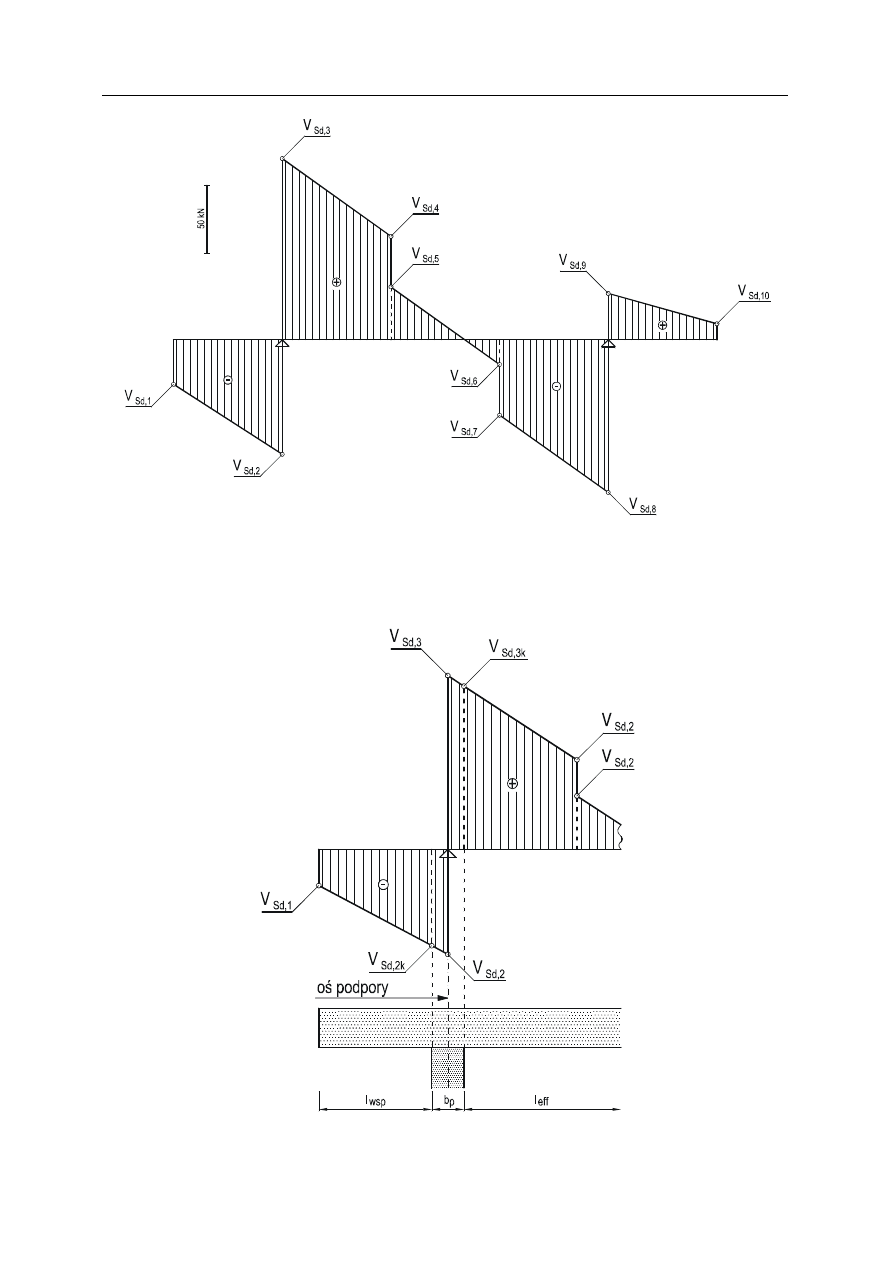
9

Rys. 6. Wykres sił poprzecznych.

2.2.1. Siły poprzeczne na krawędzi podpory

Rys. 7. Siły poprzeczne na krawędzi podpory.

Wyznaczenie w miarodajnych przekrojach wartości sił wewnętrznych

ISIE – semestr IV

10

•

Siła poprzeczna na krawędzi podpory od strony przęsła,

131

2

25

0

5

10

6

17

135

2

3

3

=

⋅

+

−

=

+

−

=

,

)

,

,

(

b

)

q

g

(

V

V

p

max

,

Sd

k

,

Sd

kN.

•

Siła poprzeczna na krawędzi podpory od strony wspornika,

5

81

2

25

0

5

10

6

17

85

2

2

2

,

,

)

,

,

(

b

)

q

g

(

V

V

p

max

,

Sd

k

,

Sd

−

=

⋅

+

+

−

=

+

+

=

kN.