
© Politechnika Lubelska
Dariusz Chocyk

© Politechnika Lubelska
Dariusz Chocyk
Każde ciało o temperaturze wyższej od temperatury bezwzględnej
wysyła i pochłania promieniowanie elektromagnetyczne (EM).
Dwie wielkości opisują emisję i absorpcję promieniowania EM
przez ciało o temperaturze T:
Zdolność emisyjna
(moc wysyłana przez jednostkę powierzchni
ciała w przedziale długości fal
[λ,λ+δλ]):
λ
λ
d
)
,
( T
e
Zdolność absorpcyjna
(jest to stosunek mocy pochłoniętej do mocy
padającej
):
(
)
(
)
pad
abs
dtdS
d
dE
dtdS
d
dE
T
a
λ
λ
λ
/
/
)
,
(
=

© Politechnika Lubelska
Dariusz Chocyk
Dla wszystkich ciał zachodzi:
λ
λ
λ
λ
λ
d
T
a
d
T
e
T
f
)
,
(
)
,
(
)
,
(
=
Gdzie f
(λ
,T) jest pewną uniwersalna funkcją długości
fali i temperatury.
Całkowita moc wypromieniowana przez jednostkę powierzchni
obliczamy przez całkowanie po wszystkich długościach fali
zdolność emisyjną.
∫
∞
=
0
)
,
(
)
(
λ
λ
d
T
e
T
P
© Politechnika Lubelska
Dariusz Chocyk
Prawo Stefana-boltzmana
4
0
)
,
(
)
(
T
d
T
e
T
P
⋅
=
=
∫
∞
σ
λ
λ
Prawo przesunięć Wiena
T
c
=
max
λ
( )
λ
λ
λ
λ
d
T
e
c
d
T
f
)
,
(
4
/
)
,
(
=
ν
ν
ν
λ
λ
λ
λ
λ
d
c
cT
F
d
T
F
d
T
f
3
4
5
)
(
)
(
)
,
(
=
⋅
=
© Politechnika Lubelska
Dariusz Chocyk
Ciało doskonale czarne (CDC)
CDC jest to takie ciało, dla którego zdolność absorpcyjna nie
zależy od długości fali i jest równa 100%. Modelem CDC może być
wnęka z małym otworem.
)
,
(
)
,
(
T
f
T
e
λ
λ
=
1
)
,
(
=
T
a
λ
© Politechnika Lubelska
Dariusz Chocyk
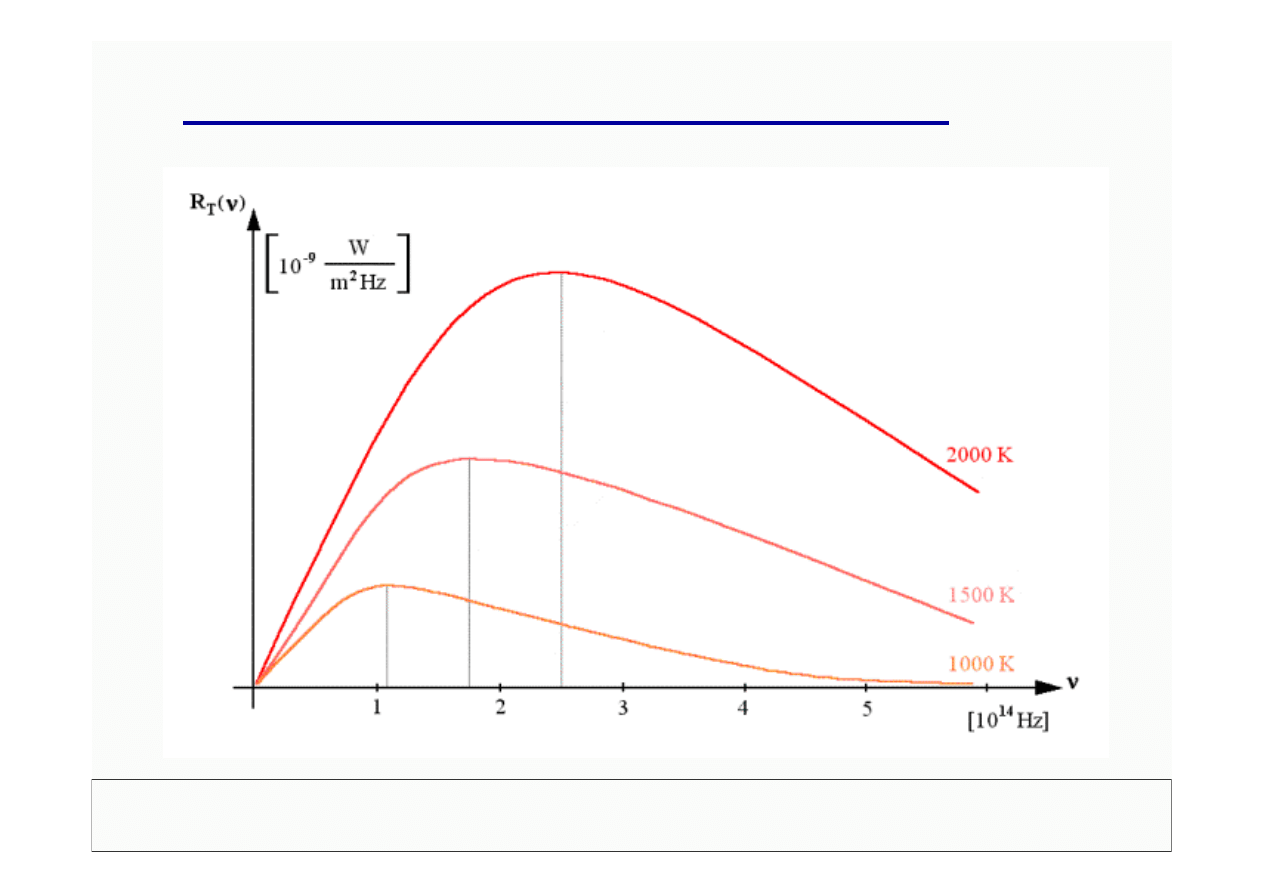
Doswiadczalne widmo promieniowania CDC:
© Politechnika Lubelska
Dariusz Chocyk
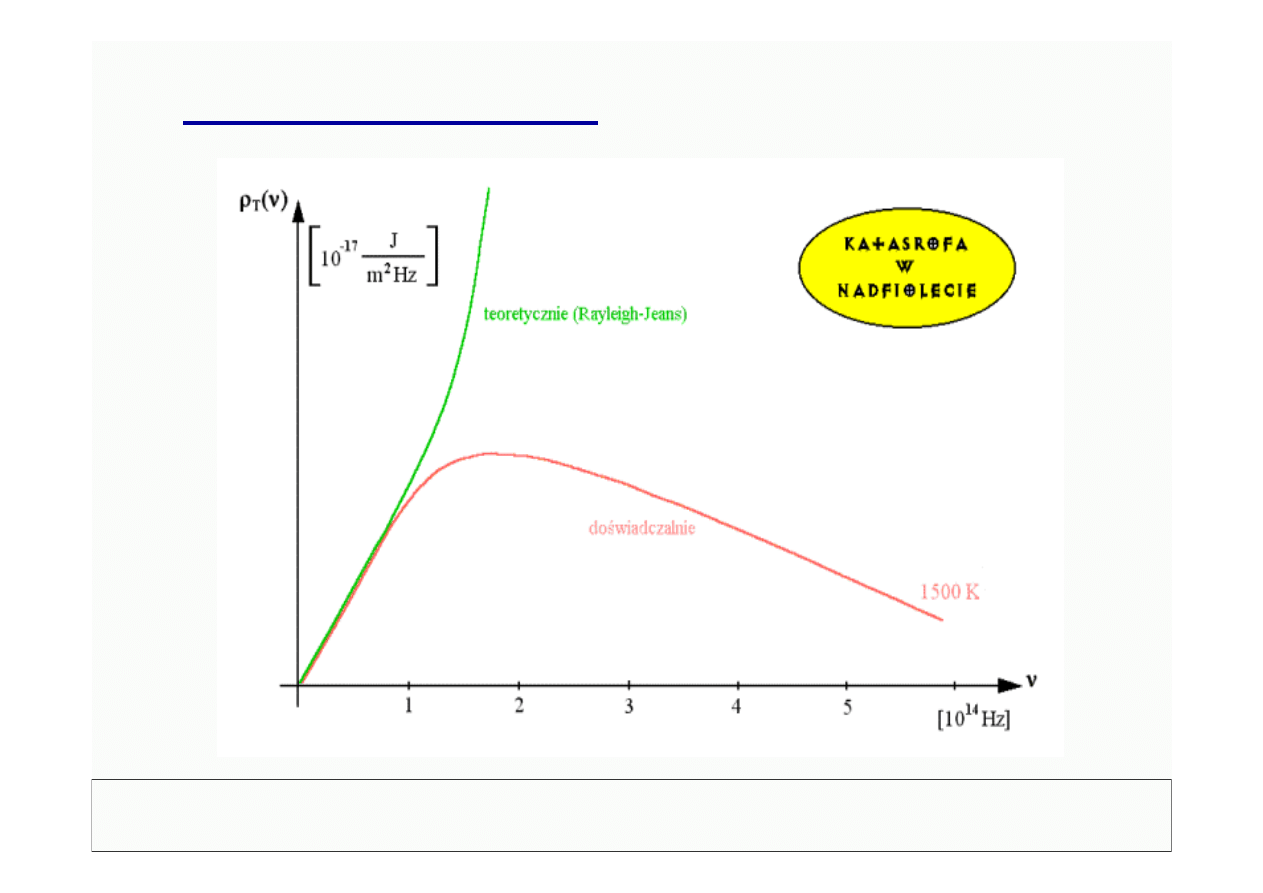
Wzór Rayleigha-Jeansa:

© Politechnika Lubelska
Dariusz Chocyk
V
E
dN
d
T
f
⋅
=
λ
λ
)
,
(
ν
ν
π
ν
ν
ν
ν
π
kTd
c
V
d
T
f
d
c
V
dN
kT
E
2
3
2
3
8
)
,
(
8
=
=
=
© Politechnika Lubelska
Dariusz Chocyk
Wzór Plancka
λ
λ
λ
λ
λ
d
e
c
d
T
f
T
c
1
1
)
,
(
2
5
1
−
=
Empiryczny:
ν
ν
π
ν
ν
ν
ν
π
d
e
e
c
V
d
T
f
d
c
V
dN
e
e
E
kT
e
kT
e
1
8
)
,
(
8
1
0
0
0
2
3
2
3
0
−
=
=
−
=

© Politechnika Lubelska
Dariusz Chocyk
Energia drgań jest zawsze całkowitą
wielokrotnością pewnej ilości energii
proporcjonalnej do częstości
ν
h
e
=
0
Teoretyczny:
λ
λ
π
λ
λ
λ
d
e
hc
d
T
f
kT
hc
1
1
8
)
,
(
5
−
=
ν
ν
π
ν
ν
ν
d
e
c
h
d
T
f
kT
h
1
1
8
)
,
(
3
3
−
=
© Politechnika Lubelska
Dariusz Chocyk
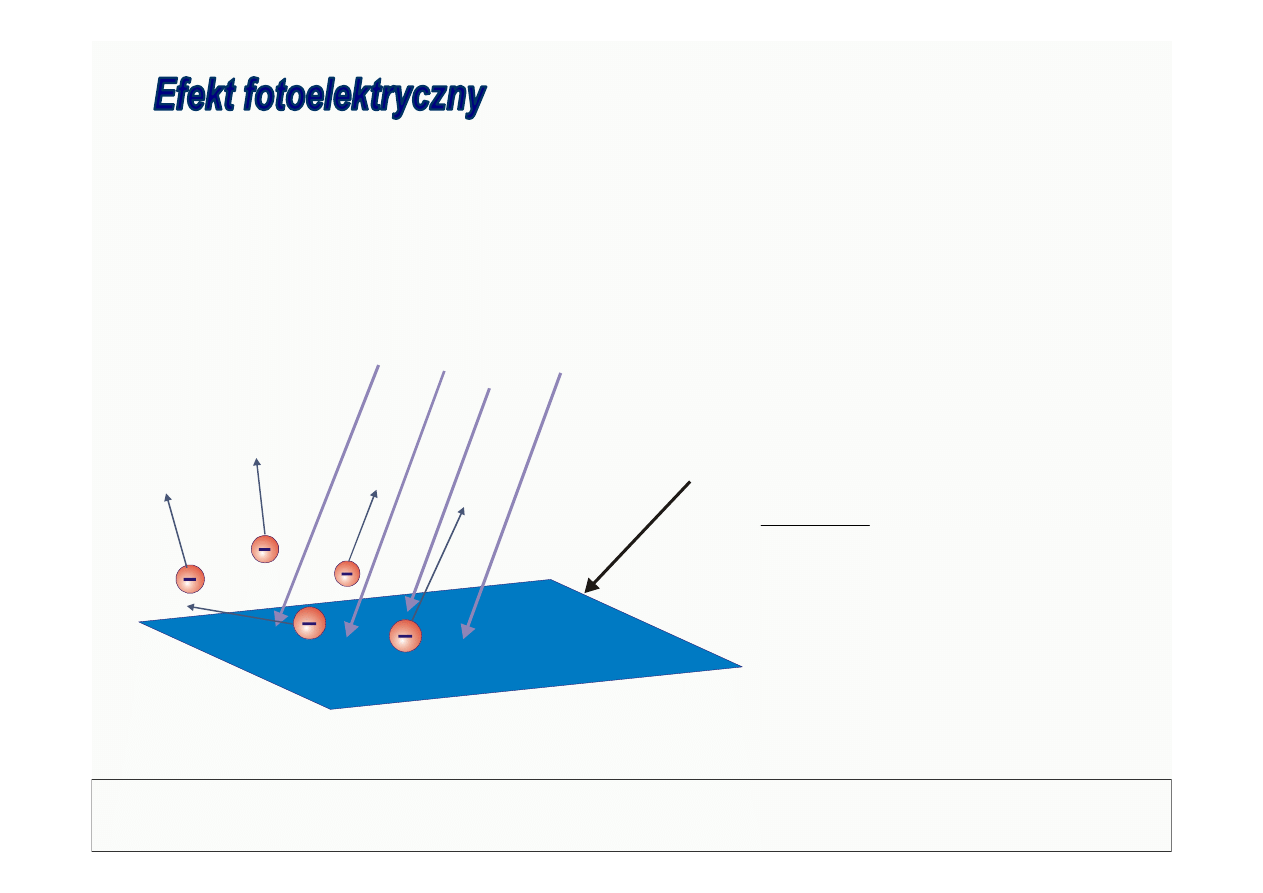
Efekt fotoelektryczny to emisja elektronów z metalu
bombardowanego promieniowaniem
elektromagnetycznym (UV).
Einstein (1905):
Metal
Promieniowanie UV
Elektrony
W
h
mv
−
=
ν
2
2
© Politechnika Lubelska
Dariusz Chocyk
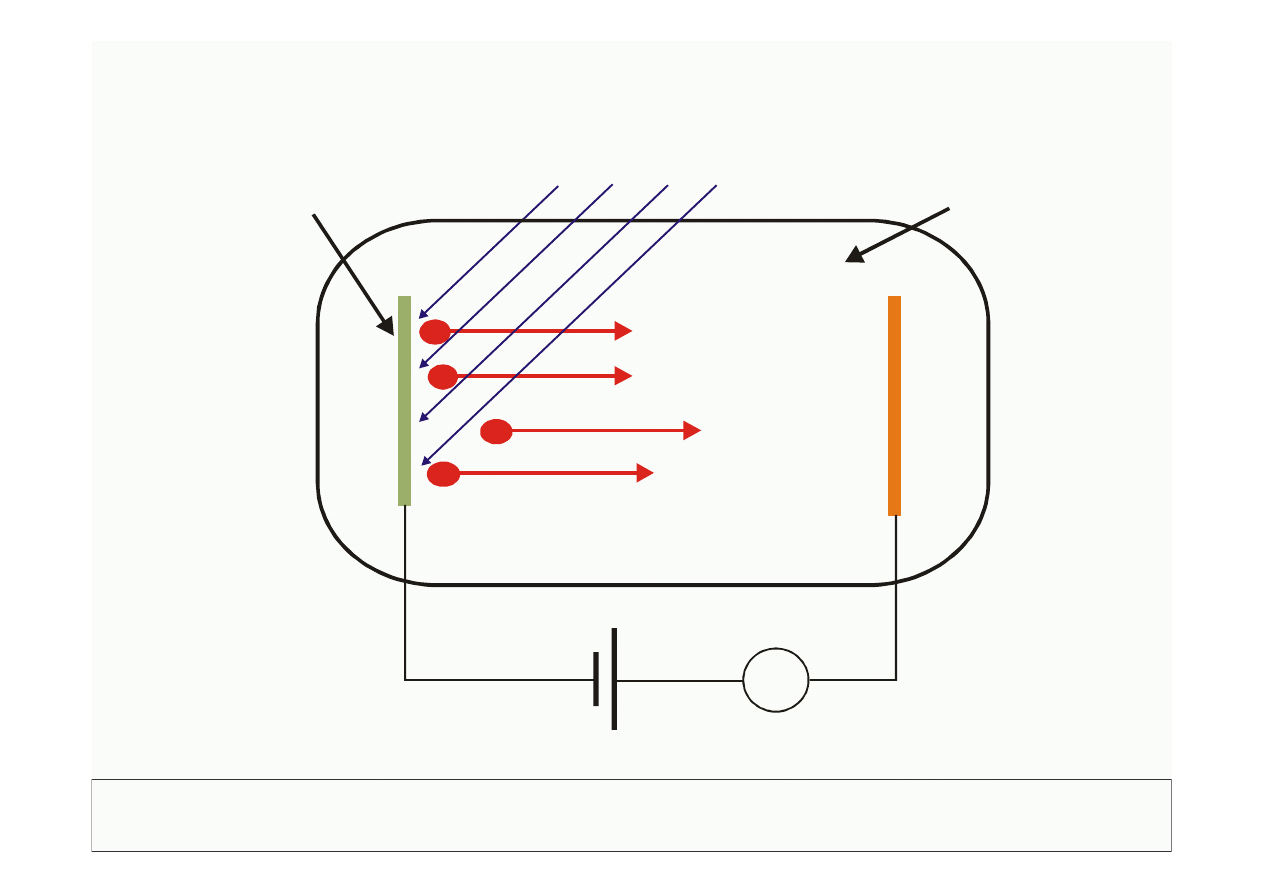
Promieniowanie UV
A
+
-
Elektrony
Katoda metalowa
Próżnia
© Politechnika Lubelska
Dariusz Chocyk
1) cząstki uwalniane z metalu pod wpływem promieniowania niosą
ładunek ujemny
UV
+
+
+
+
UV
W 1900 Lenard zmierzył stosunek ładunku do masy
(e/m) tych cząstek i zidentyfikował jajo elektrony
© Politechnika Lubelska
Dariusz Chocyk
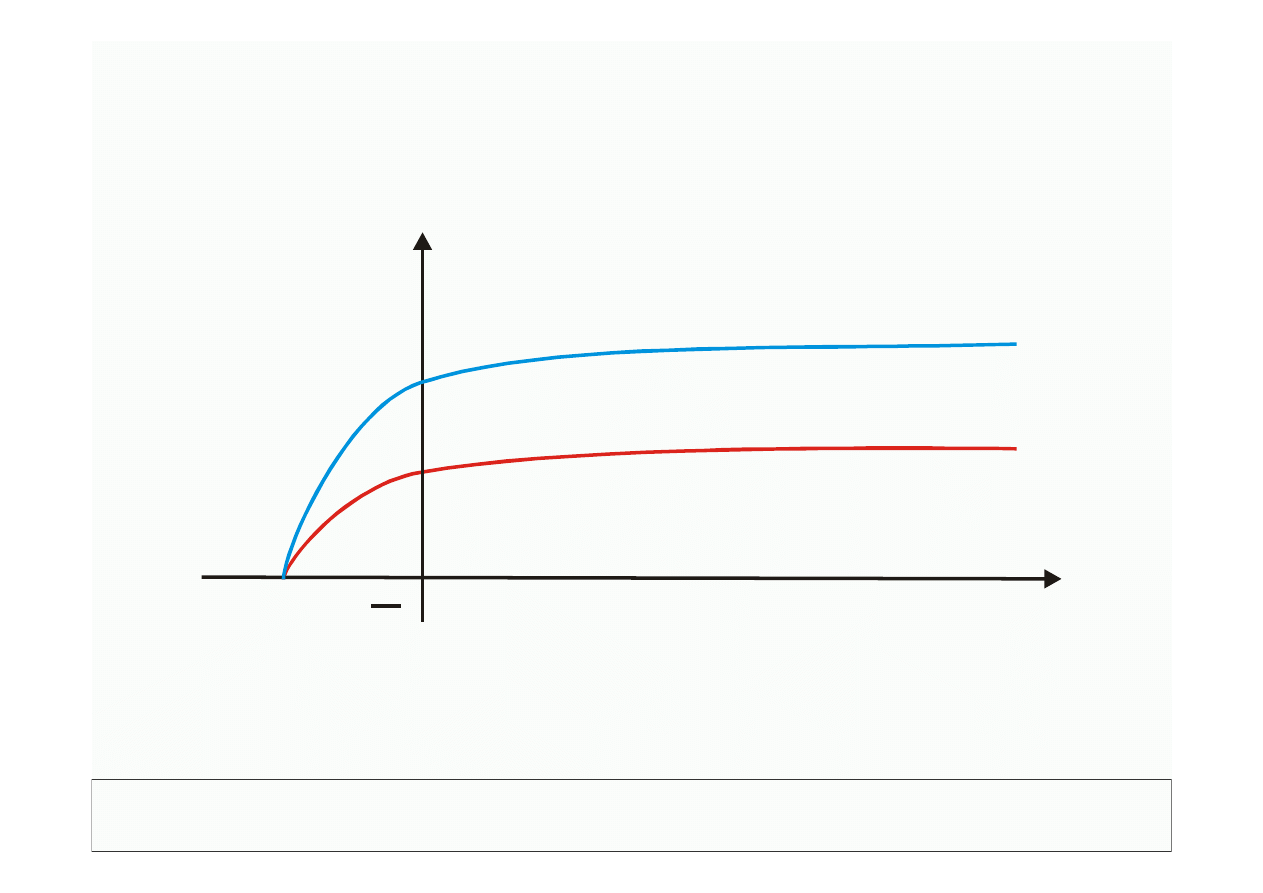
2) prąd w obwodzie wzrasta ze wzrostem natężenia fali
elektromagnetycznej
I [A]
U [V]
I
1
U
h
I
2
+
Charakterystyka prądowo-napięciowa - zależność od natężenia światła
© Politechnika Lubelska
Dariusz Chocyk
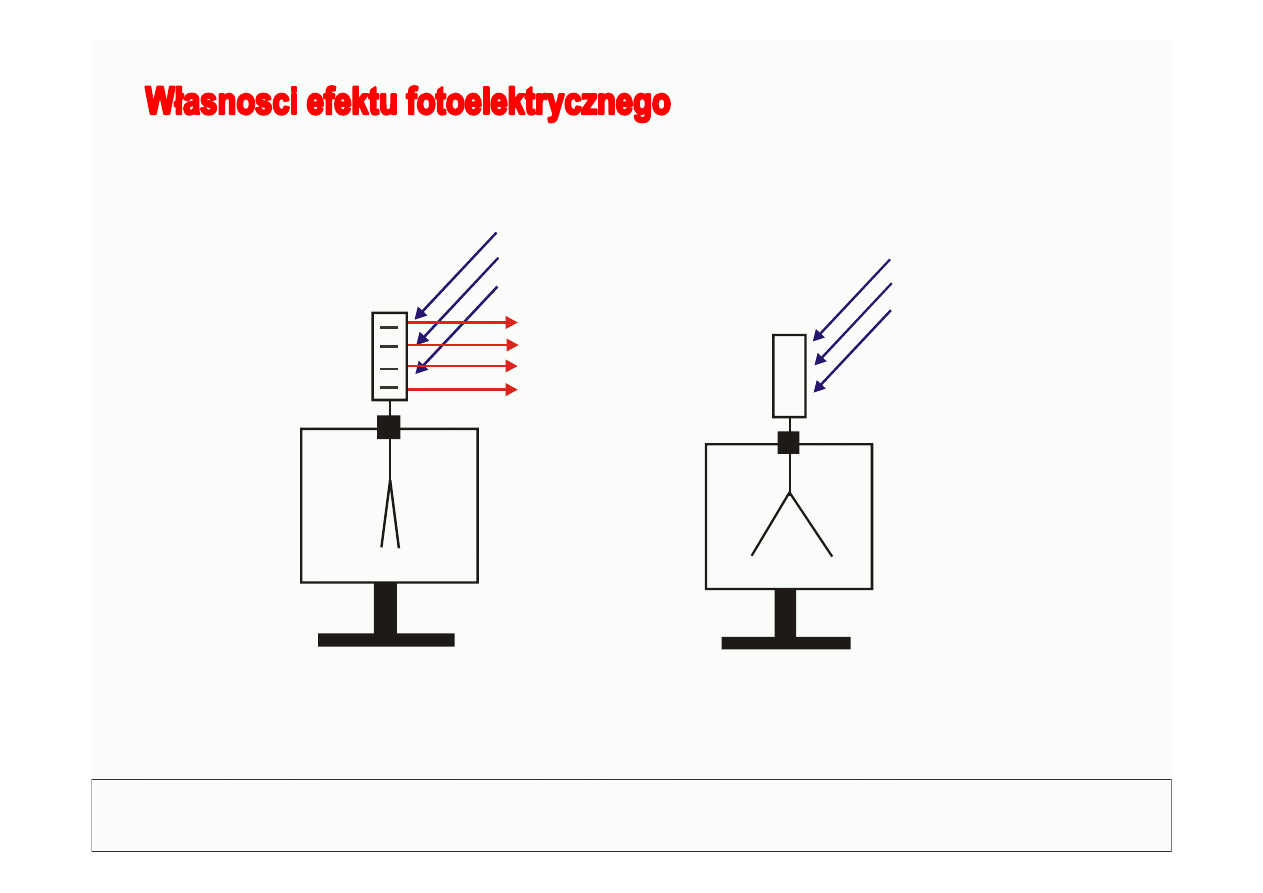
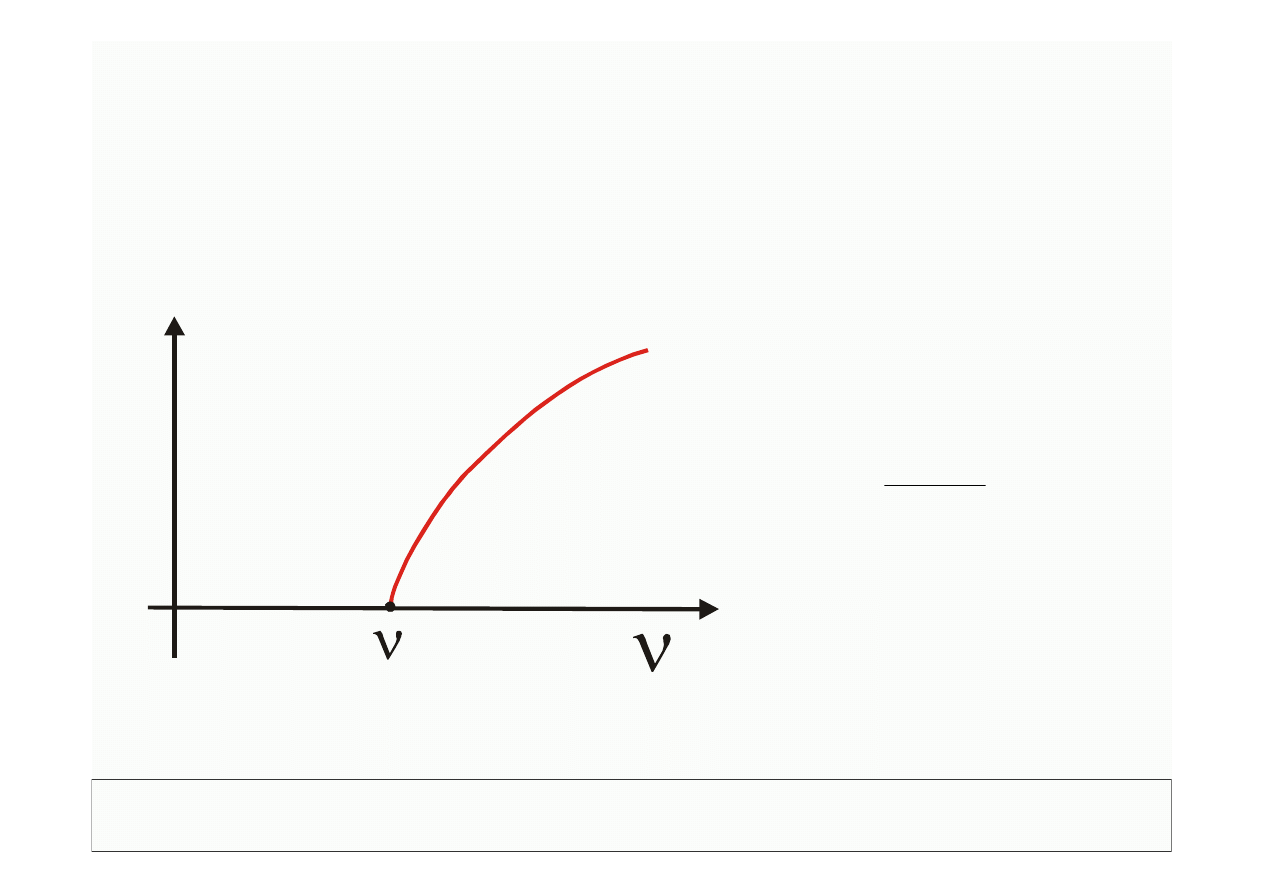
3) maksymalna energia elektronów wzrasta ze wzrostem częstości
promieniowania padającego, dla każdego materiału katody istnieje
częstość graniczna poniżej której efekt fotoelektryczny
nie zachodzi
I [A]
g
[1/s]
0
2
2
=
=
mv
h
W
ν
© Politechnika Lubelska
Dariusz Chocyk
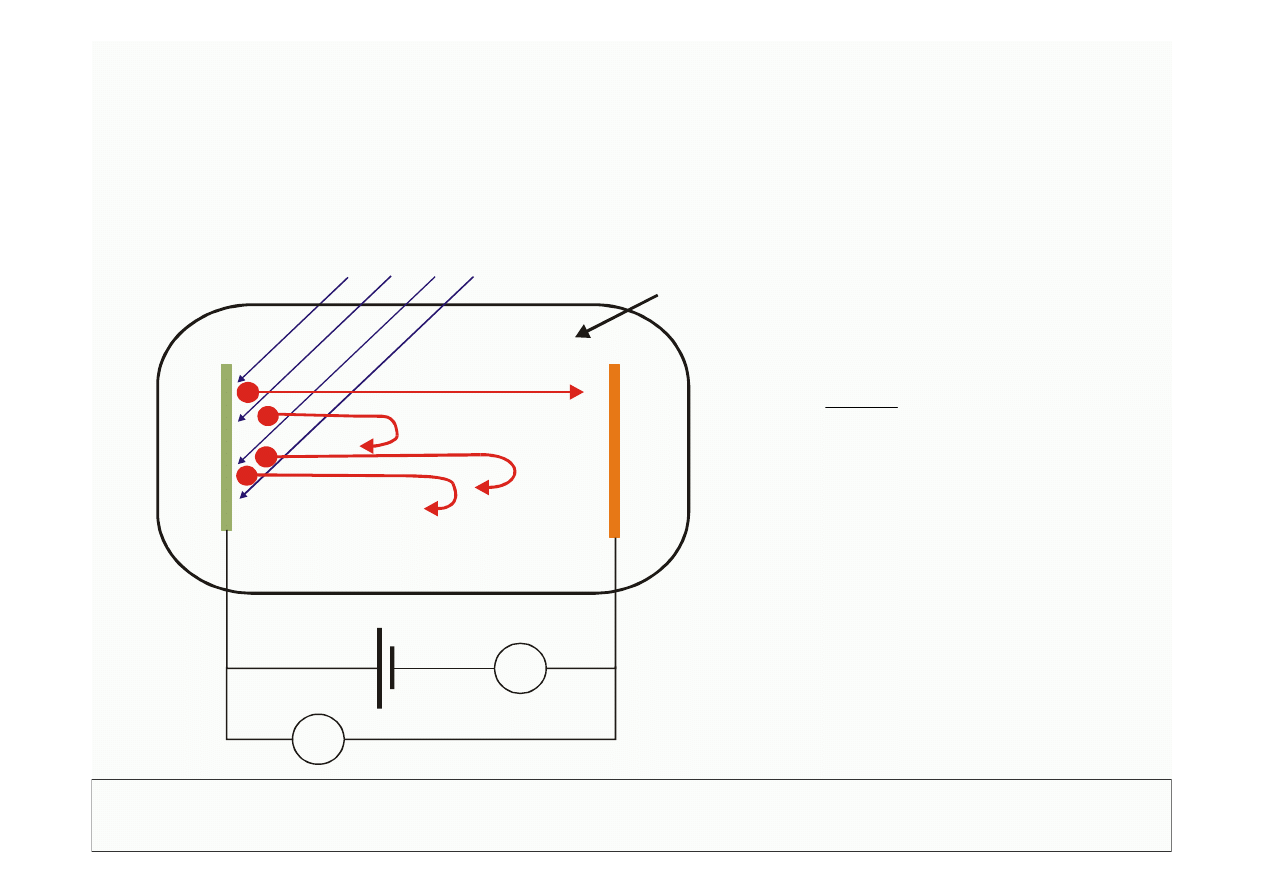
4) energia cząstek emitowanych z katody nie zależy od natężenia
fali padającej, efekt fotoelektryczny jest natychmiastowy
Pomiar maksymalnej prędkości elektronów wyemitowanych
Promieniowanie UV
A
+ -
Elektrony
Próżnia
V
0
max
2
2
eU
mv
=
© Politechnika Lubelska
Dariusz Chocyk
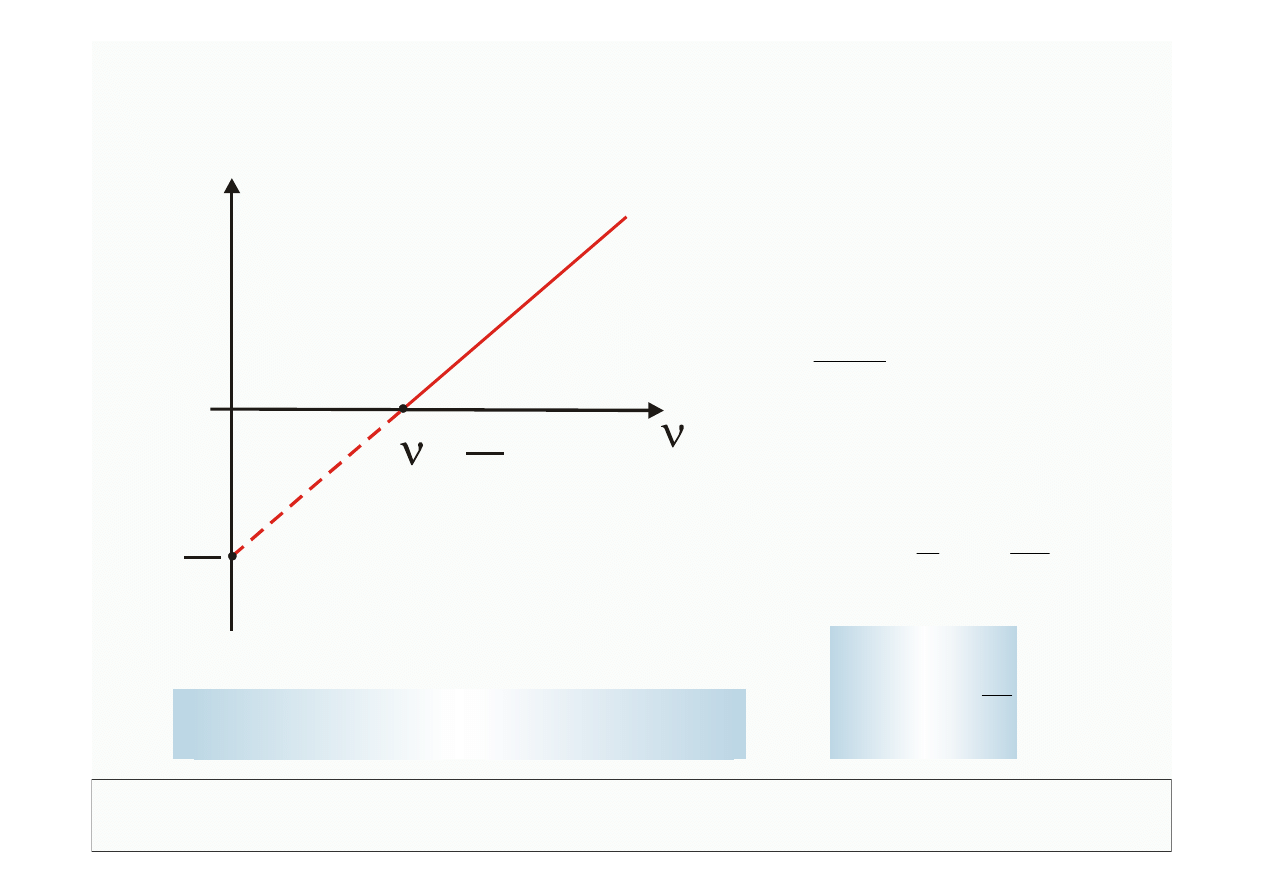
Zależność napięcia hamującego U
h
od częstości padającego
promieniowania elektromagnetycznego.
U
h
W
e
W
h
0
=
Z kąta nachylenia
możemy wyznaczyć
stałą Plancka h:
W
h
mv
−
=
ν
2
2
W
h
e
U
h
−
=
ν
e
W
e
h
U
h
−
=
ν
e
h
=
α
tg
[
]
s
J
h
⋅
⋅
=
−34
10
626755
.
6
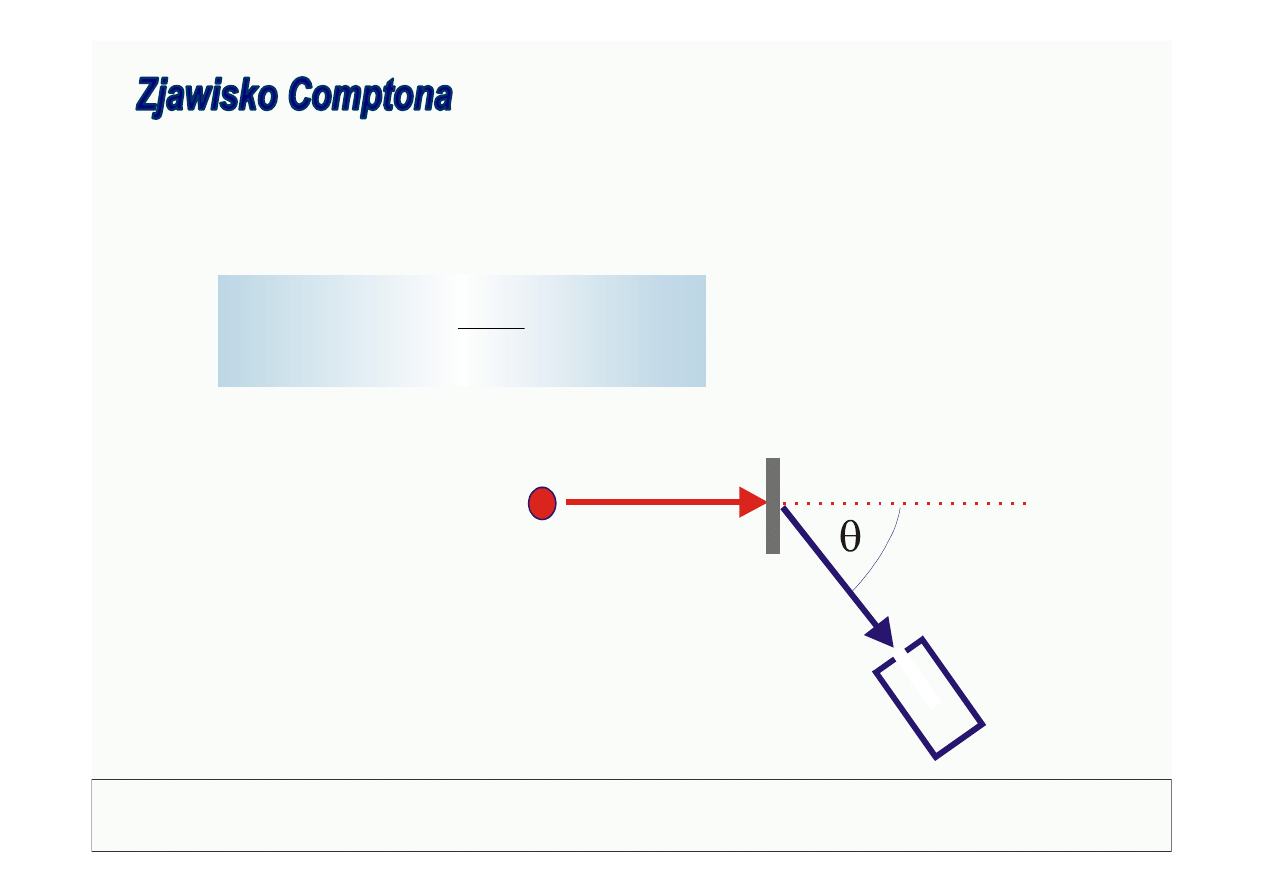
© Politechnika Lubelska
Dariusz Chocyk
Zjawisko Comptona jest to nieelastyczne (ze zmianą energii - długości
fali) rozpraszanie fotonów promieniowania elektromagnetycznego
(promieniowanie X) na niemal swobodnych elektronach atomowych.
)
cos
1
(
'
0
θ
λ
λ
λ
−
=
−
=
∆
c
m
h
źródło
grafit
λ
2
λ
1
detektor
Układ do obserwacji
zjawiska Comptona:
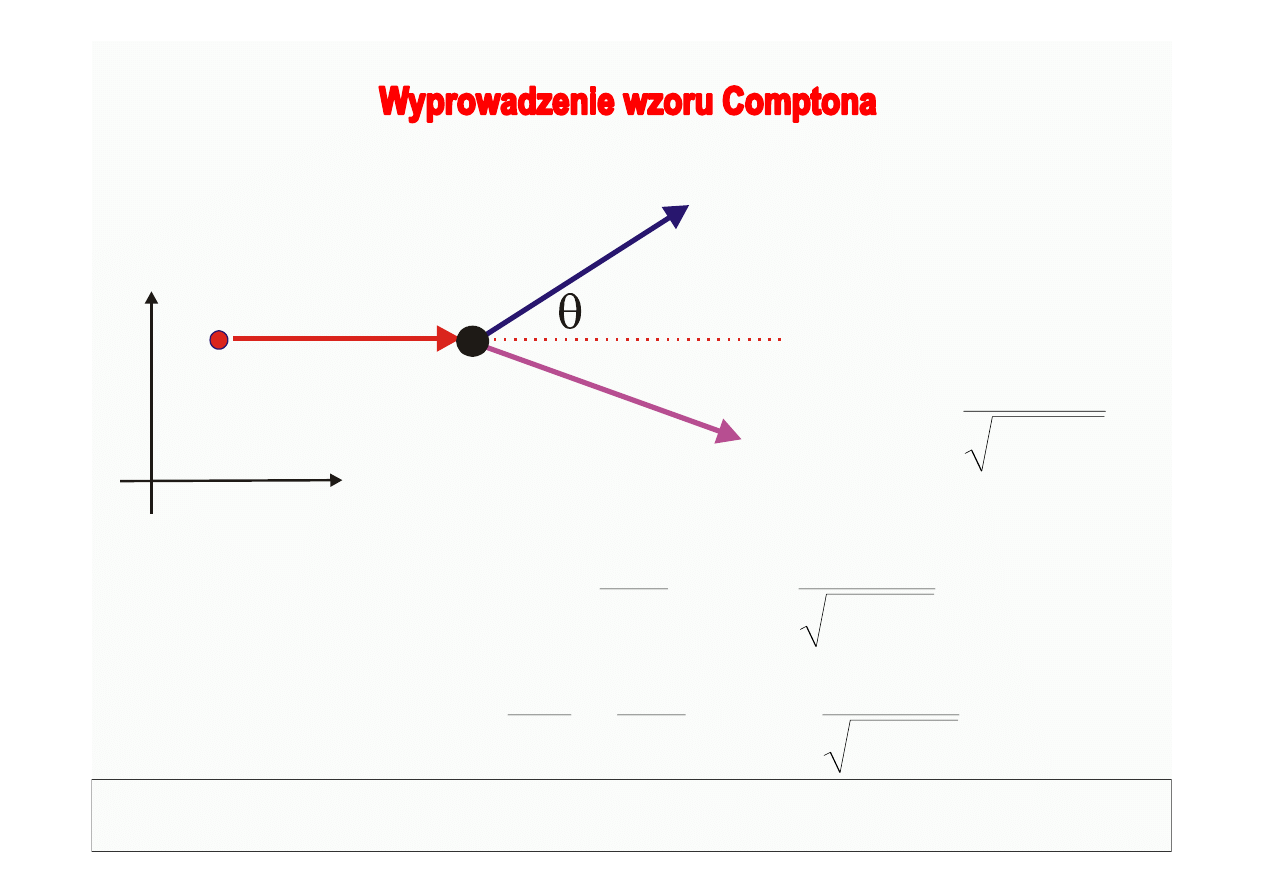
© Politechnika Lubelska
Dariusz Chocyk
λ
2
λ
1
E
1
E
e
E
2
p
1
p
2
p
e
m c
o 2
ϕ
e
-
y
x
Zasada zachowania
energii:
2
2
0
2
2
0
1
1
β
ν
ν
−
+
=
+
c
m
h
c
m
h
ϕ
β
θ
ν
sin
1
sin
0
2
0
2
−
+
=
v
m
c
h
ϕ
β
θ
ν
ν
cos
1
cos
2
0
2
1
−
+
=
v
m
c
h
c
h
Zasada
zachowania
pędu:
© Politechnika Lubelska
Dariusz Chocyk
(
)
2
2
2
0
2
2
0
1
−
=
+
∆
β
ν
c
m
c
m
h
(
)
4
2
0
2
4
2
0
2
0
2
1
2
c
m
c
m
c
m
h
h
−
−
=
∆
+
∆
β
ν
ν
ϕ
β
θ
ν
2
2
2
2
0
2
2
2
sin
1
sin
−
=
v
m
c
h
ϕ
β
θ
ν
ν
2
2
2
2
0
2
2
1
cos
1
cos
−
=
−
v
m
c
h
h
(
) (
)
2
2
2
2
0
2
2
2
2
2
1
1
sin
cos
β
θ
ν
θ
ν
ν
−
=
+
−
c
v
m
h
h
h

© Politechnika Lubelska
Dariusz Chocyk
(
)
(
)
( )
( )
[
]
2
1
2
1
2
2
2
1
2
1
2
2
2
2
1
2
2
1
2
2
2
2
0
2
cos
2
2
cos
2
1
ν
ν
θ
ν
ν
ν
ν
ν
ν
ν
θ
ν
ν
ν
β
+
−
+
−
=
+
−
=
−
h
h
h
h
c
v
m
(
)
[
]
)
cos
1
(
2
1
2
1
2
2
1
2
2
2
2
2
0
θ
ν
ν
ν
ν
β
−
+
−
=
−
h
c
v
m
Wykorzystując wzór:
2
2
2
2
0
4
2
0
2
4
2
0
1
1
β
β
−
=
−
−
c
v
m
c
m
c
m
( )
4
2
0
2
2
c
m
pc
E
+
=
(
)
(
)
[
]
)
cos
1
(
2
2
2
1
2
2
1
2
2
0
2
θ
ν
ν
ν
ν
ν
ν
−
+
−
=
∆
+
∆
h
c
m
h
h
© Politechnika Lubelska
Dariusz Chocyk
)
cos
1
(
2
1
2
0
θ
ν
ν
ν
−
=
∆
h
c
m
)
cos
1
(
1
1
2
0
2
1
2
1
2
1
θ
ν
ν
ν
ν
ν
−
=
−
=
−
c
m
h
ν
)
cos
1
(
0
2
1
2
1
θ
λ
λ
ν
ν
−
=
−
=
−
c
m
h
c
c
Comptonowska długość fali:
)
cos
1
(
0
θ
λ
−
=
∆
c
m
h
c
m
h
c
0
=
λ

© Politechnika Lubelska
Dariusz Chocyk
Zmiana długości fali w zjawisku Comptona zależy jedynie od kąta
rozproszenia, nie zależy natomiast od energii początkowej fotonu.
Maksymalna zmiana długości fali wynosi 2
λ
c
.
Comptonowska długość fali jest zbyt mała (0.0024 nm) aby
zaobserwować to zjawisko dla fal świetlnych.

© Politechnika Lubelska
Dariusz Chocyk
1) Odkrycie kwantów energii fal EM
w widmie promieniowania termicznego
(Ciało Doskonale Czarne)
2) Absorpcja kwantów EM w zjawisku
fotoelektrycznym
3) Nieelastyczne rozpraszanie kwantów
promieniowania rentgenowskiego
na elektronach (zjawisko Comptona)
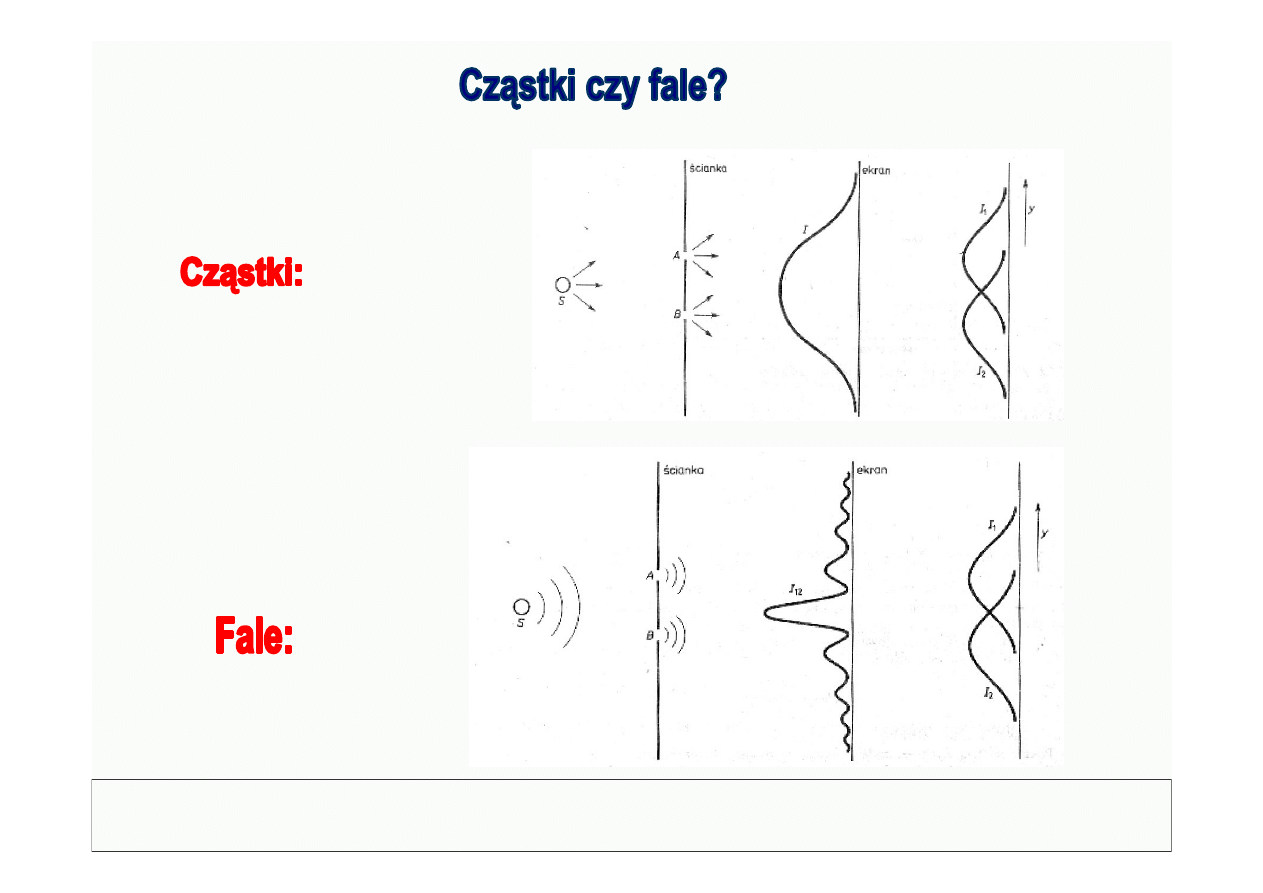
1) Zjawiska interferencji i dyfrakcji
światła, fal radiowych, promienio-
wania rentgenowskiego
2) Emisja i absorpcja promieniowania
EM opisana przez teorię elektronową
Lorenta.
© Politechnika Lubelska
Dariusz Chocyk
© Politechnika Lubelska
Dariusz Chocyk
c
=
λν
πν
ω
2
=
λ
π
2
=
k
λ
ν
h
c
h
c
E
p
=
=
=
π
2
h
=
h
π
2
h
n
rp
=
λ
π
n
p
h
n
r
=
=
2
ω
h
=
E
k
p h
=
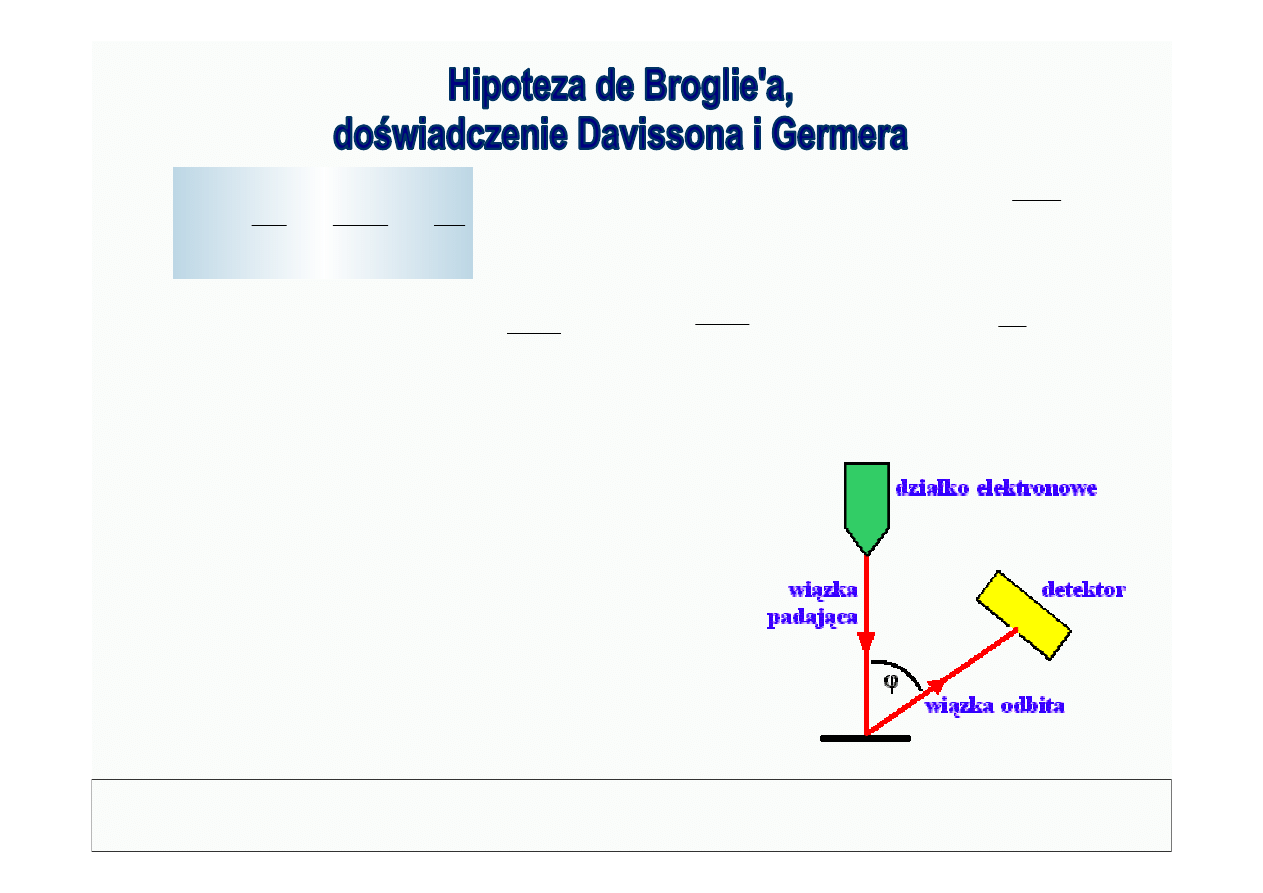
Jeśli elektrony rozchodzą się jak fale
to powinny ulegać interferencji.
W dośw. D-G wiązka elektronów o określonych
pędach (dł fali) padały na powierzchnię niklu
o stałej sieci a=3.52*10
-10
m.
Jako wynik zaobserwowano obraz interferencyjny.
© Politechnika Lubelska
Dariusz Chocyk
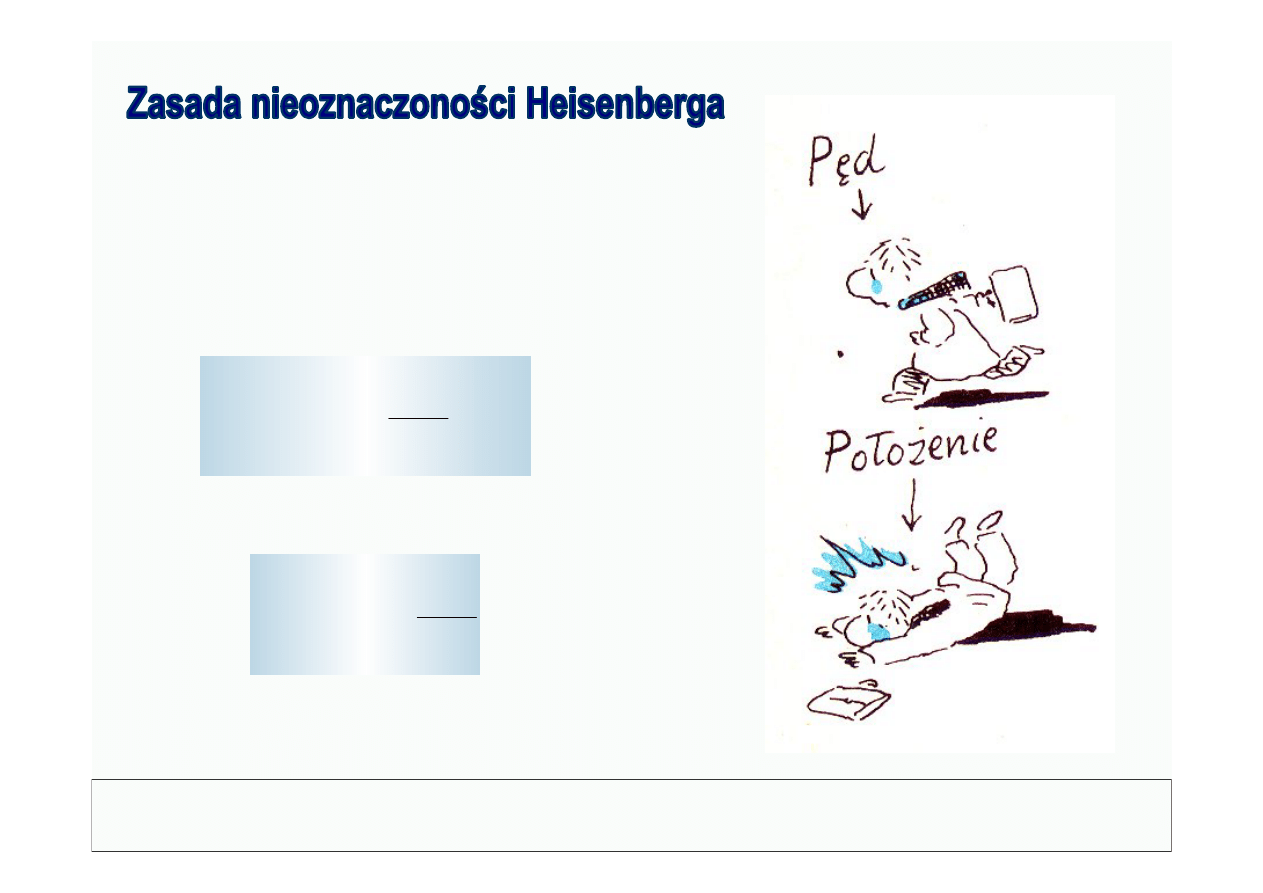
Jeśli dokładnie znamy pęd cząstki, to tym
samym nic nie możemy powiedzieć o jej
położeniu.
h
=
≥
∆
∆
π
2
h
p
x
x
π
2
h
t
E
≥
∆
∆

© Politechnika Lubelska
Dariusz Chocyk
Dowolnej, dobrze określonej obserwabli (położenie, pęd, energia,
masa, moment pędu itp.)odpowiada operator  taki, że w wyniku
pomiaru otrzymamy wartości a, które są wartościami własnymi
operatora Â.
ϕ
ϕ
a
=
Aˆ
 - operator obserwabli
a - wartość własna operatora  odpowiadająca funkcji
ϕ
ϕ
- funkcja własna operatora Â

© Politechnika Lubelska
Dariusz Chocyk
∇
−
= h
i
pˆ
x
i
p
x
∂
∂
−
= h
ˆ
ϕ
ϕ
x
p
x
i
=
∂
∂
− h
ikx
x
ip
Ae
Ae
x
=
=
h
/
h
p
k
=
ϕ
)
(
λ
+
=
x
ik
ikx
e
e
λ
λ
λ
k
i
k
e
ik
sin
cos
1
+
=
=
0
sin
,
1
cos
=
=
λ
λ
k
k
π
λ
2
=
k
λ
p
k
=
k
p
Ae
ikx
k
h
=
=
,
ϕ
© Politechnika Lubelska
Dariusz Chocyk
)
(
2
)
(
2
ˆ
Hˆ
2
2
2
r
V
m
r
V
m
p
r
h
r
+
∇
−
=
+
=
ϕ
ϕ
E
x
m
=
∂
∂
−
2
2
2
2
h
2
2
2
ˆ
∇
−
=
m
H
h
m
k
E
k
p
Ae
ikx
k
2
2
2
h
h
=
=
=
ϕ
0
2
2
2
=
+
∂
∂
ϕ
ϕ
k
x
2
2
2
h
mE
k
=
m
k
E
2
2
2
h
=
ikx
Ae
=
ϕ
ϕ
ϕ
x
p
p
=
ˆ
( )
(
)
( ) ( )
ϕ
ϕ
ϕ
ϕ
ϕ
m
k
p
m
k
m
k
p
p
m
p
H
2
ˆ
2
2
ˆ
ˆ
2
ˆ
ˆ
2
h
h
h
=
=
=
=

© Politechnika Lubelska
Dariusz Chocyk
Pomiar obserwabli A dający w wyniku wartość a pozostawia układ
w stanie
ϕ
a
, gdzie
ϕ
a
jest funkcją własną operatora Â, odpowiadającą
wartości własnej a.
ϕ
ϕ
'
xˆ
x
=
Równanie na wartości własne operatora położenia:
)
'
(
'
)
'
(
xˆ
x
x
x
x
x
−
=
−
δ
δ
)
'
(
x
x
−
δ
-funkcja delta Diraca
∫
∞
∞
−
=
−
)
(
'
)
'
(
)
'
(
x
f
dx
x
x
x
f
δ
∫
∞
∞
−
=
−
1
'
)
'
(
dx
x
x
δ

© Politechnika Lubelska
Dariusz Chocyk
Stan układu w dowolnej chwili może reprezentować funkcja stanu
ψ,
ciągła i różniczkowalna, zwana funkcją falową. Zawarte są w niej
wszystkie informacje dotyczące stanu układu. W szczególności, jeśli
układ znajduje się w stanie
ψ(r,t), to średnia wartość dowolnej
obserwabli fizycznej A związanej z układem w chwili t dana jest wzorem:
dz
d
d
Aˆ
A
*
y
x
ψ
ψ
∫
=

© Politechnika Lubelska
Dariusz Chocyk
Funkcja stanu układu zależy od czasu zgodnie z równaniem,
zwanym równaniem równaniem Schrodingera zależnym od czasu:
)
,
(
ˆ
)
,
(
t
r
H
t
r
t
i
r
r
h
ψ
ψ
=
∂
∂
gdzie H jest operatorem energii.
)
(
)
(
)
,
(
t
T
r
t
r
ϕ
=
r
r
)
(
2
)
(
Hˆ
Hˆ
2
2
r
V
m
r
r
h
r
+
∇
−
=
=
E
r
H
r
t
t
T
t
T
i
=
=
∂
∂
)
(
ˆ
)
(
1
)
(
)
(
1
r
r
h
ϕ
ϕ
ψ
)
(
)
(
ˆ
r
E
r
H
r
r
ϕ
ϕ
=
0
)
(
)
(
=
+
∂
∂
t
T
iE
t
t
T
h

© Politechnika Lubelska
Dariusz Chocyk
−
=
t
iE
A
t
T
h
exp
)
(
)
(
)
(
ˆ
r
E
r
H
n
n
n
r
r
ϕ
ϕ
=
−
=
=
t
iE
r
A
t
T
r
t
r
n
n
n
h
r
r
r
exp
)
(
)
(
)
(
)
,
(
ϕ
ϕ
ψ
m
k
E
k
2
2
2
h
=
2
2
2
/
2
kl
v
m
p
p
m
p
k
k
v
=
=
=
=
=
h
h
ω
ω
ikx
k
Ae
=
ϕ
−
=
t
iE
ikx
A
t
r
k
k
h
r
exp
)
exp(
)
,
(
ψ
[
]
)
(
exp
)
,
(
t
kx
i
A
t
r
k
ω
−
=
r
ψ
ω
h
=
k
E
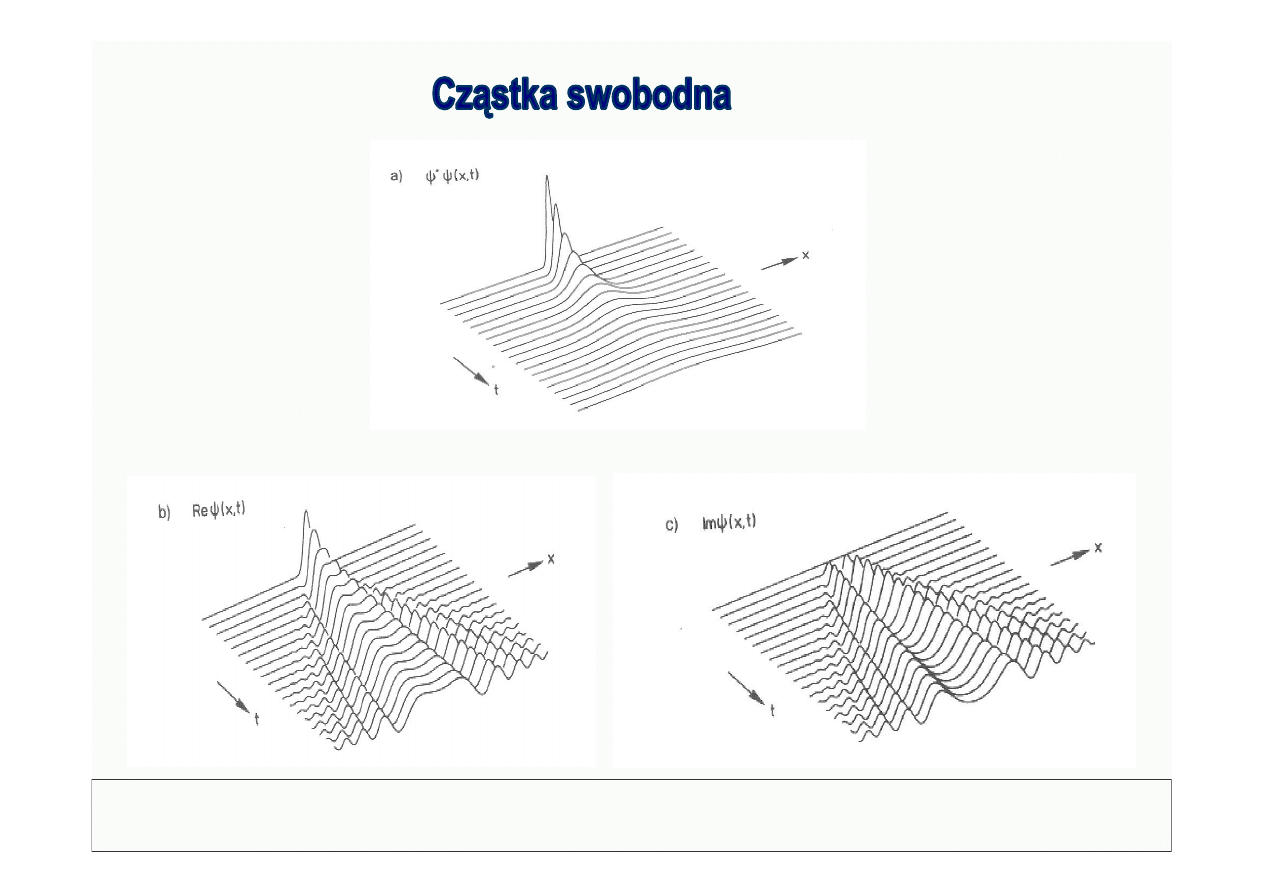
© Politechnika Lubelska
Dariusz Chocyk
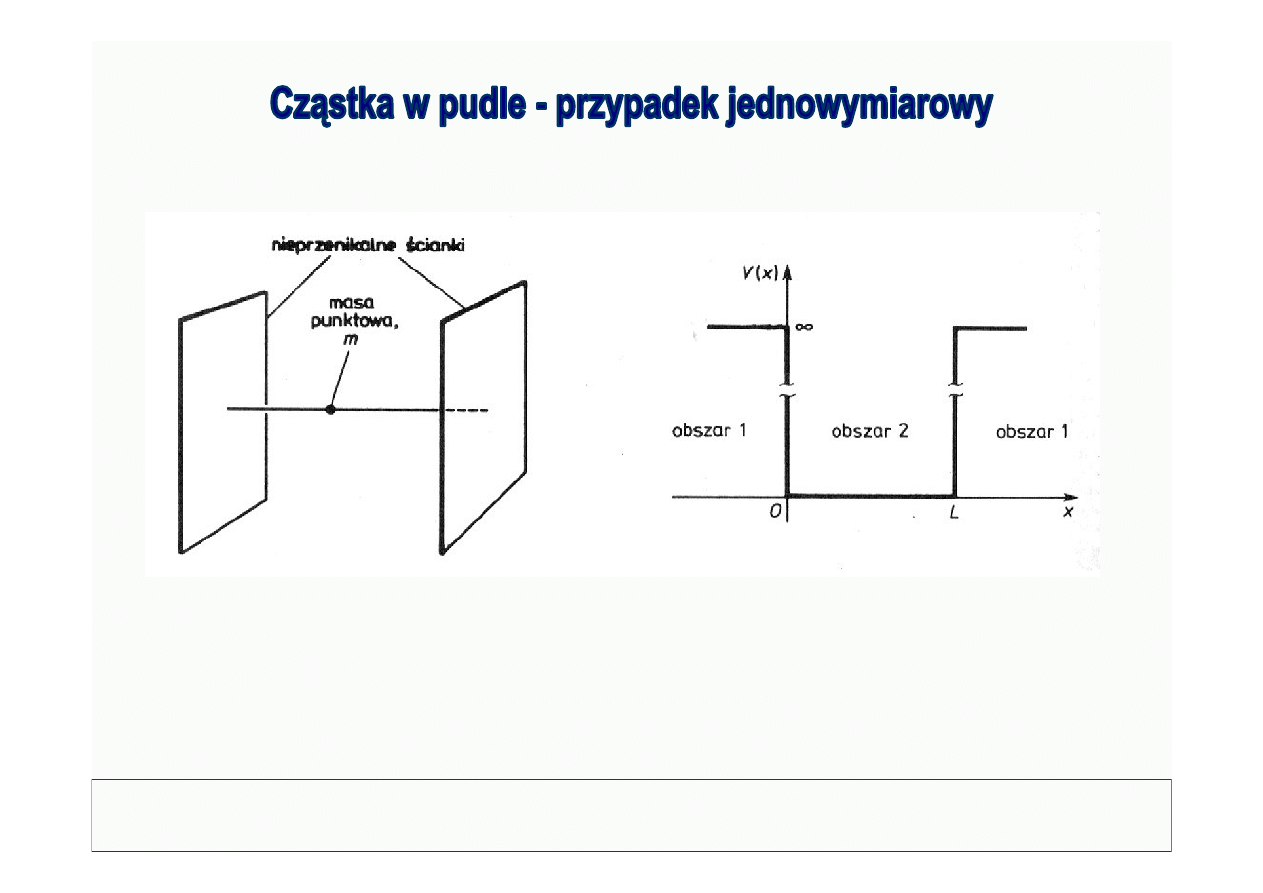
© Politechnika Lubelska
Dariusz Chocyk
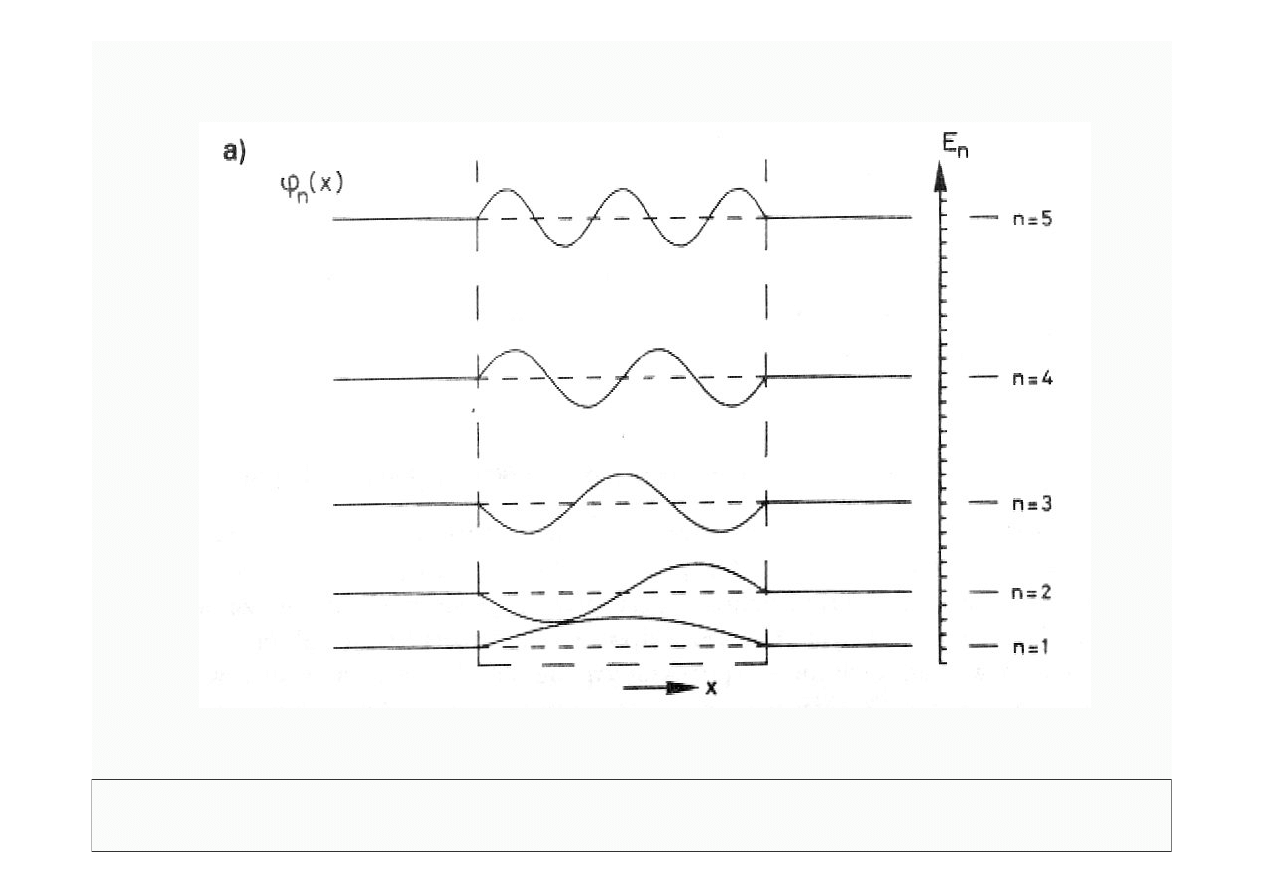
© Politechnika Lubelska
Dariusz Chocyk
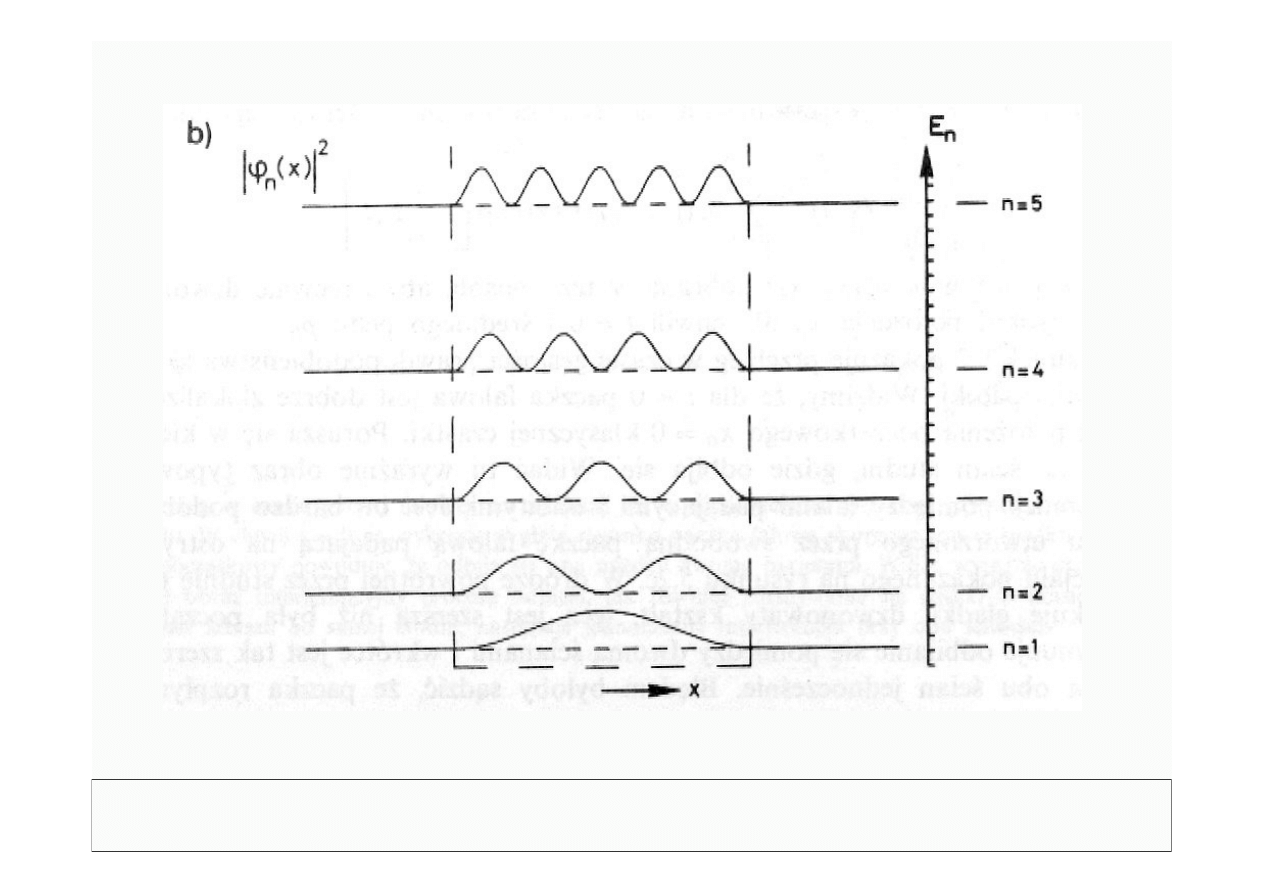
© Politechnika Lubelska
Dariusz Chocyk
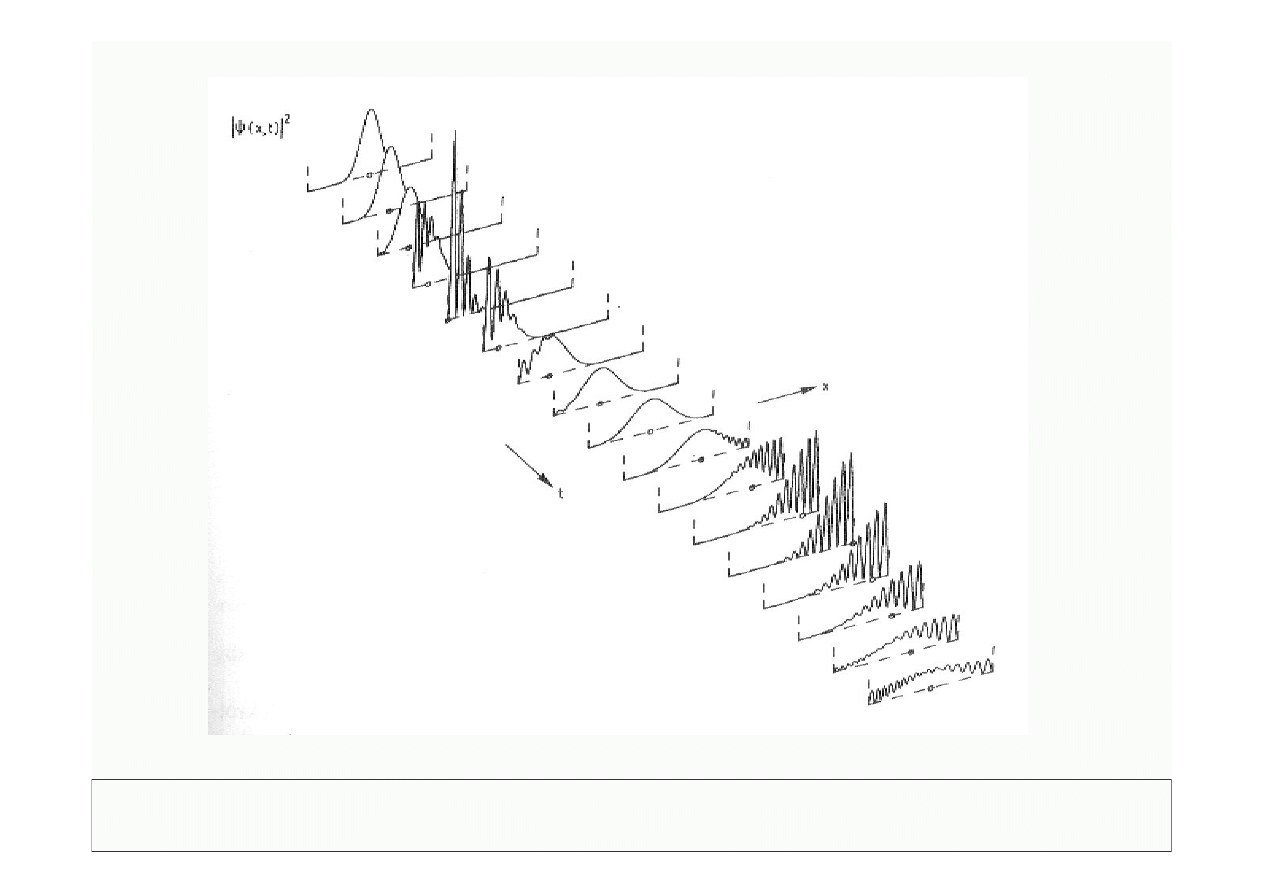
© Politechnika Lubelska
Dariusz Chocyk
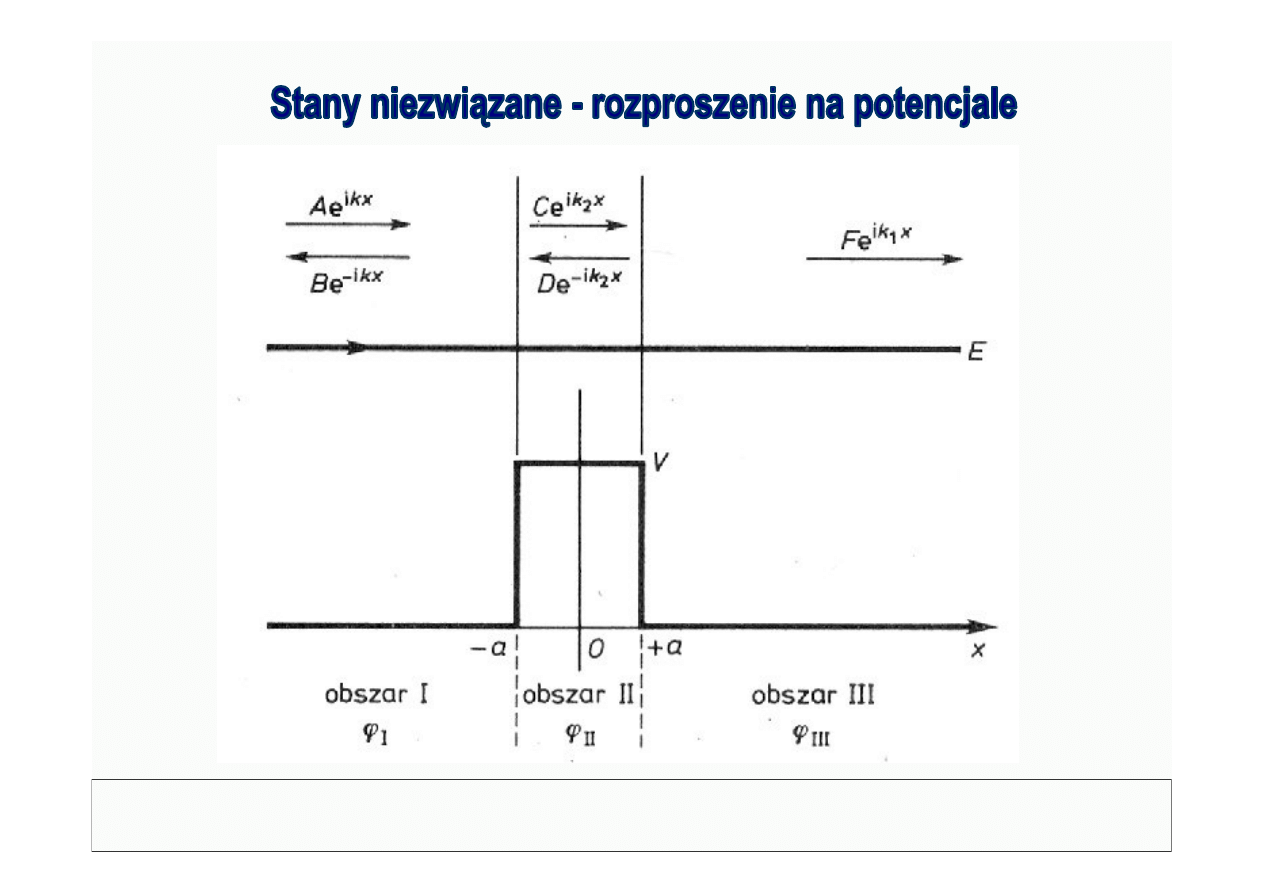
© Politechnika Lubelska
Dariusz Chocyk
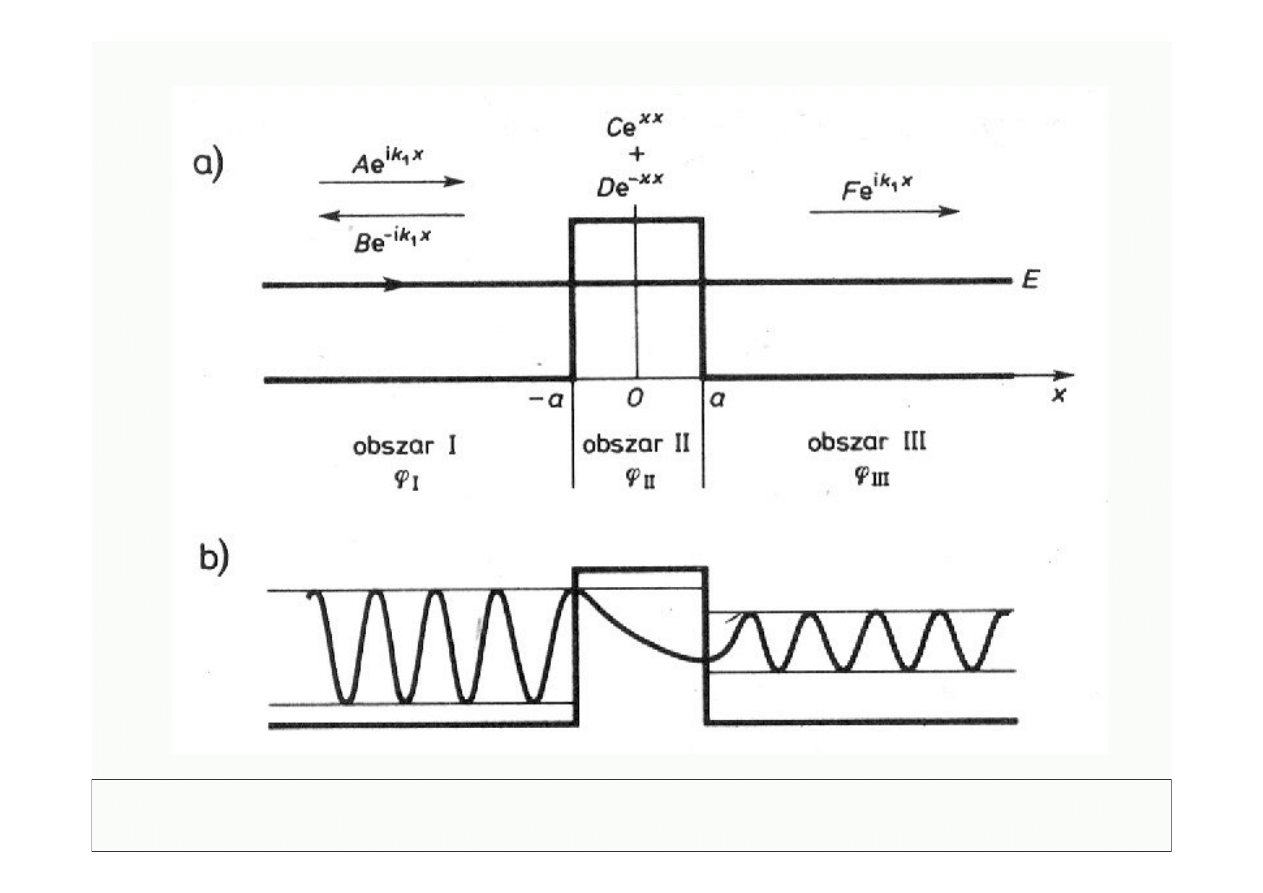
© Politechnika Lubelska
Dariusz Chocyk
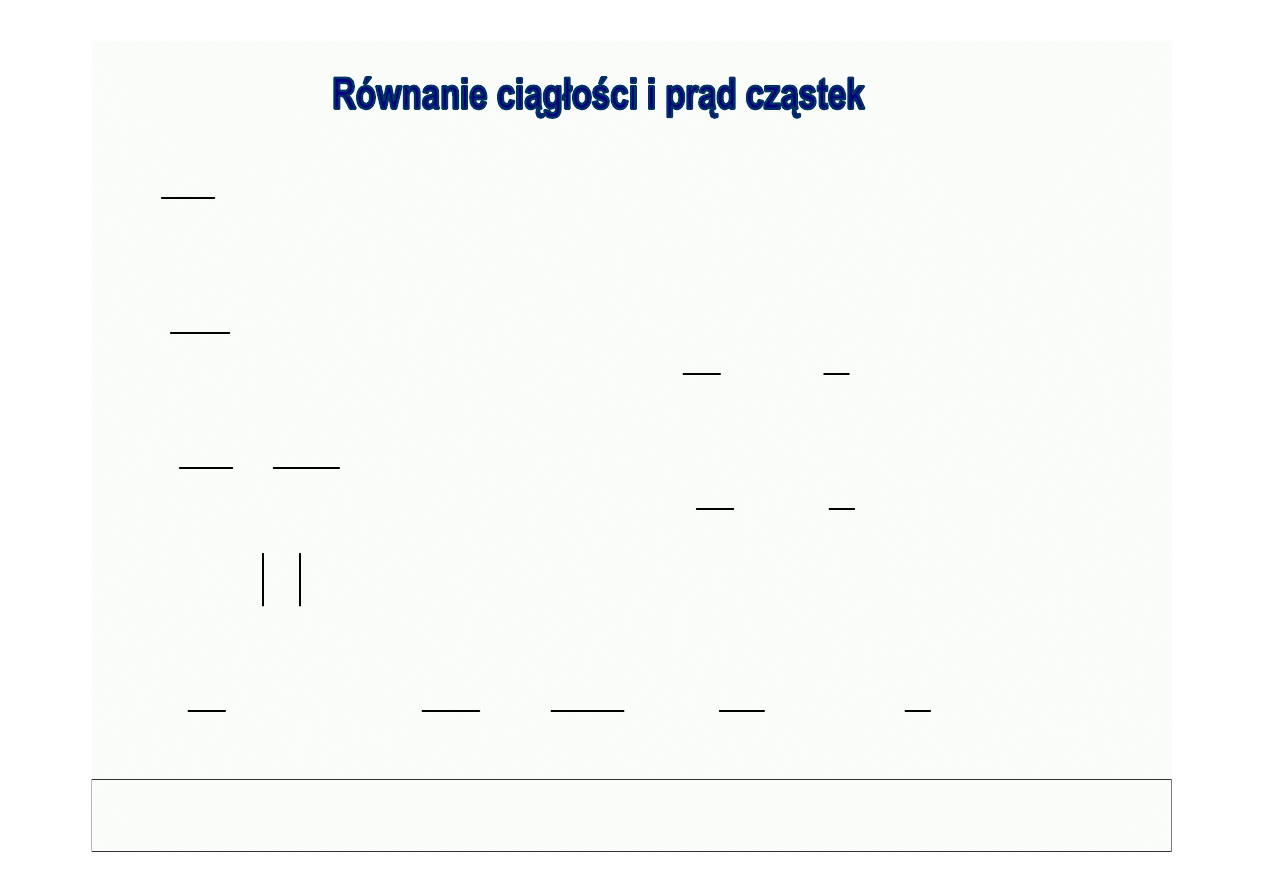
© Politechnika Lubelska
Dariusz Chocyk
0
=
⋅
∇
+
∂
∂
J
t
ρ
∫
⋅
−
=
V
r
d
N
r
ρ
∫
⋅
−
=
∂
∂
S
dS
J
t
N
ψ
ψ
H
i
t
ˆ
h
−
=
∂
∂
0
=
∂
∂
+
∂
∂
x
J
t
x
ρ
*
*
:
ˆ
ψ
ψ
H
i
t
h
=
∂
∂
2
ψ
ρ
≈
( )
*
*
:
*
*
:
*
:
ˆ
ˆ
ψ
ψ
ψ
ψ
ψ
ψ
ψ
ψ
ψψ
H
i
H
i
t
t
t
h
h
+
−
=
∂
∂
+
∂
∂
=
∂
∂
© Politechnika Lubelska
Dariusz Chocyk
x
i
p
x
∂
∂
−
= h
ˆ
)
(
2
ˆ
Hˆ
2
r
V
m
p
r
+
−
=
( )
∂
∂
−
∂
∂
=
∂
∂
2
*
2
2
2
*
:
*
:
2
x
x
m
i
t
ψ
ψ
ψ
ψ
ψψ
h
( )
0
2
*
*
:
*
:
=
∂
∂
−
∂
∂
∂
∂
+
∂
∂
x
x
mi
x
t
ψ
ψ
ψ
ψ
ψψ
h
∂
∂
−
∂
∂
=
x
x
mi
J
x
*
*
:
2
ψ
ψ
ψ
ψ
h
(
)
*
*
:
2
ψ
ψ
ψ
ψ
∇
−
∇
=
m
i
J
h
© Politechnika Lubelska
Dariusz Chocyk
pad
prz
J
J
T
=
pad
odb
J
J
R
=
2
1
2
2
A
ik
mi
J
pad
h
=
[
]
)
(
exp
1
1
t
x
k
i
A
pad
ω
ψ
−
=
[
]
)
(
exp
1
1
t
x
k
i
B
odb
ω
ψ
+
−
=
2
1
2
2
B
ik
mi
J
odb
h
−
=
[
]
)
(
exp
2
2
t
x
k
i
C
prz
ω
ψ
−
=
2
2
2
2
C
ik
mi
J
prz
h
=
2
A
B
R
=
1
2
2
k
k
A
C
T
=
© Politechnika Lubelska
Dariusz Chocyk
ϕ
ϕ
E
x
m
=
∂
∂
−
2
2
2
2
h
ϕ
ϕ
)
(
2
2
2
2
V
E
x
m
−
=
∂
∂
− h
m
k
E
2
2
1
2
h
=
m
k
V
E
2
2
2
2
h
=
−
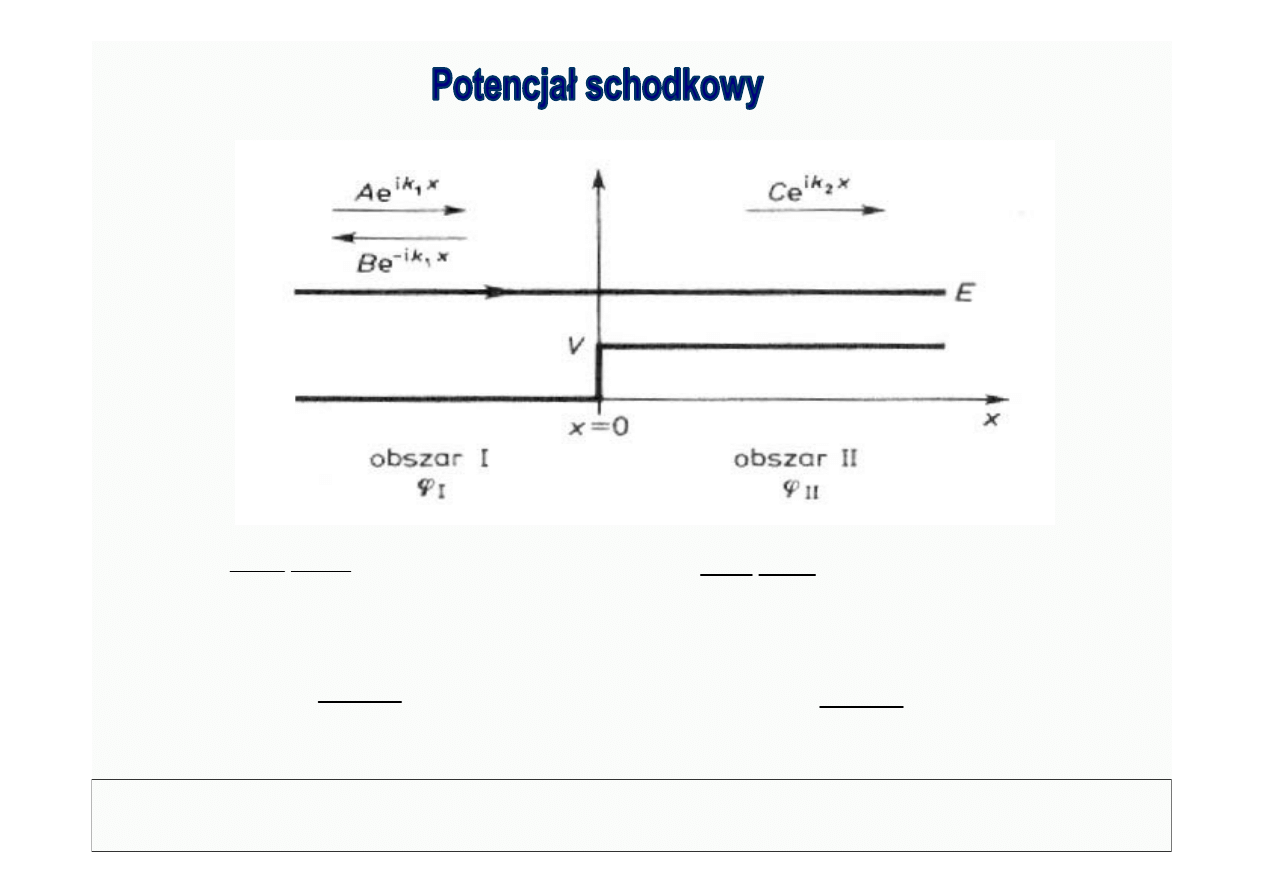
© Politechnika Lubelska
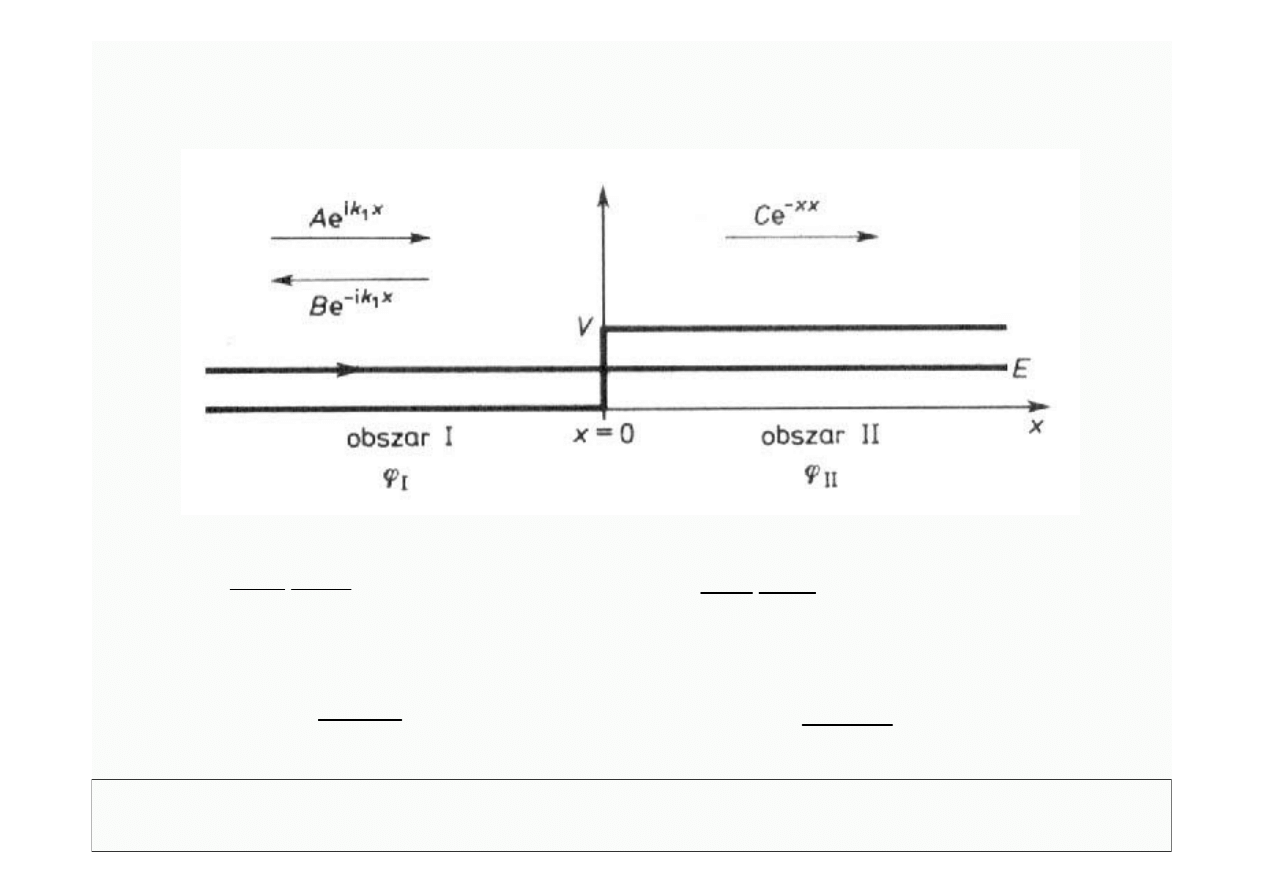
Dariusz Chocyk
x
ik
x
ik
I
Be
Ae
1
1
−
+
=
ϕ
x
ik
x
ik
II
De
Ce
2
2
−
+
=
ϕ
0
=
D
x
x
II
I
∂
∂
=
∂
∂
)
0
(
)
0
(
ϕ
ϕ
)
0
(
)
0
(
II
I
ϕ
ϕ
=
)
0
(
)
0
(
0
0
0
2
1
1
II
ik
ik
ik
I
Ce
Be
Ae
ϕ
ϕ
=
=
+
=
−
C
B
A
=
+
x
e
Cik
e
Bik
e
Aik
x
II
ik
ik
ik
I
∂
∂
=
=
−
=
∂
∂
−
)
0
(
)
0
(
0
2
0
1
0
1
2
1
1
ϕ
ϕ
1
2
k
k
C
B
A
=
−
© Politechnika Lubelska
Dariusz Chocyk
1
2
/
1
2
k
k
A
C
+
=
1
2
1
2
/
1
/
1
k
k
k
k
A
B
+
−
=
(
)
2
1
2
1
2
/
1
/
4
k
k
k
k
T
+
=
2
1
2
1
2
/
1
/
1
k
k
k
k
R
+
−
=
m
k
E
2
2
1
2
h
=
m
k
V
E
2
2
2
2
h
=
−
E
V
E
V
E
k
k
−
=
−
=
1
2
1
2
2
E
V
k
k
−
= 1
1
2
1
=
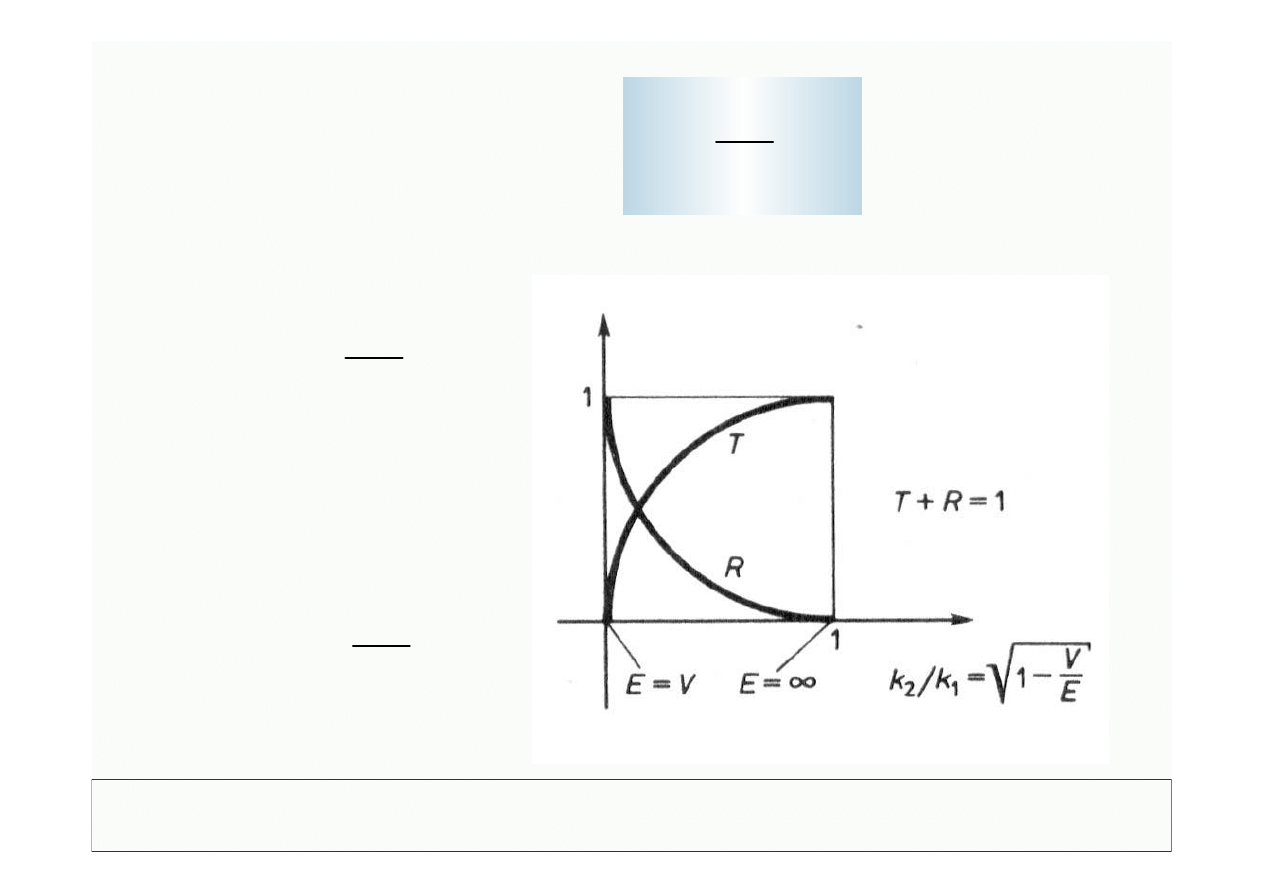
+ R
T
© Politechnika Lubelska
Dariusz Chocyk
1
0
1
2
≤
≤
k
k
mamy
Dla
V
E
>
:
Dla
V
E
>>
1
1
2
→
k
k
0
i
1
=
=
R
T
:
Dla
V
E
=
0
1
2
=
k
k
1
i
0
=
=
R
T
© Politechnika Lubelska
Dariusz Chocyk
Gdy
V
E
<
ϕ
ϕ
E
x
m
=
∂
∂
−
2
2
2
2
h
ϕ
ϕ
)
(
2
2
2
2
V
E
x
m
−
=
∂
∂
− h
m
k
E
2
2
1
2
h
=
0
2
2
2
>
=
−
m
E
V
χ
h
© Politechnika Lubelska
Dariusz Chocyk
x
ik
x
ik
I
Be
Ae
1
1
−
+
=
ϕ
x
II
Ce
χ
ϕ
−
=
A
C
A
B =
+
1
A
C
k
i
A
B
1
1
χ
=
−
1
/
1
2
k
i
A
C
χ
+
=
1
1
/
1
/
1
k
i
k
i
A
B
χ
χ
+
−
=
1
2
=
=
A
B
R
0
=
T
0
2
2
=
∂
∂
−
∂
∂
=
−
−
−
−
x
e
e
x
e
e
C
mi
J
x
x
x
x
prze
χ
χ
χ
χ
h
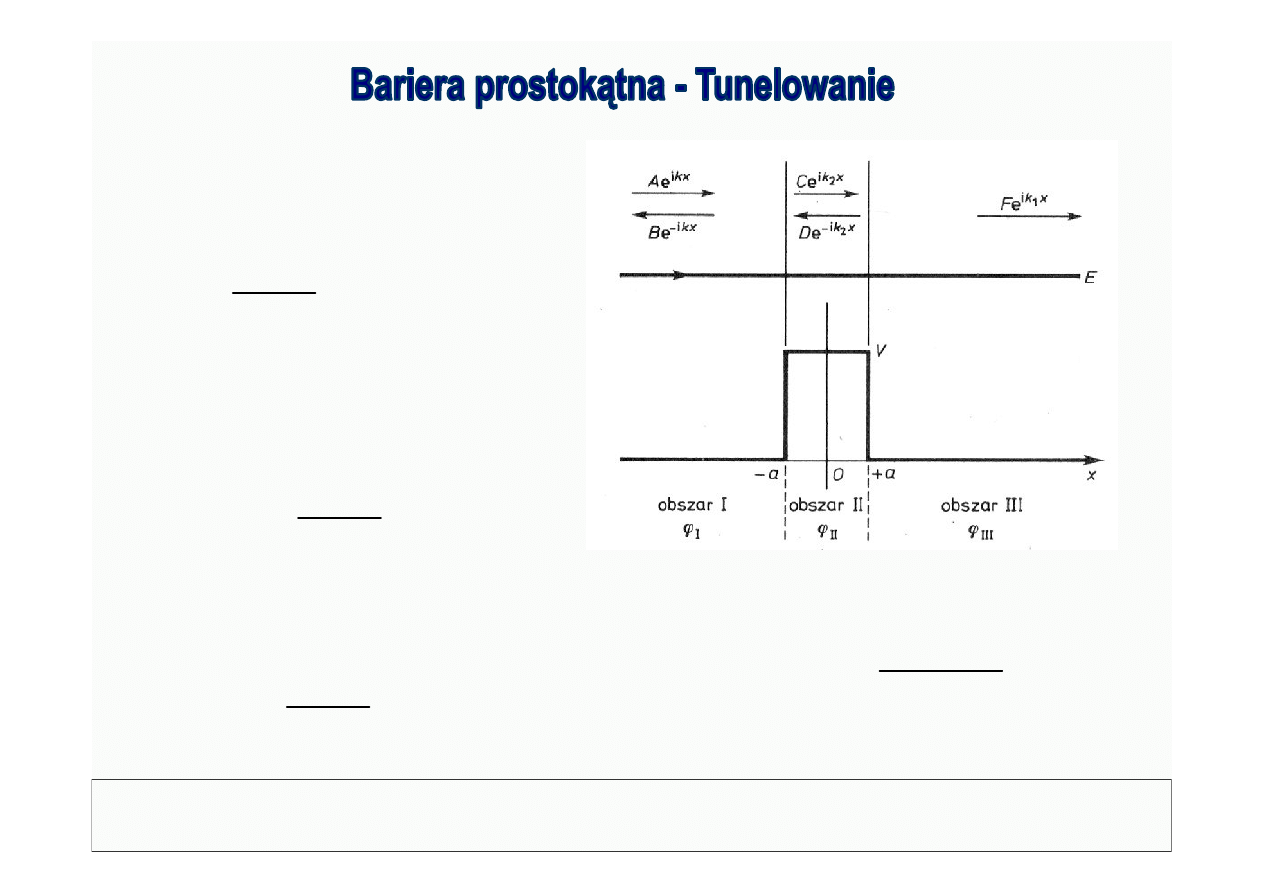
© Politechnika Lubelska
Dariusz Chocyk
x
ik
x
ik
I
Be
Ae
1
1
−
+
=
ϕ
m
k
E
2
2
1
2
h
=
x
ik
x
ik
II
De
Ce
2
2
−
+
=
ϕ
m
k
V
E
2
2
2
2
h
=
−
x
ik
III
Fe
1
=
ϕ
m
k
E
2
2
1
2
h
=
( ) ( )
2
2
2
2
2
1
2
h
V
ma
ak
ak
=
−
© Politechnika Lubelska
Dariusz Chocyk
a
ik
a
ik
a
ik
a
ik
e
A
D
e
A
C
e
A
B
e
2
2
1
1
+
=
+
−
−
−
=
−
−
−
a
ik
a
ik
a
ik
a
ik
e
A
D
e
A
C
k
e
A
B
e
k
2
2
1
1
2
1
a
ik
a
ik
a
ik
e
A
F
e
A
D
e
A
C
1
2
2
=
+
−
a
ik
a
ik
a
ik
e
A
F
k
e
A
D
e
A
C
k
1
2
2
1
2
=
−
−
1
2
2
1
2
2
2
1
2
2
sin
2
2
cos
1
−
+
−
=
a
k
k
k
k
k
i
a
k
e
A
F
a
ik
© Politechnika Lubelska
Dariusz Chocyk
a
k
k
k
k
k
A
F
i
A
B
2
2
1
2
1
2
2
2
sin
2
−
=
1
2
2
=
+
=
+
A
B
A
F
R
T
a
k
k
k
k
k
F
A
T
2
2
2
2
1
2
1
2
2
2
2
sin
4
1
1
1
−
+
=
=
Dla E>V mamy:
a
k
V
E
E
V
T
2
2
2
2
sin
)
(
4
1
1
1
−
+
=
© Politechnika Lubelska
Dariusz Chocyk
0
2
2
2
>
=
−
m
E
V
χ
h
( ) ( )
2
2
2
2
1
2
h
V
ma
a
ak
=
+
χ
z
i
iz
sinh
sin
=
χ
=
2
ik
Wiedząc, że:
a
k
k
T
χ
χ
χ
2
sinh
4
1
1
1
2
2
1
2
1
2
+
+
=
a
V
E
E
V
T
χ
2
sinh
)
(
4
1
1
1
2
2
−
+
=
a
V
E
E
V
T
χ
2
sinh
)
(
4
1
1
1
2
2
−
+
=
Gdy E<V to T<1
Jeśli
0
2
sin
2
2
=
a
k
to T=1
π
n
a
k
=
2
2

© Politechnika Lubelska
Dariusz Chocyk
100nm
400nm
Ag
200nm

© Politechnika Lubelska
Dariusz Chocyk
400nm
100nm
Au
200nm

© Politechnika Lubelska
Dariusz Chocyk
Cu
400nm
100nm
200nm
© Politechnika Lubelska
Dariusz Chocyk
Wyszukiwarka
Podobne podstrony:
kwanty dch
Wyklad4 kwantyle dystrybuanta
AMI 02 1 Kwantyfikatory
kwanty
kwantyfikatory, Matematyka
Logika dla informatyków, Sekwenty Genztena dla kwantyfikatorów
Kwanty XX
roz14 kwanty
Modul 2 Wynikanie logiczne i elementy rachunku kwantyfikatorow
5 Metody?lsyfikacji formuł na gruncie pierwszorzędowego rachunku kwantyfikatorów
ROZKLAd ch2, Kwantyle c2(p,v) rzędu p rozkładu c2 o
Kwanty światla, efekt fotoelektryczny i realność fotonów Skalski
Kwantyle rozkładu x kwadrat
kwantyle
kwantyle rozklad t studenta
06 Kwantyfikatory
19 kwanty wstęp
więcej podobnych podstron