14. Elementy fizyki mikroświata

W poprzednich rozdziałach omawiane były zjawiska z otaczającego nas świata w skalach (przestrzennych, czasowych i masowych) opowiadających bezpośrednim możliwościom percepcyjnym człowieka. W ostatnim rozdziale będzie mowa o zjawiskach zachodzących w skali mikro- i nano-, tzn. będzie mowa o zjawiskach zachodzących w bardzo krótkich czasach i w bardzo małych obszarach przestrzeni (patrz rozdział 1). Rozpoczniemy od elementów fizyki atomowej, a więc budowy materii na poziomie atomów i cząsteczek tworzących ciała materialne. Atom zbudowany jest z jądra atomowego, w którym znajdują się obojętne elektrycznie neutrony i dodatnio naładowane protony (ich wspólna nazwa to nukleony). Wokół jądra, po orbitach kołowych krążą ujemnie naładowane elektrony. Klasycznie taki ruch ładunku (z przyspieszeniem dośrodkowym) powinien spowodować emisję fali elektromagnetycznej, utratę energii elektronu i jego „spadek” na jądro atomowe. Spowodowało to konieczność wprowadzenia pewnych postulatów kwantowych.

14.1. Postulaty Bohra

Pierwszy postulat Bohra mówi, że istnieją stany stacjonarne (stabilne) atomu, w których nie emituje on energii. W stanach tych elektron atomu znajduje się na takiej orbicie, dla której moment pędu jest wielokrotnością stałej Diraca (stała Plancka podzielona przez 2
).

W równaniu tym n jest główną liczbą kwantową. Elektron obsadza ujemny poziom energetyczny:

(R - stała Rydberga)

Rys. 107 Poziomy energetyczne w atomie wodoropodobnym

Drugi postulat Bohra mówi, że atom przechodząc z jednego stanu stacjonarnego (m) do innego (n) emituje lub absorbuje porcję energii (foton, kwant) o energii
równej różnicy poziomów energetycznych obsadzanych przez elektron po i przed procesem.

14.2. Liczby kwantowe

Zastosowanie mechaniki kwantowej i rozwiązanie równania Schroedingera prowadzą do wartości momentu pędu elektronu w atomie:

,

gdzie: l jest orbitalną liczbą kwantową i przyjmuje wartości:

l = 0, 1, 2, ...,n-1 .

Wynika stąd, że n-ta powłoka elektronowa atomu (powłoki oznaczamy dużymi literami: K, L, M, N ...) składa się z n podpowłok numerowanych przez orbitalną liczbę kwantową. Te ostanie oznaczamy małymi literami s, p, d, f,...

Umieszczenie atomu w zewnętrznym polu magnetycznym powoduje, że wektor momentu pędu orientuje się tak w przestrzeni, że jego rzut na kierunek tego pola (rysunek 108) jest równy wielokrotności stałej Diraca.

m_l nazywamy orbitalną, magnetyczną liczbą kwantową. Przybiera ona 2l+1 wartości (od -l, ..., 0, ...., l).

Rys.108. Moment pędu elektronu w zewnętrznym polu magnetycznym.

Kolejna spinowa, magnetyczna liczba kwantowa: m_s przyjmuje wartości
. Wiąże się to z faktem, że rzut spinowego momentu pędu elektronu w polu magnetycznym może przyjmować tylko dwie wartości.

3. Układ okresowy pierwiastków

Powyższe informacje oraz zasada minimalizacji energii i zakaz Puliego są podstawą zrozumienia budowy układu okresowego pierwiastków. Zakaz Pauliego mówi, że w atomie nie mogą znajdować się dwa elektrony o tych samych czterech liczbach kwantowych. Zasada minimalizacji energii mówi, że w kolejnych pierwiastkach (kolejne wartości liczby porządkowej Z) elektrony obsadzają poziomy energetyczne w kolejności rosnących wartości energii (1s_1, 1s₂, 2s₁, 2s₂, 2p₁, 2p₂, 2p₃ ..... ). Z powyższych faktów wynika też, że na podpowłoce l może być co najwyżej 2(2l+1) elektronów (2, 6, 10, ...) a na powłoce n może być co najwyżej 2n² elektronów (2, 8, 18 ....).

4. Widma emisyjne i absorpcyjne

Substancja pobudzona (np. termicznie) do świecenia zawiera atomy w stanie wzbudzonym, które emitują promieniowanie charakterystyczne (liniowe) nakładające się na ciągłe tło termiczne. Mówimy wtedy o widmie emisyjnym (maksima intensywności) charakterystycznym dla atomów, z których zbudowana jest ta substancja. Zjawisko to wykorzystywane jest w spektralnej analizie jakościowej. Jeśli badana substancja znajdzie się na drodze wiązki świetlnej o widmie ciągłym wysyłanym przez źródło o wyższej temperaturze to zostaną z tej wiązki wychwycone fragmenty widma energetycznego odpowiadające różnicom poziomów energetycznych badanego materiału. Powtórna emisja fotonów odbywa się już w pełny kąt bryłowy, co prowadzi do obniżenia intensywności wiązki przechodzącej w zakresie absorbowanym przez badany materiał (rysunek 109).

Rys. 109 Widmo emisyjne (dolny wykres) i absorpcyjne (górny wykres)

Do badania widma promieniowania atomu wykorzystuje się spektrometry siatkowe lub pryzmatyczne. Pierwsze z nich charakteryzują się liniową zależnością odchylenia określonej składowej od jej długości fali. Dla małych kątów sin   
, gdzie: x oznacza odległość danego prążka od prążka zerowego a l odległość tego prążka od siatki dyfrakcyjnej. W doświadczeniu Younga uzyskano zależność wzmocnienia w k-tym rzędzie interferencyjnym:

.

Przy powyższych założeniach otrzymujemy więc:

x ~  

W rozdziale 13 wyprowadzono wzór na odchylenie  wiązki przechodzącej przez pryzmat. Odchylenie to dla małych kątów jest wprost proporcjonalne do współczynnika załamania n.

Ponieważ, poza obszarami pochłaniania (z dokładnością do stałej):

,

stąd wynika, że dla spektrometru pryzmatycznego:

.

W spektrometrze pryzmatycznym (rysunek 110) wiązka światła wychodząca z pobudzonej do świecenia substancji pada na soczewkę S₁ dającą wiązkę równoległą. Ta z kolei pada na pryzmat Pr. Na jego pierwszej powierzchni następuje załamanie i rozszczepienie wiązki na składowe. Promienie o tej samej długości fali (barwie) wychodzą z pryzmatu jako równoległe do siebie i są ogniskowane przez soczewkę S₂ w jednym miejscu jako barwny prążek.

Rys.110. Schemat spektrometru pryzmatycznego

Spektrometry wykorzystywane są zarówno do analizy jakościowej (określenie pierwiastków wchodzących w skład próbki) jak i ilościowej (skład procentowy) badanej substancji.

Rysunek 111 Przedstawia zdjęcie spektrofotometru pryzmatycznego Helios sterowanego i przetwarzającego automatycznie dane za pomocą wbudowanego komputera.

Rys.111 Sterowany komputerowo spektrofotometr Helios (z lewej, u góry - wykres transmisji dla herbaty z cytryną, niżej - automatyczny podajnik z kuwetami, z prawej - wyświetlacz i klawiatura komputera).

Promieniowanie elektromagnetyczne o dużej energii i długościach fal od 10^-12 do 10^-9 m pochodzące od emisji przy przeskokach elektronów na nisko położone poziomy energetyczne nazywamy promieniowaniem rentgenowskim. Ze względu na jego przenikliwość i długości fal znalazło ono zastosowanie do diagnostyki medycznej i w nauce do badania struktury wewnętrznej ciał.

14.5 Półprzewodniki

Jedną z najdynamiczniej rozwijających się w ostatnich dziesięcioleciach dziedzin nauki jest elektronika. Jej szybki rozwój umożliwiło zastosowanie elementów półprzewodnikowych takich jak dioda i tranzystor.

Ciała stałe, ze względu na właściwości elektryczne, dzielimy na przewodniki, półprzewodniki i izolatory. Pierwsze z nich charakteryzują się największym przewodnictwem elektrycznym. Najmniejsze przewodnictwo wykazują izolatory. Półprzewodniki charakteryzują się pośrednimi wartościami przewodnictwa właściwego σ w zakresie od 10^-6 do 10⁶ ^-1m^-1.

Przewodnictwo właściwe σ jest odwrotnością oporu właściwego ρ występującego we wzorze na rezystancję (opór) R regularnego przewodnika:

,

gdzie ρ zależy od temperatury:

,

„” jest temperaturowym współczynnikiem oporu (ρ₀ - dla temperatury 0⁰C), l oznacza długość przewodnika a S pole powierzchni jego przekroju poprzecznego.

Z ostatniego wzory wynika, że opór przewodników rośnie z temperaturą.

W poprzednim rozdziale przedstawiono układ poziomów energetycznych odosobnionego atomu. Jeśli atomy znajdują się w strukturze krystalicznej ciała stałego to wpływ sąsiednich atomów powoduje rozszczepienie poziomu energetycznego w układ bardzo blisko leżących poziomów, które nazywamy pasmem energetycznym. Na rysunku 112 przedstawiono układ pasm energetycznych dla przewodników, półprzewodników i izolatorów.

Rys. 112 Układ pasm energetycznych dla przewodników, półprzewodników i izolatorów (pp-pasmo przewodnictwa, pw-pasmo walencyjne, pe-przerwa energetyczna, pd-poziom donorowy, pa-poziom akceptorowy)

Pasmo przewodnictwa pp to najniższe pasmo posiadające wolne poziomy energetyczne. Pasmo walencyjne to najwyższe pasmo zawierające elektrony. Warunkiem przepływu prądu jest aby w danym paśmie były wolne poziomy energetyczne i nośniki prądu (elektrony, dziury). Przewodniki spełniają ten warunek ponieważ oba pasma zachodzą na siebie. W półprzewodnikach samoistnych (bez domieszek) warunek ten można uzyskać w procesie generacji par elektron - dziura przy podgrzewaniu lub naświetlaniu półprzewodnika (fotorezystor). Wprowadzenie do półprzewodnika, zbudowanego z atomów 4 grupy układu okresowego, atomów z 5 grupy układu okresowego daje elektrony na poziomie donorowym pd. Termiczne wzbudzenia przenoszą elektrony do pasma przewodnictwa gdzie biorą one udział w przewodnictwie typu n. Wprowadzenie do półprzewodnika atomów z 3 grupy układu okresowego daje poziom akceptorowy pa. Termiczne wzbudzenia przenoszą elektrony z pasma walencyjnego pw na poziom pa. Powstałe w paśmie walencyjnym wolne miejsca - dziury biorą udział w przewodnictwie typu p w tym paśmie.

Połączenie półprzewodnika typu n z półprzewodnikiem typu p daje złącze pn wykorzystywane w technice jako dioda półprzewodnikowa. Na złączu tym występuje zjawisko rekombinacji polegające na kompensowaniu przez elektrony z półprzewodnika typu n dziur w półprzewodniku typu p (na złączu). Prowadzi to do nadmiaru ładunku dodatniego w pierwszym i ujemnego w drugim. Powstająca różnica potencjałów blokuje dalszą migrację elektronów. Przyłożenie zewnętrznego napięcia + do półprzewodnika typu n i - do półprzewodnika typu p zwiększa różnicę potencjałów na złączu i uniemożliwia przepływ prądu elektrycznego. Odwrotna polaryzacja zmniejsza to napięcie i umożliwia przepływ prądu. Wynika stąd, że dioda w obwodzie prądu zmiennego stanowi element prostowniczy (zastosowanie w prostownikach). Dioda jest więc elementem nieliniowym. W przypadku diody nie ma zastosowania prawo Ohma (brak liniowej zależności natężenia prądu od napięcia - rysunek 113).

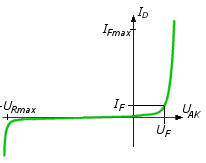
Rys.113 Charakterystyka prądowo-napięciowa i symbol graficzny diody ( strzałka wyznacza kierunek przepływu prądu przez diodę).

Wyprowadzenie diody od strony półprzewodnika p jest nazywane anodą A, a drugie jest nazywane katodą K. Prąd wsteczny diody jest zwykle o kilka rzędów mniejszy niż prąd przewodzenia dlatego przyjmuje się, że jest on równy zeru. Jest tak do momentu gdy napięcie zaporowe przekroczy pewną granicę, tak zwane napięcie przebicia. Wówczas popłynie prąd porównywalny z prądem w kierunku przewodzenia. Zjawisko to wykorzystywane jest w diodzie Zenera do stabilizacji napięcia.

Diody wykorzystywane są do prostowania jednopołówkowego (1 dioda) lub dwupołówkowego z dwoma diodami (przy podwójnym uzwojeniu wtórnym transformatora) lub z czterema w układzie Gretza (przy pojedynczym uzwojeniu wtórnym transformatora).

Na rysunku 114 przedstawiono układ trzech półprzewodników typu p-n-p stosowany w technice jako tranzystor.

Rys. 114 Rozkład prądów w tranzystorze p-n-p (E-emiter, B-baza, C-kolektor)

Pojedyncze złącze nie przepuszcza prądu w kierunku zaporowym. Wynika to z działania bariery potencjału na nośniki większościowe w obu półprzewodnikach. Bariera ta przenosiłaby jednak bez problemu nośniki mniejszościowe (przeciwny zwrot siły pola elektrycznego). Złącze BC blokuje przepływ elektronów od bazy do kolektora. Ale gdyby wstrzyknąć tam dziury to byłyby natychmiast przerzucone do obszaru kolektora. Do tego służy złącze emiter-baza, które spolaryzowane jest w kierunku przewodzenia powodując wstrzykiwanie dziur z emitera do bazy. Dla ograniczenia rekombinacji w obszarze bazy jest ona bardzo cienka co zmniejsza prawdopodobieństwo zajścia tego zjawiska. W układzie tym sterując niewielkim prądem bazy uzyskujemy duże zmiany prądu kolektora. Dlatego tranzystor wykorzystywany jest w układach elektronicznych jako wzmacniacz (prądowy i napięciowy). Stosunek przyrostu prądu kolektora do przyrostu prądu bazy określa współczynnik wzmocnienia prądowego . Jego wartość dla układu o wspólnym emiterze przekracza 10².

W technice wykorzystywane są też elementy wielowarstwowe (diaki, tyrystory, triaki) służące do regulacji małych i dużych mocy w układach elektrycznych.

14.6. Budowa jądra atomowego

Dalszym krokiem w kierunku poznania mikroświata jest model budowy jądra atomowego. Składa się ono z nukleonów (protonów i neutronów). Między protonami występują siły odpychania, które kompensowane są przez krótkozasięgowe siły przyciągania występujące między nukleonami. Oznacza to, że neutrony pełnią rolę stabilizującą trwałość jądra atomowego. Ze wzrostem liczby porządkowej Z (liczby protonów) rośnie też liczba neutronów. Gdyby policzyć masę jądra atomowego i sumę mas poszczególnych jego nukleonów to otrzymamy różnicę nazywaną defektem masy. Wykorzystując wzór Einsteina możemy przeliczyć ten defekt na tzw. energię wiązania. Dzieląc ją przez liczbę nukleonów otrzymamy tzw. właściwą energię wiązania (przypadającą na jeden nukleon). Rysunek 115 przedstawia zależność właściwej energii wiązania od liczby nukleonów A (tzw. krzywa Wszechświata).

Rys.115. Krzywa Wszechświata

14.7. Reakcje rozszczepienia i syntezy

Z rysunku tego wynika, że zarówno reakcje rozszczepienia ciężkich jąder jak i reakcje syntezy lekkich jąder prowadzą do wydzielenia energii ze względu na rosnącą wartość właściwej energii wiązania produktów końcowych. Widać też, że produkcja tej energii musi być dużo większa w przypadku reakcji syntezy. I faktycznie w niechlubnych przypadkach wybuchów bomb wodorowych (synteza wodoru w hel) uzyskiwano znacznie większe efekty energetyczne (i polityczne) niż w przypadku wybuchu konwencjonalnych bomb atomowych (rozszczepienie uranu). Warunkiem reakcji lawinowej jest w ostatnim przypadku przekroczenie tzw. masy krytycznej dla danej geometrii ładunku. W przypadku bomby wodorowej niezbędne jest też uzyskanie odpowiedniej temperatury inicjującej syntezę. Do tego celu wykorzystywana jest zapalnik w postaci bomby atomowej.

8. Promieniotwórczość

Niektóre jądra nietrwałe ulegają samorzutnemu rozpadowi na jądra lżejszych pierwiastków z jednoczesną emisją cząstek
,
i
. Rysunek 116 przedstawia zachowanie tych cząstek w polu magnetycznym.

Rys.116 Tory cząstek , , γ w polu magnetycznym (skierowanym za kartkę)

Ponieważ promienie γ nie posiadają ładunku elektrycznego, dlatego poruszają się po liniach prostych. Cząstki  to elektrony (-e) a cząstki  to jądra helu zawierające dwa protony (+2e). Porównując siłę dośrodkową i jej źródło - siłę Lorentza otrzymujemy:

,

.

Ze względu na znacznie większą wartość m/q dla cząstki  jej promień krzywizny jest większy (mniejsza krzywizna) niż dla cząstki . Ze względu na ich przeciwne znaki cząstki te odchylają się w przeciwne strony.

Wzory opisujące rozpady promieniotwórcze podano w rozdziale 2 przy omawianiu zasady zachowania ładunku elektrycznego. Rozpady te podlegają prawu rozpadu promieniotwórczego. Ilość jąder ulegających rozpadowi jest proporcjonalna do bieżącej ilości jąder i czasu dt tego rozpadu.

Znak minus oznacza ubytek bieżącej liczby jąder przy rozpadzie. Rozwiązaniem tego równania różniczkowego jest funkcja:

.

Przyjmując, że w czasie t=T_1/2 (czas połowicznego zaniku) rozpadowi uległa połowa początkowej ilości jąder otrzymujemy:

stąd:

.

Średni czas życia substancji promieniotwórczej definiuje się jako:

Po upływie czasu
aktywność substancji promieniotwórczej maleje e-krotnie.

---