10. Teoria względności

1905 – postulaty Einsteina:

I. Prawa przyrody są identyczne we wszystkich inercjalnych układach odniesienia.

II. Prędkość światła w próżni jest stała i taka sama we wszystkich inercjalnych układach
odniesienia.

1984

→ c = 299 792 458 m/s ⇒ wzorzec metra

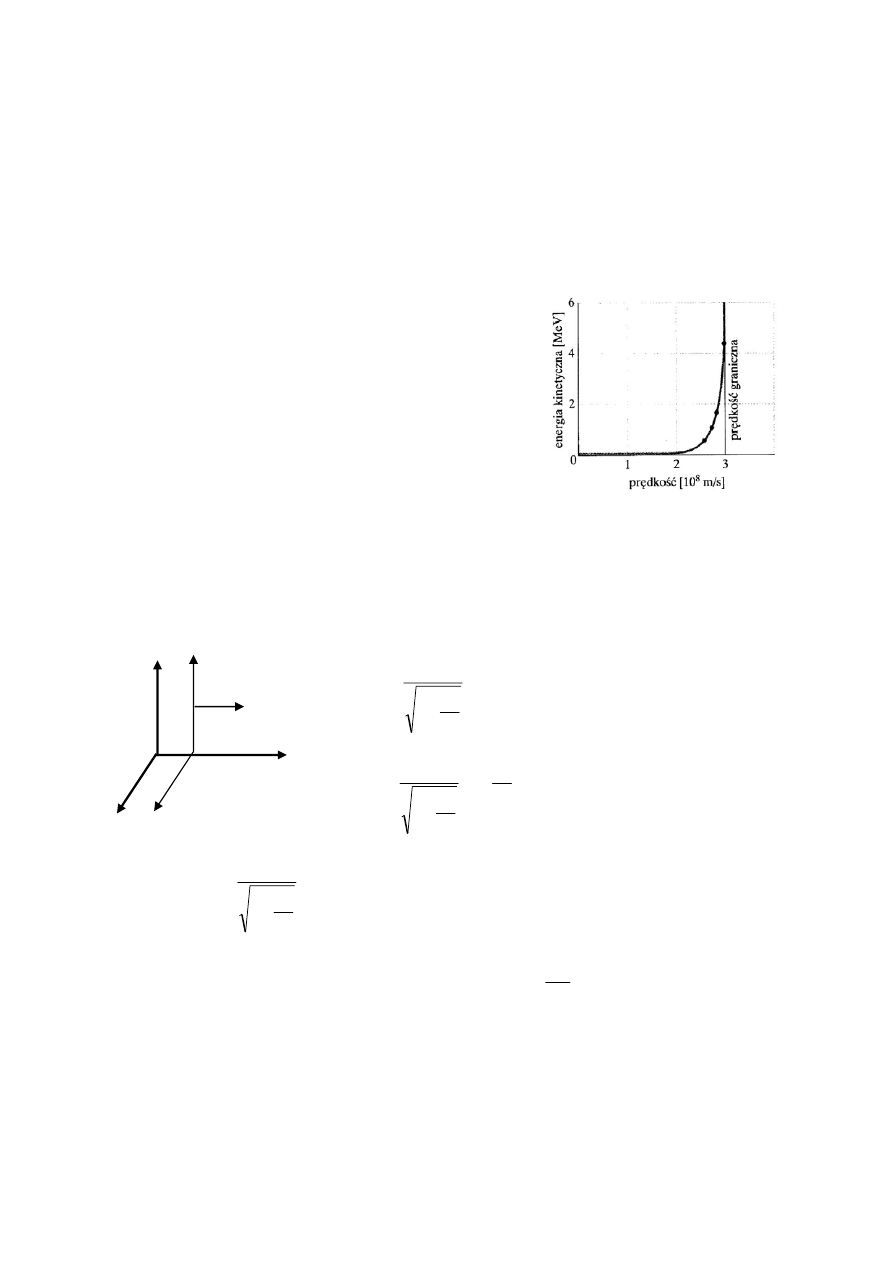
Prędkość żadnego ciała przenoszącego energię lub
informację nie może przekroczyć prędkości granicznej
(niezależnie od czasu przyspieszania!). Eksperyment
Bertozziego (1964) – przyspieszanie elektronów.

Szczególna teoria względności dotyczy jedynie
inercjalnych układów odniesienia.

10.1. Transformacja Lorentza.

1893 – hipoteza Fitzgeralda, że wszystkie poruszające się względem eteru przedmioty ulegają
skróceniu w tym samym kierunku, w którym odbywa się ruch przedmiotu.

1895 – Lorentz wzory transformacyjne dla układu poruszającego się:

(

)

vt

x

c

v

x

−

−

=

2

2

1

1

'

y’ = y

z’ = z

⎟

⎠

⎞

⎜

⎝

⎛ −

−

=

x

c

v

t

c

v

t

2

2

2

1

1

'

Z

Z’

X

X’

Y’

V

Y

Podstawiając

2

2

1

1

c

v

−

=

γ

otrzymamy dla transformacji odwrotnej wyrażenia:

x =

γ

(x’ + v

⋅

t’)

y = y’

z = z’

⎟

⎠

⎞

⎜

⎝

⎛ +

=

2

'

'

c

v

x

t

t

γ

Oczywiście gdy v << c to otrzymujemy wzory transformacji Galileusza:

x’ = x – vt

y’ = y z’ = z

t’ = t

Z postulatów Einsteina wynika konieczność innego niż dotychczas sposobu opisywania czasu
i przestrzeni.

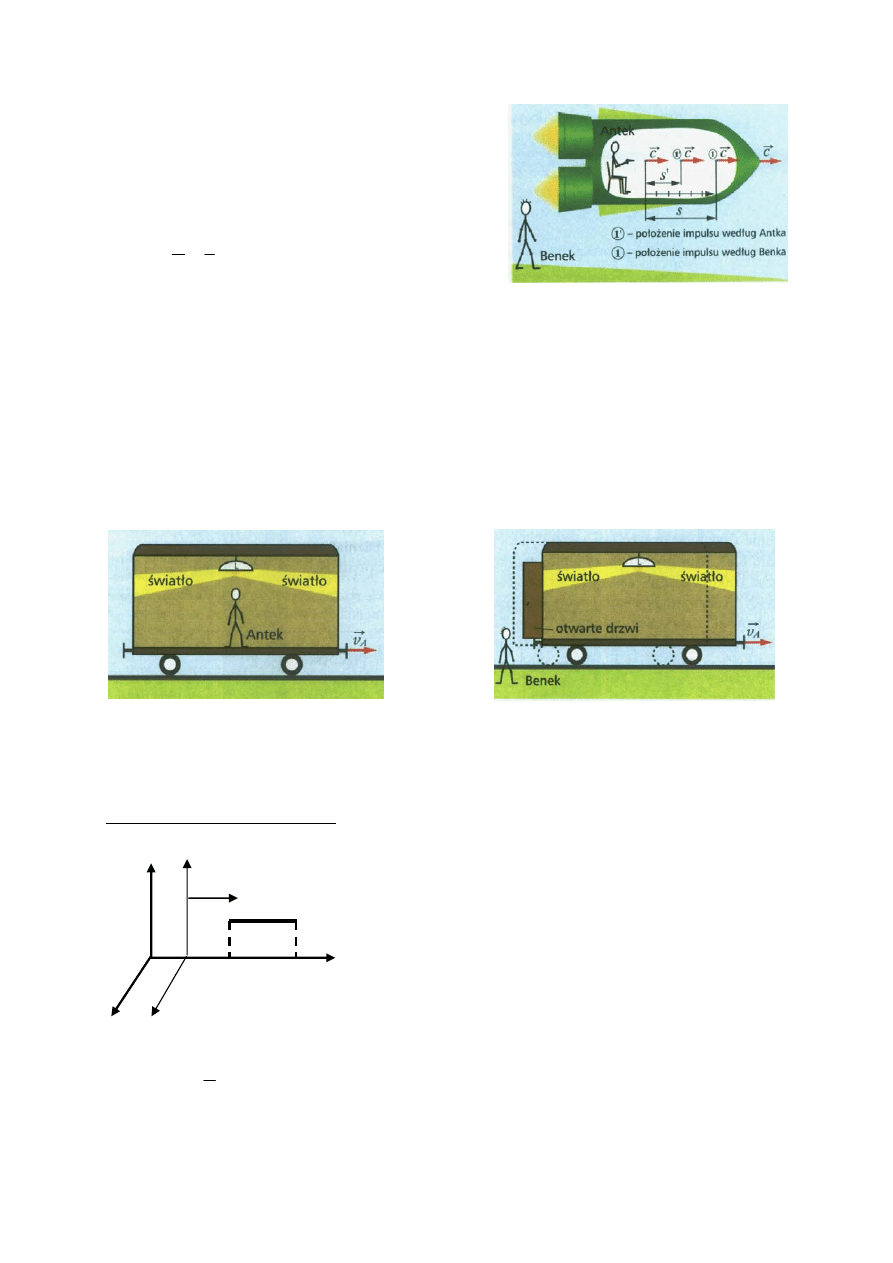
Obserwator siedzący w rakiecie obliczy prędkość
impulsu świetlnego mierząc w czasie t’ przebytą
przez impuls drogę s’. Natomiast dla obserwatora
stojący nieruchomo, impuls w czasie t przebędzie
odcinek s.

Ale:

t

s

t

s

c

=

=

'

'

wynika z tego, że s’ < s (droga

przebyta w układzie poruszającym się musi być
krótsza niż w układzie spoczywającym) oraz t’ < t (czas płynący w układzie poruszającym
się musi płynąć wolniej niż w układzie spoczywającym).

Drugą ważną konsekwencją postulatów Einsteina jest stwierdzenie, że zdarzenia jednoczesne
w jednym układzie odniesienia nie muszą być jednoczesne gdy obserwujemy je z innego
układu !

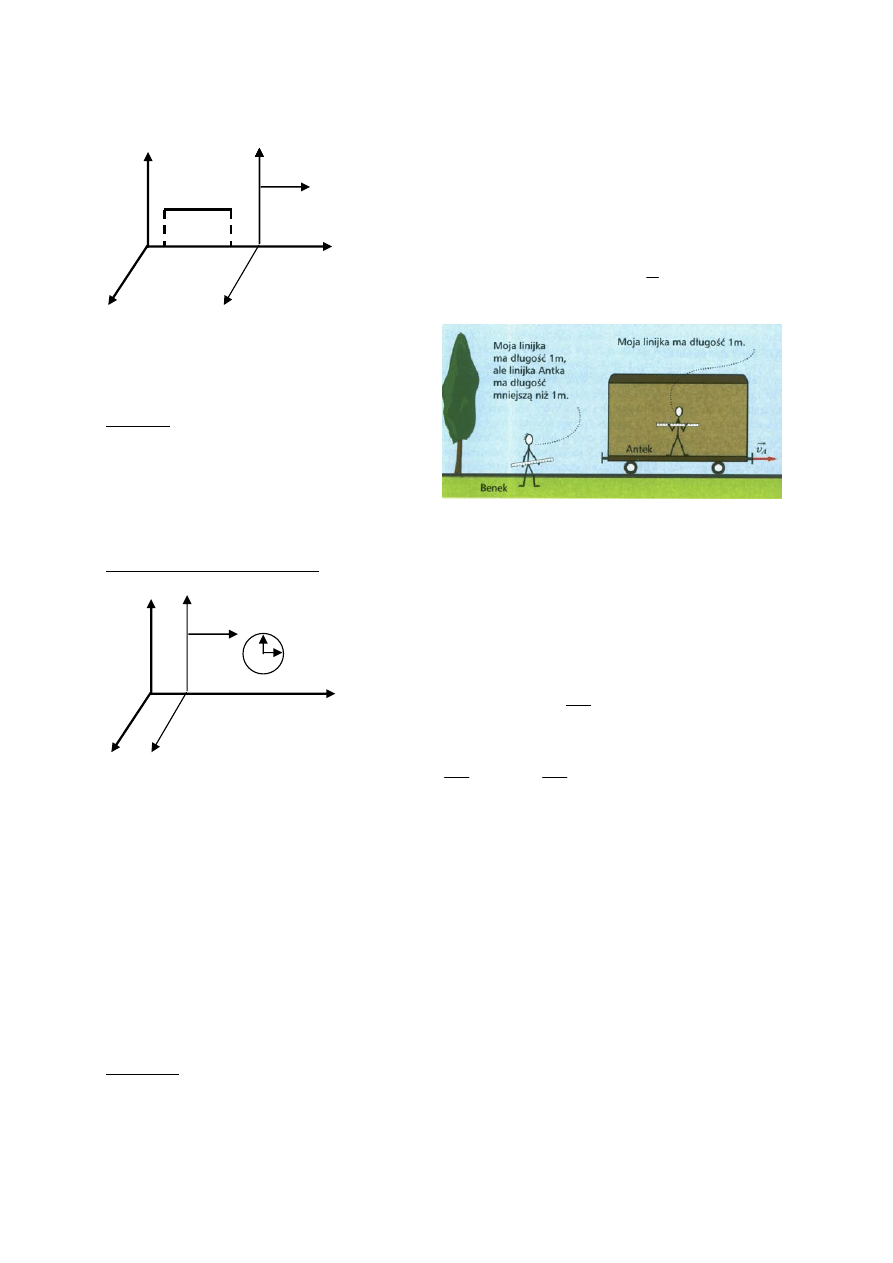
Światło z lampy umieszczonej w suficie padając na czujniki otwiera drzwi w obu końcach
wagonu. Dla obserwatora poruszającego się drzwi otworzą się jednocześnie, ale dla
obserwatora nieruchomego najpierw otworzą się tylne drzwi (które „doganiają” impuls
świetlny). Obaj maja rację !!

10.2. Kontrakcja długości, dylatacja czasu.

Skrócenie (kontrakcja) długości

Pręt jest nieruchomy względem układu O’
poruszającego się z szybkością v względem
spoczywającego układu O.

y

y’

x

x’

z

z’

V

x

1

’

x

2

’

l

0

O

O’

Długość odcinka zmierzona w układzie O’ :

l

0

= x’

2

– x’

1

=

γ

(x

2

- v

⋅

t) -

γ

(x

1

- v

⋅

t)

l

0

=

γ

(x

2

– x

1

) =

γ⋅

l

A więc

o

l

l

γ

1

=

- zmierzona w układzie spoczywającym, długość poruszającego się pręta

jest mniejsza od długości zmierzonej w układzie O’.

Jeżeli sytuacje odwrócimy:

Pręt nieruchomy w układzie O porusza się w stosunku do
układu O’

y

y’

x

x’

z

z’

V

x

1

x

2

l

0

O

O’

l

0

=

γ

(x’

2

– x’

1

) =

γ⋅

l

l

0

= x

2

– x

1

=

γ

(x’

2

+ v

⋅

t) -

γ

(x’

1

+ v

⋅

t)

o

l

l

γ

1

=

Długość

ta w ocenie obserwatora

oruszającego ę względem niego jest

mniejsza.

prę

p

si

Wniosek – zgodność z I postulatem
Einsteina, że układy inercjalne są sobie
równoważne we wszystkich układach

ydłużenie (dylatacja) czasu

odniesienia.

W

Zegar jest nieruchomy względem układu O’

⇒

Δ

t

0

y

y’

x

x’

z

z’

V

Δ

t

0

O

O

W układzie O mierzony jest przedział czasu

Δ

t

’

1

2

t

t

t

−

=

Δ

gdzie

⎟

⎠

⎞

⎛

'v

x

⎜

⎝

+

=

2

'

c

t

t

γ

(

)

1

2

2

1

2

2

'

'

'

'

'

'

t

t

t

c

v

x

t

c

v

x

t

t

−

=

Δ

⇒

⎟

⎠

⎞

⎜

⎝

⎛ +

−

⎟

⎠

⎞

⎜

⎝

⎛ +

=

Δ

γ

γ

γ

Czyli

Δ

t =

γ⋅

Δ

t

0

w

ka względem obserwatora w układzie O jest dłuższy.

dkościami v

≤

c

nauta wyruszający w kosmos będzie

Czas tr ania zjawis

Cząstki elementarne (o krótkim czasie życia) poruszające się z dużymi prę
mają długi czas życia dla obserwatora w laboratorium.

Pytanie – w znanym paradoksie bliźniąt, dlaczego astro
„młodszy” od bliźniaka pozostającego na Ziemi – skoro dla niego to właśnie Ziemia będzie
się poruszać ?

Przykłady

1. W jaki sposób i z jaką szybkością powinien poruszać się prostopadłościenny kontener o
wymiarach L

0

x L

0

x 1,5L

0

aby nieruchomy obserwator widział go jako sześcian ?

Odp. Ruch zgodny z najdłuższym wymiarem 1,5 L

0

. Widziana długość L = 1,5 L

0

ma być

równa L , a więc

0

0

0

5

,

1

L

L

L

=

=

stąd

γ

5

,

1

1

2

2

−

v

1

=

=

γ

czyli

2

2

2

2

4

1

v

v

⇒

=

−

9

9

c

c

5

c

=

Ostatecznie v = 0,75 c

2. Statek kosmiczny porusza się z szybkością 0,7c. na statku ustawiono stół konferencyjny

zdłuż osi statku. Długość stołu, jak zmierzył podczas lotu astronauta wynosiła 5m.

B. O ile krótszy stół widzieliby podczas lotu obserwatorzy z Ziemi?

C. Ile lat wg czasu pokładowego minęło od startu?

Odp. A. O ile stół się nie skurczył ze starości, to w każdym układzie względem którego stół

w

A. Jaka była długość stołu zmierzona przed odlotem z Ziemi 46 lat wcześniej?

jest nieruchomy, jego długość wynosi 5.

714

,

0

49

,

0

1

1

;

2

−

=

=

c

c

L

L

S

Z

γ

γ

Odp. B.

2

=

stąd L

Z

= 3,57 m

Δ

L = 1,43 m

Δ

t

Z

=

γ⋅

Δ

t

S

stąd

Δ

t

S

= 0,714

⋅ 46 lat

3. W wyniku oddziaływania promieniowania kosmicznego na górne warstwy atmosfery

owstają cząsteczki elementarne mezony

π

+

, których czas życia liczony w układzie własnym

(związanym z cząstką) wynosi 2,6

⋅10

-8

s (0,924c). Zakładając, że powstające mezony mają

B. Długość drogi przebytej przez powstały mezon do chwili jego rozpadu mierzonej w

Odp. C.

= 32,84 roku

p

prędkość V = 2,769

⋅10

8

m/s, obliczyć:

A. Czas życia mezonu w układzie związanym z laboratorium na Ziemi.

układzie laboratoryjnym oraz w układzie własnym mezonu.

Odp. A.

Δ

t

L

=

γ⋅

Δ

t

m

s

t

L

8

2

8

10

8

,

6

924

,

0

1

10

6

,

2

−

−

⋅

=

−

⋅

=

Δ

(ponad 2,5 razy dłuższy czas !!)

Odp.B. S

L

= v

⋅

Δ

t

L

= 1

własnym mezonu: S

8,83 m natomiast w układzie

,19m

4. Długość nieruchomego pociągu jest taka sama jak długość tunelu i wynosi L

0

. Pociąg ten

dzie z prędkością V = 0,1 c. Czy początek i koniec pociągu miną końce tunelu w tym

m

= v

⋅

Δ

t

m

= 7

je

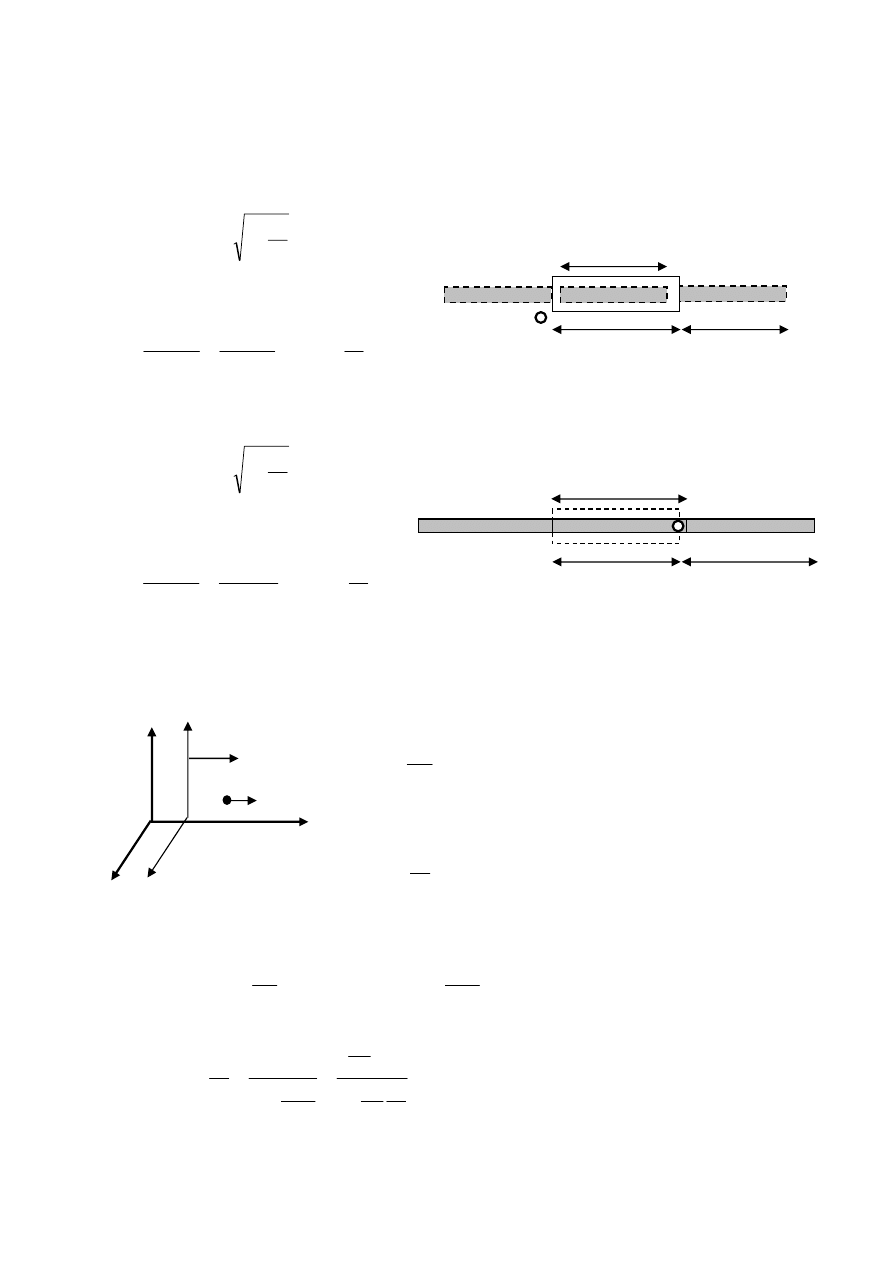
samym czasie dla obserwatorów w pociągu i tunelu ? Jak długo trwał przejazd pociągu dla
tych obserwatorów?

Odp. Dla obserwatora stojącego na ziemi długość pociągu będzie mniejsza niż długość tunelu:

L

p

< L

t

2

2

v

1

c

L

L

t

p

−

=

L

p

= 0.995

⋅

L

t

Czas przejazdu całego pociągu przez tunel:

L

t

+ L

p

L

p

t

t

p

t

Z

L

c

c

v

t

0501

,

0

1

,

0

=

=

=

L

L

L

995

,

1

+

Dla obserwatora w pociągu długość tunelu bę

L

p

> L

t

dzie mniejsza niż pociągu:

2

2

v

1

c

L

L

p

t

−

=

stąd L

p

= 1.005

⋅

L

t

łego poci

Czas przejazdu ca

ągu przez tunel:

L

p

t

t

p

t

p

L

c

c

v

t

0499

,

0

1

,

0

=

=

=

L

L

L

005

,

2

+

0.3. Prędkość w układach inercjalnych.

ładu O’ punkt materialny ma szybkość

L

t

+ L

p

1

Względem uk

'

1

1

dt

v

=

s

dx

atomia t względem układu O ma szybkość

N

dt

dx

v

=

.

2

Skoro x =

γ⋅

(x’ + vt’) to dx =

γ⋅

(dx’ + vdt’)

Z

Z’

X

X’

V

V

1

V

2

Y

Y’

Natomiast

⎟

⎞

⎜

⎛ +

=

'

'

v

x

t

γ

więc

⎟

⎠

⎞

⎜

⎛ +

=

'

dx

dt

γ

⎠

⎝

2

c

t

⎝

⋅

2

'

c

v

dt

A zatem

2

2

2

'

'

1

'

'

'

'

'

'

c

v

dt

dx

v

dt

dx

c

v

dx

dt

vdt

dx

dt

dx

v

+

+

=

⋅

+

+

=

=

2

1

1

2

1

c

v

v

v

v

v

+

+

=

Ostatecznie

dla v = 0 (układ O’ w spoczynku) v

2

= v

1

Przykłady

1. Dwa akcel

strumienie cząstek poruszające się w przeciwne stro

eratory dają

ny - każdy z

szybkością v

1

= v

2

= 0,9c. Obliczyć względną szybkość strumieni cząstek.

superpozycja: v

wzgl

= v

1

+ v

2

= 1,8 c

⇒ wynik zły !! v

wzgl

> c

Klasyczna

Dodawanie relatywistyczne:

c

c

c

v

v

v

v

v

9945

,

0

81

,

0

1

8

,

1

1

2

1

1

2

=

+

=

+

+

=

c

c

2

2

2. Podczas zbliżania rakiety lecącej z szybkością 0,7c

, wystrzelono z niej

słońca tego układu

wynosiła 0,8c. Jaka była szybkość sondy względem
rakiety ?

do pewnego układu słonecznego
sondę, której szybkość względem

Dane: v = 0,7c; v

2

= 0,8c

Klasyczne dodawanie prędkości: v

wzgl

= v

2

= v + v

1

stąd v

1

= v

2

– v = 0,1c - źle ! Wartość zaniżona!!

Dodawanie relatywistyczne:

2

c

+

2

2

1

1

7

,

0

1

7

,

0

8

,

0

v

c

c

v

c

⋅

+

=

0,8c – 0,7c = (1 – 0,56)v

1

c a zatem v

1

= 0,23c

10.4. Masa, energia.

II zasada dynamiki w ujęciu relatywistycznym:

ędu ciała jest proporcjonalny do wartości działającej na ciało siły wypadkowej i

stąd po przekształceniu

Przyrost p

czasu działania siły:

t

p

F

=

Δ

Δr

r

gdzie wartość pędu ciała wyraża się wzorem:

2

2

1

c

v

mv

p

−

=

Einstein założył, że dla dużych prędkości przestaje być słuszny wzór

v

m

p

r

r

⋅

=

gdyż

oznaczałoby to, że dow

iła działając przez odpowiednio długi czas byłab

olna s

w stanie

rozpędzić ciało nawet do prędkości przekraczających prędkość światła.

y

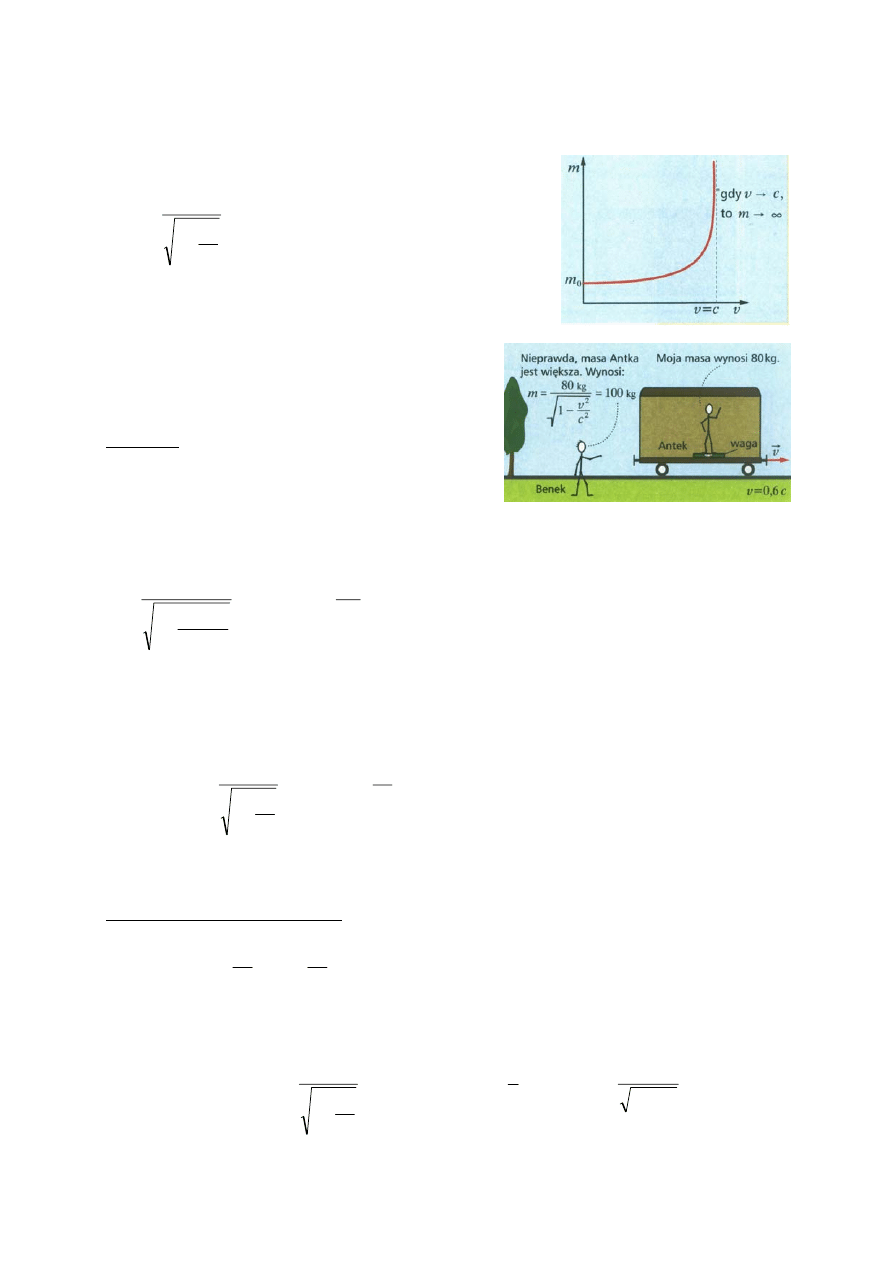
Ze wzoru Einsteina na pęd wynika, że zgodnie z teoria względności m

rośnie

prędkością układu, w którym ciało się znajduje. Tak więc wartość masy poruszającego si
obiektu można obliczyć ze wzoru:

asa ciała

wraz z

ę

0

2

2

0

1

)

(

m

m

c

v

m

v

m

⋅

=

⇒

−

=

γ

gdzie m

0

jest tzw. masą spoczynkow

masą ciała mierzoną

w układzie, w którym ciało spoczywa.

Przykłady

ą –

Oczywiście, dla v << c m = m

0

a wzory na pęd

ciała przybierają postać klasyczną.

1. Sonda, która znalazła się na orbicie
wokółsłonecznej zarejestrowała uderzenia

pochodzących z wiatru słonecznego, które poru

0,8c. Ile razy masa tych elektronów była większa od masy elektronów sondy ?

elektronów
prędkością

szały się względem słońca z

0

0

2

2

0

67

,

1

6

,

0

64

,

0

1

m

m

m

c

c

m

m

⋅

=

=

⇒

−

=

2. Z jaką co najwyżej prędkością może poruszać się pojazd kosmiczny, aby masa
podróżującej nim kosmonautki była maksymalnie o 5% większa od jej (niewielkiej zapewne)
masy spoczynkowej ?

91

,

0

1

1

05

,

1

2

2

2

2

0

0

=

−

⇒

−

=

⋅

=

c

v

c

v

m

m

m

czyli maksymalna prędkość to v = 0,3c.

Związek między masą a energią.

dt

v

dt

dv

m

dx

dt

dv

m

dx

F

dE

k

⋅

=

=

⋅

=

Pęd relatywistyczny

dp

v

dv

mv

dE

k

⋅

=

⋅

=

2

0

1

β

−

=

v

m

p

2

2

0

1

c

v

v

m

p

−

=

podstawiając

c

v

=

β

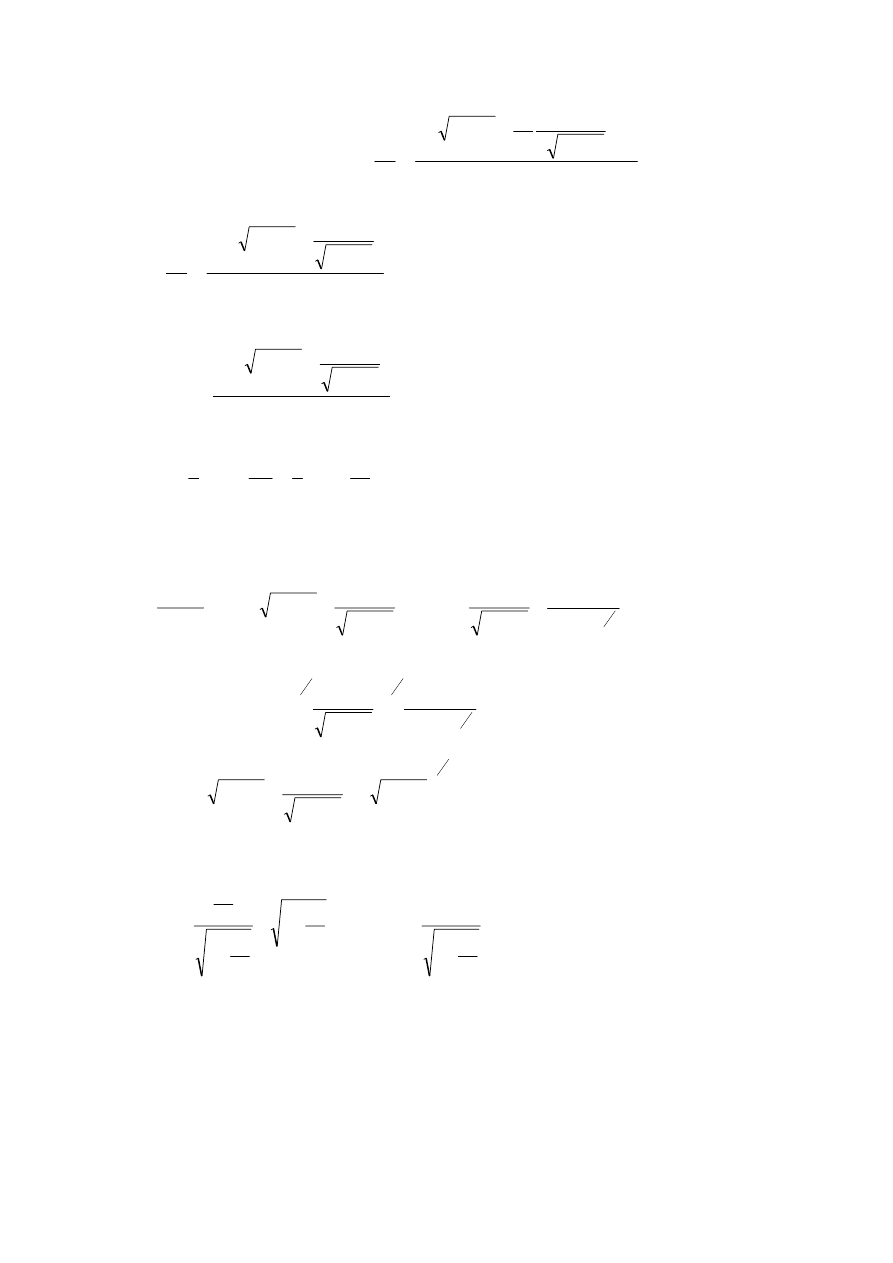
2

0

2

2

0

1

−

v

m

2

1

1

2

1

2

β

β

β

−

−

+

=

v

m

c

dv

dp

Różniczkując po v otrzymujemy

2

2

2

2

0

1

1

⎜

⎝

−

=

dp

Czyli

1

β

β

β

β

−

⎟

⎟
⎠

⎞

⎜

⎛

+

−

m

dv

A więc

dv

v

m

dE

k

⋅

−

⎟

⎟
⎠

⎞

⎜

⎜
⎝

⎛

−

+

−

=

2

2

2

2

0

1

1

1

β

β

β

β

β

β

β

d

c

dv

c

dv

d

c

v

=

⇒

=

⇒

=

1

Skoro

Podstawiając otrzymujemy:

(

)

⎟

⎟
⎠

⎞

⎜

⎜
⎝

⎛

−

+

−

⋅

=

⎟

⎟
⎠

⎞

⎜

⎜
⎝

⎛

−

+

−

⋅

−

=

2

3

2

3

2

2

0

2

2

2

2

2

0

1

1

1

1

1

β

β

β

β

β

β

β

β

β

β

β

β

d

d

c

m

d

c

m

dE

k

(

)

⎥

⎥
⎦

⎤

⎢

⎢
⎣

⎡

−

⋅

+

−

⋅

=

∫

∫

c

v

c

v

k

d

d

c

m

E

0

2

3

2

0

2

2

0

1

1

β

β

β

β

β

β

Całkując

c

v

k

0

c

m

E

0

2

2

2

2

2

1

2

1

1

⎥

⎥
⎦

⎤

⎢

⎢
⎣

⎡

−

+

−

+

−

−

=

β

β

β

β

Po podstawieniu granic całkowania otrzymujemy:

⎥

⎥

⎥

⎥

⎦

⎤

⎢

⎢

−

⎥

⎥

⎢

⎢

−

1

1

2

2

2

2

v

c

v

⎢

⎢

⎣

⎡

−

=

⎥

⎥

⎦

⎤

⎢

⎢

⎣

⎡

−

−

+

=

1

1

1

1

2

0

2

2

2

2

0

c

c

m

v

c

c

v

c

m

E

k

Ostatecznie

Każda zmiana energii związana jest ze zmianą masy -

Δ

m

2

jest to energia spoczynkowa

E = m

⋅

c – energia całkowita A więc

Δ

E =

Δ

m

⋅

c

2

{

2

0

2

2

0

2

0

2

0

)

1

(

c

m

mc

c

m

c

m

c

m

E

m

k

−

=

−

⋅

=

−

=

γ

γ

2

c

m

E

k

⋅

Δ

=

E

0

= m

0

c –

2

Przykłady

1. Wykazać, że relatywistyczna energia kinetyczna przechodzi dla v << c w klasyczną

wyrażenie

γ

w szereg:

energię kinetyczną.

Rozwijamy

...

!

2

2

3

1

1

1

1

2

1

2

2

⎟

⎞

⎜

⎛−

⎟

⎞

⎜

⎛−

⎟

⎞

⎜

⎛−

⎟⎟

⎞

⎜⎜

⎛

−

=

−

v

2

2

1

2

2

2

2

2

+

⎟⎟

⎠

⎞

⎜⎜

⎝

⎛

−

⎠

⎝

⎠

⎝

+

⎟⎟

⎠

⎞

⎜⎜

⎛

−

⎠

⎝

+

=

c

v

c

v

c

!

1

1

2

2

⎝

⎠

⎝

−

c

v

...

8

3

2

1

1

1

4

4

2

2

2

2

+

+

+

=

−

c

v

c

v

c

v

A więc energia kinetyczna:

⎟⎟

⎠

⎞

⎜⎜

⎝

⎛

−

+

+

+

=

⎥

⎥

⎢

⎢

−

1

2

2

v

⎥

⎥

⎦

⎤

⎢

⎢

⎣

⎡

−

=

1

...

8

3

2

1

1

1

4

4

2

2

2

0

2

0

c

v

c

v

c

m

c

c

m

E

k

...

8

3

2

2

4

0

2

0

+

+

=

c

v

m

v

m

E

k

co

było do udowodnienia.

e przyspieszające elektron aby uzyskał on prędkość v = c ?

E

k

= E

całk

dla c >> v

2. Ile powinno wynosić napięci

– E

0

2

0

2

c

2

2

0

1

c

m

v

c

m

=

−

=

⎥

⎥

⎥

⎥

⎦

⎤

⎢

⎢

⎢

⎢

⎣

⎡

−

−

=

⋅

1

1

1

2

2

2

0

c

v

c

m

e

U

wynika

stąd, że jeżeli v

→

c to U

→ ∝

ę na dwa, o masach spoczynkowych m

01

oraz m

02

.

W

relatywistyczne.

3. Spoczywające ciało o masie M rozpada si

yznaczyć energie kinetyczne powstałych fragmentów uwzględniając efekty

Założenie F

zew

= 0

{

2

1

.

2

E

E

Mc

a

spoczynkow

en

+

=

Gdzie E

1

i E – energie ca

2

łkowite

p

m

01

P

B

m

02

0 = p

1

+ p

2

2

2

2

0

p

c

m

c

E

więc

+

=

p

p

=

⇒

2

2

4

2

0

2

p

c

c

m

E

+

=

Skoro

2

2

2

1

2

1

p

p

−

=

4

2

02

2

4

2

01

2

1

c

m

A zatem

2

c

m

E

−

Stąd

E

−

=

(

)

2

02

2

01

4

2

2

2

1

m

m

c

E

E

−

=

−

(

)(

) (

)

(

)

M

m

m

c

E

E

Mc

E

E

E

E

E

E

2

02

2

01

2

2

1

2

2

1

2

1

2

1

−

=

−

⇐

−

=

+

−

(

)

(

)

M

m

m

c

E

Mc

E

E

2

02

2

01

2

1

2

1

2

−

=

−

−

43

42

1

Czyli

(

)

M

c

M

m

m

c

E

2

2

2

2

02

2

01

2

1

+

−

=

(

)

M

m

m

c

c

M

E

2

2

02

2

01

2

2

2

2

−

−

=

(

)

[

]

2

02

2

01

2

2

01

1

1

2

m

m

M

M

c

c

m

E

E

k

−

−

=

−

=

Ostatecznie

(

)

[

]

2

01

2

02

2

2

02

2

2

2

m

m

M

M

c

c

m

E

E

k

−

−

=

−

=

je w ciągu sekundy energię równą 6,5

⋅10

21

Wh. Przyjmując, że

promieniowanie Słońca jest niezmienne, obliczyć po jakim czasie masa Słońca zmaleje do

ołowy.

4. Słońce emitu

k

p

E =

Δ

M

⋅

c

2

oraz E = P

⋅

t

Ponieważ

2

M

M

=

Δ

Stąd

P

Mc

t

2

=

przyjmując masę Słońca M = 1,99

⋅10

30

kg

otrzymujemy: t = 1,23

⋅10

11

lat - a więc – bez obaw !!

2