Marek Jarosz
dr Andrzej Baranowski
Fizyka techniczna I rok
Wtorek 16:00 – 18:15
Wyznaczanie względnej gęstości cieczy i ciał stałych
Waga Mohr'a
Względna gęstość alkoholu
810,68 kg/m
3
Waga Jolly'ego
Ośrodek
Ciało
h
o(cm)
h
p (cm)
(górna szalka)
h
w(cm)
(dolna szalka)
Gęstość
względna
ciała
Woda destylo-
wana
Duża kostka
22,5
30,7
26,9
7,45
Średnia kostka
22,5
24,5
23,8
2,86
Mała kostka
22,5
28,0
27,5
11,0
Walec
22,5
24,6
24,3
7,0
Alkohol
Duża kostka
22,6
30,8
29,9
9,11
Średnia kostka
22,6
24,6
24,0
3,33
Mała kostka
22,6
28,0
27,6
13,5
Walec
22,6
24,6
24,4
10,0
2.Zagadnienia teoretyczne
Prawo Archimedesa – podstawowe prawo hydro- i aerostatyki określające siłę wyporu.
Nazwa prawa wywodzi się od jego odkrywcy Archimedesa z Syrakuz.
Wersja współczesna: Na ciało zanurzone w płynie (cieczy, gazie lub plazmie) działa
pionowa, skierowana ku górze siła wyporu. Wartość siły jest równa ciężarowi wypartego płynu.
Siła ta jest wypadkową wszystkich sił parcia płynu na ciało.
Stara wersja prawa: Ciało zanurzone w cieczy lub gazie traci pozornie na ciężarze tyle, ile
waży ciecz lub gaz wyparty przez to ciało.
Prawo Hooke'a – prawo mechaniki określające zależność odkształcenia od naprężenia. Głosi
ono, że odkształcenie ciała pod wpływem działającej na niego siły jest wprost proporcjonalne do tej
siły. Współczynnik między siłą a odkształceniem jest często nazywany współczynnikiem
(modułem) sprężystości.
Ta prawidłowość, sformułowana przez Roberta Hooke'a (1635-1703) w formie "ut tensio sic
vis", pozostaje prawdziwa tylko dla niezbyt dużych odkształceń, nie przekraczających tzw. granicy
Hooke'a (zwanej też granicą proporcjonalności), i tylko dla niektórych materiałów. Prawo Hooke'a
zakłada też, że odkształcenia ciała, w reakcji na działanie sił, następują w sposób natychmiastowy i
całkowicie znikają, gdy przyłożone siły przestają działać. Takie uproszczenie jest wystarczające
jedynie dla ciał o pomijalnie małej lepkości. Najprostszym przykładem zastosowania prawa
Hooke'a jest rozciąganie statyczne pręta. Względne wydłużenie takiego pręta jest wprost
proporcjonalne do siły przyłożonej do pręta, do jego długości i odwrotnie proporcjonalne do pola
przekroju poprzecznego pręta. Współczynnikiem proporcjonalności jest moduł Younga” E ”
𝐹
𝑆
= 𝐸
𝑑𝑙
𝑙
stąd
𝑑𝑙 =
𝑙 ∗ 𝐹
𝑆 ∗ 𝐸
Gdzie:
F – siła rozciągająca
S - pole przekroju
dl - wydłużenie pręta
l – długość początkowa
Zastosowanie wagi Mohra do pomiarów gęstości cieczy
Waga Mohra to aparat umożliwiający wykonywanie pomiarów gęstości cieczy za pomocą
prawa Archimedesa. Mierzoną wielkością jest siła wyporu cieczy. Waga Mohra to waga
dwuramienna. Jedna z belek podzielona jest na 10 działek o równej długości a. Na działce nr 10
znajdującej się na końcu ramienia zawieszony jest szklany nurek. Wagę ustawia się w pozycji
równowagi za pomocą śruby umieszczonej przy podstawie wagi. W zagłębieniach przy podziałce
umieszcza się specjalnie przygotowane ciężarki, o masach w stosunku 1:0,1:0,01, tzn. jeśli
najcięższy ciężarek ma masę 100 g, to pozostałe ważą 10 g i 1 g.
Zasada pomiaru wagą Mohra opiera się na prawie Archimedesa. Ciało o jakiejś objętości V,
zanurzone w cieczy o znanej gęstości, doznaje działania siły wyporu równej F
w
= Vr
w
g. Jeżeli to
samo ciało zostanie zanurzone w cieczy o nieznanej gęstości, to siła wyporu będzie równa F
x
=
Vr
x
g. Stosunek sił wyporu F
x
/F
w
jest równy stosunkowi gęstości cieczy r
x
/r
w
.
Waga Mohra umożliwia szybkie wyznaczanie wielkości F
x
/F
w
. Wagę ustawia się w
położeniu równowagi w powietrzu, a następnie zanurza nurka w naczyniu z wodą destylowaną (r
w
= 1 kg/dm
3
). Ponieważ na ciało w wodzie działa siła wyporu, waga wychyli się z położenia
równowagi. Aby z powrotem była równowaga, należy na ramieniu zawiesić ciężarki na
odpowiednich miejscach podziałki tak, aby momenty siły ciężarków zrównoważyły moment siły
wyporu. Można zapisać równanie:
F
w
×10a = Mg×l
1
a + 0,1Mg×l
2
a + 0,01Mg×l
3
a
gdzie l
1
, l
2
i l
3
to odpowiednie podziałki. Jeżeli nurka zanurzymy w innej cieczy, której gęstość
chcemy zbadać, równanie będzie miało postać
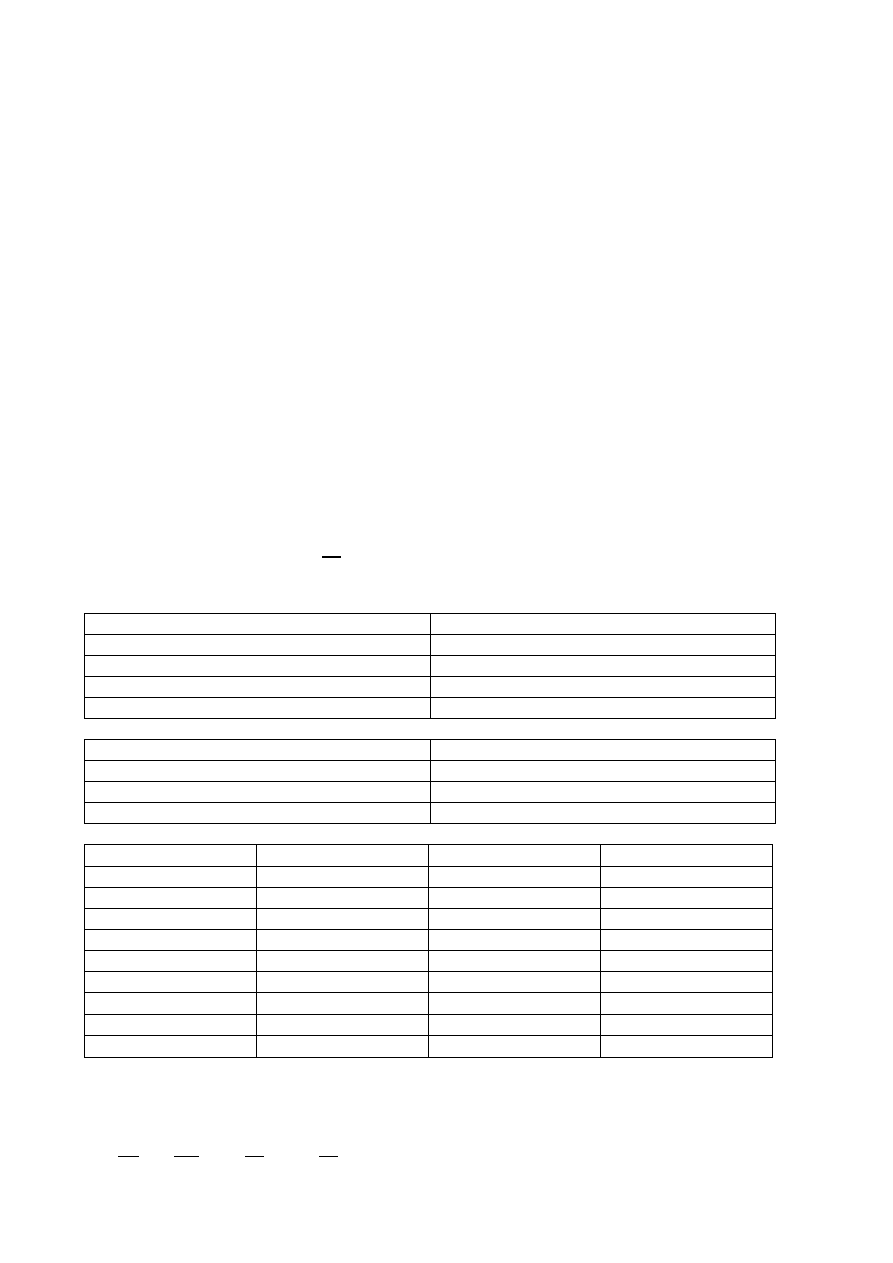
F
x
×10a = Mg×l
21
a + 0,1Mg×l
22
a + 0,01Mg×l
23
a
Stosunek sił wyporu jest równy
F
x
/F
w
= (l
21
a + l
22
a + l
23
a)/(l
1
a + l
2
a + l
3
a).
Stąd od razu odczytujemy gęstość cieczy jako
r
x
= (F
x
/F
w
) r
w
Waga Jolly'ego bardzo czuła waga dźwigniowa zaopatrzona w drugą parę szalek
zawieszonych na długich drutach. Za pomocą takiej wagi niemiecki fizyk von Jolly wyznaczył stałą
grawitacji z dokładnością większą niż Cavendish za pomocą wagi skręceń. Jolly na jednej z
dodatkowych szalek dolnych umieścił naczynie kuliste z rtęcią o masie m
1
= 5 kg. Na przeciwległej
szalce górnej umieścił odważniki równoważące tę masę. Bezpośrednio pod rtęcią ustawiona została
kula ołowiana o średnicy 1 m i masie m
2
= 5800 kg. Wyznaczenie siły oddziaływania F między
kulami z rtęci i ołowiu oraz pomiar odległości między ich środkami r pozwoliły wyznaczyć stałą
grawitacji k z zależności F = k · m
1
· m
2
· (1/r
2
).
3.Opis przeprowadzenia doświadczenia
Doświadczenie dla wagi Mohr’a
Zrównoważyłem wagę wraz z nurkiem za pomocą pionu oraz odpowiednich pokręteł przy ramieniu
wagi. Następnie wlałem ciecz wzorcową (woda destylowana) do menzurki i zanurzyłem nurka w
całości w cieczy. Zrównoważyłem wagę za pomocą koników oraz zapisałem położenie ciężarków.
Następnie wylałem ciecz z menzurki, osuszyłem nurka oraz menzurkę. Wykonałem następny
pomiar dla alkoholu na podobnych jak wcześniej zasadach.
Umieszczenie ciężarków na wadze Mohr’a dla wody: 1-1A, 3-0.1A, 1A.
Umieszczenie ciężarków na wadze Mohr’a dla alkoholu: 3-0.1A, 5-0.01A, 8-1A
Tablicowa gęstość wody
1000
𝑘𝑔
𝑚
3
Tabele pomiarów dla wagi Jolly’ego
Woda
h
o
=22.5cm =0.2 cm
Górna szalka
Dolna szalka
Duża kostka 30.7 cm
29.6 cm
Średnia kostka 24.5 cm
23.8
Mała kostka 28.0 cm
27.5
Walec 24.6
24.3
Alkohol
h
o
=22.6 cm =0.2 cm
Duża kostka 30.8 cm
29.8 cm
Średnia kostka 24.6 cm
24 cm
Mała kostka 28.0 cm
27.6 cm
Walec 24.6 cm
24.4 cm
Prawo Hooke h
o
=22.9cm =0.2 cm
1g
23.1 cm
10g
25.7 cm
2g
23.4 cm
9g
25.5 cm
3g
23.7 cm
8g
25.2 cm
4g
23.9 cm
7g
24.8 cm
5g
24.3 cm
6g
24.6 cm
6g
24.5 cm
5g
24.2 cm
7g
24.9 cm
4g
23.8 cm
8g
25.2 cm
3g
23.6 cm
9g
25.5 cm
2g
23.3 cm
10g
25.7 cm
1g
23.0 cm
4.Obliczenia
Waga Mohr'a
Woda destylowana: m = 1A*1+0,1A*3+1A*9=10,3=m
w
Alkohol: m = 1A*8+0,1A*3+0,01A*5=8,35=m
a
d
a
=
𝑚
𝑎
𝑚
𝑤
𝑑
𝑤
=
8,35
10,3
1000
𝑘𝑔
𝑚
3
=810,6
𝑘𝑔
𝑚3
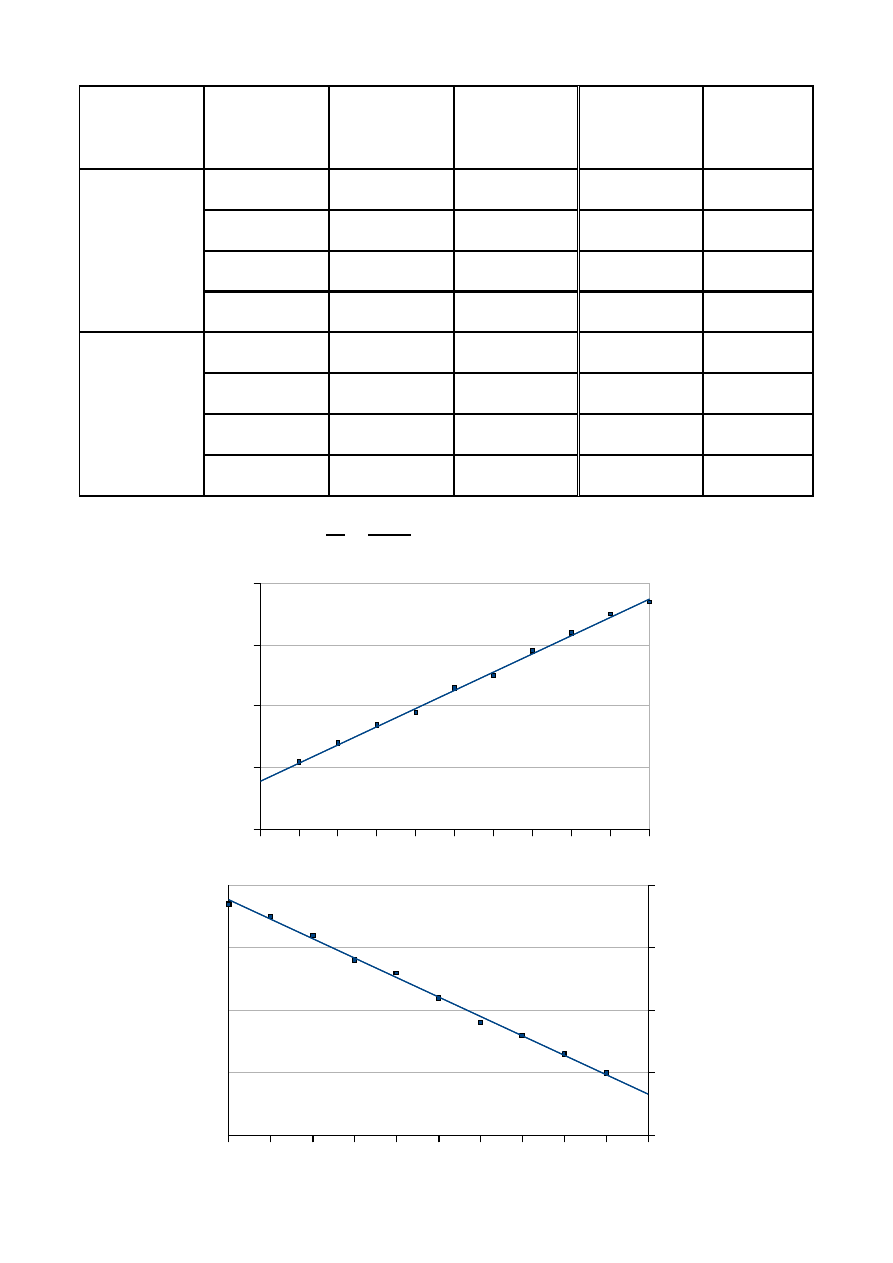
Ośrodek
Ciało
h
o(cm)
h
p (cm)
(górna szalka)
h
w(cm)
(dolna szalka)
Gęstość
względna
ciała
Woda destylo-
wana
Duża kostka
22,5
30,7
26,9
7,45
Średnia kostka
22,5
24,5
23,8
2,86
Mała kostka
22,5
28,0
27,5
11,0
Walec
22,5
24,6
24,3
7,0
Alkohol
Duża kostka
22,6
30,8
29,9
9,11
Średnia kostka
22,6
24,6
24,0
3,33
Mała kostka
22,6
28,0
27,6
13,5
Walec
22,6
24,6
24,4
10,0
Wzór na gęstość względną ciała:
𝑑
𝑐
𝑑
𝑜ś
=
𝑝
−
0
𝑝
−
𝑤
Prawo Hooke'a ( rosnące obciążenie )
Prawo Hooke'a ( malejące obciążenie )
0
1
2
3
4
5
6
7
8
9
10
22
23
24
25
26
f(x) = 0,3x + 22,79
0
1
2
3
4
5
6
7
8
9
10
22
23
24
25
26
f(x) = 0,31x + 22,67
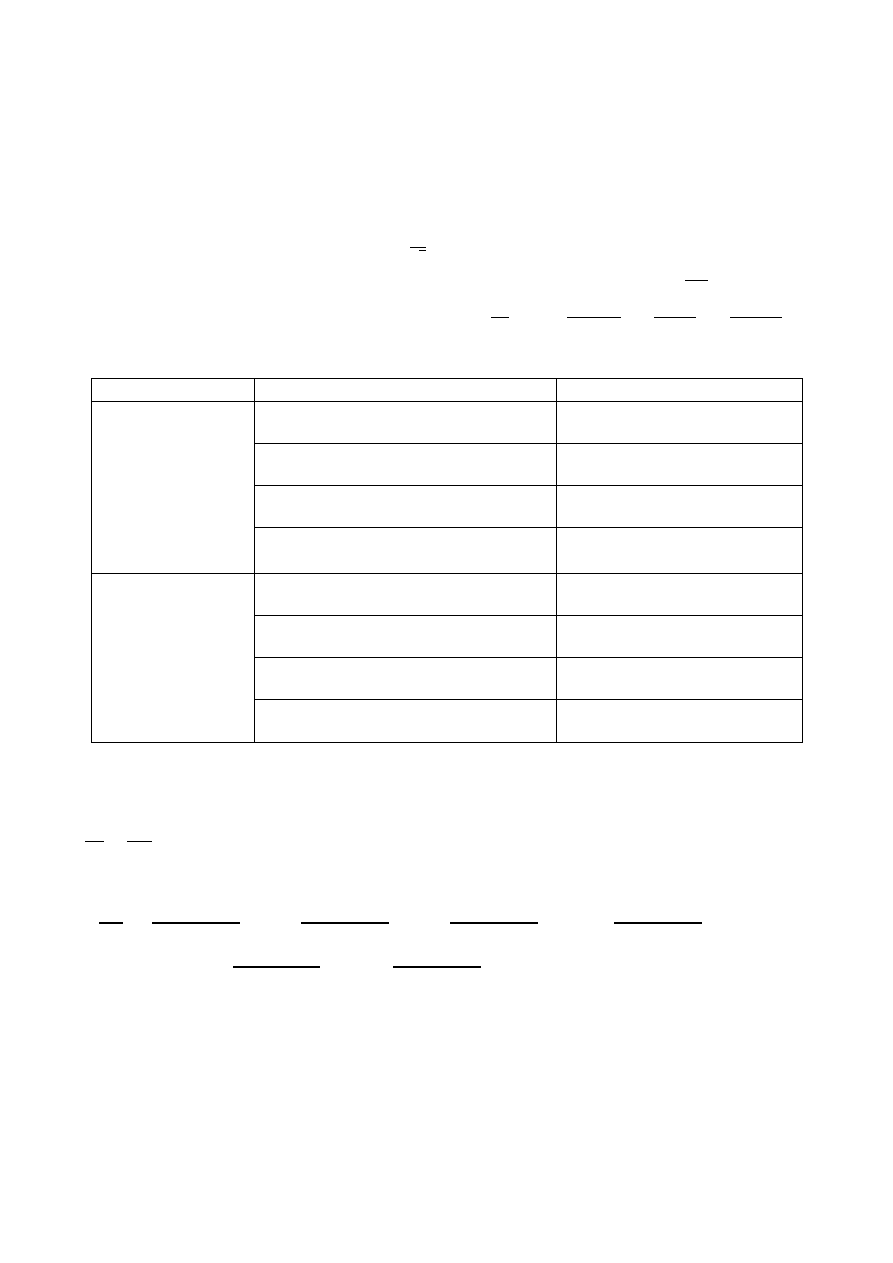
Średnia wartość współczynnika sprężystości dla wagi Jolly'ego wynosi k=0,305
5.Niepewność pomiarowa
Rachunek niepewności obliczonej wartości gęstości względnej opieram na niepewności
maksymalnej. Najpierw obliczam niepewność wszystkich mierzonych wartości
∆𝑥
𝑘
a następnie
niepewności maksymalne ∆
𝑑
𝑎
/𝑑
𝑤
- gęstość alkoholu, ∆
𝑑
𝑐
/𝑑
𝑤
i ∆𝑑
𝑐
/𝑑
𝑎
- ciała stałe w wodzie i
alkoholu korzystając z prawa przenoszenia niepewności maksymalnych.
Pomiar był wykonywany z dokładnością ∆h = 0,1cm, więc wynika z tego niepewność wynosząca
𝑢 =
∆
3
= 0,057𝑐𝑚
Rachunek niepewności dla
𝑑
𝑐
/𝑑
𝑤
i dla
𝑑
𝑐
/𝑑
𝑎
wyraża się wzorem
∆𝑦
𝜕𝑓
𝜕𝑥
𝑘
∗ ∆𝑥
𝑘
𝐾
𝑘=1
dla wody oraz alkoholu sytuacja wygląda następująco
∆
𝑑
𝑐
𝑑
𝑤
= ∆(
𝑜
−h
w
𝑝
−
𝑤
+
−1
𝑝
−
𝑤
+
𝑝
−
𝑜
(
𝑝
−
𝑤 )
)
Ośrodek
Ciało
Niepewność pomiarowa
Woda destylowana
Duża kostka
1,35
Średnia kostka
0,81
Mała kostka
4,4
Walec
4,6
Alkohol
Duża kostka
2,02
Średnia kostka
1,11
Mała kostka
6,75
Walec
10,00
Waga Mohra
Wiemy, że
m
w
= 1A + 3·0,1A + 9A = 10,3 więc a`=1+9=10, b`=3, c`=0
m
a
= 3·0,1A + 5·0,01A + 8A = 8,35 więc a`=8, b`=3, c`=5
𝑑𝑎
𝑑𝑤
=
8,35
10,3
= 0,81
∆𝑎 = ∆𝑎` = 1, ∆𝑏 = ∆𝑏` = 0,1, ∆𝑐 = ∆𝑐` = 0,01
Korzystając z poprzedniego wzoru
∆
𝑑𝑎
𝑑𝑤
=
𝑎 + 𝑏 + 𝑐
𝑎 + 𝑏 + 𝑐
∆𝑎` +
𝑎 + 𝑏 + 𝑐
𝑎 + 𝑏 + 𝑐
∆𝑏` +
𝑎 + 𝑏 + 𝑐
𝑎 + 𝑏 + 𝑐
∆𝑐` + −
𝑎` + 𝑏` + 𝑐`
𝑎 + 𝑏 + 𝑐
∆𝑎
+ −
𝑎` + 𝑏` + 𝑐`
𝑎 + 𝑏 + 𝑐
∆𝑏 + −
𝑎` + 𝑏` + 𝑐`
𝑎 + 𝑏 + 𝑐
∆𝑐 = 0,19
6.Wnioski
Obliczenia dla wagi Mohr'a są zbliżone do wartości tablicowych, brak zbieżności
najprawdopodobniej spowodowany jest niedokładnym odczytem danych, oraz zbyt dużym
zaokrąglaniem wyników. Rozbieżność dla pomiarów dla wagi Jolly'ego wynikać może ze zbyt
dużego zaokrąglenia wyników jaki i z niedokładności odczytu wskazania wagi.