Ocena Efektywności Projektów Inwestycyjnych

prof. UG, dr hab. Lucjan Czechowski

I.

Wprowadzenie do rachunku efektywności
projektów inwestycyjnych

1.

Pojęcie i zakres rachunku efektywności
inwestycji.

2.

Zasady dokonywania oceny efektywności
przedsięwzięć inwestycyjnych.

3.

Zakres stosowania metod oceny efektywności
przedsięwzięć inwestycyjnych.

II.

Proste (statyczne) metody oceny
przedsięwzięć inwestycyjnych

1.

Wprowadzenie.

2.

Przegląd statycznych metod oceny
efektywności inwestycji:



metoda prostego okresu zwrotu,



metoda porównania kosztów,



metoda porównania zysków,



metoda porównania rentowności.

III.

Dynamiczne metody oceny przedsięwzięć
inwestycyjnych

1.

Metoda wartości bieżącej netto (NPV).

2.

Metoda wewnętrznej stopy zwrotu (IRR).

3.

Zmodyfikowana wewnętrzna stopa zwrotu
(MIRR).

IV.

Ocena opłacalności inwestycji
infrastrukturalnych

1.

Wykorzystanie metody koszt

– korzyść w

ocenie inwestycji infrastrukturalnych.

2.

Ocena opłacalności projektów inwestycyjnych
z punktu widzenia oddziaływania na
środowisko naturalne.

V.

Ocena opłacalności bezpośrednich
inwestycji zagranicznych

1.

Główne elementy korzyści motywujące
inwestora zagranicznego.

2.

Korzyści kraju goszczącego z tytułu
zagranicznych inwestycji bezpośrednich.

1.

W. Behrens, P.M. Hawranek,

Poradnik przygotowania przemysłowych

studiów feasibility, UNIDO Warszawa 1993, 1997.

2.

L. Czechowski, K. Dziworska, T. Gostkowska-

Drzewicka, A. Górczyńska,

Projekty inwestycyjne

– finansowanie, metody i procedury oceny, ODDK,

Gdańsk 1999.

3.

K. Dziworska,

Decyzje inwestycyjne przedsiębiorstw, Uniwersytet

Gdański, Gdańsk 2000.

4.

Inwestycje i nieruchomości. Elementy teorii i praktyki, pod red. M.
Rymarzak, Fundacja Rozwoju Uniwersytetu Gdańskiego, Gdańsk 2009.

5.

A. Manikowski, Z. Tarapata,

Ocena projektów gospodarczych. Modele i

metody. Cześć 1, Difin, Warszawa 2001.

6.

R. Machała. Praktyczne zarządzanie finansami firm, Wydawnictwo
Naukowe PWN, Warszawa 2001.

1.

Pojęcie i zakres rachunku efektywności inwestycji.



Rachunek efektywności przedsięwzięć inwestycyjnych obejmuje:

-

przygotowanie danych i sporządzenie oceny opłacalności przedsięwzięć

inwestycyjnych,

-

analizę poziomu ryzyka związanego z ich realizacją,

-

podjęcie na podstawie wymienionych wyżej danych decyzji

inwestycyjnej.



W literaturze fachowej w odniesieniu do rachunku efektywności
przedsięwzięć inwestycyjnych stosuje się zamiennie takie pojęcia jak:

-

metody oceny efektywności (opłacalności) przedsięwzięć

inwestycyjnych,

- procedury decyzyjne rachunku inwestycyjnego,

-

techniki oceny przedsięwzięć inwestycyjnych,

-

modele w rachunku efektywności inwestycji,



W zależności od przyjętych kryteriów klasyfikacyjnych wyróżnia się kilka
rodzajów rachunku efektywności przedsięwzięć inwestycyjnych, a
mianowicie:

a)

z punktu widzenia

momentu sporządzania (a zarazem pełnionej

funkcji) rachunek efektywności inwestycji może mieć charakter:

- prospektywny (ex ante)

– przeprowadzany przed rozpoczęciem

realizacji przedsięwzięcia i oparty na danych prognostycznych;

- retrospektywny (ex post)

– przeprowadzany podczas realizacji

przedsięwzięcia inwestycyjnego lub po jego zakończeniu (na etapie
kontroli)

b)

z punktu widzenia celu

przeprowadzania rachunku efektywności

można wyróżnić:

-

rachunek bezwzględny (absolutny) – umożliwia podjęcie decyzji

inwestycyjnej dotyczącej pojedynczych przedsięwzięć inwestycyjnych
według zasady: „przyjąć – odrzucić?”,

-

rachunek względny (relatywny, porównawczy) – dokonanie wyboru

najbardziej efektywnego przedsięwzięcia inwestycyjnego spośród kilku
z nich (wybór wariantu optymalnego) wedle zasady: „który lepszy?”

c)

ze względu na sposób przeprowadzania można wyróżnić:

-

rachunek cząstkowy – oparty na zestawie wskaźników cząstkowych

dotyczących różnych aspektów przedsięwzięcia inwestycyjnego, takich
jak:



pracochłonność,



kapitałochłonność,



materiałochłonność,



rentowność,



koszty jednostkowe, itp.

- rachunek syntetyczny

(jednowskaźnikowy) – zapewniający ocenę

efektywności przedsięwzięcia inwestycyjnego w postaci jednego
syntetycznego wskaźnika, uwzględniającego podstawowe mierzalne
elementy kształtujące poziom efektywności (prosta stopa zwrotu, wartość
bieżąca netto NPV, wewnętrzna stopa zwrotu IRR, itp.).



W rozwoju rachunku efektywności zaznacza się tendencja do jego
upraszczania, co wraz z postulatem jednoznaczności skłania do
stosowania w praktyce gospodarczej rachunku syntetycznego.



Aby rachunek efektywności przedsięwzięć inwestycyjnych można było

uznać za skuteczne narzędzie oceny, musi on spełniać następujące
warunki, a mianowicie:

-

opierać się na odpowiednich, zweryfikowanych założeniach

teoretycznych, bez istnienia sprzeczności wewnętrznej;

-

właściwie odzwierciedlać rzeczywiste efekty ekonomiczne związane z

realizacją inwestycji;

-

ujmować wszystkie nakłady inwestycyjne i korzyści w całym okresie

realizacji i funkcjonowania inwestycji;

-

być uniwersalny (możliwość stosowania do oceny wszystkich rodzajów

przedsięwzięć inwestycyjnych);

-

umożliwić zarówno bezwzględną, jak i względną ocenę efektywności

inwestycji.



Charakteryzując rachunek efektywności inwestycji warto porównać go z

innymi rachunkami ekonomicznymi przeprowadzanymi w przedsiębiorstwie

np. z rachunkiem kosztów (patrz tabela nr 1).

Kryterium różnicujące

Rachunek kosztów

Rachunek

efektywności

Częstotliwość

przeprowadzania

regularnie w

określonych odstępach

czasu

w miarę potrzeby (bez

regularności czasowej)

Okres planowania

jednookresowy

wielookresowy

Obiekt, którego

dotyczy

przedsiębiorstwo jako

całość

wyodrębnione

przedsięwzięcia

inwestycyjne

Cel przeprowadzania

krótkoterminowa

kontrola i zarządzanie

przedsiębiorstwem

podejmowanie decyzji

inwestycyjnych

Elementy oceny

koszty i przychody

nakłady i korzyści



Dane zawarte w tabeli nr 1 pozwalają na wysunięcie wniosku, że rachunek
efektywności przedsięwzięć inwestycyjnych jest bardziej złożony i ma
większe znaczenie dla przyszłej sytuacji ekonomicznej przedsiębiorstwa niż
rachunek kosztów.

2.

Zasady dokonywania oceny efektywności przedsięwzięć
inwestycyjnych



Teoretyczna poprawność oceny efektywności przedsięwzięć inwestycyjnych
wymaga spełnienia pewnych wymogów formalnych, które przyjmują postać
określonych zasad jej przeprowadzania.



W literaturze ekonomicznej poświęconej inwestycjom wymienia się
najczęściej siedem podstawowych zasad poprawności rachunku
efektywności inwestycji, a mianowicie:

a)

Zasada przyrostowości dotyczy postępującego (przyrostowego)
ujmowania finansowych elementów uwzględnianych w ocenie efektywności
i oznacza konieczność ujmowania przyrostów nakładów i efektów, które
następują w związku z realizacją danego przedsięwzięcia inwestycyjnego,
nie zaś ich wartości nominalnych.

b)

Zasada uniwersalności postuluje stosowanie takich metod (formuł)
oceny efektywności, które bez zmian lub przy niewielkich tylko
modyfikacjach mogłyby służyć do oceny opłacalności różnych
przedsięwzięć ( na przykład odtworzeniowych, modernizacyjnych i
rozwojowych, typowych lub nietypowych), a także pozwalałyby
podejmować decyzje dotyczące zarówno pojedynczych przedsięwzięć
inwestycyjnych, jak i inwestycji wzajemnie się wykluczających.

c)

Zasada porównywalności dotyczy możliwości bezpośredniego
porównywania – przeprowadzonego w aspekcie przedmiotowym i
czasowym

– nakładów i efektów związanych z realizacją ocenianych

przedsięwzięć inwestycyjnych. Warunek korelacji przedmiotowej
oznacza konieczność przestrzegania zależności przyczynowo –
skutkowej między nakładami a efektami (w ocenie efektywności mogą
być uwzględnione tylko te efekty, które są rezultatem poniesionych
nakładów, i tylko te nakłady, które są niezbędne do uzyskania założonych
efektów). Warunek korelacji czasowej wiąże się z tym, że zarówno
nakłady, jak i efekty występują w różnych, często odległych okresach , a
ponadto są rozłożone w czasie, co powoduje brak możliwości ich
prostego porównywania.

d)

Zasada kompleksowości polega na uwzględnieniu wszystkich

nakładów i efektów, które powstają w jakimś związku z ocenianym

przedsięwzięciem inwestycyjnym.

e)

Zasada jednoznaczności wyników oceny efektywności oznacza

ustalenie takiej procedury jej prowadzenia, aby uzyskane za pomocą

danej metody rezultaty były takie same niezależnie od tego, kto

sporządzał daną ocenę.

f)

Zasada obiektywności dotyczy głównie danych liczbowych

uwzględnianych w ocenie, które muszą być obiektywne, a nie
subiektywne.

g)

Zasada spójności zakłada konsekwentne traktowanie w ocenie

efektywności takich elementów, jak stopa dyskontowa, inflacja i rodzaj

waluty, w jakiej jest dokonywana ocena efektywności.

3.

Zakres stosowania metod oceny efektywności przedsięwzięć
inwestycyjnych



Wśród czynników i zjawisk ekonomicznych oraz postaw i przekonań,
które w ciągu ostatnich kilkudziesięciu lat ukształtowały współczesne
metody oceny efektywności przedsięwzięć inwestycyjnych, należy
wymienić:

a)

wzrost znaczenia procesów inflacyjnych i konieczność ich uwzględniania
w procesie oceny efektywności przedsięwzięć inwestycyjnych,

b)

wzrost poziomu niepewności i ryzyka prowadzenia działalności
gospodarczej (odrzucenie jednego z podstawowych założeń klasycznej
formuły oceny efektywności, które uwzględniało deterministyczny, nie zaś
probabilistyczny charakter procesów inwestycyjnych),

c)

Konieczność uwzględniania dominującego znaczenia skutków
zewnętrznych przedsięwzięć inwestycyjnych dla gospodarki (na przykład
w zakresie stanu środowiska naturalnego) i starania o ich ujęcie w
metodyce oceny efektywności,

d)

internacjonalizację procesów inwestycyjnych i konieczność
uwzględniania jej skutków w ocenie poszczególnych przedsięwzięć
inwestycyjnych,

e)

kompleksowe programy inwestycyjne przygotowane przez poszczególne
podmioty gospodarcze (przedsiębiorstwa, rząd, władze lokalne lub
instytucje międzynarodowe) i potrzebę syntetycznej oceny ich
efektywności,

f)

zmianę i ciągłe różnicowanie form inwestowania oraz konieczność
dostosowania algorytmów i formuł oceny efektywności (wzrost liczby
przedsięwzięć nietypowych),

g)

rozwój teoretycznych podstaw oceny efektywności i techniki
obliczeniowej.



Obecnie można wyodrębnić dwa główne nurty poszukiwań i doskonalenia
metod prowadzenia oceny efektywności przedsięwzięć inwestycyjnych:

a)

pierwszy nurt

przejawia się opracowywaniem teoretycznych założeń dla

coraz bardziej skomplikowanych formuł i algorytmów oceny efektywności
inwestycji, uwzględniających coraz większą liczbę zmiennych i coraz
bardziej złożone warunki gospodarowania;

b)

z kolei drugi nurt

skupia się na modyfikowaniu oraz wskazaniu zalet i wad

istniejących już metod oceny efektywności, a także określaniu możliwości
ich stosowania w praktyce gospodarczej.



Rosnący stopień skomplikowania postulowanych przez teorię złożonych
metod efektywności przedsięwzięć inwestycyjnych nie zawsze zachęca
praktyków do ich stosowania.



Podstawowym warunkiem ich użyteczności jest bowiem posiadanie
odpowiedniej liczby pewnych, zweryfikowanych informacji dotyczących
stosunkowo dużej ilości zjawisk i procesów zarówno wewnętrznych, jak i
zewnętrznych.



Brak czy duża niepewność takich danych powodowały, że mimo formalnie
dużej precyzji takie metody oceny inwestycji nie przynosiły – jak dowodziła
praktyka

– lepszych wyników niż mniej wysublimowane kryteria oceny,

jakimi są np. proste metody oceny projektów inwestycyjnych.



Reasumując można powiedzieć, iż ocena efektywności inwestycji jest próbą
poszukiwania odpowiedzi na pytanie, czy przyszłe korzyści finansowe
przewyższą lub co najmniej zrównoważą ponoszone wydatki.



Pytanie to może być uzupełnione lub modyfikowane na kilka sposobów, a
mianowicie:



w jakim czasie nastąpi zrównoważenie wydatków przez korzyści?



jaka będzie łączna kwota nadwyżki korzyści nad nakładami?



jaka będzie średnioroczna stopa zwrotu wydatków przez korzyści?

1.

Wprowadzenie



We współczesnej gospodarce rynkowej dużego znaczenia w zarządzaniu

przedsiębiorstwem nabiera konieczność poszukiwania najefektywniejszych

sposobów wykorzystania kapitału.



Warunkiem opłacalnej jego alokacji jest posługiwanie się rachunkiem

inwestycji, na który składają się poprawne metody oceniające ich

racjonalność.



W teorii i praktyce inwestycyjnej wyróżnia się szereg różnych metod
(technik) rachunku inwestycji.



Najbardziej znany jest ich podział ze względu na wpływ czynnika czasu.



Kryterium to pozwala wyróżnić następujące grupy metod oceny inwestycji,
a mianowicie:

a)

metody statyczne (proste, uproszczone, jednoroczne, tradycyjne,
niedyskontowe)

b)

metody dynamiczne

(dyskontowe, złożone, rozwinięte).



Metody statyczne

– nieuwzględniające zmienności wartości pieniądza w

czasie i oparte na zysku jako miary korzyści netto projektu (np. 1000 zł

wydane obecnie na projekt równe będzie 1000 zł efektów z projektu za

kilka czy kilkanaście lat).



W metodach tych wykorzystywane są przeciętne wielkości rocznych

wydatków i wpływów liczone dla arbitralnie wybranego okresu

działalności projektu inwestycyjnego lub suma spodziewanych nakładów

i efektów.



W ocenie opłacalności przedsięwzięć inwestycyjnych metody statyczne

są stosowane:

◦

we wstępnych fazach procesu przygotowania projektów inwestycyjnych,

gdy nie ma jeszcze szczegółowej i rozbudowanej informacji dotyczącej

danego przedsięwzięcia (projekt jest mało zaawansowany),

◦

w wypadku projektów o relatywnie krótkim ekonomicznie cyklu życia, gdy

różne rozłożenie w czasie nakładów i efektów nie wpływa w decydujący

sposób na ocenę opłacalności przedsięwzięcia,

◦

w wypadku projektów o niewielkiej skali (wartości), gdy zarówno nakłady,
jak i efekty są niewielkie i nie naruszają pozycji rynkowej oraz sytuacji
ekonomiczno

– finansowej firmy, realizującej dane przedsięwzięcie

inwestycyjne,

◦

do wstępnej selekcji wielu projektów inwestycyjnych.



Za stosowaniem metod statycznych w ocenie opłacalności inwestycji
przemawiają następujące okoliczności:

◦

nieskomplikowany charakter i prostota obliczeń,

◦

komunikatywność i jasność stosowanych formuł rachunkowych,

◦

łatwa interpretacja uzyskanych za ich pomocą wyników,

◦

nie wymagają głębokiej znajomości teorii ekonomicznych, co dla
szerokiego grona praktyków o wykształceniu technicznym ma
niebagatelne znaczenie (akceptacja i zrozumienie metod bardziej
złożonych nie są powszechne w gospodarce).



Zasadniczym mankamentem

metod statycznych jest nieuwzględnianie

zmienności czasowego rozkładu nakładów i efektów (nieuwzględnianie

zmiennej wartości pieniądza w czasie), co skutkuje nierównocennością

wydatków i wpływów w różnym czasie.



Z kolei metody dynamiczne

uwzględniają w sposób całościowy zmienność

wartości pieniądza w czasie, biorąc pod uwagę cały okres życia projektu.



Wykorzystanie w nich rachunku dyskontowego pozwala na wyrażenie

wszystkich przyszłych wydatków i wpływów w dzisiejszej wartości pieniądza

(najczęściej jest to tzw. t=0 czyli czas oddania inwestycji do eksploatacji).



Dochód (korzyść) netto ujmowany jest w nich w kategorii przepływu

pieniężnego (strumieni pieniężnych) netto, a nie dochodu występującego jako
wynik finansowy (bilansowy).



Strumień dochodów pieniężnych netto (NCF-net cash flows) tworzą kwoty

pieniężne, będące do swobodnej dyspozycji właściciela w poszczególnych

latach analizowanego okresu życia projektu, czyli zysk netto i amortyzacja.



W publikacjach dotyczących rachunku efektywności inwestycji wymieniane

są także słabe strony metod dyskontowych. Zarzuca się im m.in.:



zbyt wąską perspektywę spojrzenia na opłacalność inwestycji, wynikającą z

ograniczenia oceny efektów inwestycyjnych do części przedsiębiorstwa (np.

oddziału), którego bezpośrednio dotyczy dane przedsięwzięcie
inwestycyjne,



wyłączenie oceny korzyści niefinansowych, zwłaszcza w wypadku

projektów sektora publicznego, czy przedsięwzięć inwestycyjnych o
charakterze niematerialnym i prawnym,



podatność tych metod na błędy metodologiczne, co wynika z konieczności

uwzględniania licznych założeń oraz zasad dotyczących np. szacowania

korzyści netto i stopy dyskontowej (za najczęściej występujący mankament

uznaje się nieprzestrzeganie zasady spójności),



ich poprawne stosowanie wymaga dosyć gruntownej wiedzy z zakresu

ekonomii, marketingu, bankowości, matematyki finansowej, rynków

kapitałowych czy badań operacyjnych.



W praktyce gospodarczej metody statyczne i dynamiczne są stosowane do
tych samych przedsięwzięć, najpierw metody statyczne do wstępnej
oceny i selekcji ogólnie zarysowanych wariantów, a następnie metody
dynamiczne

do oceny ostatecznej i selekcji wariantów, które przeszły

wstępną selekcję i zostały już dokładniej zaprojektowane.



Wstępna ocena i selekcja są potrzebne po to, aby nie ponosić wydatków na
projektowanie zbyt wielu wariantów przedsięwzięć inwestycyjnych.

2.

Przegląd statycznych metod oceny efektywności inwestycji



Do najbardziej popularnych w praktyce gospodarczej statycznych metod
oceny przedsięwzięć inwestycyjnych należą:

1)

metoda prostego okresu zwrotu,

2)

metoda porównania kosztów

3)

metoda porównania zysków,

4)

metoda porównania rentowności.

Ad 1) Metoda prostego okresu zwrotu nazywana jest w j. ang. okresem

spłaty z inwestycji (payback period – PP)



Szacuje ona długość okresu, jaki jest potrzebny, aby nakłady inwestycyjne
poniesione na realizację danego przedsięwzięcia inwestycyjnego zostały w
pełni pokryte (zrównoważone) korzyściami netto generowanymi przez to
przedsięwzięcie.



Ogólną postać algorytmu tej metody można przedstawić za pomocą
następującej formuły:

n = 1/KN

gdzie:

I

– zaangażowany kapitał (nakłady inwestycyjne podlegające zwrotowi),

KN

– korzyści netto, z których mają się zwrócić nakłady inwestycyjne.



W literaturze poświęconej rachunkowi efektywności inwestycji występuje
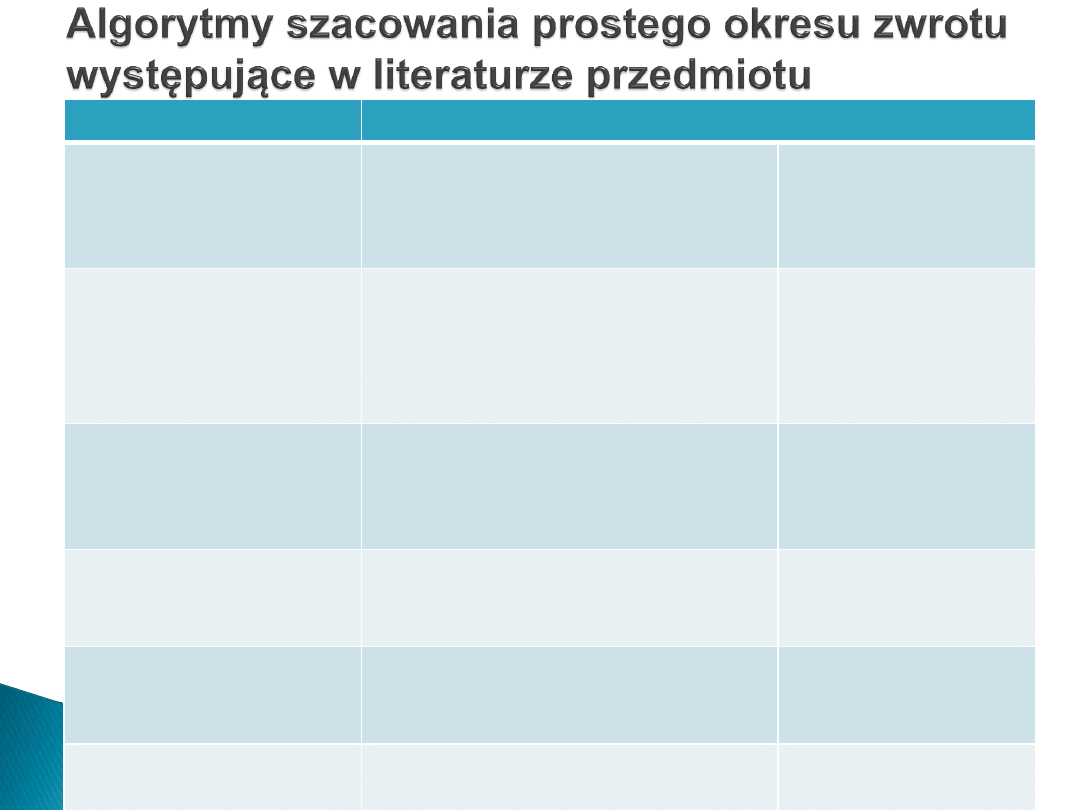
wiele wariantów metody prostego okresu zwrotu, co obrazuje poniższa
tabela.

Autor

Algorytm

korzyści netto, z

których mają się

zwrócić nakłady

inwestycyjne (KN)

nakłady inwestycyjne

podlegające zwrotowi (I)

A. Rutkowski (2000);
Rachunkowość zarządcza
(1999); M. Poszwa (1999); V.
Jog, C. Suszyński (2000);
Budżetowanie kapitałów
(2000); M. Siudak (1999); R.
Machała (2001); E.F. Brigham,
L.C. Gapenski (2000)

wpływy pieniężne netto

poniesione wydatki
inwestycyjne (rozumiane
jako ujemny strumień
pieniężny)

W. Flak (2000); M. Sierpińska,
T. Jachna (1997)

zysk netto + amortyzacja;
zysk netto + amortyzacja
+ odsetki

nakłady inwestycyjne

P. Szczepankowski

zysk operacyjny; zysk
netto; zysk netto +
amortyzacja; zysk netto +
amortyzacja +/- zmiany w
kapitale obrotowym

nakłady inwestycyjne

Autor

Algorytm

korzyści netto, z których mają się

zwrócić nakłady inwestycyjne

(KN)

nakłady

inwestycyjne

podlegające

zwrotowi (I)

H. Johnson (2000); R.A.
Brealey, S.C. Myers
(1999); S.A. Ross, R.W.
Westerfield, B.D. Jordan
(1999)

dodatnie

przepływy pieniężne netto

(operacyjne, finansowe,
inwestycyjne)

nakłady inwestycyjne

S. Wrzosek

roczny zysk netto; zysk netto +
amortyzacja; (drugi algorytm jest
uzasadniony, gdy nie przewiduje się
reinwestowania amortyzacji)

nakłady inwestycyjne

Projekty inwestycyjne
(1996)

zysk netto + amortyzacja

nakłady inwestycyjne
– księgowa wartość
rezydualna

Z. Leszczyński, A.
Skowronek-Mielczarek
(2000)

zysk netto + amortyzacja; zysk netto;
zysk netto + odsetki od kredytów

nakłady inwestycyjne

S.

Ryżewska (1999)

zysk netto + amortyzacja + odsetki
od kredytów

nakłady inwestycyjne



Brak zgodności w sformułowaniu algorytmu w metodzie prostego okresu
zwrotu, szczególnie w odniesieniu do korzyści netto, wynika ze sposobu
finansowania nakładów inwestycyjnych, które mogą być bowiem
finansowane z kapitału własnego (korzyść netto = zysk netto i amortyzacja),
jak i własnego oraz obcego (korzyść netto + zysk operacyjny lub jako suma
zysku netto, amortyzacji i odsetek).



Faktycznie obliczony okres zwrotu danego przedsięwzięcia inwestycyjnego
(n) jest porównywany z wartością progową, nazywaną także granicznym
okresem zwrotu (n

gr

).



Podjęcie decyzji inwestycyjnej na podstawie tego kryterium (okresu zwrotu)
wymaga zatem wcześniejszego ustalenia krytycznego (najdłuższego,
dopuszczalnego) okresu zwrotu (n

gr

).



Sposób wyznaczania wartości progowej (n

gr

) nie jest jednoznacznie

określony. Korzysta się tu z ogólnie uznawanych zasad, jak np.:



w wypadku przedsięwzięć finansowanych kredytem może to być
okres spłaty kredytu,



dla przedsięwzięć o wysokim poziomie ryzyka wymagane są
relatywnie krótsze okresy zwrotu,



w wypadku projektów wzajemnie wykluczających się – gdy wybór
jednego z nich powoduje odrzucenie drugiego

– wybiera się projekt o

krótszym okresie zwrotu,



w innych sytuacjach wartość progową ustala się na podstawie
średnich okresów zwrotu z podobnych przedsięwzięć inwestycyjnych
realizowanych w danym sektorze, np. hipermarketów,



w praktyce wartość ta jest określana subiektywnie przez inwestora.



Bezwzględne kryterium decyzyjne oparte na metodzie prostego okresu
zwrotu przedstawia się następująco:



jeżeli n < n

gr

, to przedsięwzięcie inwestycyjne jest opłacalne i można

je zaakceptować,



jeżeli n> n

gr

, to dane przedsięwzięcie jest nieopłacalne i należy je

odrzucić,



jeżeli n = n

gr

, to o przyjęciu lub odrzuceniu danego przedsięwzięcia

powinny decydować inne czynniki nieuwzględnione w tej metodzie.



Warto zwrócić uwagę na fakt, iż wartość progowa powinna obejmować
wszystkie okresy cyklu życia inwestycji, tzn. okres operacyjny i okres
realizacji przedsięwzięcia inwestycyjnego.



Zalety i wady metody prostego okresu zwrotu ilustruje poniższa tabela.

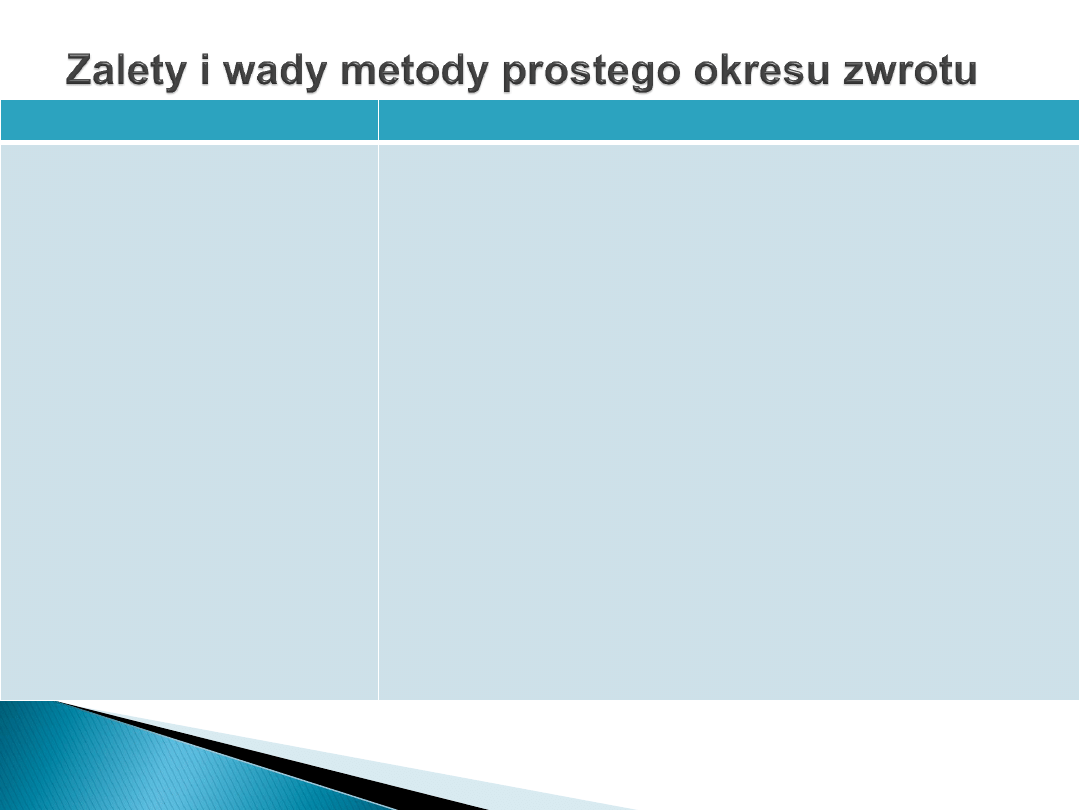
Zalety

Wady

•Jest prosta i zrozumiała.
• Uwzględnia wyższe ryzyko

przedsięwzięć długookresowych

- ogranicza ryzyko.
• Sprzyja zachowaniu płynności

zaangażowanych w

przedsiębiorstwie kapitałów

(preferuje przedsięwzięcia

krótkoterminowe).

• Opłacalność przedsięwzięcia

jest wyrażona przez czas (miara

ta lepiej przemawia do

wyobraźni decydenta, gdyż jest

intuicyjna, odpowiada też na

najczęściej zadawane pytanie o

to kiedy zwrócą się nakłady

wyłożone na realizację danego

przedsięwzięcia).

•Nie uwzględnia zmienności wartości pieniądza w czasie
• Opiera się na memoriałowym mierniku korzyści netto (zysku),
z którego poniesione nakłady inwestycyjne mają się zwrócić.
• Nie informuje o opłacalności przedsięwzięcia inwestycyjnego,

lecz o jego płynności.

• Nie można na jej podstawie skonstruować obiektywnego

bezwzględnego kryterium decyzyjnego (wymaga często

subiektywnego ustalenia granicznego okresu zwrotu nakładów

inwestycyjnych).
• Nie uwzględnia korzyści netto generowanych przez

przedsięwzięcie inwestycyjne po okresie, kiedy nakłady

inwestycyjne w pełni się zwrócą.

• Preferuje przedsięwzięcia inwestycyjne o krótkim

ekonomicznym cyklu życia.

• Nie nadaje się do bezwzględnej oceny opłacalności

niekonwencjonalnych przedsięwzięć inwestycyjnych (gdy

nakłady inwestycyjne są ponoszone nie tylko w okresie

realizacji przedsięwzięcia inwestycyjnego, ale również w

okresie eksploatacji, czy likwidacji).

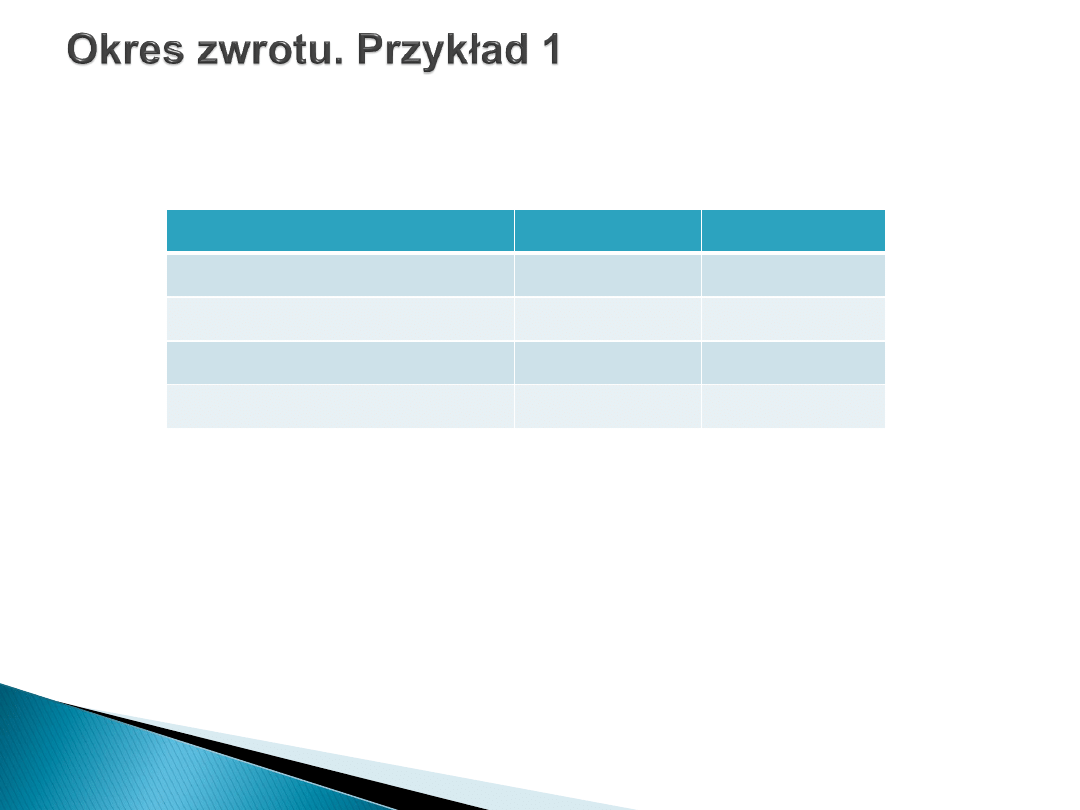
Przedmiotem oceny rachunku zwrotu nakładów inwestycyjnych są dwa

urządzenia o następujących parametrach techniczno – ekonomicznych:

Obliczenia okresu zwrotu:
T

I

= 70 : 14 + 16 = 2,33

T

II

= 90 : 18 + 25 = 2,09

Inwestor zapewne zdecyduje się na zakup urządzenia II, gdyż zwrot

zainwestowanego kapitału nastąpi wcześniej o 0,24 roku, tj. prawie 3

miesiące wcześniej, niż w przypadku urządzenia I.

Wyszczególnienie

Urządzenie I

Urządzenie II

Nakłady inwestycyjne (tys. zł)

70

90

Okres eksploatacji (lata)

5

5

Amortyzacja (tys. zł)

14

18

Zysk (tys. zł)

16

25

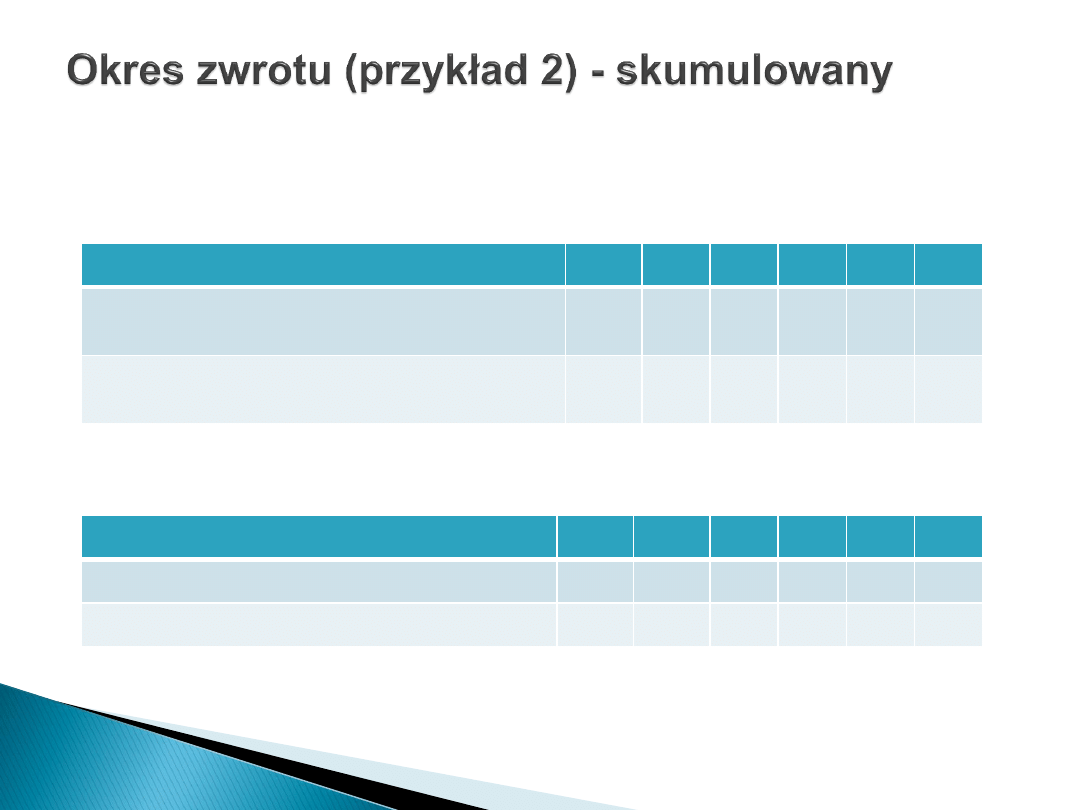
Firma zamierza zakupić nowy środek trwały. Ma do dyspozycji dwa
projekty: A i B.

Projekt A

Projekt B

Rok

0

1

2

3

4

5

Przepływy środków pieniężnych NCF
(zwrot kapitału roczny)

-120

60

50

40

30

20

Skumulowane NCF (zwrot kapitału
skumulowany)

-120

-60

-10

30

60

80

Rok

0

1

2

3

4

5

Zwrot kapitału roczny

-120

20

30

50

70

80

Zwrot kapitału skumulowany

-120 -100

-70

-20

90

130

Z powyższych wyliczeń wynika, że zwrot zainwestowanego kapitału w projekt

A nastąpi na początku trzeciego roku eksploatacji (po 2 roku), natomiast w

projekcie B na początku 4 roku. Inwestor najprawdopodobniej zdecyduje się

na projekt A, gdyż czas zamrożenia kapitału w tym projekcie jest krótszy o 1

rok. Projekt A jest także korzystniejszy ze względu na rozkład nadwyżek

pieniężnych (NCF). Dla firmy korzystniejsze jest bowiem odzyskanie

wyższej części nakładów inwestycyjnych w początkowej fazie okresu

zwrotu niż w jego późniejszym etapie.

Wyliczenie okresu zwrotu:

nie pokryty koszt na początku roku

T = (rok przed zakończeniem spłaty) + [ ]

przepływy śr. pieniężnych w ciągu roku

T

A

= 2 +

10

/

40

= 2,25 lat, czyli 2 lata i 3 m-ce,

T

B

= 3 +

20

/

70

= 3,28 lat, czyli 3 lata i 3,5 m-ca.

Ad. 2)

Metoda porównania kosztów – służy ocenie inwestycji

odtworzeniowo

– modernizacyjnych, a więc w takich przypadkach jak:



zastępowanie starego (zamortyzowanego) środka trwałego (maszyny,
urządzenia, środki transportu) nowym środkiem trwałym,



zamianie środka trwałego przed jego całkowitym zużyciem
(technicznym lub ekonomicznym) na nowy, bardziej wydajny i
nowoczesny,



określenie progowego poziomu produkcji wyrobów pozwalającego
zastosować nowoczesne urządzenie.



Przy ocenie efektywności projektów inwestycyjnych na podstawie tej
metody, zakłada się stałość warunków zewnętrznych, do których zalicza się
poziom zysku, cen, wielkość popytu itp. dla analizowanych wariantów
projektów.



Rachunek porównawczy kosztów próbuje – porównując koszty dwóch lub
większej liczby projektów – znaleźć (wybrać) ten projekt, który wymaga
najmniejszego nakładu kosztów.



W metodzie porównania kosztów ocenia się zatem zmienność kosztów w
zależności od rozmiarów produkcji i sprzedaży wynikających z inwestycji.



W metodzie tej stosuje się podział kosztów (K) na:

◦

koszty operacyjne

(wytwórcze) – k

op

, dotyczące wynagrodzeń,

materiałów, remontów,

◦

koszty inwestycyjne

(kapitałowe) k

k

, na które składają się amortyzacja

A oraz zysk kalkulacyjny (kalkulacyjna stopa zwrotu, koszt
alternatywny, utracona korzyść) Z.



Zakładając długość okresu eksploatacji inwestycji na n lat, poniesione
nakłady inwestycyjne – M oraz liniowy system amortyzacji środków
trwałych, amortyzację A wyznaczamy z następującej zależności:

lub

Gdzie:

R

– wartość końcowa (rezydualna) określająca cenę, po jakiej można

sprzedać majątek trwały po zakończeniu jego eksploatacji.

n

M

A



n

R

M

A







Zysk kalkulacyjny

oznacza ile można byłoby zyskać inwestując z i-tą

stopą zwrotu kapitał M

p

stanowiący średnią wielkość nakładów

inwestycyjnych.



Zakładając, że wielkość zainwestowanego na początku kapitału wynosi M,
przy liniowym systemie amortyzacji, średnia wielkość nakładów
inwestycyjnych Mp w alternatywną inwestycję wyraża się następującą
zależnością:



Wykorzystując powyższą zależność, zysk kalkulacyjny Z wyliczamy ze
wzoru:

2

R

M

P

M





i

R

M

i

P

M

Z

2









Na podstawie przeprowadzonej analizy dotyczącej amortyzacji i zysku

kalkulacyjnego, roczny koszt kapitałowy (inwestycyjny) można określić jako

sumę amortyzacji A i zysku kalkulacyjnego Z, a mianowicie:



Uwzględniając natomiast koszty operacyjne, całkowite koszty K

wyznaczamy ze wzoru jak niżej:



Zalety metody porównania kosztów:



znajduje szerokie zastosowanie w ocenie wstępnej różnych projektów

inwestycyjnych polegających na zakupie nowych środków trwałych,

wymianie przestarzałych elementów majątku na nowe itp.



Użyteczność tej metody jako narzędzia oceny efektywności inwestycji

ograniczają:



krótki okres analizy (w rachunku tym ze względów praktycznych przyjmuje

się wartości z pierwszego roku eksploatacji obiektu, które są uznawane za

reprezentatywne dla dalszych okresów analizy),



nieuwzględnianie przychodów, cen, jakości produkcji,



trudności z podziałem kosztów na stałe i zmienne.

i

R

M

n

R

M

k

k

2









op

k

i

n

R

M

n

R

M

K











Firma rozważa zakup jednego z dwóch urządzeń. Dane podstawowe

kształtują się następująco:

Z obliczeń wynika, że firma powinna zakupić urządzenie II.

Wyszczególnienie

Wariant I

Wariant II

Koszt nabycia urządzenia

100

150

Roczne koszty operacyjne

30

20

Wartość końcowa

0

0

Czas eksploatacji w latach

10

10

Kalkulacyjna stopa zysku w %

10

10

45

30

1

,

0

2

100

10

100

2















x

op

K

xi

M

n

M

I

K

5

,

42

20

1

,

0

2

150

10

150

2















x

op

K

xi

M

n

M

II

K

Założenie: okres eksploatacji urządzenia I jest dwukrotnie dłuższy w

porównaniu z urządzeniem II.

Wyszczególnienie

Wariant I

Wariant II

Koszt nabycia

400

200

Roczne koszty operacyjne

63

40

Wartość końcowa po 3 latach

0

8

Wartość końcowa po 6 latach

16

0

Czas eksploatacji w latach

6

3

Kalkulacyjna stopa zysku

10

10

W tym wypadku należy wydłużyć okres obrachunkowy wariantu II, przyjmując

jego kolejne powtórzenia niezbędne do zrównania czasu eksploatacyjnego
z wariantem I. Zakłada się, że po upływie 3 lat inwestycja II zostanie
powtórzona.

Z obliczeń wynika, że korzystniejszy jest wariant II.

II

K

I

K



8

,

124

40

8

,

20

64

40

1

,

0

2

16

400

6

16

400

2

)

(

2

2

)

(

2

































II

K

o

K

i

R

M

n

R

M

II

K

8

,

147

63

8

,

20

64

63

1

,

0

2

16

400

6

16

400

2

































I

K

o

K

i

R

M

n

R

M

I

K

Ad. 3)

Metoda porównania zysków



W gospodarce wolnorynkowej zysk jest podstawową, syntetyczną miarą

efektywności działania firmy, a więc również opłacalności jej różnych

przedsięwzięć inwestycyjnych.



Osiągnięcie zysku jest wynikiem wyboru najbardziej opłacalnych technologii

oraz wsadu materiałowego w celu minimalizacji kosztów wytwarzania, a z
drugiej strony

– umiejętności promowania i sprzedaży wyrobów firmy.



Kryteria oceny, które polegają na porównaniu kosztów mają dość ograniczony

zasięg i są przydatne jedynie do oceny opłacalności projektów, które

zapewniają jednorodny produkt i jednakowe rozmiary produkcji, nie przewidują

zaś zmiany asortymentu i jakości wyrobów.



Toteż ocena efektywności inwestycji na podstawie uniwersalnej i szerokiej

formuły, jaką jest zysk, umożliwia uwzględnienie w rachunku o wiele większej

liczby danych i porównanie różnych przypuszczalnych sytuacji rynkowych.



Za punkt wyjścia w tej metodzie bierze się zarówno koszty, jak i przychody

uzyskane w wyniku wdrożenia danej inwestycji.



W metodzie porównania zysków za kryterium racjonalizacji decyzji inwestycyjnej

przyjmuje się maksymalizację zysku absolutnego (globalnego) lub zysku
jednostkowego.



Niech G oznacza zysk z nowej inwestycji, zaś P – przychód, natomiast K –
koszty



Wtedy: G= P – K



Inwestycję uznajemy za opłacalną, jeśli:

G > 0



Gdy mamy do wyboru dwa warianty inwestycji wybieramy ten, dla którego

zysk jest większy, tzn. jeśli zachodzi:

to wtedy spośród wariantów A i B wybieramy wariant A.



Posługując się wielkościami jednostkowymi zysk dla konkretnego wariantu
inwestycji zostanie wyznaczony ze wzoru:

gdzie:

p

– jednostkowa cena sprzedaży,

x

– wielkość produkcji,

kz

– jednostkowe koszty zmienne,

Ks

– całkowite koszty stałe,

B

G

A

G



s

K

x

z

k

x

p

x

p

G











)

,

(



Zalety metody porównania zysków:



wiąże jednocześnie przychody z kosztami ich uzyskania w stosunku
rocznym,



może być podstawą podjęcia decyzji o likwidacji dotąd eksploatowanego
środka trwałego i zastąpienia go „nowym” urządzeniem.



Wady:



ze względu na roczny okres rachunku ma on znaczenie orientacyjne i jest
stosowany w projektach drobnych, związanych z zakupem maszyn i
urządzeń o stosunkowo małej wartości,



nadaje się do oceny zamierzeń inwestycyjnych oddziałujących silniej na
sytuację przychodową firmy, a więc zwłaszcza w przypadku inwestycji
nowych,



zysk globalny uzyskany z różnych projektów inwestycyjnych nie jest dobrą
miarą porównywalności bo nie uwzględnia skali (wielkości)
zaangażowanego kapitału, jako punktu odniesienia.

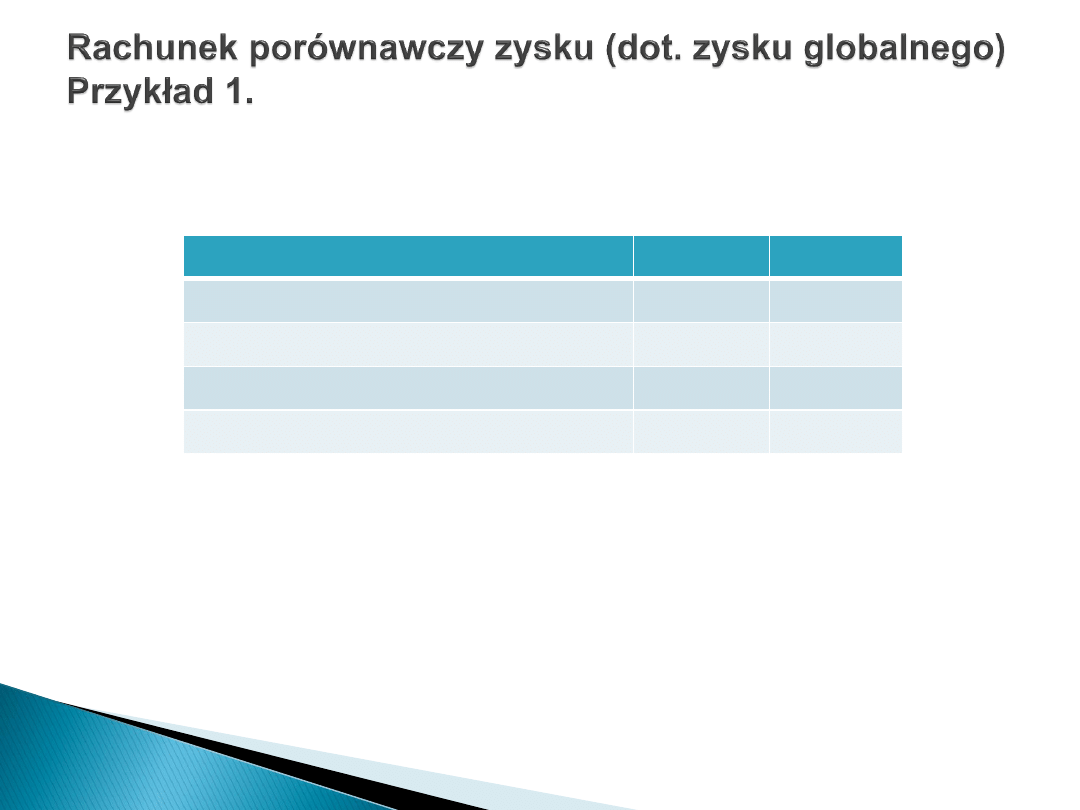
Przyjmijmy następujące parametry dwóch branych pod uwagę wariantów

inwestycyjnych:

Obliczamy zysk globalny „G”:
G

I

= 700

– 455 = 245 tys. zł

G

II

= 650

– 430 = 220 tys. zł

Powyższy wynik wskazuje na wyższą efektywność wariantu I rozpatrywanego

projektu inwestycyjnego.

Wyszczególnienie

Wariant I

Wariant II

1.

Przychód (tys. zł/rok)

700

650

2.

Koszty stałe (tys. zł/rok)

85

70

3.

Koszty zmienne (tys. zł/rok)

370

360

4.

Koszty ogółem (tys. zł/rok; poz. 2+3)

455

430

Określamy efektywność dwóch alternatywnych rozwiązań (wariant I i wariant

II) posługując się rachunkiem zysku. Przyjmijmy, że warianty projektów
inwestycyjnych charakteryzują wielkości przedstawione w poniższym
zestawieniu:

Obliczamy najpierw zysk globalny:

Wyszczególnienie

Wariant I

Wariant II

Wydajność (szt./rok)

20.000

30.000

Cena (zł/szt.)

80

75

Koszty

stałe

8.500

7.000

Koszty jednostkowe
zmienne (zł/szt.)

62

63

zł

II

G

zł

I

G

000

.

353

7000

000

.

30

63

000

.

30

75

500

.

351

500

.

8

000

.

20

62

000

.

20

80

























Następnie obliczamy zysk jednostkowy:

Wnioski:
Biorąc pod uwagę zysk globalny to korzystniejszy wydaje się wariant II.
Tymczasem uwzględniając w ocenie zysk jednostkowy o wiele korzystniejszy
okazuje się wariant I projektu.

sztuce

zł

jII

G

sztuce

zł

jI

G

/

8

,

11

000

.

30

000

.

353

/

6

,

17

000

.

20

500

.

351









Ad. 4)

Metoda porównania rentowności inwestycji



Ostatnią z omawianej grupy prostych metod oceny opłacalności

przedsięwzięć inwestycyjnych jest metoda porównania rentowności

inwestycji, zwana też rachunkiem rentowności inwestycji.



Najogólniej rentowność inwestycji jest relacją korzyści netto generowanych

przez oceniane przedsięwzięcie inwestycyjne do nakładu (kapitału), jaki

musi być poniesiony na jego realizację.



W literaturze ekonomicznej poświęconej efektywności inwestycji występują

różne warianty algorytmu wykorzystywanego w tej metodzie.



Różnice dotyczą zarówno formuły licznika, jak i mianownika rachunku.



W liczniku formuły jako miary korzyści netto można użyć:



zysku netto powiększonego o odsetki od kredytów, w sytuacji gdy w

mianowniku bierzemy pod uwagę cały zaangażowany kapitał inwestycyjny,

łącznie z kapitałem obcym,



samego zysku netto, gdy w mianowniku uwzględniamy tylko kapitał własny

zaangażowany w przedsięwzięcie,



wielkości średnich (księgowych) z całego cyklu życia projektu lub wielkości

rocznych obliczonych dla każdego okresu oddzielnie.



Z kolei w mianowniku formuły umieszcza się:

-

wartość początkową nakładów inwestycyjnych,

-

wartość średnią (księgową) nakładów inwestycyjnych.



Jeśli w formule licznika i mianownika przyjmujemy wielkości roczne to
będziemy mieli do czynienia z prostą stopą zwrotu z nakładów
inwestycyjnych, która jest odwrotnością prostego okresu zwrotu:

Prosta stopa zwrotu



Z kolei jeśli w formule licznika i mianownika umieścimy średni zysk netto z
całego cyklu życia projektu i wartość średnią nakładów inwestycyjnych to
otrzymamy tzw.

księgowa stopę zwrotu ARR (accounting rate of return),

określaną także jako średni księgowy zwrot AAR (avarage accounting
return).



Stosując każdą z tych formuł rachunku rentowności inwestycji otrzymamy
różne wyniki.

)

(

_

_

1

n

zwrotu

okres

prosty

e

R





Ogólną postać prostej stopy zwrotu można przedstawić za pomocą
następującej formuły:

Z

– zysk roczny,

I

– wartość początkowa nakładów inwestycyjnych.



Najwłaściwszym algorytmem szacowania księgowej stopy zwrotu jest
formuła zaproponowana przez R. Machałę w: Praktyczne zarządzanie
finansami firmy (2001), a mianowicie:

ARR

– księgowa stopa zwrotu z inwestycji, od m+1 do n – kolejne okresy

ekonomicznego cyklu życia projektu, w których generuje on dodatnie
korzyści netto (zysk),

zysk netto

– zysk netto w i-tym roku okresu operacyjnego projektu,

I

Z

e

R



2

_

1

WKI

WPI

d

netto

zysk

ARR

n

m

t











WPI

– wartość początkowa inwestycji (nakłady inwestycyjne),

WKI

– księgowa wartość rezydualna (końcowa) projektu,

d

– liczba okresów, w których projekt generuje zysk.



Powyższy wzór ma zastosowanie, jeśli założono liniową amortyzację
nakładów inwestycyjnych, dlatego w mianowniku znajduje się wyrażenie



Gdy jest wykorzystywana amortyzacja nieliniowa, wówczas w mianowniku
wzoru należy umieścić sumę księgowej wartości netto nakładów
inwestycyjnych na koniec okresu.



Do realizacji są przyjmowane te przedsięwzięcia, dla których księgowa
stopa zwrotu jest wyższa niż określona subiektywnie przez decydenta
wartość progowa, a odrzucane są te inwestycje, których księgowa stopa
zwrotu jest niższa od wartości progowej, na przykład średniej księgowej
stopy zwrotu z aktywów dla danego sektora.

2

WKI

WPI





W odniesieniu do prostej stopy zwrotu można mówić o tych samych
zaletach i wadach w ocenie projektów, co i w wypadku prostego okresu
zwrotu.



Natomiast zalety i wady metody księgowej stopy zwrotu prezentuje tabela.

Zalety

Wady

• jest prosta i zrozumiała,
• ułatwia prowadzenie obliczeń –
niezbędne informacje są zwykle dostępne

• nie uwzględnia zmienności wartości
pieniądza w czasie,
• opiera się na zysku jako mierniku korzyści
netto przedsięwzięcia inwestycyjnego,
• na jej podstawie nie można zbudować
obiektywnego

bezwzględnego kryterium

decyzyjnego (wymaga arbitralnego i
subiektywnego ustalenia wartości
granicznej stopy zwrotu),
• nie można jej stosować dla przedsięwzięć
inwestycyjnych cechujących się różnym
poziomem ryzyka.

Firma handlowa zamierza zakupić nowy samochód dostawczy.
Ma do wyboru dwa warianty kupna, jak niżej:

Stosując następujący wzór:

, gdzie:

Wyszczególnienie

Wariant I

Wariant II

Nakłady inwestycyjne (tys. zł)

300

320

Wartość końcowa

60

70

Przychód (tys. zł)

360

432

Czas eksploatacji (lata)

6

6

Koszty stałe (tys. zł)

54

58

Koszty zmienne (tys. zł)

216

227

%

100







k

D

K

P

e

R

2

R

M

k

D





otrzymamy:

Odpowiedź: Rentowność wariantu II jest o 27,4% wyższa niż wariantu I.

Rachunek stóp zwrotu (rentowności). Przykład 2.

Firma handlowa zamierza kupić nowy agregat chłodniczy za 50 tys. zł. Koszt

jego eksploatacji wyniesie 4 tys. zł rocznie. Koszt eksploatacji
dotychczasowego agregatu chłodniczego wynosi 7 tys. zł rocznie. Jaka jest
rentowność planowanego przedsięwzięcia inwestycyjnego?

Odpowiedź:

%

50

%

100

180

90

%

100

2

60

300

)

216

54

(

360

















eI

R

%

4

,

77

%

100

195

151

%

100

2

70

320

)

227

54

(

432

















eII

R

%

100







k

D

B

K

A

K

e

R

%

6

%

100

06

,

0

%

100

50000

4000

7000













e

R

Dysponując następującymi danymi:

Oblicz okres i stopę zwrotu.

Rok

Nakłady

Czynnik zwracający

nakład kapitałowy

Wartość

skumulowana

0

1000

0

-1000

1

0

220

-780

2

0

290

-490

3

0

320

-170

4

0

250

80

5

0

160

240



Zwrot następuje, gdy wartość skumulowana osiąga poziom zera. W w/w
przykładzie nastąpiło to pomiędzy 3 a 4 rokiem, interpolując:

lat = 3 lata i 8 miesięcy (0,68 x 12)



Tradycyjnie liczony okres zwrotu wyniesie:

1000

T = =

średnia wartość roczna czynnika zwracającego

lata



Stopa zwrotu

68

,

3

250

170





T

03

,

4

248

1000

5

:

)

160

250

320

290

220

(

1000















%

8

,

24

%

100

1000

248

1























T

1.

Metoda wartości bieżącej netto

◦

Wartość bieżąca netto (net present value, NPV) w polskiej literaturze

przedmiotu występuje również jako:



teraźniejsza wartość netto,



wartość kapitałowa inwestycji



aktualna wartość nadwyżki netto,



aktualna wartość nadwyżki finansowej netto,



aktualna wartość netto,



wartość bieżąca netto.



Założenia teoretyczne metody NPV

Metoda NPV opiera się na następujących założeniach

teoretycznych:



określona jest długość cyklu życia przedsięwzięcia inwestycyjnego
(okresu obliczeniowego),



znana jest oczekiwana struktura (tzw. wielkość i rozkład w czasie)

korzyści netto (przepływów pieniężnych netto) w całym cyklu życia

przedsięwzięcia inwestycyjnego,



przedsięwzięcie inwestycyjne charakteryzuje sie konwencjonalnym

(typowym) rozkładem w czasie przepływów pieniężnych netto,

•

nakłady inwestycyjne są ponoszone nieodwracalnie,

•

jedyną alternatywą wobec realizacji przedsięwzięcia inwestycyjnego
jest inwestycja na rynku kapitałowym (inwestycja kapitałowa), metoda
NPV pozwala bowiem uzyskać informację o tym, co jest dla firmy
bardziej opłacalne – inwestowanie w konkretne przedsięwzięcie
inwestycyjne czy bezpośrednie inwestycje na rynku kapitałowym,
zakładając, że nakłady i cykl życia obu inwestycji są identyczne, a
poziom ryzyka jest zbliżony,

•

zakłada się płaski kształt krzywej rentowności w całym cyklu życia
przedsięwzięcia inwestycyjnego (stałą stopę dyskontową w całym
okresie)

•

przyjmuje się, że dodatnie przepływy pieniężne netto (NCF,”+”) są
reinwestowane ze stopą reinwestycji (k

rei

)

równą stopie dyskontowej

(k),

•

zakłada się, że przepływy pieniężne netto (NCF) powstają z końcem
roku, podczas gdy w rzeczywistości są tworzone stopniowo w ciągu
roku, co powoduje pewne niedoszacowanie wartości NPV (założenie
to jest jednak bezpieczne, gdyż prowadzi do zaniżenia, nie zaś
zawyżenia wartości NPV),

•

nakłady inwestycyjne traktuje się jako wydatki,

•

nakłady na odtworzenie czy modernizację środków trwałych w okresie
obliczeniowym traktuje się również jako wydatki,

•

amortyzacji nie traktuje się jako wydatku, co powiększa przepływy
pieniężne netto (NCE) oraz przyjmuje sie pełną amortyzację projektu w
okresie jego eksploatacji,

•

zmiany kapitału obrotowego netto uwzględnia sie w rachunku (+ -),

•

wydatkami firmy są również: podatek dochodowy, koszty operacyjne, koszty
marketingowe, odsetki i raty kredytów,

•

wartość likwidacyjna, zwłaszcza budynków, budowli oraz odzyskany
majątek obrotowy traktuje się jako wartość netto w końcu okresu
obliczeniowego,

•

okres dyskontowania powinien być równy okresowi realizacji i eksploatacji
projektu,

•

wpływy i wydatki dyskontuje się na rok t = 0, to jest rok bezpośrednio
poprzedzający realizację projektu (współczynnik dyskontowy dla t = 0
wynosi 1).



Metoda wartości bieżącej NPV jest jedną z podstawowych metod
uwzględniających czynnik czasu w ocenach projektów inwestycyjnych i ma
szerokie zastosowanie w praktyce gospodarczej.



Pozwala ona na określenie rzeczywistej (aktualnej) wartości nakładów i
efektów związanych z danym przedsięwzięciem.



NPV jest wartością otrzymaną przez zdyskontowanie, oddzielnie dla
każdego roku, różnicy między wpływami i wydatkami w całym okresie
funkcjonowania przedsięwzięcia, przy stałym poziomie stopy dyskontowej
(różnica ta dyskontowana jest na moment, w którym przewidziane jest
rozpoczęcie budowy obiektu),



Inaczej:



NPV

– to łączna (skumulowana z całego ekonomicznego cyklu życia

projektu) przedstawiona w bieżącej wartości pieniądza korzyść netto

przedsięwzięcia inwestycyjnego,



NPV stanowi różnicę między wartością zdyskontowanych dodatnich

przepływów pieniężnych netto a wartością zdyskontowanych ujemnych

przepływów pieniężnych netto,



NPV można także interpretować jako skumulowaną bieżącą korzyść netto z

przedsięwzięcia inwestycyjnego,



NPV obliczana jest jako różnica między sumą zdyskontowanych przyszłych

przepływów gotówkowych generowanych przez projekt a wartością

nakładów niezbędnych do jego uruchomienia, co można wyrazić wzorem:

gdzie:

NCF

– wartość przepływów pieniężnych netto,

t + 0, 1, 2, …, n – kolejny rok okresu obliczeniowego,
i

– zakładana w obliczeniach stopa dyskontowa,

I

– wielkośc poniesionych na początku nakładów inwestycyjnych.

I

t

i

NCF

n

t

NPV











)

1

(

0



Badany projekt jest opłacalny, jeżeli NPV > 0, neutralny, jeżeli NPV = 0 oraz
nieopłacalny jeżeli NPV < 0 (ocena bezwzględna). Zasada: „przyjąć –
odrzucić?”



Z kolei w ocenie względnej wybiera się wariant o największej NPV, według
zasady

„który lepszy?”



Gdy NPV > 0 oznacza to, że dzisiejsza wartość wszystkich wpływów jest
większa od wartości poniesionych nakładów i wydatków związanych z
funkcjonowaniem obiektu.



Równocześnie oznacza to, że stopa rentowności projektu jest wyższa od
zakładanej stopy zwrotu inwestora wyrażonej w stopie dyskontowej.



Poziom NPV zależy od:



wielkości i rozkładu w czasie przepływów pieniężnych netto,



przyjętej stopy dyskontowej (prezentuje to wykres poniżej).

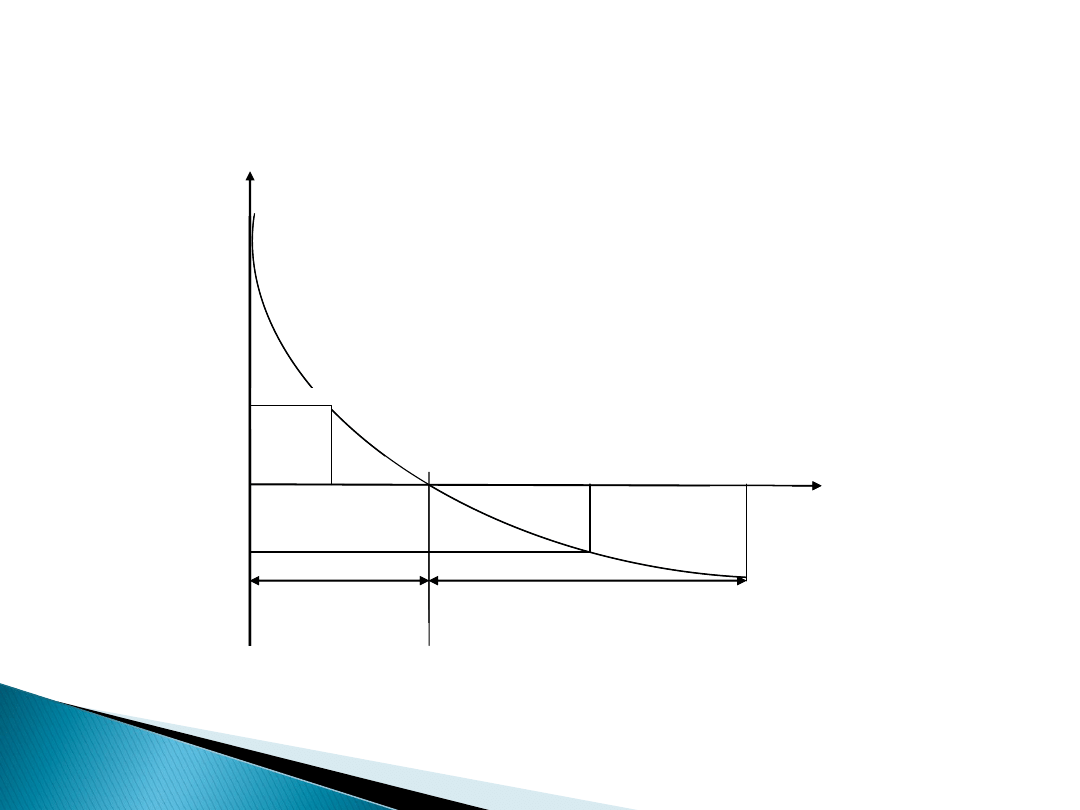
Profil NPV typowego przedsiębiorstwa inwestycyjnego dla

przyjętej stopy dyskontowej

NPV

1

k

2

> k

gr

0

k

NPV

2

NPV

2

< 0

k

gr

NPV

k

1

< k

gr

NPV

1

> 0

NPV

gr

= 0

Profil NPV typowego przedsiębiorstwa inwestycyjnego dla

przyjętej stopy dyskontowej

NPV

1

k

2

> k

gr

0

k

NPV

2

NPV

2

< 0

k

gr

NPV

k

1

< k

gr

NPV

1

> 0

NPV

gr

= 0



Profil NPV ma nachylenie ujemne, co oznacza, że wraz ze wzrostem stopy
dyskontowej maleje wartość NPV (wraz ze wzrostem wartości stopy
dyskontowej maleje wartość współczynnika dyskonta i tym samym
zmniejszają się poszczególne wartości NCF). Zależność ta nie jest jednak
liniowa, lecz wykładnicza.



Stopa dyskontowa wyraża graniczną, oczekiwaną stopę zwrotu od
zainwestowanego kapitału.



Wraz ze wzrostem stopy dyskontowej maleje wartość NPV (wraz ze
wzrostem wartości stopy dyskontowej maleje wartość współczynnika
dyskonta i tym samym zmniejszają się poszczególne wartości NCF).



Poziom stopy dyskontowej uwzględnia dwa czynniki, a mianowicie:



oczekiwaną stopę zwrotu,



ryzyko.



Oczekiwana stopa zwrotu

wyraża minimalną rentowność, przy której

inwestor jest gotów zaangażować swój kapitał w przedsięwzięcie i może

być ustalona na poziomie stopy oprocentowania wolnych od ryzyka

państwowych długoterminowych lokat kapitałowych, np. obligacji i bonów
skarbowych.



Drugą częścią stopy dyskontowej jest premia za ryzyko inwestowania.



W praktyce przypisuje się liczbową wartość tej premii zależnie od
subiektywnej oceny skali ryzyka, np.



-

5% dla projektu zakładającego modernizację istniejących mocy

wytwórczych,



- 10 % dla projektu nowego,



-

20 % dla przedsięwzięcia o charakterze spekulacyjnym.



Trzecim składnikiem stopy dyskontowej mogłaby być stopa inflacji
przewidywana w okresie projekcji przepływów pieniężnych.



Wymagałoby to jednak prognozowania wpływów i wydatków w cenach
bieżących i obarczone byłoby znacznym marginesem błędu.



Dlatego też w praktycznych rachunkach NPV pomija się stopę inflacji jako
składnika stopy dyskontowej, a prognozowane przepływy pieniężne wyraża
się w cenach stałych.



Stosowanie metody NPV wiąże sie z szacowaniem opłacalności projektu w
wartościach bezwzględnych (kwotowych), a nie relatywnych
(procentowych).



Wadę tę można wyeliminować, odnosząc wartość NPV projektu do wartości
nakładów inwestycyjnych poniesionych na jego realizację.



W tym celu wykorzystuje się wskaźnik wartości bieżącej netto (NPVR –
net present value ratio),

który wyraża skumulowaną zdyskontowaną

wartość korzyści netto (NPV) przypadającą na jednostkę zdyskontowanych

nakładów inwestycyjnych i przyjmuje postać:

gdzie:


PVI

– wartość bieżąca nakładów inwestycyjnych.



Przy czym, jeśli:



NPVR > 0 projekt jest opłacalny,



NPVR = 0 projekt jest neutralny i można go zaakceptować,



NPVR < 0 projekt jest nieopłacalny.



Wartość bieżąca netto jest najważniejszym i nadrzędnym w stosunku do

wszystkich innych kryterium oceny projektów inwestycyjnych i jedynym w

pełni zgodnym z zasadą maksymalizacji wartości firmy.



Oznacza to, że wybór projektu charakteryzującego się najwyższą NPV

powinien spowodować największy wzrost wartości firmy.



Pozostałe zalety i wady metody NPV zostały ukazane w tabeli jak niżej.

PVI

NPV

NPVR



Zalety

Wady

• Korzyść netto jest wyrażona przepływem
pieniężnym netto.
• Uwzględnia zmienność wartości pieniądza w
czasie.
• Zakłada ujmowanie w bezwzględnej ocenie
opłacalności korzyści netto z całego cyklu życia
przedsięwzięcia inwestycyjnego.
• Pozwala zbudować obiektywne bezwzględne
kryterium decyzyjne.
• Wiąże przedsięwzięcie inwestycyjne z
długofalowym celem działania firmy (wzrost
wartości).
• Może być stosowana do szacowania
opłacalności zarówno dla przedsięwzięć
konwencjonalnych, jak i niekonwencjonalnych.
• Pozwala prowadzić analizy związane z
ryzykiem przedsięwzięcia inwestycyjnego i
umożliwia prostą interpretację uzyskanych
wyników.
• Spełnia zasadę addytywności (NVP

A

+ NVP

B

=

NVP

(A + B)

, a także 2 x NVP

A

= NVP

(2 x A)

).

• Jest metodą multiplikatywną.

• Utrudniony wybór odpowiedniego poziomu
stopy dyskontowej.
• Nie pokazuje relatywnej opłacalności
przedsięwzięcia inwestycyjnego (metoda
bezwzględna nierelatywna).
• Zakłada płaską krzywą rentowności (stałość
stopy dyskontowej w całym cyklu życia
przedsięwzięcia inwestycyjnego).
• Przyjmuje założenie o równości stopy
dyskontowej oraz stopy kapitalizacji
wykorzystywanej do reinwestycji dodatnich
przepływów pieniężnych netto (problem
reinwestycji).
• Ma statyczny charakter (ogranicza aktywne
zarządzanie przedsięwzięciem inwestycyjnym
po rozpoczęciu jego realizacji), nie uwzględnia
bowiem możliwości dostosowania
przedsięwzięcia inwestycyjnego do zmian
otoczenia (przesunięcie momentu realizacji
przedsięwzięcia inwestycyjnego, wycofanie się z
przedsięwzięcia inwestycyjnego, zmniejszenie
lub zwiększenie jego skali, czasowe
wstrzymanie jego eksploatacji).

2.

Metoda wewnętrznej stopy zwrotu (IRR)



Omówiona wcześniej metoda NPV nie wskazuje skąd brać odpowiednią
wartość stopy dyskontowej „i”.



Inwestora natomiast może interesować, przy jakiej stopie dyskontowej
zwróci mu się w zakładanym okresie zainwestowany kapitał.



Wewnętrzna stopa zwrotu IRR (internal rate of return) określana jest jako
stopa dyskontowa, przy której wartość bieżąca strumienia wpływów
zrównuje się z nakładami inicjującymi, czyli jako stopa dyskontowa, przy
której NPV = 0.



IRR określa więc, przy jakiej stopie procentowej suma zdyskontowanych
dochodów zrówna się z sumą zdyskontowanych nakładów kapitałowych,
przy założonym okresie „n” lat opłacalnej eksploatacji projektu.



W metodzie tej wykorzystuje się założenie, że przepływy środków
pieniężnych z projektu są reinwestowane według stopy IRR, w tym
gotówka pozostająca w firmie.



Formuła wewnętrznej stopy zwrotu ma następującą postać:

lub

gdzie:

NPV

– wartość bieżąca netto,

NCF

– przepływy pieniężne netto.



IRR wyznacza wewnętrzną, rzeczywistą stopę rentowności projektu
inwestycyjnego.



W wypadku, gdy stopa ta jest wyższa (lub co najmniej równa) od

stopy dyskontowej przyjętej do wyliczania NPV, ocena projektu

wypada korzystnie.

i

IRR

I

t

i

t

NCF

n

t

NPV

















0

)

1

(

1

0

)

1

(

1











t

IRR

t

NCF

n

t

NPV



IRR niższa od stopy dyskontowej przyjętej do wyliczania NPV nakazuje
odrzucenie projektu

– oznacza to bowiem, że rzeczywista stopa

rentowności rozpatrywanego projektu inwestycyjnego jest niższa od

oczekiwanej przez inwestora stopy zwrotu od zainwestowanego kapitału.



IRR jest też określana metodą kolejnych przybliżeń, które przebiegają

według następującej procedury:



przygotowujemy tabelę przepływów pieniężnych NCF,



zakładamy prawdopodobny poziom stopy dyskontowej „i” , przy której

zdyskontowana wartość netto NCF byłaby zbliżona do zera,



obliczamy dla tego poziomu „i” wartość zdyskontowaną netto NCF0,



gdy NCF0 > 0, obliczenia powtarzamy, zmieniając odpowiednio wartość
stopy dyskontowej,



gdy nadal NCF0 >0, w dalszym ciągu podwyższamy stopę „i” aż do
otrzymania NCF0 <0,

gdy ujemne i dodatnie wartości NCF0, obliczone dla różnych poziomów
stopy dyskontowej zbliżone są do zera, można precyzyjnie (tym
precyzyjniej, im bliższe zera są wartości NCF0) ustalić IRR, wykorzystując
następujący wzór:

gdzie:

i

1

– stopa dyskontowa niższa dla NCF0 >0,

i

2

– stopa dyskontowa wyższa dla NCF0 <0,

NCF

01,

NCF

02

-

wartość zdyskontowana netto dla niższego i wyższego

poziomu stopy dyskontowej.



W procedurze tej należy mieć na uwadze fakt, aby „i

2

” oraz „i

1

”, nie różniły

się więcej niż o 1 punkt procentowy.



IRR można wyliczyć również przez odpowiednią funkcję finansową w
arkuszu kalkulacyjnym (np. Excel), lub za pomocą kalkulatora.

0

02

01

)

1

2

(

01











NCF

NCF

i

i

NCF

i

IRR

Metoda wewnętrznej stopy zwrotu IRR w profilu NPV dla

typowego przedsięwzięcia inwestycyjnego

NPV

1

k

2

0

k

NPV

2

NPV < 0

IRR

NPV

k

1

k

gr

NPV > 0

NPV= 0



Określenie wartości IRR możliwe jest tylko w odniesieniu do projektów

typowych (tzw. czystych), tj. takich, w których najpierw następują przepływy

ujemne spowodowane koniecznością poniesienia kosztów w celu

uruchomienia projektu, a następnie w kolejnych okresach generowane są

przez projekt już wyłącznie przepływy dodatnie.



Z kolei w wypadku projektów „odwrotnych” do typowych, tj. takich, w

których najpierw następują przepływy dodatnie, a następnie wyłącznie

przepływy ujemne, zasada IRR działa również w sposób odwrotny, tzn.

projekt jest akceptowany do dalszej analizy, jeżeli IRR jest niższa od stopy

dyskontowej (kryterium IRR ulega tu odwróceniu).



Przykładem projektów „odwrotnych” do typowych mogą być wszelkie

operacje, w których najpierw następuje zapłata (wpływ gotówki), a dopiero

później wykonywany jest przedmiot umowy (np. spółdzielnia mieszkaniowa

lub firma deweloperska otrzymuje z góry równowartość budowanego

mieszkania lub domu, a dopiero później ponosi koszty realizacji umowy).



W takich sytuacjach wyższa stopa dyskontowa oznacza wyższe korzyści z

reinwestycji środków otrzymanych z góry.



Zalety i wady metody wewnętrznej stopy zwrotu (IRR) przedstawia tabela.

Zalety

Wady

• Korzyść netto jest wyrażona przez przepływ
pieniężny netto.
• Jest prosta w interpretacji (efekt
psychologiczny związany z preferowaniem
mierników opłacalności wyrażonych
procentowo).
• Ujmuje w bezwzględnej ocenie opłacalności
korzyści netto z całego cyklu życia
przedsięwzięcia inwestycyjnego.
• Zawiera informacje o poziomie marginesu
bezpieczeństwa (IRR – k

gr

).

• Pozwala określić graniczny koszt kapitału, jaki
może być wykorzystany do sfinansowania
danego przedsięwzięcia inwestycyjnego.
• Pozwala zbudować obiektywne bezwzględne
kryterium decyzyjne.
• Może być stosowana w bezwzględnej ocenie
opłacalności przedsięwzięcia inwestycyjnego
także w sytuacji, gdy nie jest jeszcze znana
stopa dyskontowa.

• Nie może być w sposób bezpośredni
wykorzystywana do bezwzględnej oceny
opłacalności nietypowych przedsięwzięć
inwestycyjnych (nie spełnia zasady
uniwersalności).
• Zakłada, że stopa reinwestycji dodatnich
przepływów pieniężnych netto równa się
obliczanej wewnętrznej stopie zwrotu.
• Nie uwzględnia w pełni zmienności wartości
pieniądza w czasie (zakłada, że wartość
pieniądza w czasie jest równa wewnętrznej
stopie zwrotu danego przedsięwzięcia
inwestycyjnego).
•Zakłada płaską krzywą rentowności, co utrudnia
sformułowanie bezwzględnego kryterium
decyzyjnego dla modelu ze zmienną w czasie
stopą dyskontową (więcej niż jedna wartość
granicznej stopy zwrotu).
•Nie spełnia zasady addytywności: (IRR

A

+ IRR

B

)

jest różne od IRR

(A+B)

.

3.

Zmodyfikowana wewnętrzna stopa zwrotu (MIRR)



Metoda zmodyfikowanej wewnętrznej stopy zwrotu MIRR (modified
internal rate of return) eliminuje dwie istotne wady IRR, a mianowicie:

a)

pozwala szacować wszystkie rodzaje przedsięwzięć inwestycyjnych:



typowych,



typowych odwrotnych,

o których była mowa wcześniej,



nietypowych,

w których kilkakrotnie (więcej niż raz) następuje zmiana

znaku przepływów, np. najpierw następuje wypływ związany z konieczną

inwestycją, następnie projekt generuje przepływy dodatnie, a następnie

przepływy ujemne. Przykładem może być budowa kopalni, w której najpierw

wymagane nakłady inwestycyjne powodują powstanie przepływów

ujemnych, następnie eksploatacja kopalni generuje przepływy dodatnie i na
koniec wydatki konieczne do likwidacji kopalni (rekultywacja terenu)

ponownie powodują przepływy ujemne.

b)

dzięki zastosowaniu właściwej stopy reinwestycji i właściwej stopy

dyskontowej uwzględnia się proces reinwestycji dodatnich przepływów

pieniężnych netto.

Zmodyfikowana wewnętrzna stopa zwrotu jest oparta o relację tzw.

wartości końcowej projektu (terminal value of project) do zdyskontowanych

nakładów.

Jeśli relację tę spierwiastkujemy liczbą lat horyzontu czasowego projektu i

odejmiemy od tego jedność, to uzyskamy średnią, roczną stopę

wyrażającą dynamikę wzrostu, z jakim początkowy (inicjujący) nakład

przekształca się w ową wartość „terminalną”.

Wartość tę uzyskujemy przy założeniu, że przepływy gotówkowe netto

otrzymywane w okresie eksploatacji projektu są rekapitalizowane za

pomocą stopy żądanej przez inwestora „i”.

Tym samym wielkość stopy MIRR staje się bardziej realistyczna od stopy

IRR, albowiem przy obliczaniu tej ostatniej również zakładamy

rekapitalizację uzyskiwanych wyników, ale przez samą siebie, a

mianowicie stopę IRR.



Wzór na zmodyfikowaną wewnętrzną stopę zwrotu przedstawia się

następująco:

Gdzie:
NCF

t

– przepływ gotówki netto roku t, bez inicjujących nakładów

kapitałowych,

I

t

– inicjujące nakłady kapitałowe roku t.



Wzajemne ukształtowanie się stóp „i”, IRR oraz MIRR można

przedstawić następująco:

◦

gdy NPV = 0, to i = MRR = IRR,

◦

gdy NPV > 0, to i <MIRR < IRR,

◦

gdy NPV < 0, to i > MIRR > IRR.



Zalety i wady metody zmodyfikowanej wewnętrznej stopy zwrotu

prezentuje tabela.

1

)

1

(

1

)

1

(

0

0





















n

t

i

I

n

i

NCF

MIRR

n

t

t

n

t

t

Zalety

Wady

• Korzyść netto jest wyrażona przez przepływ pieniężny
netto.
• Jest prosta w interpretacji (efekt psychologiczny związany
z preferowaniem mierników opłacalności wyrażonych
procentowo).
• Zawiera informację o poziomie marginesu bezpieczeństwa
(MIRR

– k

gr

).

• Pozwala określić graniczną stopę zwrotu, która może być
bezpośrednio porównywana z kosztem kapitału.
• Pozwala zbudować obiektywne kryterium decyzyjne dla
bezwzględnej decyzji inwestycyjnej.
• Uwzględnia w bezwzględnej ocenie opłacalności korzyści
netto z całego cyklu życia przedsięwzięcia inwestycyjnego.
• Może być stosowana do szacowania bezwzględnej
opłacalności przedsięwzięcia inwestycyjnego w sytuacji, gdy
nie jest jeszcze znana stopa dyskontowa.
• Nie wymaga przyjęcia założenia o równości stopy
reinwestycji dodatnich przepływów pieniężnych netto i
wewnętrznej stopy zwrotu.

• Nie spełnia zasady addytywności:
(MIRR

A

+ IRR

B

) ≠ MIRR

(A + B)

.

• Trudności w formułowaniu
bezwzględnego kryterium
decyzyjnego dla modelu ze zmienną
w czasie stopą dyskontową (więcej
niż jedna wartość stopy granicznej).

1)

Wykorzystanie metody koszt

– korzyść w ocenie inwestycji

infrastrukturalnych



Infrastrukturę definiuje się jako zespół urządzeń i instytucji

stwarzających podstawę zarówno dla funkcjonowania na danym terenie

gospodarki narodowej, jak i życia ludności, np.:



autostrady i drogi, w tym mosty,



linie energetyczne,



urządzenia melioracyjne,



urządzenia komunalne (wodociągi, kanalizacja, gazociągi, linie
telekomunikacyjne),



szpitale i przychodnie,



szkoły, przedszkola i żłobki,



lotniska, itd.



Infrastrukturę charakteryzuje makroekonomiczne i społeczne

znaczenie oraz publiczny wymiar zapotrzebowania na jej usługi.



Jedną z podstawowych metod oceny projektów inwestycyjnych z zakresu
infrastruktury i ochrony środowiska jest metoda koszt - korzyść (ang. cost
benefit analysis

– CBA).



Istotą tej metody jest porównanie z jednej strony korzyści z tytułu
realizowanej inwestycji typu infrastrukturalnego, a z drugiej kosztów
związanych z jej przygotowaniem i realizacją.



W projektach infrastrukturalnych w miarę dokładnie można policzyć tylko
koszty inwestycji i późniejsze koszty ich eksploatacji.



Natomiast korzyści płynące z realizacji takich projektów można tylko
wyceniać metodami szacunkowymi.



Wycena taka zawsze będzie zawierać pewien stopień subiektywności.



Kryterium wyboru projektu infrastrukturalnego jest maksymalizacja korzyści
netto.



Korzyści z projektów infrastrukturalnych dzielą się na:

-

korzyści społeczne (social impact analysis –SIA)

-

korzyści zewnętrzne (external effects – EE).



Korzyści społeczne dotyczą wpływu projektu infrastrukturalnego na

społeczność lokalną oraz jakość środowiska naturalnego.



Korzyść zewnętrzne (eksternalia) – pojawiają się w różnych sferach

gospodarki na skutek realizacji danego przedsięwzięcia i są uzyskiwane
przez podmioty spoza projektu.



Przykładowo do najważniejszych korzyści społecznych wynikających z

wybudowania zapory wodnej na Wiśle we Włocławku można zaliczyć:

1.

Wytwarzanie energii elektrycznej.

2.

Realizację usług transportowych.

3.

Oszczędności budżetowe wynikające z:

◦

rezygnacji z budowy alternatywnego mostu,

◦

dotychczasowych kosztów utrzymania rzeki Wisły na odcinku objętym

inwestycją,

◦

zaniechania robót zabezpieczających przed powodziami,

◦

ograniczenia wypłat zasiłków dla bezrobotnych przez utworzenie nowych
miejsc pracy przy budowie i eksploatacji stopni wodnych oraz przy

obsłudze ruchu turystyczno – wypoczynkowego.

4.

Ograniczenie emisji spalin przez elektrownie węglowe zastąpione

hydroelektrownią we Włocławku.

5.

Ograniczenie emisji spalin przez pojazdy korzystające ze skróconej drogi
przez nowo wybudowany most na zaporze.



Z kolei

korzyści zewnętrzne (pośrednie), czyli wtórne wobec inwestycji

podstawowej, osiągane przez podmioty gospodarcze, ludność i budżet
wskutek sprzyjających warunków, stworzonych przez tę inwestycję w
postaci netto wystąpią jako:

◦

przyrost produkcji rybackiej i rolniczej,

◦

podatki od wzrostu wartości gruntów i przyrost podatków od
nieruchomości w stosunku do podatku gruntowego,

◦

podatki od dochodów z działalności dotyczącej turystyki i
wypoczynku,

◦

oszczędności na zużyciu paliwa przez pojazdy skracające podróż
przy korzystaniu z mostu na zaporze.



Przykład procedury określającej opłacalność budowy autostrady
(drogi):

1.

Określenie rodzaju drogi i jej funkcji.

2.

Określenie rozwiązań alternatywnych, np. autostrada lub droga szybkiego
ruchu.

3.

Określenie korzyści bezpośrednich:



oszczędności w eksploatacji pojazdów (zmniejszone zużycie paliwa i

pojazdów)



oszczędności kosztów utrzymania dróg (im lepiej – wyższym kosztem –

droga jest wykonana, tym niższe będą koszty jej utrzymania),



oszczędności czasu przejazdu,



poprawa komfortu jazdy,



poprawa warunków ekologicznych.



zmniejszenie liczby wypadków.

4.

Określenie korzyści pośrednich:



wpływ inwestycji drogowej na rozwój procesów integracji międzyregionalnej
i turystyki,



wzrost prestiżu kraju i regionu,



zwiększenie możliwości wymiany handlowej zarówno krajowej, jak i
międzynarodowej,



wzrost zatrudnienia i dochodów ludności (aktywizacja terenów
przydrogowych),



zwiększony napływ kapitału zagranicznego w pobliżu autostrad i głównych
dróg.

2)

Ocena opłacalności projektów inwestycyjnych z punktu widzenia
oddziaływania na środowisko naturalne.



Celem oceny projektów inwestycyjnych z punktu widzenia ich
oddziaływania na środowisko naturalne jest zminimalizowanie
(wyeliminowanie) niekorzystnego wpływu projektów na to środowisko,
poprzez wnikliwą analizę wszystkich czynników związanych z realizacją
projektów i znalezienie rozwiązań (projektów) najmniej szkodliwych dla
środowiska naturalnego.



Ekonomiczna ocena inwestycji w ochronie środowiska jest jednym z
podstawowych wymogów szeroko rozumianej racjonalności decyzji
ekologicznych.



Ocena projektów inwestycyjnych o szerokim zasięgu środowiskowym
dokonuje się według następującej procedury (tzw. schematu analizy
wpływu środowiskowego EIA – environmental impact analysis):

1.

opis projektu wraz z uzasadnieniem jego podjęcia, dane dotyczące

lokalizacji, charakterystyka funkcjonowania;

2.

opis środowiska zawierający w szczególności dane o gruncie, stanie wody
i atmosfery, cechach krajobrazu, cechach społeczno – ekonomicznych, a
także cechach związanych z unikatowością historyczną, archeologiczną
lub tzw. wrażliwością obszaru,

3.

określenie wpływu projektu na środowisko, łącznie z fazą przygotowania
lokalizacji, w zakresie jakości wody i atmosfery, zmian ekosystemu, emisji
odpadów i ścieków, możliwości wystąpienia zagrożeń ekologicznych;

4.

określenie najbardziej prawdopodobnych negatywnych efektów
środowiskowych;

5.

określenie powiązań projektu z planami zagospodarowania
przestrzennego;

6.

przedstawienie alternatyw względem rozpatrywanego projektu;

7.

określenie relacji między krótkookresowymi i długookresowymi efektami
projektu;

8.

rozważenie różnych dopuszczalnych wariantów projektu wraz z próbą ich
zweryfikowania w aspekcie kosztów i korzyści;

9.

przeprowadzenie konsultacji wśród społeczności lokalnych;

10.

ocena projektu z punktu widzenia lokalnego oraz w wymiarze
makroekonomicznym;

11.

wnioski i rekomendacje projektu dla podmiotu decyzyjnego.



Oprócz metody koszt – korzyść w ocenie projektów dotyczących ochrony
środowiska stosowana jest również metoda minimalizacji kosztów (CEA –
cost efectiveness analysis).



Stosowana jest ona zwykle dla projektów, których korzyści są dość
precyzyjnie określone, natomiast kryterium decyzyjnym jest osiągnięcie
założonego celu po jak najniższych kosztach.

Przykład: zapewnienie dostaw wody dla miejscowości liczącej 25 tys.
mieszkańców na najbliższe 20 lat najmniejszym nakładem kosztów, np.
wybór najtańszej z możliwych technologii uzdatniania wody.

1.

Główne elementy korzyści motywujące inwestora zagranicznego



Przez bezpośrednie inwestycje zagraniczne (BIZ) rozumie się lokaty

kapitału poza granicami kraju, dokonywane w celu podjęcia przez

inwestora działalności gospodarczej od podstaw lub nabycia praw

własności w przedsiębiorstwie już istniejącym w skali umożliwiającej

bezpośredni udział w zarządzaniu (ang. FDI – foreign direct investment).



Dla NBP inwestycję bezpośrednią za granicą stanowi inwestycja

dokonywana w celu osiągnięcia długotrwałej korzyści z kapitału

zaangażowanego w przedsiębiorstwo bezpośredniego inwestowania.



Z kolei przedsiębiorstwem bezpośredniego inwestowania jest taka

jednostka organizacyjna, w której zagraniczny inwestor posiada co

najmniej 10% udziału w kapitale spółki.



Bezpośrednie inwestycje zagraniczne łączą w sobie trzy płaszczyzny

przedsiębiorczości, a mianowicie:



kapitał finansowy,



doświadczenie i wiedzę techniczną (know-how),



nowe systemy i metody zarządzania.



Inwestor zagraniczny dąży do poprawienia efektywności zastosowania
posiadanych środków.



Korzyści, których w tym celu poszukuje to:

1)

Nowe rynki zbytu,

do których zdobędzie dostęp inwestując za granicą.

Toteż na decyzje inwestora w tym względzie wpłyną:

o

rozmiary rynku wewnętrznego (klienci i ich dochody), oczekiwany wzrost
popytu na tym rynku,

o

bariery wejścia na rynek – taryfowe i nietaryfowe,

o

koszty transportu,

o

konieczność dopasowania produktu do wymagań rynku.

2)

Dostęp do zasobów:

o

zasoby surowców,

o

lokalne zasoby wytwórcze,

o

synergia z innymi istniejącymi już w danym kraju zakładami produkcyjnymi,

o

zasoby taniej i odpowiednio wykwalifikowanej siły roboczej.



Poniższe zestawienie ukazuje Chiny, jako miejsce do korzystnego
lokowania np. przemysłu odzieżowego w porównaniu do RFN.

Porównanie elementów kosztów robocizny w RFN i Chinach

Wyszczególnienie

RFN

Chiny

Dni robocze w roku

223

294

Święta i urlopy (dni/rok)

38

19

Dni robocze w tygodniu

5

6

Godziny pracy / tydzień

38

48

Godziny

pracy / dzień

7,6

8

Wydajność pracy

100%

60%

Płaca godzinowa z premią

17 EUR

0,60 EUR

Koszty socjalne w %

70

25

3)

Inne czynniki zwiększające efektywność inwestycji lokowanych za

granicą:



korzyści skali,



obniżenie kosztów transakcyjnych,



elastyczność potencjalnych zmian profilu produkcji,



poszerzenie świadomości marki,



brak wystarczającej konkurencji ze strony rodzimych i zagranicznych

przedsiębiorstw



możliwość transferu zysków,



możliwość wycofania kapitału,



zwolnienia podatkowe w kraju przyjmującym,



bliskość innych rynków zbytu, np. w przypadku Polski – Wspólnoty

Niepodległych Państw,



dobry klimat społeczny dla BIZ



dobra infrastruktura otoczenia biznesu (sieć bankowa, instytucje
ubezpieczeniowe) itp.,



warunki mieszkaniowe i wypoczynkowe dla kadry zarządzającej i jej rodzin.

2.

Korzyści kraju goszczącego z tytułu zagranicznych inwestycji

bezpośrednich



Bilans korzyści dla kraju przyjmującego kapitał w formie bezpośrednich
inwestycji zagranicznych jest bardzo szeroki i obejmuje:

◦

efekt demokratyzacji

– przyczynia się do stabilizowania i utrwalania tzw.

młodych demokracji,

◦

efekt modernizacji

– dynamizuje i zmienia system społeczno –

gospodarczy w kierunku modelu nowoczesnych społeczeństw
zachodnich,

◦

efekt wzrostowy

– wspiera wzrost gospodarczy, łagodząc niedobór

kapitału i managmentu,

◦

efekt bilansu płatniczego - zwiększa wpływy dewizowe przez import

kapitału, podejmowanie produkcji zastępującej import oraz eksport,

◦

efekt zatrudnienia

– tworzy nowe miejsca pracy,

◦

efekt konkurencji

– zwiększa konkurencję na rynku,

◦

efekt poziomu cen

– przyczynia się do stabilizacji cen dzięki masowej

produkcji charakteryzującej się niskimi kosztami,

◦

efekt dyfuzji

– wspiera postęp techniczny dzięki wysokim wydatkom na

badania i import technologii,

◦

efekt środowiska naturalnego – inwestuje w technologie przyjazne

środowisku naturalnemu,

◦

efekt płacowy – świadczy ponadprzeciętne wynagrodzenia i inne
świadczenia,

◦

efekt awansu społecznego – umożliwia np. Polakom zrobienie kariery
w ramach międzynarodowych struktur koncernów zagranicznych,

◦

efekt podnoszenia kwalifikacji

– szkoli w szerokim zakresie

pracowników,

◦

efekt kooperacji

– zaopatruje się w materiały, surowce, podzespoły oraz

korzysta z usług niezbędnych przy prowadzeniu działalności
gospodarczej na rynku wewnętrznym.



Ocena efektywności inwestycji zagranicznych, podobnie jak ocena
inwestycji na rynku lokalnym, skupia się na oszacowaniu przyrostowych
przepływów pieniężnych generowanych przez projekt.



Przy określaniu tych przepływów należy uwzględnić wiele czynników
charakterystycznych wyłącznie dla działań na arenie międzynarodowej.



Wartość obecna inwestycji jest funkcją przyszłych przepływów pieniężnych
dostępnych centrali koncernu.



W ocenie efektywności projektów zagranicznych najczęściej stosuje się
pięć podstawowych metod oceny efektywności, a mianowicie:



okres zwrotu,



zdyskontowany okres zwrotu,



wartość obecną netto (NPV),



wewnętrzną stopę zwrotu (IRR),



zmodyfikowaną wewnętrzną stopę zwrotu (MIRR)



Jednakże należy zwrócić uwagę na fakt, że szacunki przepływów
pieniężnych są bardziej złożone w przypadku inwestycji zagranicznych.



Problemy, jakie pojawiają się w tym zakresie to:

•

zachodzi różnica pomiędzy przepływami samego projektu
inwestycyjnego a przepływami dostępnymi firmie macierzystej, np. w
wyniku ograniczeń w wymienialności walut,

•

część nakładów firmy macierzystej ma postać aportów rzeczowych,

•

oczekuje się, że kurs wymiany walut nie będzie stabilny w okresie
realizacji inwestycji,

•

inne stawki podatkowe w kraju, w którym podejmuje się inwestycje, a
inne w kraju, w którym znajduje się siedziba podmiotu inwestującego,

•

istotną rolę odgrywają opłaty licencyjne i opłaty za zarządzanie,

•

nie ma możliwości przekazania firmie macierzystej wszystkich strumieni
pieniężnych pochodzących z realizacji projektu.