8. METODY OCENY EFEKTYWNOŚCI PROJEKTÓW INWESTYCYJNYCH

Zagadnienia mierzenia i oceny efektywności funkcjonowania przedsiębiorstw należą do najważniejszych problemów analizy i diagnozowania stanu i perspektyw firm działających w otoczeniu rynkowym .

Badanie ekonomicznej efektywności jest niezbędną procedurą poprzedzającą podjęcie każdej decyzji inwestycyjnej .

Ocena każdego projektu inwestycyjnego powinna nastąpić w sposób :

• absolutny - czyli odpowiedzieć na pytanie czy podjęcie danego projektu jest ekonomicznie uzasadnione ?

• relatywny - czyli wyłonić spośród realnych wariantów inwestycyjnych ten o największej efektywności ekonomicznej.

Rachunek ekonomiczny dla dużych , długotrwałych , kosztownych i ryzykownych przedsięwzięć inwestycyjnych powinien być sporządzony wg kilku metod i powinien być uaktualniany w miarę potrzeb i możliwości.

Wiarygodność wyniku rachunku ekonomicznego jest w dużym stopniu uzależniona od odpowiedniego dobrania metody przeprowadzania rachunku do danego przedsięwzięcia oraz od jakości danych ekonomiczno-finansowych będących podstawą tego rachunku .

Przyjmując za kryteria klasyfikacyjne zakres przedmiotowy przedsięwzięć inwestycyjnych (pojedyncze inwestycje lub programy inwestycyjne) oraz warunki realizacji (deterministyczne lub niedeterministyczne) dzielimy je na cztery klasy .

Pojedyncze przedsięwzięcia w warunkach deterministycznych oceniane są za pomocą metod klasy I , do których należą m.in. metody statyczne i dynamiczne. Pojedyncze przedsięwzięcia w warunkach niedeterministycznych oceniane są za pomocą metod klasy II , do których zaliczamy m.in. analizę wrażliwości i metodę drzewa decyzyjnego czy analizę ryzyka.

METODY

1. Okres zwrotu -PB (Payback Period)

2. Zdyskontowany PB

3. Wartość obecna netto inwestycji, NPV (Net Present Value)

4.Wewnętrzna stopa zwrotu, IRR (Internal Rate of Return)

5.Wskaźnik zyskowności, PI (Profitability Index).

1. Okres zwrotu

a) dla równych rocznych wpływów gotówkowych w kolejnych latach życia projektu, NCFi = const, i = 1,2,...,n

PB = NINV/NCF

b) dla różnych NCFi

PB = t + (b-c)/d-c), gdzie

t- ostatni pełny rok, w którym skumulowana NCF jest mniejsza niż wydatek inwestycyjny,

b - wydatek inwestycyjny -NINV,

c - skumulowane wpływy gotówkowe w roku t,

d - skumulowane wpływy gotówkowe w roku t+1.

Przykład: Rozważmy dwa projekty A oraz B. W obu przypadkach wydatek inwestycyjny jest jednorazowy i wynosi 50 000zł. Przewiduje się 6-letni czas życia projektu. Wpływy gotówkowe z obu projektach w zł. przedstawia tabela #.

Tab. # Wpływy gotówki w rozważanym projekcie.

	Projekt A		Projekt B
rok	NCF	Skumul.NCF	NCF	Skumul. NCF
1	12 500	12 500	5 000	5 000
2	12 500	25 000	10 000	15 000
3	12 500	37 500	15 000	30 000
4	12 500	50 000	15 000	45 000
5	12 500	62 500	25 000	70 000
6	12 500	75 000	30 000	100 000

Wówczas

PBA = 50 000/12 5000 = 4 lata

PBB = 4 + (50 000 - 45 000)/(70 000 - 45 000) = 4 + 5 000/25 000 = 4.2 roku

2. Zdyskontowany PB.

Zdyskontowany PB oblicza się podobnie jak PB, ale wcześniej należy obliczyć zdyskontowane wartości NCF, przy założonej stopie dyskontowej i dopiero potem obliczać skumulowane wartości.

3. Metoda NPV

W metodzie NPV dokonuje się porównania zdyskontowanych wydatków inwestycyjnych ze zdyskontowanymi wpływami

NPV = PVNCF - NINV = NCF1/(1+k)1 + NCF2/(1+k)2 +....+NCFn/(1+k)n - NINV =

= NCFi/(1+k)i - NINV,

gdzie

k - żądana stopa zwrotu z inwestycji (koszt kapitału inwestycyjnego),

n - okres życia projektu.

Przykład.

Rozważmy projekty inwestycyjne A, B z przykładu #, w którym wykorzystano kapitał inwestycyjny o koszcie kapitału 14%.

Projekt A.

PVNCF - skumulowaną wartość obecną zdyskontowanych wpływów można obliczyć korzystając z wzoru na 6-letnia rentę (annuity) o rocznych płatnościach 12 5000zł. przy oprocentowaniu 14%.

PVNCF = 12 500*(PVFA0.14, 6) = 12 500*3.889 = 48 612.500zł

i wówczas

NPV = 48 612.500 - 50 000 = -1387.500

Projekt B.

Tab. # Obliczanie NPV dla projektu B.

lata	NCF	PVIF	PV(NCF)
1	5 000	0.877	4 385
2	10 000	0.769	7 690
3	15 000	0.675	10 125
4	15 000	0.592	8 880
5	25 000	0.519	12 975
6	30 000	0.456	13 680
RAZEM			57 735

NPV = 57 735zł.- 50 000zł. = 7 735zł

4. Wewnętrzna stopa zwrotu

IRR jest stopa zwrotu generowana przez rozważany projekt. Inaczej mówiąc jest to wartość stopy dyskontowej, przy której

PVNCF = NINV,

NCFi/(1+r)i = NINV , to r =?

Stopę tę oblicza się w sposób rekurencyjny metodą kolejnych przybliżeń, Rys. #

Krok 1. Założyć stopę dyskontową

krok 2. Wykorzystując tę stopę obliczyć NPV

Krok 3. Jeśli NPV>0, przyjąć wyższą stopę dyskontową,

jeśli NPV<0 przyjąć niższą stopę dyskontowa

Krok 4. Powtarzać kroki aż NPV będzie bliskie lub równe zero.

Przykład.

dalszy ciąg przykładu # dla projektu B, dla którego przy r = 14%, NPV = 7 735zł

Wiadomo, że dla r=14%, NPV= 7 735zł., zatem IRR powinno być wyższe. Załóżmy stopę dyskontową w wysokości 15%, wówczas

r = 15% , to NPV = 5 745zł

Ponieważ NPV wciąż jest dodatnie zakładamy wyższą stopę, np. 19%, wówczas

r = 19%, to NPV = -1 325zł

Otrzymaliśmy ujemną wartość NPV, zatem zmniejszamy niższą stopę dyskontową, np. 18%, wówczas

r = 18%, to NPV = 315 zł.

Zatem IRR generowany przez projekt B wynosi około 18%. Jeśli koszt kapitału inwestycyjnego jest niższy niż 18%, projekt można realizować, ponieważ w efekcie będzie generowany zysk.

5. Wskaźnik zyskowności , PI

Wskaźnik ten oblicza się jako stosunek sumy zdyskontowanych wpływów gotówkowych do sumy zdyskontowanych wydatków inwestycyjnych

PI = [NCFi/(1+r)i ]/NINV

Jeśli PI przyjmuje wartość większą niż 1, to przyjmuje się, że projekt jest opłacalny.

Przedstawione metody nie zawsze dają podobne efekty. Projekt, który jedna z metod zakwalifikuje jako opłacalny, inna metoda może zakwalifikować jako nieopłacalny. Również przy porównywaniu opłacalności projektów inwestycyjnych należy mieć na uwadze, że każda z metod kwalifikuje projekty według odmiennych kryteriów. A więc wyniki tylko jednej metody nie mogą być podstawą stwierdzenia o tym, że jeden projekt jest lepszy od drugiego. Przy wyborze projektów należy w pierwszej kolejności ustalić cel badania opłacalności projektów inwestycyjnych, a następnie które kryterium jest w danym konkretnym przypadku ważniejsze.

Rys. 2. Wartości NPV oraz IRR dla projektów inwestycyjnych I, II, III

2. METODY SZACOWANIA OPŁACALNOŚCI INWESTYCJI W WARUNKACH RYZYKA

Przy stosowaniu modeli PB, NPV, IRR, PI i ich modyfikacjach zakłada się, że ryzyko rozważanych projektów jest takie samo, oraz że ryzyko związane z projektem inwestycyjnym jest identyczne jak ryzyko dla całej firmy. Ryzyko projektu może być większe, mniejsze lub równe ryzyku globalnemu przedsiębiorstwa, dlatego w dzisiejszej ekonomii istotnym problemem staje się rozważenie ryzyka projektu w kontekście ryzyka firmy, rozumianego jako ryzyko portfela.

Stopę zwrotu, która odzwierciedla stopę zwrotu z projektu w kontekście całej firmy, otrzymuje się zwykle z o wiele mniejszym ryzykiem niż ryzyko pojedynczego projektu. Oczywiście, wszystko zależy od tego, w co się inwestuje i kto inwestuje. Chociaż wpływ ryzyka pojedynczego projektu inwestycyjnego na ryzyko firmy (traktowanej jako portfel działalności) nie jest zbyt duży, to jednak należy zwracać uwagę na ryzyko projektu, ryzyko firmy oraz wpływ ryzyka projektu na ryzyko firmy.

1. Metoda subiektywna

W wielu sytuacjach podejmowania decyzji wiedza i doświadczenie dają lepsze wyniki niż stosowanie najbardziej skomplikowanych metod. Menedżer ocenia ryzyko subiektywnie. Na podstawie tej subiektywnej oceny dokonuje wyboru projektu inwestycyjnego. Oczywiście, jeśli dwa projekty są tak samo ryzykowne, wybiera ten, który oferuje wyższą stopę zwrotu. Jeśli dwa projekty mają takie samo NPV, ale różny stopień ryzyka - wybiera projekt o mniejszym ryzyku. Gorzej, gdy zgodnie z regułą rynkową im wyższe NPV, tym większe ryzyko. I wówczas, albo doświadczenie menedżera podpowie, który projekt wybrać, albo należy się jednak odwołać do innych technik wspierania decyzji.

2. Metoda NPV/PB

Podstawą szacowania opłacalności projektów inwestycyjnych jest CF_t. Zgodnie z wcześniejszymi rozważaniami przyjmuje się, że im CF_t bardziej odsunięte w czasie, tym bardziej niepewne. Zastosowanie ilorazu

do oceny opłacalności projektu inwestycyjnego ułatwia podjęcie decyzji. Stosunek ten obrazuje średnie NPV przypadające na 1 rok okresu zwrotu. Oczywiście, gdy CF_t nie jest równomiernie rozłożony w czasie, przydatność tego sposobu nie jest oczywista. Wiele projektów generuje CF_t bardzo szybko, wiele zaś późno. Ryzyko tych drugich jest o wiele większe. Zastosowanie metody NPV/PB powinno być poprzedzone dokładną analizą CF_t.

3. Metoda dodawania ryzyka do stopy dyskontowej - RADRA (risk adjusted discount rate approach)

W metodzie NPV do dyskontowania CF_t rozważanych projektów wykorzystuje się koszt kapitału firmy. W metodzie RADAR proponuje się stosowanie różnych stóp dyskontowych do wyznaczania NPV dla różnych projektów, w zależności od poziomu ryzyka projektu. Premia za ryzyko

Θ = k - r_f,

gdzie:

Θ - premia za ryzyko,

r_f - stopa wolna od ryzyka,

k    - żądana stopa zwrotu dla projektów o średnim poziomie ryzyka; często przyjmo-
 wana na poziomie kosztu kapitału firmy.

W związku z tym CF_t projektów o ryzyku większym niż ryzyko średnie powinno być dyskontowane po wyższej stopie k*, która uwzględnia premię za ryzyko (cenę ryzyka) rozważanych projektów. Występuje tu problem szacowania premii za ryzyko dla poszczególnych projektów. W metodzie RADAR proponuje się subiektywne ustalenie premii za ryzyko, zależne od rodzaju projektu inwestycyjnego lub korzystanie z rynkowych szacunków ceny ryzyka.

4. Metoda progowa (hurdle rate approach)

Metoda progowa jest bardzo podobna do metody RADAR. Podstawą jej jest zastosowanie metody IRR do szacowania opłacalności inwestycji. Jeżeli w metodzie RADAR żądana stopa zwrotu (stopa dyskontowania CF_t) jest oszacowana na poziomie k*, opłacalność projektu należy porównywać z k*, a nie z kosztem kapitału firmy. Stopę k* nazywa się progiem opłacalności.

5. Metoda ekwiwalentu pewności

W tej metodzie oczekiwany NCF oblicza się przez dyskontowanie szacowanego CF_t po r_f (stopie wolnej od ryzyka), a następnie - po uwzględnieniu niepewności, ryzykowności otrzymania NCF_t - mnoży się jego wartość przez pewien współczynnik pewności α_t [7],

Współczynnik α_t [0,1] odzwierciedla szansę uzyskania oczekiwanego NCF_t w chwili t i wówczas

.

Dyskontowanie następuje po stopie wolnej od ryzyka, a nie po koszcie kapitału firmy, ponieważ α_t zawiera w sobie całe ryzyko. Zwykle im t większe, tym α_t mniejsze, jako że z odległością w czasie zwiększa się niepewność otrzymania oczekiwanego NCF_t. Dla różnych projektów rozważanych w firmie α_t są różne, w zależności od ryzyka samego projektu.

6. Symulacja

Metoda symulacyjna jest zwykle stosowana w analizie dużych projektów. Rozwój technik mikrokomputerowych pozwala stosować ją w każdej sytuacji.

Strumień gotówki netto NCF_t oblicza się następująco [1], [7]

NCF_t = [np - n(c + s) - A] [1 - T] + A,

gdzie:

n - liczba sztuk wyrobu,

p - cena jednostkowa sprzedaży wyrobu,

c - jednostkowy koszt produkcji,

s - jednostkowy koszt sprzedaży,

A - amortyzacja,

T - stopa podatku dochodowego.

Wykonując symulację NPV zakłada się (lub estymuje) dla każdej zmiennej (lub wybranych) odpowiednie rozkłady prawdopodobieństwa. W wyniku symulacji otrzyma się

jako zmienną losową o wartości oczekiwanej oraz wariancji σ²_NPV lub odchyleniu standardowym σ_NPV. Można również otrzymać odpowiednią dystrybuantę zmiennej losowej NPV

7. Metoda uwzględniania β-ryzyka

Metodę tę stosuje się wtedy, gdy konieczne jest rozważenie ryzyka projektów i przy założeniu, że stopy zwrotu z rozważanych projektów są dodatnio skorelowane ze stopą zwrotu firmy jako całości (ryzyko mierzone  można wykorzystać również w metodzie RADAR, dla firm, których akcje są w publicznym obrocie). W metodzie tej firmę rozpatruje się jako portfel projektów o różnym ryzyku systematycznym. Ryzyko systematyczne firmy jako całości zakłada się jako średnią ważoną ryzyka projektów indywidualnych. W zależności od wartości β_i rozważanego i-tego projektu (jego ryzyka), zgodnie z modelem wyceny aktywów kapitałowych CAPM, żądana stopa zwrotu R_i jest inna - niższa dla mniej ryzykownych projektów inwestycyjnych (niższa wartość  ) i wyższa dla większej wartości , wówczas

R_i = R_f + β_i (R_m - R_f)

i służy do szacowania opłacalności projektu. Sposób wyznaczenia R_i przedstawiono na rysunku 7.

Uwzględnienie β_i w procesie szacowania opłacalności inwestycji może dać zaskakujące wyniki w porównaniu ze zwykłymi metodami, odnoszącymi IRR do ważonego średniego kosztu kapitału WACC. Rozważmy 4 projekty P₁, P₂, P₃, P₄ (rys. 5.11).

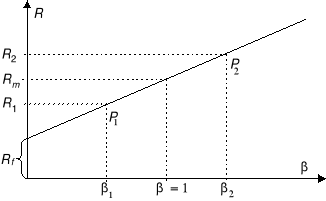
Rys. 7. Rynkowa linia papieru wartościowego - SML firmy i rozważane projekty (na podstawie pracy

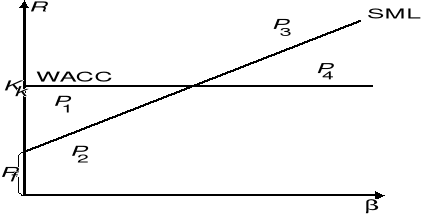
Rys. 8. Uwzględnienie  versus średni ważony koszt kapitału WACC (na podstawie pracy

W zadaniu szacowania opłacalności projektów inwestycyjnych, po zastosowaniu metody IRR i porównaniu wewnętrznej stopy zwrotu projektów z ważonym kosztem kapitału, menedżer zaakceptuje projekty P₃ i P₄, ponieważ stopy zwrotu R₃ i R₄ są większe od ważonego kosztu kapitału K_k. Uwzględnienie  powoduje, że menedżer powinien zaakceptować projekty P₁ i P₃, ponieważ R₁ i R₃ leżą ponad SML, czyli oferują więcej niż można uzyskać średnio na rynku. Obserwacja zachowania się akcji firm z interesującej branży na giełdzie, tzn. obserwacja firm, których akcje są w publicznym obrocie, a które są charakterystyczne dla rozważanych projektów, ułatwia szacowanie β_i projektów indywidualnych.

Omawiane w tym artkule modele szacowania opłacalności inwestycji są stosowane do badania efektywności projektów pojedynczych. Ryzyko portfela projektów, złożonego z dwóch projektów o wysokim ryzyku, może być o wiele niższe niż ryzyko indywidualne. Również więc i ocena efektywności portfela może być różna od efektywności sugerowanej przez projekty pojedyncze.

WIELOKRYTERIALNE METODY OCENY OPŁACALNOŚCI INWESTYCJI

Obecnie coraz częściej spotyka się opinie , iż uwzględnianie przy ocenie projektów inwestycyjnych wyłącznie takich metod jak NPV , IRR czy innych metod o podobnej konstrukcji może prowadzić do poważnych błędów w decyzjach inwestycyjnych .

Marketingowcy np. uważają , iż często korzystniejsza jest dla firmy taka inwestycja , która umożliwia jej wejście na zupełnie nowy segment rynku , niż inwestycja , która ma szczególnie korzystne NPV czy IRR .

Metody dynamiczne nie uwzględniają również innych aspektów niefinansowych planowanej inwestycji takich jak :

• stopień zgodności z przyjętą wcześniej strategią firmy ,

• uwarunkowania techniczno-technologiczne ,

• uwarunkowania ekologiczne ,

• uwarunkowania prawne .

Stąd też coraz częściej stosuje się wielokryterialne metody oceny inwestycji uwzględniające , oprócz kryteriów o charakterze finansowym , również rynkowych , ekologicznych , technicznych , prawnych etc.

Metody te składają się z szeregu następujących po sobie etapów .

Etap I to wyznaczenie kryteriów wstępnych (progowych) , które określają jakie warunki muszą być spełnione , aby inwestycja była zaakceptowana .

Mogą być nimi przykładowo następujące stwierdzenia :

• wartość bieżąca netto (NPV) ma być większa od zera ,

• wewnętrzna stopa zwrotu (IRR) ma być większa od stopy procentowej ,

• projekt inwestycyjny ma zmieścić się w z góry określonym budżecie ,

• projekt inwestycyjny ma być zgodny z przyjętą strategią rozwojową przedsiębiorstwa .

Jeśli kryteria wstępne są spełnione , to projekt przechodzi do etapu kolejnego .

Przykład :

Rozpatrujemy 5 projektów inwestycyjnych A , B , C , D i E , ale kryteria wstępne spełniły tylko projekty A , C i D i tylko one przechodzą do etapu II .

W etapie II określonym kryteriom oceny przypisywane są konkretne wagi (maksymalne liczby punktów do zdobycia przez dane kryterium) .

Mamy 5 kryteriów oceny projektów i ilość maksymalnych punktów w poszczególnych kryteriach jest następująca : 40 , 30 ,10 , 5 , 15 (maksymalna do zdobycia przez projekt suma punktów wynosi więc 100)

Etap III polega na przypisaniu do poszczególnych kryteriów liczby punktów ,,zdobytych'' przez oceniany projekt .

Projektowi A przypisujemy następującą liczbę punktów w poszczególnych kryteriach : 30 , 25 , 10 , 5 ,10 (łącznie więc projekt uzyskał 80 punktów) ; podobnie postępujemy z pozostałymi projektami (C i D) .

Etap IV to porównanie rezultatów ,,uzyskanych'' przez poszczególne projekty i wybranie tego , który uzyska wynik najlepszy jako ,,wielokryterialnie'' najbardziej atrakcyjnego .

Projekt C uzyskał łącznie 65 pkt. , zaś projekt D 72 pkt. Wybieramy więc do realizacji projekt A jak najatrakcyjniejszy z całej piątki rozpatrywanych projektów .

Oczywiście rangowanie projektów może być stosowane nie tylko dla kryteriów o charakterze jakościowym i niemierzalnym , ale również dla kryteriów wyrażanych liczbowo (np. określonym wartościom NPV czy IRR przypisujemy określoną wartość punktów) .

W stosowaniu wielokryterialnych , wieloetapowych metod oceny inwestycji szczególnie ,,lubują się'' banki , które muszą odpowiedzieć sobie na pytanie, czy powinny finansować określone przedsięwzięcia przedsiębiorstwa .

Stosują one własne , dopasowane do swoich potrzeb procedury oceny projektów inwestycyjnych, ale cały proces oceny przebiega z reguły wg następującego schematu :

• analiza standingu finansowego przedsiębiorstwa ,

• ocena finansowa projektu (szczególny nacisk kładzie się na analizę finansowej wykonalności projektu) ,

• łączna ocena jakości i atrakcyjności projektu inwestycyjnego ,

• decyzja o podjęciu się , bądź rezygnacji z (ewentualnie o spełnieniu pewnych dodatkowych wymogów) , finansowania danego projektu inwestycyjnego , a w przypadku pozytywnej decyzji - również określenie warunków szczegółowych .

Istnieją również pewne niebezpieczeństwa związane ze stosowaniem metod wielokryterialnych takie jak : możliwość złego doboru kryteriów oceny czy ich wag , nie odpowiednie ,,wmontowanie'' kryteriów finansowych w system oceny czy nadmierne skomplikowanie procedury oceny .

Bardzo szerokie pole do działania w zakresie udoskonalania tego systemu mają więc osoby zajmujące się profesjonalnie problematyką inwestycji .

Pewne niedoskonałości metod wielokryterialnych nie pomniejszają jednak znacząco ich roli i wydaje się , iż będą one coraz częściej stosowane w polskich przedsiębiorstwach .

Przykład

Firma TOR Corporation rozważa projekty inwestycyjne na przyszły rok. Po wstępnej selekcji, dalszej analizie są poddane inwestycje o takiej samej stopie ryzyka [48], dla których IRR jest większe niż 10% (tab. 7.22).

Tab. 7.24 Projektowane inwestycje.

Nazwa projektu	Żądany kapitał inwestycyjny [mln. zł]	Wewnętrzna stopa zwrotu - IRR [%]
A	4,0	13,8
B	8,0	13,5
C	6,0	12,5
D	5,0	12,0
E	8,0	11,0
F	4,0	10,0

Aktualna struktura kapitału firmy jest następująca: 40 % - kapitał obcy, 10 % - kapitał akcyjny preferowany, 50 % - kapitał akcyjny zwykły. W strategii finansowej firmy nie przewiduje się zmiany struktury kapitałowej. Firma może uzyskać następujące fundusze:

• dług: 5 mln. zł - kredyt bankowy oprocentowany w wysokości i_d = 9 % rocznie; więcej niż 5 mln. zł - i_d = 10 % rocznie

• kapitał własny: wykorzystanie własnych źródeł finansowania zgodnie z przyjętą strategią finansową powinno uwzględniać następujące ograniczenia:

- zaangażowanie 10 mln. zł funduszu własnego w postaci zysku zatrzymanego,

- akcje preferowane, których stopa kosztu wynosi k_ap = 10 % (roczna stopa dywidendy),

- dywidenda dla akcji zwykłych D_o = 2 zł płacona jest za 1 akcję zwykłą, której aktualna cena wynosi P_o = 25 zł,

- nowo wyemitowane akcje zwykłe będzie można sprzedać po cenie P_o' = 24 zł za 1 akcję,

- przewiduje się g = 7 % wzrost firmy,

- firma płaci t = 40 % podatku dochodowego.

Aby optymalnie dobrać fundusz inwestycyjny należy teraz obliczyć koszt kapitału inwestycyjnego oraz wyznaczyć budżet optymalny.

I. Obliczenie kosztu kapitału inwestycyjnego.

1) Koszt długu k_d

k_d = i_d (1 - t) = 9% * 0,6 = 5,4 % dla kredytu
5 mln. zł

k'_d =i'_d (1 - t) = 10% * 0,6 = 6 % dla kredytu
5 mln. zł

2) Koszt akcji preferowanej k_ap = 10 %

3) Koszt kapitału własnego

- zaangażowanego zysku (do 10 mln. zł); zaangażowanie kapitału wiąże się z niewypłaceniem dywidendy akcjonariuszom, a więc

k_e = D_o (1+g) / P_o + g = 2 zł(1 + 0,07) / 25 zł + 0,07 = 15,6 %,

- emisji nowych akcji zwykłych

k'_e = D_o (1+g) /
+ g = 15,9 %.

Po określeniu kosztu poszczególnych składników kapitału oblicza się możliwe do uzyskania najtańszym sposobem kwoty kapitału zgodne z istniejącą strukturą kapitału firmy.

4) Średni ważony koszt kapitału inwestycyjnego.

a. Najtańszą formą pozyskania kapitału inwestycyjnego jest zaciągnięcie kredytu bankowego w wysokości 5 mln. zł. Ponieważ zgodnie z celową strukturą kapitału firmy, ta forma finansowania stanowi 40 % całego funduszu, a więc wielkość kapitału inwestycyjnego W₁ uzyskanego najniższym kosztem może wynosić najwyżej

W₁ = = 12,5 mln. zł.

Na kwotę tę składa się:

5 mln. zł - kredyt bankowy (0.4), 1,25 mln. zł - akcje preferowane (0.1), reszta - 6,25 mln. zł - kapitał własny (0.5).

Średni ważony koszt 12,5 mln. zł kapitału inwestycyjnego wynosi

k(W₁) = 0,40 * 5,4 % + 0,1 * 10 % + 0,5 * 15,6 % = 10, 96 %

b. Kapitał inwestycyjny przekraczający 12,5 mln. zł będzie kosztował więcej, ponieważ koszt kredytu bankowego większego niż 5 mln. zł wynosi już 6 %. Zysku zatrzymanego zostało do wykorzystania tylko 10mln. zł - 6,25mln. zł = 3,75 mln. zł. Zatem wielkość kapitału inwestycyjnego W₂, możliwego do uzyskania po kosztach wyższych niż W₁, ale niższych niż koszt maksymalny wynosi

W₂ = = 7,5 mln. zł

Na kwotę tę (zgodnie z celową strukturą finansowania) składają się: 3 mln. zł - kredyt bankowy (0.4) z 6 % kosztem, 0,75 mln. zł - akcje preferowane (0.1) z 10 % kosztem, 3,75mln. zł - środki obrotowe własne (0.5) z 15,6 % kosztem.

Średni ważony koszt kapitału W₂ wynosi

k(W₂) = 0,4 * 6 % + 0,1 * 10 % + 0,5 * 15,6 % = 11,2 %

c. Ponieważ są już wyczerpane możliwości korzystania z tańszych form finansowania, firma może uzyskać dowolną kwotę W₃ kapitału inwestycyjnego po koszcie

k(W₃) = 0,4 * 6 % + 0,1 * 10 % + 0,5 * 15,9 % = 11, 35 %.

II. Wyznaczenie optymalnego budżetu inwestycyjnego.

Optymalny budżet inwestycyjny otrzymuje się przez porównanie średniego ważonego kosztu kapitału oraz oczekiwanych stóp zwrotu z inwestycji (rys. 7.6). Wyznacza go punkt przecięcia się krzywej korzyści z krzywą marginalnych kosztów kapitału.

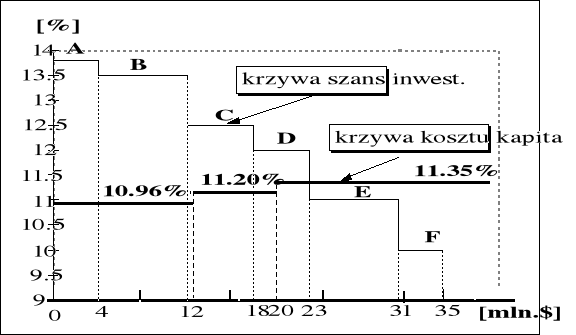
Rys.. Krzywa stopy zwrotu inwestycji i krzywa marginalnych kosztów kapitału.

Optymalny budżet TOR Corporation wynosi 23 mln. zł. Będą realizowane projekty A, B, C, D. Realizacja dodatkowych projektów E i F spowodowałaby zmniejszenie średniej stopy zwrotu z inwestycji, ponieważ koszt kapitału inwestycyjnego przewyższającego 23 mln. zł jest wyższy niż oczekiwana wewnętrzna stopa zwrotu z inwestycji E i F.

3

---