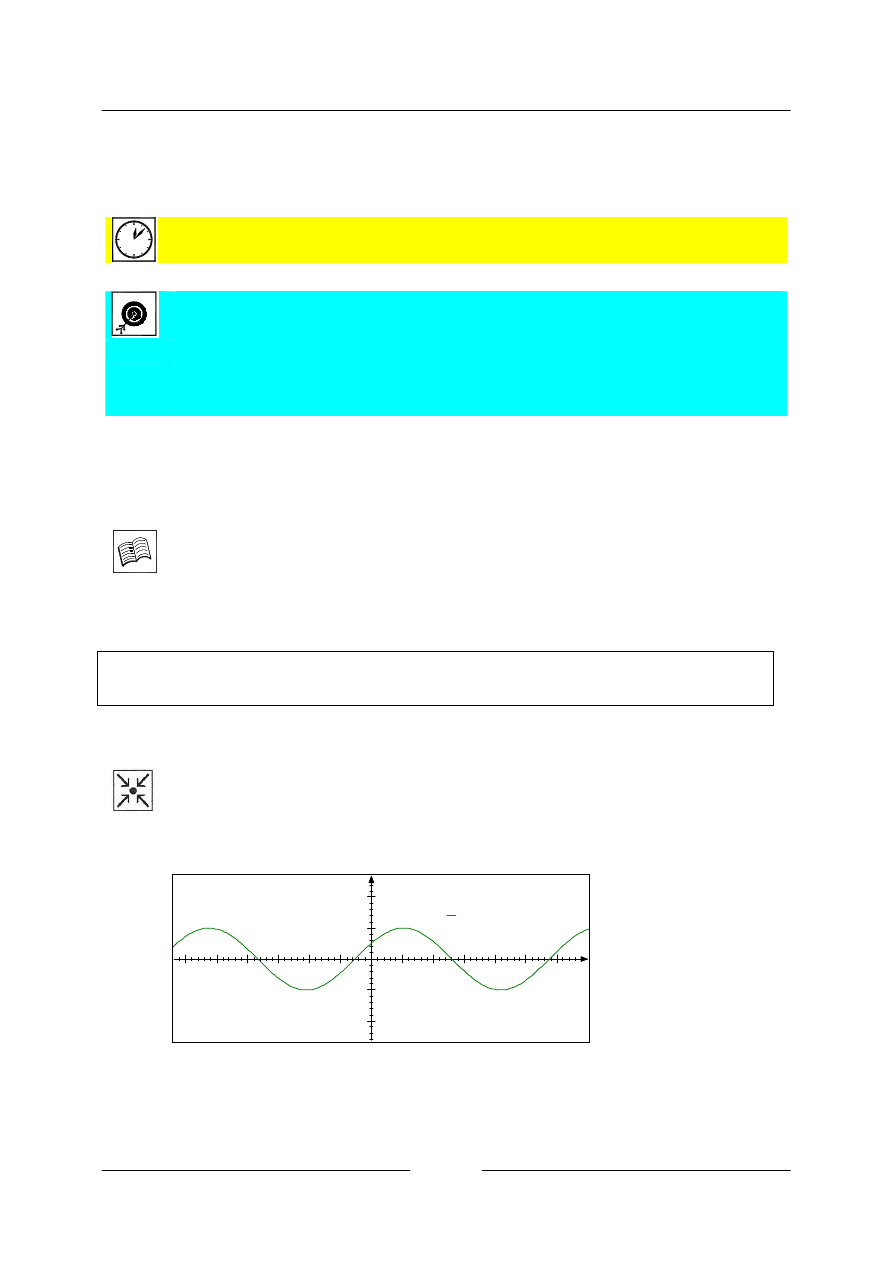
3. Funkce

97

3. FUNKCE

Čas ke studiu: 6

hodin

Cíl

•

Seznámíte se s pojmem funkce, možností zadání funkce, dále pak elementárními
funkcemi, jejich vlastnostmi a grafy.

Funkce jsou základním stavebním kamenem matematiky, bez jejich znalostí se nebudete moci
v dalším studiu seznámit s pojmy limita, derivace, integrál… Pojem funkce je důležitý také ve fyzice a
ostatních technických předmětech.

Než se budeme zabývat funkcemi, zavedeme si pojem zobrazení, bez kterého bychom se do studia
funkcí nemohli pustit.

Zobrazením nazýváme množinu uspořádaných dvojic

[ ]

y

x,

, kdy

B

y

A

x

∈

∈ ,

, pro které

platí, že ke každému

A

x

∈

existuje nejvýše jedno

B

y

∈ .

POZOR ! Pro

y

x

≠

platí

[ ] [ ]

x

y

y

x

,

,

≠

.

Řešený příklad

• Rozhodněte, zda se jedná o zobrazení, či nikoli.

a)

Řešení

Toto je zobrazení, každému

x

přísluší jediné

y

.

-1

-2

-3

-4

-5

-6

1

2

3

4

5

6

-1

-2

1

0

x

y

-1

-2

-3

-4

-5

-6

1

2

3

4

5

6

-1

-2

1

0

x

y

y=cos( π

3

- x)

3. Funkce

98

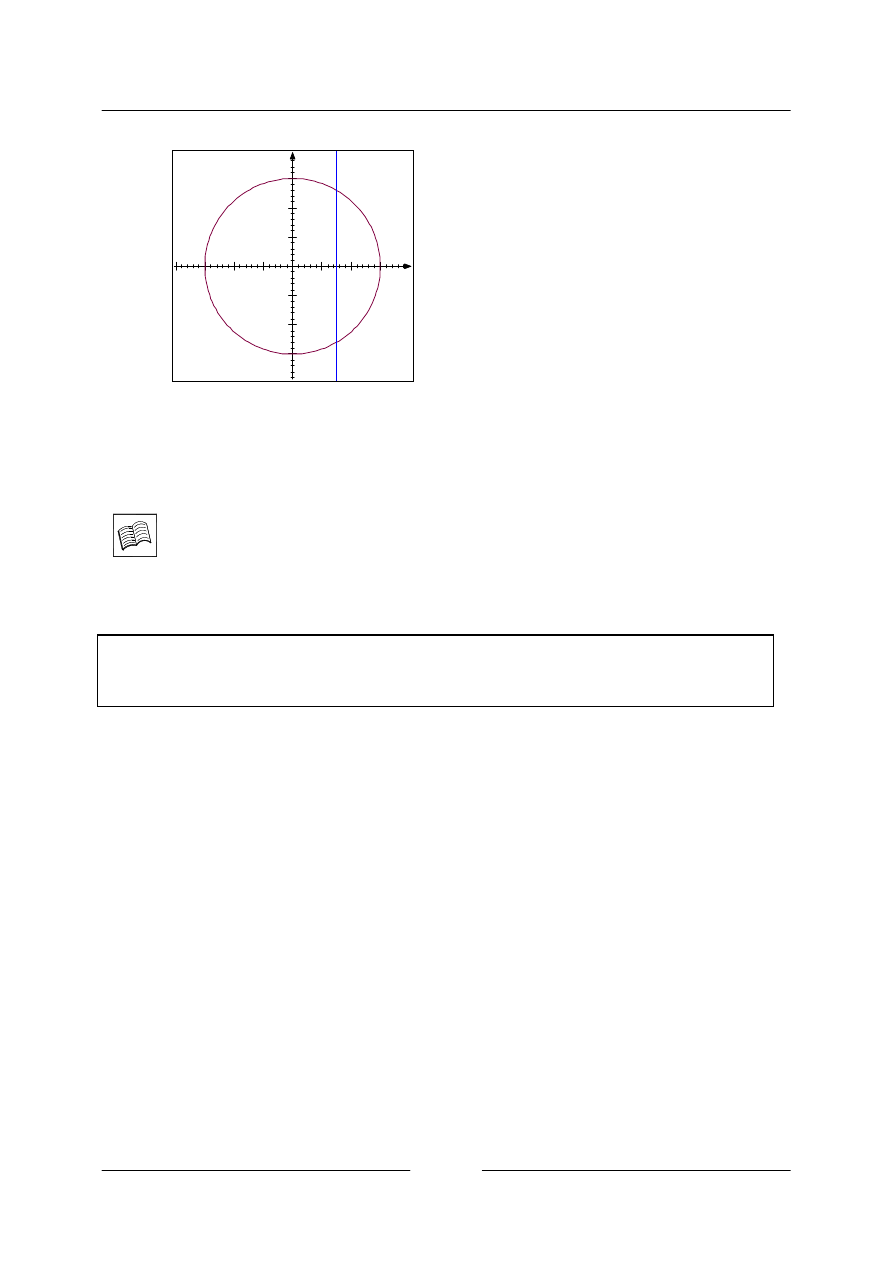
b)

Řešení

V tomto případě se o zobrazení nejedná, pro

5

,

1

=

x

nacházíme dvě funkční hodnoty, tato situace je

stejná pro všechna

(

)

3

,

3

−

∈

x

.

Nyní zavedeme pojem funkce a uvedeme její vlastnosti. Tyto vlastnosti budeme používat i v dalších
kapitolách.

Funkcí

na množině

R

⊂

A

rozumíme zobrazení, které číslu z množiny

R

⊂

A

přiřadí

právě jedno reálné číslo. Množinu

R

⊂

A

nazýváme definiční obor funkce.

Ozn.

( )

f

D

.

2

r

S

π

=

je funkční předpis vyjadřující závislost velikosti obsahu

S

kruhu na jeho poloměru

r

.

Velikost poloměru si volíme –

r

je nezávislá proměnná.

Obsah kruhu vypočítáme ze vzorce –

S

je závislá proměnná.

Označme si naši funkci

2

:

r

S

g

π

=

.

Čísla, která můžeme dosadit za

r

, určují definiční obor. Je zřejmé, že nelze za

r

dosadit

záporné číslo a nulu. Definiční obor značíme

( ) ( )

∞

= ,

0

g

D

Hodnotu funkce

g

v bodě

o

r

označíme

( )

o

o

S

r

g

=

a budeme nazývat funkční hodnota v

o

r

. Množinu všech výsledků , kterou dostaneme postupným dosazováním všech hodnot

( )

g

D

r

∈

do

funkčního předpisu, nazýváme obor hodnot funkce

g

a značíme

( ) ( )

∞

= ,

0

g

H

.

Obecně, budeme-li mít dánu funkci

f

, ve které je číslu

( )

f

D

x

o

∈

přiřazeno číslo

o

y

, označíme

tento fakt

( )

o

o

y

x

f

=

Jiná možnost zadání funkce je tabulkou nebo grafem.

-1

-2

-3

1

2

3

-1

-2

-3

1

2

3

0

x

y

-1

-2

-3

1

2

3

-1

-2

-3

1

2

3

0

x

y

3. Funkce

99

Tabulka:

r

0,1

0,5

1

1,2

1,5

2

r

S

π

=

0,0314

0,785

3,14

4,5216

7,06

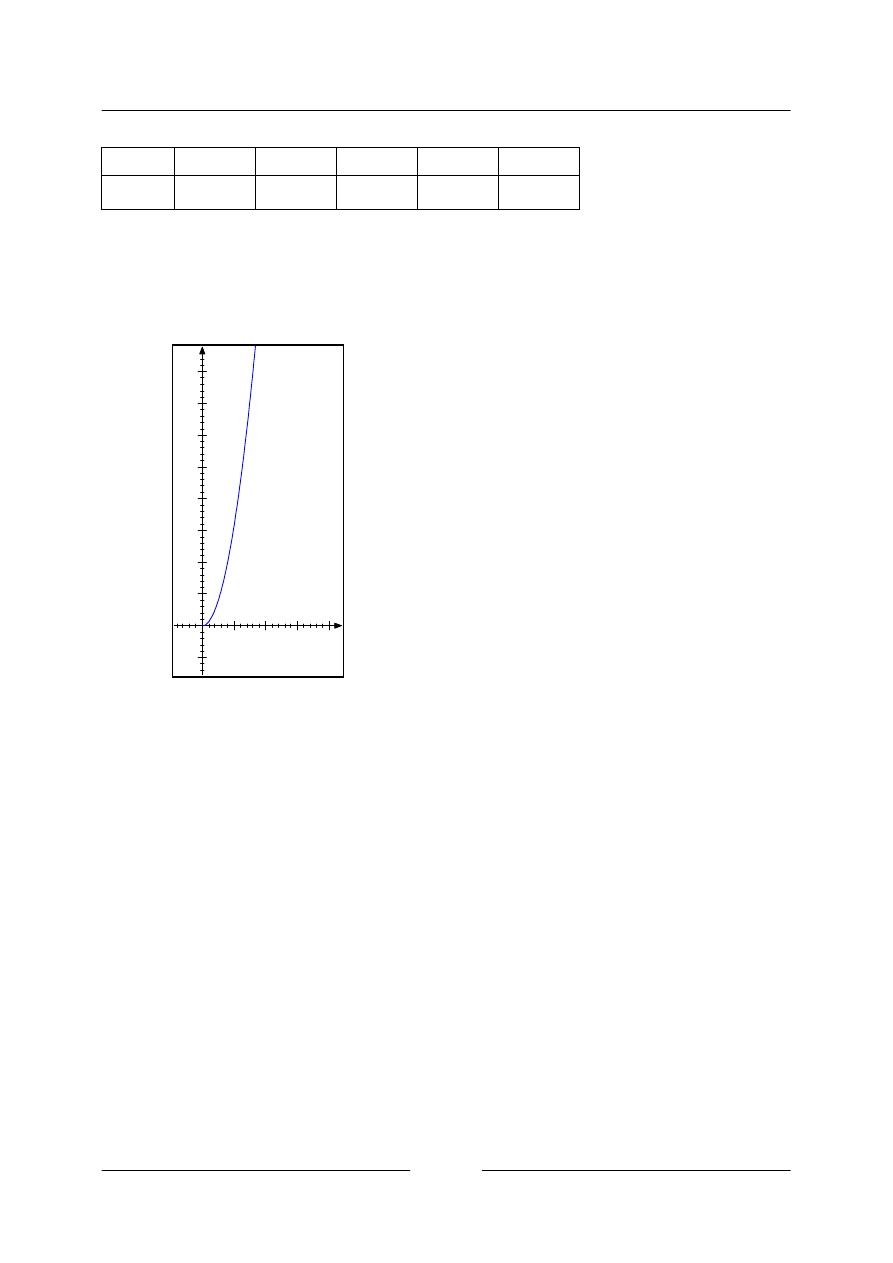
Graf:

Grafem funkce

f

ve zvolené soustavě souřadnic ( SS ) v rovině je množina všech bodů

( )

[

]

x

f

x

X ,

,

kde

( )

f

D

x

∈

.

Na obrázku je graf funkce

g

pro výpočet obsahu kruhu. Graf neprochází počátkem SS, protože

( )

g

D

∉

0

.

1

2

3

-1

1

2

3

4

5

6

7

0

x

y

1

2

3

-1

1

2

3

4

5

6

7

0

x

y

S=πr

2

3. Funkce

100

3.1. Základní vlastnosti

‰

Parita, sudost nebo lichost funkce

Funkce je sudá, platí-li

( )

( )

x

f

x

f

=

−

. Graf sudé funkce je souměrný podle osy y.

Funkce je lichá, platí-li

( )

( )

x

f

x

f

−

=

−

. Graf lidé funkce je souměrný podle počátku SS.

Nenastane-li ani jedna z uvedených možností, není funkce ani sudá ani lichá.

Řešený příklad

• Z grafu určete, zda je funkce lichá nebo sudá.

a)

b)

c)

-1

-2

-3

-4

-5

-6

1

2

3

4

5

6

-1

-2

3

1

2

0

x

y

-1

-2

-3

-4

-5

-6

1

2

3

4

5

6

-1

-2

3

1

2

0

x

y

-1

-2

-3

-4

-5

-6

1

2

3

4

5

6

-1

-2

-3

1

2

0

x

y

-1

-2

-3

-4

-5

-6

1

2

3

4

5

6

-1

-2

-3

1

2

0

x

y

-1

-2

-3

-4

-5

-6

1

2

3

4

5

6

-1

-2

-3

1

2

0

x

y

-1

-2

-3

-4

-5

-6

1

2

3

4

5

6

-1

-2

-3

1

2

0

x

y

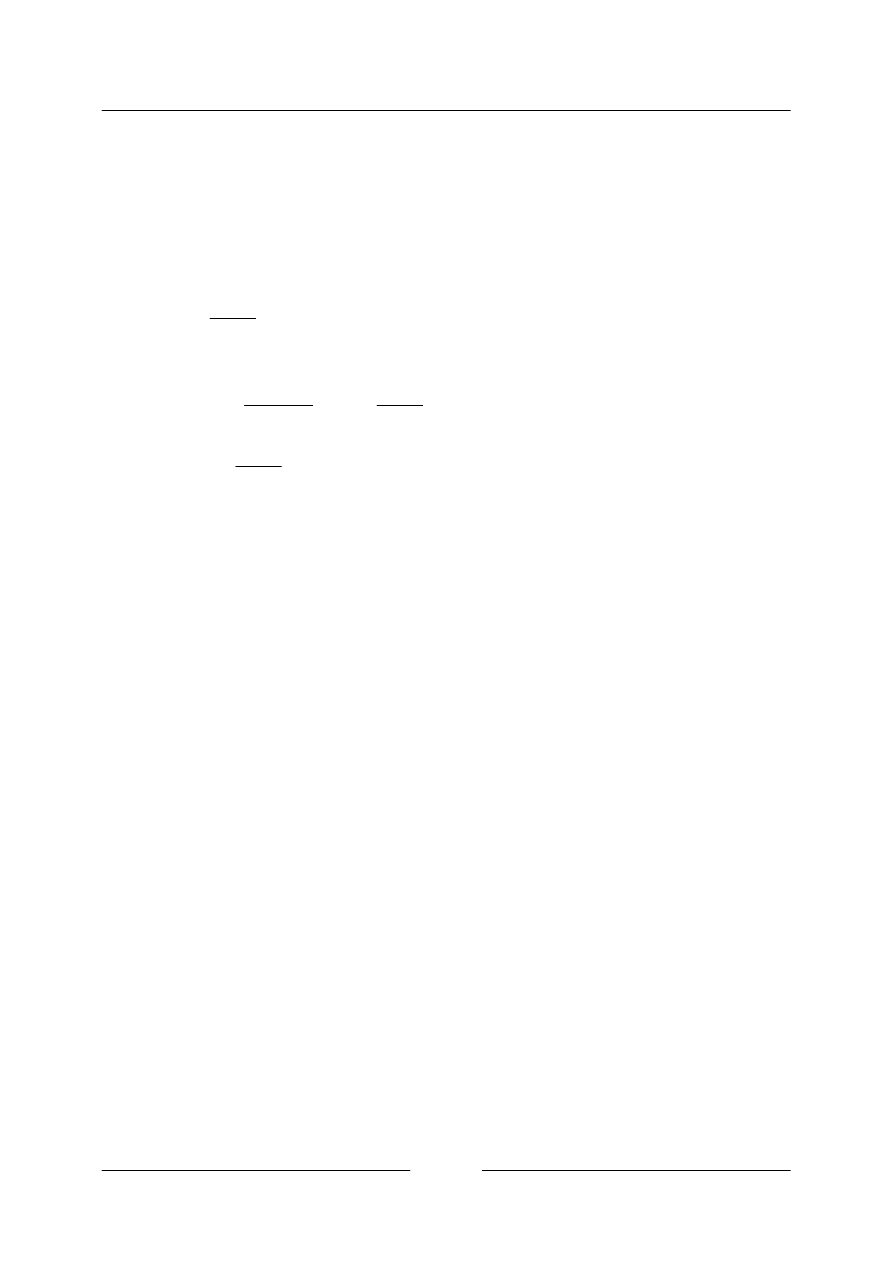
3. Funkce

101

Řešení

a) funkce je sudá, je souměrná podle osy

y

b) funkce je lichá, je souměrná podle počátku

c) funkce není ani sudá ani lichá

• Rozhodněte, zda je funkce sudá či lichá.

2

4

2

5

3

x

x

x

y

−

−

=

Řešení

)

(

5

3

)

(

5

)

(

)

(

3

)

(

2

4

2

2

4

2

x

f

x

x

x

x

x

x

x

f

=

−

−

=

−

−

−

−

−

=

−

Funkce

2

4

2

5

3

x

x

x

y

−

−

=

je sudá.

3. Funkce

102

‰

Monotónnost funkce, funkce rostoucí a klesající

Funkce se nazývá rostoucí, právě když pro všechna

( )

f

D

x

x

∈

2

1

,

platí:

2

1

x

x

<

,

pak

( )

( )

2

1

x

f

x

f

<

.

Funkce se nazývá klesající, právě když pro všechna

( )

f

D

x

x

∈

2

1

,

platí:

2

1

x

x

>

,

pak

( )

( )

2

1

x

f

x

f

>

.

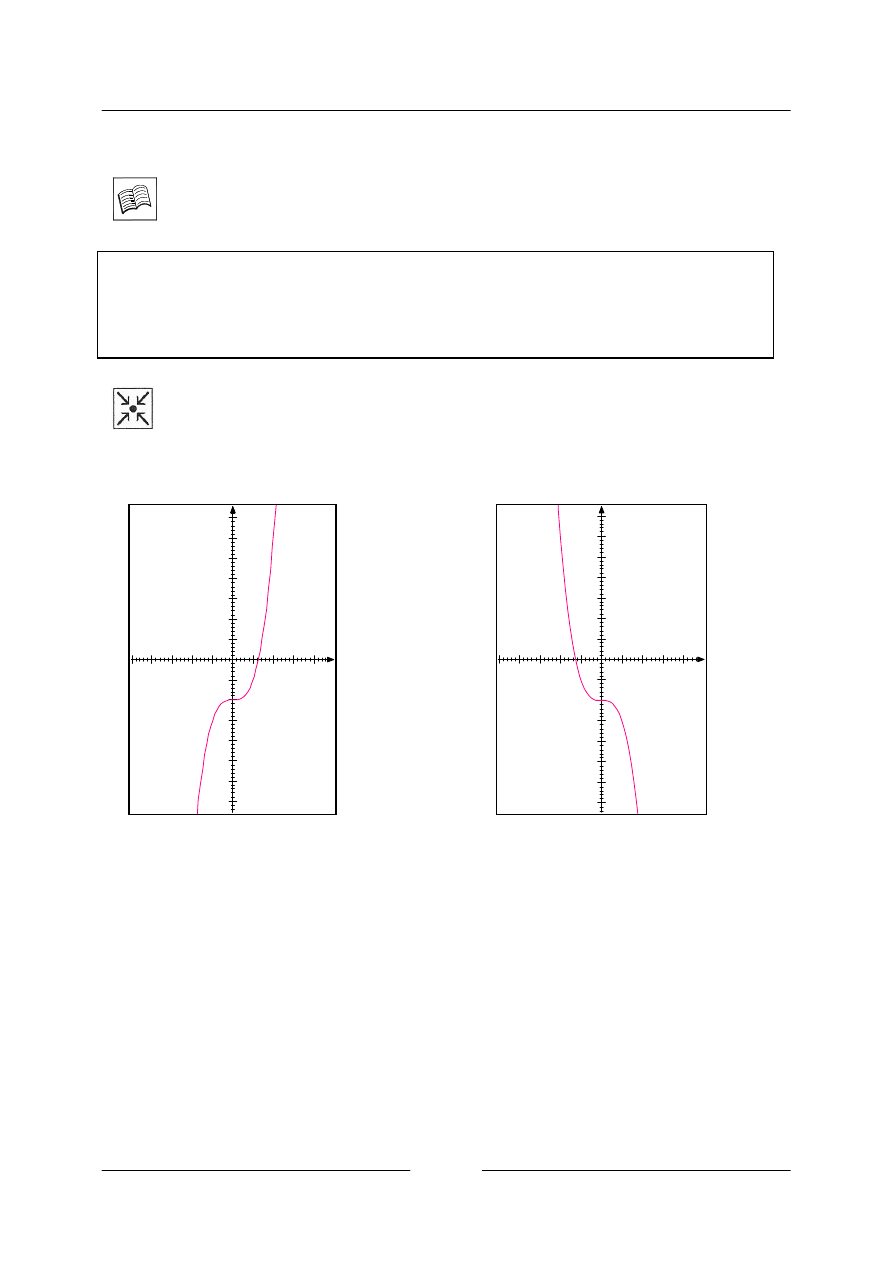
Řešený příklad

Rostoucí funkce na

)

(

f

D

Klesající funkce na

)

(

f

D

-1

-2

-3

-4

1

2

3

4

-1

-2

-3

-4

-5

-6

-7

1

2

3

4

5

6

0

x

y

-1

-2

-3

-4

1

2

3

4

-1

-2

-3

-4

-5

-6

-7

1

2

3

4

5

6

0

x

y

y=-x

3

-2

-1

-2

-3

-4

1

2

3

4

-1

-2

-3

-4

-5

-6

-7

1

2

3

4

5

6

0

x

y

-1

-2

-3

-4

1

2

3

4

-1

-2

-3

-4

-5

-6

-7

1

2

3

4

5

6

0

x

y

y=x

3

-2

3. Funkce

103

Je dána funkce

f a interval I , který je částí jejího definičního oboru

( )

(

)

f

D

I

⊂

.

Funkce se nazývá rostoucí na intervalu

I , právě když pro všechna

( )

f

D

x

x

∈

2

1

,

platí:

2

1

x

x

<

, pak

( ) ( )

2

1

x

f

x

f

<

.

Funkce se nazývá klesající, právě když pro všechna

( )

f

D

x

x

∈

2

1

,

platí:

2

1

x

x

>

, pak

( )

( )

2

1

x

f

x

f

>

.

Řešený příklad

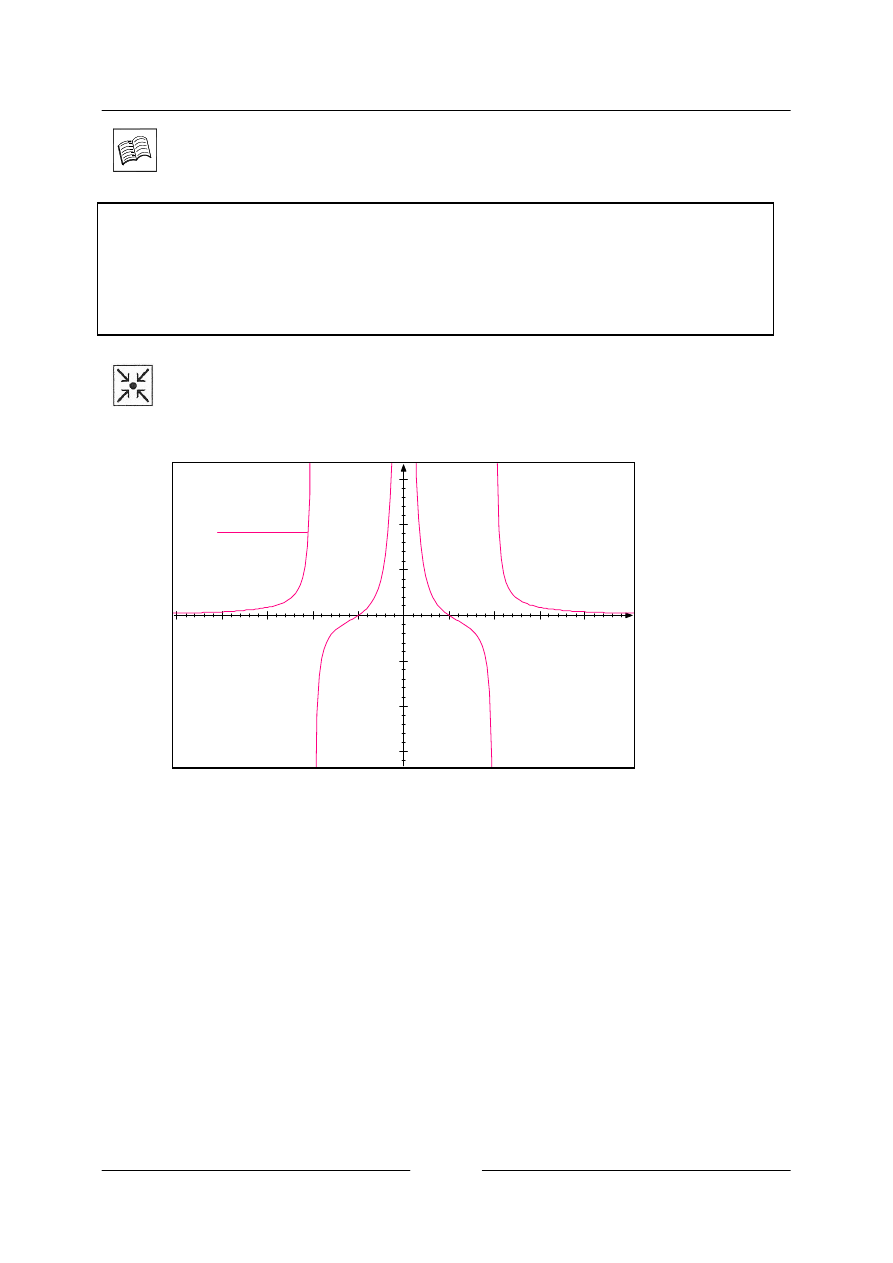
• Z grafu rozhodněte, kde je funkce rostoucí a kde klesající.

Řešení

Funkce je rostoucí na intervalu

)

(

2

,

−

∞

−

a

)

(

0

,

2

−

, na intervalu

( )

2

,

0

a na

)

(

∞

,

2

klesá.

-1

-2

-3

-4

1

2

3

4

-1

-2

-3

1

2

0

x

y

-1

-2

-3

-4

1

2

3

4

-1

-2

-3

1

2

0

x

y

y=

(x-1).(x+1)

x

2

.(x+2).(x-2)

3. Funkce

104

‰

Prostá funkce

Funkce se nazývá prostá, právě když pro všechna

( )

f

D

x

x

∈

2

1

,

platí: Je-li

2

1

x

x

≠

, pak

( )

( )

2

1

x

f

x

f

≠

.

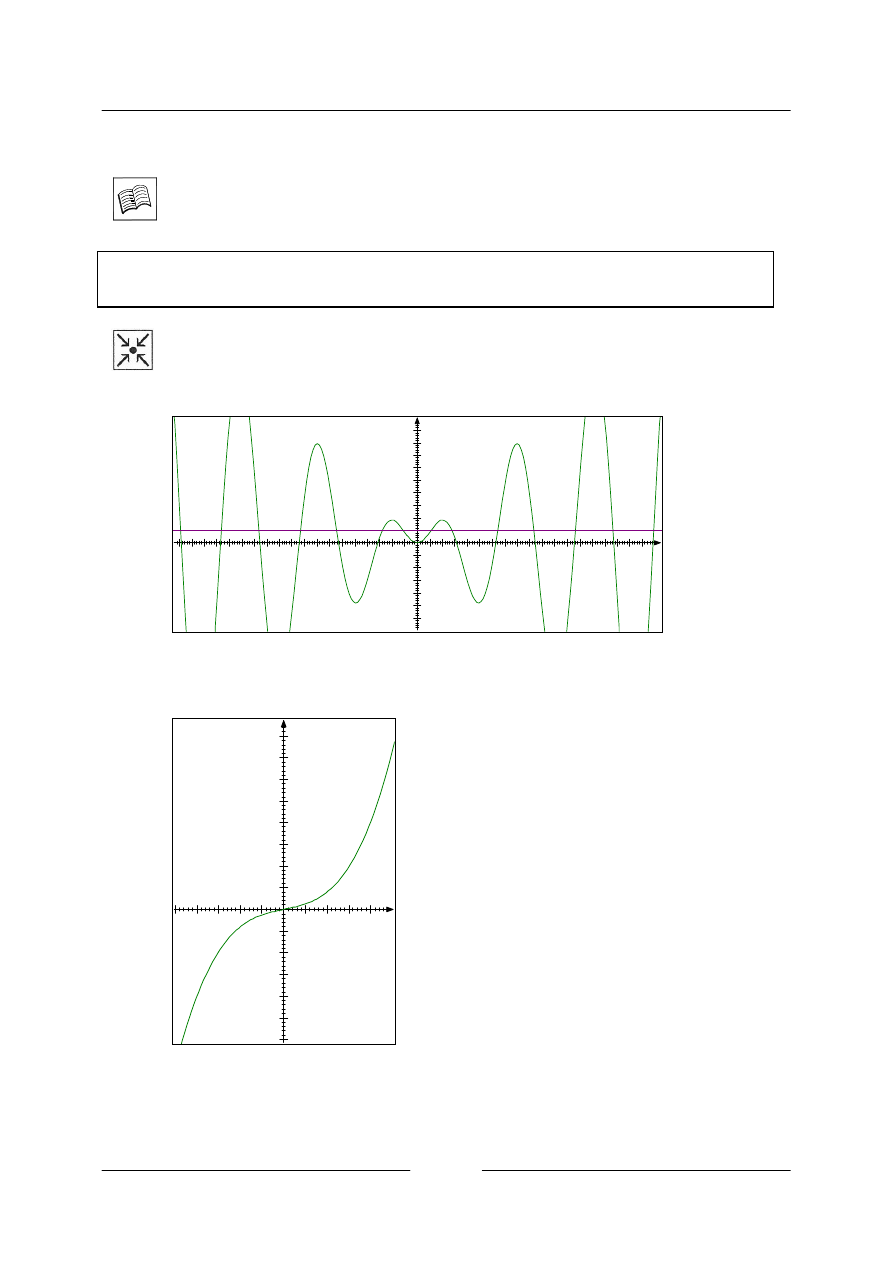
Řešený příklad

• Rozhodněte, zda je funkce prostá.

a)

Řešení

Funkce není prostá, pro různá

x

existují stejné funkční hodnoty.

b)

Řešení

Funkce je prostá, platí definice. Z obrázku vidíme, že funkce rostoucí nebo klesající je prostá.

-1

-2

-3

-4

-5

-6

-7

-8

-9

-10

-11

-12

-13

-14

-15

-16

-17

-18

-19

1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18

-1
-2
-3
-4
-5
-6

1

2

3

4

5

6

7

8

0

x

y

-1

-2

-3

-4

-5

-6

-7

-8

-9

-10

-11

-12

-13

-14

-15

-16

-17

-18

-19

1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18

-1
-2
-3
-4
-5
-6

1

2

3

4

5

6

7

8

0

x

y

x.sinx

-1

-2

-3

-4

1

2

3

4

-1

-2

-3

-4

-5

1

2

3

4

5

6

7

0

x

y

-1

-2

-3

-4

1

2

3

4

-1

-2

-3

-4

-5

1

2

3

4

5

6

7

0

x

y

0,05.x

3

+0,2.x

3. Funkce

105

‰

Periodická funkce

Funkce se nazývá periodická, právě když existuje takové číslo

0

>

p

, že pro každé

Z

∈

k

platí následující podmínky:
a) Je-li

( )

f

D

x

∈

, pak

( )

f

D

p

k

x

∈

+ .

;

b)

(

)

( )

x

f

p

k

x

f

=

+ .

.

Číslo

p se nazývá perioda funkce f .

Řešený příklad

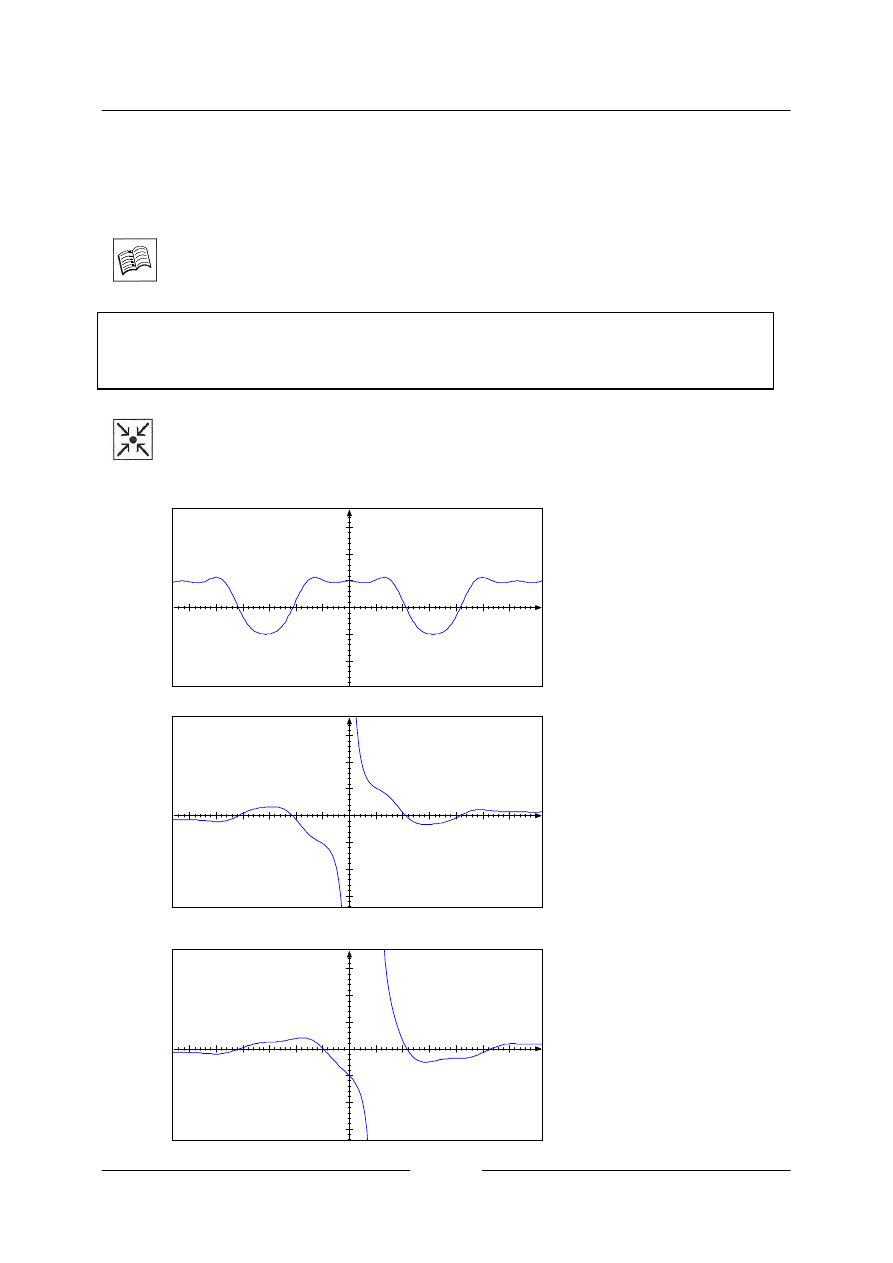
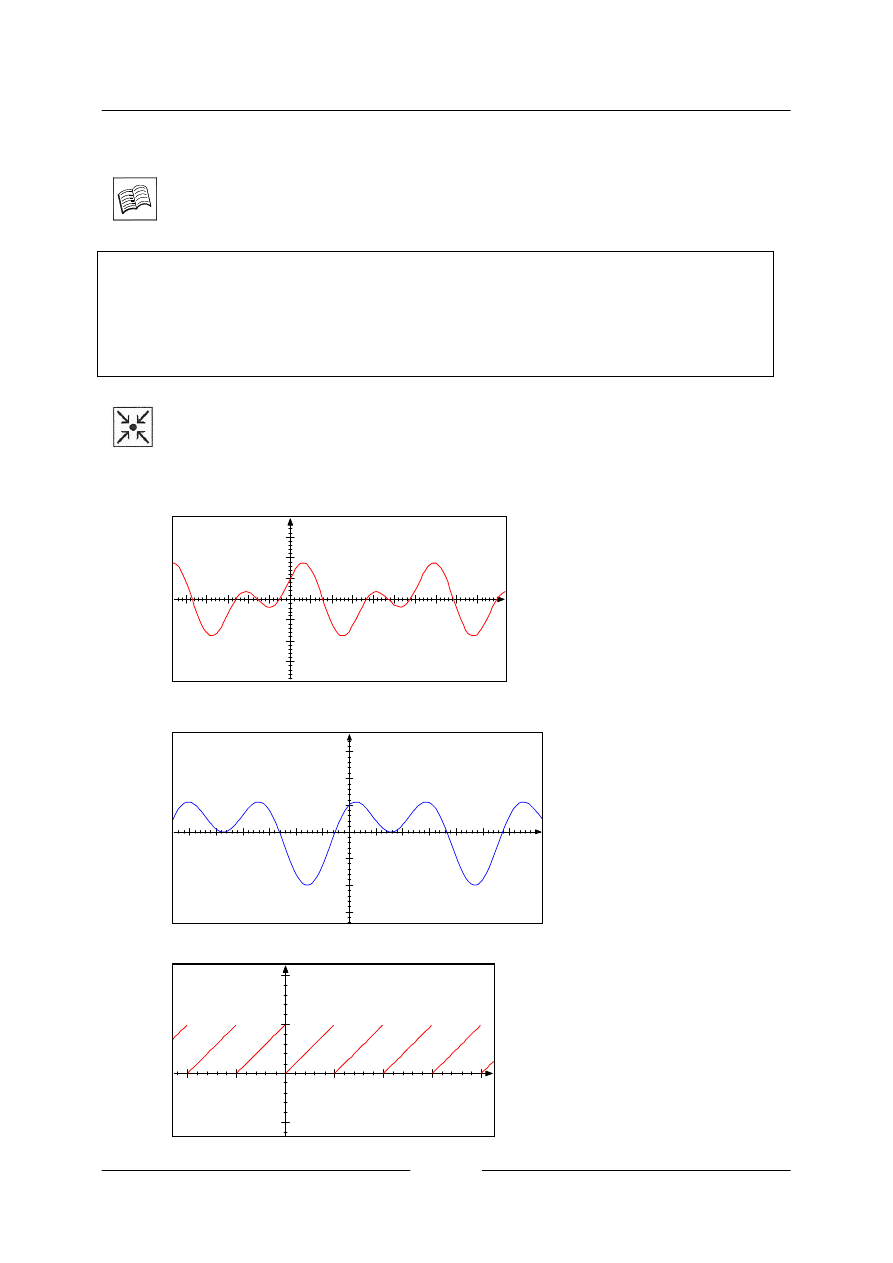
• Příklady periodických funkcí

a)

b)

c)

-1

-2

-3

-4

-5

-6

1

2

3

4

5

6

-1

-2

-3

1

2

0

x

y

-1

-2

-3

-4

-5

-6

1

2

3

4

5

6

-1

-2

-3

1

2

0

x

y

-1

-2

-3

-4

-5

1

2

3

4

5

6

7

8

9

-1

-2

-3

1

2

0

x

y

-1

-2

-3

-4

-5

1

2

3

4

5

6

7

8

9

-1

-2

-3

1

2

0

x

y

y=cosx+sin2x

-1

-2

1

2

3

-1

1

0

x

y

-1

-2

1

2

3

-1

1

0

x

y

y=x-[x]

3. Funkce

106

• Určete periodu funkce

x

2

sin

Řešení

(

)

(

)

x

x

p

k

p

k

x

p

k

x

p

k

x

2

sin

2

cos

.

.

2

sin

.

2

cos

.

2

sin

.

2

2

sin

.

2

sin

=

+

=

+

=

+

Porovnáme upravený tvar s pravou stranou: u

1

.

2

cos

...

2

sin

=

p

k

x

u

0

.

2

sin

...

2

cos

=

p

k

x

Z první rovnice je

p

rovno celočíselným násobkům

π

, z druhé je rovno celočíselným násobkům

2

π

.

Výsledná perioda je

π

=

p

.

3. Funkce

107

‰

Inverzní funkce

Inverzní funkce

k prosté funkci

f je

1

−

f , pro kterou platí:

f

f

H

D

=

−1

, každému

1

−

∈

f

D

y

je přiřazeno právě to

f

D

x

∈

, pro které je

( )

y

x

f

=

.

Oborem hodnot inverzní funkce je definiční obor původní funkce:

f

f

D

H

=

−1

Grafy obou funkcí jsou souměrné podle osy I. a II. kvadrantu

x

y

= .

Inverzním funkcím bude věnována samostatná kapitola.

3. Funkce

108

Úlohy k řešení

Úloha 3.1.

Rozhodněte, zda je funkce sudá či lichá:

a)

2

5

2

3

4

3

−

−

+

−

=

x

x

x

x

y

,

b)

2

3

5

x

x

x

y

−

−

=

,

c)

(

)

x

x

x

x

y

sin

cos

−

=

,

d)

x

x

y

2

ln

=

,

e)

x

x

x

x

e

e

e

e

y

−

−

+

−

=

,

f)

(

)

x

x

x

x

y

sin

2

3

−

=

,

g)

5

2

2

−

+

=

x

x

y

.

♦

Úloha 3.2.

Určete periodu funkce
a)

x

3

cos

b)

2

cos

x

♦

3. Funkce

109

Klíč k řešení a výsledky

3.1.

a)

2

5

2

3

2

5

)

(

2

)

(

)

(

3

)

(

4

3

4

3

−

−

−

−

−

−

=

−

−

−

−

+

−

−

−

=

−

x

x

x

x

x

x

x

x

x

f

ANI SUDÁ ANI LICHÁ

b)

)

(

5

5

)

(

)

(

5

)

(

2

3

2

3

2

3

x

f

x

x

x

x

x

x

x

x

x

x

f

−

=

−

=

+

−

−

=

−

−

−

−

−

=

−

LICHÁ

c)

( )

( ) ( ) ( )

(

)

(

)

(

)

(

)

( )

x

f

x

x

x

x

x

x

x

x

x

x

x

x

x

f

−

=

−

−

=

−

+

−

=

−

−

−

−

−

=

−

sin

cos

sin

cos

sin

cos

LICHÁ

d)

( )

( )

x

f

x

x

x

f

x

x

=

=

−

=

−

−

2

ln

2

ln

SUDÁ

e)

( )

( )

( )

(

)

( )

x

f

e

e

e

e

e

e

e

e

e

e

e

e

x

f

x

x

x

x

x

x

x

x

x

x

x

x

−

=

+

−

−

=

+

−

=

+

−

=

−

−

−

−

−

−

−

−

−

−

−

LICHÁ

f)

(

)

(

) (

)

)

(

sin

sin

)

sin(

)

(

)

(

)

(

2

3

2

3

2

3

x

f

x

x

x

x

x

x

x

x

x

x

x

x

x

f

−

=

−

=

+

−

−

=

−

−

−

−

−

=

−

LICHÁ

g)

5

2

5

)

(

2

)

(

)

(

2

2

−

−

=

−

−

+

−

=

−

x

x

x

x

x

f

ANI SUDÁ ANI LICHÁ

3.2.

a)

3

2

π

=

p

b)

π

4

=

p