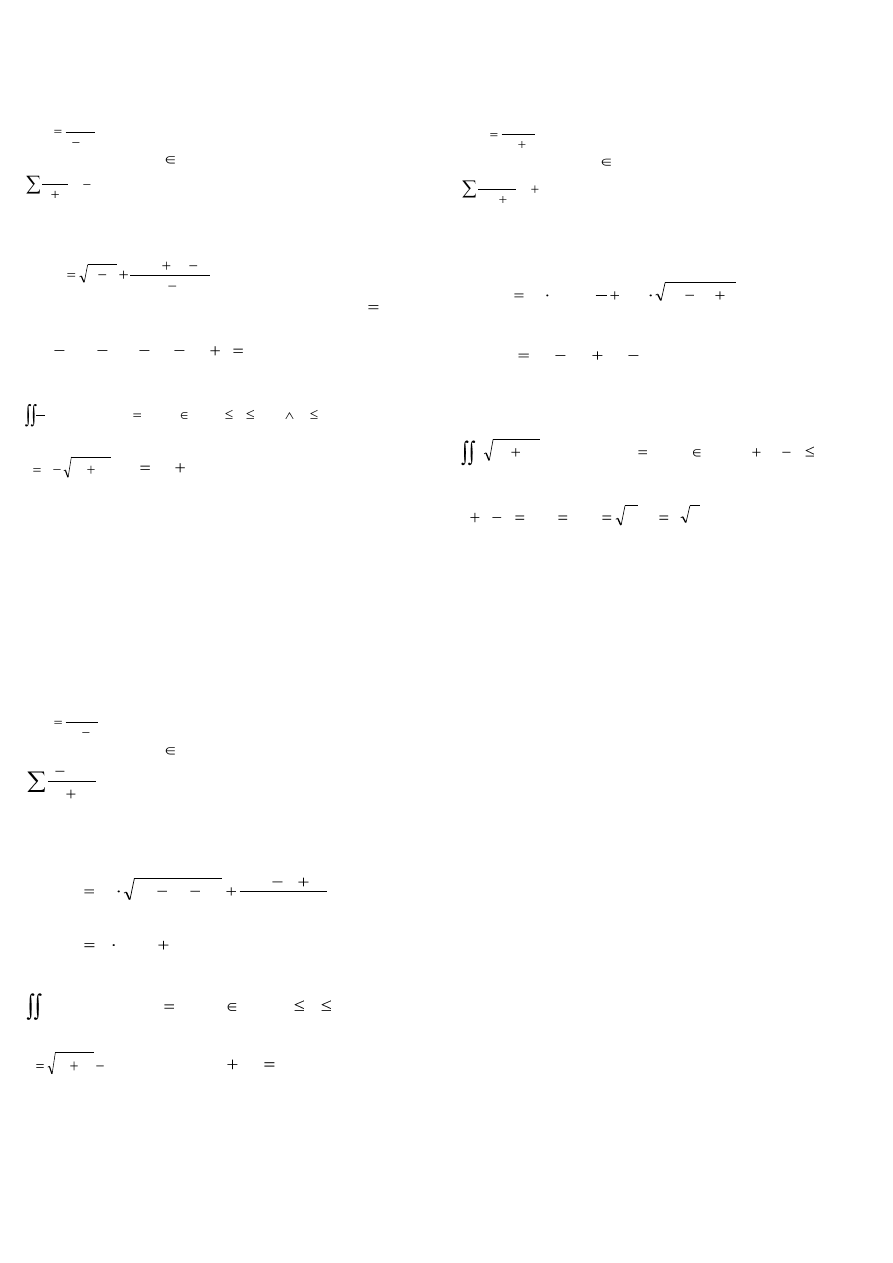
ZiIP, MATEMATYKA II, KOLOKWIUM 2,
zestaw przykładowy nr 1
Zad. 1.
a) Rozwinąć poniższą funkcję w szereg Maclaurina:
x
x
x
f
5
1
3
)
(
b) Wyznaczyć zbiór
R
x
, dla których zbieżny jest szereg:
)
2
(
3
2
n
x
n
Zad. 2.
a) Wyznaczyć dziedzinę D, narysować zbiór D i policzyć
pochodne cząstkowe I-go rzędu funkcji:
1
)
1
ln(
)
(
2
2
y
y
x
y
x
x,y
f
b) Wyznaczyć ekstrema lokalne, o ile istnieją, funkcji
)
(x
y
y
określonej równaniem:
0
1
6
2
y
3
2
x
2
2
y
x
xy
Zad. 3.
a) Obliczyć całkę:
D
x
y
y
x
dxdy
x
y
e}
x
ln
0
:
)
,
{(
D
gdzie
,
2
R
b) Obliczyć objętość bryły ograniczonej powierzchniami:
2
2
6
y
x
z
,
2
2
y
x
z
ZiIP, MATEMATYKA II, KOLOKWIUM 2,
zestaw przykładowy nr 2
Zad. 1.
a) Rozwinąć poniższą funkcję w szereg Maclaurina:
5
4
2
)
(
x
x
x
f
b) Wyznaczyć zbiór
R
x
, dla których zbieżny jest szereg:
7
3
)
4
(
n
n
n
x
Zad. 2.
a) Wyznaczyć dziedzinę D, narysować zbiór D i policzyć
pochodne cząstkowe I-go rzędu funkcji:
.
)
3
ln(
6
)
(
2
2
3
y
y
x
y
x
y
x
x,y
f
b) Wyznaczyć ekstrema lokalne, o ile istnieją, funkcji :
).
ln(
)
(
2
y
x
y
x,y
f
Zad. 3.
a) Obliczyć całkę:
D
y
y
x
y
y
x
dxdy
e
}
:
)
,
{(
D
gdzie
,
2
2
R
b) Obliczyć pole płata wyciętego z powierzchni
2
2
2
y
x
z
przez walec
.
2
2
2
x
y
x
ZiIP, MATEMATYKA II, KOLOKWIUM 2,
zestaw przykładowy nr 3
Zad. 1.
a) Rozwinąć poniższą funkcję w szereg Maclaurina:
7
2
)
(
2
x
x
x
f
b) Wyznaczyć zbiór
R
x
, dla których zbieżny jest szereg:
)
1
(
2
3
(-1)
2
n
n
x
n
Zad. 2.
a) Wyznaczyć dziedzinę D, narysować zbiór D i policzyć
pochodne cząstkowe I-go rzędu funkcji:
.
2
3
1
arccos
)
(
2
5
2
x
x
e
y
x
x,y
f
xy
b)
Wyznaczyć ekstrema globalne funkcji
2
3
3
)
,
(
y
xy
y
x
y
x
f
na trójkącie domkniętym o wierzchołkach A(-2,0), B(1,0), C(1,-3).
Zad. 3.
a) Obliczyć całkę:
D
y
y
x
y
x
dxdy
y
x
y
}
0
:
)
,
{(
D
gdzie
,
2
2
2
2
2
R
b) Obliczyć objętość bryły ograniczonej powierzchniami:
.
2
,
,
0
,
0
4
x
y
x
y
z
z
x