Fizyka 1 (2005/2006) Wykład IV 1/4
Fizyka I sem
Informatyka
Wykład nr 4
18 10 2005
PRACA
W
=F
x
x
W
=F cos x
W
= F⋅ds
Praca przy zmiennej sile:
W
= lim
x
i
0
∑
i
F
xi
x
i
W
=
∫
x
1
x
2
F
x
dx
Przykład: Sprężyna (Nasza praca przy rozciąganiu sprężyny)
W
x
1
, x
2
=
∫
x
1
x
2
F x⋅dx =
∫
x
1
x
2
kx dx
=
1
2
k
x
2
2
−
1
2
k
x
1
2
Ostateczny zapis pracy
W
=
∫
s
1
s
2
F⋅ds
Jeśli działa więcej sił na ciało:
dW
=
F
1
⋅ds
F
2
⋅ds... =
∑
i
F
i
⋅ds
Energia potencjalna
Jeśli
W
p AB
jest pracą sił pola na drodze AB to zachodzi zależność
E
B
=E
A
− W
p
AB
Dlaczego minus?
Jeśli wyobrazimy sobie, że to my przemieszczamy ciało ze stałą prędkością z punktu A do B to
musimy cały czas działać siłą równą co do wartości sile jaką działa pole w każdym punkcie toru na
ciało. Nasza siła musi być jednak przeciwnie skierowana. Można więc napisać dla pracy
W
z
AB
wykonanej przeciwko siłom pola
E
B
=E
A
W
z
AB
Dlaczego teraz plus?
W polu zachowawczym praca sił pola (a także przeciwko siłom pola) na drodze z A do B jest
zawsze taka sama
W
p
AB
= − W
z
AB
© M. Krasiński 2005
Fizyka 1 (2005/2006) Wykład IV 2/4
W
p
AB
= W '
p
AB
na każdej drodze
Można więc wprowadzić jednoznaczną funkcję
E
x , y , z
zależną TYLKO od położenia,
charakteryzującą pole, definiowaną jako:
E
x , y , z=E
0
x
0 ,
y
0 ,
z
0
− W
p
[x
0 ,
y
0 ,
z
0
x , y , z]
^ To jest definicja energii potencjalnej ^
Tę samą definicje można zapisać używając sił zewnętrznych (przeciwko siłom pola) jako:
E
x , y , z=E
0
x
0 ,
y
0 ,
z
0
W
z
[ x
0 ,
y
0 ,
z
0
x , y , z]
Ta definicja ma sens jedynie wtedy gdy
W
z
[ x
0 ,
y
0 ,
z
0
x , y , z]
(a więc także
W
p
[x
0 ,
y
0 ,
z
0
x , y , z]
) nie zależy od drogi po której wykonujemy (lub pole wykonuje)
pracę.
W każdym innym przypadku, startując z punktu początkowego gdzie energia wynosi
E
0
otrzymamy bardzo wiele wartości na energię końcową E w zależności od drogi. Taka funkcja
byłaby zupełnie bezwartościowa.
Energię potencjalną można więc wprowadzić wyłącznie w polach zachowawczych (zwanych
inaczej potencjalnymi).
Skąd ta nazwa?
Problem wyboru
E
0
Ponieważ przedstawiona definicja pozwala określić energię potencjalną pola w każdym punkcie z
wyjątkiem jednego (tego od którego zaczęliśmy) to wartość dla punktu początkowego jest w
zasadzie dowolna! Kierujemy się głównie wygodą rachunkową i pewną dozą zdrowego rozsądku.
Przykład pola grawitacyjnego
Problem nieskończoności
E
∞
=E
A
W
z
A∞
Sensownie jest założyć, iż energia w nieskończoności jest zero gdyż tam już nie ma oddziaływań
E
∞
=0
to 0
=E
A
W
z
A∞
to E
A
=− W
z
A∞
Ponieważ praca
W
z
A∞
0
bo siła zewnętrzna działa zgodnie z przesunięciem (praca
przeciwko sile grawitacji) więc
E
A
0
Wyliczenie energii potencjalnej pola grawitacyjnego
siła grawitacji
F = −G
M m
r
2
r
r
Uwaga! Dlaczego piszemy znak minus?
siła przeciwna
F = G
M m
r
2
r
r
w takim razie korzystając zależności
E
∞
=E
A
W
z
A∞
mamy praca
0
=E
A
W
z
A∞
czyli
E
A
=−W
z
A∞
© M. Krasiński 2005
Fizyka 1 (2005/2006) Wykład IV 3/4
W takim razie energia potencjalna w punkcie A wynosi
E
A
=−W
z
A∞
= −
∫
r
A
∞
F dr = −
∫
r
A
∞
G
M m
r
3
r⋅dr = −G M m
∫
r
A
∞
1
r
2
dr
E
A
= −G M m
[
−1
r
∞
−
−1
r
A
]
= −G
M m
r
A
Siła jako gradient energii potencjalnej
F
x
=−
∂E
p
∂ x
F
y
=−
∂E
p
∂ y
F
z
= −
∂E
p
∂z
albo bardziej formalnie
F =− grad E
p
=−
∇ E
p
gdzie operator nabla
∇ = ∂
∂x
i ∂
∂ y
j ∂
∂z
k
a więc ostatecznie
F =−
∇ E
p
=−
∂E
p
∂ x
i
∂E
p
∂ y
j
∂E
p
∂ z
k
ZAPAMIĘTAJ!
•
Energia potencjalna ? Ale czego ? Pamiętaj zawsze o podaniu jakich oddziaływań dotyczy ta
energia!
•
NIE KAŻDA
ENERGIA POTENCJALNA WYNOSI E=mgh !!!!
•
Jeśli w jakimś punkcie
F=0
to
nie
znaczy, że
E
pot
=0
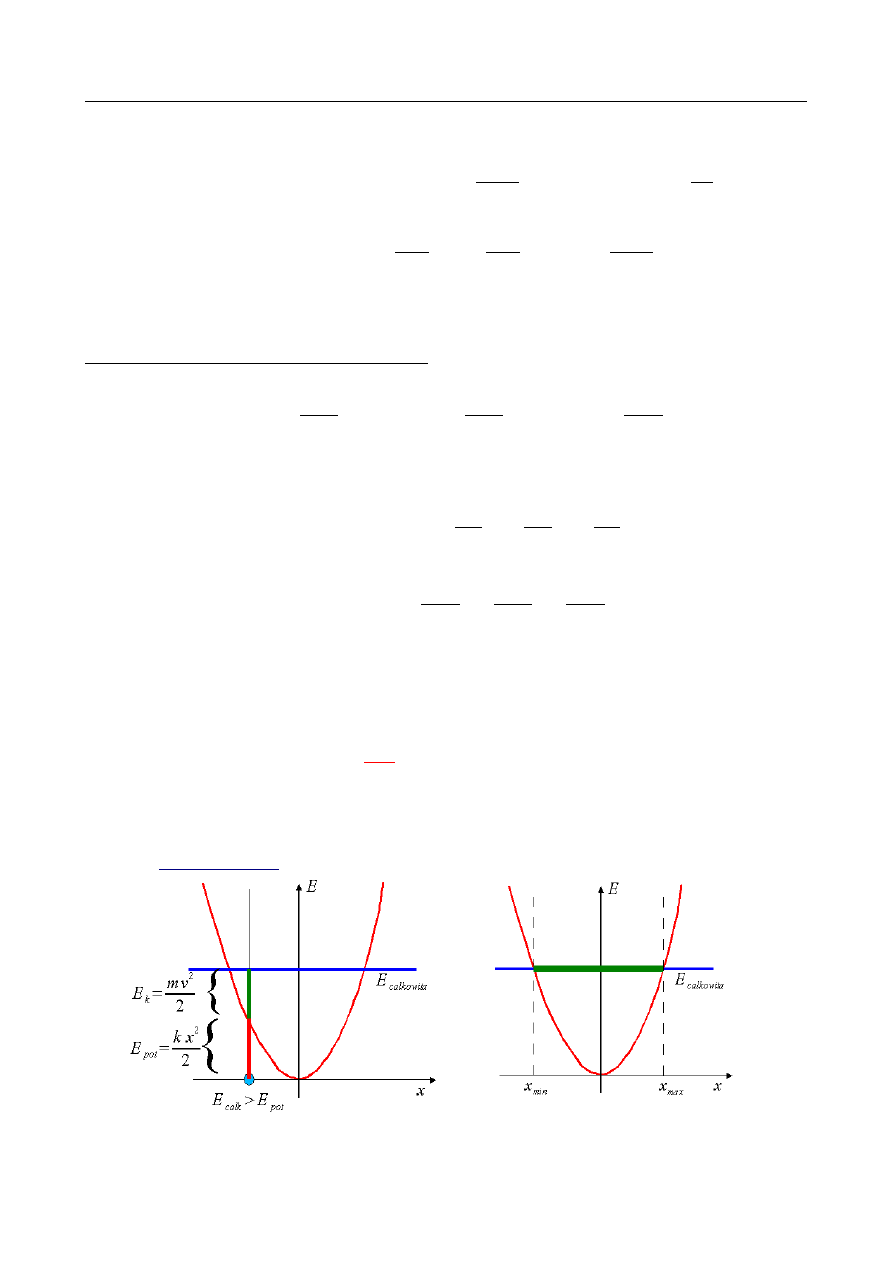
Energia na wykresie
•
Analogia grawitacyjna dla dowolnej energii
•
Jak czytać wykresy energetyczne?
•
zobacz animację
© M. Krasiński 2005
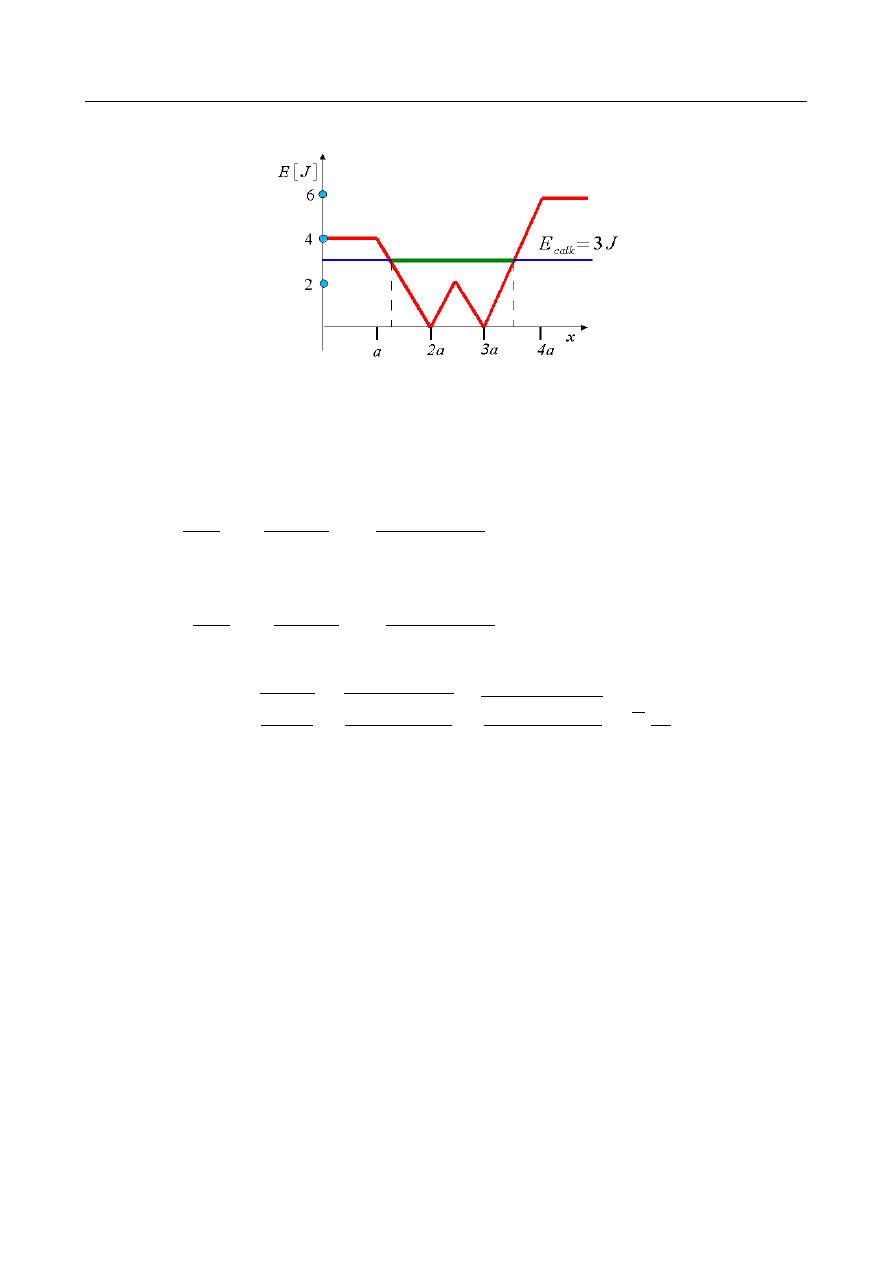
Fizyka 1 (2005/2006) Wykład IV 4/4
Dla wykresu powyżej przyjmijmy, że a = 1 m oraz m =1 kg:
•
Siła działająca na obiekt w punkcie x = 3,9 m wynosi........... Ciała nigdy nie ma w tym
punkcie!
•
Siła działająca na obiekt w punkcie x = 3,2 m wynosi:
F
x
=−
∂E
p
∂ x
= −
E
2
−E
1
x
2
−x
1
= −
6 [J]
−0 [J]
4 m
−3 m
=− 6 N
i działa w lewo (znak minus)
•
Siła działająca na obiekt w punkcie x = 1,8 m wynosi:
F
x
=−
∂E
p
∂ x
= −
E
2
−E
1
x
2
−x
1
=−
0 [J]
−4 [J]
2 m
−1 m
= 4 N
i działa w prawo (znak plus)
•
Prędkość ciała w x = 2,5 m wynosi
v
=
2 E
kin
m
=
2
E
C
−E
pot
m
=
2
3 J−2 J
1 kg
=
2
m
s
2
Pochodzenie zasad zachowania
zachowanie energii
-
jednorodność czasu
zachowanie pędu
-
jednorodność przestrzeni
zachowanie momentu pędu -
izotropowość przestrzeni
© M. Krasiński 2005