Wykład 9

Fizyka I (Informatyka 2005/06)

06 12 2005

c

Mariusz Krasiński 2005

Spis treści

1

Ruch harmoniczny wymuszony c.d.

1

1.1

Dynamiczny eliminator drgań . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . .

1

2

FALE

2

2.1

Dwaj wędkarze . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . .

2

2.2

Równanie fali . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . .

3

2.3

Prędkość fazowa

. . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . .

4

3

Fala stojąca

4

3.1

Fale stojące na strunie . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . .

6

3.2

Fale stojące na wodzie . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . .

6

3.2.1

Sejsze . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . .

7

3.2.2

Fala stojąca a przypływy. . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . .

7

3.2.3

Tsunami . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . .

7

4

Prędkość grupowa

8

UWAGA! Część rysunków wymaga własnoręcznego dopisania oznaczeń!

1

Ruch harmoniczny wymuszony c.d.

1.1

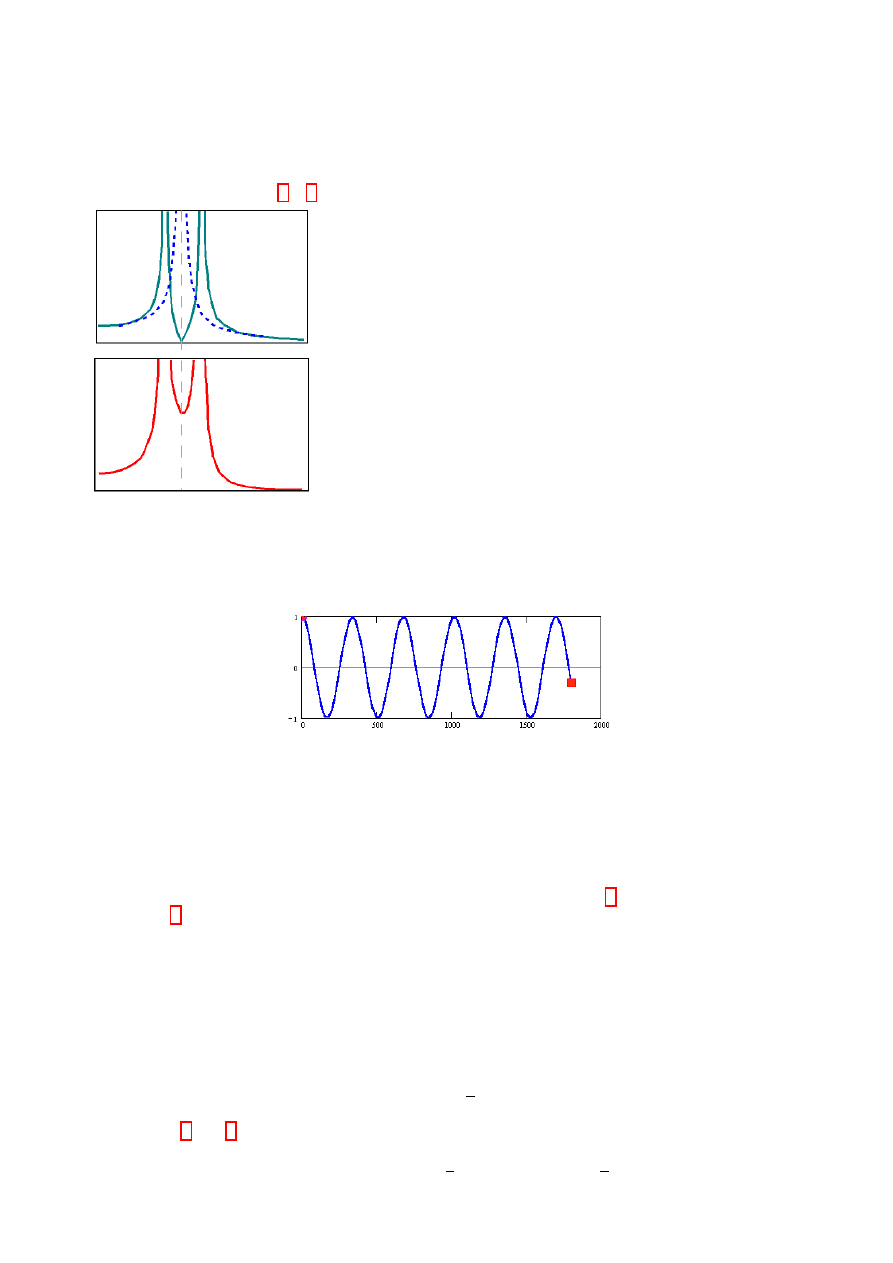
Dynamiczny eliminator drgań

Równania ruchu dla układu powyżej mają postać:

1

2

FALE

2

m

1

a

1

= −k

1

x

1

+ k

2

(x

2

− x

1

) + F

0

cos(ωt)

(1)

m

2

a

2

= −k

2

(x

2

− x

1

)

(2)

Rozwiązanie układu równań (1), (2) przedstawiono poniżej

Dodaj opisy na wykładzie

2

FALE

2.1

Dwaj wędkarze

(dopisz oznaczenia)

Drgania źródła opisuje równanie

y(x = 0, t) = A cos(ωt)

(3)

Co rejestruje obserwator?

y(x, t) = ?

Drgania w miejscu gdzie stoi obserwator można opisać przy pomocy równania (3) ale dla obserwatora musimy
w równaniu (3) zamienić czas (dlaczego?)

t → t − ∆t

(4)

otrzymując wychylenie w punkcie o współrzędnej x równe

y(x, t) = A cos [ω(t − ∆t)]

(5)

gdzie

∆t =

x

v

(6)

Podstawiając (6) do (5) otrzymamy więc równanie drgań w miejscu x gdzie stoi obserwator

y(x, t) = A cos

h

ω

t −

x

v

i

= A cos

ωt − ω

x

v

(7)

2

FALE

3

Ponieważ

ω

v

=

2π

T

v

=

2π

vT

=

2π

λ

to równanie (7) przyjmuje ostateczną postać

y(x, t) = A cos

ωt −

2π

λ

x

= A cos(ωt − kx)

(8)

gdzie

k =

2π

λ

(9)

nazywamy liczbą falową

2.2

Równanie fali

Liczymy pochodne cząstkowe wychylenia y względem

• położenia x

∂y

∂x

=

∂

∂x

(A cos(ωt − kx)) = Ak sin(ωt − kx)

∂

2

y

∂x

2

=

∂

∂x

(Ak sin(ωt − kx)) = −Ak

2

cos(ωt − kx) = −k

2

y

(10)

• oraz czasu t

∂y

∂t

=

∂

∂t

(A cos(ωt − kx)) = −Aω sin(ωt − kx)

∂

2

y

∂t

2

=

∂

∂t

(−Aω sin(ωt − kx))

= −Aω

2

cos(ωt − kx ) = −ω

2

y

(11)

Przyrównując wychylenie y wyliczone z równań (10) i (11) otrzymujemy

∂

2

y

∂x

2

1

k

2

=

∂

2

y

∂t

2

1

ω

2

albo zapisując inaczej

∂

2

y

∂x

2

=

k

2

ω

2

∂

2

y

∂t

2

(12)

gdzie

k

2

ω

2

=

"

2π

λ

2π

T

#

2

=

T

λ

2

=

1

v

2

(13)

Ostatecznie więc równanie (12) przyjmuje postać

∂

2

y

∂x

2

=

1

v

2

∂

2

y

∂t

2

(14)

W trzech wymiarach równanie (14) ma postać

∂

2

U

∂x

2

+

∂

2

U

∂y

2

+

∂

2

U

∂z

2

=

1

v

2

∂

2

U

∂t

2

(15)

gdzie wychylenie oznaczono jako U dla uniknięcia pomyłki ze współrzędną y.

Równanie (15) można zapisać w bardziej zwartej postaci

∇

2

U =

1

v

2

∂

2

U

∂t

2

(16)

3

FALA STOJĄCA

4

gdzie wyrażenie

∇

2

=

∂

2

∂x

2

+

∂

2

∂y

2

+

∂

2

∂z

2

nazywa się operatorem Laplace’a albo laplasjanem

Rozwiązanie równania falowego (16) w trzech wymiarach, w przypadku fali płaskiej, ma postać

U (~

r) = A cos(ωt − ~

k · ~

r)

(17)

gdzie ~

k nazywa się wektorem falowym.

2.3

Prędkość fazowa

Chcemy dowiedzieć się jak przemieszcza się faza fali

y = A cos(ωt − kx)

Jako charakterystyczny punkt wybieramy jeden z grzbietów

y = max

⇒

cos(ωt − kx) = 1

⇒

ωt − kx = 0

⇒

x =

ω

k

t

Jeśli t rośnie to x też rośnie - czyli fala porusza się zgodnie z kierunkiem osi x (w tym przypadku w prawo).
Wielkość

v

f

=

ω

k

jest prędkością przemieszczania się fazy czyli prędkością fazową.

Analogicznie możemy pokazać, że równanie

y = A cos(ωt + kx)

opisuje falę, która porusza się przeciwnie do kierunku osi x (w tym przypadku w lewo).

Jest tak, ponieważ dla grzbietu fali zachodzą relacje

y = max

⇒

cos(ωt + kx) = 1

⇒

ωt + kx = 0

⇒

x = −

ω

k

t

3

Fala stojąca

(dodaj opisy!)

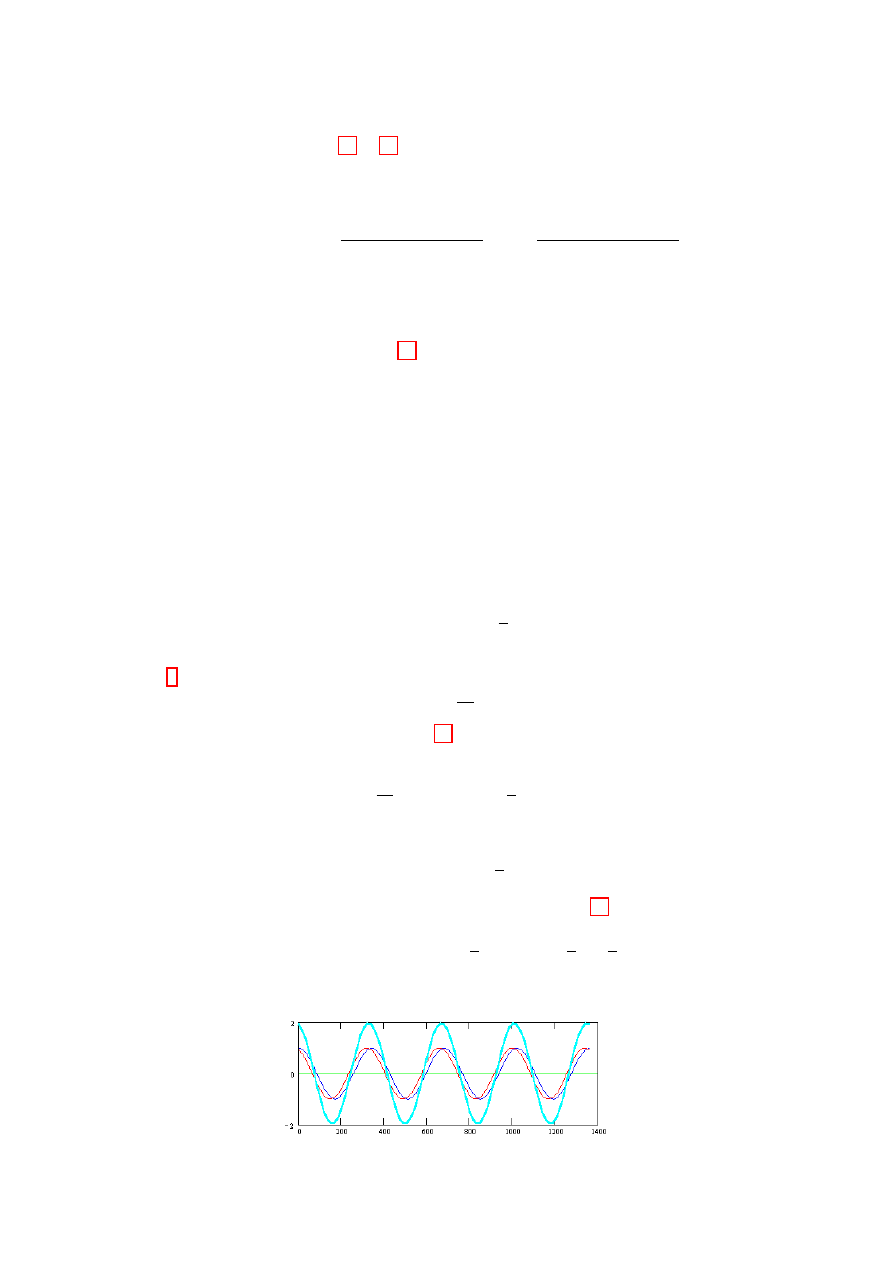
Co się stanie kiedy w pewnym miejscu, o współrzędnej x spotkają się dwie identyczne fale, biegnące z przeciwnych
stron?

Fale te opisujemy równaniami

y

1

(x, t) = A cos(ωt − kx)

(18)

3

FALA STOJĄCA

5

y

2

(x, t) = A cos(ωt + kx)

(19)

Dodając drgania wywołane przez fale (18) i (19) w dowolnym punkcie x otrzymujemy

y

w

(x, t) = y

1

(x, t) + y

2

(x, t) = A cos(ωt − kx) + A cos(ωt + kx)

y

w

(x, t) = 2A cos

ωt − kx + ωt + kx

2

cos

ωt − kx − ωt − kx

2

i ostatecznie

y

w

(x, t) = 2A cos (ωt) cos (−kx ) = [ 2A cos(kx) ] cos(ωt)

(20)

Wyrażenie w nawiasie kwadratowym równania (20)

A

0

(x) = 2A cos(kx)

zależy wyłącznie od położenia (x) a nie od czasu (t)! Jest to więc amplituda drgań wypadkowych, zależna od
położenia. Wychylenie w dowolnym punkcie x można więc opisać równaniem

y

w

(x, t) = A

0

(x) cos(ωt)

Amplituda A

0

(x) może, na przykład, w niektórych punktach być zawsze równa zero

A

0

(x) = 0 = 2A cos(kx)

Jest tak dla punktów o współrzednych spełniających warunek

kx

N

= (2N + 1)

π

2

(21)

gdzie N jest liczbą naturalną.

Ponieważ z (9) wiemy, że

k =

2π

λ

więc wykorzystując powyższą zależność w równaniu (21) otrzymamy że amplituda drgań będzie równa zero w
miejscach, których współrzędne x

N

spełniają zależność

2π

λ

x

N

= (2N + 1)

π

2

czyli

x

N

= (2N + 1)

λ

4

(22)

Odległość między dwoma kolejnymi (N , N + 1) takimi punktami, zgodnie z (22), wynosi

x

N +1

− x

N

= [2(N + 1) + 1]

λ

4

− (2N + 1)

λ

4

=

λ

2

(23)

Interpretacja na wykładzie

dopisz oznaczenia!

3

FALA STOJĄCA

6

3.1

Fale stojące na strunie

Prędkość fali poprzecznej na strunie wynosi

c =

s

F

µ

(24)

gdzie F - siła naprężająca strunę, µ - gęstość liniowa struny

kgm

−1

Częstość drgań struny, w której rozchodzi się taka fala poprzeczna wynosi

f =

1

T

=

1

λ

c

=

c

λ

=

1

λ

s

F

µ

(25)

W przypadku gitary:

• F regulujemy przez.....

• µ regulujemy przez.....

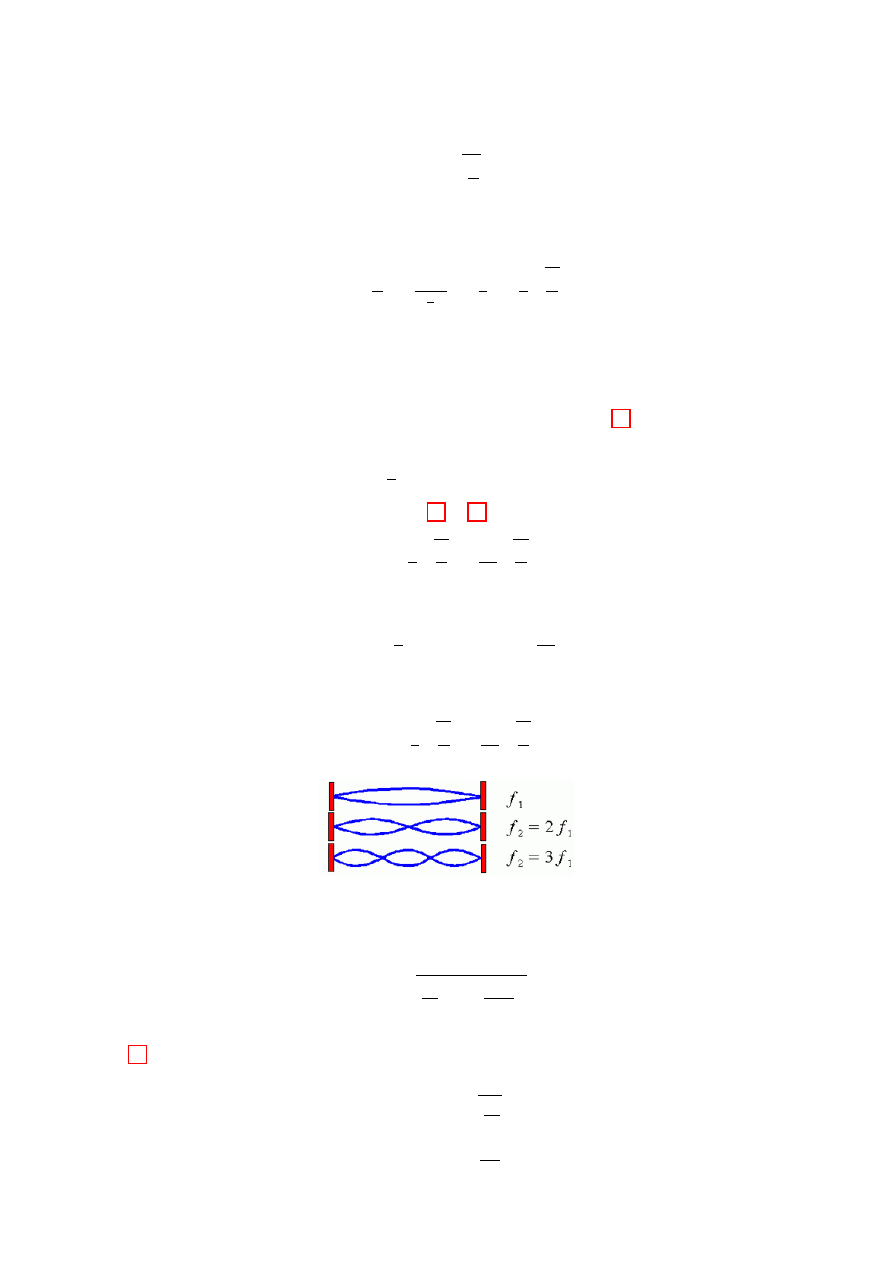
Fale stojące na strunie muszą mieć węzły na końcach. W takim razie, zgodnie z (23), podstawowa (najdłuższa)
fala stojąca jaka może powstać na strunie o długości L ma długość

L =

λ

2

⇒

λ = 2L

(26)

zaś częstotliwość drgań takiej struny, na podstawie (25) i (26), wynosi

f

1

=

1

λ

s

F

µ

=

1

2L

s

F

µ

(27)

Możliwe są też inne (krótsze) fale stojące, spełniające warunek

L = N

λ

2

⇒

λ =

2L

N

gdzie N jest liczbą naturalną.

Odpowiadające im częstotliwości drgań struny f

N

wynoszą

f

N

=

1

λ

s

F

µ

=

N

2L

s

F

µ

(28)

3.2

Fale stojące na wodzie

Prędkość fali na wodzie wynosi

c =

s

gλ

2π

tgh

2πH

λ

(29)

pod warunkiem, że wysokość fali H = 2A spełnia zależność H λ

Wzór (29) trochę się upraszcza w szczególnych przypadkach:

• “Głęboka” woda (głębokość > λ/2 )

c =

r

gλ

2π

• “Płytka woda” (glębokość < λ/20 )

c =

p

gh

3

FALA STOJĄCA

7

3.2.1

Sejsze

Dopisz oznaczenia i komentarz na wykładzie

3.2.2

Fala stojąca a przypływy.

Dopisz oznaczenia i komentarz na wykładzie

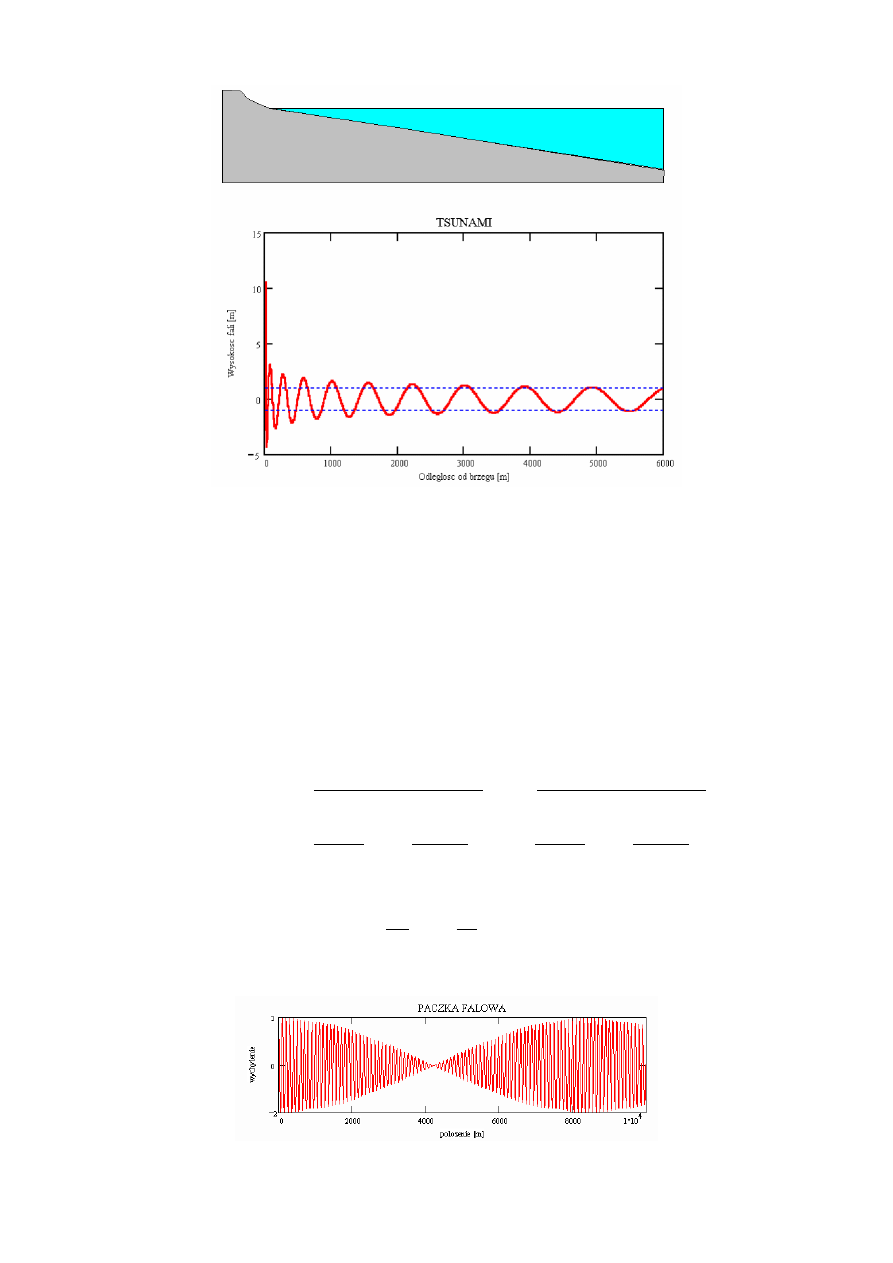
3.2.3

Tsunami

Model zjawiska

• długość wzniesienia l = 6 km

• głębokość (daleko od brzegu) h = 1058

• nachylenie wzniesienia α = arctg (h/l) = 10, 26

o

• częstość drgań ω = 0, 54 Hz

• amplituda początkowa a = 1 m

• prędkość fali c =

√

gh = 367 km/godz

• długość fali λ = c

2π

ω

= 1185 km

Wynik

• amplituda w pobliżu brzegu H(x) wynosi

H(x) = a

J 0

2ω

q

x

αg

J 0

2ω

q

l

αg

4

PRĘDKOŚĆ GRUPOWA

8

4

Prędkość grupowa

W jednym kierunku podążają dwie fale, różniące się nieznacznie częstością (i liczbą falową)

y

1

(x, t) = A cos(ω

1

t − k

1

x)

y

2

(x, t) = A cos(ω

2

t − k

2

x)

W dowolnym punkcie x na drodze fal, wychylenie wypadkowe y

w

w chwili t wynosi

y

w

(x, t) = y

1

(x, t) + y

2

(x, t) = A cos(ω

1

t − k

1

x) + A cos(ω

2

t − k

2

x)

y

w

(x, t) = 2A cos

ω

1

t − k

1

x + ω

2

t − k

2

x

2

cos

ω

1

t − k

1

x − ω

2

t + k

2

x

2

y

w

(x, t) = 2A cos

ω

1

+ ω

2

2

t −

k

1

+ k

2

2

x

cos

ω

1

− ω

2

2

t −

k

1

− k

2

2

x

Uwaga! zmieniamy kolejność wyrażeń.

y

w

(x, t) =

2A cos

∆ω

2

t −

∆k

2

x

cos (ω

sr

t − k

sr

x)

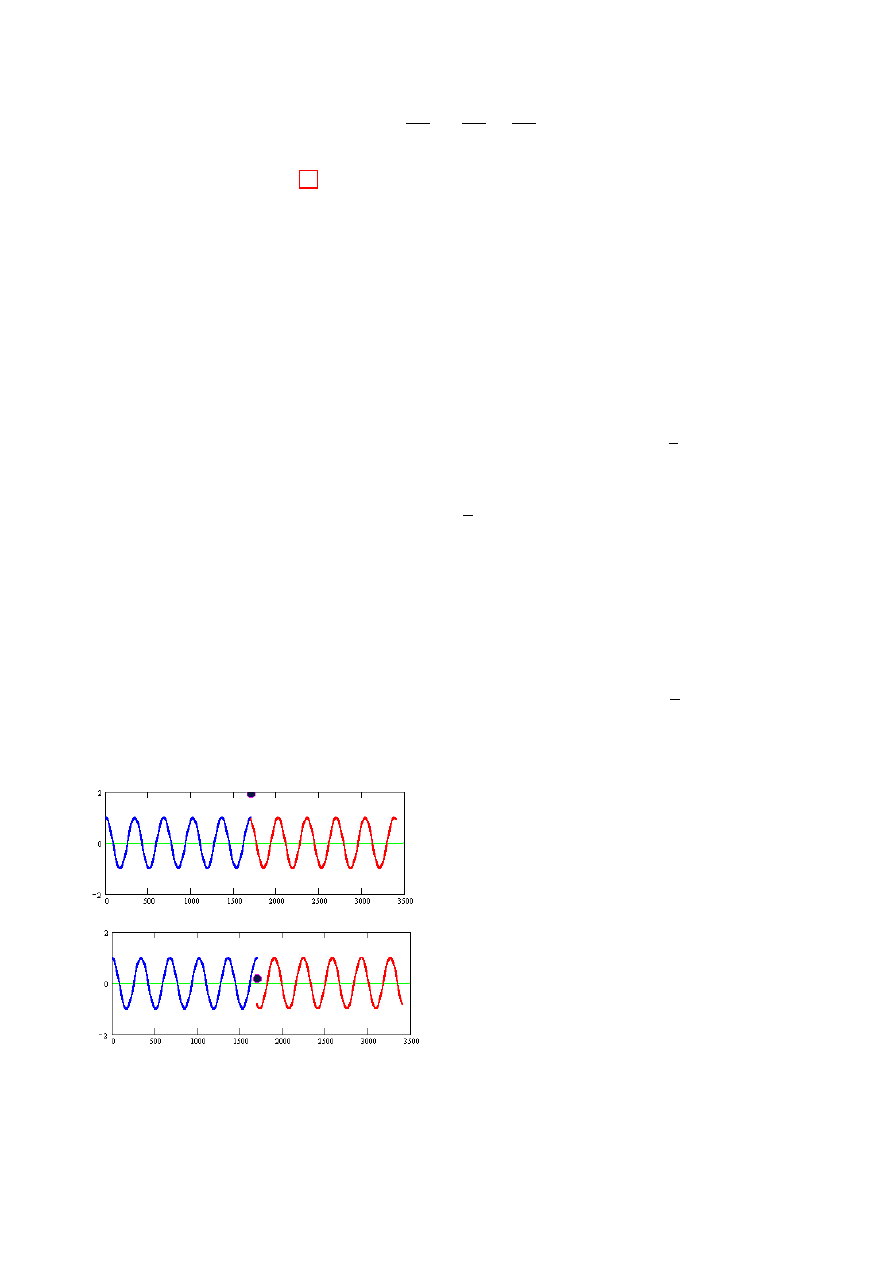
(30)

Poniżej, graficzna prezentacja wyniku

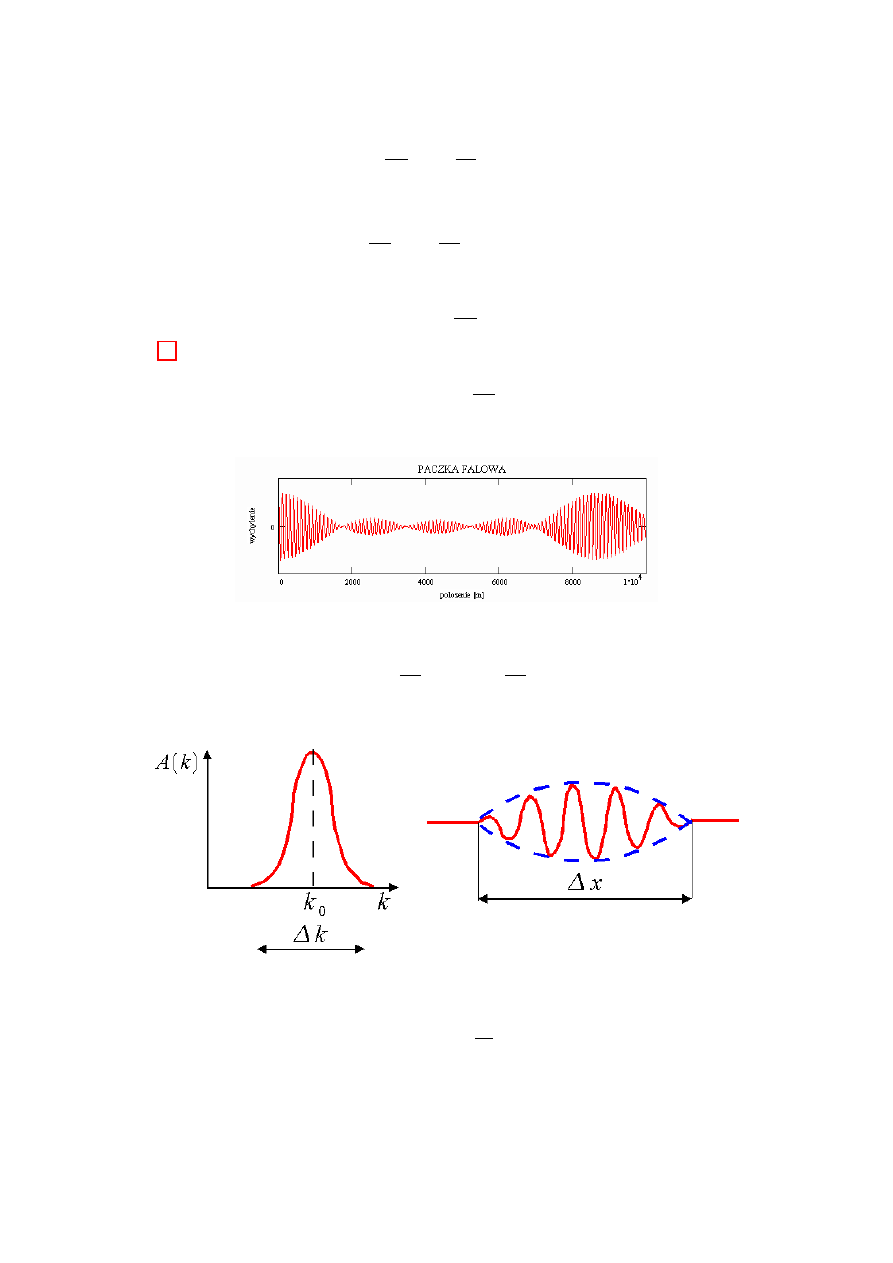
4

PRĘDKOŚĆ GRUPOWA

9

Liczymy prędkość grupy w podobny sposób jak liczyliśmy prędkość przemieszczania się fazy. Wybieramy mak-
simum grupy:

2A cos

∆ω

2

t −

∆k

2

x

g

= 2A

Wtedy

∆ω

2

t −

∆k

2

x

g

= 0

i ostatecznie

x

g

=

∆ω

∆k

t

(31)

Równanie (31) pokazuje, że prędkość grupy v

grupy

wynosi

v

grupy

=

∆ω

∆k

Kiedy grupa składa się z większej ilości fal, obraz ulega zmianie

Kiedy użyjemy nieskończenie wielu fal o liczbach falowych z pewnego zakresu

k

0

−

∆k

2

< k < k

0

+

∆k

2

otrzymamy pojedynczą paczkę falową

Ogólny wzór na prędkość grupową ma postać

v

grupy

=

dω

dk