•

Odpowiedzi należy wpisywać tylko

w pozostawionych miejscach,

•

W pytaniach wystarczą 2-3 zdania odpowiedzi,

najlepiej w punktach i ewentualnie odręczny

szkic,

•

Odpowiedzi nieczytelne, zupełnie nie na temat

lub z elementarnymi błędami mogą zostać

ocenione punktem ujemnym,

•

Do zaliczenia wymagane jest 10 punktów.

KOLOKWIUM Z FUNDAMENTOWANIA II (KB)

Imię i nazwisko studenta:

. . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . .
Numer albumu: Data:
Zadanie 1

max 8p.

Zadanie 2

max. 4p.

Pytanie 1

max 3p.

Pytanie 2

max 3p.

Pytanie 3

max 2p.

RAZEM

max 20p.

ξ

EI, B

C

M

o

M

o

ξ

o

=0

π

π

f ( )

ξ =

e

−ξ

ξ

cos

e

−ξ

ξ

sin

d f

d

2

2

ξ

=

2e

−ξ

ξ

sin

− −

2e

ξ

ξ

cos

d f

d

3

3

ξ

=

− −

+ −

2

2

e

e

ξ

ξ

ξ

ξ

sin

cos

2

2

e

e

−

+ −

ξ

ξ

ξ

ξ

cos

sin

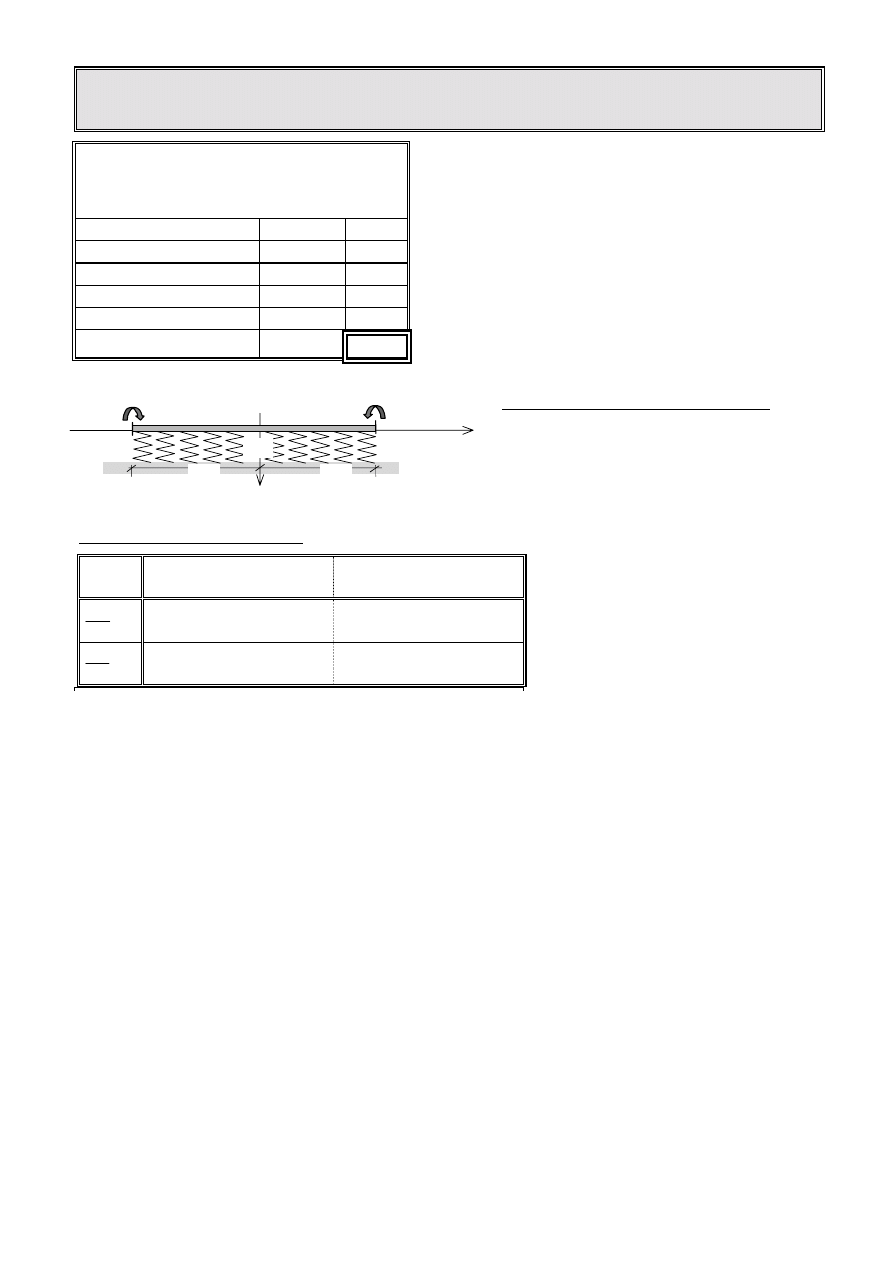
Zadanie 1. (za 8 punktów, ok. 20min):
Belka na podłożu Winklera ma
bezwymiarową długość 2

π

i jest obciążona na

obu końcach momentem skupionym M

o

.

Obliczyć osiadanie środka tej belki, y(0) = ?

Można wykorzystać oś symetrii w przekroju

ξ

o

= 0.

Zastosować rozwiązanie ogólne i podane niżej pochodne funkcji.

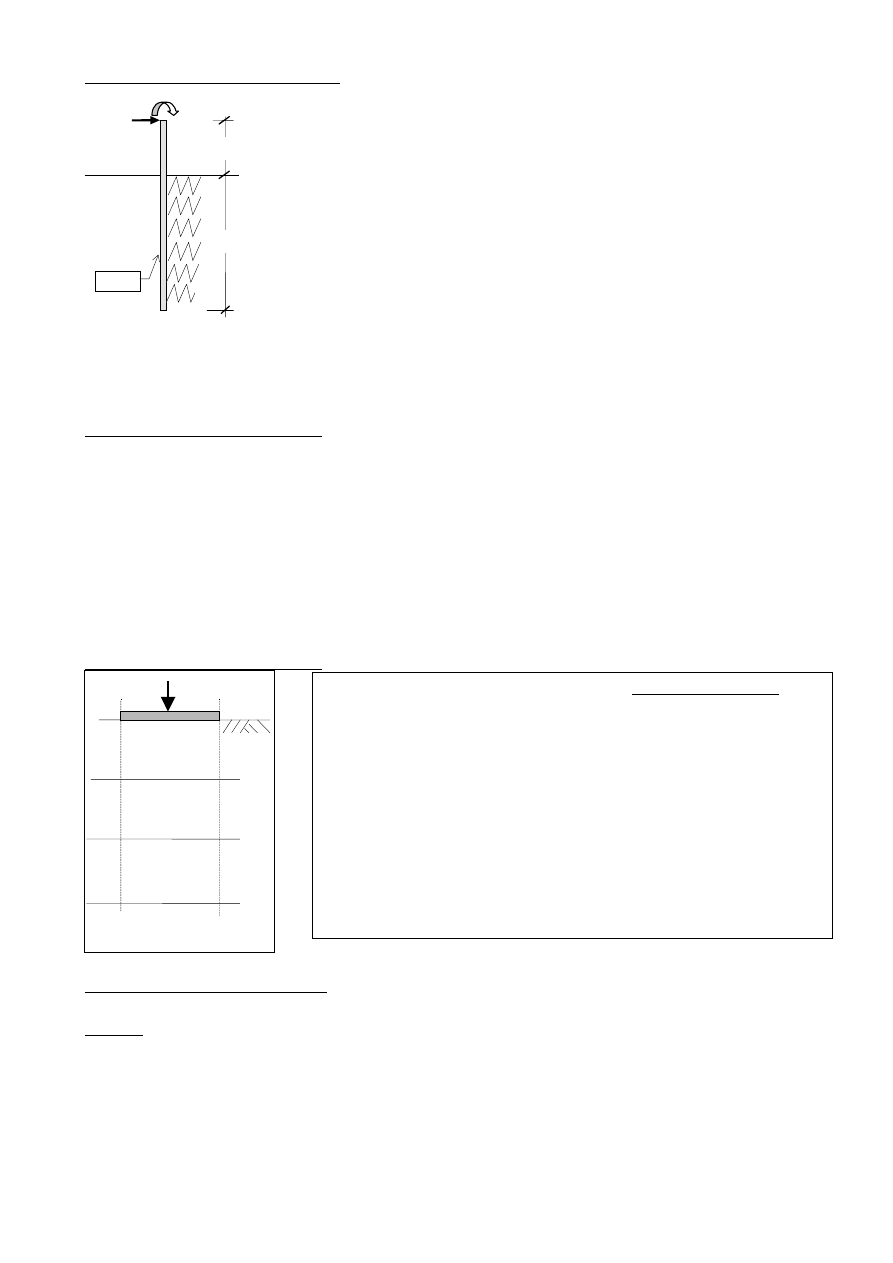
Zadanie 2. (za 4 punkty, ok. 10min)

Modelem pala w ośrodku sprężystym jest belka o długości H+h,
spoczywająca na podłożu Winklera o stałej C.
Zaproponować sposób analitycznego wyznaczenia poziomego przemieszczenia
głowicy pojedynczego pala obciążonej momentem M

o

i siłą poziomą P

o

na dużej

wysokości h ponad poziomem terenu.

Pytanie 1. (za 3 punkty, ok. 5min)
Belkę jednostronnie nieskończenie długą na jednorodnym podłożu Winklera łatwo rozwiązuje się za
pomocą metody Bleicha. A za pomocą metody Zawrijewa?

Pytanie 2. (za 3 punkty, ok. 5min)

Pytanie 3. (za 2 punkty, ok. 5min):
Podać przykład sytuacji, w której podstawowe znaczenie ma sprawdzenie masywnej ściany oporowej
na obrót względem zewnętrznej krawędzi fundamentu, a nie sprawdzenie nośności na wypieranie Q

fNB

.

P

o

h

H

EI, B

C

M

o

Nieskończenie sztywna ława fundamentowa na podłożu Winklera jest
obciążona siłą pionową bez mimośrodu. Na rysunku obok naszkicować
typowy wykres reakcji podłoża (pionowe naprężenia pod ławą):

A) przed wystąpieniem deformacji górniczej:

B) po wystąpieniu wklęsłej w dół krzywizny terenu górniczego o
promieniu 0 > R

gr

> R:

C) po wystąpieniu wklęsłej w dół krzywizny terenu górniczego o
promieniu 0 > R > R

gr

:

A

B

C