Przewodnik dla nauczycieli

Krótkie posumowanie

Przedstawiono geometrię najbliższego pierścienia wokół Supernowej 1987A. Następnie zdefiniowano skalę
zdjęcia Supernowej wykonanego przez Hubble'a. To pozwoliło na znalezienie kątowej średnicy i nachylenia
(inklinacji) pierścienia w stosunku do płaszczyzny nieba.

Obserwacje prowadzone z Ziemi pokazały w jaki sposób światło Supernowej dochodzi do różnych części
pierścienia. Wykorzystując pomiar natężenia światła i znajomość jego prędkości można znaleźć liniowy
rozmiar pierścienia. Mając wyznaczony kątowy i liniowy rozmiar pierścienia możemy wyznaczyć odległość do
SN 1987A.

Przewodnik dla nauczycieli zawiera rozwiązania problemów wraz z komentarzami oraz dyskusją przybliżeń i
uproszczeń, które poczyniliśmy. Jego celem jest maksymalizacja użyteczności ćwiczenia i pomoc w
przygotowaniu planu przedstawienia zagadnienia.

Zadanie 1

Przykładowe pomiary, robione ręcznie, na wydrukowanym obrazku o rozmiarach 149 mm x 151 mm
(rozmiar wydrukowanego obrazka zależy od ustawienia i rodzaju drukarki):

Zadanie 2

Kątową średnicę pierścienia znaleźliśmy mierząc największy wymiar widomej elipsy. Projekcja okręgu będzie
zawsze ukazywała jego średnicę, niezależnie od tego jak bardzo będzie on nachylony.

Zmierzona widoma średnica pierścienia: 51 mm.
Zamiana na radiany:

a = 51 mm * 0.03111 sekund łuku/mm * 4.848 *10-6 rad/sekundę łuku = 7.6919 *10

-6

rad

Zadanie 3

Niektórzy mogą mieć problemy z trójwymiarową percepcją patrząc na dwuwymiarowy obraz - tj. ze
"zdekodowaniem" rysunku, który zawiera perspektywę na dwuwymiarowym przekroju (na przykład projekcja
izometryczna) . Jeśli będzie to konieczne, połóżcie większy nacisk na zagadnienia i komentarze związane z
rysunkami. Przyjęte przybliżenie, mówiące o tym, że promienie światła, które dochodzą do Ziemi z odległego
obiektu, są do siebie równoległe jest ogólnie dobrze znane uczniom (w podobny sposób postępujemy
w przypadku promieni światła dochodzących do nas ze Słońca).

Każdą elipsę możemy rozpatrywać jako projekcję okręgu nachylonego pod kątem inklinacji, i, do płaszczyzny
nieba (płaszczyzna ta jest prostopadła do linii patrzenia). Duża oś elipsy jest równa średnicy okręgu, zaś jego
mała oś jest równa cos(i) pomnożonemu przez dużą oś.

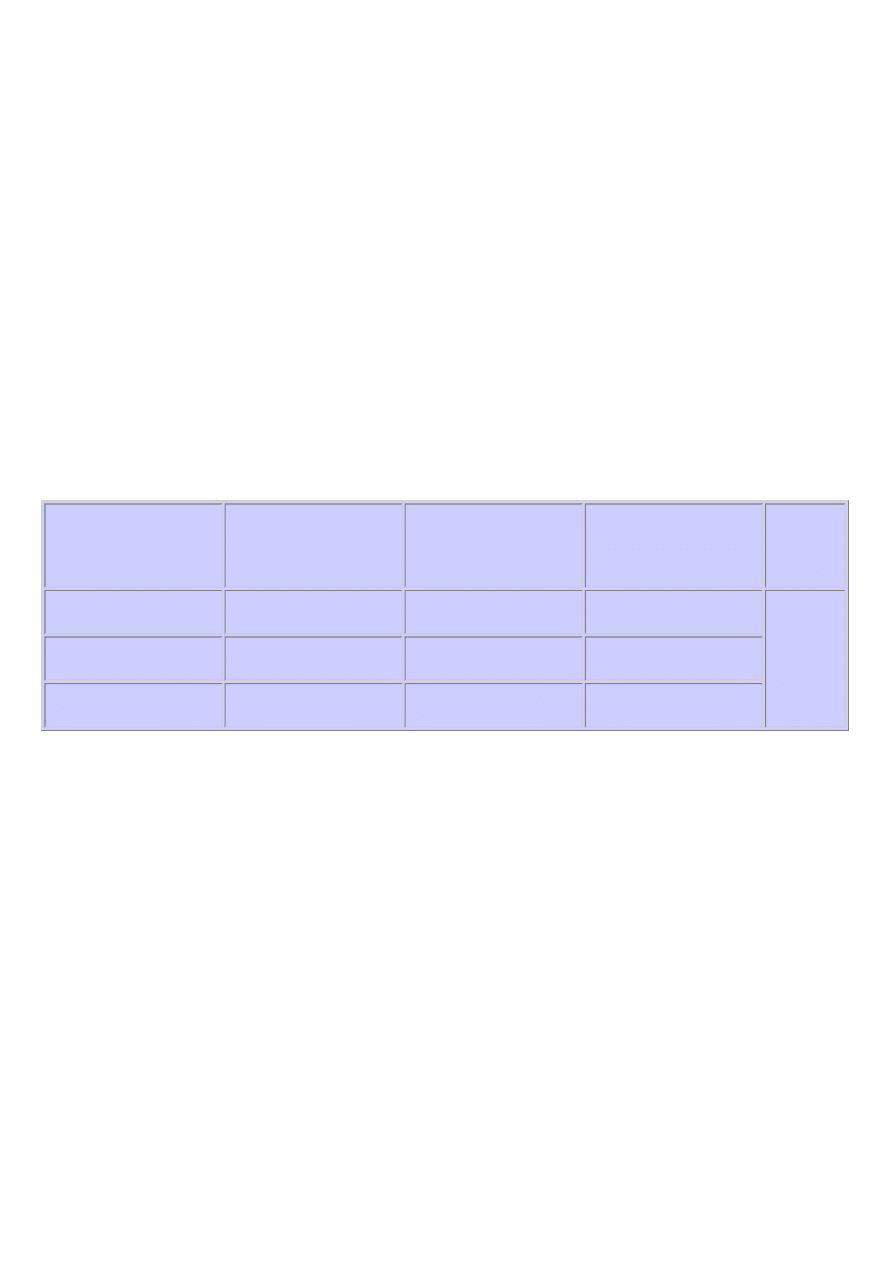
Odległość
(mm)

Odległość
(sekundy łuku)

Skala
(sekundy łuku/mm)

Średnia
skala
(sekundy
łuku/mm)

Gwiazda 2 z gwiazdą
1

89

3.0

0.03371

0.03111

Gwiazda 3 z gwiazdą
1

50

1.4

0.02800

Gwiazda 3 z gwiazdą
2

136

4.3

0.03162

Strona 1 z 2

Otrzymujemy związek:
cos i=(mała oś)/(wielka oś)=37mm/51mm
i = cos

-1

(37/51) = 0.7591 rad = 43.49 stopni

Zadanie 4

Na diagramie zmian jasności możecie zmierzyć odległość na osi czasu pomiędzy początkiem zaświecenia
się pierścienia, a maksimum jego jasności. Nam wyszło t = 399 dni (to, że okres ten jest w przybliżeniu równy
jednemu rokowi jest czystym przypadkiem). Gdyby nachylenie pierścienia wynosiło 90

o

, wtedy widzielibyśmy

go jako odcinek. W tym przypadku różnica czasu pomiędzy chwilą, w której pojaśniał pierwszy fragment
pierścienia, a momentem, w którym doleciało do nas światło z najbardziej oddalonej części pierścienia byłaby
niczym innym jak jego średnicą podzieloną przez prędkość światła.

Zadanie 5

sin(i) = d

p

/d => d = d

p

/ sin(i)

d

p

= c * t

To daje:
d = d

p

/ sin(i) = (c * t)/sin(i) = (2.977 * 108 * 339 * 24 * 3600)/ sin(43.49) = 1.4912 * 10

16

m

Zadanie 6

D = d/a = (1.4912 * 1016)/(7.6915 * 10

-6

) = 1.9439 * 10

21

m = 63.0 kpc

Odległość liczona przez

Panagia i innych

na podstawie oryginalnych danych (naukowcy ci używali bardziej

wyrafinowanych metod obliczeniowych) wynosi D = 51.2 ± 3.1 kpc. (Wartość, którą my uzyskaliśmy mieści
się w granicy 20%-owego błędu.)

Źródła błędów

Dyskusja błędów może być dobrym powodem do wprowadzenia bardziej formalnych rachunków zakresu
błędów. Można poprosić uczniów o powtórzenie rachunków dla największej i najmniejszej wartości uzyskanej
z pomiarów. Oto jaki wpływ mogą mieć przeszacowania jednych wielkości na wartość innych:

Za duży rozmiar kątowy, a => za małe D (coś co jest bliżej, wygląda na większe)
Za duża widoma średnica => za małe D
Za duża stała przeliczenia => za małe D
Za małe t => za małe D
Za duże i => za małe D

Dobrym ćwiczeniem dla uczniów może być samodzielne rozpatrzenie powyższych zależności.

Problem pochodzenia dwóch zewnętrznych pierścieni.

Pytanie o zewnętrzne pierścienie wokół Supernowej jest dobrym przykładem prostego pytania naukowego, na
które nie znamy odpowiedzi (zdarza się to bardzo często w dynamicznie rozwijających się naukach, do których
należy także astronomia). Świat naukowy nie zna co prawda wyjaśnienia tłumaczącego mechanizm
powstawania pierścieni, ale jest pewien, że materia tworząca je oderwała się od macierzystej gwiazdy przeszło
20 000 lat przed wybuchem supernowej. Pozostaje tajemnicą dlaczego zachowały one formę niemalże
idealnych okręgów. Powszechnie przyjmuje się, że czerwony gigant (gwiazda będąca w ostatniej fazie
ewolucji, tuż przed wybuchem supernowej) odrzuca swą zewnętrzną otoczkę jednorodnie we wszystkich
kierunkach.

Strona 2 z 2