prof. dr hab. inż. Idzi Gajderowicz
Uniwersytet Warmińsko – Mazurski w Olsztynie

Ocena dokładności i stabilności

polskiej sieci niwelacji precyzyjnej

I klasy

Kraków, wrzesień 2004

Parametry geometryczne sieci niwelacyjnej I klasy

* 382 linie niwelacyjne o łącznej długości 17516 km

* 16150 odcinków niwelacyjnych

średnia długość odcinka: 1.085 km

* 245 węzłów i punktów końcowych linii dowiązanych

jednostronnie, w tym 28 punktów przygranicznych

Okres pomiaru

* kampania pomiarowa od kwietnia 1999 roku

do końca czerwca 2002 roku

* do sieci włączono także linię pomierzoną w połowie 1997 r.

i linię pomierzoną w październiku 2003 r.

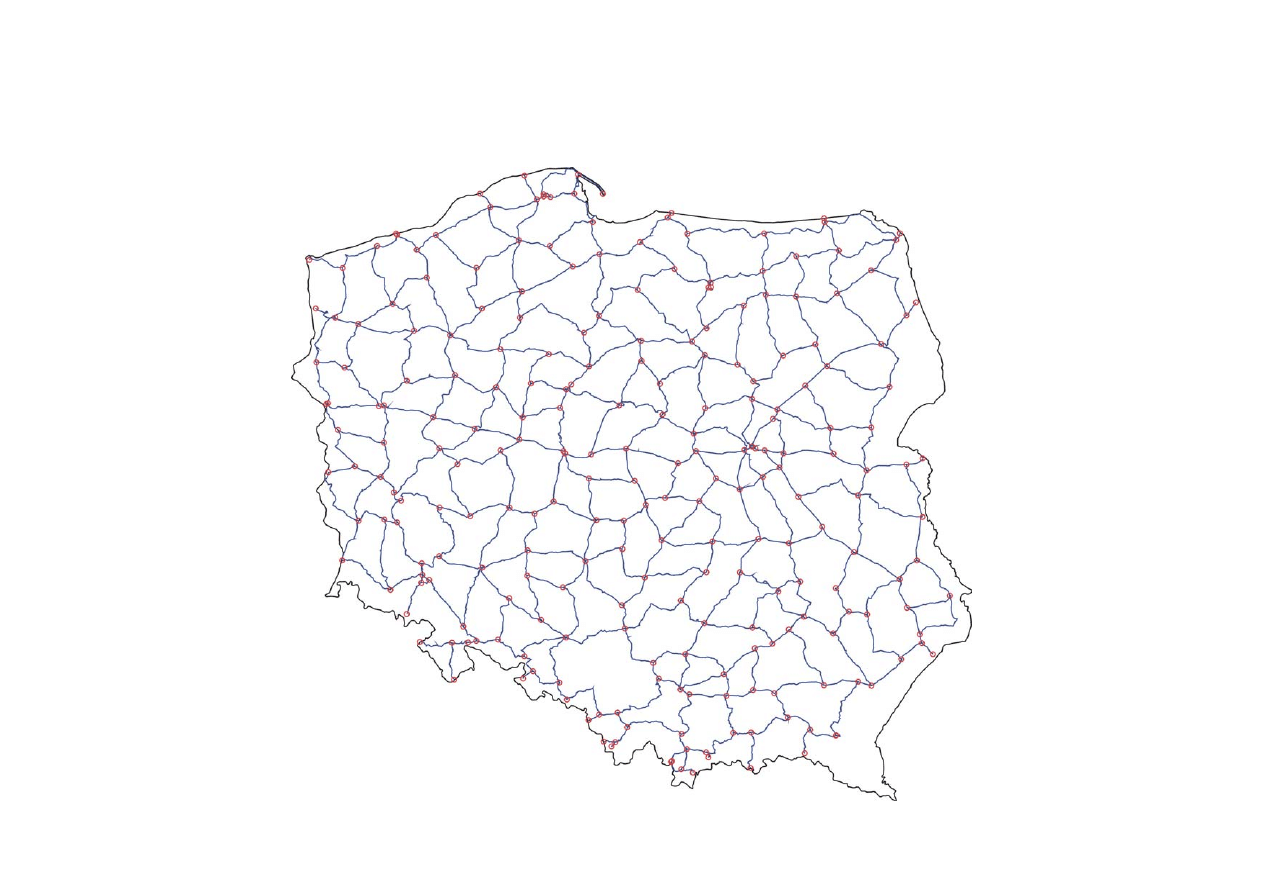
Szkic sieci niwelacyjnej I klasy.

* Błąd średni m

1

pomiaru 1 km niwelacji obliczony w oparciu o

o różnice

ρ między wynikami pomiarów odcinków w kierunku

głównym i powrotnym

m

1

= 0.278 mm/

√km

* Błąd przypadkowy

η i błąd systematyczny σ

obliczone według wzorów Lallemanda

η = 0.261 mm/√km

σ = 0.088 mm/km

Ocena dokładności – parametry dotyczące instrumentów

.088

.261

.278

393

Cała sieć

.084
.096
.094

.266
.244
.328

.282
.263
.344

259
123

11

Zeiss Ni002
Zeiss DiNi11
Topcon NJ

σ

η

m

1

n

lin

Instrument

gdzie n

lin

– liczba linii lub sekcji

Ocena dokładności – parametry dotyczące obserwatorów

.088

.261

.278

393

Cała sieć

.077
.081
.098
.082
.104
.098
.072
.060
.106
.046
.063
.069
.109
.120
.118

.246
.245
.236
.236
.271
.268
.295
.260
.271
.297
.274
.239
.286
.284
.297

.257
.257
.255
.265
.293
.287
.302
.270
.291
.303
.281
.258
.314
.322
.327

54
52
41
34
32
27
24
19
17
17
17
15
14

8

22

Z. Strzeszewski
K. Ryszkowski
J. Grabczak
Z. Rodak
R. Kryński
M. Bogusz
A. Gąsior
W. Frontczak
K. Ciechoniec
K. Tarnowski
A. Romanowski
M. Lisik
Z. Bednarz
W. Sałgut
Pozostali (9 obs.)

σ

η

m

1

n

lin

Obserwator

* Jak ocenić podwójne pomiary linii ?

Błąd średni m

2

pomiaru 1 km niwelacji obliczony w oparciu

o różnice

λ między wynikami pomiarów linii

w kierunku głównym i powrotnym
przy założeniu, że różnice

λ

mają charakter błędów przypadkowych
( dla każdej linii

λ=[ρ] )

m

2

= 0.516 mm/

√km

* Zamknięcia poligonów niwelacyjnych i błąd średni m

3

Błąd średni m

3

pomiaru 1 km niwelacji obliczony w oparciu

o błędy zamknięcia poligonów

m

3

=0.833 mm/

√km

Wyrównanie testowe sieci

Przyjęty system wysokości

•System wysokości normalnych

•Anomalie Faye’a odniesione do wzoru Helmerta 1901-1908

na przyspieszenie normalne

•Jeden stały punkt – reper węzłowy Warszawa-Wola,

którego wysokość przyjęto z wyników opracowania sieci 1974-1982.

Wyniki wyrównania sieci metodą najmniejszych kwadratów

* Błąd średni m

0

typowej obserwacji

czyli podwójnej niwelacji odcinka o długości 1 km

m

0

= 0.88 mm/

√km

* Błąd średni pomiaru typowej linii niwelacyjnej AB( L

AB

=45.8km )

m

AB

= m

0

√L

AB

= 6.0 mm

* Błędy średnie wysokości punktów węzłowych

tylko na skrajach sieci przekraczają wielkość 10 mm.

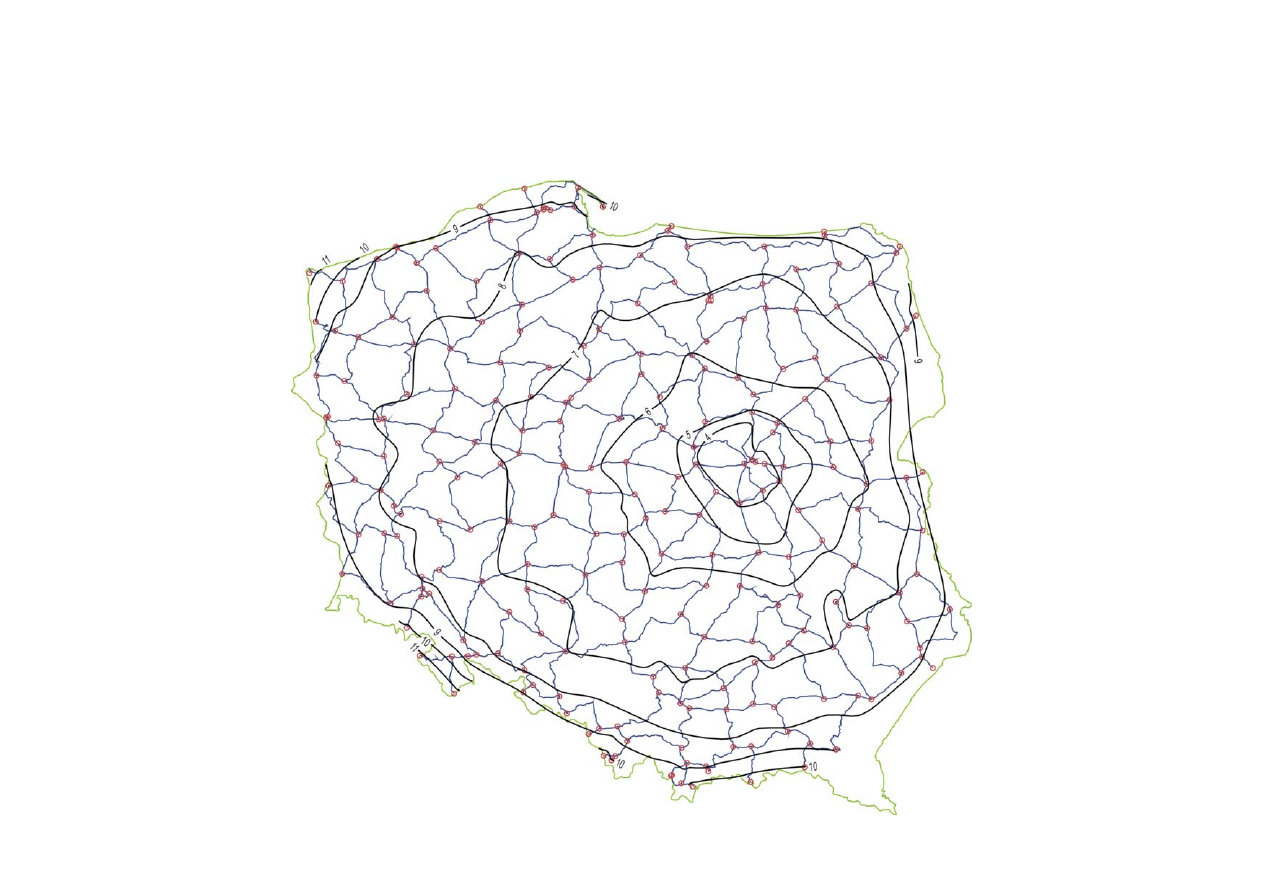
Izolinie błędów średnich wyrównanych
wysokości punktów węzłowych.

Porównanie parametrów dokładnościowych
kampanii 1974-1982 i 1997-2003.

Parametry dokładnościowe kampanii

niwelacyjnej 1974-1982 można znaleźć w
(Niwelacja Precyzyjna (1993), Rozdział 10.74).

0.88 mm/√km

0.844 mm/√km

m

0

0.278 mm/√km
0.516 mm/√km
0.833 mm/√km
0.261 mm/√km

0.088 mm/km

0.288 mm/√km
0.534 mm/√km
0.922 mm/√km
0.277 mm/√km

0.082 mm/km

m

1

m

2

m

3

η
σ

Kampania

1977-2003

Kampania

1974-1982

Parametr

Wielkości parametrów dokładnościowych nowej kampanii
obserwacyjnej są bardzo zbliżone do wielkości odpowiednich
parametrów poprzedniej kampanii.
Wynika to z faktu, że w obu przypadkach mierzono prawie taką
samą sieć, stosując te same lub równorzędne instrumenty.

Na uwagę zasługuje jeszcze parametr m

0

starej sieci, którą

wyrównano jako sieć nawiązaną wielopunktowo.
Jeśli tę sieć wyrównać jako sieć nawiązaną jednopunktowo,
to parametr wynosi 0.88 mm/√km i jest równy parametrowi
m

0

otrzymanemu w procesie wyrównania wyników pomiarów

nowej sieci.

Porównanie nowych wysokości ze starymi

Dla każdego reperu danej linii obliczono

∆

i

= (H

n

– H

s

)

i

– (a +b*(SR)

i

)

Parametry a, b wyznaczano oddzielnie dla każdej linii
metodą najmniejszych kwadratów

Dla większości linii m

0

< 6mm

Dla 22 linii 6mm < m

0

< 9mm

Przyjęto, że reper i-ty był niestabilny, jeśli

∆

i

 > 2.5 m

0

gdy m

0

< 6mm

lub

∆

i

 > 2.0 m

0

gdy m

0

> 6mm

Znaleziono 923 niestabilne repery

Porównanie nowych i starych różnic wysokości

Dla każdego odcinka niwelacyjnego i-j sprawdzono czy

dH

ij

stare

- dH

ij

nowe

 < (2.5√R + 2.0)mm

gdzie R jest długością odcinka

Przyjęto, że reper był niestabilny jeśli oba sąsiednie odcinki
niwelacyjne nie spełniały powyższej nierówności.

Znaleziono w ten sposób dodatkowo 297 niestabilnych reperów

Statystyka dotycząca stabilności reperów

Stabilnych 11810 73.8 %
Niestabilnych 1120 7.6 %
Nowych 2983 18.6 %
-----------------------------------------
Razem 16013

Obliczanie wysokości
nowych reperów i reperów niestabilnych
w starym systemie wysokości

na zasadzie „wklejania” nakładek (łatek)
do starych linii
w oparciu o wyniki nowych pomiarów.

W procesie wklejania kilku tysięcy łatek otrzymano:

m

0

= 2.0 mm/

√km

Wniosek:
Stara sieć niwelacyjna I klasy ma teraz obniżoną dokładność.
Parametr m

0

= 2.0 mm/

√km wskazuje, że jest to dokładność

typowa dla II klasy.