Rok akademicki:

2011/2012

INŻYNIERIA MATERIAŁOWA

Statystyczna analiza wyników badań

Konsultował:

Projekt wykonał:

dr inż. Janusz Konkol

Adam Wasilewski P8

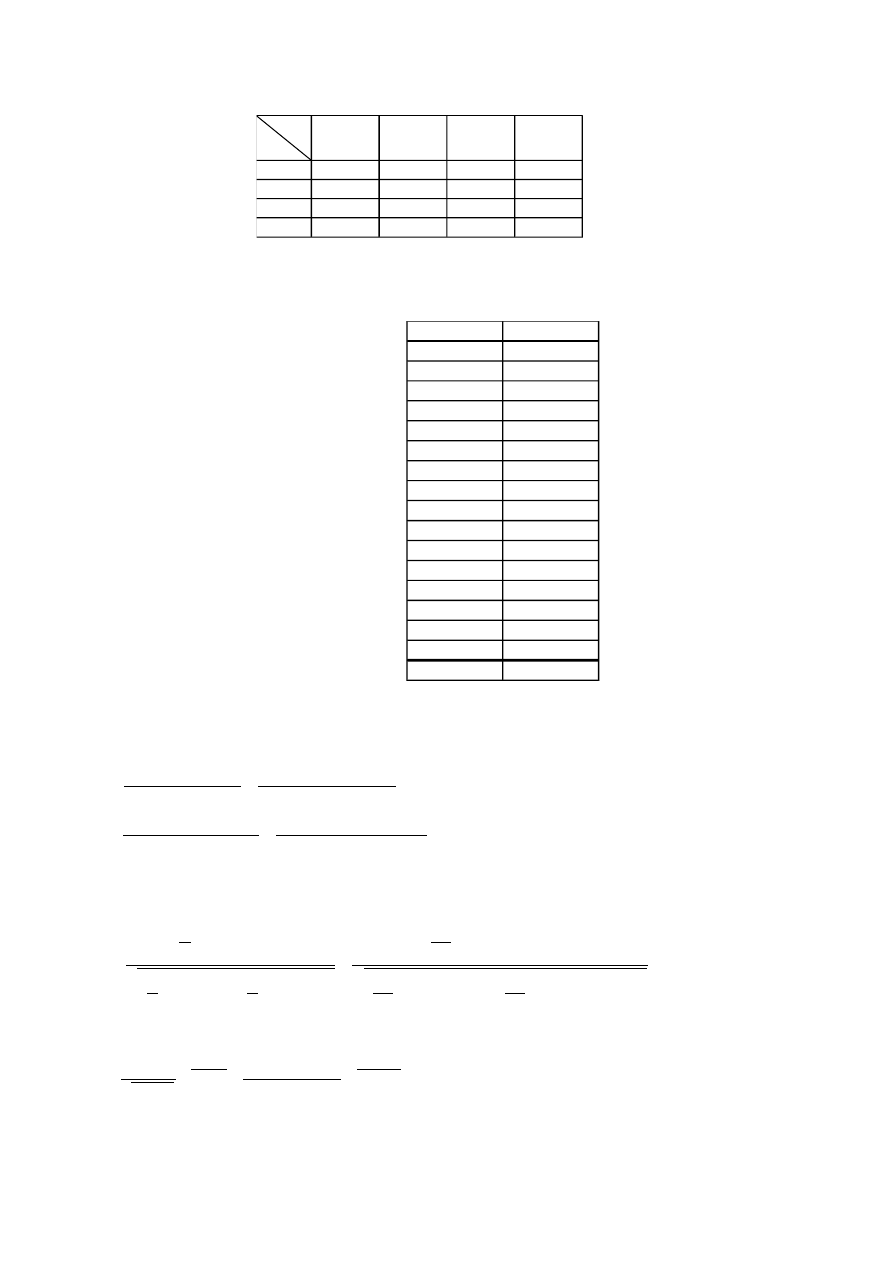
Dane wejściowe:

Wyznaczenie funkcji regresji liniowej y=ax+b metodą najmniejszych kwadratów.

Zbiór punktów:
Wartości potrzebne do wyznaczenie współczynników a i b:

Σ

xy=191,3

Σ

x=7,2

Σ

y =432

Σ

x

2

=

3,44

n=16

a=

n⋅Σ xy−Σ x⋅Σ y

n⋅Σ x

2

−( Σ

x )

2

=

16⋅191,3−7,2⋅432

16⋅3,44−(7,2)

2

=−

15,5

b=

Σ

y⋅Σ x

2

−Σ

x⋅Σ xy

n⋅Σ x

2

−(Σ

x )

2

=

432⋅3,44−7,2⋅191,3

16⋅3,44−(7,2)

2

=

33,975

Zatem funkcja regresji liniowej ma postać:

y=−15,5⋅x +33,975

Współczynnik korelacji:

̄x=0,45

̄y=27

R=

1
n

⋅Σ

x

i

y

i

−̄x⋅̄y

√

(

1
n

⋅Σ

x

i

2

−̄x

2

)

⋅

(

1
n

⋅Σ

y

i

2

−̄y

2

)

=

1

16

⋅

191,3−0,45⋅27

√

(

1

16

⋅

3,44−0,45

2

)

⋅

(

1

16

⋅

11716,92−27

2

)

=−

0,953

Istotność współczynnika korelacji:

t=

R

√

1− R

2

⋅

√

n−2=

−

0,953

1−(−0,953)

2

⋅

√

16−2=−11,75

Sprawdzenie hipotez

Hipoteza początkowa H

0

– Brak korelacji liniowej

1

0,3

0,4

0,5

0,6

29,2

28,2

26,9

25,2

28,5

27,5

26,5

24,8

29,5

27,8

27

24,2

30,1

26,9

25,9

23,8

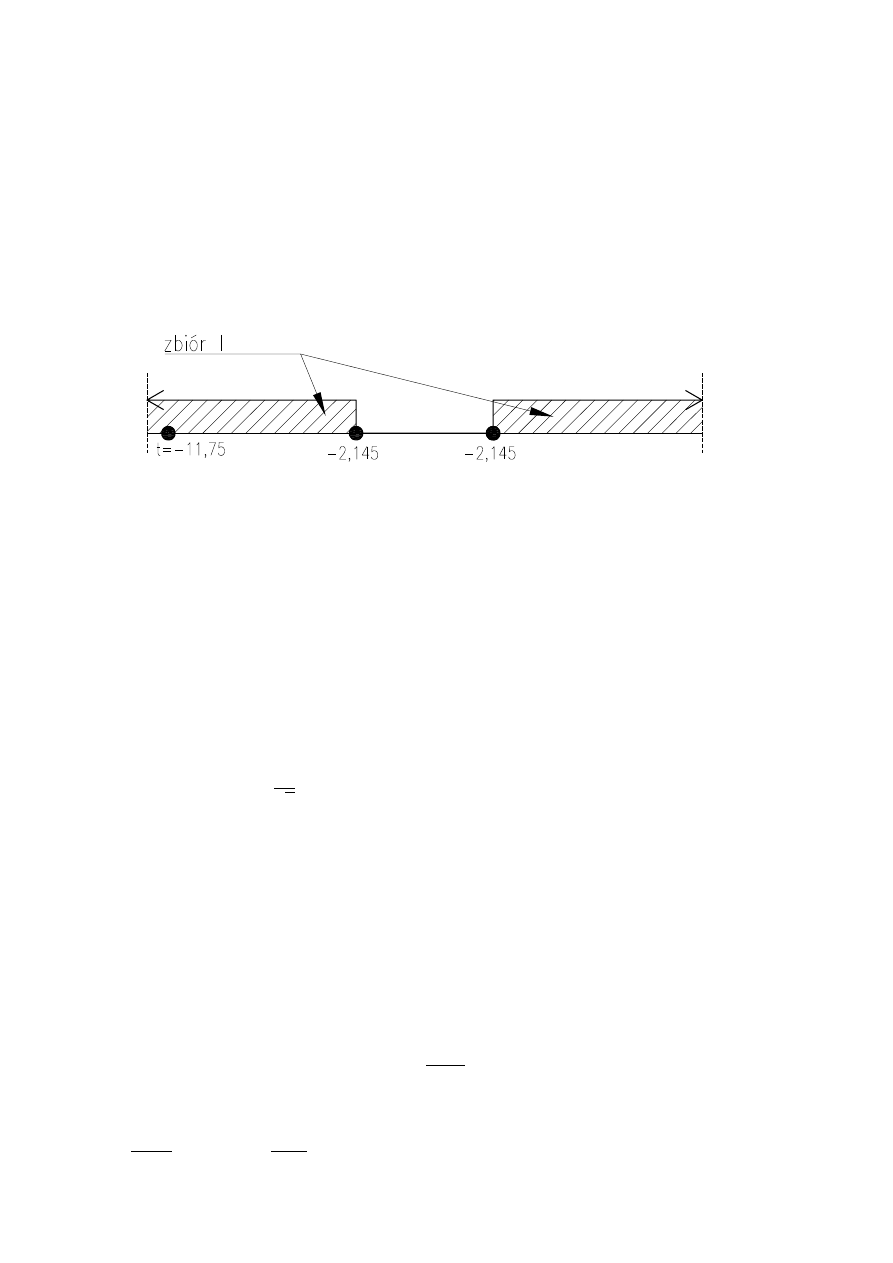
x

y

y

0,3

29,2

0,3

28,5

0,3

29,5

0,3

30,1

0,4

28,2

0,4

27,5

0,4

27,8

0,4

26,9

0,5

26,9

0,5

26,5

0,5

27

0,5

25,9

0,6

25,2

0,6

24,8

0,6

24,2

0,6

23,8

Σ

7,2

432

x

Hipoteza alternatywna H

1

– Korelacja jest liniowa

Statystyka testu – t

H

0

jest prawdziwa, jeśli t ∉I

Poziom istotności: α=0,05

I – zbiór krytyczny: I =(−∞ ,−t (1−0,5 α , ν)>∪<t (1−0,5α , ν),+∞)
gdzie ν=n−2

t (1−0,5 α , ν)=t(1−0,5⋅0,05 ,16−2)=t (0,975 ,14)

Kwantyl t(0,975 , 14) rzędu 0,975 rozkładu Studenta o 14 stopniach swobody wynosi 2,145.

Ponieważ t ∈I , hipoteza początkowa jest nieprawdziwa, zatem korelacja jest liniowa.

Wartości średnie:
x=0,3 ̄y=29,325

x=0,4 ̄y=27,6

x=0,5 ̄y=26,575

x=0,6 ̄y=24,5

Odchylenie standardowe na podstawie próbki:
x=0,3 s=0,665
x=0,4 s=0,548
x=0,5 s=0,499
x=0,6 s=0,622

Błąd standardowy: ̄s=

s

√

r

r – liczba próbek

x=0,3 ̄s=0,333

x=0,4 ̄s=0,274

x=0,5 ̄s=0,250

x=0,6 ̄s=0,311

Wielomianowa funkcja regresji:
Za pomocą programu Origin dopasowano funkcję wielomianową o wzorze:

y=−291,67⋅x

3

+

385⋅x

2

−

178,83⋅x +56,2

Określenie liczby pomiarów dla x=0,3 żeby błąd wynosił d=0,4.

Liczba pomiarów jest wyrażona wzorem: n=

t

α

2

⋅

S

2

d

2

d=0,4 – założony błąd
S

2

– wariancja z małej próby wstępnej o liczebności n

0

=4

S

2

=

1

n

0

−

1

⋅Σ

i=1

n

0

(

x

i

−̄x)

2

=

1

4−1

⋅

1,3275=0,4425

2

∞

∞

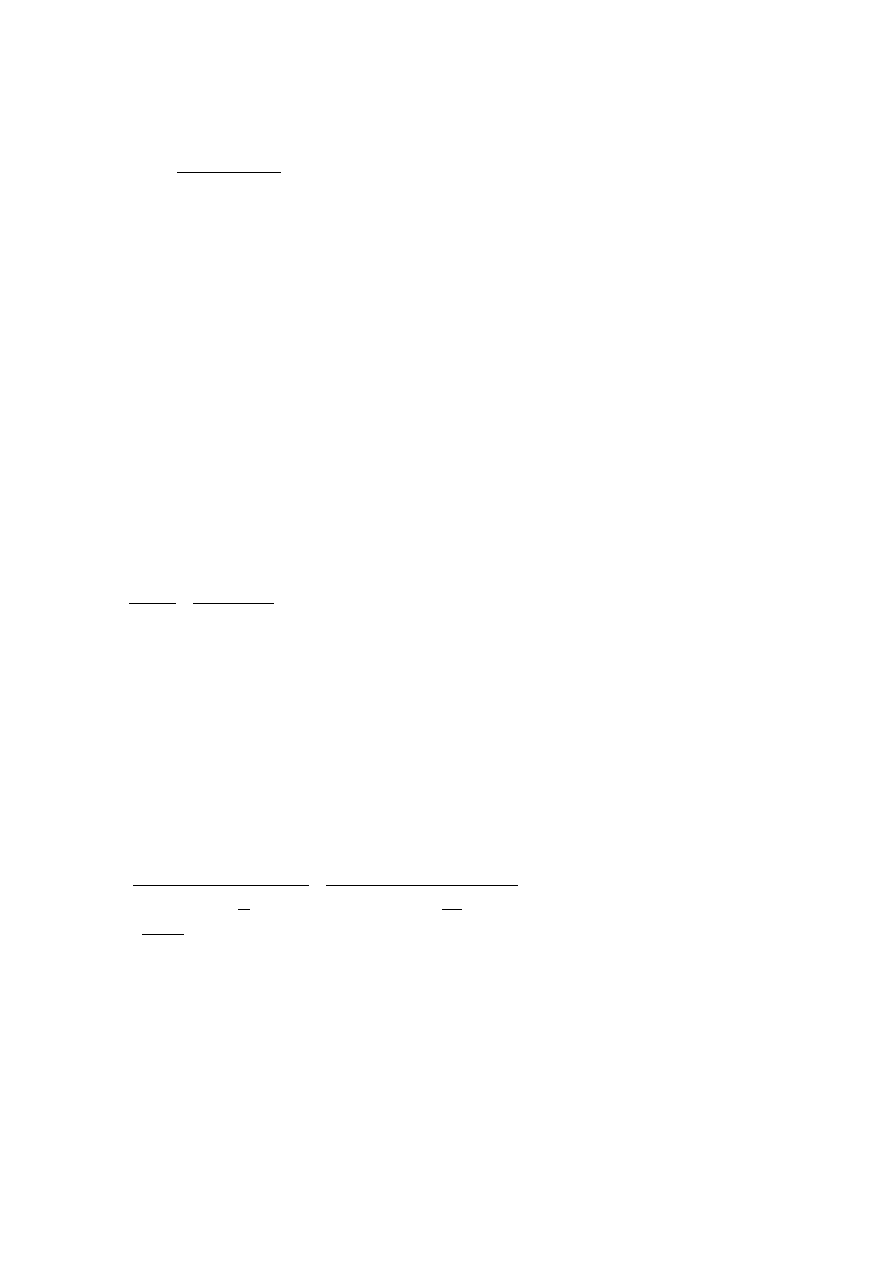
t

α

=2,353

– wartość t Studenta odczytana z tablicy dla współczynnika ufności 1-

α

i dla n

0

-1 stopni

swobody.

Zatem: n=

2,353

2

⋅

0,4425

0,4

2

=

15,3≈16

Ponieważ n=16>4=n

0

, zatem należy wykonać 12 dodatkowych pomiarów by uzyskać błąd

maksymalny 0,4.

Test na przynależność wartości ekstremalnej do tej samej populacji, co reszta pomiarów.

Sprawdzenie dla x=0,5 czy wartość minimalną należy odrzucić, uporządkowano więc wartości
rosnąco:

Hipoteza H

0

– wartość ekstremalną należy odrzucić

Hipoteza H

1

– Nie ma podstaw do odrzucenia wartości ekstremalnej

Statystyka testu: r

ij

Poziom istotności: α=0,05

Hipoteza H

0

jest prawdziwa jeśli r

ij

>r

10

, jeśli nie, hipoteza H

1

ma zastosowanie.

r

ij

=

z

2

−

z

1

z

n

−

z

1

=

26,5−25,9

27−25,9

=

0,545

r

10

dla poziomu istotności

α

=0,05 i liczby pomiarów r=4 wynosi: r

10

=0,765

Ponieważ r

ij

=0,545<0,765=r

10

, hipoteza H

0

jest nie prawdziwa. Zatem nie ma podstaw do

odrzucenia minimalnej wartości.

Badanie istotności współczynników równania y=-15,5x+33,975

Określenie zbioru ufności współczynnika regresji liniowej a.

Zbiór ufności współczynnika a: a−S

A

⋅

t (0,975 ,14)<a <a+S

A

⋅

t (0,975 ,14)

t (0,975 , 14)=2,145

S

A

2

=

Σ(

y

i

−

y

i

'

)

2

(

n−1)⋅

[

Σ

x

i

2

−

1
n

⋅(Σ

x

i

)

2

]

=

4,87

(

16−1)⋅

[

3,44−

1

16

⋅(

7,2)

2

]

=

1,623

S

A

=

√

1,623=1,274

Zatem: −15,5−1,274⋅2,145=−18,23<a <−12,77=−15,5+1,274⋅2,145

Więc a=−15,5 ± 2,73 , na tej podstawie stwierdzono że współczynnik a jest istotny.

Określenie zbioru ufności współczynnika regresji liniowej b.

Zbiór ufności współczynnika b: b−S

B

⋅

t (0,975 , 14)<b<b +S

B

⋅

t (0,975 ,14)

t (0,975 , 14)=2,145

3

25,9
26,5
26,9

27

z

1

z

2

z

3

z

4

S

B

2

=

Σ(

y

i

−

y

i

'

)

2

⋅Σ

x

i

2

(

n−2)⋅

[

n⋅Σ x

i

2

−(Σ

x

i

)

2

]

=

4,87⋅3,44

(

16−2)⋅

[

16⋅3,44−(7,2)

2

]

=

0,374

S

B

=

√

0,374=0,612

Zatem: 33,975−0,612⋅2,145=32,66<b<35,29=33,975+0,612⋅2,145

Więc b=33,975 ±1,31 , na tej podstawie stwierdzono że współczynnik b jest istotny.

4